A Block Coordinate Descent-Based Projected Gradient Algorithm for Orthogonal Non-Negative Matrix Factorization

Abstract

This article uses the projected gradient method (PG) for a non-negative matrix factorization problem (NMF), where one or both matrix factors must have orthonormal columns or rows. We penalize the orthonormality constraints and apply the PG method via a block coordinate descent approach. This means that at a certain time one matrix factor is fixed and the other is updated by moving along the steepest descent direction computed from the penalized objective function and projecting onto the space of non-negative matrices. Our method is tested on two sets of synthetic data for various values of penalty parameters. The performance is compared to the well-known multiplicative update (MU) method from Ding (2006), and with a modified global convergent variant of the MU algorithm recently proposed by Mirzal (2014). We provide extensive numerical results coupled with appropriate visualizations, which demonstrate that our method is very competitive and usually outperforms the other two methods.

1. Introduction

1.1. Motivation

Many machine learning applications require processing large and high dimensional data. The data could be images, videos, kernel matrices, spectral graphs, etc., represented as an $m\times n$ matrix R. The data size and the amount of redundancy increase rapidly when m and n grow. To make the analysis and the interpretation easier, it is favorable to obtain compact and concise low rank approximation of the original data R. This low-rank approximation is known to be very efficient in a wide range of applications, such as: text mining [1,2,3], document classification [4], clustering [5,6], spectral data analysis [1,7], face recognition [8], and many more.

There exist many different low rank approximation methods. For instance, two well-known strategies, broadly used for data analysis, are singular value decomposition (SVD) [9] and principle component analysis (PCA) [10]. Much of real-world data are non-negative, and the related hidden parts express physical features only when the non-negativity holds. The factorizing matrices in SVD or PCA can have negative entries, making it hard or impossible to put a physical interpretation on them. Non-negative matrix factorization was introduced as an attempt to overcome this drawback, i.e., to provide the desired low rank non-negative matrix factors.

1.2. Problem Formulation

A non-negative matrix factorization problem (NMF) is a problem of factorizing the input non-negative matrix R into the product of two lower rank non-negative matrices G and H:

$$\begin{array}{c}\hfill R\approx GH,\end{array}$$

(1)

where $R\in {\mathbb{R}}_{+}^{m\times n}$ usually corresponds to the data matrix, $G\in {\mathbb{R}}_{+}^{m\times p}$ represents the basis matrix, and $H\in {\mathbb{R}}_{+}^{p\times n}$ is the coefficient matrix. With p we denote the number of factors for which it is desired that $p\ll min(m,n)$. If we consider each of the n columns of R being a sample of m-dimensional vector data, the factorization represents each instance (column) as a non-negative linear combination of the columns of G, where the coefficients correspond to the columns of H. The columns of G can be therefore interpreted as the p pieces that constitute the data R. To compute G and H, condition (1) is usually rewritten as a minimization problem using the Frobenius norm:

$$\underset{G,H}{min}f(G,H)=\frac{1}{2}{∥R-GH∥}_F^2,G\ge 0,H\ge 0.$$

(NMF)

It is demonstrated in certain applications that the performance of the standard NMF in (NMF) can often be improved by adding auxiliary constraints which could be sparseness, smoothness, and orthogonality. Orthogonal NMF (ONMF) was introduced by Ding et al. [11]. To improve the clustering capability of the standard NMF, they imposed orthogonality constraints on columns of G or on rows of H. Considering the orthogonality on columns of G, it is formulated as follows:

$$\underset{G,H}{min}f(G,H)=\frac{1}{2}{∥R-GH∥}_F^2,\mathrm{s}.\mathrm{t}.G\ge 0,H\ge 0,G^{T}G=I.$$

(ONMF)

If we enforce orthogonality on the columns of G and on rows of H, we obtain the bi-orthogonal ONMF (bi-ONMF), which is formulated as

$$\underset{G,H}{min}f(G,H)=\frac{1}{2}{∥R-GH∥}_F^2,\mathrm{s}.\mathrm{t}.G\ge 0,H\ge 0,G^{T}G=I,H{H}^T=I,$$

(bi-ONMF)

where I denotes the identity matrix.

While the classic non-negative matrix factorization problem (NMF) has achieved a great attention in the recent decade, see also the recent book [12], and several methods have been devised to compute approximate optimal solutions, the problems with the orthogonality constraints (ONMF)–(bi-ONMF) were much less studied and the list of available methods is much shorter. Most of them are related to the fixed point method and to some variant of update rules. Especially meeting both orthogonality constraints in (bi-ONMF), which is relevant for co-clustering of the data, is still challenging and very limited research has been done in this direction, especially with methods that are not related to the fixed point method approach.

1.3. Related Work

The NMF was firstly studied by Paatero et al. [13,14] and was made popular by Lee and Seung [15,16]. There are several different existing methods to solve (NMF). The most used approach to minimize (NMF) is a simple MU method proposed by Lee and Seung [15,16]. In Chu et al. [17], several gradient-type approaches have been mentioned. Chu et al., reformulated (NMF) as an unconstrained optimization problem, and then applied the standard gradient descent method. Considering both G and H as variables in (NMF), it is obvious that $f(G,H)$ is a non-convex function. However, considering G and H separately, we can find two convex sub-problems. Accordingly, a block-coordinate descent (BCD) approach [16] is applied to obtain values for G and H that correspond to a local minimum of $f(G,H)$. Generally, the scheme adopted by BCD algorithms is to recurrently update blocks of variables only, while the remaining variables are fixed. NMF methods which adopt this optimization technique are, e.g., the MU rule [15], the active-set-like method [18], or the PG method for NMF [19]. In [19], two PG methods were proposed for the standard NMF. The first one is an alternating least squares (ALS) method using projected gradients. This way, H is fixed first and a new G is obtained by PG. Then, with the fixed G at the new value, the PG method looks for a new H. The objective function in each least squares problem is quadratic. This enabled the author to use Taylor’s extension of the objective function to obtain an equivalent condition with the Armijo rule, while checking the sufficient decrease of the objective function as a termination criterion in a step-size selection procedure. The other method proposed in [19] is a direct application of the PG method to (NMF). There is also a hierarchical ALS method for NMF which was originally proposed in [20,21] as an improvement to the ALS method. It consists of a BCD method with single component vectors as coordinate blocks.

As the original ONMF algorithms in [5,6] and their variants [22,23,24] are all based on the MU rule, there has been no convergence guarantee for these algorithms. For example, Ding et al. [11] only prove that the successive updates of the orthogonal factors will converge to a local minimum of the problem. Because the orthogonality constraints cannot be rewritten into a non-negatively constrained ALS framework, convergent algorithms for the standard NMF (e.g., see [19,25,26,27]) cannot be used for solving the ONMF problems. Thus, no convergent algorithm was available for ONMF until recently. Mirzal [28] developed a convergent algorithm for ONMF. The proposed algorithm was designed by generalizing the work of Lin [29] in which a convergent algorithm was provided for the standard NMF based on a modified version of the additive update (AU) technique of Lee [16]. Mirzal [28] provides the global convergence for his algorithm solving the ONMF problem. In fact, he first proves the non-increasing property of the objective function evaluated by the sequence of the iterates. Secondly, he shows that every limit point of the generated sequence is a stationary point, and finally he proves that the sequence of the iterates possesses a limit point. In more recent literature, NMF is used in very applicative areas. In [30], a procedure for mining biologically meaningful biomarkers from microarray datasets of different tumor histotypes is illustrated. The proposed methodology allows automatically identifying a subset of potentially informative genes from microarray data matrices, which differs either in the number of rows (genes) and columns (patients). The methodology integrates NMF to allow the analysis of omics input data with different row size. In [31], the authors propose the correntropy-based orthogonal nonnegative matrix tri-factorization algorithm, which is robust to noisy data contaminated by non-Gaussian noise and outliers. In contrast to previous NMF algorithms, this algorithm firstly applies correntropy, which is defined as a measure of similarity between two random variables, to non-negative matrix tri-factorization problem to measure the similarity, and preserves double orthogonality conditions and dual graph regularization. Then, they adapt the half-quadratic technique which is based on conjugate function theory to solve the resulting optimization problem, and derive the multiplicative update rules. In [32], the blind audio source separation problem which consists of isolating and extracting each of the sources is studied. To perform this task, the authors use NMF based on the Kullback-Leibler and Itakura-Saito $\beta$-divergences as a standard technique that itself uses the time-frequency representation of the signal. The new NMF model is based on the minimization of $\beta$-divergences along with a penalty term that promotes the columns of the dictionary matrix to have a small volume. In [33], the authors use NMF to analyze microarray data which are a kind of numerical non-negative data used to collect gene expression profiles. Since the number of genes in DNA is huge, they are usually high dimensional, therefore they require dimensionality reduction and clustering techniques to extract useful information. The authors use NMF for dimensionality reduction to simplify the data and the relations in the data. To improve the sparseness of the base matrix in incremental NMF, the authors of [34] present a new method, orthogonal incremental NMF algorithm, which combines the orthogonality constraint with incremental learning. This approach adopts batch update in the process of incremental learning.

1.4. Our Contribution

In this paper, we consider the penalty reformulation of (bi-ONMF), i.e., we add the orthogonality constraints multiplied with penalty parameters to the objective function to obtain reformulated problems (ONMF) and (bi-ONMF). The main contributions are:

• We develop an algorithm for (ONMF) and (bi-ONMF), which is essentially a BCD algorithm, in the literature also known as alternating minimization, coordinate relaxation, the Gauss-Seidel method, subspace correction, domain decomposition, etc., see e.g., [35,36]. For each block optimization, we use a PG method and Armijo rule to find a suitable step-size.
• We construct synthetic data sets of instances for (ONMF) and (bi-ONMF), for which we know the optimum value by construction.
• We use MATLAB [37] to implement our algorithm and two well-known (MU-based) algorithms: the algorithm of Ding [11] and of Mirzal [28]. The code is available upon request.
• The implemented algorithms are compared on the constructed synthetic data-sets in terms of: (i) the accuracy of the reconstruction, and (ii) the deviation of the factors from the orthonormality. This deviation is a measure the feasibility of the obtained solution and has not been analyzed in the work Of Ding [11] and Mirzal [28]. Accuracy is measured by the so-called root-square error (RSE), defined as

  $$\begin{array}{c}\hfill \mathrm{RSE}:=\frac{{∥R-GH∥}_F}{1+{∥R∥}_F},\end{array}$$

  (2)
  Please note that we added 1 to the denominator in the formula above to prevent numerical difficulties when the data matrix R has a very small Frobenius norm.
  Deviations from the orthonormality are computed using Formulas (17) and (18) from Section 4. Our numerical results show that our algorithm is very competitive and almost always outperforms the MU based algorithms.

1.5. Notations

Some notations used throughout our work are described here. We denote scalars and indices by lower-case Latin letters, vectors by lowercase boldface Latin letters, and matrices by capital Latin letters. ${\mathbb{R}}^{m\times n}$ denotes the set of m by n real matrices, and I symbolizes the identity matrix. We use the notation ∇ to show the gradient of a real-valued function. We define ${\nabla }^{+}$ and ${\nabla }^{-}$ as the positive and (unsigned) negative parts of ∇, respectively, i.e., $\nabla ={\nabla }^{+}-{\nabla }^{-}$. ⊙ and ⊘ denote the element-wise multiplication and the element-wise division, respectively.

1.6. Structure of the Paper

The rest of our work is organized as follows. In Section 2, we review the well-known MU method and the rules being used for updating the factors per iteration in our computations. We also outline the global convergent MU version of Mirzal [28]. We then present our PG method and discuss the stopping criteria for it. Section 4 presents the synthetic data and the result of implementation of the three decomposition methods presented in Section 3. This implementation is done for both the problem (ONMF), as well as (bi-ONMF). Some concluding results are presented in Section 5.

2. Existing Methods to Solve (NMF)

2.1. The Method of Ding

Several popular approaches to solve (NMF) are based on so-called MU algorithms, which are simple to implement and often yield good results. The MU algorithms originate from the work of Lee and Seung [16]. Various MU variants were later proposed by several researchers, for an overview see [38]. At each iteration of these methods, the elements of G and H are multiplied by certain updating factors.

As already mentioned, (ONMF) was proposed by Ding et al. [11] as a tool to improve the clustering capability of the associated optimization approaches. To adapt the MU algorithm for this problem, they employed standard Lagrangian techniques: they introduced the Lagrangian multiplier $\Lambda$ (a symmetric matrix of size $p\times p$) for the orthogonality constraint, and minimized the Lagrangian function where the orthogonality constraint is moved to the objective function as the penalty term $\mathrm{Trace}(\Lambda (G^{T}G-I))$. The complementarity conditions from the related KKT conditions can be rewritten as a fixed point relation, which finally can lead to the following MU rule for (ONMF):

$$\begin{array}{c}{G}_{ij}=G_{ij}\sqrt{\frac{{\left(R{H}^T\right)}_{ij}}{{\left(G{G}^{T}R{H}^T\right)}_{ij}}},i=1,\dots ,m,j=1,\dots ,p,\\ H_{st}=H_{st}\sqrt{\frac{{\left(R^{T}G\right)}_{st}}{{\left(H^T{G}^{T}G\right)}_{st}}},s=1,\dots ,p,t=1,\dots ,n.\end{array}$$

(3)

They extended this approach to non-negative three factor factorization with demand that two factors satisfy orthogonality conditions, which is a generalization of (bi-ONMF). The MU rules (28)–(30) from [11], adapted to (bi-ONMF), are the main ingredients of Algorithm 1, which we will call Ding’s algorithm.

Algorithm 1: Ding’s MU algorithm for (bi-ONMF).

INPUT: $R\in {\mathbb{R}}_{+}^{m\times n}$, $p\in N$

1.  Initialize: generate $G\ge 0$ as an $m\times p$ random matrix and $H\ge 0$ as a $p\times n$ random matrix.

2.  Repeat

$$\begin{array}{c}{G}_{ij}=G_{ij}\sqrt{\frac{{\left(R{H}^T\right)}_{ij}}{{\left(G{G}^{T}R{H}^T\right)}_{ij}+\delta }},i=1,\dots ,m,j=1,\dots ,p,\\ H_{st}=H_{st}\sqrt{\frac{{\left(G^{T}R\right)}_{st}}{{\left(G^{T}R{H}^{T}H\right)}_{st}+\delta }},s=1,\dots ,p,t=1,\dots ,n.\end{array}$$ (4)

3.  Until convergence or a maximum number of iterations or maximum time is reached.

OUTPUT:$G,H$.

Algorithm 1 converges in the sense that the solution pairs G and H generated by this algorithm yield a sequence of decreasing RSEs, see [11], Theorems 5 and 7.

If R has zero vector as columns or rows, a division by zero may occur. In contrast, denominators close to zero may still cause numerical problems. To escape this situation, we follow [39] and add a small positive number $\delta$ to the denominators of the MU terms (4). Pleas note that Algorithm 1 can be easily adapted to solve (ONMF) by replacing the second MU rule from (4) with the second MU rule of (3).

2.2. The Method of Mirzal

In [28], Mirzal proposed an algorithm for (ONMF) which is designed by generalizing the work of Lin [29]. Mirzal used the so-called modified additive update rule (the MAU rule), where the updated term is added to the current value for each of the factors. This additive rule has been used by Lin in [29] in the context of a standard NMF. He also provided in his paper a convergence proof, stating that the iterates generated by his algorithm converge in the sense that RSE is decreasing and the limit point is a stationary point. In [28], Mirzal discussed the orthogonality constraint on the rows of H, while in [40] the same results are developed for the case of (bi-ONMF).

Here we review the Mirzal’s algorithm for (bi-ONMF), presented in the unpublished paper [40]. This algorithm actually solves the equivalent problem (pen-ONMF) where the orthogonality constraints are moved into the objective function (the so-called penalty approach), and the importance of the orthogonality constraints are controlled by the penalty parameters $\alpha ,\beta$:

$$\begin{array}{ccc}\hfill \underset{G,H}{min}F(G,H)& =& \frac{1}{2}{∥R-GH∥}_F^2+\frac{\alpha }{2}{∥H{H}^T-I∥}_F^2+\frac{\beta }{2}{∥G^{T}G-I∥}_F^2,\hfill \\ \hfill \mathrm{s}.\mathrm{t}.& & G\ge 0,H\ge 0\hfill \end{array}$$

(pen-ONMF)

The gradients of the objective function with respect to G and H are:

$$\begin{array}{c}{\nabla }_{G}f(G,H)=GH{H}^T-R{H}^T+\beta G{G}^{T}G-\beta G,\\ {\nabla }_{H}f(G,H)=G^{T}GH-G^{T}R+\alpha H{H}^{T}H-\alpha H.\end{array}$$

(5)

For the objective function in (pen-ONMF), Mirzal proposed the MAU rules along with the use of $\overline{G}={\left(\overline{g}\right)}_{ij}$ and $\overline{H}={\left(\overline{h}\right)}_{ij}$, instead of G and H, to avoid the zero locking phenomenon [28], Section 2:

$$\begin{array}{c}\hfill {\overline{g}}_{ij}=\left\{\begin{array}{cc}{g}_{ij},\hfill & \mathrm{if}{\nabla }_{G}f{(G,H)}_{ij}\ge 0\hfill \\ max\{g_{ij},\nu \},\hfill & \mathrm{if}{\nabla }_{G}f{(G,H)}_{ij}<0\hfill \end{array}\right.\end{array}$$

(6)

$$\begin{array}{c}\hfill {\overline{h}}_{st}=\left\{\begin{array}{cc}{h}_{st},\hfill & \mathrm{if}{\nabla }_{H}f{(G,H)}_{st}\ge 0\hfill \\ max\{h_{st},\nu \},\hfill & \mathrm{if}{\nabla }_{H}f{(G,H)}_{st}<0\hfill \end{array}\right.\end{array}$$

(7)

where $\nu$ is a small positive number.

Please note that the algorithms working with the MU rules for (pen-ONMF) must be initialized with positive matrices to avoid zero locking from the start, but non-negative matrices can be used to initialize the algorithm working with the MAU rules (see [40]).

Mirzal [40] used the MAU rules with some modifications by considering $\overline{G}$ and $\overline{H}$ in order to guarantee the non-increasing property, with a constant step to make ${\delta }_G$ and ${\delta }_H$ grow in order to satisfy the property. Here, ${\delta }_G$ and ${\delta }_H$ are the values added within the MAU terms to the denominator of update terms for G and H, respectively. The proposed algorithm by Mirzal [40] is summarised as Algorithm 2 below.

Algorithm 2: Mirzal’s algorithm for bi-ONMF [40]

INPUT: inner dimension p, maximum number of iterations: maxit; small positive $\delta$, small positive $step$ to increase $\delta$.

1.  Compute initial $G^0\ge 0$ and $H^0\ge 0$.

2.  For $k=0:\mathrm{maxit}$

${\delta }_G=\delta$;

Repeat

$g_{ij}^{(k+1)}=g_{ij}^{\left(k\right)}-\frac{{\overline{g}}_{ij}^{\left(k\right)}·{\nabla }_{G}f{(G^{\left(k\right)},H^{\left(k\right)})}_{ij}}{{({\overline{G}}^{\left(k\right)}{H}^{\left(k\right)}{H}^{\left(kT\right)}+\beta {\overline{G}}^{\left(k\right)}{\overline{G}}^{\left(kT\right)}{\overline{G}}^{\left(k\right)})}_{ij}+{\delta }_G^{\left(k\right)}},i=1\dots m,j=1,\dots p$;

${\delta }_G={\delta }_G·\mathrm{step}$;

Until $f(G^{(k+1)},H^{\left(k\right)})\le f(G^{\left(k\right)},H^{\left(k\right)})$

${\delta }_H=\delta$;

Repeat

$h_{st}^{(k+1)}=h_{st}^{\left(k\right)}-\frac{{\overline{h}}_{st}^{\left(k\right)}·{\nabla }_{H}f(G^{(k+1)},H^{\left(k\right)})st}{{(G^{(k+1)T}{G}^{(k+1)}{\overline{H}}^{\left(k\right)}+\alpha {\overline{H}}^{\left(k\right)}{\overline{H}}^{\left(kT\right)}{\overline{H}}^{\left(k\right)})}_{st}+{\delta }_H^{\left(k\right)}},s=1,\dots p,t=1,\dots n$;

${\delta }_H={\delta }_H·\mathrm{step}$;

Until $f(G^{(k+1)},H^{(k+1)})\le f(G^{(k+1)},H^{\left(k\right)})$

${\delta }_H=\delta$;

OUTPUT: $G,H$.

3. PG Method for (ONMF) and (bi-ONMF)

3.1. Main Steps of PG Method

In this subsection we adapt the PG method proposed by Lin [19] to solve both (ONMF) as well as (bi-ONMF). Lin applied PG to (NMF) in two ways. The first approach is actually a BCD method. This method consecutively fixes one block of variables (G or H) and minimizes the simplified problem in the other variable. The second approach by Lin directly minimizes (NMF). Lin’s main focus was on the first approach and we follow it. We again try to solve the penalized version of the problem (pen-ONMF) by the block coordinate descent method, which is summarised in Algorithm 3.

Algorithm 3: BCD method for (pen-ONMF)

INPUT: inner dimension p, initial matrices $G^0,H^0$.

1.  Set $k=0$.

2.  Repeat

Fix $H:=H^k$ and compute new G as follows:

$$\begin{array}{c}\hfill G^{k+1}:={\mathrm{argmin}}_{G\ge 0}\frac{1}{2}{∥R-G{H}^k∥}_F^2+\frac{\alpha }{2}{∥H^k{H}^{kT}-I∥}_F^2+\frac{\beta }{2}{∥G^{T}G-I∥}_F^2\end{array}$$ (8)

Fix $G:=G^{k+1}$ and compute new H as follows:

$$\begin{array}{c}\hfill H^{k+1}:={\mathrm{argmin}}_{H\ge 0}\frac{1}{2}{∥R-G^{k+1}H∥}_F^2+\frac{\alpha }{2}{∥H{H}^T-I∥}_F^T+\frac{\beta }{2}{∥G^{(k+1)T}{G}^{k+1}-I∥}_F^2\end{array}$$ (9)

$k:=k+1$

3.  Until some stopping criteria is satisfied

OUTPUT: $G,H$.

The objective function in (pen-ONMF) is not quadratic any more, so we lose the nice properties about Armijo’s rule that represent advantages for Lin. We managed to use the Armijo rule directly and still obtained good numerical results, see Section 4. Armijo [41] was the first to establish convergence to stationary points of smooth functions using an inexact line search with a simple “sufficient decrease” condition. The Armijo condition ensures that the line search step is not too large.

We refer to (8) or (9) as sub-problems. Obviously, solving these sub-problems in every iteration could be more costly than Algorithms 1 and 2. Therefore, we must find effective methods for solving these sub-problems. Similarly to Lin, we apply the PG method to solve the sub-problems (8) and (9). Algorithm 4 contains the main steps of the PG method for solving the latter and can be straightforwardly adapted for the former.

For the sake of simplicity, we denote by $F_H$ the function that we optimize in (8), which is actually a simplified version (pure H terms removed) of the objective function from (pen-ONMF) for H fixed:

$$F_H\left(G\right):=\frac{1}{2}{∥R-GH∥}_F^2+\frac{\beta }{2}{∥G^{T}G-I∥}_F^2.$$

Similarly, for G is fixed, the objective function from (9) will be denoted by:

$$F_G\left(H\right):=\frac{1}{2}{∥R-GH∥}_F^2+\frac{\alpha }{2}{∥H{H}^T-I∥}_F^T.$$

In Algorithm 4, P is the projection operator which projects the new point (matrix) on the cone of non-negative matrices (we simply put negative entries to 0).

Inequality (10) shows the Armijo rule to find a suitable step-size guaranteeing a sufficient decrease. Searching for ${\lambda }_k$ is a time-consuming operation, therefore we strive to do only a small number of trials for new $\lambda$ in Step 3.1.

Similarly to Lin [19], we allow for $\lambda$ any positive value. More precisely, we start with $\lambda =1$ and if the Armijo rule (10) is satisfied, we increase the value of $\lambda$ by dividing it with $\gamma <1$. We repeat this until (10) is no longer satisfied or the same matrix $H_{\lambda }$ as in the previous iteration is obtained. If the starting $\lambda =1$ does not yield $H_{\lambda }$ which would satisfy the Armijo rule (10), then we decrease it by a factor $\gamma$ and repeat this until (10) is satisfied. The numerical results obtained using different values of parameters $\gamma$ (updating factor for $\lambda$) and $\sigma$ (parameter to check (10)) are reported in the following subsections.

Algorithm 4: PG method using Armijo rule to solve sub-problem (9)

INPUT: $0<\sigma <1,\gamma <1$, and initial $H^0$.

1.  Set $k=0$

2.  Repeat

Find a $\lambda$ (using updating factor $\gamma$) such that for $H_{\lambda }:=P[H^k-\lambda \nabla F_G\left(H^k\right)]$

we have

$$\begin{array}{c}\hfill F_G\left(H_{\lambda }\right)-F_G\left(H^k\right)\le \sigma \nabla F_G\left(H^k\right)(H_{\lambda }-H^k);\end{array}$$ (10)

Set $H^{k+1}:=H_{\lambda }$

Set $k=k+1$;

3.  Until some stopping criteria is satisfied.

OUTPUT: $H=H^{k+1}$.

3.2. Stopping Criteria for Algorithms 3 and 4

As practiced in the literature (e.g., see [42]), in a constrained optimization problem with the non-negativity constraint on the variable x, a common condition to check whether a point $x^k$ is close to a stationary point is

$$\begin{array}{c}\hfill ∥{\nabla }^{P}f\left(x^k\right)∥\le \epsilon ∥\nabla f\left(x^0\right)∥,\end{array}$$

(11)

where f is the differentiable function that we try to optimize and ${\nabla }^{P}f\left(x^k\right)$ is the projected gradient defined as

$$\begin{array}{c}\hfill {\nabla }^{P}f{\left(x\right)}_i=\left\{\begin{array}{c}\nabla f{\left(x\right)}_i,\mathrm{if}{x}_i>0,\hfill \\ min\{0,\nabla f{\left(x\right)}_i\},\mathrm{if}{x}_i=0,\hfill \end{array}\right.\end{array}$$

(12)

and $\epsilon$ is a small positive tolerance. For Algorithm 3, (11) becomes

$$\begin{array}{c}\hfill {∥{\nabla }^{P}F\left(G^k,H^k\right)∥}_F\le {∥\epsilon \nabla F\left(G^0,H^0\right)∥}_F.\end{array}$$

(13)

We impose a time limit in seconds and a maximum number of iterations for Algorithm 4 as well. Following [19], we also define stopping conditions for the sub-problems. The matrices $G^{k+1}$ and $H^{k+1}$ returned by Algorithm 4, respectively, must satisfy

$$\begin{array}{c}\hfill \begin{array}{c}{∥{\nabla }_G^{P}F\left(G^{k+1},H^k\right)∥}_F\le {\overline{\epsilon }}_G,\\ {∥{\nabla }_H^{P}F\left(G^{k+1},H^{k+1}\right)∥}_F\le {\overline{\epsilon }}_H,\end{array}\end{array}$$

(14)

where

$$\begin{array}{c}\hfill {\overline{\epsilon }}_G={\overline{\epsilon }}_H=max\{{10}^{-7},\epsilon \}{∥\nabla F\left(G^0,H^0\right)∥}_F,\end{array}$$

(15)

and $\epsilon$ is the same tolerance used in (13). If the PG method for solving the sub-problem (8) or (9) stops after the first iteration, then we decrease the stopping tolerance as follows:

$${\overline{\epsilon }}_G⟵\tau {\overline{\epsilon }}_G,{\overline{\epsilon }}_H⟵\tau {\overline{\epsilon }}_H,$$

(16)

where $\tau$ is a constant smaller then 1.

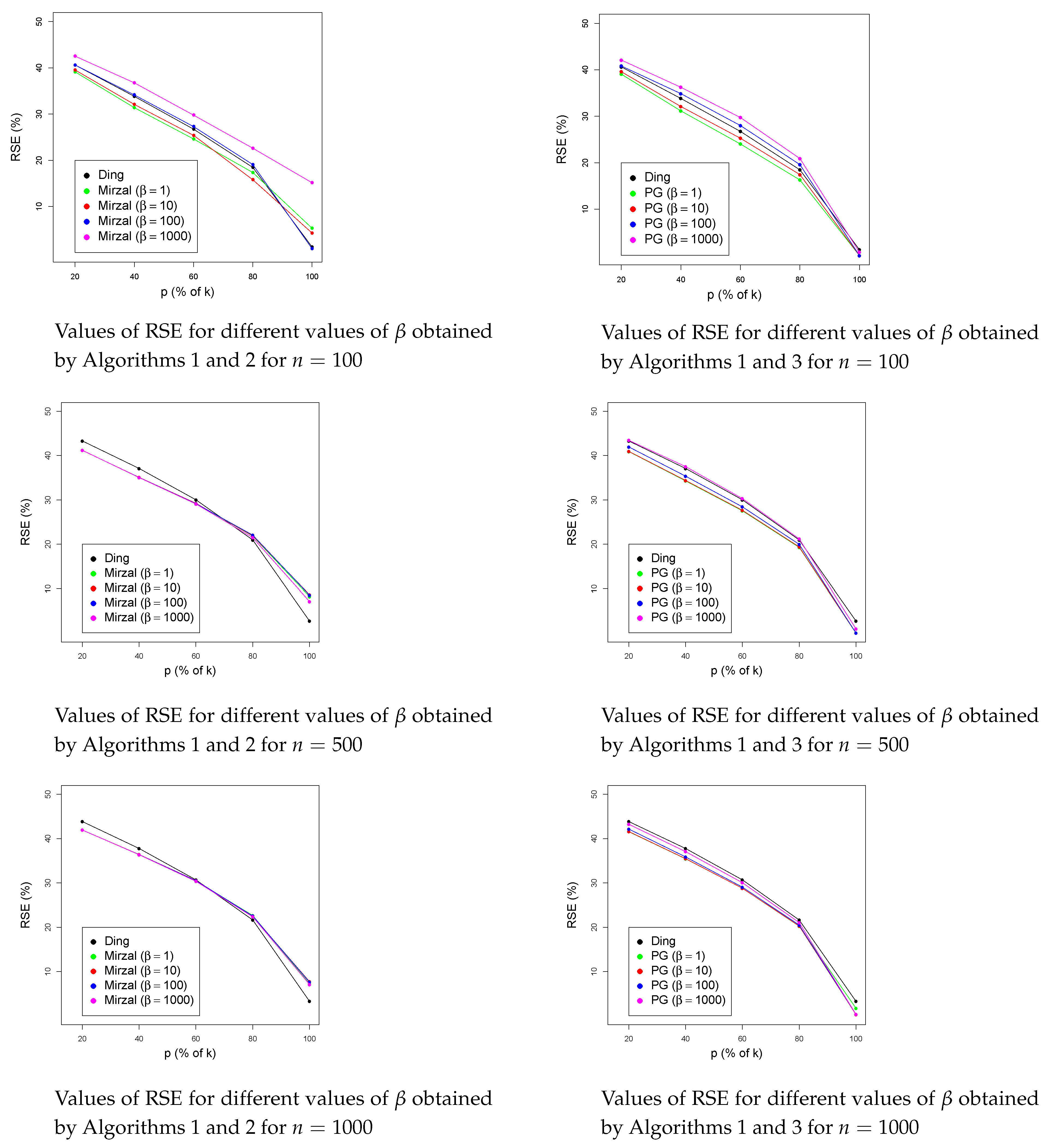
4. Numerical Results

In this section we demonstrate, how the PG method described in Section 3, performs compared to the MU-based algorithms of Ding and Mirzal, which were described in Section 2.1 and Section 2.2, respectively.

4.1. Artificial Data

We created three sets of synthetic data using MATLAB [37]. The first set we call bi-orthonormal set (BION). It consists of instances of matrix $R\in {\mathbb{R}}_{+}^{n\times n}$, which were created as products of G and H, where $G\in {\mathbb{R}}_{+}^{n\times k}$ has orthonormal columns while $H\in {\mathbb{R}}_{+}^{k\times n}$ has orthonormal rows. We created five instances of R, for each pair $(n,k_1)$ and $(n,k_2)$ from

Table 1. Paris $(n,k)$ for which we created UNION and BION datasets.

n	50	100	200	500	1000
k${}_1$	10	20	40	100	200
k${}_2$	20	40	80	200	400

.

Matrices G were created in two phases: firstly, we randomly (uniform distribution) selected a position in each row; secondly, we selected a random number from $(0,1)$ (uniform distribution) for the selected position in each row. Finally, if it happens that after this procedure some column of G is zero or has a norm below ${10}^{-8}$, we find the first non-zero element in the largest column of G (according to Euclidean norm) and move it into the zero column. Then we normalized the columns of G. We created H similarly.

Each triple $(R,G,H)$ was saved as a triple of txt files. For example, NMF_BIOG_data_R_n=200_k=80_id=5.txt contains $200\times 200$ matrix R obtained by multiplying matrices $G\in {\mathbb{R}}^{200\times 80}$ and $H\in {\mathbb{R}}^{80\times 200}$, which were generated as explained above. With id=5, we denote that this is a 5th matrix corresponding to this pair $(n,k)$.

The second set contains similar data to BION, but only one factor (G) is orthonormal, while the other (H) is non-negative but not necessarily orthonormal. We call this dataset uni-orthonormal (UNION).

The third data set is a nosy variant of the first data set. For each triple $R,G,H$ from the BION data, we computed a new nosy $R_n=R+E$, where E is a random matrix of the same size as R, with entries uniformly distributed on $[0,\overline{\mu }]$. Parameter $\overline{\mu }$ is defined such that the expected value of RSE satisfies:

$$\mathbb{E}\left(\frac{\parallel R_n{-GH\parallel }_F}{1+\parallel R_n{\parallel }_F}\right)=\mathbb{E}\left(\frac{{\parallel E\parallel }_F}{1+\parallel R_n{\parallel }_F}\right)\le \frac{\mathbb{E}(\parallel E{\parallel }_F)}{1+{\parallel GH\parallel }_F}\le \mu ,$$

where $\mu$ is parameter chosen by us and was set to ${10}^{-2},{10}^{-4},{10}^{-6}$. By using basic properties of the uniform distribution, we can easily derive that $\overline{\mu }\le {\mu (1+\parallel GH\parallel }_F)\sqrt{3}/n$, where n is the order of square matrix R. We indeed used the right hand side term of this inequality to generate the noise matrices E.

All computations are done using MATLAB [37] and a high performance computer available at Faculty of Mechanical Engineering of University of Ljubljana. This is Intel Xeon X5670 (1536 hyper-cores) HPC cluster and an E5-2680 V3 (1008 hyper-cores) DP cluster, with an IB QDR interconnection, 164 TB of LUSTRE storage, 4.6 TB RAM and with 24 TFlop/s performance.

4.2. Numerical Results for UNION

In this subsection, we present numerical results, obtained by Ding’s, Mirzal’s, and our algorithm for a uni-orthogonal problem (ONMF), using the UNION data, introduced in the previous subsection. We adapted the last two algorithms (Algorithms 2 and 3) for UNION data by setting $\alpha =0$ in the problem formulation (bi-ONMF) and in all formulas underlying these two algorithms.

The maximum number of outer iterations for all three algorithms was set to 1000. In practices, we stop Algorithms 1 and 3 only when the maximum number of iterations is reached, while for Algorithm 2, the stopping condition involved also checking the progress of RSE. If this is too small (below ${10}^{-5}$) we also stop.

Recall that for UNION data we have for each pair $n,k$ from Table 1 five symmetric matrices R for which we try to solve (ONMF) by Algorithms 1–3. Please note that all these algorithms demand as input the internal dimension k, i.e., the number of columns of factor G, which is in general not known in advance. Even though, we know this dimension by construction for UNION data, we tested the algorithms using internal dimensions p equal to $20\%,40\%,\dots ,100\%$ of k. For $p=k$, we know the optimum of the problem, which is 0, so for this case we can also estimate how good are the tested algorithms in terms of finding the global optimum.

The first question we had to answer was which value of $\beta$ to use in Mirzal’s and PG algorithms. It is obvious that larger values of $\beta$ moves the focus from optimizing the RSE to guaranteeing the orthonormality, i.e., feasibility for the original problem. We decided not to fix the value of $\beta$ but to run both algorithms for $\beta \in \{1,10,100,1000\}$ and report the results.

For each solution pair $G,H$ returned by all algorithms, the non-negativity constraints are held by the construction of algorithms, so we only need to consider deviation of G from orthonormality, which we call infeasibility and define it as

$$\begin{array}{c}\hfill {\mathrm{infeas}}_G:=\frac{{∥G^{T}G-I∥}_F}{1+{∥I∥}_F}.\end{array}$$

(17)

The computational results that follow in the rest of this subsection were obtained by setting the tolerance in the stopping criterion to $\epsilon ={10}^{-10}$, the maximum number of iterations to 1000 in Algorithm 3 and to 20 in Algorithm 4.

We also set a time limit to 3600 seconds. Additionally, for $\sigma$ and $\gamma$ (updating parameter for $\lambda$ in Algorithm 4) we choose $0.001$ and $0.1$, respectively. Finally, for $\tau$ from (16) we set a value of $0.1$.

In general, Algorithm 3 converges to a solution in early iterations and the norm of the projected gradient falls below the tolerance shortly after running the algorithm.

Results in

Table 2. In this table we demonstrate how good RSE is achieved by Algorithms 1–3 on UNION dataset. For each $n\in \{50,100,200,500,1000\}$ we take all 10 matrices R (five of them corresponding to $k=0.2n$ and five to $k=0.4n$). We run all three algorithms on these matrices with inner dimensions $p\in \{0.2k,0.4k,\dots ,1.0k\}$ with all possible values of $\beta \in \{1,10,100,1000\}$. Each row represents the average (arithmetic mean value) RSE obtained on instances corresponding to given n. For example, the last row shows the average value of RSE in 10 instances of dimension 1000 (five of them corresponding to $k=200$ and five to $k=400$) obtained by all three algorithms for all four values of $\beta$, which were run with the input dimension $p=k$. The bold number is the smallest one in each line.

n	p	RSE of	RSE of Algorithm 2				RSE of Algorithm 3
	(% of k)	Algorithm 1	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$
50	40	0.3143	0.2965	0.3070	0.3329	0.3898	0.2963	0.3081	0.3425	0.3508
50	60	0.2348	0.2227	0.2356	0.2676	0.3459	0.2201	0.2382	0.2733	0.2765
50	80	0.1738	0.1492	0.1634	0.1894	0.3277	0.1468	0.1620	0.1953	0.2053
50	100	0.0002	0.0133	0.0004	0.0932	0.2973	0.0000	0.0000	0.0000	0.0000
100	20	0.4063	0.3914	0.3955	0.4063	0.4254	0.3906	0.3959	0.4083	0.4210
100	40	0.3384	0.3139	0.3210	0.3415	0.3677	0.3116	0.3210	0.3488	0.3625
100	60	0.2674	0.2462	0.2541	0.2730	0.2978	0.2403	0.2528	0.2801	0.2974
100	80	0.1847	0.1737	0.1581	0.1909	0.2263	0.1629	0.1744	0.1959	0.2090
100	100	0.0126	0.0532	0.0427	0.0089	0.1515	0.0000	0.0000	0.0000	0.0075
200	20	0.4213	0.4024	0.4077	0.4080	0.4257	0.4005	0.4032	0.4162	0.4337
200	40	0.3562	0.3315	0.3398	0.3401	0.3647	0.3270	0.3313	0.3497	0.3738
200	60	0.2845	0.2675	0.2746	0.2748	0.2955	0.2573	0.2617	0.2812	0.3061
200	80	0.1959	0.1958	0.2013	0.1996	0.2085	0.1773	0.1819	0.1960	0.2133
200	100	0.0191	0.0753	0.0632	0.0622	0.0415	0.0000	0.0000	0.0069	0.0181
500	20	0.4332	0.4120	0.4119	0.4120	0.4121	0.4092	0.4096	0.4197	0.4346
500	40	0.3711	0.3506	0.3509	0.3507	0.3505	0.3430	0.3440	0.3537	0.3753
500	60	0.3003	0.2919	0.2923	0.2916	0.2909	0.2756	0.2766	0.2845	0.3031
500	80	0.2098	0.2186	0.2192	0.2207	0.2151	0.1931	0.1941	0.1999	0.2122
500	100	0.0273	0.0822	0.0864	0.0853	0.0713	0.0002	0.0003	0.0002	0.0097
1000	20	0.4386	0.4195	0.4194	0.4193	0.4195	0.4156	0.4160	0.4216	0.4324
1000	40	0.3777	0.3641	0.3640	0.3638	0.3637	0.3545	0.3548	0.3588	0.3707
1000	60	0.3070	0.3047	0.3055	0.3051	0.3036	0.2881	0.2880	0.2906	0.3006
1000	80	0.2164	0.2265	0.2248	0.2254	0.2236	0.2024	0.2029	0.2050	0.2106
1000	100	0.0329	0.0725	0.0772	0.0761	0.0709	0.0173	0.0030	0.0035	0.0035

and

Table 3. In this table we demonstrate how feasible (orthonormal) the solutions are G computed by Algorithms 1–3 on UNION data set, i.e., in this table we report the average infeasibility of the solutions underlying Table 2. The bold number is the smallest one in each line.

n	p	Infeas. of	Infeas. of Algorithm 2				Infeas. of Algorithm 3
	(% of k)	Algorithm 1	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$
50	20	0.0964	0.2490	0.0924	0.0155	0.0038	0.2298	0.0909	0.0154	0.0022
50	40	0.0740	0.1886	0.0676	0.0131	0.0040	0.1845	0.0670	0.0135	0.0023
50	60	0.0553	0.1324	0.0465	0.0068	0.0040	0.1245	0.0440	0.0091	0.0015
50	80	0.0324	0.0964	0.0241	0.0053	0.0034	0.0789	0.0250	0.0069	0.0020
50	100	0.0023	0.0257	0.0022	0.0023	0.0039	0.0000	0.0000	0.0000	0.0000
100	20	0.0774	0.2624	0.1441	0.0258	0.0064	0.2588	0.1308	0.0258	0.0036
100	40	0.0539	0.1754	0.0928	0.0168	0.0036	0.1654	0.0819	0.0182	0.0035
100	60	0.0400	0.1205	0.0545	0.0102	0.0024	0.1109	0.0487	0.0138	0.0033
100	80	0.0239	0.0890	0.0324	0.0062	0.0022	0.0623	0.0258	0.0083	0.0018
100	100	0.0062	0.0452	0.0153	0.0009	0.0016	0.0002	0.0000	0.0000	0.0000
200	20	0.0584	0.2157	0.1437	0.1433	0.0054	0.2087	0.1512	0.0348	0.0074
200	40	0.0356	0.1379	0.1004	0.1000	0.0036	0.1240	0.0806	0.0207	0.0053
200	60	0.0260	0.0955	0.0791	0.0793	0.0031	0.0754	0.0434	0.0143	0.0047
200	80	0.0154	0.0657	0.0634	0.0629	0.0017	0.0416	0.0218	0.0080	0.0026
200	100	0.0059	0.0412	0.0517	0.0512	0.0016	0.0002	0.0001	0.0002	0.0001
500	20	0.0332	0.1587	0.1894	0.1908	0.1908	0.1475	0.1268	0.0436	0.0087
500	40	0.0189	0.1155	0.1343	0.1349	0.1347	0.0770	0.0621	0.0227	0.0069
500	60	0.0134	0.0889	0.1095	0.1102	0.1055	0.0412	0.0312	0.0123	0.0038
500	80	0.0084	0.0656	0.0946	0.0954	0.0826	0.0300	0.0154	0.0061	0.0021
500	100	0.0050	0.0499	0.0847	0.0853	0.0693	0.0249	0.0003	0.0001	0.0001
1000	20	0.0211	0.1200	0.1344	0.1349	0.1350	0.1043	0.0970	0.0471	0.0097
1000	40	0.0122	0.0863	0.0951	0.0954	0.0954	0.0542	0.0422	0.0199	0.0059
1000	60	0.0073	0.0662	0.0776	0.0779	0.0779	0.0414	0.0205	0.0098	0.0037
1000	80	0.0045	0.0539	0.0671	0.0675	0.0675	0.0336	0.0103	0.0047	0.0018
1000	100	0.0040	0.0475	0.0600	0.0603	0.0604	0.0296	0.0066	0.0005	0.0003

and their visualizations in Figure 1 and Figure 2 confirm expectations. More precisely, we can see that the smaller the value of $\beta$, the better RSE. Likewise, the larger the value of $\beta$, the smaller the infeasibility ${\mathrm{infeas}}_G$. In practice, we want to reach both criteria: small RSE and small infeasibility, so some compromise should be made. If RSE is more important than infeasibility, we choose the smaller value of $\beta$ and vice versa. We can also observe that regarding RSE the three compared algorithms do not differ a lot. However, when the input dimension p approaches the real inner dimension k, Algorithm 3 comes closest to the global optimum $\mathrm{RSE}=0$. The situation with infeasibility is a bit different. While Algorithm 1 performs very well in all instances, Algorithm 2 reaches better feasibility for smaller values of n. Algorithm 3 outperforms the others for $\beta =1000$.

Results from Table 3, corresponding to $n=100,500,1000$ are depicted in Figure 2.

4.3. Numerical Results for Bi-Orthonormal Data (BION)

In this subsection, we provide the same type of results as in the previous subsection, but for the BION dataset. We used almost the same setting as for UNION dataset: $\epsilon ={10}^{-10}$, maxit $=1000$, $\sigma =0.001$ and time limit = 3600 s. Parameters $\gamma ,\tau$ were slightly changed (based on experimental observations): $\gamma =0.75$ and $\tau =0.5$. Additionally, we decided to take the same values for $\alpha ,\beta$ in Algorithms 2 and 3, since the matrices R in BION dataset are symmetric and both orthogonality constraints are equally important. We computed the results for values of $\alpha =\beta$ from $\{1,10,100,1000\}$. In

Table 4. RSE obtained by Algorithms 1–3 on the BION data. For the latter two algorithms, we used $\alpha =\beta \in \{1,10,100,1000\}$. For each $n\in \{50,100,200,500,1000\}$ we take all ten matrices R (five of them corresponding to $k=0.2n$ and five to $k=0.4n$). We run all three algorithms on these matrices with inner dimensions $p\in \{0.2k,0.4k,\dots ,1.0k\}$ with all possible values of $\alpha =\beta$. Like before, each row represents the average (arithmetic mean value) of RSE obtained on instances corresponding to given n and given p as a percentage of k. We can see that the larger the $\beta$, the worse the RSE, which is consistent with expectations. The bold number is the smallest one in each line.

n	p	RSE of	RSE of Algorithm 2				RSE of Algorithm 3
	(% of k)	Algorithm 1	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$
50	20	0.7053	0.7053	0.7053	0.7053	0.8283	0.7053	0.7053	0.7055	0.8259
50	40	0.6108	0.6108	0.6108	0.6108	0.9066	0.6108	0.6108	0.6108	0.6631
50	60	0.4987	0.4987	0.4987	0.5442	0.9665	0.4987	0.4987	0.4987	0.5000
50	80	0.3526	0.3671	0.3742	0.4497	1.0282	0.3526	0.3796	0.3527	0.4374
50	100	0.0607	0.1712	0.2786	0.5198	1.0781	0.1145	0.1820	0.2604	0.3689
100	20	0.7516	0.7516	0.7516	0.7517	0.9070	0.7516	0.7516	0.7517	0.8224
100	40	0.6509	0.6509	0.6509	0.7174	0.9779	0.6509	0.6509	0.6509	0.6514
100	60	0.5315	0.5315	0.5315	0.5504	1.0401	0.5315	0.5315	0.5315	0.5352
100	80	0.3758	0.3787	0.4106	0.4542	1.1082	0.3801	0.3888	0.3917	0.3898
100	100	0.1377	0.1993	0.3311	0.4898	1.1734	0.0457	0.1016	0.2758	0.3757
200	20	0.7884	0.7884	0.7884	0.7884	0.9499	0.7884	0.7884	0.7884	0.7888
200	40	0.6828	0.6828	0.6828	0.6828	1.0325	0.6828	0.6828	0.6828	0.6828
200	60	0.5575	0.5575	0.5575	0.5647	1.0938	0.5575	0.5575	0.5575	0.5610
200	80	0.3942	0.3942	0.3965	0.5019	1.1618	0.3942	0.3942	0.3942	0.4373
200	100	0.1447	0.1851	0.3014	0.5400	1.2297	0.0202	0.1429	0.2964	0.3315
500	20	0.8242	0.8242	0.8242	0.8242	0.9956	0.8242	0.8242	0.8242	0.8243
500	40	0.7138	0.7138	0.7138	0.7138	1.0679	0.7138	0.7138	0.7138	0.7138
500	60	0.5828	0.5828	0.5828	0.6045	1.1534	0.5828	0.5828	0.5828	0.5828
500	80	0.4121	0.4121	0.4203	0.5285	1.2160	0.4121	0.4121	0.4121	0.4334
500	100	0.1405	0.1814	0.3401	0.5854	1.2822	0.0067	0.1059	0.2044	0.3378
1000	20	0.8436	0.8436	0.8436	0.8436	1.0261	0.8436	0.8436	0.8436	0.8436
1000	40	0.7306	0.7306	0.7306	0.7309	1.0916	0.7306	0.7306	0.7306	0.7306
1000	60	0.5965	0.5965	0.5965	0.6121	1.1669	0.5965	0.5965	0.5965	0.5968
1000	80	0.4218	0.4218	0.4256	0.5338	1.2389	0.4218	0.4218	0.4218	0.4397
1000	100	0.1346	0.1635	0.3324	0.5755	1.3080	0.0096	0.0697	0.1661	0.2188

and

Table 5. In this table we demonstrate how feasible (orthonormal) are the solutions G and H computed by Algorithms 1–3 on the BION dataset, i.e., in this table we report the average infeasibility (18) of the solutions underlying Table 4. We can observe that with these settings of all algorithms we can bring infeasibility to order of ${10}^{-3}$ very often, for all values of $\beta$. The bold number is the smallest one in each line.

n	p	Infeas. of	Infeas. of Algorithm 2				Infeas. of Algorithm 3
	(% of k)	Algorithm 1	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$	$\mathit{\beta }=1$	$\mathit{\beta }=10$	$\mathit{\beta }=100$	$\mathit{\beta }=1000$
50	20	0.0001	0.0070	0.0036	0.0010	0.0068	0.0017	0.0021	0.0021	0.0026
50	40	0.0000	0.0041	0.0021	0.0004	0.0056	0.0008	0.0012	0.0012	0.0014
50	60	0.0000	0.0030	0.0009	0.0032	0.0038	0.0005	0.0008	0.0009	0.0009
50	80	0.0000	0.0183	0.0030	0.0021	0.0028	0.0004	0.0202	0.0006	0.0013
50	100	0.0355	0.0533	0.0127	0.0045	0.0027	0.0418	0.0478	0.0123	0.0021
100	20	0.0001	0.0051	0.0024	0.0006	0.0063	0.0010	0.0012	0.0013	0.0016
100	40	0.0000	0.0029	0.0017	0.0066	0.0040	0.0004	0.0006	0.0007	0.0007
100	60	0.0000	0.0019	0.0008	0.0009	0.0027	0.0003	0.0004	0.0005	0.0005
100	80	0.0000	0.0039	0.0048	0.0015	0.0021	0.0062	0.0149	0.0037	0.0006
100	100	0.0606	0.0454	0.0105	0.0022	0.0018	0.0106	0.0228	0.0173	0.0028
200	20	0.0002	0.0033	0.0019	0.0005	0.0043	0.0005	0.0007	0.0007	0.0007
200	40	0.0001	0.0017	0.0010	0.0002	0.0027	0.0002	0.0003	0.0004	0.0003
200	60	0.0001	0.0010	0.0005	0.0004	0.0019	0.0001	0.0002	0.0002	0.0004
200	80	0.0000	0.0006	0.0006	0.0015	0.0014	0.0001	0.0001	0.0002	0.0013
200	100	0.0425	0.0280	0.0064	0.0019	0.0015	0.0046	0.0224	0.0240	0.0034
500	20	0.0001	0.0017	0.0011	0.0003	0.0025	0.0002	0.0003	0.0003	0.0003
500	40	0.0001	0.0008	0.0005	0.0001	0.0016	0.0001	0.0001	0.0002	0.0002
500	60	0.0000	0.0005	0.0003	0.0006	0.0013	0.0001	0.0001	0.0001	0.0002
500	80	0.0000	0.0003	0.0009	0.0009	0.0008	0.0000	0.0001	0.0001	0.0016
500	100	0.0258	0.0184	0.0045	0.0013	0.0007	0.0017	0.0101	0.0175	0.0053
1000	20	0.0001	0.0010	0.0006	0.0002	0.0024	0.0001	0.0002	0.0002	0.0002
1000	40	0.0000	0.0005	0.0003	0.0001	0.0009	0.0001	0.0002	0.0003	0.0002
1000	60	0.0000	0.0003	0.0002	0.0004	0.0009	0.0003	0.0002	0.0003	0.0003
1000	80	0.0000	0.0002	0.0005	0.0007	0.0006	0.0040	0.0001	0.0002	0.0020
1000	100	0.0173	0.0117	0.0031	0.0009	0.0005	0.0043	0.0050	0.0121	0.0060

we report average RSE and average infeasibility, respectively, of the solutions obtained by Algorithms 1–3. Since for this dataset we need to monitor how orthonormal are both matrices G and H, we adapt the measure for infeasibility as follows:

$$\begin{array}{c}\hfill {\mathrm{infeas}}_{G,H}:=\frac{{∥G^{T}G-I∥}_F+{∥H{H}^T-I∥}_F}{1+{∥I∥}_F}.\end{array}$$

(18)

Figure 3 and Figure 4 depict RSE and infeasibility reached by the three compared algorithms, for $n=100,500,1000$. We can see that all three algorithms behave well; however, Algorithm 3 is more stable and less dependent on the choice of $\beta$. It is interesting to see that $\beta$ does not have a big impact on RSE and infeasibility for Algorithm 3, a significant difference can be observed only when the internal dimension is equal to the real internal dimension, i.e., when $p=100\%$. Based on these numerical results, we can conclude that smaller $\beta$ achieve better RSE and almost the same infeasibility, so it would make sense to use $\beta =1$.

For Algorithm 2 these differences are bigger and it is less obvious which $\beta$ is appropriate. Again, if RSE is more important then smaller values of $\beta$ should be taken, otherwise larger values.

4.4. Numerical Results on the Noisy BION Dataset

In this subsection, we report RSE and infeasibility computed on the noisy BION dataset with dimension $n=200$. We decided to skip the other dimension since this n is already well representative for the whole noisy dataset and implies a large new

Table 6. This table contains numerical data obtained by running all three algorithms on the third dataset—BION data with three levels of noise, represented by $\mu \in \{{10}^{-2},{10}^{-4},{10}^{-6}\}$. The bold number is the smallest one in each line.

			Algorithm 1			Algorithm 2			Algorithm 3
$\mathbf{\mu }$	$\mathbf{n}$	$\mathbf{p}$	RSE	${\mathbf{infeas}}_{\mathbf{G}}$	${\mathbf{infeas}}_{\mathbf{H}}$	RSE	${\mathbf{infeas}}_{\mathbf{G}}$	${\mathbf{infeas}}_{\mathbf{H}}$	RSE	${\mathbf{infeas}}_{\mathbf{G}}$	${\mathbf{infeas}}_{\mathbf{H}}$
${10}^{-2}$	20	200	0.7877	0.0019	0.0019	0.7877	0.0041	0.0041	0.7877	0.0042	0.0042
	40	200	0.6821	0.0014	0.0014	0.6823	0.0024	0.0024	0.6821	0.0027	0.0028
	60	200	0.5570	0.0010	0.0010	0.5571	0.0015	0.0015	0.5569	0.0020	0.0020
	80	200	0.3939	0.0007	0.0007	0.3939	0.0010	0.0010	0.3938	0.0015	0.0015
	100	200	0.0072	0.0003	0.0003	0.1327	0.0097	0.0098	0.0039	0.0010	0.0010
	120	200	0.0278	0.0483	0.0483	0.1325	0.0283	0.0326	0.0036	0.0465	0.0141
	140	200	0.0344	0.0589	0.0590	0.1909	0.0366	0.0363	0.0034	0.0565	0.0188
${10}^{-4}$	20	200	0.7884	0.0002	0.0002	0.7884	0.0018	0.0018	0.7884	0.0003	0.0003
	40	200	0.6828	0.0001	0.0001	0.6828	0.0009	0.0009	0.6828	0.0001	0.0001
	60	200	0.5575	0.0001	0.0001	0.5575	0.0006	0.0006	0.5575	0.0001	0.0001
	80	200	0.3942	0.0000	0.0000	0.3942	0.0004	0.0003	0.3942	0.0001	0.0001
	100	200	0.0575	0.0086	0.0086	0.1717	0.0089	0.0192	0.0001	0.0004	0.0004
	120	200	0.0043	0.0490	0.0489	0.1407	0.0275	0.0321	0.0003	0.0468	0.0159
	140	200	0.0049	0.0596	0.0596	0.1743	0.0363	0.0390	0.0003	0.0558	0.0221
${10}^{-6}$	20	200	0.7884	0.0001	0.0001	0.7884	0.0017	0.0017	0.7884	0.0002	0.0002
	40	200	0.6828	0.0000	0.0000	0.6828	0.0009	0.0008	0.6828	0.0001	0.0001
	60	200	0.5575	0.0000	0.0000	0.5575	0.0005	0.0005	0.5575	0.0001	0.0001
	80	200	0.3942	0.0000	0.0000	0.3942	0.0003	0.0003	0.3942	0.0001	0.0001
	100	200	0.0624	0.0092	0.0091	0.1966	0.0159	0.0167	0.0137	0.0029	0.0006
	120	200	0.0031	0.0490	0.0492	0.1250	0.0301	0.0309	0.0003	0.0478	0.0179
	140	200	0.0051	0.0595	0.0597	0.1692	0.0367	0.0381	0.0003	0.0562	0.0268

and six new plots in Figure 5. For Algorithms 2 and 3, we included results only for $\beta =1$, according to conclusions from Section 4.3. We can see that with increasing noise, the computed RSE also increase. However, we can see that all three algorithms are robust to noise, i.e., the resulting RSE for the noisy and the original BION data are very close. The same holds for the infeasibility, depicted in Figure 5.

On the noisy dataset, we also demonstrate what happens if the internal dimension is larger than the true internal dimension (this is demonstrated by $p=120\%,140\%)$. Algorithm 1 finds solution that is slightly closer to the optimum compared to the non-noisy data. Algorithm 2 does not improve RSE, actually RSE slightly increases with p. Algorithm 3 has best performance. It comes with RSE very close to 0 and stays there with increasing p.

Regarding infeasibility, the situation from Figure 4 can be observed also on the noisy dataset. Figure 5 shows that with $p>100\%$ the infeasibility increases. This is not surprising, the higher the internal dimension, the more difficult is to achieve orthonormality. However, resulting vales of ${infeas}_{G,H}$ are still surprisingly small.

We also analyzed how close are the matrices $\tilde{G}$ and $\tilde{H}$, computed by all three algorithms, to the matrices G and H that were used to generate the data matrices R. This comparison is possible only when the inner dimension is equal to the real inner dimension ($p=100\%$). We figured out that the Frobenious norms between these pairs of matrices, i.e., $\parallel \tilde{G}{-G\parallel }_F$ and $\parallel \tilde{H}{-H\parallel }_F$ are quite large (of order $\sqrt{k}$), which means that on a first glance, the solutions are quite different. However, since for every pair $G,H$ and every permutation matrix $\Pi$, we have $GH=G\Pi {\Pi }^{T}H$, the differences between the computed pairs matrices are mainly due to the fact that they have permuted columns (G) or rows (H).

4.5. Time Complexity of All Algorithms

Based on the previous subsections, we can observe that Algorithm 3 is best performing regarding RSE and infeasibility. In this section we perform time complexity analysis of all three algorithms. Following their descriptions we can see that Algorithms 1 has the most simple descriptions and also its implementation is rather simple, only few lines of code. Algorithms 2 and 3 are more involved regarding their theoretical description and implementation, since both involve computations of gradients.

In practices, we stop all three algorithms after 1000 iterations of (outer) loop. For Algorithms 1 and 3, this is the only stopping criteria, while for Algorithm 2, the stopping condition involves also checking the progress of RSE. If this is too small (below ${10}^{-5}$) we also stop.

We first demonstrate how RSE decreases with iterations. The left plot in Figure 6 depicts that Algorithm 3 has the fastest decrease with the number of iterations and needs only a few dozens of iterations to reach optimum RSE. The other two algorithms need much more iterations. However, in each iteration, Algorithm 3 involves solving two sub-problems (9). This results in much higher times needed for one iteration. The right plot of Figure 6 depicts how RSE is decreasing with time. We can see that Algorithms 1 and 2 are much faster. We could decrease this difference by involving more advanced stopping criteria for Algorithm 3, which will be addressed during our future research.

5. Discussion and Conclusions

We presented a projected gradient method to solve the orthogonal non-negative matrix factorization problem. We penalized the deviation from orthonormality with some positive parameters and added the resulted terms to the objective function of the standard non-negative matrix factorization problem. Then, we considered minimizing the resulted objective function under the non-negativity conditions only, in a block coordinate decent approach. The method was tested on three sets of synthetic data: the first containing the uni-orthonormal matrices, the second containing the bi-orthonormal matrices and the third containing the noisy variants of the bi-orthonormal matrices. Different values for penalising parameters were applied in the implementation to determine recommendations which values shall be used in practise.

The performance of our algorithm was compared with two algorithms based on multiplicative updates rules. Algorithms were compared regarding the quality of factorization (RSE) and how much the resulting factors deviate from orthonormality. We provided an extensive list of numerical results which demonstrate that our method is very competitive and outperforms the others in terms of quality of the solution, measured by RSE, and feasibility of the solution, measured by ${\mathrm{infeas}}_G$ or ${\mathrm{infeas}}_{G,H}$. If we take into account also the computing time, the Ding’s Algorithm 1 is also very competitive, since it computes solutions with slightly worse RSE and ${\mathrm{infeas}}_{G,H}$, but in much shorter time.

We expect that the difference in time complexity between Algorithms 1 and 3 can be reduced if we implement more advanced stopping criteria for the latter algorithm. This will be addressed in our future research.