Revisiting the French Didactic Tradition through Technological Lenses
Abstract
:1. Introduction
2. The French Didactic Tradition: Some Important Characteristics
3. A Tradition Seen through the Lens of Dynamic Geometry
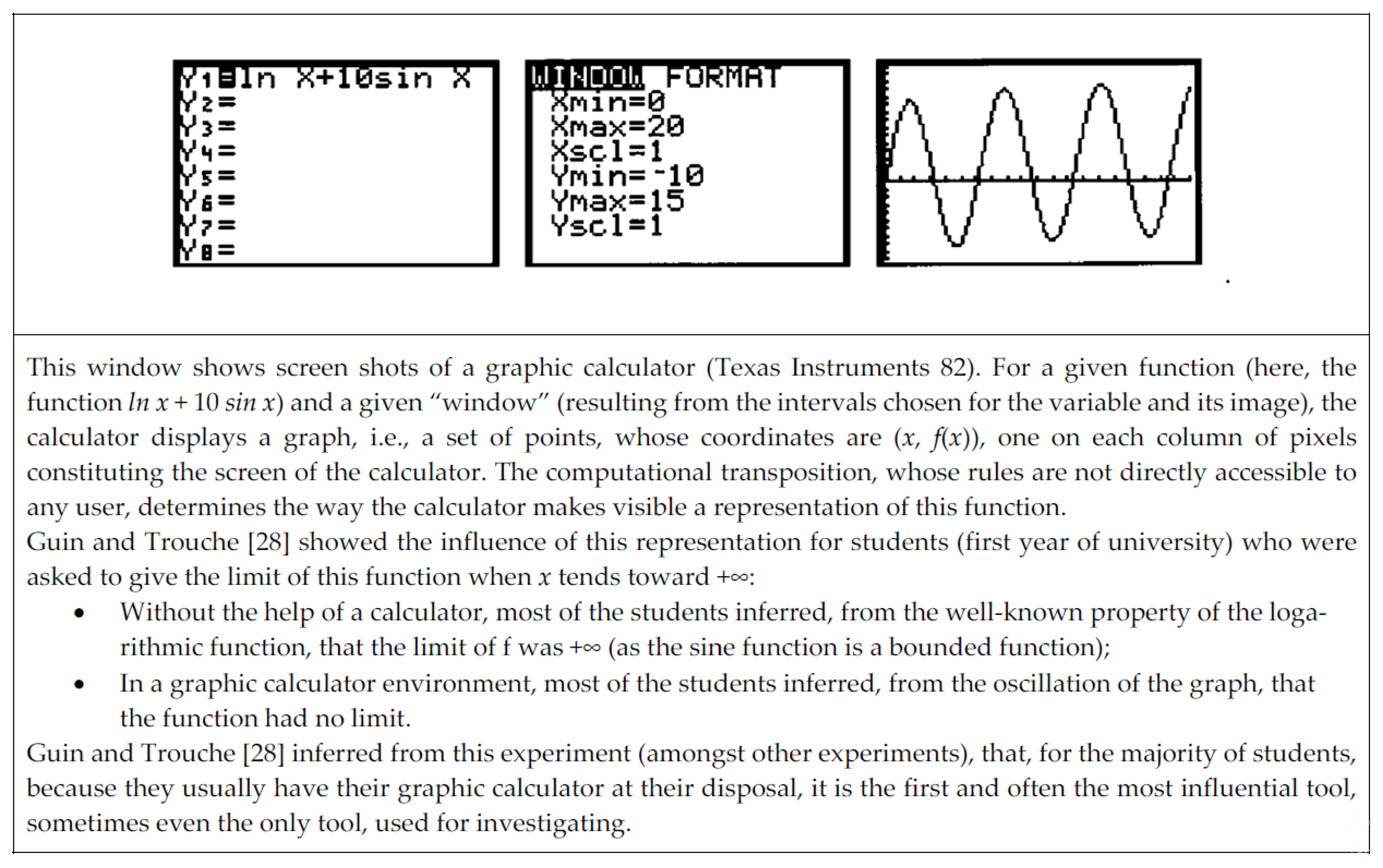
4. A Tradition Seen through the Lens of Calculators and Computer Algebra Systems
- An artefact/instrument dialectic: each artefact, defined as a product and means of human activity, is engaged by the subject in the course of their situated activity; the instrument is developed, from this artefact, by the subject. It is defined as a hybrid entity, composed of the part of the artefact actually used and the scheme of use;
- An instrumentation/instrumentalization dialectic: instrumentation is the process by which the use of the artefact influences the activity of the subject; instrumentalization is the process by which the subject adapts/enriches the artefact to make it more efficient and more suited to their needs.
- That of instrumental orchestrations, defined by Trouche [50] and further developed in a joint work with Drijvers [51] as “the systematic arrangement by an intentional agent of the elements (artefacts and humans) of an environment in order to implement a didactical situation”, taking up the notion of “didactical exploitation scenario” already introduced by Chevallard [48];
- That of double didactic and mathematical genesis [52], expressing the fact that, for a teacher and a given digital artefact, two instrumental geneses take place, the first one transforming it into a mathematical instrument and the second one transforming it into a didactical instrument;
- That of genesis of technology uses by teachers [53], taking account of the fact that the teacher’s activity combines the use of diverse artefacts, digital or not, as well as the fact, in line with the double approach mentioned above, that the analysis of teachers’ instrumented practices cannot be isolated from a more global approach to their practices.
5. A Tradition Seen through the Lens of Digital Resources
- For many different mathematical contents, she prepared lesson frames comprising texts with empty slots, particularly when a new formula is presented;
- She reported that she had taught the same lesson for 3 years, using word processing software, several websites, the digital textbook, the interactive whiteboard, and a paper form to be filled in by students.
- The DAD develops a holistic point of view on the teacher’s work, embracing not only some predominant artefacts, but all the resources in this work: material and symbolic; coming from Internet, as well as from the interactions with colleagues or students; resources already “there” or collected for addressing a new issue. These views lead to the productive notion of resource system embracing the diversity of resources a teacher interacts with;
- It recognizes as essential the process of instrumentalization, considering that adopting a resource is always adapting it (whereas it was not, at the beginning at least, the case in the instrumental approach, as the adaptation of environments such as CAS was not so obvious). In the documentational approach, the processes of usage and design appear as intrinsically linked, as announced by the seminal lecture by Folcher [65];
- Lastly, the DAD is interested in “ordinary” classes, trying to take into account, as much as possible, the institutional conditions constraining teacher activity.
- The connection still alive with the three main frameworks grounding the French didactics (the dialectic scheme/situation from the TCF, the institutional constraints of teacher work from the ATD, and the analysis of task design for TDS);
- The application of DAD in various cultural contexts beyond the French one, for example, in China [77], making it possible to deepen the conditions of teachers’ collective work;
- The interaction with other traditions of research, for example, with Ruthven [78] for deepening the notion of resource system, with the field of research on textbooks [79], for better understanding the critical role of “traditional” resources, or, more generally, with the field of research on curricular resources [80], for taking into account the institutional conditions of teacher documentation work.
6. Discussion
- The Aplusix project initiated by Jean-François Nicaud [87], a computer scientist of the EIAH community, and continuously developed over three decades, already mentioned in the introduction;
- The Pépite project that emerged from the Grugeon doctoral thesis [88] and the multidimensional diagnostic tool of students’ competences in elementary algebra developed in it, transformed into a digital diagnostic tool, Pépite [89], thanks to the collaboration between didacticians and computer scientists, continuously refined until today.
- The cKc (conception, knowing, concept) framework, created by Balacheff [90], drawing out Vergnaud’s frame of conceptualization, for an efficient design of teaching situations and learning environments, be they digital or not, with the additional ambition to build a bridge between research in mathematics education and research in educational technology;
- The modeling of the learner and their relationship with knowledge, developed in the frame of the ATD, throughout the notion of personal praxeology [91], evidencing the emergence of the cognitive subject inside the ATD;
- The “media–milieu dialectic” (dialectique media–milieu, in French), developed by Chevallard [92], for questioning the interactions, in the frame of a given institution, between existing media and the milieu (§ 2), a medium being a system constituted for representing a part of the world to a given audience, including, but not restricted to, the digital environments.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Short Biography of Authors
 | Michèle Artigue: Michèle Artigue is an Emeritus Professor at the Université de Paris and an associate researcher of the Laboratoire de Didactique André Revuz. She gained a doctorate in mathematical logic (1972) and then a habilitation in the didactics of mathematics (1987) at the University Paris 7, where she spent most of her academic career. After her doctorate, she progressively engaged in didactic research. Her main research areas have been the didactics of calculus and analysis, as well as the teaching and learning of mathematics with technology. She has offered theoretical contributions on different themes concerning epistemology and didactics, didactical engineering, the instrumental approach, and the networking of theories. She has had and still has many editorial and scientific responsibilities. From 1998 to 2009, she was Vice President and then President of the International Commission on Mathematical Instruction (ICMI). She was awarded the ICMI Felix Klein Medal in 2013 and the Luis Santaló Medal in 2015. |
 | Luc Trouche: Luc Trouche is an Emeritus Professor at the Ecole Normale Supérieure de Lyon and an associate researcher of the S2HEP Laboratory. He gained a doctorate in didactics of mathematics (1996) at the University Montpellier 2 and then a habilitation (2003) at the University Paris 7. He spent his academic career first in Montpellier (Research Institute for the Teaching of Mathematics) and then in Lyon, at the French Institute of Education. His main research areas have been the teaching and learning of mathematics with technology and teacher professional development, seen particularly through their interactions with resources. He has offered theoretical contributions on different themes, mainly the instrumental approach and the documentational approach to didactics. From 2012 to 2016, he was President of the French Commission on Mathematical Instruction |
References
- Blum, W.; Artigue, M.; Mariotti, M.A.; Sträßer, R.; Van den Heuvel-Panhuizen, M. (Eds.) European Traditions in Didactics of Mathematics (ICME-13 Monograph); Springer: Cham, Switzerland, 2019. [Google Scholar]
- Artigue, M.; Bosch, M.; Chaachoua, H.; Chellougui, F.; Chesnais, A.; Durand-Guerrier, V.; Knipping, C.; Maschietto, M.; Romo-Vázquez, A.; Trouche, L. The French didactics tradition in mathematics. In European Traditions in Didactics of Mathematics (ICME-13 Monograph); Blum, W., Artigue, M., Mariotti, M.A., Sträßer, R., Van den Heuvel-Panhuizen, M., Eds.; Springer: Cham, Switzerland, 2019; pp. 11–55. [Google Scholar]
- Artigue, M. (Ed.) La Tradition Didactique Française au-delà des Frontières. Exemples de Collaborations avec l’Afrique, l’Amérique Latine et l’Asie; Commission Française pour l’Enseignement des Mathématiques: Lyon, France, 2016. Available online: http://www.cfem.asso.fr/cfem/Collaborationsdidactiquesfrancaises.pdf (accessed on 13 March 2021).
- Trouche, L. From Artifact to Instrument: Mathematics Teaching Mediated by Symbolic Calculators. Interact. Comput. 2003, 15, 783–800. [Google Scholar] [CrossRef]
- Trouche, L.; Gueudet, G.; Pepin, B. Documentational approach to didactics. In Encyclopedia of Mathematics Education, 2nd ed.; Lerman, S., Ed.; Springer: Cham: Switzerland, 2020; pp. 307–313. [Google Scholar] [CrossRef] [Green Version]
- Balacheff, N.; Vivet, M. (Eds.) Didactique et Intelligence Artificielle; La Pensée Sauvage Éditions: Grenoble, France, 1994. [Google Scholar]
- Vergnaud, G.; Brousseau, G.; Hulin, M. Didactique des Acquisitions des Connaissances Scientifiques. Actes du Colloque de Sèvres. Mai 1987; La Pensée Sauvage Éditions: Grenoble, France, 1988. [Google Scholar]
- Brousseau, G. Theory of Didactical Situations in Mathematics; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997. [Google Scholar]
- Vergnaud, G. The theory of conceptual fields. Hum. Dev. 2009, 52, 83–94. [Google Scholar] [CrossRef]
- Chevallard, Y. Introducing the Anthropological Theory of the Didactic: An attempt at a principled approach. Hiroshima J. Math. Educ. 2019, 12, 1–44. [Google Scholar]
- Robert, A.; Rogalski, J. Le système complexe et cohérent des pratiques des enseignants de mathématiques: Une double approche. Rev. Can. L’enseign. Sci. Math. Technol. 2002, 2, 505–528. [Google Scholar] [CrossRef]
- Gispert, H. Mathematics education in France, 1900–1980. In Handbook on the History of Mathematics Education; Springer: Cham, Switzerland, 2014; pp. 229–240. [Google Scholar]
- Trouche, L. Didactics of Mathematics: Concepts, Roots, Interactions and Dynamics from France. In Tools and Mathematics, Instruments for Learning; Monaghan, J., Trouche, L., Borwein, J.M., Eds.; Springer: Cham, Switzerland, 2016; pp. 219–256. [Google Scholar]
- Artigue, M. Perspectives on Design Research: The Case of Didactical Engineering. In Approaches to Qualitative Research in Mathematics Education; Bikner-Ahsbahs, A., Knipping, C., Presmeg, N., Eds.; Springer: New York, NY, USA, 2014; pp. 467–496. [Google Scholar]
- Chevallard, Y. La Transposition Didactique; La Pensée Sauvage Éditions: Grenoble, France, 1985. [Google Scholar]
- Brousseau, G.; Brousseau, N.; Warfield, V. Teaching Fractions through Situations: A fundamental Experiment; Springer: New York, NY, USA, 2014. [Google Scholar]
- Laborde, J.M. Technology-Enhanced Teaching/Learning at a New Level with Dynamic Mathematics as Implemented in the New Cabri. In Digital Curricula in School Mathematics. Part I: Creating Digital Curriculum; Beates, M., Usiskin, Z., Eds.; The University of Chicago: Chicago, CH, USA, 2016; pp. 53–74. [Google Scholar]
- Laborde, C.; Capponi, B. Cabri-géomètre constituant d’un milieu pour l’apprentissage de la notion de figure géométrique. Rech. Didact. Math. 1994, 14, 165–210. [Google Scholar]
- Parzysz, B. Knowing vs Seeing. Problems of the plane representation of space geometry figures. Educ. Stud. Math. 1988, 19, 79–92. [Google Scholar] [CrossRef]
- Laborde, C. Integration of geometry in the design of geometry tasks with Cabri-geometry. Int. J. Comput. Math. Learn. 2001, 6, 283–317. [Google Scholar] [CrossRef]
- Falcade, R.; Laborde, C.; Mariotti, M.A. Approaching functions: Cabri tools as instruments of semiotic mediation. Educ. Stud. Math. 2007, 66, 317–333. [Google Scholar] [CrossRef]
- Healy, L. Identifying and explaining geometrical relationship: Interactions with robust and soft Cabri constructions. In Proceedings of the 24th Conference of the International Group for the Psychology of Mathematics Education, Hiroshima, Japan, 23–27 July 2000; Tadao Nakahara, Masataka Koyama: Hiroshima, Japan, 2000; Volume 1, pp. 103–117. [Google Scholar]
- Arzarello, F.; Gallino, G.; Micheletti, C.; Olivero, F.; Paola, D.; Robutti, O. Dragging in Cabri and modalities of transition from conjectures to proofs in geometry. In Proceedings of the 22nd Conference of the International Group for the Psychology of Mathematics Education, Stellenbuch, South Africa, 12–17 July 1998; Volume 2, pp. 32–39. [Google Scholar]
- Laborde, C.; Assude, T.; Grugeon, B.; Soury-Lavergne, S. Study of a teacher professional problem: How to take into account the instrumental dimension when using Cabri-geometry? In Proceedings of the Seventeenth ICMI Study Conference “Technology Revisited”, Hanoi, Vietnam, 3–8 December 2006; Hoyles, C., Lagrange, J.-B., Son, L.-H., Sinclair, N., Eds.; Hanoi Institute of Technology: Hanoi, Vietnam, 2006; pp. 317–325. [Google Scholar]
- Guin, D.; Trouche, L. The Complex Process of Converting Tools into Mathematical Instruments. The Case of Calculators. Int. J. Comput. Math. Learn. 1998, 3, 195–227. [Google Scholar] [CrossRef]
- Artigue, M. Le logiciel DERIVE comme révélateur de phénomènes didactiques liés à l’utilisation d’environnements informatiques pour l’apprentissage. Educ. Stud. Math. 1997, 33, 133–169. [Google Scholar] [CrossRef]
- Hirlimann, A. (Ed.) Enseignement des Mathématiques et Logiciels de Calcul Formel; Ministère de l’Education Nationale, DITEN B2: Paris, France, 1994. [Google Scholar]
- Guin, D.; Trouche, L. Seeing is Reality: How Graphic Calculators May Influence the Conceptualization of Limits. In Proceedings of the PME 20, Valencia, Spain, 8–12 July 1996; Puig, L., Gutiérrez, A., Eds.; Universitat de València: València, Spain, 1996; Volume 4, pp. 323–330. [Google Scholar]
- Balacheff, N. Didactique et intelligence artificielle. Rech. Didact. Math. 1994, 14, 9–42. [Google Scholar]
- Rabardel, P. Les Hommes et les Technologies. Approche Cognitive des Instruments Contemporains; Armand Colin: Paris, France, 1995. [Google Scholar]
- Verillon, P.; Rabardel, P. Cognition and artifact: A contribution to the study of thought in relation to instrument activity. Eur. J. Psychol. Educ. 1995, 9, 77–101. [Google Scholar] [CrossRef]
- Artigue, L. Rapports entre dimensions technique et conceptuelle dans l’activité mathématique avec des systèmes de mathématiques symboliques. In Actes de l’Université d’été « Des Outils Informatiques dans la Classe aux Calculatrices Symboliques et Géométriques: Quelles Perspectives pour L’enseignement des Mathématiques; IREM: Rennes, France, 1997; pp. 19–40. [Google Scholar]
- Trouche, L. A la recherche d’une méthode d’étude de l’action instrumentée. In Actes de l’Université d’été «Des Outils Informatiques dans la Classe aux Calculatrices Symboliques et Géométriques: Quelles Perspectives pour L’enseignement des Mathématiques»; IREM: Rennes, France, 1997; pp. 113–148. [Google Scholar]
- Defouad, B. Étude de Genèses Instrumentales Liées à L’utilisation D’une Calculatrice Symbolique en Classe de Première S. Ph.D. Thesis, Paris 7 University, Paris, France, 2000. [Google Scholar]
- Trouche, L. A Propos de L’apprentissage des Limites de Fonctions, Etude des Rapports Entre Processus D’instrumentation et Processus de Conceptualisation. Ph.D. Thesis, Montpellier 2 University, Montpellier, France, 1996. [Google Scholar]
- Maschietto, M. L’enseignement de L’analyse au Lycée: Les Débuts du jeu Global/Local Dans L’environnement de Calculatrices. Ph.D. Thesis, Paris 7 University, Paris, France, 2002. [Google Scholar]
- Guin, D.; Trouche, L. Analyser l’usage didactique d’un EIAH en mathématiques, une tâche nécessairement complexe. Sci. Tech. Educ. 2001, 8, 61–74. [Google Scholar] [CrossRef] [Green Version]
- Restrepo, A. Genèse Instrumentale du Déplacement en Géométrie Dynamique Chez des Elèves de 6ème. Ph.D. Thesis, Grenoble 1 University, Grenoble, France, 2008. [Google Scholar]
- Haspekian, M. Intégration D’outils Informatiques dans L’enseignement des Mathématiques: Étude du cas des Tableurs. Ph.D. Thesis, Paris 7 University, Paris, France, 2005. [Google Scholar]
- Rabardel, P. Éléments pour une approche instrumentale en didactique des mathématiques. In Actes de L’école d’été de Didactique des Mathématiques; Bailleul, M., Ed.; ARDM & IUFM: Caen, France, 2000; pp. 202–213. [Google Scholar]
- Lagrange, J.-B. Les instruments de calcul formel. In Actes de la Dixième Université d’été de Didactique des Mathématiques; Bailleul, M., Ed.; IUFM & ARDM: Caen, France, 1999; pp. 235–244. [Google Scholar]
- Laborde, C. L’activité instrumentée par des logiciels de géométrie dynamique. In Actes de la Dixième Université d’été de Didactique des Mathématiques; Bailleul, M., Ed.; IUFM & ARDM: Caen, France, 1999; pp. 214–234. [Google Scholar]
- Guin, D. (Ed.) Calculatrices Symboliques et Géométriques dans L’enseignement des Mathématiques. Actes du Colloque Francophone Européen de La Grande-Motte; IREM, Université Montpellier 2: Montpellier, France, 1998. [Google Scholar]
- Artigue, M. Learning mathematics in a CAS environment: The genesis of a reflection about instrumentation and the dialectics between technical and conceptual work. Int. J. Comput. Math. Learn. 2002, 7, 245–274. [Google Scholar] [CrossRef]
- Guin, D.; Ruthven, K.; Trouche, L. (Eds.) The Didactical Challenge of Symbolic Calculators: Turning a Computational Device into a Mathematical Instrument; Springer: New York, NY, USA, 2005. [Google Scholar]
- Hoyles, C.; Lagrange, J.-B. Mathematics Education and Technology-Rethinking the Terrain. The 17th ICMI Study; Springer: New York, NY, USA, 2010. [Google Scholar]
- Lagrange, J.-B.; Artigue, M.; Laborde, C.; Trouche, L. Technology and mathematics education: A multidimensional study of the evolution of research and innovation. In Second International Handbook of Mathematics Education; Bishop, A.J., Clements, M.A., Keitel, C., Kilpatrick, J., Leung, F.K.S., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2003; pp. 239–271. [Google Scholar]
- Chevallard, Y. Familière et problématique, la figure du professeur. Rech. Didact. Math. 1997, 17, 17–54. [Google Scholar]
- Margolinas, C. Situations, milieux, connaissances: Analyse de l’activité du professeur. In Actes de la 11ème Ecole d’Eté de Didactique des Mathématiques; Dorier, J.-L., Artaud, M., Artigue, M., Berthelot, R., Floris, R., Eds.; La Pensée Sauvage Éditions: Grenoble, France, 2002; pp. 141–156. [Google Scholar]
- Trouche, L. Managing the complexity of human/machine interactions in computerized learning environments: Guiding students’ command process through instrumental orchestrations. Int. J. Comput. Math. Learn. 2004, 9, 281–307. [Google Scholar] [CrossRef]
- Trouche, L.; Drijvers, P. Handheld technology for mathematics education, flashback to the future. ZDM Int. J. Math. Educ. 2010, 42, 667–681. [Google Scholar] [CrossRef]
- Haspekian, M. The co-construction of a mathematical and a didactical instrument. In Proceedings of the CERME 7, Rzeszów, Poland, 9–13 February 2011; Pytak, M., Swoboda, E., Rowland, T., Eds.; University of Rzeszów and ERME: Rzeszów, Poland, 2011; pp. 2298–2307. [Google Scholar]
- Abboud, M.; Vandebrouck, F. Geneses of technology uses: A theoretical model to study the development of teachers’ practices in technology environments. In Proceedings of the CERME 8, Antalya, Turkey, 6–10 February 2013; Ubuz, B., Haser, C., Mariotti, M.A., Eds.; Université de Sherbrooke: Sherbrooke, QC, Canada, 2013; pp. 2504–2513. [Google Scholar]
- Artigue, M.; Groupe TICE IREM de Paris. Lutilisation de ressources en ligne pour lenseignement des mathématiques au lycée: Du suivi d’une expérimentation régionale à un objet de recherche. In Actes du Colloque EMF 2006. L’enseignement des Mathématiques Face aux Défis de L’école et des Communautés; Bednarz, N., Mary, C., Eds.; Université de Sherbrooke: Sherbrooke, QC, Canada, 2008; Thème 5; pp. 1–11. [Google Scholar]
- Guin, D.; Trouche, L. Distance training, a key mode to support teachers in the integration of ICT? In Proceedings of the Fourth European Conference on Research on Mathematics Education, Sant Feliu de Guíxols, Spain, 17–21 February 2005; Bosch, M., Ed.; FUNDEMI IQS, Universitat Ramon LLull: Barcelona, Spain, 2005; pp. 1020–1029. [Google Scholar]
- Lagrange, J.-B.; Abboud Blanchard, M.; Loisy, C.; Vandebrouck, F. Rapport final de la Recherche Genèse d’usages Professionnels des Technologies par les Enseignants. 2009. Available online: http://gupten.free.fr/ (accessed on 13 March 2021).
- Sokhna, M. Formation à Distance des Professeurs de Mathématiques au Sénégal, Genèse Instrumentale de Ressources Pédagogiques. Ph.D. Thesis, Montpellier 2 University, Montpellier, France, 2006. [Google Scholar]
- Lagrange, J.-B. Complex calculators in the classroom: Theoretical and practical reflections on teaching pre-calculus. Int. J. Comput. Math. Learn. 1999, 4, 51–81. [Google Scholar] [CrossRef]
- Monaghan, J. Computer algebra, instrumentation and the anthropological approach. Int. J. Technol. Math. Educ. 2007, 14, 63–71. [Google Scholar]
- Gueudet, G.; Trouche, L. Conceptions et usages de ressources pour et par les professeurs, développement associatif et développement professionnel. Doss. L’ingénierie Educ. 2009, 65, 76–80. [Google Scholar]
- Gueudet, G. Studying teachers’ documentation work. In The ‘Resource’ Approach to Mathematics Education; Trouche, L., Gueudet, G., Pepin, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 17–42. [Google Scholar]
- Adler, J. Conceptualising resources as a theme for teacher education. J. Math. Teach. Educ. 2000, 3, 205–224. [Google Scholar] [CrossRef]
- Baron, M.; Guin, D.; Trouche, L. (Eds.) Environnements Informatisés et Ressources Numériques pour l’apprentissage: Conception et Usages, Regards Croisés; Hermès: Paris, France, 2007. [Google Scholar]
- Pédauque, R.T. Le Document à la Lumière du Numérique; C & F Éditions: Caen, France, 2006. [Google Scholar]
- Folcher, V. Conception pour l’usage, conception dans l’usage: Quelles ressources pour quelles activités? In Nouvelles Perspectives en Didactique des Mathématiques; Bloch, I., Conne, F., Eds.; La Pensée Sauvage: Grenoble, France, 2009; pp. 95–108. [Google Scholar]
- Gueudet, G.; Trouche, L. Vers de nouveaux systèmes documentaires des professeurs de mathématiques. In Nouvelles Perspectives en Didactique des Mathématiques; Bloch, I., Conne, F., Eds.; La Pensée Sauvage Éditions: Grenoble, France, 2009; pp. 109–133. [Google Scholar]
- Margolinas, C.; Wozniak, F. Place des documents dans l’élaboration d’un enseignement de mathématiques à l’école primaire. In Nouvelles Perspectives en Didactique des Mathématiques; Bloch, I., Conne, F., Eds.; La Pensée Sauvage Éditions: Grenoble, France, 2009; pp. 135–146. [Google Scholar]
- Gueudet, G.; Trouche, L. Teachers’ work with resources: Documentation geneses and professional geneses. In From Text to ‘Lived’ Resources: Mathematics Curriculum Materials and Teacher Development; Gueudet, G., Pepin, B., Trouche, L., Eds.; Springer: New York, NY, USA, 2012; pp. 23–41. [Google Scholar]
- Gueudet, G.; Buteau, C.; Mesa, V.; Misfeldt, M. Instrumental and documentational approaches: From technology use to documentation systems in university mathematics education. Res. Math. Educ. 2014, 16, 139–155. [Google Scholar] [CrossRef]
- Gueudet, G.; Trouche, L. Étudier les interactions professeurs-ressources: Questions de méthode. Educ. Didact. 2021. to appear. [Google Scholar]
- Sabra, H. L’étude des rapports entre documentations individuelle et collective: Incidents, connaissances et ressources mathématiques. Rech. Didact. Math. 2016, 36, 49–95. [Google Scholar]
- Hammoud, R. Le Travail Collectif des Professeurs en Chimie Comme Levier pour la Mise en Œuvre de Démarches D’investigation et le Développement des Connaissances Professionnelles. Contribution au développement de L’approche Documentaire du Didactique. Ph.D. Thesis, Lyon 1 University and Lebanese University, Villeurbanne, France, 2012. [Google Scholar]
- Rocha, K. Une étude des Effets du Travail Documentaire et Collectif sur le Développement Professionnel des Enseignants de Mathématiques: Apport des Concepts D’expérience et de Trajectoire Documentaires. Ph.D. Thesis, ENS de Lyon, Lyon, France, 2019. [Google Scholar]
- Gueudet, G.; Trouche, L. Du travail documentaire des enseignants: Genèses, collectifs, communautés. Le cas des mathématiques. Educ. Didact. 2008, 2, 7–33. [Google Scholar] [CrossRef] [Green Version]
- Pepin, B.; Gueudet, G.; Trouche, L. Re-sourcing teachers’ work and interactions: A collective perspective on resources, their use and transformation. ZDM Math. Educ. 2013, 45, 929–944. [Google Scholar] [CrossRef] [Green Version]
- Besnier, S. Le Travail Documentaire des Professeurs à L’épreuve des Ressources Technologiques. Le cas de L’enseignement du Nombre à l’école Maternelle. Ph.D. Thesis, Brittany University, Rennes, France, 2016. [Google Scholar]
- Pepin, B.; Xu, B.; Trouche, L.; Wang, C. Developing a deeper understanding of mathematics teaching expertise: Chinese mathematics teachers’ resource systems as windows into their work and expertise. Educ. Stud. Math. 2017, 94, 257–274. [Google Scholar] [CrossRef] [Green Version]
- Ruthven, K. The Construct of ‘Resource System’ as an Analytic Tool in Understanding the Work of Teaching. In The ‘Ressource’ Approach to Mathematics Education; Trouche, L., Gueudet, G., Pepin, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 43–59. [Google Scholar]
- Fan, L.; Trouche, L.; Qi, C.; Rezat, S.; Visnovska, J. (Eds.) Research on Mathematics Textbooks and Teachers’ Resources: Advances and issues; Springer: Cham, Switzerland, 2018. [Google Scholar]
- Remillard, J.T. Examining key concepts in research on teachers’ use of mathematics curricula. Rev. Educ. Res. 2005, 75, 211–246. [Google Scholar] [CrossRef] [Green Version]
- Gueudet, G.; Trouche, L. (Eds.) Ressources Vives, la Documentation des Professeurs en Mathématiques; PUR & INRP: Rennes, France, 2010. [Google Scholar]
- Gueudet, G.; Pepin, B.; Trouche, L. (Eds.) From Text to ‘Lived’ Resources: Mathematics Curriculum Materials and Teacher Development; Springer: New York, NY, USA, 2012. [Google Scholar]
- Gitirana, V.; Miyakawa, T.; Rafalska, M.; Soury-Lavergne, S.; Trouche, L. (Eds.) Proceedings of the Re(s)sources 2018 International Conference. Available online: https://hal.archives-ouvertes.fr/hal-01764563v3/document (accessed on 13 March 2021).
- Trouche, L. Evidencing missing resources of the documentational approach to didactics. Towards ten programs of research/development for enriching this approach. In The ‘Ressource’ Approach to Mathematics Education; Trouche, L., Gueudet, G., Pepin, B., Eds.; Springer: Cham, Switzerland, 2019; pp. 447–489. [Google Scholar]
- Trouche, L.; Adler, J.; Remillard, J. (Eds.) Conceptualizing teachers’ interactions with resources in crossing languages and cultures. Special issue. In ZDM Math. Educ.; to be published in 2023.
- Cornu, B.; Ralston, A. The Influence of Computers and Informatics on Mathematics and its Teaching, 2nd ed.; UNESCO: Paris, France, 1992. [Google Scholar]
- Bouhineau, D.; Nicaud, J.F. APLUSIX, un EIAH de l’algèbre. In Environnements Informatiques et Apprentissage Humain; Grandbastien, M., Labat, J.-M., Eds.; Hermès-Lavoisier: Paris, France, 2006; pp. 333–350. [Google Scholar]
- Grugeon-Allys, B. Etude des Rapports Institutionnels et des Rapports Personnels des Elèves à L’algèbre Elémentaire dans la Transition Entre deux Cycles D’enseignement: BEP et Première G. Ph.D. Thesis, Paris 7 University, Paris, France, 1995. [Google Scholar]
- Grugeon-Allys, B.; Chenevotot-Quentin, F.; Pilet, J.; Prévit, D. Online automated assessment and student learning: The Pepite project in elementary algebra. In Uses of Technology in K-12 Mathematics Education: Tools, Topics and Trends; Ball, L., Drijvers, P., Ladel, S., Siller, H.-S., Tabach, M., Vale, C., Eds.; Springer: New York, NY, USA, 2018; pp. 245–266. [Google Scholar]
- Balacheff, N. A knowledge model drawn from an understanding of students understanding. Didactical principles and model specifications. In Baghera Assessment Project, Designing an Hybrid and Emergent Educational Society; Soury-Lavergne, S., Ed.; Cahier Leibniz: Grenoble, France, 2003; pp. 3–22. [Google Scholar]
- Crozet, M.-C.; Chaachoua, H. Une réponse à la prise en compte de l’apprenant dans la TAD: La praxéologie personnelle. Rech. Didact. Math. 2016, 36, 161–196. [Google Scholar]
- Chevallard, Y. Un concept en émergence: La dialectique des médias et des milieux. In Actes du Séminaire National de Didactique des Mathématiques; Gueudet, G., Matheron, Y., Eds.; ARDM et IREM: Paris, France, 2007; pp. 344–366. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artigue, M.; Trouche, L. Revisiting the French Didactic Tradition through Technological Lenses. Mathematics 2021, 9, 629. https://doi.org/10.3390/math9060629
Artigue M, Trouche L. Revisiting the French Didactic Tradition through Technological Lenses. Mathematics. 2021; 9(6):629. https://doi.org/10.3390/math9060629
Chicago/Turabian StyleArtigue, Michèle, and Luc Trouche. 2021. "Revisiting the French Didactic Tradition through Technological Lenses" Mathematics 9, no. 6: 629. https://doi.org/10.3390/math9060629
APA StyleArtigue, M., & Trouche, L. (2021). Revisiting the French Didactic Tradition through Technological Lenses. Mathematics, 9(6), 629. https://doi.org/10.3390/math9060629






