Multi-Way Fluorescence Technique Combined with Four-Way Calibration for the Determination of Thiabendazole and Carbaryl in Apple
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals and Reagents
2.2. Instruments and Software
2.3. Sample Preparation
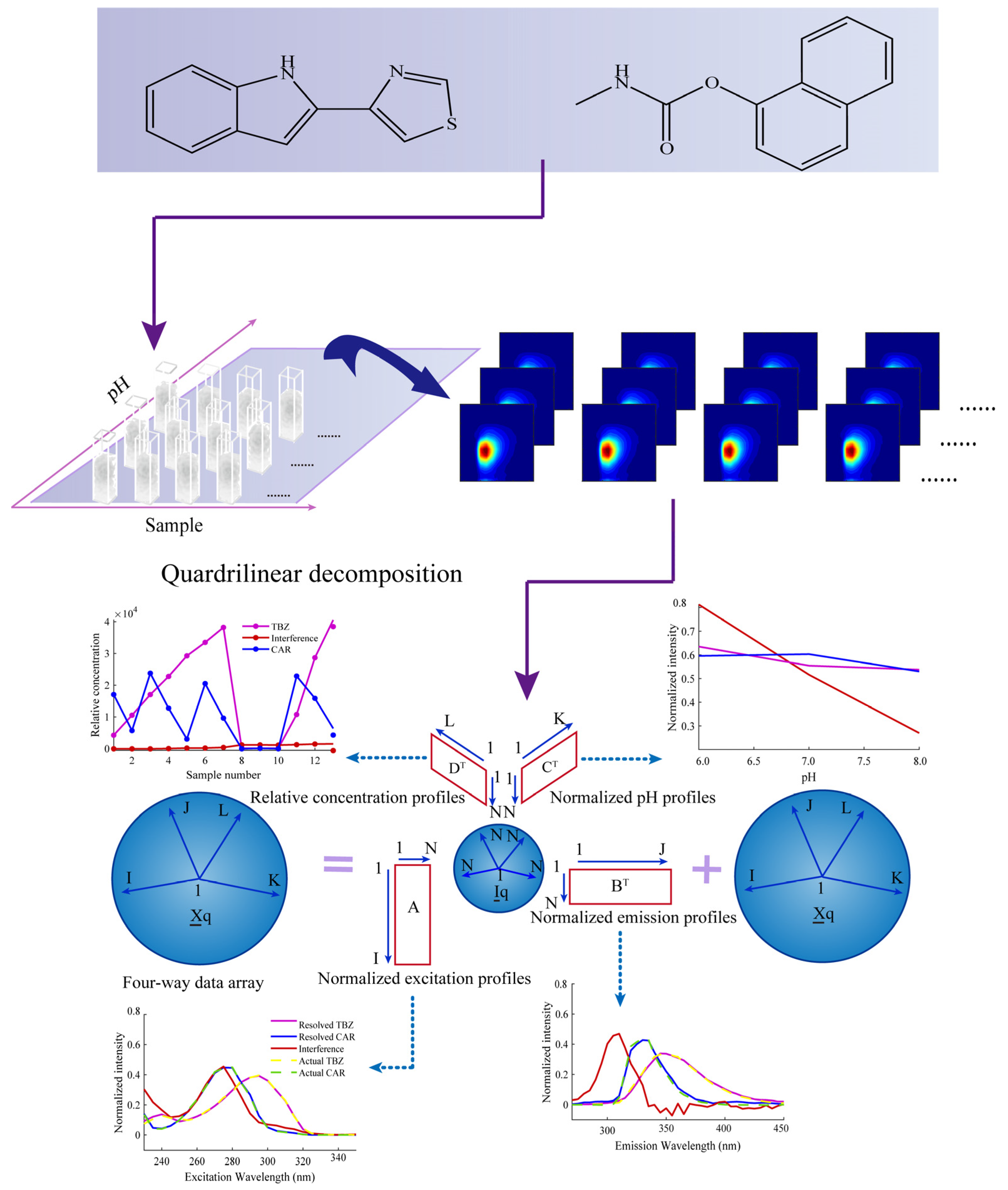
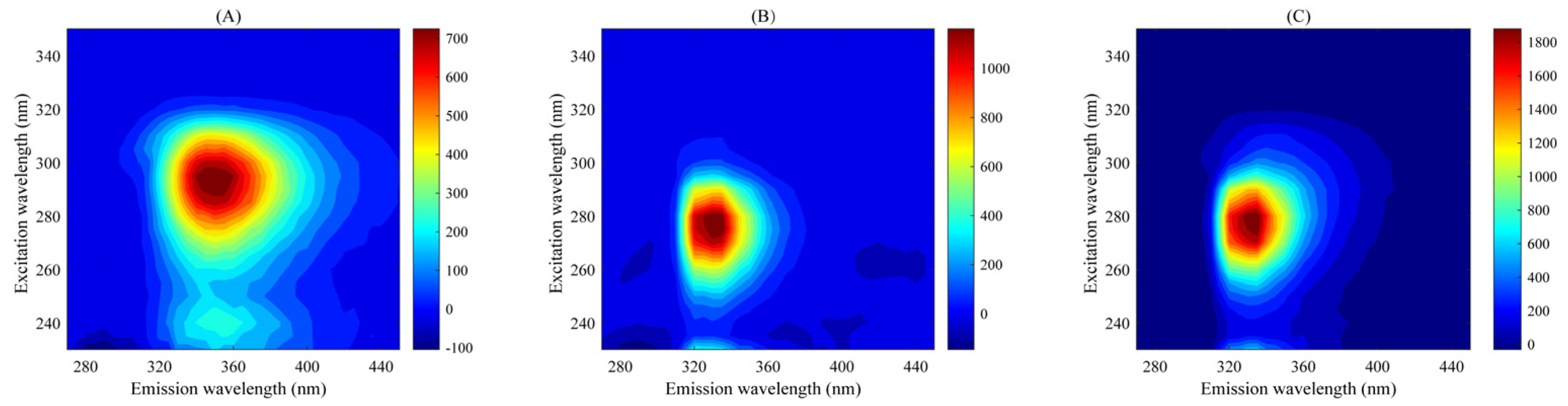
2.4. Acquisition of Four-Way Data Array
2.5. Theory
2.5.1. Quadrilinear Component Model
2.5.2. Alternating Quadrilinear Decomposition (AQLD) Algorithm
2.5.3. Alternating Normalization Weighted Error (ANWE) Algorithm
2.5.4. Method Evaluation
3. Results and Discussion
3.1. Estimating the Number of Components
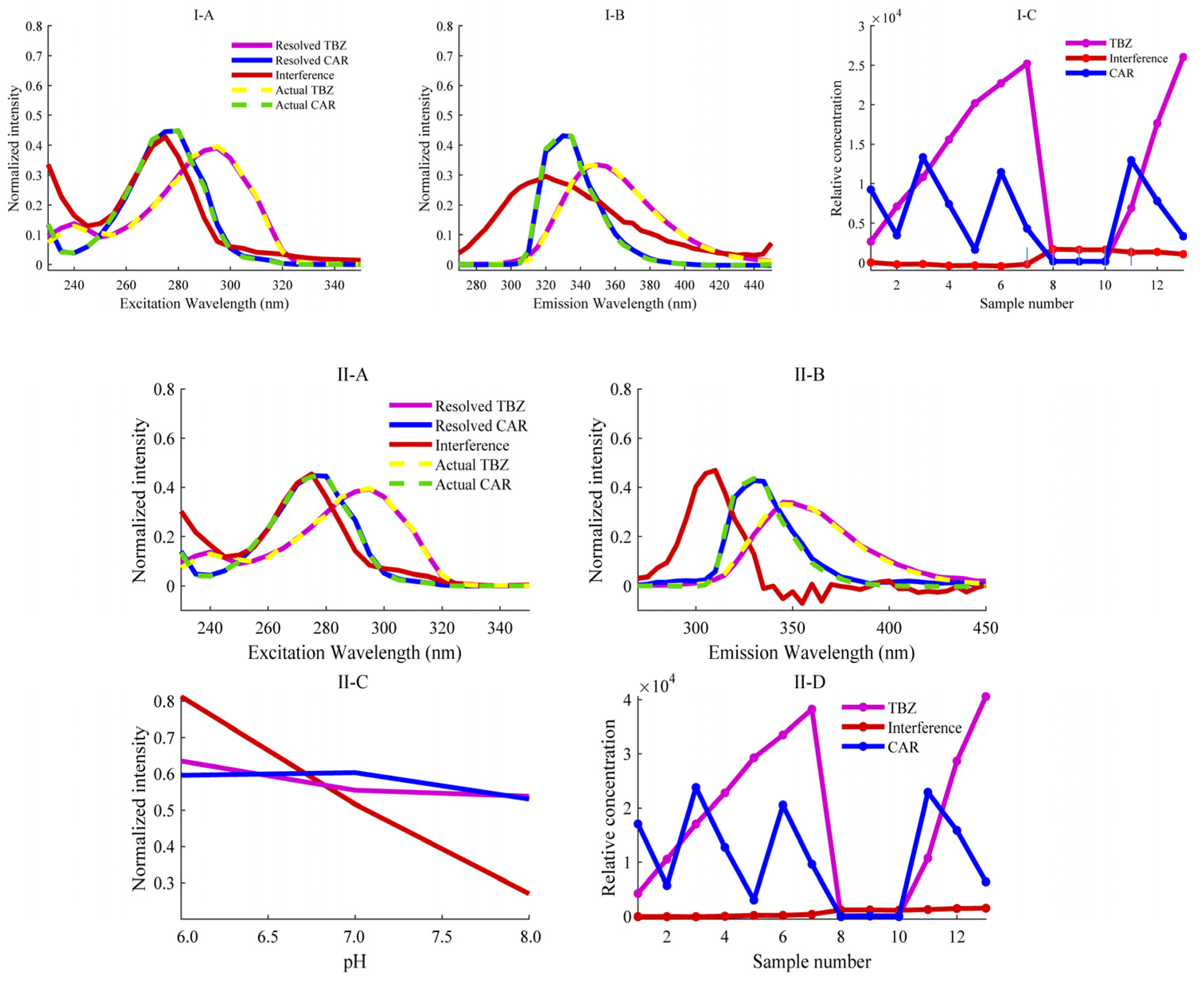
3.2. Spectral Characteristics
3.3. Simultaneous Quantitative Analysis of TBZ and CAR in Apple
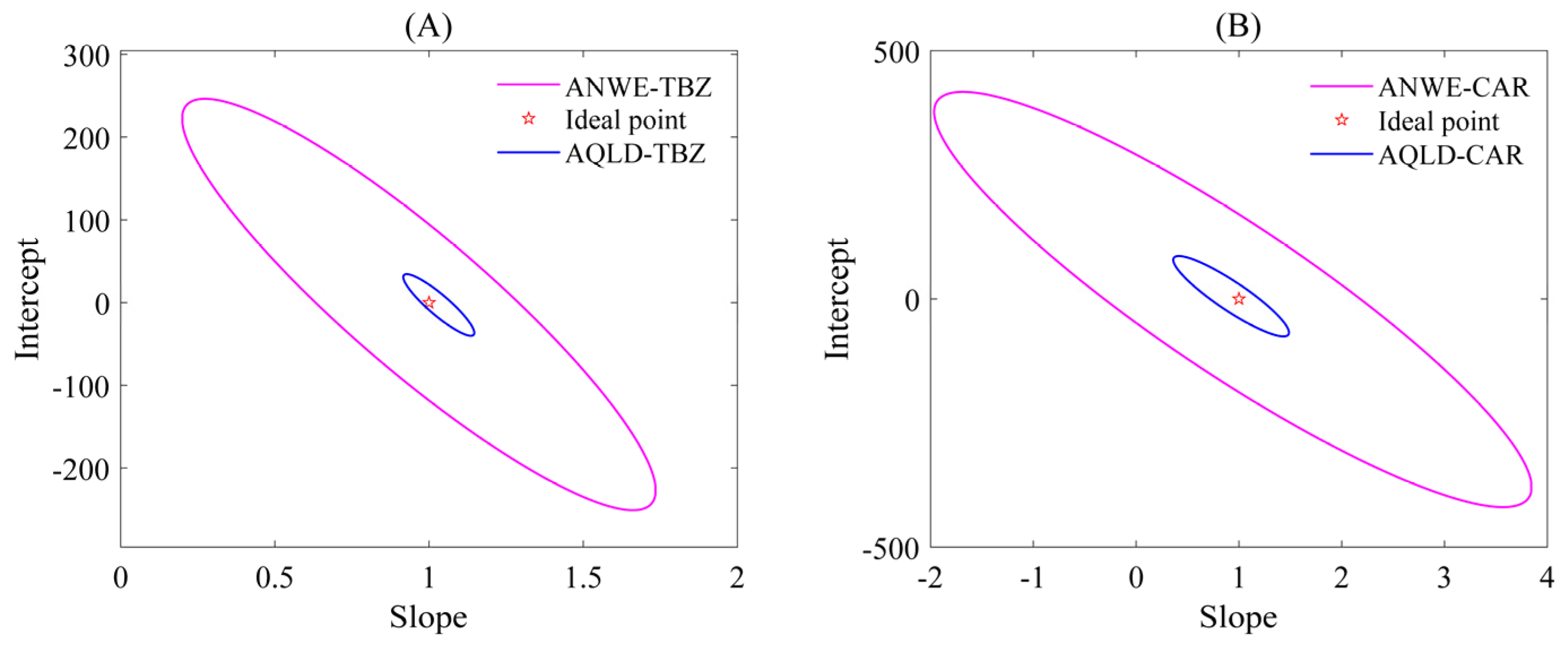
3.4. Analytical Figures of Merit
3.5. Comparison of Three-Way and Four-Way Calibration Methods
3.6. HPLC-DAD Method for Confirmation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Goh, M.S.; Lam, S.D.; Yang, Y.; Naqiuddin, M.; Addis, S.N.K.; Yong, W.T.L.; Luang-In, V.; Sonne, C.; Ma, N.L. Omics technologies used in pesticide residue detection and mitigation in crop. J. Hazard. Mater. 2021, 420, 126624. [Google Scholar] [CrossRef] [PubMed]
- Rejman, K.; Górska-Warsewicz, H.; Kaczorowska, J.; Laskowski, W. Nutritional Significance of Fruit and Fruit Products in the Average Polish Diet. Nutrients 2021, 13, 2079. [Google Scholar] [CrossRef] [PubMed]
- Budetić, M.; Kopf, D.; Dandić, A.; Samardžić, M. Review of Characteristics and Analytical Methods for Determination of Thiabendazole. Molecules 2023, 28, 3926. [Google Scholar] [CrossRef] [PubMed]
- European Food Safety Authority. Revision of the review of the existing maximum residue levels for thiabendazole. EFSA J. 2016, 14, e04516. [Google Scholar] [CrossRef]
- Choi, S.-I.; Han, X.; Lee, S.-J.; Men, X.; Oh, G.; Lee, D.-S.; Lee, O.-H. Validation of an Analytical Method for the Determination of Thiabendazole in Various Food Matrices. Separations 2022, 9, 135. [Google Scholar] [CrossRef]
- Saquib, Q.; Siddiqui, M.A.; Ansari, S.M.; Alwathnani, H.A.; Musarrat, J.; Al-Khedhairy, A.A. Cytotoxicity and genotoxicity of methomyl, carbaryl, metalaxyl, and pendimethalin in human umbilical vein endothelial cells. J. Appl. Toxicol. JAT 2021, 41, 832–846. [Google Scholar] [CrossRef]
- Lerman, Y.; Hirshberg, A.; Shteger, Z. Organophosphate and carbamate pesticide poisoning: The usefulness of a computerized clinical information system. Am. J. Ind. Med. 1984, 6, 17–26. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, H.-L.; Wang, T.; Sun, X.-D.; Liu, B.-B.; Chang, Y.-Y.; Chen, J.-C.; Ding, Y.-J.; Yu, R.-Q. Quantitative analysis of carbaryl and thiabendazole in complex matrices using excitation-emission fluorescence matrices with second-order calibration methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 264, 120267. [Google Scholar] [CrossRef]
- Ke, Z.; Zhu, Q.; Jiang, W.; Zhou, Y.; Zhang, M.; Jiang, M.; Hong, Q. Heterologous expression and exploration of the enzymatic properties of the carbaryl hydrolase CarH from a newly isolated carbaryl-degrading strain. Ecotoxicol. Environ. Saf. 2021, 224, 112666. [Google Scholar] [CrossRef]
- Khan, N.; Yaqub, G.; Hafeez, T.; Tariq, M. Assessment of Health Risk due to Pesticide Residues in Fruits, Vegetables, Soil, and Water. J. Chem. 2020, 2020, 5497952. [Google Scholar] [CrossRef]
- Kaczyński, P.; Rutkowska, E.; Jankowska, M.; Hrynko, I. Evaluation of pesticide residues in fruit from Poland and health risk assessment. Agric. Sci. 2013, 4, 106. [Google Scholar]
- Kowalska, G.; Kowalski, R. Pestycydy-zakres i ryzyko stosowania, korzyści i zagrożenia. Praca przeglądowa. Ann. Hortic. 2019, 29, 5–25. [Google Scholar] [CrossRef]
- Bempah, C.; Buah-Kwofie, A.; Denutsui, D.; Asomaning, J.; Asamoah, A. Monitoring of Pesticide Residues in Fruits and Vegetables and Related Health Risk Assessment in Kumasi Metropolis, Ghana. Res. J. Environ. Earth Sci. 2011, 3, 761–771. [Google Scholar]
- Narenderan, S.T.; Meyyanathan, S.N.; Babu, B. Review of pesticide residue analysis in fruits and vegetables. Pre-treatment, extraction and detection techniques. Food Res. Int. 2020, 133, 109141. [Google Scholar] [CrossRef]
- Xu, X.; Long, N.; Lv, J.; Wang, L.; Zhang, M.; Qi, X.; Zhang, L. Functionalized Multiwalled Carbon Nanotube as Dispersive Solid-Phase Extraction Materials Combined with High-Performance Liquid Chromatography for Thiabendazole Analysis in Environmental and Food Samples. Food Anal. Methods 2015, 9, 30–37. [Google Scholar] [CrossRef]
- Ferreira, J.A.; Ferreira, J.M.S.; Talamini, V.; Facco, J.d.F.; Rizzetti, T.M.; Prestes, O.D.; Adaime, M.B.; Zanella, R.; Bottoli, C.B.G. Determination of pesticides in coconut (Cocos nucifera Linn.) water and pulp using modified QuEChERS and LC–MS/MS. Food Chem. 2016, 213, 616–624. [Google Scholar] [CrossRef]
- Tomai, P.; Gentili, A.; Fanali, S.; Picó, Y. Multi-residue determination of organic micro-pollutants in river sediment by stir-disc solid phase extraction based on oxidized buckypaper. J. Chromatogr. A 2020, 1621, 461080. [Google Scholar] [CrossRef]
- Tanaka, A.; Fujimoto, Y. Gas chromatographic determination of thiabendazole in fruits as its methyl derivative. J. Chromatogr. A 1976, 117, 149–160. [Google Scholar] [CrossRef]
- Gionfriddo, E.; Gruszecka, D.; Li, X.; Pawliszyn, J. Direct-immersion SPME in soy milk for pesticide analysis at trace levels by means of a matrix-compatible coating. Talanta 2020, 211, 120746. [Google Scholar] [CrossRef]
- Alamgir Zaman Chowdhury, M.; Fakhruddin, A.N.M.; Nazrul Islam, M.; Moniruzzaman, M.; Gan, S.H.; Khorshed Alam, M. Detection of the residues of nineteen pesticides in fresh vegetable samples using gas chromatography–mass spectrometry. Food Control 2013, 34, 457–465. [Google Scholar] [CrossRef]
- Peng, X.-X.; Bao, G.-M.; Zhong, Y.-F.; Zhang, L.; Zeng, K.-B.; He, J.-X.; Xiao, W.; Xia, Y.-F.; Fan, Q.; Yuan, H.-Q. Highly sensitive and rapid detection of thiabendazole residues in oranges based on a luminescent Tb3+-functionalized MOF. Food Chem. 2021, 343, 128504. [Google Scholar] [CrossRef]
- Fan, L.; Tong, C.; Cao, Y.; Long, R.; Wei, Q.; Wang, F.; Tong, X.; Shi, S.; Guo, Y. Highly specific esterase activated AIE plus ESIPT probe for sensitive ratiometric detection of carbaryl. Talanta 2022, 246, 123517. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Mehedi Hassan, M.; Wang, J.; Wei, W.; Zou, M.; Ouyang, Q.; Chen, Q. Investigation of nonlinear relationship of surface enhanced Raman scattering signal for robust prediction of thiabendazole in apple. Food Chem. 2021, 339, 127843. [Google Scholar] [CrossRef] [PubMed]
- Cheng, F.; Liao, X.; Huang, Z.; Xu, L.; Zhou, Y.; Zhang, X. Highly Sensitive Detection of Thiabendazole Residues in Food Samples Based on Multiwall Carbon Nanotubes Decorated Two-Dimensional Layered Molybdenum Disulfide. Food Anal. Methods 2020, 13, 811–822. [Google Scholar] [CrossRef]
- Dorozhko, E.V.; Gashevskay, A.S.; Korotkova, E.I.; Barek, J.; Vyskocil, V.; Eremin, S.A.; Galunin, E.V.; Saqib, M. A copper nanoparticle-based electrochemical immunosensor for carbaryl detection. Talanta 2021, 228, 122174. [Google Scholar] [CrossRef]
- Zhu, D.; Ren, X.; Wei, L.; Cao, X.; Ge, Y.; Liu, H.; Li, J. Collaborative analysis on difference of apple fruits flavour using electronic nose and electronic tongue. Sci. Hortic. 2020, 260, 108879. [Google Scholar] [CrossRef]
- Slavin, J.L.; Lloyd, B. Health benefits of fruits and vegetables. Adv. Nutr. 2012, 3, 506–516. [Google Scholar] [CrossRef]
- Muroski, A.R.; Booksh, K.S.; Myrick, M.J.A.C. Single-measurement excitation/emission matrix spectrofluorometer for determination of hydrocarbons in ocean water. 1. Instrumentation and background correction. Anal. Chem. 1996, 68, 3534–3538. [Google Scholar] [CrossRef]
- Booksh, K.S.; Muroski, A.R.; Myrick, M.J.A.C. Single-measurement excitation/emission matrix spectrofluorometer for determination of hydrocarbons in ocean water. 2. Calibration and quantitation of naphthalene and styrene. Anal. Chem. 1996, 68, 3539–3544. [Google Scholar] [CrossRef]
- Olivieri, A.C. Analytical Advantages of Multivariate Data Processing. One, Two, Three, Infinity? Anal. Chem. 2008, 80, 5713–5720. [Google Scholar] [CrossRef]
- Wu, H.-L.; Kang, C.; Li, Y.; Yu, R.-Q. Chapter 4—Practical Analytical Applications of Multiway Calibration Methods Based on Alternating Multilinear Decomposition. In Data Handling in Science and Technology; de la Peña, A.M., Goicoechea, H.C., Escandar, G.M., Olivieri, A.C., Eds.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 29, pp. 167–246. [Google Scholar]
- Kang, C.; Wu, H.-L.; Yu, Y.-J.; Liu, Y.-J.; Zhang, S.-R.; Zhang, X.-H.; Yu, R.-Q. An alternative quadrilinear decomposition algorithm for four-way calibration with application to analysis of four-way fluorescence excitation–emission–pH data array. Anal. Chim. Acta 2013, 758, 45–57. [Google Scholar] [CrossRef] [PubMed]
- Qing, X.-D.; Wu, H.-L.; Yan, X.-F.; Li, Y.; Ouyang, L.-Q.; Nie, C.-C.; Yu, R.-Q. Development of a novel alternating quadrilinear decomposition algorithm for the kinetic analysis of four-way room-temperature phosphorescence data. Chemom. Intell. Lab. Syst. 2014, 132, 8–17. [Google Scholar] [CrossRef]
- Xia, A.L.; Wu, H.-L.; Zhu, S.-H.; Han, Q.-J.; Zhang, Y.; Yu, R.-Q. Determination of Psoralen in Human Plasma Using Excitation-Emission Matrix Fluorescence Coupled to Second-Order Calibration. Anal. Sci. 2008, 24, 1171–1176. [Google Scholar] [CrossRef]
- Olivieri, A.C.; Faber, N.M. Standard error of prediction in parallel factor analysis of three-way data. Chemom. Intell. Lab. Syst. 2004, 70, 75–82. [Google Scholar] [CrossRef]
- Olivieri, A.C. Computing Sensitivity and Selectivity in Parallel Factor Analysis and Related Multiway Techniques: The Need for Further Developments in Net Analyte Signal Theory. Anal. Chem. 2005, 77, 4936–4946. [Google Scholar] [CrossRef]
- Olivieri, A.C.; Faber, N.M. A closed-form expression for computing the sensitivity in second-order bilinear calibration. J. Chemom. 2005, 19, 583–592. [Google Scholar] [CrossRef]
- Olivieri, A.C.; Faber, K. New Developments for the Sensitivity Estimation in Four-Way Calibration with the Quadrilinear Parallel Factor Model. Anal. Chem. 2012, 84, 186–193. [Google Scholar] [CrossRef]
- Messick, N.J.; Kalivas, J.H.; Lang, P.M. Selectivity and Related Measures for nth-Order Data. Anal. Chem. 1996, 68, 1572–1579. [Google Scholar] [CrossRef]
- Olivieri, A.C. Analytical Figures of Merit: From Univariate to Multiway Calibration. Chem. Rev. 2014, 114, 5358–5378. [Google Scholar] [CrossRef]
- Bro, R.; Kiers, H.A.L. A new efficient method for determining the number of components in PARAFAC models. J. Chemom. 2003, 17, 274–286. [Google Scholar] [CrossRef]
- Bahram, M.; Bro, R.; Stedmon, C.; Afkhami, A. Handling of Rayleigh and Raman scatter for PARAFAC modeling of fluorescence data using interpolation. J. Chemom. 2006, 20, 99–105. [Google Scholar] [CrossRef]
| AQLD | ANWE | |||||
|---|---|---|---|---|---|---|
| Added Concentration (ng mL−1) | Predicted Concentration (ng mL−1) | Predicted Concentration (ng mL−1) | ||||
| [Spiked Recovery (%)] | [Spiked Recovery (%)] | |||||
| Sample | TBZ | CAR | TBZ | CAR | TBZ | CAR |
| SP01 | 112.5 | 200.0 | 112.8 [100.3] a | 191.6 [95.8] | 109.5 [97.3] | 194.4 [97.2] |
| SP02 | 315.0 | 140.0 | 323.2 [102.6] | 132.4 [94.6] | 294.9 [93.6] | 117.9 [84.2] |
| SP03 | 450.0 | 50.0 | 463.1 [102.9] | 52.4 [104.8] | 440.2 [97.8] | 51.8 [103.5] |
| AVG ± S.D.(%) b | 101.9 ± 1.4 | 98.4 ± 5.6 | 96.2 ± 2.3 | 95.0 ± 9.8 | ||
| RMSEP (ng mL−1) | 9.5 | 6.5 | 12.4 | 13.05 | ||
| Performance Parameter | AQLD | ANWE | ||
|---|---|---|---|---|
| TBZ | CAR | TBZ | CAR | |
| r | 0.9997 | 0.9991 | 0.9949 | 0.9958 |
| LOD (ng mL−1) | 0.13 | 0.18 | 0.19 | 0.36 |
| LOQ (ng mL−1) | 0.38 | 0.56 | 0.57 | 1.08 |
| SEN (mL ng−1) | 51.53 | 60.76 | 25.70 | 14.76 |
| SEL | 0.42 | 0.47 | 0.45 | 0.22 |
| Intra-day a (RSD%) | 0.83 | 0.54 | 1.18 | 0.47 |
| Inter-day b (RSD%) | 1.81 | 4.57 | 2.04 | 0.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, H.; Wu, H.; Wang, T.; Wang, X.; Yu, R. Multi-Way Fluorescence Technique Combined with Four-Way Calibration for the Determination of Thiabendazole and Carbaryl in Apple. Chemosensors 2025, 13, 107. https://doi.org/10.3390/chemosensors13030107
Chang H, Wu H, Wang T, Wang X, Yu R. Multi-Way Fluorescence Technique Combined with Four-Way Calibration for the Determination of Thiabendazole and Carbaryl in Apple. Chemosensors. 2025; 13(3):107. https://doi.org/10.3390/chemosensors13030107
Chicago/Turabian StyleChang, Haiyan, Hailong Wu, Tong Wang, Xiaozhi Wang, and Ruqin Yu. 2025. "Multi-Way Fluorescence Technique Combined with Four-Way Calibration for the Determination of Thiabendazole and Carbaryl in Apple" Chemosensors 13, no. 3: 107. https://doi.org/10.3390/chemosensors13030107
APA StyleChang, H., Wu, H., Wang, T., Wang, X., & Yu, R. (2025). Multi-Way Fluorescence Technique Combined with Four-Way Calibration for the Determination of Thiabendazole and Carbaryl in Apple. Chemosensors, 13(3), 107. https://doi.org/10.3390/chemosensors13030107







