Stochastic Claims Reserve in the Healthcare System: A Methodology Applied to Italian Data

Abstract

One of the challenges in the healthcare sector is making accurate forecasts across insurance years for claims reserve. Healthcare claims present huge variability and heterogeneity influenced by random decisions of the courts and intrinsic characteristics of the damaged parties, which makes traditional methods for estimating reserves inadequate. We propose a new methodology to estimate claim reserves in the healthcare insurance system based on generalized linear models using the Overdispersed Poisson distribution function. In this context, we developed a method to estimate the parameters of the quasi-likelihood function using a Gauss–Newton algorithm optimized through a genetic algorithm. The genetic algorithm plays a crucial role in glimpsing the position of the global minimum to ensure a correct convergence of the Gauss–Newton method, where the choice of the initial guess is fundamental. This methodology is applied as a case study to the healthcare system of the Tuscany region. The results were validated by comparing them with state-of-the-art measurement of the confidence intervals of the Overdispersed Poisson distribution parameters with better outcomes. Hence, local healthcare authorities could use the proposed and improved methodology to allocate resources dedicated to healthcare and global management.

1. Introduction

The term “medical malpractice” is intended to define those damages (tending to be biological, but also in perspective moral) arising from errors in the health sector of the practitioner and closely related to clinical activity in the strict sense USI (2000). This damage is closely correlated with civil liability in healthcare, which profoundly impacts the economy and society. Indeed, healthcare expenditure was estimated for 2019 at 8.7% of the national Gross Domestic Product (GDP), which is below the EU average of 9.9% OECD (2021). It should be noted that approximately 15% of hospital expenditure in high-income countries is used to correct complications of care and patient harm OECD (2018). However, in these countries which have efficient healthcare systems, adverse events seem to be progressively decreasing. It is estimated that 10% of patients experience an adverse event during medical–surgical treatment resulting in a malpractice injury. The most frequently reported types of adverse events, on a global level, undoubtedly include surgical procedures—with significant peaks among orthopaedics and traumatology, general surgery, and obstetrics and gynaecology Mushinski et al. (2022)—diagnostic errors, accidental falls, and the contraction of nosocomial infections, in reference to which specific investigation would be due. In Italy, no official national published statistics on medical adverse events and/or claims exist. However, some regions have published independent reports on hospital claims in the past, showing that most complaints are received in the above-mentioned operational areas Bertoli and Grembi (2018); Grembi and Garoupa (2013). When an adverse event occurs, Italian healthcare liability is imposed on healthcare organizations and, potentially, the healthcare professionals who committed the error. Public and private healthcare institutions are liable with contractual liability for the behaviour of healthcare professionals whose services they employ, with reference to professionals, including researchers, under any contract of the National Health Service. For this reason, public and private health and social care facilities must be provided with insurance coverage or other similar measures for third parties’ liability and that of employees. Other measures include the possibility for organizations to utilize cover funds from internal provisions to cover all or part of the health liability risk. The money to pay insurance premiums or to provide coverage funds is derived from the national health fund, which is then distributed to different regions. In turn, they may distribute the money to their health organizations or centralize the resources to shield against claims. Therefore, insurance or self-insurance coverage must be provided to be operative in the event of a medical malpractice claim. However, given the significant fluctuation in medical malpractice claims, the challenge arises regarding how much money should be allocated annually to guarantee the fulfilment of financial commitments and the payment of compensation for damages. In this study, the authors aim to address the following research questions: (1) Which models are appropriate for estimating claims reserves in the healthcare sector? (2) How can the models be adapted to enhance the state-of-the-art (SoA) models to fit our specific context?

The proposed work can be positioned in the context described above to build a solid procedure to estimate and manage the claims reserve. The treatment developed here will be technical because the authors want to provide a complete mathematical and computational tool for the healthcare system to allocate appropriate resources. The paper is organized as follows: (1) the first part is focused on the mathematical background behind the GLM to underline the foundation of the applied methodology, jointly with the definition of the quasi-likelihood function to model the response variables, as well as the algorithms to locate the best parameters that maximize these functions and the corresponding errors associated to the parameters of the quasi-likelihood function; (2) the second part of the work is focused on the validation of the developed models by providing a detailed comparison with the present SoA, based on the confidence intervals of the parameters that maximize the quasi-likelihood function; (3) in the third part, the authors illustrate an application of the developed methodology to the disposable data coming from the Tuscany region1 to show its capability compared to the available SoA; (4) finally, a discussion and conclusions are provided with improvements and future development. All the numerical analyses and computations described in this work have been implemented with the Matlab software package (R2022b release).

2. Structure and Main Ideas

The generalized linear model (GLM) has become a significant reality in claims reserve analysis in the last few years England and Verrall (1999, 2002); Kendall and Stuart (1967); Larsen (2007); Verrall (2000). The present work supplies the context of their forecast and applicability. The authors found the necessity, at first, to better describe and elucidate the mathematical background of the subject and to assemble a coherent and well-defined model. In this context, the authors contributed to creating a new framework that could provide adequate and complete results in claims reserve.

The basis to estimate the claims reserve is through the construction of Run-Off triangles Schmidt (2006) that estimate the total paid amount of claims incurred that are not yet reported to the insurance agency. A common methodology to estimate claims reserve is the Chain-Ladder (CL) method Hindley (2017); Schmidt (2012); Verrall (1991). The CL method aims to approximate the value of claims reserves that have been incurred but not yet reported and to predict the ultimate loss amounts in general insurance. The fundamental assumption on which the CL is based is that the patterns observed in historical loss development must hold for future loss development. The previous assumption represents one of the limitations of the CL and other deterministic methods because they do not extrapolate the tail factors England and Verrall (2002) to increase the prediction performance for the paid amount. Several modifications of the CL have been proposed in the literature to improve the prediction of the claims reserve Hess and Schmidt (2002); Verdonck et al. (2009), and various stochastic claim reserving models have been developed for general insurance to extrapolate the tail factors.

The employment of stochastic models replicates the conventional reserve estimates produced by the CL methods, including parametric curves and smoothing techniques to reshape the Run-Off triangles, enabling estimation of the tail factors through extrapolation. Stochastic models offer a significant benefit in providing precision measures for claims reserve, particularly emphasising the mean squared error of the prediction. However, understanding the stochastic distribution function of the claims reserve outcome is crucial to provide good prediction performance Renshaw and Verrall (1998). In this regard, the GLM has become, in the last years, a robust stochastic methodology for predicting claims reserve Hindley (2017); Nelder and Wedderburn (1972). The GLM represents a wide range of models that allow the definition and estimation of parameters by maximizing the likelihood function Nelder and Wedderburn (1972). In this framework, the likelihood function is employed to evaluate the goodness of fit for a distribution that belongs to the exponential family of random variables. To define the likelihood function, one must specify the analytical form of the response variable distribution. In the works of Wedderburn (1974, 1976), the last assumption has been overcome by introducing the quasi-likelihood function, which only needs the definition of the mean–variance relation of the response variable without any assumption on the shape of its distribution. Following the work of Strascia and Tripodi (2018), the authors assume a logarithmic mean–variance relation, which provides the well-known Overdispersed Poisson (ODP) distribution model. The maximization of the ODP quasi-likelihood function is performed using the Gauss–Newton (GN) algorithm Fletcher (2000); Strascia and Tripodi (2018). This methodology has several benefits, but at the same time, it presents some crucial weaknesses that need to be considered and addressed.

Concerning the SoA, we propose a methodology to compute parameters in the framework of the GLM, which allows making good predictions for expectation value and errors without increased computational costs. Compared with other methods proposed in the SoA, our approach allows forecasting the claims reserve values and the corresponding standard errors by optimizing two different residuals. Consequently, it gives a better overview of the claims reserve in the healthcare sector, where the strong aleatory and peculiar nature of claims’ lifespan needs particular attention. The authors performed specific tests on different data-sets to validate the developed model. Firstly, the authors conducted a validation of the developed model to estimate the claims reserve on the data-sets present in the SoA, particularly from Strascia and Tripodi (2018) and Verdonck et al. (2009). These validation tests helped to understand whether the developed model outperforms the ones in the literature. Subsequently, the developed model was tested in the health insurance claims database of the Tuscany region (Italy), which covers the period from 2010 to 2021. Dealing with this kind of database in the healthcare system is extremely rare and represents a flaw in estimating the claims reserve.

3. Theoretical Background

In this Section, the authors present the theoretical background for estimating claims reserve. Section 3.1 describes the CL approach and how to construct the Run-Off triangles that represent the applied basis of the developed methodology. Section 3.2 provides an introduction to GLM to understand the context in which our methodology is applied. Section 3.3 introduces the definition of the quasi-likelihood function to make predictions of the response variable defined in the GLM framework. Section 3.4 describes the implementation of the Gauss–Newton (GN) algorithm that maximizes the quasi-likelihood function and its limitation. Section 3.5 depicts the deployment of the genetic algorithm (GA), which overcomes the limitation problems of the GN algorithm, to provide consistent results and predictions. Finally, Section 3.6 provides a workflow for how to estimate the errors of the quasi-likelihood function.

3.1. Run-Off Triangles and Chain-Ladder Approach

The characteristic feature of claims is their recognizable time lag from the point of incidence until they are reported to the insurance agency. As the reported claims are documented yearly, the insurance agency will face a significant amount of claims in a given calendar year, where each of them has a typical time delay. In this context, Run-Off triangles Schmidt (2006) estimate the total paid amount of claims incurred during a period (e.g., fiscal year) that are not yet reported, and they help insurance agencies to estimate the amount of money that they will need to set aside to cover future claims that have already been incurred but have not been reported. For this reason, a reserve must be set aside for this purpose.

The Run-Off triangle is divided into cells where the row corresponds to the ith “incurred” year with $i\in [1,I]$, i.e., the year in which the claims happen, and the column corresponds to the jth “progression” year with $j\in [0,J]$, i.e., the delayed year of the payments from when the claims have been incurred. Each cell of the Run-Off triangle indicates the total paid amount $y_{i,j}$ for claims that have been incurred in the ith year and effectively paid in the jth year. In the following,

Table 1. Example of Run-Off triangle. The variable $y_{i,j}$ indicates the paid amount relative to a claim that has occurred in the ith incurred year where the effective payment has been delayed in the jth year.

$\mathit{i}/\mathit{j}$	0	1	…	j	…	$\mathit{J}-1$	J
1	$y_{1,0}$	$y_{1,1}$	…	$y_{1,j}$	…	$y_{1,J-1}$	$y_{1,J}$
2	$y_{2,0}$	$y_{2,1}$	…	$y_{2,j}$	…	$y_{2,J-1}$
⋮	⋮	⋮.		⋮
i	$y_{i,0}$	$y_{i,1}$	…	$y_{i,j}$
⋮	⋮	⋮
$I-1$	$y_{I-1,0}$	$y_{I-1,1}$
I	$y_{I,0}$

shows a representation of a Run-Off triangle.

The most common approach used to calculate the claims reserve is the CL approach. Considering the definition of the Run-Off triangle represented in Table 1, and according to Strascia and Tripodi (2018) and Schmidt (2006), the first step of the CL approach is the definition of a Run-Off triangle of the cumulative payments, which is shown in the following Equation (1):

$$C_{i,j}=\sum _{k=0}^j{y}_{i,k}$$

(1)

where the variable $C_{i,j}$ represents the cumulative payment concerning the incurred year i relative to the delayed year j. The idea behind the CL method is that the cumulative payments of two adjacent anti-duration years, i.e., the $y_{i,j-1}$ and $y_{i,j}$ year, are proportional to each other, barring an erratic component $ϵ$ with zero expectation value. Another vital assumption of the CL is that the system is not susceptible to structural changes over time. Therefore, the estimate of the ultimate cumulative paid ${\widehat{C}}_{i,J}$ is obtained through the dilation factors ${\widehat{f}}_j^{\left(t\right)}$ (called link-ratio), according to Equation (2):

$${\widehat{C}}_{i,J}^{\left(t\right)}=C_{i,t-i}\prod _{j=t-i}^{J-1}{\widehat{f}}_j^{\left(t\right)}$$

(2)

where the index $t\in [1,I]$ indicates the generic budget year, while the term ${\widehat{f}}_j^{\left(t\right)}$ represents the link-ratio which is defined through the following Equation (3):

$${\widehat{f}}_j^{\left(t\right)}={\displaystyle \frac{{\sum }_{k=1}^{t-j-1}{C}_{k,j+1}}{{\sum }_{k=1}^{t-j-1}{C}_{k,j}}}$$

(3)

Hence, given Equations (2) and (3), the CL method is able to estimate the claims reserve ${\widehat{R}}_i^{\left(t\right)}$ given by Equation (4):

$${\widehat{R}}_i^{\left(t\right)}={\widehat{C}}_{i,J}^{\left(t\right)}-C_{i,t-1}$$

(4)

In addition, in order to estimate the claims reserve per year, the stochastic approach allows the calculation of the complete claims reserve, which predicts the total payment amount for all the incurred and delayed years. In the following Sections, the authors will show the procedure to develop the stochastic model with the related theoretical approach to estimate the entire claims reserve, including the associated errors.

3.2. Generalized Linear Model

The GLM was introduced in the work of Nelder and Wedderburn (1972) as a methodology to unify and generalize various statistical methods such as linear regression, logistic regression, etc. In ordinary linear regression, given a random variable Y, called response variable, one can assume that it is defined as a linear combination of some explicative variables or predictors with small variation $\epsilon$ with expectations value $E\left[\epsilon \right]=0$ and variance var$\left[\epsilon \right]={\sigma }^2$. In this framework, the estimation of Y became an algebraic problem of inverting matrices, but despite the simplicity of this methodology, this method has strong limitations, specifically when:

• The relation between the response variable and the explicative variables is not linear;
• The explicative variables Y do not take values from the interval $(-\infty ,\infty )$;
• The variance ${\sigma }^2$ is not constant;
• It is not possible to assume the response variable Y following the normal distribution.

The GLM allows the user to overcome previous limitations by expanding the sets of applicability of the standard linear model and has became a common tool in statistical analysis and prediction theory. Indeed, the GLM needs a unique starting hypothesis about the behaviour of the probability distribution function (PDF) of Y, which is only required to belong to the class of exponential family PDF, which includes Normal, Poisson, Binomial, Gamma, and Inverse Gaussian distribution. Moreover, if more response variables (Y) exist, they must be stochastically independent. Therefore, in general terms, the authors consider a response variable that follows a PDF parameterized by $\beta$ as defined in Equation (5):

$$f(y;\beta ,\varphi )=e^{\alpha \left(\varphi \right)\left[y\beta -g\left(\beta \right)+h\left(y\right)\right]+\alpha (\varphi ,y)}$$

(5)

where y stands for a single realization of Y, while the variable $\varphi$ represents the nuisance parameter2 and $\alpha \left(\varphi \right)$ is a positive definite function. In order to define the moments of the distributions, we introduce the likelihood $L\left(\beta \right|y)$ and the log-likelihood $\mathcal{L}\left(\beta \right|y)$ functions as shown in Equation (6). In the following, the single realization (y) of the response variable (Y) refers to incremental payments as shown in Table 1.

$$L\left(\beta \right|y)=ln\mathcal{L}\left(\beta \right|y)=ln\prod _{i=1}^{m}f(y_i;\beta ,\varphi )=\sum _{i=1}^{m}f(y_i;\beta ,\varphi )$$

(6)

For the sake of simplicity, the authors moved from a matrix-like notation to a vector-like notation (with a single index). Therefore, the vectorial response variable $y_i$, which is in one-to-one correspondence with the previous $y_{i,j}$, is defined as in the following

Table 2. One-to-one correspondence between matrix-like and vector-like notation.

	Response Variable	Entries
Matrix-like Notation (Table 1)	$y_{i,j}$	$y_{1,1},y_{1,2},\dots ,y_{k,l},\dots ,y_{m,n}$
Vector-like Notation	$y_i$	$y_1,y_2,\dots ,y_k,\dots ,y_m$

:

Based on the results of Kendall and Stuart (1967), it is possible to derive two crucial properties of the log-likelihood function shown in Equation (7):

$$\begin{array}{cc}\hfill E\left[{\displaystyle \frac{\partial \mathcal{L}}{\partial \beta }}\right]& =0\hfill \\ \hfill E\left[{\displaystyle \frac{{\partial }^2\mathcal{L}}{\partial {\beta }^2}}\right]& =-E{\left[{\displaystyle \frac{\partial \mathcal{L}}{\partial \beta }}\right]}^2\hfill \end{array}$$

(7)

which provides the statement shown in Equation (8) for the generic exponential function (Equation (6)):

$$\begin{array}{cc}\hfill E\left[{\displaystyle \frac{\partial \mathcal{L}}{\partial \beta }}\right]& =E\left[\alpha \left(\varphi \right)[y-g^{\prime }\left(\beta \right)]\right]=0\hfill \\ \hfill & \Rightarrow E\left[y\right]\equiv \mu =g^{\prime }\left(\beta \right)\hfill \end{array}$$

(8)

together with the quadratic expectation value:

$$\begin{array}{cc}\hfill E\left[{\displaystyle \frac{{\partial }^2\mathcal{L}}{\partial {\beta }^2}}\right]& =E[-\alpha \left(\varphi \right)g^{″}\left(\beta \right)]\hfill \\ \hfill & \Rightarrow E\left[\alpha \left(\varphi \right)g^{″}\left(\beta \right)\right]=E\left[{\alpha }^2\left(\varphi \right){(y-\mu )}^2\right]\hfill \end{array}$$

(9)

and hence,

$$g^{″}\left(\beta \right)=\alpha \left(\varphi \right)E\left[{(y-\mu )}^2\right]$$

(10)

which finally provides the expression for the variance of y (Equation (11)):

$$\alpha \left(\varphi \right)\mathrm{var}\left(y\right)=g^{″}\left(\beta \right)=V\left(\mu \right)$$

(11)

It is easy to prove that for a response variable Y normally distributed, the GLM reduces to the ordinary linear model.

3.3. Quasi-Likelihood Function

To make predictions and estimations concerning the response variables Y in the GLM frameworks, it is necessary at first to estimate parameters of the log-likelihood function, commonly with the least-squares method. This procedure has a substantial limitation: the necessity to make a forecast hypothesis on the specific shape of the distribution (Equation (6)). In the work of Wedderburn (1974), a new methodology was proposed introducing the so-called quasi-likelihood function, which only needs to fix the relationship between the first two moments of the distribution, so, mean and variance. The mean–variance relation is entirely defined by the link function (g) as shown in Equation (12).

$$\begin{array}{cc}\hfill \mathrm{var}\left(y\right)& ={\displaystyle \frac{1}{\alpha \left(\varphi \right)}}V\left(\mu \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\alpha \left(\varphi \right)}}{g}^{″}\left(\beta \right)\hfill \\ \hfill & ={\displaystyle \frac{1}{\alpha \left(\varphi \right)}}{g}^{″}\left({\left(g^{\prime }\right)}^{-1}\left(\mu \right)\right)\hfill \end{array}$$

(12)

In Equation (12), the term ${\left(g^{\prime }\right)}^{-1}$ represents the inverse function of the first derivative of the link function (g) according to Equation (8).

Furthermore, we will assume, without any lack of generality, an exponential link function. Our proposed model robustly represents the well-known GLM with Overdispersed Poisson distribution (ODP). It is possible to prove that the overall function $\alpha \left(\varphi \right)$ is proportional to the inverse of the nuisance parameter multiplied by a proportional constant representing a weight parameter relative to the single realization of Y. For the sake of simplicity, we will assume all the weights equal to unity. Therefore, Equation (12) can be written as indicated in Equation (13):

$$\mathrm{var}\left(y\right)=\varphi g^{″}\left({\left(g^{\prime }\right)}^{-1}\left(\mu \right)\right)$$

(13)

Consequently, for an exponential link function, the mean–variance relation is given by Equation (14):

$$E\left[y\right]=\mu ={\displaystyle \frac{1}{\varphi }}\mathrm{var}\left(y\right)=V\left(\mu \right)$$

(14)

Considering that $V\left(\mu \right)=\mu$ in Equation (14), the nuisance parameter is estimated by the Pearson statistics:

$$\varphi \equiv \widehat{\varphi }={\displaystyle \frac{1}{m-n}}\sum _{i=1}^m{\displaystyle \frac{{(y_i-{\mu }_i)}^2}{V\left({\mu }_i\right)}}⟹\varphi ={\displaystyle \frac{1}{m-n}}\sum _{i=1}^m{\displaystyle \frac{{(y_i-{\mu }_i)}^2}{{\mu }_i}}$$

(15)

where m is the number of observable data, n is the number of parameters of the quasi-likelihood function, and the difference $m-n$, indeed, represents the degree of freedom (DOF) of the system.

At this point, given the i-realization of the response variable Y, the quasi-likelihood function $K(y_i,{\mu }_i)$ is defined in Equation (16):

$${\displaystyle \frac{\partial K(y_i,{\mu }_i)}{\partial {\mu }_i}}={\displaystyle \frac{y_i-{\mu }_i}{\mathrm{var}\left(y_i\right)}}={\displaystyle \frac{y_i-{\mu }_i}{\varphi V\left({\mu }_i\right)}}$$

(16)

or equivalently employing its integral form (Equation (17)):

$$K(y_i,{\mu }_i)=\int {\displaystyle \frac{y_i-{\mu }_i^{\prime }}{\varphi V\left({\mu }_i^{\prime }\right)}}d{\mu }_i^{\prime }+c\left(y_i\right)$$

(17)

where the index i indicates the single observations. The variable $c\left(y_i\right)$ represents a function of $y_i$, which in the future will be omitted for simplicity. For a complete overview of the properties and theorems concerning the quasi-likelihood function, we refer to the work of Wedderburn (1974). Therefore, substituting Equation (14) into Equation (17) and integrating over the i-interval $[y_i,{\mu }_i]$, we obtain the following expression (Equation (18)) for the quasi-likelihood function of the ODP model:

$$\begin{array}{cc}\hfill K(y_i,{\mu }_i)={\int }_{y_i}^{{\mu }_i}{\displaystyle \frac{y_i-{\mu }_i^{\prime }}{\varphi V\left({\mu }_i^{\prime }\right)}}d{\mu }_i^{\prime }& ={\int }_{y_i}^{{\mu }_i}{\displaystyle \frac{y_i-{\mu }_i^{\prime }}{\varphi {\mu }_i^{\prime }}}d{\mu }_i^{\prime }\hfill \\ \hfill & ={\displaystyle \frac{1}{\varphi }}\left[y_{i}ln{\displaystyle \frac{{\mu }_i}{y_i}}-{\mu }_i+y_i\right]\hfill \end{array}$$

(18)

Finally, summing over the complete set of the Y realization, it is possible to obtain the complete quasi-likelihood function in terms of y, $\beta$, and $\varphi$:

$$K(y,\beta ,\varphi )={\displaystyle \frac{1}{\varphi }}\sum _{i=1}^m\left[y_{i}ln{\displaystyle \frac{{\mu }_i}{y_i}}-{\mu }_i+y_i\right]$$

(19)

At this point, in the quasi-likelihood analysis, to obtain correct predictions for the response variable, it is necessary to estimate the parameters which maximize the function $K(y_i,{\mu }_i)$. In this regard, the non-linear link function requires an iterative algorithm to solve the problem. The adopted solution to estimate the parameters which maximize the function $K(y_i,{\mu }_i)$ is the Gauss–Newton algorithm (GN). The following Section will present the GN iterative methodology to estimate the parameters that maximize the $K(y_i,{\mu }_i)$ function. For clarity, the variable ${\mu }_i$ will be indicated as ${\mu }_i\left(\beta \right)$ because it represents the model that contains the parameters $\beta$ that maximize the quasi-likelihood function. Additionally, the details of its convergence problem and a solution to this problem will be proposed for a better choice of initial guesses. In the following Sections, the authors will employ the vectorial notation for the $\beta$ parameters for completeness.

3.4. Gauss–Newton Algorithm

Taking $\mathit{\beta }=({\beta }_1,\cdots ,{\beta }_n)$ as the vector of parameters on which the response variable depends, to determine the ${\mathit{\beta }}^{*}$ vector that maximizes the quasi-likelihood function (see Equation (18)), we need to solve the following system of non-linear Equation (20):

$${\displaystyle \frac{\partial K(y_i,{\mu }_i\left(\mathit{\beta }\right))}{\partial {\beta }_k}}=0$$

(20)

An iterative algorithm is required to locate the kth parameters of the $\mathit{\beta }$ vector, where $k\in [1,n]$, that solve the non-linear equation system shown in Equation (20). Therefore, the GN algorithm has been deployed based on the guidelines provided in the work of Wedderburn (1974). Given a set of generic functions (called residuals) ${\left\{r_i\left(\mathit{\beta }\right)\right\}}_{i=1}^m$, the GN locates the set of ${\beta }_k$ parameters that minimize the function $S\left(\mathit{\beta }\right)$ defined in Equation (21):

$$S\left(\mathit{\beta }\right)=\sum _{i=1}^m{r}_i^2\left(\mathit{\beta }\right)$$

(21)

where the specific choice of the residual function $r_i\left(\mathit{\beta }\right)$ is crucial in the entire process of parameter estimation. Furthermore, the authors tested two different $r_i\left(\mathit{\beta }\right)$ functions, which we will define later, providing different results. Starting from the quasi-likelihood function $K(y_i,{\mu }_i\left(\mathit{\beta }\right))$, the Taylor expansion around the parameters $\mathit{\beta }$ is needed to minimize the function $S\left(\mathit{\beta }\right)$. Considering an expansion step $\mathit{\delta }$ given by Equation (22):

$$\mathit{\delta }={\mathit{\beta }}^{*}-\mathit{\beta }$$

(22)

The first-order Taylor expansion in $\mathit{\delta }$ can be written in Equation (23):

$$K(y_i,{\mu }_i\left({\mathit{\beta }}^{*}\right))=K(y_i,{\mu }_i\left(\mathit{\beta }\right))+\frac{\partial K(y_i,{\mu }_i\left(\mathit{\beta }\right))}{\partial \mathit{\beta }}{|}_{\mathit{\beta }}\mathit{\delta }+o\left({\mathit{\delta }}^2\right)$$

(23)

It is important to note that, because the function $K(y_i,{\mu }_i\left(\mathit{\beta }\right))$ is maximized by ${\mathit{\beta }}^{*}$, its first derivative in Equation (23) is null when $\mathit{\beta }={\mathit{\beta }}^{*}$; therefore, a maximization procedure must be developed to locate the ${\mathit{\delta }}^{*}$ parameters. The GN works directly on the function $S\left(\mathit{\beta }\right)$ defined in Equation (21), which has no triviality problem. Subsequently, it remains to define a consistent definition of the function $r_i\left(\mathit{\beta }\right)$ to start the optimization procedure properly and minimize the $S\left(\mathit{\beta }\right)$ function through the GN methodology. In this Section, we propose two different definitions of residuals $r_i\left(\mathit{\beta }\right)$, which allows us to work separately on forecasting the claims reserves and their corresponding standard errors. The two definitions are consistent with providing the best estimation for the reserves and trying to reduce the related CI.

The first formulation of the residuals, as characterised by Strascia and Tripodi (2018), concerns the direct optimization of the parameters inside the quasi-likelihood $K(y_i,{\mu }_i\left(\mathit{\beta }\right))$, and it is given by Equation (24):

$$r_i\left(\mathit{\beta }\right)=\frac{y_i}{\varphi }-K(y_i,{\mu }_i\left(\mathit{\beta }\right))⟹r_i\left(\mathit{\beta }\right)={\displaystyle \frac{1}{\varphi }}\left[{\mu }_i\left(\mathit{\beta }\right)-y_{i}ln{\displaystyle \frac{{\mu }_i\left(\mathit{\beta }\right)}{y_i}}\right]$$

(24)

The second formulation of the residuals, developed by the authors, concerns the optimization of the dispersion parameters ($\varphi$-see Equation (15)), and it is given by the Equation (25):

$$r_i\left(\mathit{\beta }\right)={\displaystyle \frac{y_i-{\mu }_i\left(\mathit{\beta }\right)}{\sqrt{{\mu }_i\left(\mathit{\beta }\right)}}}$$

(25)

Regarding the following steps, the authors will not use one of the previous definitions of residuals but will keep the discussion in general terms. The comparison of the two specific formulations of $r_i\left(\mathit{\beta }\right)$ (Equations (24) and (25)) will be discussed in Section 4 and Section 5, where the results related to comparison with the SoA, and the data from the Tuscany region are presented, respectively. The function $S\left(\mathit{\beta }\right)$ does not present triviality problems compared to the quasi-likelihood function. Therefore, the first-order Taylor expansion of Equation (21) can be performed in $\mathit{\delta }$ (see Equation (22)) around the initial point $\mathit{\beta }$ using a vectorial formalism which provides Equation (26):

$$\begin{array}{cc}\hfill S\left({\mathit{\beta }}^{*}\right)& =S\left(\mathit{\beta }\right)+{\displaystyle \frac{\partial S\left(\mathit{\beta }\right)}{\partial \mathit{\beta }}}{|}_{\mathit{\beta }}\mathit{\delta }+o\left({\mathit{\delta }}^2\right)\hfill \\ \hfill & =S\left(\mathit{\beta }\right)+2{\mathit{r}}^T\left(\mathit{\beta }\right)·{\displaystyle \frac{\partial \mathit{r}\left(\mathit{\beta }\right)}{\partial \mathit{\beta }}}{|}_{\mathit{\beta }}\mathit{\delta }+o\left({\mathit{\delta }}^2\right)\hfill \end{array}$$

(26)

The first derivative in Equation (26) represents the Jacobian matrix of the residuals computed in the initial point $\mathit{\beta }$. More precisely, the first derivative appearing in Equation (26) depends on the definition of residuals (see Equations (24) and (25)). Therefore, the single elements of the Jacobian matrix can be defined by the following Equations (27) and (28):

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial r_i\left(\mathit{\beta }\right)}{\partial {\beta }_k}}{|}_{\mathit{\beta }}& =-{\displaystyle \frac{1}{\varphi }}{\displaystyle \frac{\partial {\mu }_i\left(\mathit{\beta }\right)}{\partial {\beta }_k}}{|}_{\mathit{\beta }}{\displaystyle \frac{y_i-{\mu }_i\left(\mathit{\beta }\right)}{{\mu }_i\left(\mathit{\beta }\right)}}\equiv J_{ik}\left(\mathit{\beta }\right)(\mathrm{see}\mathrm{Equation}(24))\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial r_i\left(\mathit{\beta }\right)}{\partial {\beta }_k}}{|}_{\mathit{\beta }}& =-{\displaystyle \frac{1}{2}}{\displaystyle \frac{\partial {\mu }_i\left(\mathit{\beta }\right)}{\partial {\beta }_k}}{|}_{\mathit{\beta }}{\displaystyle \frac{y_i+{\mu }_i\left(\mathit{\beta }\right)}{{\mu }_i{\left(\mathit{\beta }\right)}^{\frac{3}{2}}}}\equiv J_{ik}\left(\mathit{\beta }\right)(\mathrm{see}\mathrm{Equation}(25))\hfill \end{array}$$

(28)

The term appearing on the left-hand side of Equations (27) and (28) represents the derivative of the ith-residual $r_i\left(\mathit{\beta }\right)$ space with respect to every ${\beta }_k$-parameter. The variable $J_{ik}\left(\mathit{\beta }\right)$ appearing on the right-hand side of Equations (27) and (28) represents the i-row and k-column of the Jacobian matrix defined in Equation (26); thus, the Jacobian matrix has a dimension of $m\times n$ where m is the number of residuals and n represents the number of parameters (i.e., the length of the $\mathit{\beta }$ vector). At this step, the previous Taylor expansion shown in Equation (26) can be rewritten as follows (Equation (29)):

$$\begin{array}{cc}\hfill S\left({\mathit{\beta }}^{*}\right)& =S\left(\mathit{\beta }\right)+2{\mathit{r}}^T\left(\mathit{\beta }\right)·\mathit{J}\left(\mathit{\beta }\right)·\mathit{\delta }+o\left({\mathit{\delta }}^2\right)\hfill \\ \hfill & ={\mathit{r}}^T\left(\mathit{\beta }\right)·\mathit{r}\left(\mathit{\beta }\right)+2{\mathit{r}}^T\left(\mathit{\beta }\right)·\mathit{J}\left(\mathit{\beta }\right)·\mathit{\delta }+o\left({\mathit{\delta }}^2\right)\hfill \end{array}$$

(29)

The term $\mathit{J}\left(\mathit{\beta }\right)$ appearing in Equation (29) represents the Jacobian matrix in a vectorial formalism computed in the initial point $\mathit{\beta }$. The variable $S\left(\mathit{\beta }\right)$ in Equation (29) is expressed by performing the dot product between the residuals $\mathit{r}\left(\mathit{\beta }\right)$ and its vectorial transpose. For the sake of simplicity, the variables $\mathit{J}\left(\mathit{\beta }\right)$ and $\mathit{r}\left(\mathit{\beta }\right)$ will be indicated as $\mathit{J}$ and $\mathit{r}$, respectively. At this point, it is possible to compute the gradient of the $S\left(\mathit{\beta }\right)$ function in the stationary point ${\mathit{\beta }}^{*}$ as it appears in Equation (29):

$${\displaystyle \frac{\partial S\left(\mathit{\beta }\right)}{\partial \mathit{\beta }}}{|}_{{\mathit{\beta }}^{*}}=2{\mathit{J}}^T\mathit{r}+2{\mathit{J}}^T\mathit{J}\mathit{\delta }+2{\mathit{r}}^T{\displaystyle \frac{\partial \mathit{J}}{\partial \mathit{\beta }}}{|}_{\mathit{\beta }}\mathit{\delta }$$

(30)

Since the gradient of $S\left(\mathit{\beta }\right)$ is computed in the stationary point ${\mathit{\beta }}^{*}$, the derivatives of this gradient are null. Additionally, Equation (30) can be further simplified by neglecting the term containing the derivative of the Jacobian matrix. Therefore, Equation (30) can be rewritten as follows:

$${\displaystyle \frac{\partial S\left(\mathit{\beta }\right)}{\partial \mathit{\beta }}}{|}_{{\mathit{\beta }}^{*}}=2{\mathit{J}}^T\mathit{r}+2{\mathit{J}}^T\mathit{J}\mathit{\delta }=0$$

(31)

Therefore, the $\mathit{\delta }$ can be recalculated as a function of ${\mathit{\beta }}^{*}$ (see Equation (22)) as follows:

$$\mathit{\delta }=-{\left({\mathit{J}}^T\mathit{J}\right)}^{-1}{\mathit{J}}^T\mathit{r}⟹{\mathit{\beta }}^{*}=\mathit{\beta }-{\left({\mathit{J}}^T\mathit{J}\right)}^{-1}{\mathit{J}}^T\mathit{r}$$

(32)

In practice, the GN algorithm computes a ${\mathit{\beta }}^{\left(s\right)}$ value at every iterative step (s) starting from an initial guess of ${\mathit{\beta }}^{\left(0\right)}$. Therefore, the ${\mathit{\delta }}^{\left(s\right)}$ value is calculated using Equation (33):

$${\mathit{\delta }}^{\left(s\right)}=-{\left({\mathit{J}}^T\left({\mathit{\beta }}^{\left(s\right)}\right)·\mathit{J}\left({\mathit{\beta }}^{\left(s\right)}\right)\right)}^{-1}{\mathit{J}}^T\left({\mathit{\beta }}^{\left(s\right)}\right)·\mathit{r}\left({\mathit{\beta }}^{\left(s\right)}\right)$$

(33)

The iterative procedure described in Equation (33) is carried on until the following condition is verified (Equation (34)):

$$∥{\mathit{\delta }}^{\left(s\right)}∥\equiv ∥{\mathit{\beta }}^{(s+1)}-{\mathit{\beta }}^{\left(s\right)}∥<ϵ$$

(34)

where the variable $ϵ$ represents an arbitrary user-defined tolerance which the GN algorithm must reach to stop the iterations. At this point, the GN algorithm has found the $\mathit{\beta }$ parameters which minimize the function $S\left(\mathit{\beta }\right)$ and therefore, the final value of $\mathit{\beta }$ is given as follows (Equation (35)):

$${\mathit{\beta }}^{*}\equiv {\mathit{\beta }}^{(s+1)}={\mathit{\beta }}^{\left(s\right)}-{\left({\mathit{J}}^T\left({\mathit{\beta }}^{\left(s\right)}\right)·\mathit{J}\left({\mathit{\beta }}^{\left(s\right)}\right)\right)}^{-1}{\mathit{J}}^T\left({\mathit{\beta }}^{\left(s\right)}\right)·\mathit{r}\left({\mathit{\beta }}^{\left(s\right)}\right)$$

(35)

The described procedure represents an iterative methodology to locate the stationary point that maximizes the quasi-likelihood function $K(y_i,{\mu }_i\left(\mathit{\beta }\right))$, and it can be iterated until the $∥\mathit{\delta }∥$ reaches an arbitrary tolerance value ($ϵ$ = 10⁻¹⁵) defined by the user. For each step of the iterative method, the $\mathit{\beta }$ is updated closer to the value that minimizes the $S\left(\mathit{\beta }\right)$ function. The choice of a good initial guess for $\mathit{\beta }$ is a crucial point for the iterative GN method to have success in locating the global minimum of the $S\left(\mathit{\beta }\right)$ function. However, estimating a good initial guess of the multi-parametric function $S\left(\mathit{\beta }\right)$ to force the convergence of the GN method to a global minimum requires additional concerns and tools that must be addressed.

3.4.1. The Hessian Modification

The convergence of the GN algorithm (Equation (35)) is not guaranteed for the residuals defined in Equations (24) and (25). The main reason that the GN algorithm fails to reach the convergence is due to the approximation introduced in Equation (31) where the derivative of the Jacobian matrix ($\mathit{J}$) with respect to $\mathit{\beta }$ is ignored. In order to be able to apply Equation (35), the following approximation must hold:

$$\left|{\mathit{J}}^T\mathit{J}\right|\gg \left|{\mathit{r}}^T{\displaystyle \frac{\partial \mathit{J}}{\partial \mathit{\beta }}}\right|$$

(36)

In order to expect the convergence of the GN algorithm using Equation (35), the approximation highlighted in Equation (36) must be valid in one of the two cases: (1) the residuals $\mathit{r}\left(\mathit{\beta }\right)$ are small compared to the derivatives of the Jacobian ($\partial \mathit{J}/\partial \mathit{\beta }$) around the stationary point ${\mathit{\beta }}^{*}$; (2) the residuals $\mathit{r}\left(\mathit{\beta }\right)$ are blandly non-linear in such a way that the derivatives of the Jacobian are negligible Nocedal and Wright (2006). Therefore, in the case for which the approximation (36) cannot hold, the key equation of the GN algorithm (Equation (35)) must be modified. Starting from Equation (30), it can be rearranged in the following equation:

$$\begin{array}{cc}\hfill {\displaystyle \frac{\partial S\left(\mathit{\beta }\right)}{\partial \mathit{\beta }}}{|}_{{\mathit{\beta }}^{*}}& =2{\mathit{J}}^T\mathit{r}+2\left[{\mathit{J}}^T\mathit{J}+2{\mathit{r}}^T{\displaystyle \frac{\partial \mathit{J}}{\partial \mathit{\beta }}}{|}_{\mathit{\beta }}\right]·\mathit{\delta }\hfill \\ \hfill \nabla S\left({\mathit{\beta }}^{*}\right)& =\nabla S\left(\mathit{\beta }\right)+\mathit{H}\left(S\left(\mathit{\beta }\right)\right)·\mathit{\delta }\hfill \end{array}$$

(37)

The variable $\nabla S\left(\mathit{\beta }\right)$ in Equation (37) represents the gradient of the function $S\left(\mathit{\beta }\right)$ (see Equation (21)) computed in the initial point $\mathit{\beta }$; the term $\mathit{H}\left(S\left(\mathit{\beta }\right)\right)$ indicates the Hessian of the function $S\left(\mathit{\beta }\right)$ computed in the initial point $\mathit{\beta }$. The Hessian is a matrix with a dimension of $n\times n$ where n represents the number of parameters (i.e., the length of the $\mathit{\beta }$ vector), where each element of this matrix contains the second derivatives of the function $S\left(\mathit{\beta }\right)$. For simplicity, the gradient $\nabla S\left(\mathit{\beta }\right)$ will be indicated as $\mathit{g}$, and the Hessian $\mathit{H}\left(S\left(\mathit{\beta }\right)\right)$ will be indicated as $\mathit{H}$. Since the gradient $\nabla S\left({\mathit{\beta }}^{*}\right)$ is computed in the stationary point ${\mathit{\beta }}^{*}$, the derivatives of this gradient are null. Therefore, Equation (37) can be rewritten as follows:

$$\begin{array}{cc}\hfill \nabla S\left({\mathit{\beta }}^{*}\right)& =\mathit{g}+\mathit{H}·\mathit{\delta }=0⟹\hfill \\ \hfill \mathit{\delta }& =-{\mathit{H}}^{-1}·\mathit{g}\hfill \end{array}$$

(38)

Therefore, the $\mathit{\delta }$ can be recalculated as function of ${\mathit{\beta }}^{*}$ (see Equation (22)) as follows:

$${\mathit{\beta }}^{*}=\mathit{\beta }-{\mathit{H}}^{-1}·\mathit{g}$$

(39)

In this case, the GN algorithm computes a ${\mathit{\beta }}^{\left(s\right)}$ value at every iterative step (s) starting from an initial guess of ${\mathit{\beta }}^{\left(0\right)}$. Therefore, the ${\mathit{\delta }}^{\left(s\right)}$ value is calculated using the following Equation (40):

$${\mathit{\delta }}^{\left(s\right)}=-{\left(\mathit{H}\left({\mathit{\beta }}^{\left(s\right)}\right)\right)}^{-1}·\mathit{g}\left({\mathit{\beta }}^{\left(s\right)}\right)$$

(40)

The iterative procedure described in Equation (40) is carried on until the condition $∥\mathit{\delta }∥<ϵ$ is verified. The variable $ϵ$ represents an arbitrary user-defined tolerance which the GN algorithm must reach to stop the iterations. At this point, the GN algorithm has found the $\mathit{\beta }$ parameters which minimize the function $S\left(\mathit{\beta }\right)$; therefore, the final value of $\mathit{\beta }$ is given as follows (35):

$${\mathit{\beta }}^{*}\equiv {\mathit{\beta }}^{(s+1)}={\mathit{\beta }}^{\left(s\right)}-{\left(\mathit{H}\left({\mathit{\beta }}^{\left(s\right)}\right)\right)}^{-1}·\mathit{g}\left({\mathit{\beta }}^{\left(s\right)}\right)$$

(41)

The described procedure represents an alternative iterative methodology to locate the stationary point (${\mathit{\beta }}^{*}$) that maximizes the quasi-likelihood function $K(y_i,{\mu }_i\left(\mathit{\beta }\right))$, and it can be adopted when the previous methodology (see Section 3.4) fails completely to locate the stationary point.

3.4.2. Limits of the GN Algorithm

The convergence of the GN algorithm using the Jacobian matrix (see Section 3.4) and its Hessian modification (see Section 3.4.1) is not always guaranteed, as proved and discussed by Nocedal and Wright (2006) and Mascarenhas (2013). Even local convergence could fail for the following reasons: (1) the initial guess ${\mathit{\beta }}^{\left(0\right)}$ is far from the stationary point ${\mathit{\beta }}^{*}$; (2) the ${\mathit{J}}^T\mathit{J}$ matrix described in Equation (32) is ill conditioned; (3) the Hessian matrix $\mathit{H}$ in Equation (39) is ill conditioned. Therefore, in order to perform claims reserve estimation in this framework, it is necessary to address and solve the problem of GN convergence and provide a method to ensure efficiency in finding the global minimum by the algorithm. Local convergence allows us to predict acceptable results for the claims reserve but could provide huge errors associated with the estimated $\mathit{\beta }$ parameters. Thus, providing an instrument that guarantees the GN algorithm’s global convergence is necessary to offer good results for claims reserve estimation and associated errors without increasing computational costs. In this regard, the author aims to derive a good initial guess of the $\mathit{\beta }$ parameters to prevent divergence or local convergence of the GN algorithm. The genetic algorithm (GA) has been employed to help locate a good initial guess of the $\mathit{\beta }$ parameters to solve the convergence problem.

3.5. The Genetic Algorithm

The GA is a methodology for solving constrained and unconstrained optimization problems based on a natural selection process that mimics biological evolution. The GA alters a present population of $\mathit{\beta }$ parameters by randomly picking and processing them as parents to create the next generation’s offspring. Over generations, the population evolves to the solution represented by a global minimum. The GA behaves differently from classical, derivative-based optimization algorithms, i.e., it can address issues that conventional optimization algorithms may not be able to process, such as discontinuous, non-differentiable, or highly non-linear objective functions. A detailed description and explanation of how the GA works is presented in the following references: Conn et al. (1991, 1997); Goldberg (1989). The algorithm, at each iteration, creates a sequence of new populations of individuals starting from the current generation. In order to avoid a huge computational cost, the author decided to implement a population of 2000 individuals, with 20,000 generations as the maximum number of generations, and 5000 generations as the maximum stall generation number for which the fitness function remains constant during the optimization.

The creation process is based on the following steps. Each population individual is associated with a score called “fitness” value, allowing the algorithm to select specific members. The fitness value is calculated by a fitness function represented by the residuals defined in Equation (24) or Equation (25). Individuals with high fitness are chosen as the elite population. Hence, they are selected as the elite population to create the next generation of individuals from which the children are produced by manipulating the $\beta$ parameters by combining them as an entry of a pair of parents-crossover or a single parent-mutation. The parent-crossover procedure follows the well-known technique described by Haupt and Haupt (2004), where two elite individuals are selected to generate the children for the subsequent generation. Let us suppose that the two parents are labelled as a and b, where their corresponding $\beta$-parameters are defined as the following vectors [${\beta }_1^a$, ${\beta }_2^a$] and [${\beta }_1^b$, ${\beta }_2^b$], respectively. The procedure involves the random selection of a single ${\beta }_i$-parameter which will serve as the crossover point, and subsequently, a random number ($\eta$), which ranges from 0 to 1, is introduced to determine the new ${\beta }_i$-parameters for the children in the next generation. The calculation of the new ${\beta }_i$-parameter is given by the following Equation (42):

$$\begin{array}{cc}\hfill {\beta }_{i1}& =(1-\eta ){\beta }_i^a+\eta {\beta }_i^b\hfill \end{array}$$

(42)

$$\begin{array}{cc}\hfill {\beta }_{i2}& =(1-\eta ){\beta }_i^b+\eta {\beta }_i^a\hfill \end{array}$$

(43)

The other $\beta$-parameter, which is ${\beta }_2$ in our example, is directly inherited from each respective parent chromosome. At this point, suppose that the two children are labelled as c and d; the complete set of $\beta$-values for the next generation is given by the following vectors: [${\beta }_{i1}^c$, ${\beta }_2^c$] and [${\beta }_{i2}^d$, ${\beta }_2^d$]. The described methodology combines the characteristics of both parent chromosomes using a single crossover point jointly with a $\eta$ random value to obtain a new set of chromosomes. In contrast, the parent-mutation involves a random change of a single ${\beta }_i$-parameter within a user-defined range [${\beta }_i^{min}$, ${\beta }_i^{max}$]. The new parent parameter for the next generation is given by the following relationship (44):

$${\beta }_i={\beta }_i^{min}+\eta ({\beta }_i^{max}-{\beta }_i^{min})\mathrm{with}\eta \in [0,1]$$

(44)

Additionally, the GA excludes individuals with low fitness who are not participating in the selection process. Finally, the stopping criterion of the GA is given by reaching a certain deviation threshold (fixed at ${10}^{-10}$) within the $\beta$-parameters in the fitness values for all the selected population Conn et al. (1991, 1997). The employment of the GA enforces the stability of the GN algorithm by increasing the convergence speed with a consequent reduction of the number of iterations needed to null the gradient represented in Equation (38) and ensuring that the global minimum is reached within the user-defined domain of the $\mathit{\beta }$ parameter.

3.6. Expectation Values and Error Estimation

Following the approach described in Section 3.4, the parameterization of the $\mathit{\beta }$ vector for the quasi-likelihood function defined in Equation (17) must be carried out. The parameterization described by Strascia and Tripodi (2018) has been followed to define the $\mathit{\beta }$ vector as shown in Equation (45):

$$\mathit{\beta }=(c,a_1,\dots ,a_n,b_1,\dots ,b_m)$$

(45)

where the authors have used a different definition of the indexes n and m with respect to Section 3.4, which is the one that will be used in the following. Therefore, the index is $k\in [1,n+m+1]$ and it labels the k-parameters of the $\mathit{\beta }$ vector. The variable c represents the intercept, the variable $a_{n_i}$ (with $n_i\in [1,n]$) is associated with the $n_i^{th}$ rows of the Run-Off triangles, i.e., the incurred year, and the variable $b_{m_i}$ (with $m_i\in [1,m]$) corresponds to the $m_i^{th}$ columns of the Run-Off triangles, i.e., the progression year. In this case, this notation has the advantage that the subscript index (i) indicates the ith residual, which embeds the index couple $(n_i,m_i)$ where $n_i$ can be ≠ from $m_i$. In the ODP framework, the exponential function with the parameterization $\mathit{\beta }$ is represented by Equation (46) and indicates the expectation value of the $y_i$ observable:

$$E\left[y_i\right]={\mu }_i\left(\mathit{\beta }\right)=\left\{\begin{array}{cc}{e}^c\hfill & \mathrm{if}{n}_i=m_i=1\hfill \\ e^{c+a_{n_i}}\hfill & \mathrm{if}{m}_i=1\mathrm{and}{n}_i\ne 1\hfill \\ e^{c+b_{m_i}}\hfill & \mathrm{if}{n}_i=1\mathrm{and}{m}_i\ne 1\hfill \\ e^{c+a_{n_i}+b_{m_i}}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(46)

Once the ODP framework has been chosen, the methodology discussed in Section 3.4 can be applied. The main goal is to find the best estimate of the $\mathit{\beta }$ parameters associated with the generic ${\mu }_i$ model (Equation (46)) to fill the Run-Off triangle and estimate the claims reserve jointly with their confidence interval. Therefore, it is necessary to find the parameters that maximize the quasi-likelihood function (17) by substituting it in Equation (46). In this manner, it is possible to obtain Equation (47):

$$K(y_i,{\mu }_i\left(\mathit{\beta }\right))={\displaystyle \frac{1}{\varphi }}\left[y_i(c+a_{n_i}+b_{m_i})-y_{i}log{y}_i-e^{c+a_{n_i}+b_{m_i}}+y_i\right]$$

(47)

At this step, the function $S\left(\mathit{\beta }\right)$ defined in Equation (21) has been built with the two residuals $r_i\left(\mathit{\beta }\right)$ (Equations (24) and (25)) defined in Section 3.4 and it depends directly on the parameter $\mathit{\beta }$. In the ODP framework, the residuals are defined as the following Equations (48) and (49):

$$\begin{array}{cc}\hfill r_i\left(\mathit{\beta }\right)={\displaystyle \frac{1}{\varphi }}\left[e^{c+a_{n_i}+b_{m_i}}+y_{i}log{y}_i-y_i(c+a_{n_i}+b_{m_i})\right]& \left(\mathrm{Equation}\right(24\left)\right)\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill r_i\left(\mathit{\beta }\right)={\displaystyle \frac{y_i-e^{c+a_{n_i}+b_{m_i}}}{e^{\frac{1}{2}(c+a_{n_i}+b_{m_i})}}}& \left(\mathrm{Equation}\right(25\left)\right)\hfill \end{array}$$

(49)

At this step, considering the total number of residuals (N) which corresponds to the number of observations, the Jacobian matrix ($\mathit{J}$) to apply the GN algorithm (see Equation (35)) is defined as follows (Equation (50)):

$$\mathit{J}=\left(\begin{array}{ccccccc}{\displaystyle \frac{\partial r_1}{\partial c}}& {\displaystyle \frac{\partial r_1}{\partial a_1}}& \dots & {\displaystyle \frac{\partial r_1}{\partial a_n}}& {\displaystyle \frac{\partial r_1}{\partial b_1}}& \dots & {\displaystyle \frac{\partial r_1}{\partial b_m}}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ {\displaystyle \frac{\partial r_i}{\partial c}}& {\displaystyle \frac{\partial r_i}{\partial a_1}}& \dots & {\displaystyle \frac{\partial r_i}{\partial a_n}}& {\displaystyle \frac{\partial r_i}{\partial b_1}}& \dots & {\displaystyle \frac{\partial r_i}{\partial b_m}}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ {\displaystyle \frac{\partial r_N}{\partial c}}& {\displaystyle \frac{\partial r_N}{\partial a_1}}& \dots & {\displaystyle \frac{\partial r_N}{\partial a_n}}& {\displaystyle \frac{\partial r_N}{\partial b_1}}& \dots & {\displaystyle \frac{\partial r_N}{\partial b_m}}\end{array}\right)$$

(50)

Starting from the initial guess ${\mathit{\beta }}^{\left(0\right)}$ provided by the GA (Section 3.5), the GN algorithm updates the Jacobian matrix (Equation (50)) using one of the two residuals defined in Equations (48) or (49) to compute iteratively the parameters ${\mathit{\beta }}^{*}$ which minimize the function $S\left(\mathit{\beta }\right)$ through Equation (35). During the iterative process using the Jacobian matrix, the relation (36) must hold to reach the convergence of the calculus. If Equation (36) cannot hold, the Hessian modification of the GN algorithm (Section 3.4.1) must be applied. In this case, the gradient ($\mathit{g}$) and the Hessian ($\mathit{H}$) of the function $S\left(\mathit{\beta }\right)$ are defined as follows (for simplicity, the variable $S\left(\mathit{\beta }\right)$ is denoted as S):

$$\mathit{g}={\left[\left({\displaystyle \frac{\partial S}{\partial c}}\right),\left({\displaystyle \frac{\partial S}{\partial a_1}}\right),\dots ,\left({\displaystyle \frac{\partial S}{\partial a_n}}\right),\left({\displaystyle \frac{\partial S}{\partial b_1}}\right),\dots ,\left({\displaystyle \frac{\partial S}{\partial b_m}}\right)\right]}^T$$

(51)

$$\mathit{H}=\left(\begin{array}{ccccccc}{\displaystyle \frac{{\partial }^{2}S}{\partial c^2}}& {\displaystyle \frac{{\partial }^{2}S}{\partial c\partial a_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial c\partial a_n}}& {\displaystyle \frac{{\partial }^{2}S}{\partial c\partial b_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial c\partial b_m}}\\ {\displaystyle \frac{{\partial }^{2}S}{\partial a_1\partial c}}& {\displaystyle \frac{{\partial }^{2}S}{\partial a_1^2}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial a_1\partial a_n}}& {\displaystyle \frac{{\partial }^{2}S}{\partial a_1\partial b_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial a_1\partial b_m}}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ {\displaystyle \frac{{\partial }^{2}S}{\partial a_n\partial c}}& {\displaystyle \frac{{\partial }^{2}S}{\partial a_n\partial a_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial a_n^2}}& {\displaystyle \frac{{\partial }^{2}S}{\partial a_n\partial b_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial a_n\partial b_m}}\\ {\displaystyle \frac{{\partial }^{2}S}{\partial b_1\partial c}}& {\displaystyle \frac{{\partial }^{2}S}{\partial b_1\partial a_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial b_1\partial a_n}}& {\displaystyle \frac{{\partial }^{2}S}{\partial b_1^2}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial b_1\partial b_m}}\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ {\displaystyle \frac{{\partial }^{2}S}{\partial b_m\partial c}}& {\displaystyle \frac{{\partial }^{2}S}{\partial b_m\partial a_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial b_m\partial a_n}}& {\displaystyle \frac{{\partial }^{2}S}{\partial b_m\partial b_1}}& \dots & {\displaystyle \frac{{\partial }^{2}S}{\partial b_m^2}}\end{array}\right)$$

(52)

At that point, it is possible to fill the entire Run-Off table with the complete set of estimations given by Equation (53):

$${\mu }_i\left({\mathit{\beta }}^{*}\right)=\left\{\begin{array}{cc}{e}^{c^{*}}\hfill & \mathrm{if}{n}_i=m_i=1\hfill \\ e^{c^{*}+a_{n_i}^{*}}\hfill & \mathrm{if}{m}_i=1\mathrm{and}{n}_i\ne 1\hfill \\ e^{c^{*}+b_{m_i}^{*}}\hfill & \mathrm{if}{n}_i=1\mathrm{and}{m}_i\ne 1\hfill \\ e^{c^{*}+a_{n_i}^{*}+b_{m_i}^{*}}\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(53)

Concurrently with the estimation of the expectation values, the corresponding errors on the ${\mathit{\beta }}^{*}$ parameters have been computed starting from the Hessian matrix $\mathit{H}\left(K(y,{\mathit{\beta }}^{*},\varphi )\right)$ of the complete quasi-likelihood function defined in Equation (19), where each element of the Hessian matrix ($H_{jk}$) is computed using Equation (54):

$$H_{jk}={\displaystyle \frac{{\partial }^{2}K(y,{\mathit{\beta }}^{*},\varphi )}{\partial {\beta }_j\partial {\beta }_k}}$$

(54)

Therefore, the variance ($\delta {\mathit{\beta }}^2$) associated with each ${\mathit{\beta }}^{*}$ parameter is computed by performing the inverse of the Hessian matrix ($\mathit{H}$), and then taking the diagonal elements of the matrix changing the sign as shown in Equation (55). For the sake of simplicity, the ${\mathit{\beta }}^{*}$ term is indicated as $\mathit{\beta }$, and the variable $\mathit{H}$ indicates the Hessian of the complete quasi-likelihood function $\mathit{H}\left(K(y,{\mathit{\beta }}^{*},\varphi )\right)$.

$$\delta {\mathit{\beta }}^2=\left(\delta c^2,\delta a_1^2,\dots ,\delta a_n^2,\delta b_1^2,\dots ,\delta b_m^2\right)=-\mathrm{diag}\left({\mathit{H}}^{-1}\right)$$

(55)

In order to provide the complete estimation of the standard errors for the expectation values ${\mu }_i\left(\mathit{\beta }\right)$, the authors applied the theory of error propagation. Therefore, they computed the differential of the generic expectation values ${\mu }_i\left(\mathit{\beta }\right)$ (see Equation (53)), which is given by Equation (56):

$$d{\mu }_i=d\left(e^{c+a_{n_i}+b_{m_i}}\right)=e^{c+a_{n_i}+b_{m_i}}(dc+d{a}_{n_i}+d{b}_{m_i})$$

(56)

Hence, substituting the parameter errors $\delta c$, $\delta a_{n_i}$, and $\delta b_{m_i}$ with the corresponding differentials in Equation (56):

$$\delta {\mu }_i=e^{c+a_{n_i}+b_{m_i}}(\delta c+\delta a_{n_i}+\delta b_{m_i})$$

(57)

The variance $\delta {\mu }_i$ of the expectation values is given by the squared sum of the single term of the previous Equation (57):

$$\delta {\mu }_i^2=e^{2(c+a_{n_i}+b_{m_i})}(\delta c^2+\delta a_{n_i}^2+\delta b_{m_i}^2+2\delta c\delta a_{n_i}+2\delta c\delta b_{m_i}+2\delta a_{n_i}\delta b_{m_i})$$

(58)

where the mixed terms are negligible for independent variables. In this framework, the standard errors of the expectation value $\Delta {\mu }_i$ are defined as follows (59):

$$\Delta {\mu }_i=e^{c+a_{n_i}+b_{m_i}}\sqrt{d{c}^2+d{a}_{n_i}^2+d{b}_{m_i}^2}$$

(59)

This Section completes the treatment of the GLM methods using the GN algorithm to estimate parameters with an initial guess provided via the GA algorithm. Starting from the SoA approach, the procedure developed in Section 3.3, Section 3.4 and Section 3.5 is used by the authors to provide results in the context of the healthcare sector, and specifically for the Tuscany region case study. The aim is to provide results in the form given by the theoretical background of Section 3.2, composed by expectation value and corresponding standard error. The authors are now able to present, in the next Section, a validation of the developed approach by comparison with the available SoA.

4. Comparison with SoA Models

To validate the proposed methodology, the authors performed a comparison with two works present in the SoA. The first comparison concerns the work of Strascia and Tripodi (2018), which primarily inspired the authors because it presents a similar methodology, presenting a sweetened data-set from a context different from healthcare (i.e., RC cars in Italy). The data-set of Strascia and Tripodi (2018) provides a complete calculation of the expectation values with the corresponding errors to the estimated parameters ($\mathit{\beta }$). The second comparison concerns the work of Verdonck et al. (2009), which is a good data-set that contains predictions coming from a robustification of the CL method with highly homogeneous data. The aim is to apply the methodology developed in the previous Sections (i.e., Section 3.4, Section 3.5 and Section 3.6) and improve the results compared with the ones in the SoA. Following, the authors show two different figures for each of the mentioned works to compare the results coming from the different choices of the residuals defined, respectively, in Equations (48) and (49). The key performance indicators (KPIs) used to compare our methodology with the ones proposed in the literature are the function $S\left(\mathit{\beta }\right)$ computed as shown in Equation (21) using the values of the $\mathit{\beta }$ vector that minimize the residuals after applying the GN algorithm (${\mathit{\beta }}^{*}$), the dispersion parameter ($\varphi$) computed as shown in Equation (15), and the claims reserve amount ($R_{tot}$) that must be set aside including the corresponding errors of the expectation value.

The developed stochastic model allows us to compute claims reserve differently with respect to the CL method described in Section 3.1. After computing the ${\mathit{\beta }}^{*}$ parameters of the stationary point through the GN algorithm, the expectation values shown in Equation (53) can be calculated and they correspond to every single cell of the Run-Off triangle. Considering the two-indices notation adopted in the Run-Off triangle of Table 1, the developed stochastic approach is able to calculate the complete set of expectation values in order to estimate the entire claims reserve. For clarity, the expectation values are indicated in the following

Table 3. Complete set of expectation values ${\mu }_{i,j}$ computed using the developed stochastic model.

$\mathit{i}/\mathit{j}$	0	1	…	j	…	$\mathit{J}-1$	J
1	${\mu }_{1,0}$	${\mu }_{1,1}$	…	${\mu }_{1,j}$	…	${\mu }_{1,J-1}$	${\mu }_{1,J}$
2	${\mu }_{2,0}$	${\mu }_{2,1}$	…	${\mu }_{2,j}$	…	${\mu }_{2,J-1}$	${\mu }_{2,J}$
⋮	⋮	⋮		⋮		⋮	⋮
i	${\mu }_{i,0}$	${\mu }_{i,1}$	…	${\mu }_{i,j}$	…	${\mu }_{i,J-1}$	${\mu }_{i,J}$
⋮	⋮.	⋮		⋮		⋮	⋮
$I-1$	${\mu }_{I-1,0}$	${\mu }_{I-1,1}$	…	${\mu }_{I-1,j}$	…	${\mu }_{I-1,J-1}$	${\mu }_{I-1,J}$
I	${\mu }_{I,0}$	${\mu }_{I,1}$	…	${\mu }_{I,j}$	…	${\mu }_{I,J-1}$	${\mu }_{I,J}$

.

The coloured cells in “light blue” as shown in Table 3 represent the expectation values ${\mu }_{i,j}$ with $i+j\le I$ coming from the application of the GN algorithm. In other words, they correspond to the generic model ${\mu }_i\left({\mathit{\beta }}^{*}\right)$ indicated in Section 3.6, for which they have been used to construct the residuals $r_i\left(\mathit{\beta }\right)$ in the Equations (48) and (49). Additionally, these expectation values (${\mu }_{i,j}$) are important to understand the dispersion of the observable data ($y_{i,j}$ in Table 1) and therefore compute the dispersion parameter ($\varphi$). In contrast, the coloured cells in “light orange” as shown in Table 3 represent the expectation values ${\mu }_{i,j}$ with $i+j>I$ that are estimated using Equation (53), and they are being used to predict the claims reserve for the generic budget year ($t>I$) through Equation (60):

$$R^{\left(t\right)}=\sum _{i+j=t}{\mu }_{i,j}\mathrm{with}t\in [I+1,I+J]$$

(60)

In order to predict the entire claims reserve $R_{tot}$, i.e., the total amount to be set aside, it is necessary to sum over every budget year $t\in [I+1,I+J]$, through Equation (61):

$$R_{tot}=\sum _{t=I+1}^{I+J}{R}^{\left(t\right)}$$

(61)

Furthermore, concerning the comparison with the current SoA, the total paid amount for a specific budget year ($t\in [1,I]$) is computed using Equation (62):

$$R^{\left(t\right)}=\sum _{i+j=t}{y}_{i,j}\mathrm{with}t\in [1,I]$$

(62)

where the variable $y_{i,j}$ represents the single payments as indicated in Table 1 (see Section 3.1). Since the variables $y_{i,j}$ represent the observation values, they are not used as KPIs to perform the comparison with the SoA. In the following Section, the comparison with the literature using the developed stochastic model for both residuals will be shown, jointly with the obtained values of the $S\left(\mathit{\beta }\right)$ function for each residual, the dispersion parameters $\varphi$, the prediction of the claims reserves for each individual budget year $R^{\left(t\right)}$, and the entire claims reserve $R_{tot}$ to be set aside with the associated absolute errors. For this comparison, the authors used the data-sets of Strascia and Tripodi (2018) and Verdonck et al. (2009), both of which are accessible in their entirety within their respective articles. For the sake of simplicity, in the following the authors will only report the results of the comparison between the results in the aforementioned works and those given by their methodology, described in Section 3. The source data, arranged in Run-Off triangles, were selected for comparison as they relate to incremental payments over time in the claims reserve context, though not appropriate to the healthcare context specifically addressed in this paper. The comparison, based on the specific KPIs described above, is made to show how with the methodology proposed by the authors the results of the SoA can be reproduced with greater absolute and percentage accuracy, thanks to the implementation of the GA which is fundamental in the choice of the initial guess, a step not envisaged in the proposed literature.

4.1. Comparison with Strascia and Tripodi (2018)

The data-set used in the work of Strascia and Tripodi (2018) presents a Run-Off triangle filled in the context of “RC cars”, which is a well-known benchmark to test and validate the new methodology and theory of forecasting model especially in claims reserve estimation due to their small data dispersion and homogeneity. The authors applied the method previously described, using both residuals defined in Section 3.4, to reproduce the results of Strascia and Tripodi (2018). The developed stochastic approach has been applied to predict the claims reserve $R^{\left(t\right)}$ for the generic budget year (t) using Equation (60), and it has been compared with the one provided by the optimization of Strascia and Tripodi (2018). The results concerning the predicted claims reserve $R^{\left(t\right)}$ for the generic budget year (t), are depicted in the following two figures. Figure 1 shows the paid amount ($R^{\left(t\right)}$ in Equation (62)) and the predicted claims reserve ($R^{\left(t\right)}$ in Equation (60)) relative to the comparison between Strascia and Tripodi (2018) and our methodology using the residual defined in Equation (48). Figure 2 shows the paid amount and the predicted claims reserve relative to the comparison between Strascia and Tripodi (2018) and our methodology using the residual defined in Equation (49). The obtained numerical results for the predicted claims reserve for a specific budget year are summarized in

Table 4. Comparison between our developed methodology and the work of Strascia and Tripodi (2018) in predicting claims reserve $R^{\left(t\right)}$ for the specific budget year $t\in [I+1,I+J]$ for the two residuals.

Budget Year (t)	Paid (${10}^3$ €) Literature	${\mathit{R}}^{\left(\mathit{t}\right)}$ (${10}^3$ €) Literature	${\mathit{R}}^{\left(\mathit{t}\right)}$ (${10}^3$ €) Residual (Equation (48))	${\mathit{R}}^{\left(\mathit{t}\right)}$ (${10}^3$ €) Residual (Equation (49))
0	22.60	-	22.60 ± 1.43	22.60 ± 1.43
1	62.32	-	62.32 ± 5.70	62.32 ± 5.65
2	101.93	-	101.93 ± 9.25	101.93 ± 9.03
3	124.59	-	124.59 ± 12.12	124.59 ± 11.57
4	152.04	-	152.04 ± 14.82	152.04 ± 13.85
5	188.65	-	188.65 ± 17.33	188.65 ± 16.03
6	185.31	-	185.31 ± 19.72	185.31 ± 18.45
7	203.38	-	203.38 ± 21.77	203.38 ± 20.40
8	213.67	-	213.67 ± 23.03	213.67 ± 21.37
9	207.65	-	207.65 ± 23.39	207.65 ± 21.63
10	197.67	-	197.67 ± 23.64	197.67 ± 21.84
11	184.68	-	184.68 ± 24.99	184.68 ± 23.10
12	194.08	-	194.08 ± 29.10	194.08 ± 27.00
13	-	177.71 ± 41.39	183.87 ± 27.96	179.53 ± 25.78
14	-	139.04 ± 33.41	146.17 ± 22.90	140.69 ± 20.80
15	-	112.39 ± 27.91	119.75 ± 19.38	113.99 ± 17.43
16	-	93.69 ± 24.06	101.15 ± 16.98	95.37 ± 15.13
17	-	80.55 ± 21.36	85.66 ± 14.89	81.93 ± 13.48
18	-	66.73 ± 18.32	71.52 ± 12.90	67.97 ± 11.61
19	-	52.05 ± 14.84	57.26 ± 10.72	53.14 ± 9.43
20	-	38.71 ± 11.50	42.30 ± 8.21	39.44 ± 7.26
21	-	29.33 ± 9.05	32.14 ± 6.44	29.97 ± 5.71
22	-	23.89 ± 7.62	26.14 ± 5.41	24.38 ± 4.78
23	-	18.78 ± 6.39	20.36 ± 4.50	19.19 ± 4.00
24	-	12.95 ± 4.93	13.69 ± 3.40	12.85 ± 3.01

.

The obtained numerical results describing the value of the $S\left({\mathit{\beta }}^{*}\right)$ function, the corresponding dispersion parameter ($\varphi$), and the total predicted total claims reserve amount $R_{tot}$ are summarized in

Table 5. Comparison between the work of Strascia and Tripodi (2018) and our proposed methodology concerning the $S\left({\beta }^{*}\right)$ function (Equation (21)), the dispersion parameter $\varphi$ (Equation (15)), and the total predicted claims reserve amount $R_{tot}$ (Equation (61)) for both residuals (Section 3.4).

Residual (Equation (48))	Reference	$\mathit{S}\left({\mathit{\beta }}^{*}\right)$	$\mathit{\varphi }$	${\mathit{R}}_{\mathit{t}\mathit{o}\mathit{t}}$ (${10}^5$ €)
	Strascia and Tripodi (2018)	$3.65\times {10}^5$	$4.11\times {10}^2$	8.46 ± 2.20
	Our work	$3.00\times {10}^5$	$4.53\times {10}^2$	9.00 ± 1.54
Residual (Equation (49))	Reference	$\mathit{S}\left({\mathit{\beta }}^{*}\right)$	$\mathit{\varphi }$	${\mathit{R}}_{\mathit{t}\mathit{o}\mathit{t}}$ (${10}^5$ €)
	Strascia and Tripodi (2018)	$2.71\times {10}^4$	$4.11\times {10}^2$	8.46 ± 2.20
	Our work	$2.68\times {10}^4$	$4.06\times {10}^2$	8.58 ± 1.38

.

It is essential to mention that in both cases, i.e., in the estimation provided by the authors, the convergence of the GN algorithm is improved because the authors used the GA to calculate the initial guess of parameters $\mathit{\beta }$ (see Section 3.5). In contrast, concerning the work of Strascia and Tripodi (2018), the algorithm’s convergence might converge to a local minimum without starting with an appropriate initial guess, leading to an increase in the errors associated with the $\mathit{\beta }$ parameters. Additionally, it is important to mention that the computed values of the $S\left({\mathit{\beta }}^{*}\right)$ function, the dispersion parameter ($\varphi$), and the total predicted claims reserve amount $R_{tot}$ for the work of Strascia and Tripodi (2018) have been obtained using the ${\mathit{\beta }}^{*}$ parameters resulting from their calculation. The errors in the predicted claims reserve for the specific year $R^{\left(t\right)}$ have been calculated using the error propagation by summing the errors relative to every single cell of the predicted values ($\Delta {\mu }_i$—see Equation (59)). The error propagation theory has been applied to calculate the entire predicted claims reserve $R_{tot}$. Furthermore, using the two different definitions of the residuals, the estimation of the claims reserve performed by the authors provides confidence intervals slightly lower than the ones provided by Strascia and Tripodi (2018). Even if the difference between the two residuals is negligible for this case, the high dispersion and aleatory data in other contexts, such as healthcare, might produce more prominent confidence intervals.

4.2. Comparison with Verdonck et al. (2009)

In this Section, the authors performed the validation approach of Section 4.1 with the Run-Off triangle presented in the work of Verdonck et al. (2009). In this case, Verdonck et al. (2009) did not compute the errors associated with their stochastic model because they focused on developing a robustification of the CL method. However, the possibility to reproduce and improve the results presented in the work of Verdonck et al. (2009) represents an excellent manner to validate further the methodology described in this paper since they present a low-dispersion data-set. Following an identical procedure to the one of Section 4.1, the authors show the results of the developed stochastic model using the two definitions of the residuals in Equations (48) and (49), respectively. The results concerning the predicted claims reserve $R^{\left(t\right)}$ for the generic budget year (t), are depicted in the following two figures. Figure 3 shows the paid amount ($R^{\left(t\right)}$ in Equation (62)) and the predicted claims reserve ($R^{\left(t\right)}$ in Equation (60)) relative to the comparison between Strascia and Tripodi (2018) and our methodology using the residual defined in Equation (48). Figure 4 shows the paid amount and the predicted claims reserve relative to the comparison between Verdonck et al. (2009) and our methodology using the residual defined in Equation (49). The obtained numerical results for the predicted claims reserve for a specific budget year are summarized in

Table 6. Comparison between our developed methodology and the work of Verdonck et al. (2009) in predicting claims reserve $R^{\left(t\right)}$ for the specific budget year $t\in [I+1,I+J]$ for the two residuals.

Budget Year (t)	Paid (${10}^6$ €) Literature	${\mathit{R}}^{\left(\mathit{t}\right)}$ (${10}^6$ €) Literature	${\mathit{R}}^{\left(\mathit{t}\right)}$ (${10}^6$ €) Residual (Equation (48))	${\mathit{R}}^{\left(\mathit{t}\right)}$ (${10}^6$ €) Residual (Equation (49))
0	135.34	-	135.34 ± 3.05	135.34 ± 2.92
1	216.03	-	216.03 ± 7.56	216.03 ± 7.38
2	294.31	-	294.31 ± 11.12	294.31 ± 10.84
3	353.38	-	353.38 ± 14.22	353.38 ± 13.84
4	431.01	-	431.01 ± 17.14	431.01 ± 16.69
5	463.80	-	463.80 ± 19.19	463.80 ± 18.65
6	478.03	-	478.03 ± 20.99	478.03 ± 20.33
7	493.10	-	493.10 ± 22.89	493.10 ± 22.20
8	507.59	-	507.59 ± 25.35	507.59 ± 24.53
9	535.26	-	535.26 ± 28.75	535.26 ± 27.84
10	-	401.96	403.74 ± 23.07	402.54 ± 22.35
11	-	309.07	310.82 ± 18.74	309.57 ± 18.13
12	-	236.98	238.43 ± 15.25	237.42 ± 14.75
13	-	178.16	179.39 ± 12.26	178.56 ± 11.86
14	-	129.86	131.02 ± 9.57	130.23 ± 9.24
15	-	92.78	93.62 ± 7.45	93.08 ± 7.19
16	-	62.85	63.36 ± 5.61	63.08 ± 5.43
17	-	36.63	37.03 ± 3.82	36.83 ± 3.69
18	-	15.12	14.87 ± 1.93	15.11 ± 1.90

.

In this case, the authors provided the results concerning the value of the $S\left({\mathit{\beta }}^{*}\right)$ function, the corresponding dispersion parameter ($\varphi$), and the claims reserve amount applied to the Run-Off in the work of Verdonck et al. (2009). The results are shown in

Table 7. Comparison between the work of Verdonck et al. (2009) and our proposed methodology concerning the $S\left({\beta }^{*}\right)$ function (Equation (21)), the dispersion parameter $\varphi$ (Equation (15)), and the total predicted claims reserve amount $R_{tot}$ (Equation (61)) for both residuals (Section 3.4).

Residual (Equation (48))	Reference	$\mathit{S}\left({\mathit{\beta }}^{*}\right)$	$\mathit{\varphi }$	${\mathit{R}}_{\mathit{t}\mathit{o}\mathit{t}}$ (${10}^9$ €)
	Verdonck et al. (2009)	-	-	1.46
	Our work	$8.57\times {10}^6$	$2.02\times {10}^5$	1.47 ± 0.09
Residual (Equation (49))	Reference	$\mathit{S}\left({\mathit{\beta }}^{*}\right)$	$\mathit{\varphi }$	${\mathit{R}}_{\mathit{t}\mathit{o}\mathit{t}}$ (${10}^9$ €)
	Verdonck et al. (2009)	-	-	1.46
	Our work	$6.81\times {10}^6$	$1.89\times {10}^5$	1.47 ± 0.09

. Since Verdonck et al. (2009) did not provide the errors associated with their stochastic model, the authors are unable to perform a consistent comparison with this work in the literature, but they only provide the claims reserve amount coming from a robustification of the CL method.

Even in this case, and in both cases in the estimation provided by the authors, the convergence of the GN algorithm is improved because the authors used the GA to calculate the initial guess of parameters $\mathit{\beta }$ (see Section 3.5). Furthermore, using the two different definitions of the residuals, the calculation performed by the authors provides confidence intervals for the claims reserve that include the values calculated by Verdonck et al. (2009) using a completely different approach.

5. The Healthcare Study: The Case of Claims in the Tuscany Region

The main objective is to apply the developed methodology to predict the total claims reserve to be set aside by an insurance agency. Specifically, the authors worked on the health insurance context of claims concerning the Tuscany region in Italy to provide results for the reserve amount required by the region to manage the yearly balance finance system in healthcare. It is essential to notice that the authors carried out a stochastic analysis on claims reserve employing the two definitions of residuals described in Section 3.4, providing accordingly to the SoA a new methodology to deal with claims reserve and the corresponding errors. The novelty and the contribution of our research take credit not only from the improvements compared with the SoA but also in the healthcare context. In order to test our methodology in the healthcare insurance system of the Tuscany region, the authors proceeded in the following manner. Firstly, the authors performed a preliminary analysis of the available healthcare insurance data-set to understand the useful information that could be retrieved in order to compile the Run-Off triangle. Secondly, the authors compared the CL methodology with the developed stochastic approach. The CL is a deterministic method used in different contexts to compute a one-year reserve. Subsequently, the authors reproduced the deterministic result with the developed stochastic model. Finally, the authors found the optimal parameters of the ODP to perform prediction for the entire claims reserve to provide an outcome for the region which could be used in management, together with the corresponding confidence intervals.

5.1. Preliminary Analysis

The authors worked with the Centro Gestione Rischio Clinico of the Tuscany region database concerning the healthcare claims reported from 2010 to 2021. In this Section, the authors performed a preliminary analysis retrieving the following information:

• Time evolution of the paid claims;
• Single payment for years of the specific claim;
• Total paid amounts.

Starting from the provided data-set, it is possible to compile the following Run-Off triangle, which is the base of our research (Section 3.1). The rows of the Run-Off triangle are filled with the incurred years (i.e., from 2010 to 2021). The columns of the Run-Off triangle are filled with the progression of the payments towards the years. In this way, each cell represents the delayed payment with respect to the corresponding incurred year. The Run-Off triangle of health insurance claims for the Tuscany region is shown in

Table 8. Paid amount of the Run-Off triangle for health insurance claims for the Tuscany region from 2010 to 2021 (10⁶ €).

${\mathit{y}}_{\mathit{i},\mathit{j}}$	0	1	2	3	4	5	6	7	8	9	10	11
2010	2.80	5.94	10.1	5.00	4.06	4.28	2.74	1.98	2.64	1.06	1.20	1.27
2011	2.13	11.3	6.15	1.79	2.82	4.29	5.26	7.76	4.91	3.35	1.43
2012	0.95	7.61	7.19	3.25	4.77	3.08	5.03	5.65	3.64	1.74
2013	0.72	8.66	5.68	1.63	3.44	4.06	4.89	3.95	2.50
2014	0.97	9.76	7.67	6.49	4.07	5.66	4.41	3.90
2015	1.50	11.4	7.17	3.95	6.52	5.76	7.87
2016	1.15	5.14	9.14	9.74	3.33	2.95
2017	0.19	6.96	8.92	5.77	3.63
2018	0.10	5.90	9.36	3.68
2019	2.35	5.55	10.9
2020	0.27	6.57
2021	0.81

:

The variable $y_{i,j}$ in Table 8 identifies the paid amount of the payment for claims that have been incurred in the ith year with a delay occurring in the jth year. As previously discussed, the authors present the deterministic analysis of the Run-Off triangle shown in Table 8 employing the well-known CL approach. This analysis represents the benchmark of our research, as it will be compared with the proposed stochastic method by the authors in the following Sections.

5.2. Chain-Ladder Results

The CL method provides a mechanism to forecast future loss development trends based on historical patterns. It offers a deterministic perspective on reserving losses for the subsequent year. This Section outlines the results of the CL method applied to the previous Run-Off triangle. This approach has been comprehensively explained in the referenced studies Strascia and Tripodi (2018); Verrall (1991). The results obtained by applying the CL method to the health insurance context of the Tuscany region are summarized in

Table 9. Predicted claims reserve amount $R^{\left(t\right)}$ for every single incurred year $\left(t\right)$ using the CL method.

t	${\mathit{R}}^{\left(\mathit{t}\right)}$ (€)
2011	$1.56\times {10}^6$
2012	$2.59\times {10}^6$
2013	$3.97\times {10}^6$
2014	$9.19\times {10}^6$
2015	$16.83\times {10}^6$
2016	$19.17\times {10}^6$
2017	$22.24\times {10}^6$
2018	$23.21\times {10}^6$
2019	$34.07\times {10}^6$
2020	$29.78\times {10}^6$
2021	$31.70\times {10}^6$

.

In this case, the predicted claims reserve amount $R^{\left(t\right)}$ appearing in Table 9 has been calculated using Equation (4), while the total predicted claims reserve amount for the Tuscany region in the incurred years 2010–2021 is roughly: $R_{tot}=194.32$ × 10⁶ €. Figure 5 shows the predicted claims reserve amount $R^{\left(t\right)}$ for every single incurred year (2010–2021) employing the CL methodology. Despite the simplicity of the CL method, several issues make it unsuitable for performing our analysis. Indeed it cannot provide and predict changes in the model, and it can only predict the one-year estimate of the claims reserve. Therefore, a stochastic method is needed to provide more complete results for claims reserve predictions and confidence intervals. In the following Section 5.3, the authors present the developed stochastic approach with the corresponding numerical results compared to the CL approach.

5.3. Stochastic Approach Results

The results obtained by applying the developed stochastic approach to estimate the claims reserve for the Tuscany region are presented in this Section. Here, the values and the corresponding errors of the parameters (${\mathit{\beta }}^{*}$) resulting from the developed stochastic approach are shown for the Tuscany region insurance claims using both residual defined in Equations (48) and (49). The procedure described in Section 3.4 and Section 3.5 has been applied to calculate the ${\mathit{\beta }}^{*}$ parameters needed to compile the Run-Off triangle. The GA has been applied firstly to obtain a good initial guess of $\mathit{\beta }$ parameters, and subsequently, the GN algorithm has been applied to reach the stationary point ${\mathit{\beta }}^{*}$. The following

Table 10. Estimated parameters (${\beta }^{*}$) using both residuals defined in Equations (48) and (49).

Residual (Equation (48))			Residual (Equation  (49))
Variable	Value	Error	Variable	Value	Error
c	14.183	0.221	c	14.109	0.226
$a_1$	0.175	0.155	$a_1$	0.197	0.156
$a_2$	−0.022	0.164	$a_2$	0.002	0.165
$a_3$	−0.103	0.170	$a_3$	−0.114	0.172
$a_4$	0.126	0.165	$a_4$	0.140	0.166
$a_5$	0.286	0.165	$a_5$	0.313	0.166
$a_6$	0.191	0.177	$a_6$	0.178	0.179
$a_7$	0.048	0.193	$a_7$	0.055	0.195
$a_8$	−0.011	0.209	$a_8$	−0.047	0.213
$a_9$	0.164	0.217	$a_9$	0.190	0.216
$a_{10}$	−0.158	0.313	$a_{10}$	−0.191	0.320
$a_{11}$	−0.572	0.889	$a_{11}$	−0.498	0.883
$b_1$	1.655	0.205	$b_1$	1.701	0.210
$b_2$	1.682	0.207	$b_2$	1.740	0.212
$b_3$	1.244	0.220	$b_3$	1.247	0.226
$b_4$	0.994	0.233	$b_4$	1.034	0.237
$b_5$	1.026	0.237	$b_5$	1.075	0.241
$b_6$	1.216	0.238	$b_6$	1.248	0.242
$b_7$	1.239	0.248	$b_7$	1.252	0.253
$b_8$	0.894	0.285	$b_8$	0.925	0.289
$b_9$	0.430	0.355	$b_9$	0.418	0.364
$b_{10}$	−0.186	0.522	$b_{10}$	−0.124	0.519
$b_{11}$	−0.125	0.724	$b_{11}$	−0.051	0.719

provides the results of the entire estimation for the $\mathit{\beta }$ parameters and the corresponding errors.

At this step, it is possible to compute the expectation value ${\mu }_{i,j}$ for each insurance year (2010–2021) and fulfil the Run-Off triangle as shown in Section 4. The following

Table 11. Expectation values ${\mu }_{i,j}$ (10⁶ €) computed using the residual defined in Equation (48).

${\mathit{\mu }}_{\mathit{i},\mathit{j}}$	0	1	2	3	4	5	6	7	8	9	10	11
2010	1.44	7.55	7.76	5.01	3.90	4.03	4.87	4.98	3.53	2.22	1.20	1.27
2011	1.72	9.00	9.24	5.97	4.65	4.80	5.80	5.94	4.20	2.64	1.43	1.52
2012	1.41	7.39	7.59	4.90	3.82	3.94	4.77	4.87	3.45	2.17	1.17	1.25
2013	1.30	6.81	7.00	4.52	3.52	3.63	4.39	4.49	3.18	2.00	1.08	1.15
2014	1.64	8.57	8.80	5.68	4.42	4.57	5.52	5.65	4.00	2.52	1.36	1.44
2015	1.92	10.1	10.3	6.67	5.19	5.36	6.48	6.63	4.70	2.95	1.60	1.70
2016	1.75	9.14	9.39	6.06	4.72	4.88	5.89	6.03	4.27	2.69	1.45	1.54
2017	1.52	7.93	8.14	5.26	4.09	4.23	5.11	5.23	3.70	2.33	1.26	1.34
2018	1.43	7.47	7.68	4.96	3.86	3.99	4.82	4.93	3.49	2.20	1.19	1.26
2019	1.70	8.90	9.14	5.90	4.60	4.75	5.74	5.87	4.16	2.62	1.41	1.50
2020	1.23	6.45	6.63	4.28	3.33	3.44	4.16	4.25	3.01	1.90	1.02	1.09
2021	0.81	4.26	4.38	2.83	2.20	2.27	2.75	2.81	1.99	1.25	0.68	0.72

and

Table 12. Expectation values ${\mu }_{i,j}$ (10⁶ €) computed using the residual defined in Equation (49).

${\mathit{\mu }}_{\mathit{i},\mathit{j}}$	0	1	2	3	4	5	6	7	8	9	10	11
2010	1.34	7.35	7.64	4.67	3.77	3.93	4.67	4.69	3.38	2.04	1.18	1.27
2011	1.63	8.95	9.30	5.68	4.59	4.79	5.69	5.71	4.12	2.48	1.44	1.55
2012	1.34	7.36	7.66	4.68	3.78	3.94	4.68	4.70	3.39	2.04	1.19	1.28
2013	1.20	6.56	6.82	4.17	3.37	3.51	4.17	4.19	3.02	1.82	1.06	1.14
2014	1.54	8.45	8.79	5.37	4.34	4.52	5.37	5.40	3.89	2.34	1.36	1.47
2015	1.83	10.0	10.4	6.38	5.16	5.37	6.38	6.41	4.62	2.79	1.62	1.74
2016	1.60	8.78	9.13	5.58	4.51	4.70	5.58	5.61	4.04	2.43	1.42	1.52
2017	1.42	7.77	8.07	4.93	3.99	4.15	4.93	4.96	3.58	2.15	1.25	1.35
2018	1.28	7.01	7.29	4.45	3.60	3.75	4.46	4.48	3.23	1.94	1.13	1.22
2019	1.62	8.88	9.24	5.64	4.56	4.75	5.64	5.67	4.09	2.46	1.43	1.54
2020	1.11	6.07	6.31	3.86	3.12	3.25	3.86	3.88	2.79	1.68	0.98	1.05
2021	0.81	4.47	4.64	2.84	2.29	2.39	2.84	2.85	2.06	1.24	0.72	0.77

represent the Run-Off triangles compiled with the estimation provided by the entire procedure described in Section 3.4 and Section 3.6.

Given the expectation values ${\mu }_{i,j}$ shown in the previous Table 11 and Table 12, the authors provide the following figures representing the paid amount and the predicted claims reserve $R^{\left(t\right)}$ for the generic budget year (t) from 2010 to 2031 in the Tuscany region.

Referring to the previous Figure 6 and Figure 7,

Table 13. Representation of the paid amount and predicted claims reserve $R^{\left(t\right)}$ for the generic budget year provided with the two different definitions of the residuals. From the budget year 2022 to 2031, the values of $R^{\left(t\right)}$ are fully predicted.

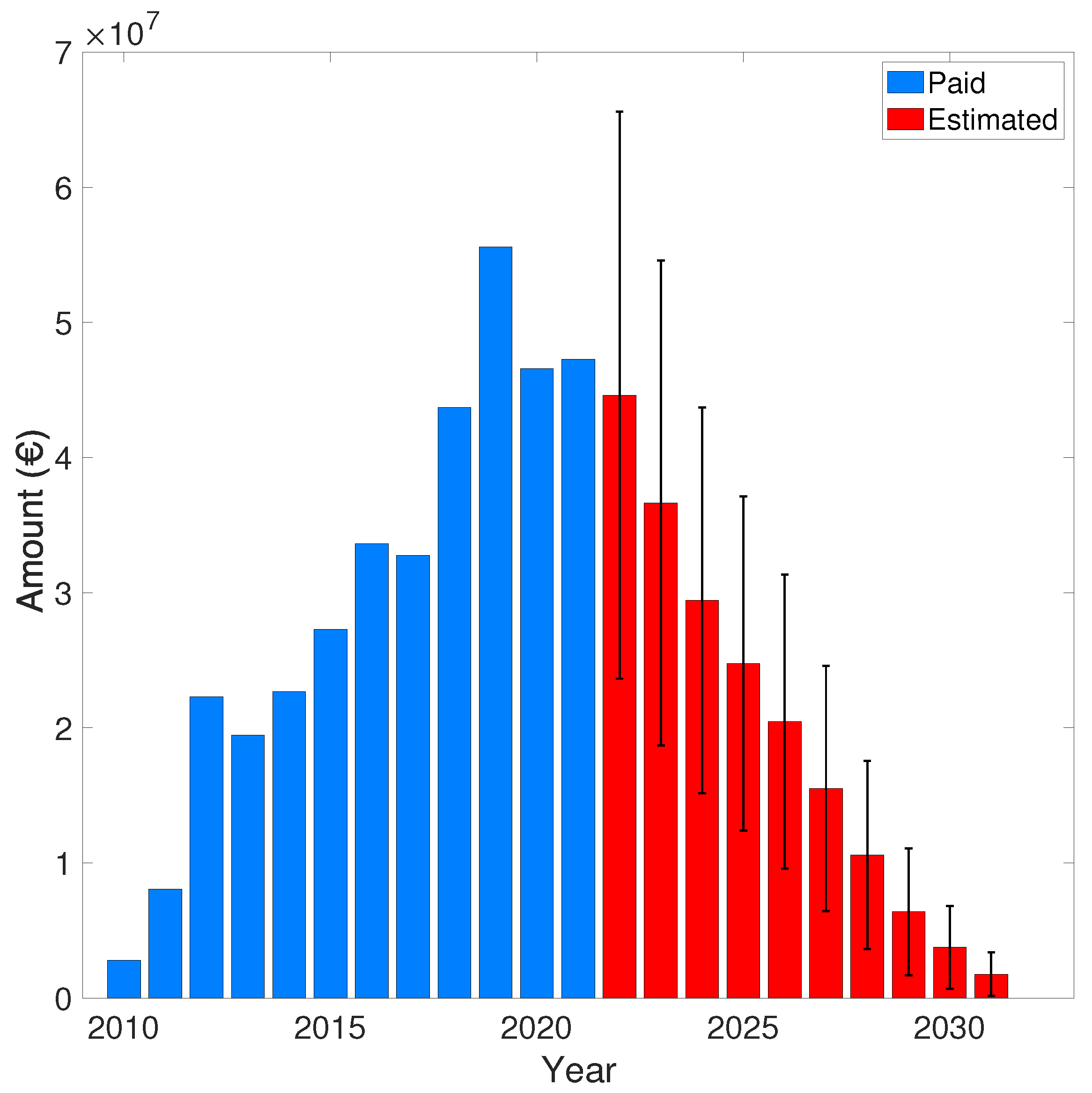
Budget Year (t)	${\mathit{R}}^{\left(\mathit{t}\right)}$ (106 €) Paid Amount	${\mathit{R}}^{\left(\mathit{t}\right)}$ (106 €) Residual (Equation (48))	${\mathit{R}}^{\left(\mathit{t}\right)}$ (106 €) Residual (Equation (49))
2010	2.80	1.44 ± 0.32	1.34 ± 0.30
2011	8.08	9.27 ± 2.74	8.98 ± 2.71
2012	22.3	18.2 ± 5.79	17.9 ± 5.83
2013	19.5	22.9 ± 7.61	22.5 ± 7.63
2014	22.7	25.9 ± 8.76	25.2 ± 8.69
2015	27.3	31.1 ± 10.6	30.3 ± 10.5
2016	33.6	38.6 ± 13.3	37.8 ± 13.3
2017	32.8	44.9 ± 15.7	43.7 ± 15.5
2018	43.7	47.7 ± 17.0	46.2 ± 16.8
2019	55.6	48.8 ± 17.9	47.0 ± 17.5
2020	46.6	50.5 ± 19.1	48.7 ± 18.8
2021	47.3	50.5 ± 20.7	48.8 ± 20.3
2022	-	46.1 ± 21.2	44.6 ± 21.0
2023	-	37.9 ± 18.1	36.7 ± 17.9
2024	-	30.7 ± 14.6	29.4 ± 14.3
2025	-	25.7 ± 12.6	24.8 ± 12.4
2026	-	21.3 ± 11.1	20.5 ± 10.9
2027	-	16.2 ± 9.27	15.5 ± 9.08
2028	-	11.0 ± 7.10	10.6 ± 6.97
2029	-	6.56 ± 4.75	6.39 ± 4.69
2030	-	3.78 ± 3.08	3.76 ± 3.06
2031	-	1.76 ± 1.60	1.77 ± 1.62

presents the complete set of values concerning the paid amount and the predicted claims reserve $R^{\left(t\right)}$ for the generic budget year (t) from 2010 to 2031 in the Tuscany region.

In

Table 14. Results concerning the Tuscany region analysis providing the values of the KPIs such as $S\left({\beta }^{*}\right)$ function (Equation (21)), the dispersion parameter $\varphi$ (Equation (15)), the predicted claims reserve amount for the 2021 incurred year $R^{\left(2021\right)}$, and the total predicted claims reserve $R_{tot}$.

	$\mathit{S}\left({\mathit{\beta }}^{*}\right)$	$\mathit{\varphi }$	${\mathit{R}}^{\left(2021\right)}$ (106 €)	${\mathit{R}}_{\mathit{tot}}$ (106 €)
Measured	-	-	47.3	-
CL (Table 9)	-	-	31.7	-
Residual (Equation (48))	6.78 × 103	6.05 × 105	50.5 ± 20.7	201 ± 103
Residual (Equation (49))	3.27 × 107	5.94 × 105	48.8 ± 20.3	194 ± 102

, the authors provided the values of the KPIs resulting from the estimation of the total reserve to be set aside for the Tuscany region insurance claims. Specifically, the value of the $S\left({\mathit{\beta }}^{*}\right)$ function, the corresponding dispersion parameter ($\varphi$), the predicted claims reserve amount for the 2021 incurred year $R^{\left(2021\right)}$, and the total predicted claims reserve $R_{tot}$ are computed using Equation (61).

The results in Table 14 illustrate the predictive accuracy of the stochastic model developed by the authors, which was previously validated as described in Section 4. It is important to note that the absolute errors on the predicted claims reserve are considerably off an interval of acceptability (i.e., the estimated errors are roughly 50% of the predicted values for the claims reserve). The reason for this is the high data dispersion that the stochastic model is unable to overcome. Nevertheless, compared to the current SoA, the analysis conducted by the authors for the healthcare sector is entirely satisfactory, as it represents a notable initial approach to estimating the claims reserve in a highly heterogeneous and mutable context.

6. Conclusions

In this work, the authors contributed to creating a robust protocol to deal with claims reserve in the healthcare system context. Even if the SoA already presented a well-defined approach for claims reserve, in the healthcare system, the wide variability, peculiarity, and aleatory nature of claims made reformulation and subsequent improvements of the stochastic methodology usually adopted necessary. Therefore, the authors contributed to the SoA, improving the management of claims reserve in such a way that is easy to reproduce by the institutions that are the final users (i.e., the Tuscany region) without increasing computational costs. This study wants to prove how it is possible to handle healthcare claims using the well-known GLM with an Overdispersed Poisson function with an improvement in the estimation of the parameters of the quasi-likelihood function, with an initial guess optimized by a genetic algorithm which glimpses the position of the global minimum solving the convergence of the Gauss–Newton algorithm. This step is crucial for the peculiarity and variability of healthcare databases. Possible developments of the study concern the possibility of expanding the Run-Off tables, predicting the durability of the entire claim life, and defining a method to better improve error estimations also for highly dispersed databases such as the one treated in this work in the healthcare context. Furthermore, it is necessary to create a unique protocol for data management to improve the quality and accessibility of the data and develop a robust analysis of the incurred velocity.

[custom] References