External Wetting Efficiency in a Three-Phase Fixed Bed Loaded with Porous and Non-Porous Packings
Abstract
1. Introduction
- (1)
- The tracer method [21,22,23,24,25]. The wetting efficiency is defined as the square root of the ratio of the apparent diffusivity of the tracer in a porous particle in a trickle-bed reactor to the diffusivity obtained in a liquid-full reactor. Diffusivities are obtained from the variance of the impulse response of the tracer. Based on a comprehensive theoretical analysis, Julcour-Lebigue et al. [26] demonstrated that under the usual low axial dispersion conditions, factors including the external mass transfer resistance, adsorption of the tracer, flow pattern of the wetted zone, and heterogeneity of wetting on the reactor scale have only a slight effect on the wetting efficiency and, therefore, wetting efficiency can accurately be evaluated from RTD data. The tracer technique has been compared satisfactorily to the direct measurements of partial wetting obtained by dye adsorption [27,28]. In another work by Lappalainen et al. [29], in a hydrodynamic model establishment for wetting efficiency, all wetting efficiency data points were recommended to be obtained from the tracer method, in view of the high reliability of this method.
- (2)
- The dye adsorption method [27,28,30,31]. Wetting efficiency can be obtained at the pellet scale using this method by colorimetric tracing via dye adsorption. However, this method requires tedious experimental work, since the packing can only be used once and needs to be replaced by a fresh one for the next run. The reactor should be disassembled several times to obtain cross-sectional photographs of the packing.
- (3)
- The hydrodynamic method. Pironti et al. [32] and Kundu et al. [33] applied the shear stress method for wetting efficiency evaluation by comparing the liquid–solid shear stress times of the specific area in the two-phase flow to that in a liquid-full bed at the same intrinsic liquid and gas velocities. The advantage of this method is that the wetting efficiency can be determined directly from the pressure drop and liquid holdup measurements, which is quite convenient compared to the tracer and colorimetric methods. Its accuracy needs to be improved in view of the remarkable discrepancy from the literature reports. On the other hand, the liquid morphology observation has also been used for the wetting efficiency estimation, as shown in the work of Sederman and Gladden [14]. The authors attempted to obtain the wetting efficiency from the fraction of surface voxels that contain liquid. A wetting efficiency of 0.56 was obtained at a liquid flow rate of 5.8 mm·s−1 and gas superficial velocity of 66 mm/s. This shows that the MRI method appears to be a very promising tool for obtaining flow features and quantitative analysis.
- (4)
- The reaction method. This method was initially proposed by comparison of reaction rates in a two-phase operation and in a reactor completely filled with liquid [34,35]. An innovative parallel hydrogenation for the quantification of wetting efficiency in a trickle-bed reactor was introduced by van Houwelingen and Nicol [36]. In this method, the reaction rates of two first-order liquid-limited hydrogenation reactions occurring in parallel were measured under upflow and trickle flow conditions. The higher conversion in the upflow operation was explained by the complete wetting and better liquid–solid mass transfer characteristics.
2. Liquid Flow Texture Modeling
3. Experimental Work
4. Results and Discussion
4.1. Experimental Results
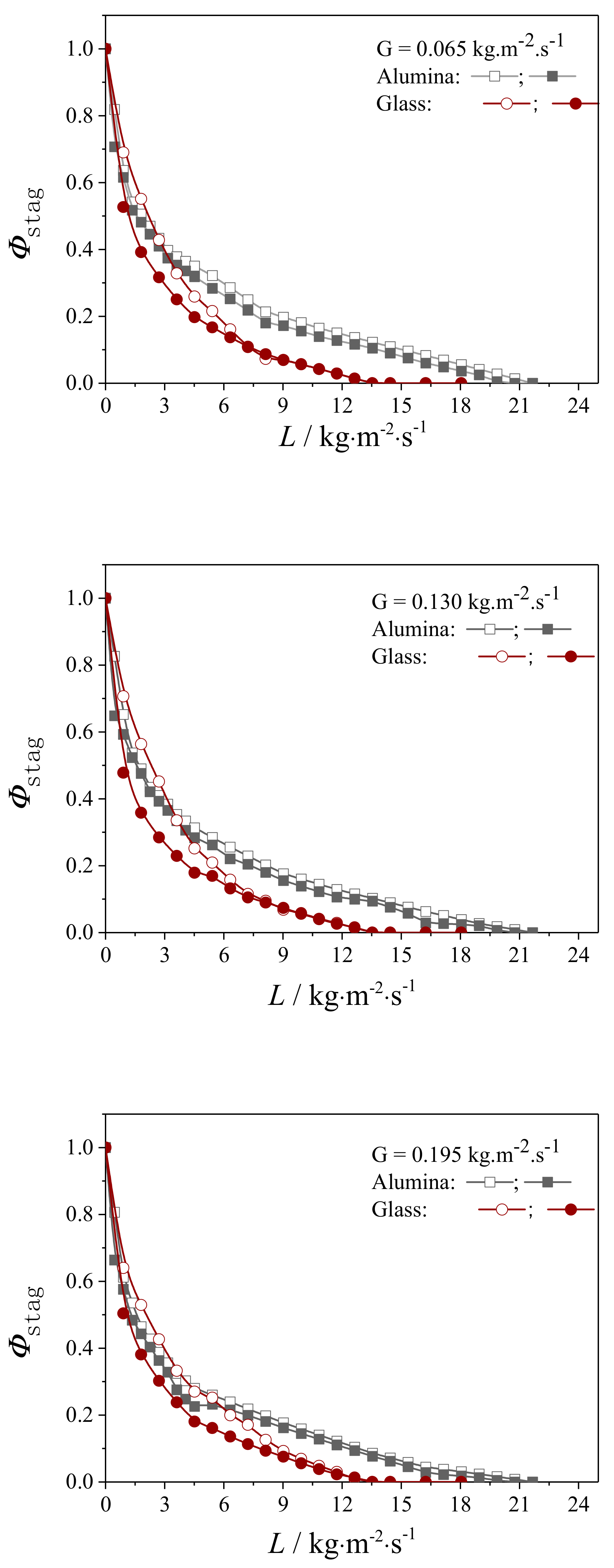
4.1.1. The Static Liquid Holdup
4.1.2. Hysteresis in Dynamic Liquid Holdup
4.1.3. Hysteresis in Pressure Drop
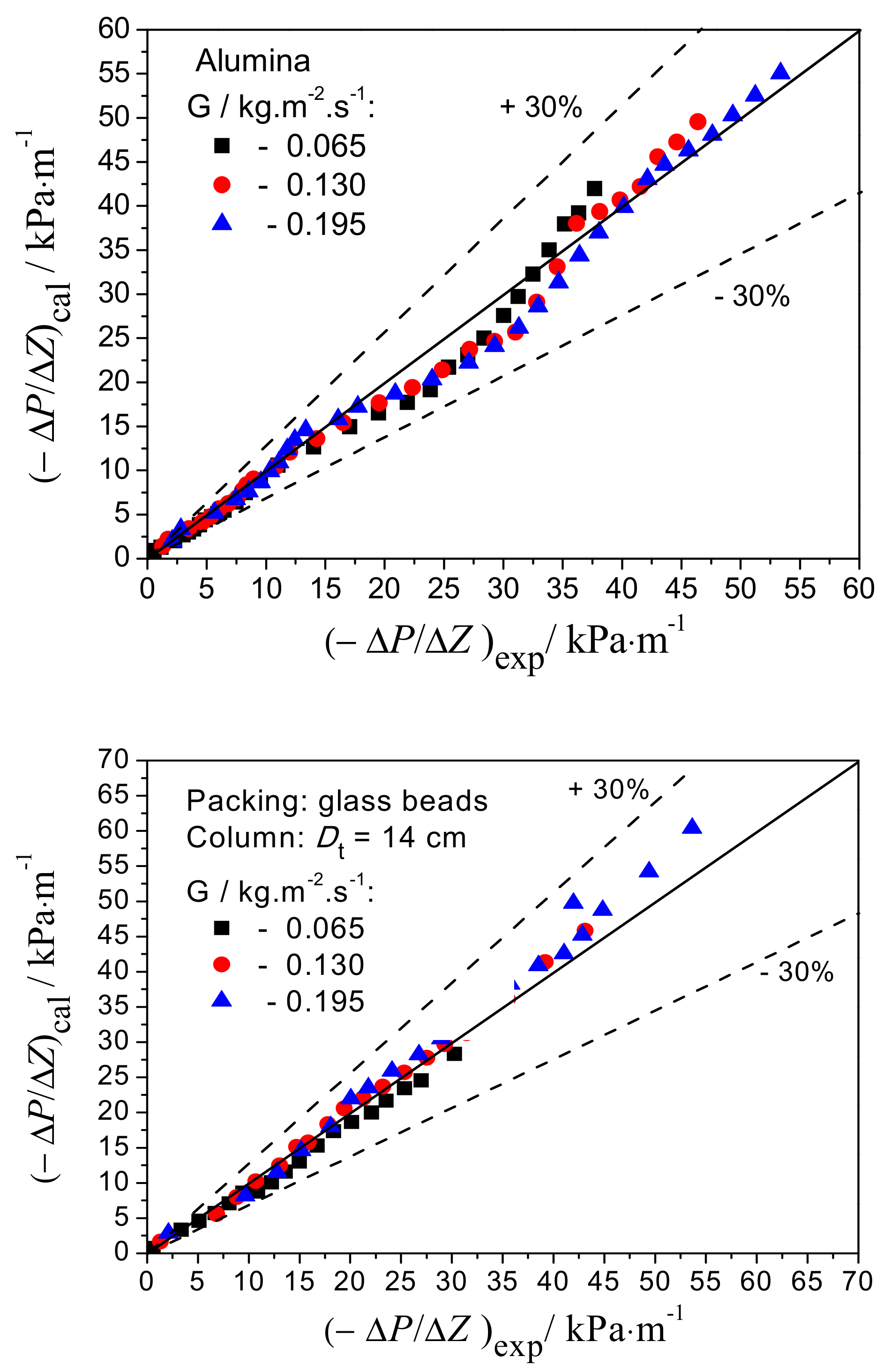
4.2. Modeling Results
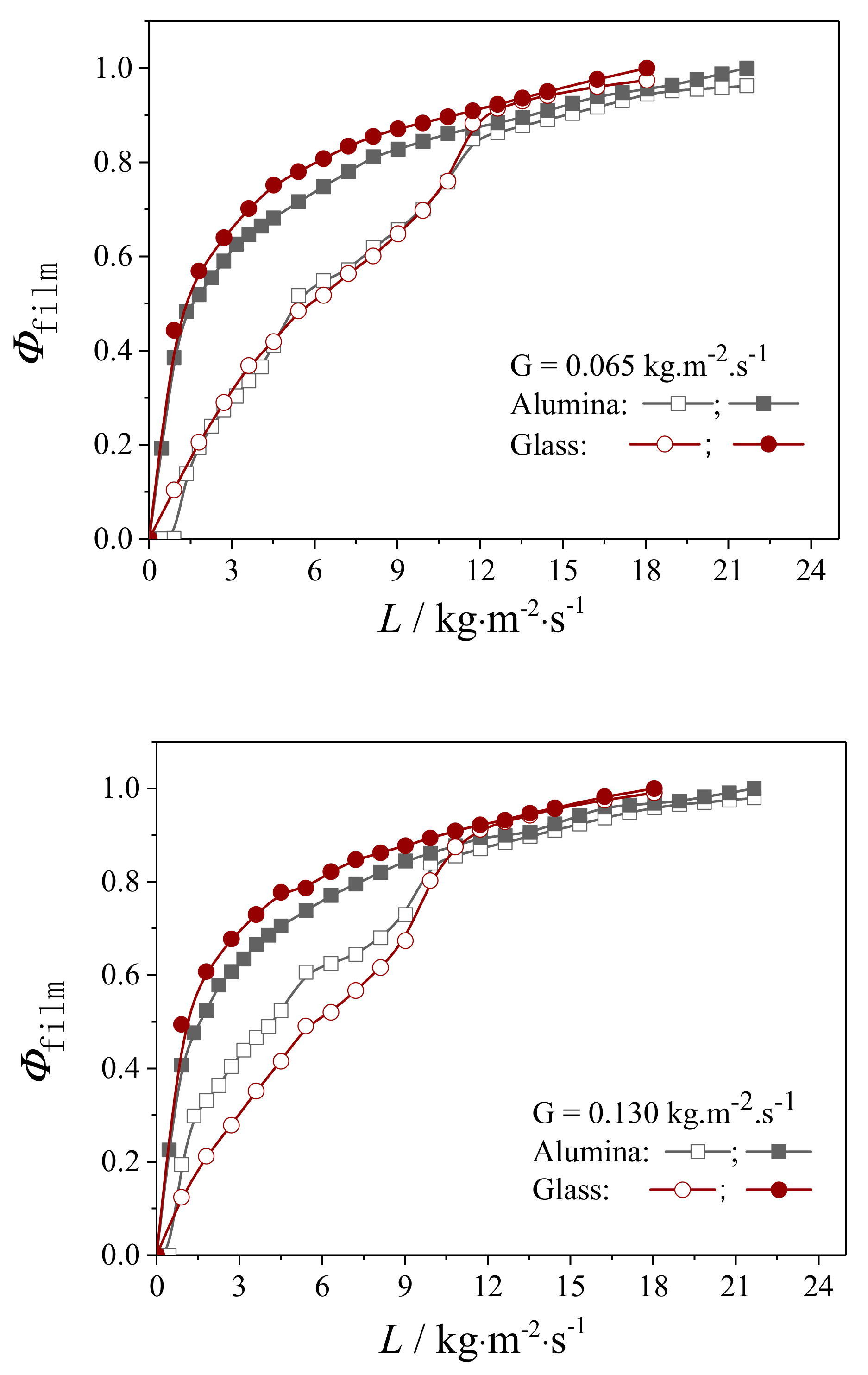
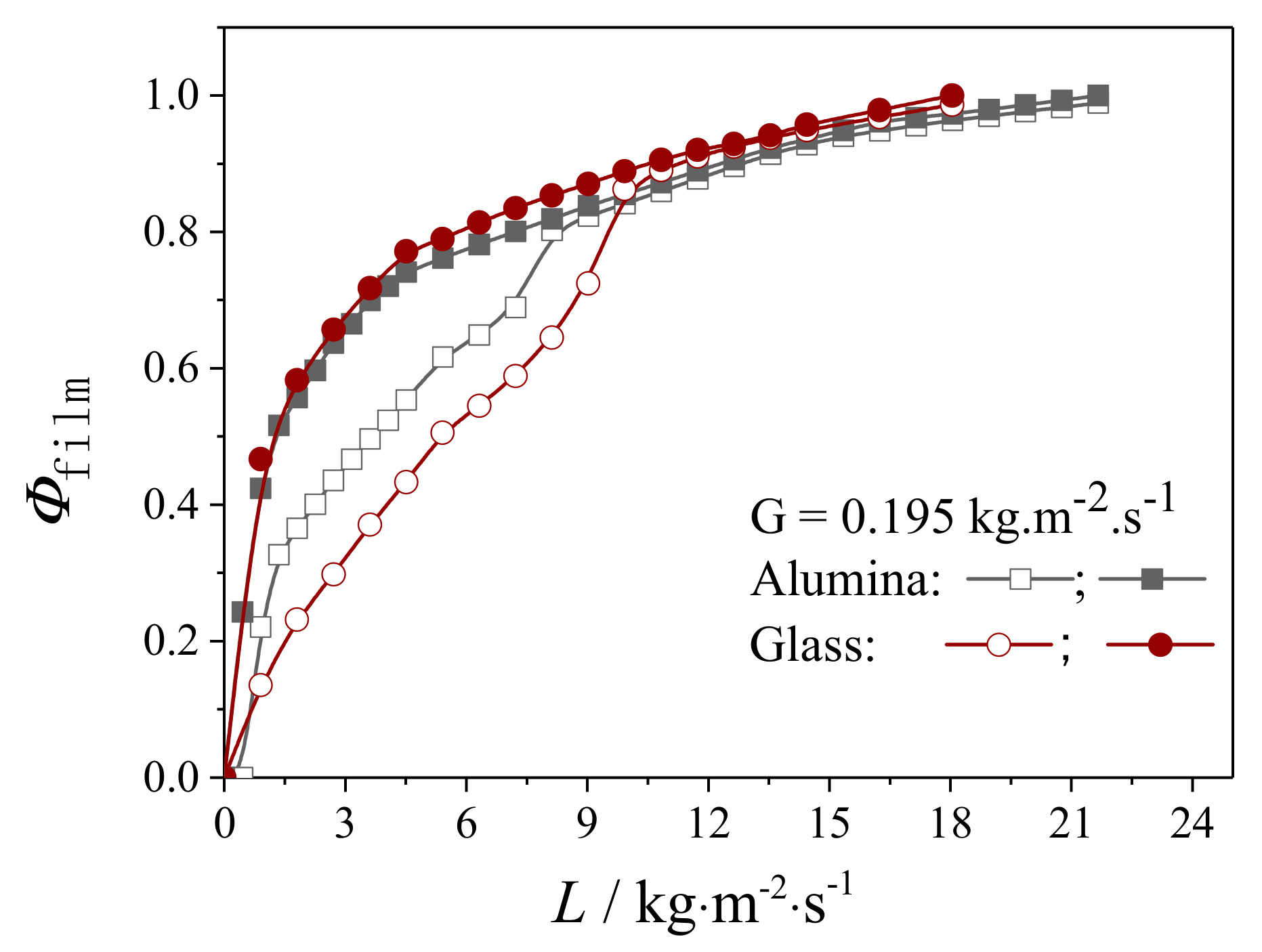
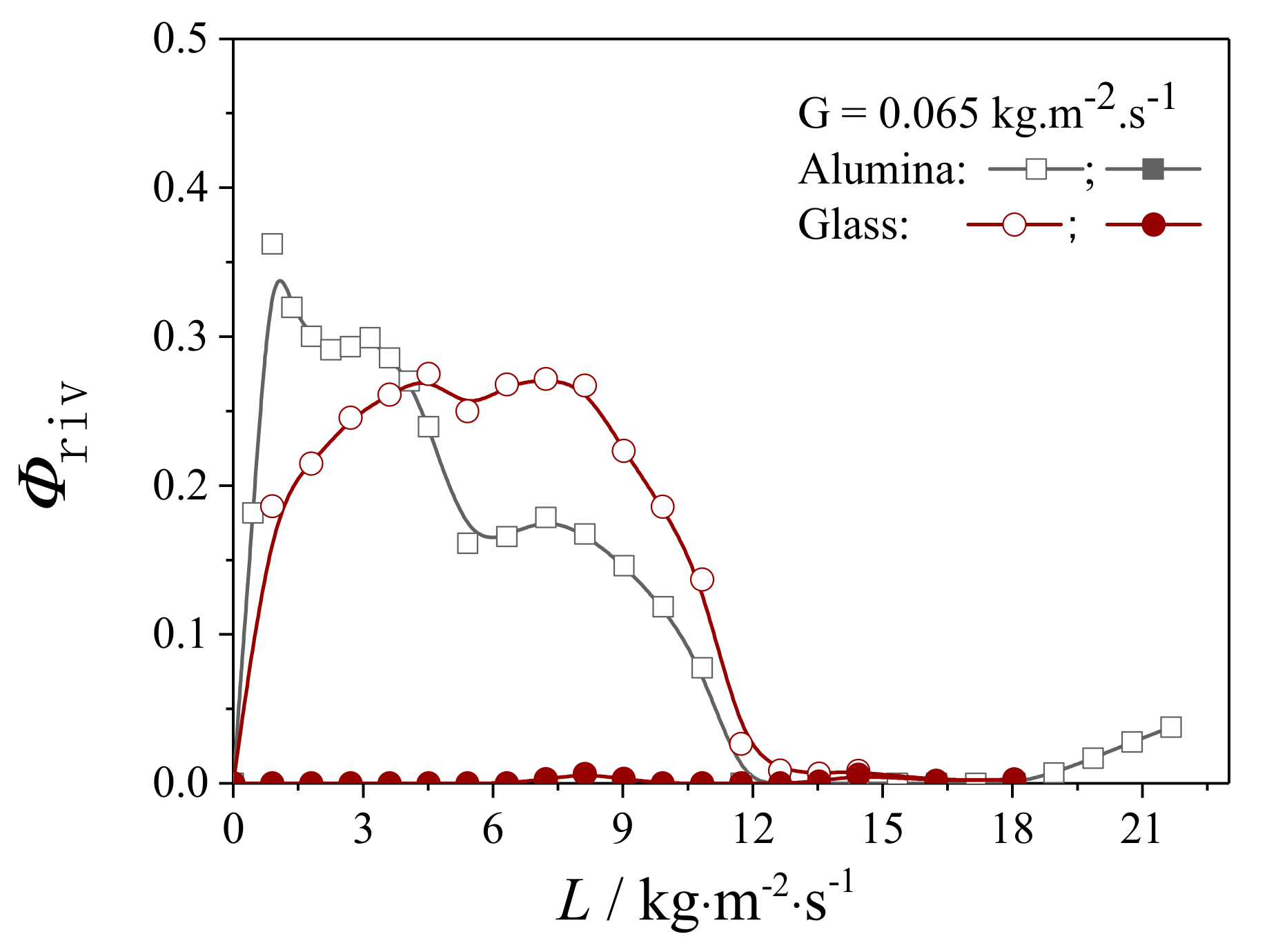
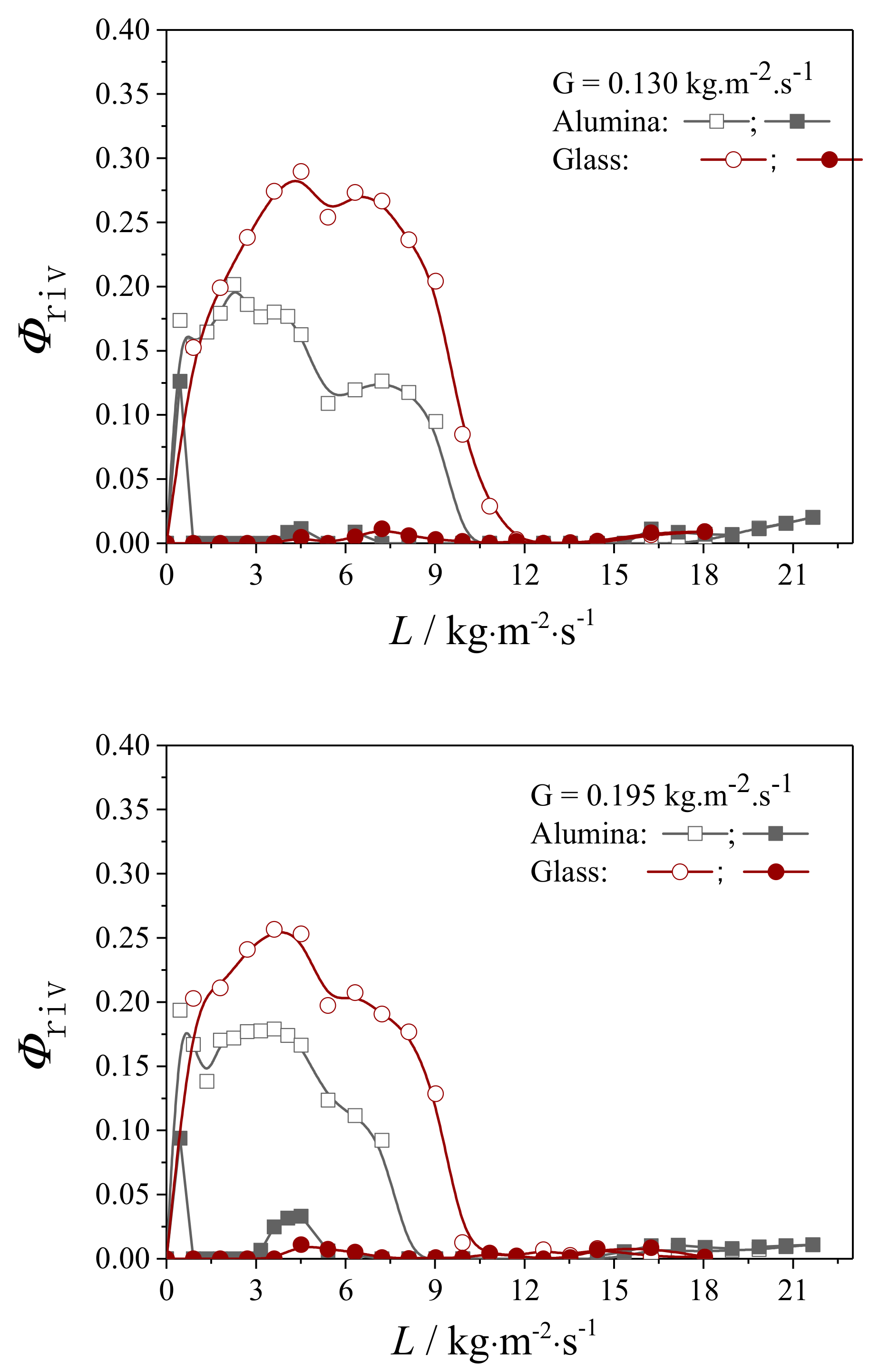
4.2.1. Liquid Flow Texture Characterization
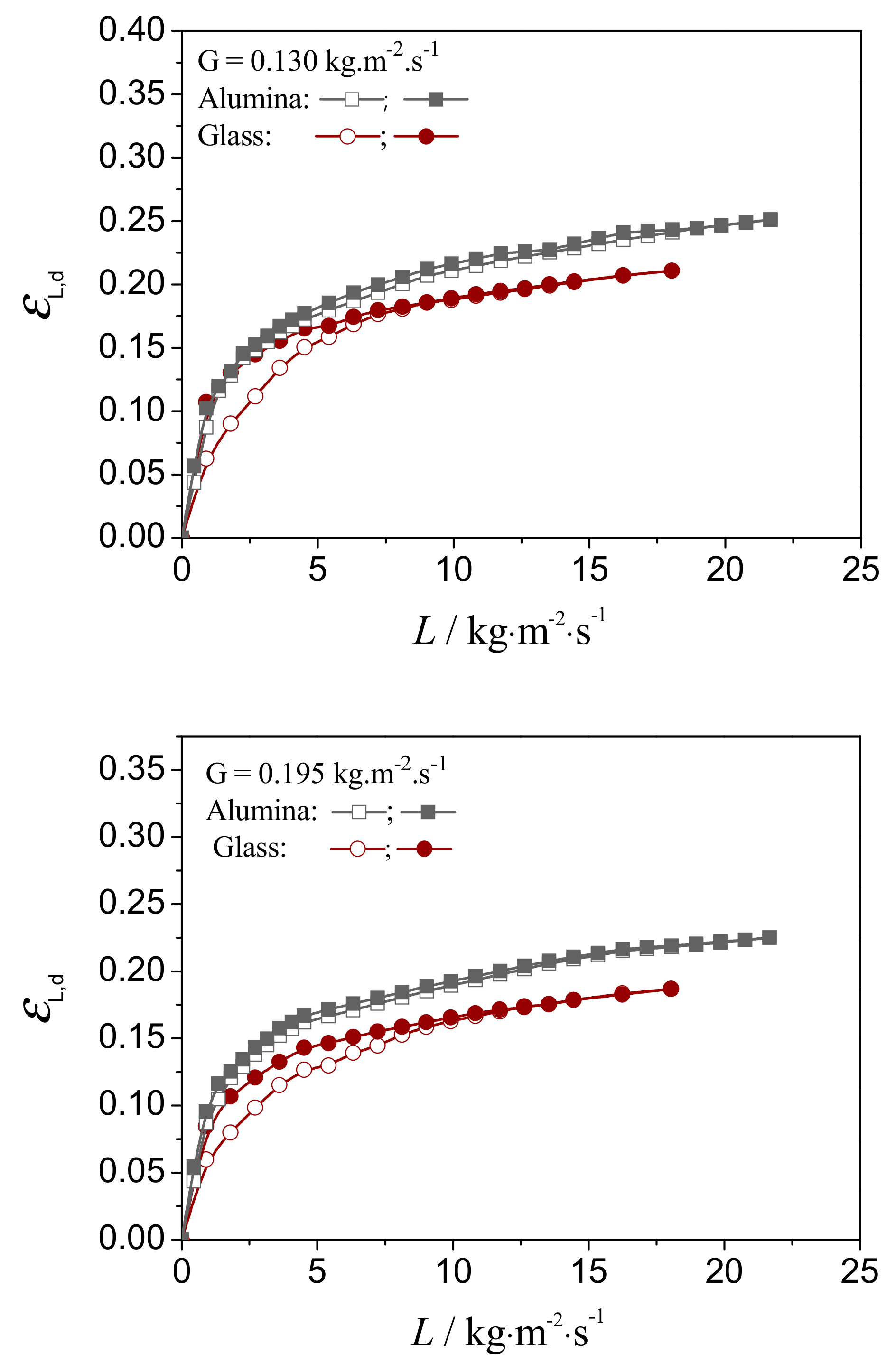
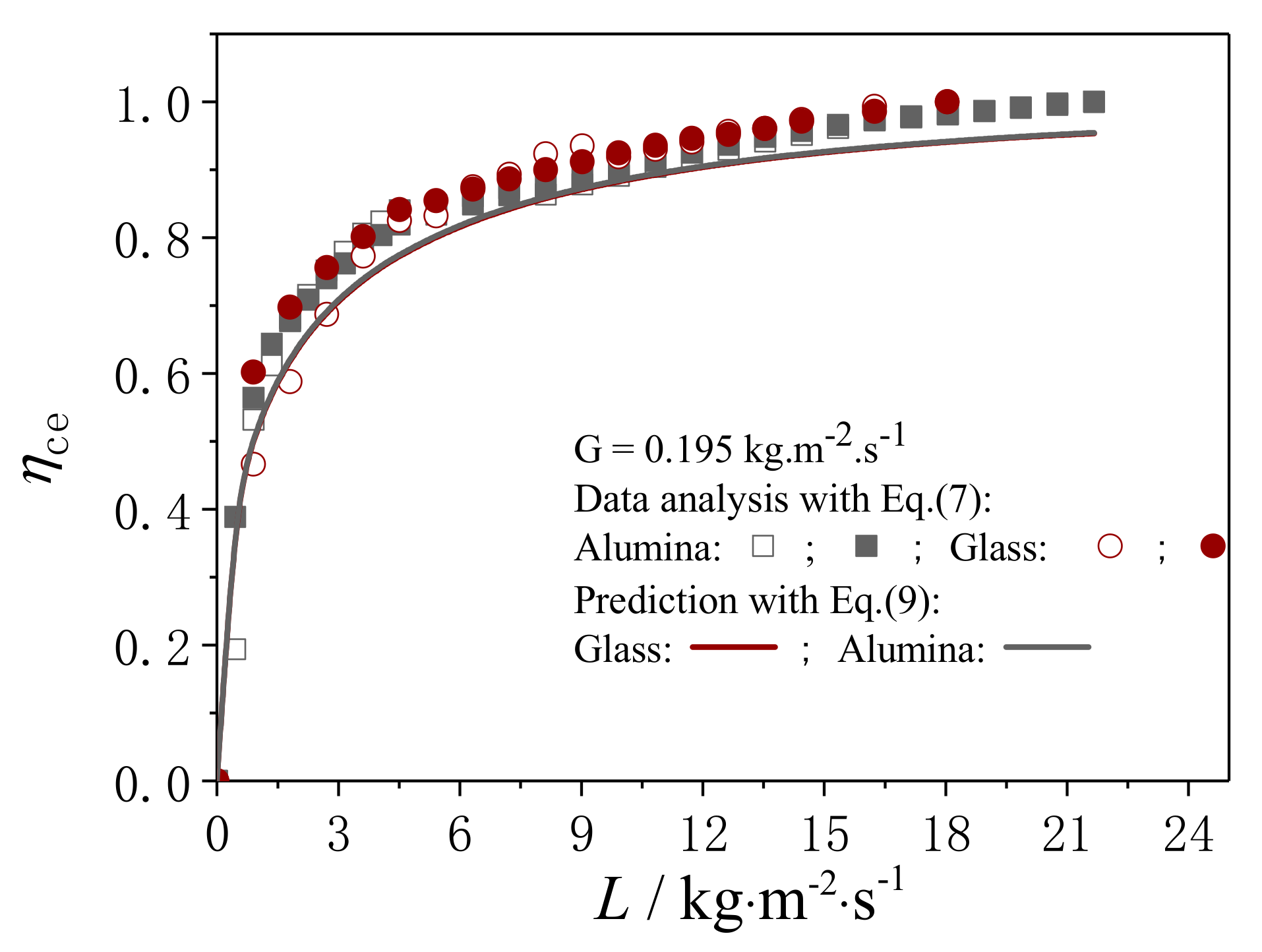
4.2.2. Evaluation on the External Wetting Efficiency
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| packing external surface area per unit volume of reactor | |
| A, B | Ergun equation coefficients, defined in Equation (1) |
| dp | packing diameter, m |
| Eötvos number, defined in Equation (11) | |
| Wetting fraction of the packing surface | |
| g | gravitational acceleration, 9.81 m·s−2 |
| G | gas flow rate, kg·m−2·s−1 |
| Galileo number, | |
| modified Galileo number, | |
| k | relative permeability |
| L | liquid flow rate, kg·m−2·s−1 |
| P | Pressure, N·m−2 |
| Reynolds number, | |
| modified Reynolds number, | |
| S | saturation degree, degree in Equation (4) |
| u | superficial velocity, m·s−1 |
| Z | axial distance, m |
| Greek letters | |
| α | coefficient in Equation (3) |
| β | exponent in Equation (3) |
| ε | porosity or holdup |
| ρ | density, kg·m−3 |
| σ | surface tension, N·m−1 |
| Φ | volumetric fraction, defined in Equation (5) |
| η | wetting efficiency |
| μ | viscosity, Pa·s |
| ψ | dimensionless pressure drop, defined in Equation (2) |
| Subscripts | |
| b | the bed averaged |
| ce | contacting efficiency |
| p | packing |
| L | liquid phase |
| G | gas phase |
| film | film flow |
| riv | rivulet flow |
| s | static liquid |
| stag | stagnant liquid |
References
- Mary, G.; Esmaeili, A.; Chaouki, J. Simulation of the Selective Hydrogenation of C3-Cut in the Liquid Phase. Int. J. Chem. React. Eng. 2016, 14, 859–874. [Google Scholar] [CrossRef]
- Guan, D.; Chen, Z.; Chen, X.; Zhang, Y.; Qi, Q.; Shi, Q.; Zhao, S.; Xu, C.; Zhang, L. Molecular-level heavy petroleum hydrotreating modeling and comparison with high-resolution mass spectrometry. Fuel 2021, 297, 120792. [Google Scholar] [CrossRef]
- Mohammed, A.E.; Jarullah, A.T.; Gheni, S.A.; Mujtaba, I.M. Optimal design and operation of an industrial three phase reactor for the oxidation of phenol. Comput. Chem. Eng. 2016, 94, 257–271. [Google Scholar] [CrossRef]
- Kasperczyk, D.; Urbaniec, K.; Barbusinski, K.; Rene, E.R.; Colmenares-Quintero, R.F. Application of a compact trickle-bed bioreactor for the removal of odor and volatile organic compounds emitted from a wastewater treatment plant. J. Environ. Manag. 2019, 236, 413–419. [Google Scholar] [CrossRef] [PubMed]
- Russo, V.; Kilpiö, T.; Di Serio, M.; Tesser, R.; Santacesaria, E.; Murzin, D.Y.; Salmi, T. Dynamic non-isothermal trickle bed reactor with both internal diffusion and heat conduction: Sugar hydrogenation as a case study. Chem. Eng. Res. Des. 2015, 102, 171–185. [Google Scholar] [CrossRef]
- Schubert, M.; Kost, S.; Lange, R.; Salmi, T.; Haase, S.; Hampel, U. Maldistribution susceptibility of monolith reactors: Case study of glucose hydrogenation performance. AIChE J. 2016, 62, 4346–4364. [Google Scholar] [CrossRef]
- Srifa, A.; Faungnawakij, K.; Itthibenchapong, V.; Assabumrungrat, S. Roles of monometallic catalysts in hydrodeoxygenation of palm oil to green diesel. Chem. Eng. J. 2015, 278, 249–258. [Google Scholar] [CrossRef]
- Aho, A.; Rosales, C.; Eränen, K.; Salmi, T.; Murzin, D.Y.; Grénman, H. Biohydrogen from dilute side streams-Influence of reaction conditions on the conversion and selectivity in aqueous phase reforming of xylitol. Biomass-Bioenergy 2020, 138, 105590. [Google Scholar] [CrossRef]
- Thema, M.; Weidlich, T.; Kaul, A.; Böllmann, A.; Huber, H.; Bellack, A.; Karl, J.; Sterner, M. Optimized biological CO2-methanation with a pure culture of thermophilic methanogenic archaea in a trickle-bed reactor. Bioresour. Technol. 2021, 333, 125135. [Google Scholar] [CrossRef]
- Hickman, D.A.; Degenstein, J.C.; Ribeiro, F.H. Fundamental principles of laboratory fixed bed reactor design. Curr. Opin. Chem. Eng. 2016, 13, 1–9. [Google Scholar] [CrossRef]
- Hickman, D.A.; Holbrook, M.T.; Mistretta, S.; Rozeveld, S.J. Successful Scale-up of an Industrial Trickle Bed Hydrogenation Using Laboratory Reactor Data. Ind. Eng. Chem. Res. 2013, 52, 15287–15292. [Google Scholar] [CrossRef]
- Zimmerman, S.P.; Ng, K.M. Liquid distribution in trickling flow trickle-bed reactors. Chem. Eng. Sci. 1986, 41, 861–866. [Google Scholar] [CrossRef]
- Lutran, P.G.; Ng, K.M.; Delikat, E.P. Liquid distribution in trickle-beds. An experimental study using computer-assisted tomography. Ind. Eng. Chem. Res. 1991, 30, 1270–1280. [Google Scholar] [CrossRef]
- Sederman, A.J.; Gladden, L.F. Magnetic resonance imaging as a quantitative probe of gas–liquid distribution and wetting efficiency in trickle-bed reactors. Chem. Eng. Sci. 2001, 56, 2615–2628. [Google Scholar] [CrossRef]
- Van der Merwe, W.; Nicol, W.; de Beer, F. Trickle flow distribution and stability by X-ray radiography. Chem. Eng. J. 2007, 132, 47–59. [Google Scholar] [CrossRef]
- Salleh, K.A.M.; Lee, H.K.; Al-Dahhan, M.H. Studying local liquid velocity in liquid–solid packed bed using the newly developed X-ray DIR technique. Flow Meas. Instrum. 2015, 42, 1–5. [Google Scholar] [CrossRef]
- Solomenko, Z.; Haroun, Y.; Fourati, M.; Larachi, F.; Boyer, C.; Augier, F. Liquid spreading in trickle-bed reactors: Experiments and numerical simulations using Eulerian–Eulerian two-fluid approach. Chem. Eng. Sci. 2015, 126, 698–710. [Google Scholar] [CrossRef]
- Markthaler, S.; Plankenbühler, T.; Weidlich, T.; Neubert, M.; Karl, J. Numerical simulation of trickle bed reactors for biological methanation. Chem. Eng. Sci. 2020, 226, 115847. [Google Scholar] [CrossRef]
- Lopes, R.J.G.; de Sousa, V.S.L.; Quinta-Ferreira, R.M. Numerical simulation of reactive pulsing flow for the catalytic wet oxidation in TBR using a VOF technique. AIChE J. 2012, 58, 493–504. [Google Scholar] [CrossRef]
- Bouras, H.; Haroun, Y.; Bodziony, F.F.; Philippe, R.; Fongarland, P.; Augier, F. Use of CFD for pressure drop, liquid saturation and wetting predictions in trickle bed reactors for different catalyst particle shapes. Chem. Eng. Sci. 2021, 249, 117315. [Google Scholar] [CrossRef]
- Schwartz, J.G.; Weger, E.; Duduković, M.P. A new tracer method for determination of liquid-solid contacting efficiency in trickle-bed reactors. AIChE J. 1976, 22, 894–904. [Google Scholar] [CrossRef]
- Colombo, A.J.; Baldi, G.; Sicardi, S. Solid-liquid contacting effectiveness in trickle bed reactors. Chem. Eng. Sci. 1976, 31, 1101–1108. [Google Scholar] [CrossRef]
- El-Hisnawi, A.A.; DudukoviĆ, M.P.; Mills, P.L. Trickle-Bed Reactors: Dynamic Tracer Tests, Reaction Studies, and Modeling of Reactor Performance. In Chemical Reaction Engineering; American Chemical Society: Boston, MA, USA, 1982; Volume 196, pp. 421–440. [Google Scholar]
- Mills, P.L.; Dudukovic, M.P. Evaluation of liquid-solid contacting in trickle-bed reactors by tracer methods. AIChE J. 1981, 27, 893–904. [Google Scholar] [CrossRef]
- Ring, Z.E.; Missen, R.W. Trickle-bed reactors: Tracer study of liquid holdup and wetting efficiency at high temperature and pressure. Can. J. Chem. Eng. 1991, 69, 1016–1020. [Google Scholar] [CrossRef]
- Julcour-Lebigue, C.; Baussaron, L.; Delmas, H.; Wilhelm, A.-M. Theoretical analysis of tracer method for the measurement of wetting efficiency. Chem. Eng. Sci. 2007, 62, 5374–5379. [Google Scholar] [CrossRef][Green Version]
- Baussaron, L.; Julcour-Lebigue, C.; Wilhelm, A.-M.; Boyer, C.; Delmas, H. Partial Wetting in Trickle Bed Reactors: Measurement Techniques and Global Wetting Efficiency. Ind. Eng. Chem. Res. 2007, 46, 8397–8405. [Google Scholar] [CrossRef]
- Baussaron, L.; Julcour-Lebigue, C.; Wilhelm, A.-M.; Delmas, H.; Boyer, C. Wetting topology in trickle bed reactors. AIChE J. 2007, 53, 1850–1860. [Google Scholar] [CrossRef]
- Lappalainen, K.; Alopaeus, V.; Manninen, M.; Aittamaa, J. Improved Hydrodynamic Model for Wetting Efficiency, Pressure Drop, and Liquid Holdup in Trickle-Bed Reactors. Ind. Eng. Chem. Res. 2008, 47, 8436–8444. [Google Scholar] [CrossRef]
- Van Houwelingen, A.J.; Sandrock, C.; Nicol, W. Particle wetting distribution in trickle-bed reactors. AIChE J. 2006, 52, 3532–3542. [Google Scholar] [CrossRef]
- Julcour-Lebigue, C.; Augier, F.; Maffre, H.; Wilhelm, A.-M.; Delmas, H. Measurements and Modeling of Wetting Efficiency in Trickle-Bed Reactors: Liquid Viscosity and Bed Packing Effects. Ind. Eng. Chem. Res. 2009, 48, 6811–6819. [Google Scholar] [CrossRef]
- Pironti, F.; Mizrahi, D.; Acosta, A.N.; González-Mendizabal, D. Liquid–solid wetting factor in trickle-bed reactors: Its determination by a physical method. Chem. Eng. Sci. 1999, 54, 3793–3800. [Google Scholar] [CrossRef]
- Kundu, A.; Nigam, K.D.P.; Verma, R.P. Catalyst wetting characteristics in trickle-bed reactors. AIChE J. 2003, 49, 2253–2263. [Google Scholar] [CrossRef]
- Satterfield, C.N. Trickle-bed reactors. AIChE J. 1975, 21, 209–228. [Google Scholar] [CrossRef]
- Morita, S.; Smith, J.M. Mass Transfer and Contacting Efficiency in a Trickle-Bed Reactor. Ind. Eng. Chem. Fund. 1978, 17, 113–120. [Google Scholar] [CrossRef]
- Van Houwelingen, A.J.; Nicol, W. Parallel hydrogenation for the quantification of wetting efficiency and liquid-solid mass transfer in a trickle-bed reactor. AIChE J. 2011, 57, 1310–1319. [Google Scholar] [CrossRef]
- Adamsom, A.; Gast, A. Physical Chemistry of Surfaces, 6th ed.; Wiley: New York, NY, USA, 1997. [Google Scholar]
- Maiti, R.N.; Khanna, R.; Sen, P.K.; Nigam, K.D.P. Enhanced liquid spreading due to porosity. Chem. Eng. Sci. 2004, 59, 2817–2820. [Google Scholar] [CrossRef]
- Ravindra, P.V.; Rao, D.P.; Rao, M.S. Liquid Flow Texture in Trickle-Bed Reactors: An Experimental Study. Ind. Eng. Chem. Res. 1997, 36, 5133–5145. [Google Scholar] [CrossRef]
- Khanna, R.; Nigam, K.D.P. Partial wetting in porous catalysts: Wettability and wetting efficiency. Chem. Eng. Sci. 2002, 57, 3401–3405. [Google Scholar] [CrossRef]
- Maiti, R.N.; Arora, R.; Khanna, R.; Nigam, K.D.P. The liquid spreading on porous solids: Dual action of pores. Chem. Eng. Sci. 2005, 60, 6235–6239. [Google Scholar] [CrossRef]
- Schubert, M.; Hessel, G.; Zippe, C.; Lange, R.; Hampel, U. Liquid flow texture analysis in trickle bed reactors using high-resolution gamma ray tomography. Chem. Eng. J. 2008, 140, 332–340. [Google Scholar] [CrossRef]
- Wang, R.; Mao, Z.-S.; Chen, J. Experimental and theoretical studies of pressure drop hysteresis in trickle bed reactors. Chem. Eng. Sci. 1995, 50, 2321–2328. [Google Scholar] [CrossRef]
- Cheng, Z.; Kong, X.; Zhu, J.; Wang, Z.; Jin, J.; Huang, Z. Hydrodynamic modeling on the external liquid–solid wetting efficiency in a trickling flow reactor. AIChE J. 2013, 59, 283–294. [Google Scholar] [CrossRef]
- Gianetto, A.; Specchia, V. Trickle-bed reactors: State of art and perspectives. Chem. Eng. Sci. 1992, 47, 3197–3213. [Google Scholar] [CrossRef]
- Sáez, A.E.; Carbonell, R.G. Hydrodynamic parameters for gas-liquid cocurrent flow in packed beds. AlChE J. 1985, 31, 52–62. [Google Scholar] [CrossRef]
- Christensen, G.; McGovern, S.J.; Sundaresan, S. Cocurrent downflow of air and water in a two-dimensional packed column. AIChE J. 1986, 32, 1677–1689. [Google Scholar] [CrossRef]
- Levec, J.; Grosser, K.; Carbonell, R.G. The hysteretic behavior of pressure drop and liquid holdup in trickle beds. AIChE J. 1988, 34, 1027–1030. [Google Scholar] [CrossRef]
- Chu, C.F.; Ng, K.M. Model for pressure drop hysteresis in trickle-beds. AIChE J. 1989, 35, 1365–1369. [Google Scholar] [CrossRef]
- Kramer, G.J. Static liquid hold-up and capillary rise in packed beds. Chem. Eng. Sci. 1998, 53, 2985–2992. [Google Scholar] [CrossRef]
- Sáez, A.E.; Yépez, M.M.; Cabrera, C.; Soria, E.M. Static liquid holdup in packed beds of spherical particles. AIChE J. 1991, 37, 1733–1736. [Google Scholar] [CrossRef]
- Ortiz-Arroyo, A.; Larachi, F.Ç.; Iliuta, I. Method for inferring contact angle and for correlating static liquid hold-up in packed beds. Chem. Eng. Sci. 2003, 58, 2835–2855. [Google Scholar] [CrossRef]




| Packing Material | Shape | dp /mm | |Exp.-Cal. *|/Cal. * | |||
|---|---|---|---|---|---|---|
| Exp. | Cal. * | |||||
| alumina | sphere | 1.6 | 0.361 | 0.07469 | 0.04975 | 50.13% |
| glass | sphere | 1.9 | 0.368 | 0.04994 | 0.04965 | 0.58% |
| Packing Material | G/kg·m2·s−1 | ||
|---|---|---|---|
| 0.065 | 0.130 | 0.195 | |
| Alumina | |||
| Glass | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Z.; Luo, G.; Tang, Y.; Ling, D.; Chen, Z.; Liu, P.; Zhang, B. External Wetting Efficiency in a Three-Phase Fixed Bed Loaded with Porous and Non-Porous Packings. Processes 2022, 10, 135. https://doi.org/10.3390/pr10010135
Cheng Z, Luo G, Tang Y, Ling D, Chen Z, Liu P, Zhang B. External Wetting Efficiency in a Three-Phase Fixed Bed Loaded with Porous and Non-Porous Packings. Processes. 2022; 10(1):135. https://doi.org/10.3390/pr10010135
Chicago/Turabian StyleCheng, Zhenmin, Gang Luo, Yanling Tang, Dan Ling, Zhaoxuan Chen, Peng Liu, and Bo Zhang. 2022. "External Wetting Efficiency in a Three-Phase Fixed Bed Loaded with Porous and Non-Porous Packings" Processes 10, no. 1: 135. https://doi.org/10.3390/pr10010135
APA StyleCheng, Z., Luo, G., Tang, Y., Ling, D., Chen, Z., Liu, P., & Zhang, B. (2022). External Wetting Efficiency in a Three-Phase Fixed Bed Loaded with Porous and Non-Porous Packings. Processes, 10(1), 135. https://doi.org/10.3390/pr10010135








