Design, Heat Transfer, and Visualization of the Milli-Reactor by CFD and ANN
Abstract
:1. Introduction
2. Numerical Simulation and Experiment
2.1. Numerical Calculation
2.1.1. Geometric Model
2.1.2. Governing Equations and Boundary Conditions
2.1.3. Data Reduction
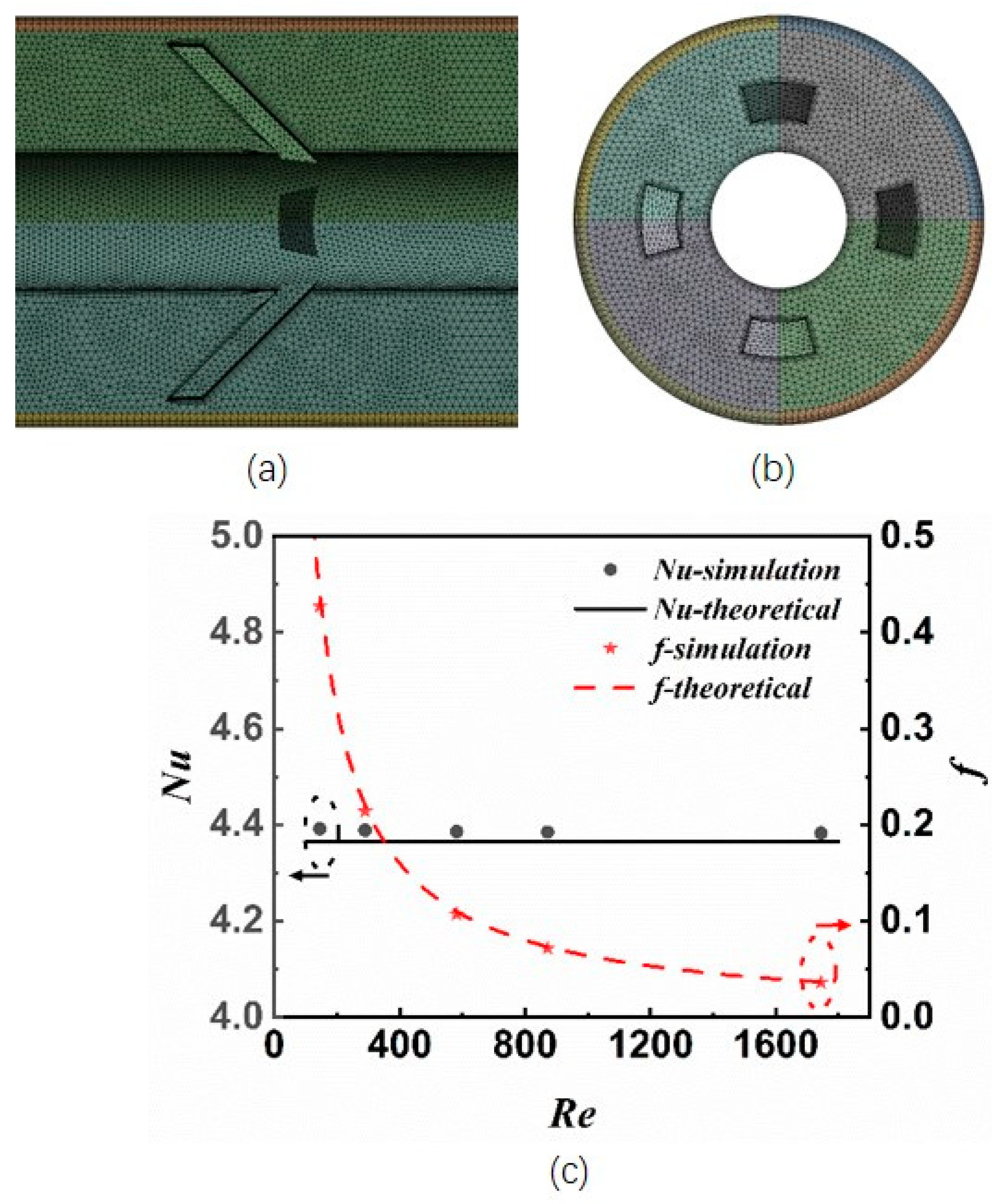
2.1.4. Grid Generation and Verification of Accuracy
2.2. PIV Visualization Experiment
2.3. Stability Criterion
2.4. Neural Network
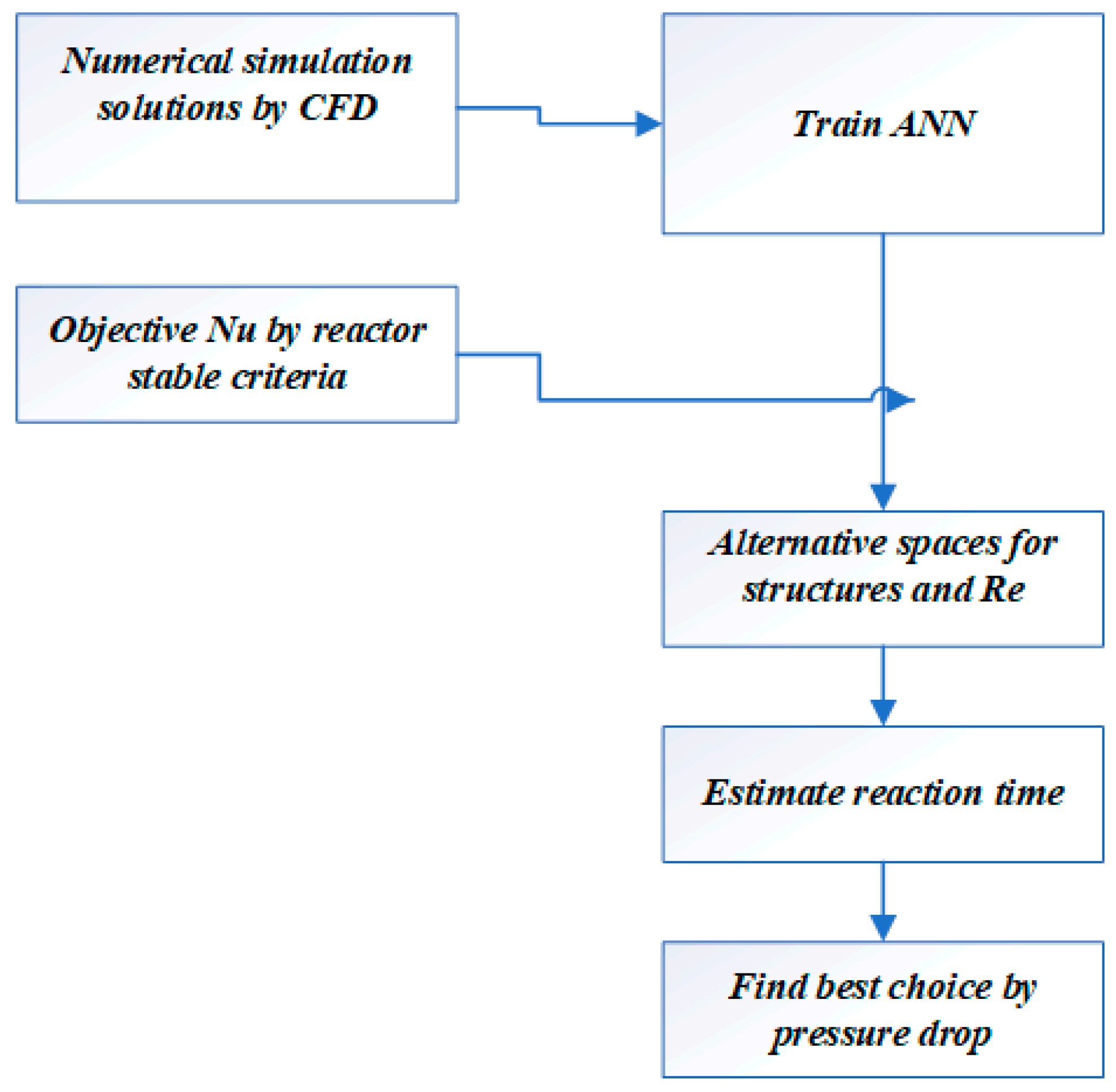
2.5. Milli-Reactor Design Process
3. Results and Discussion
3.1. Thermal-Hydraulic Characteristics
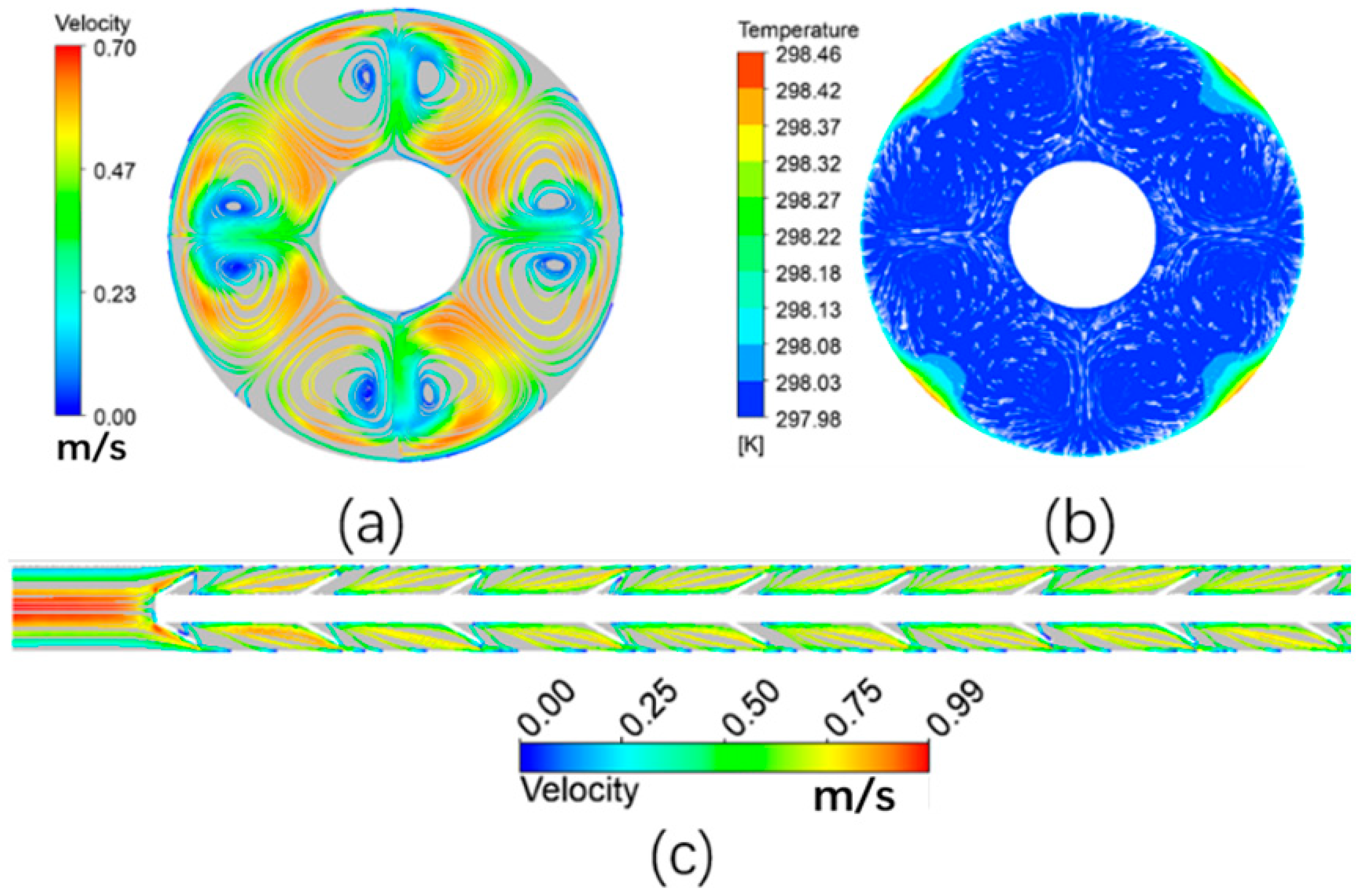
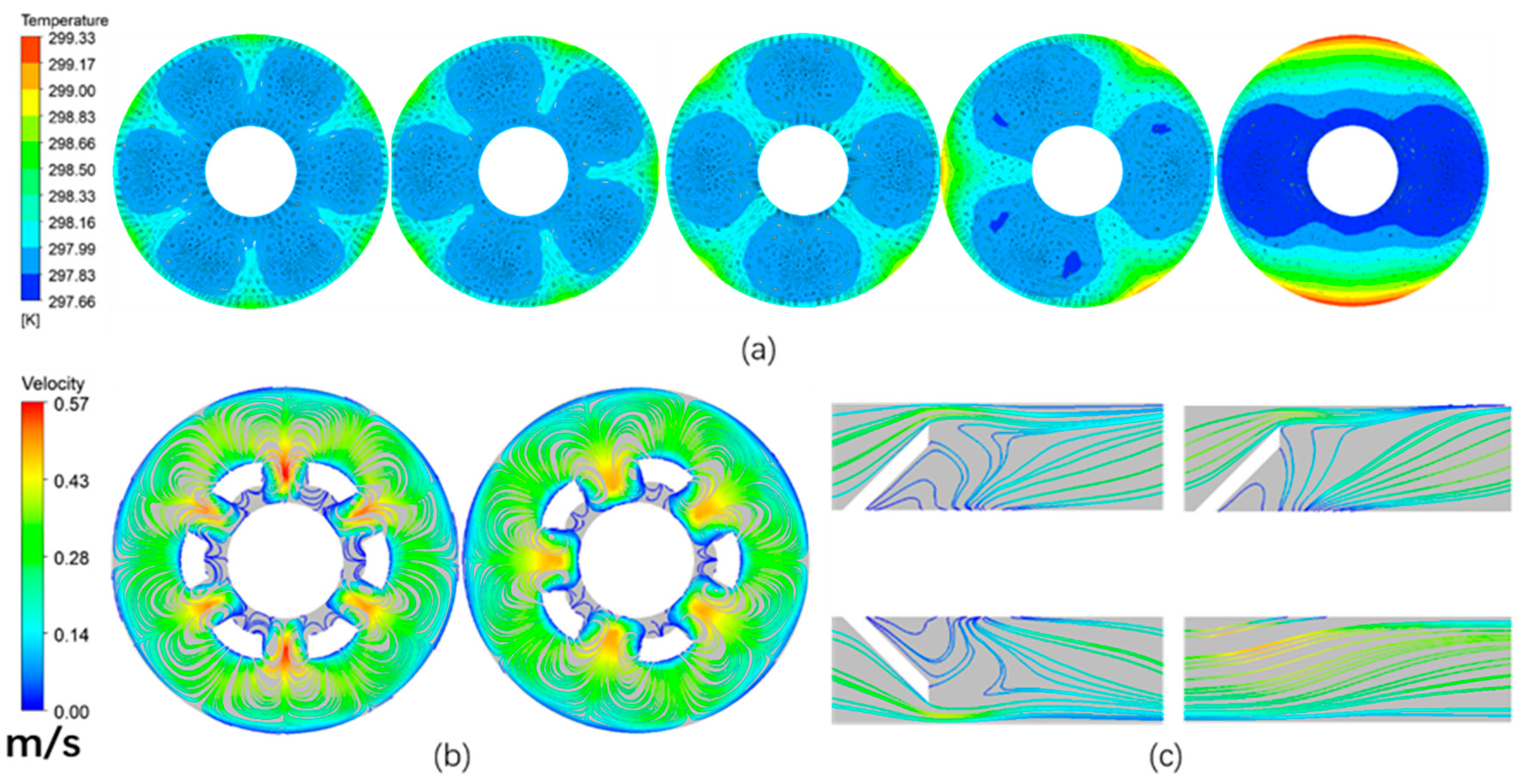
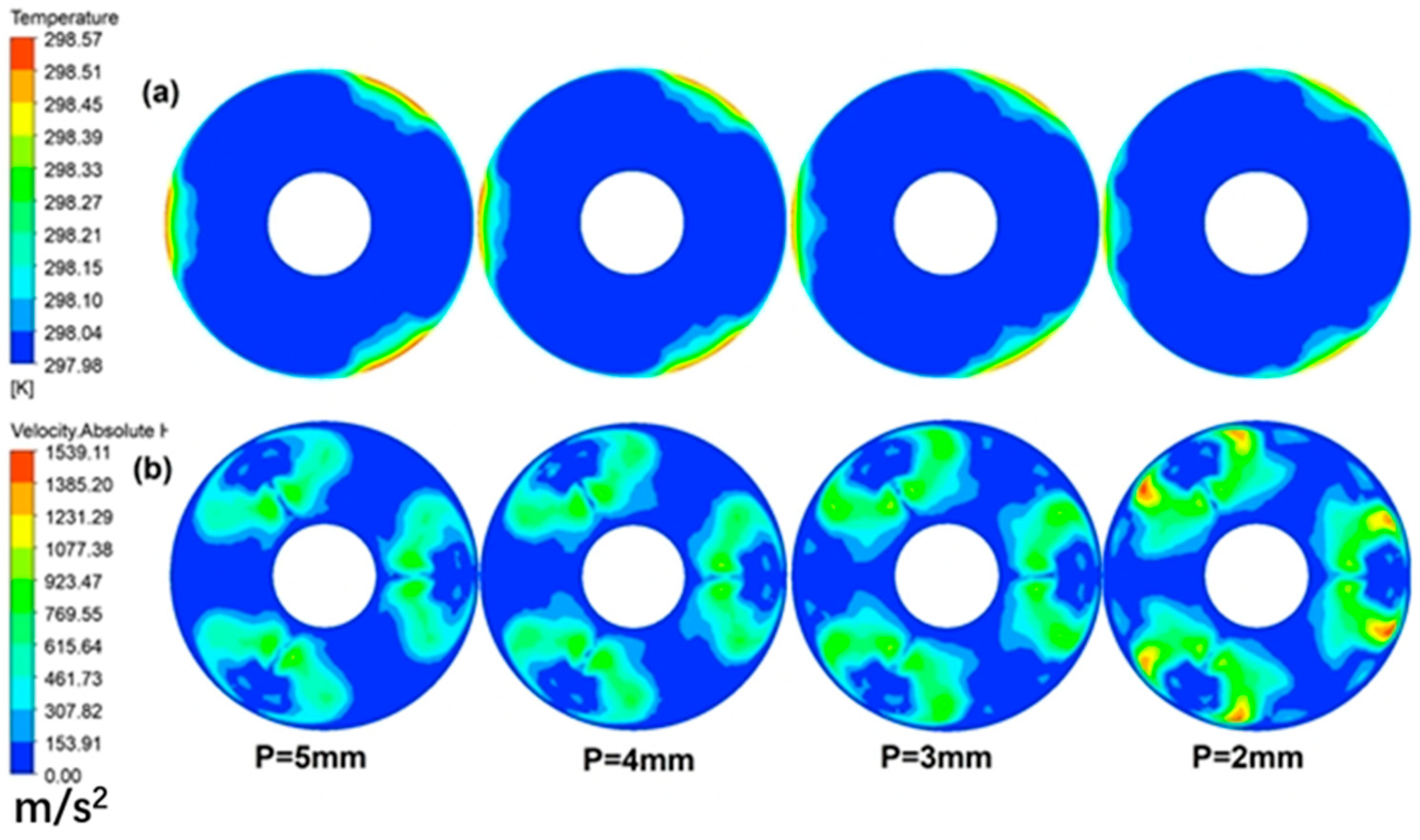
3.1.1. Heat Transfer Mechanism
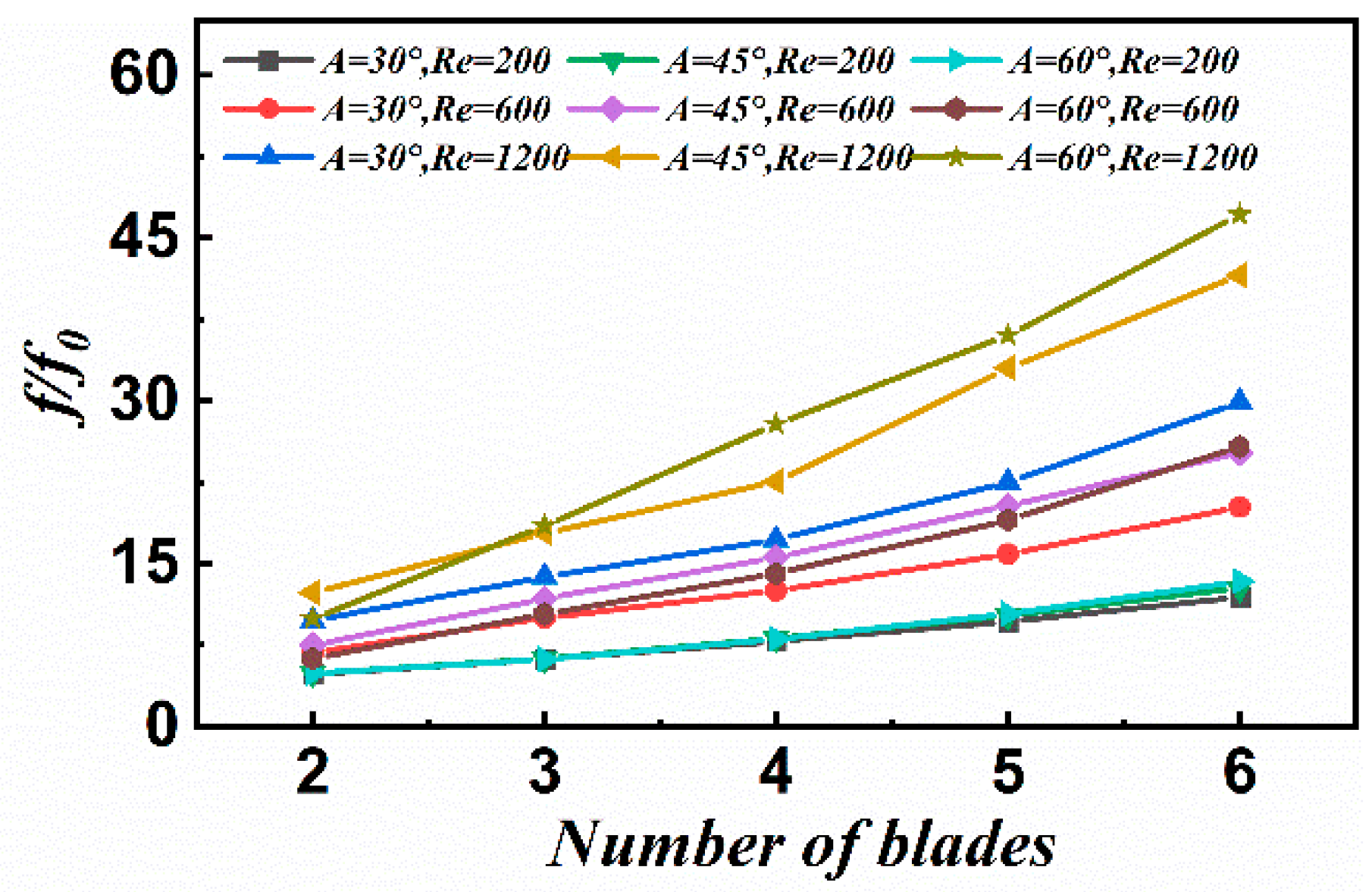
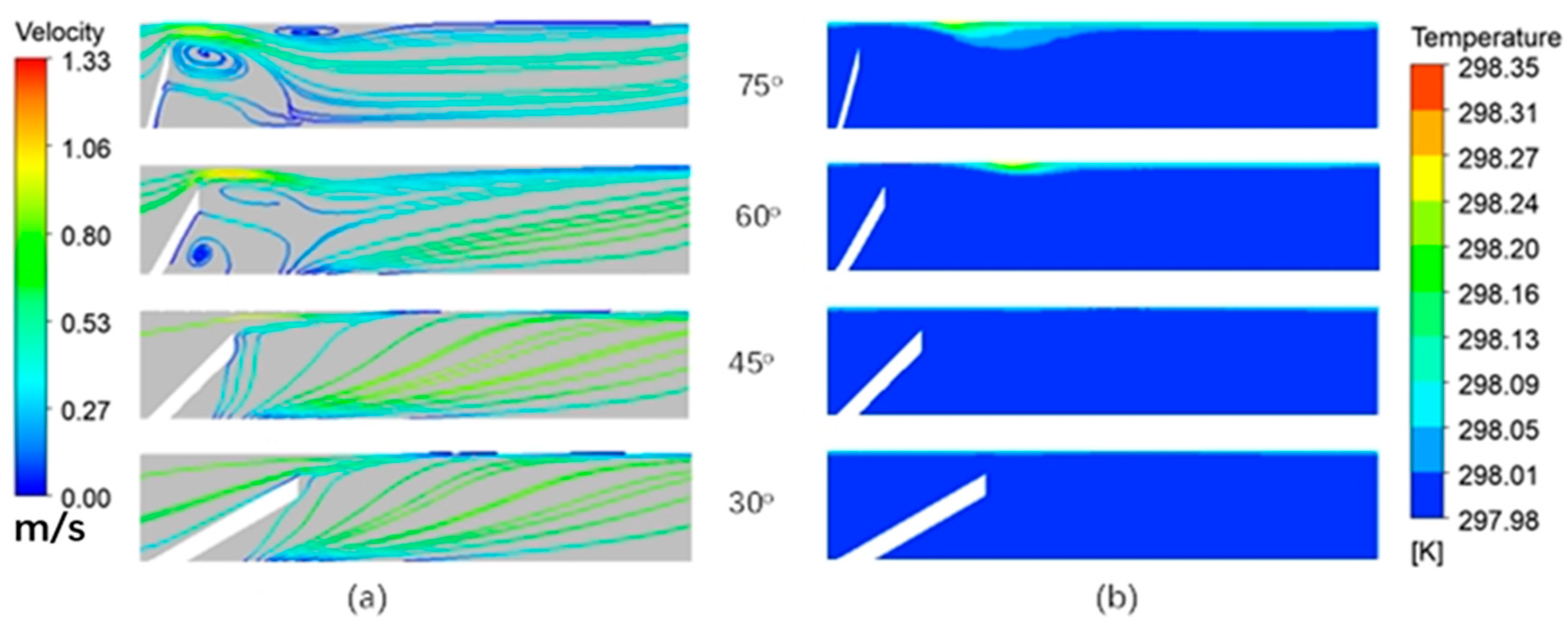
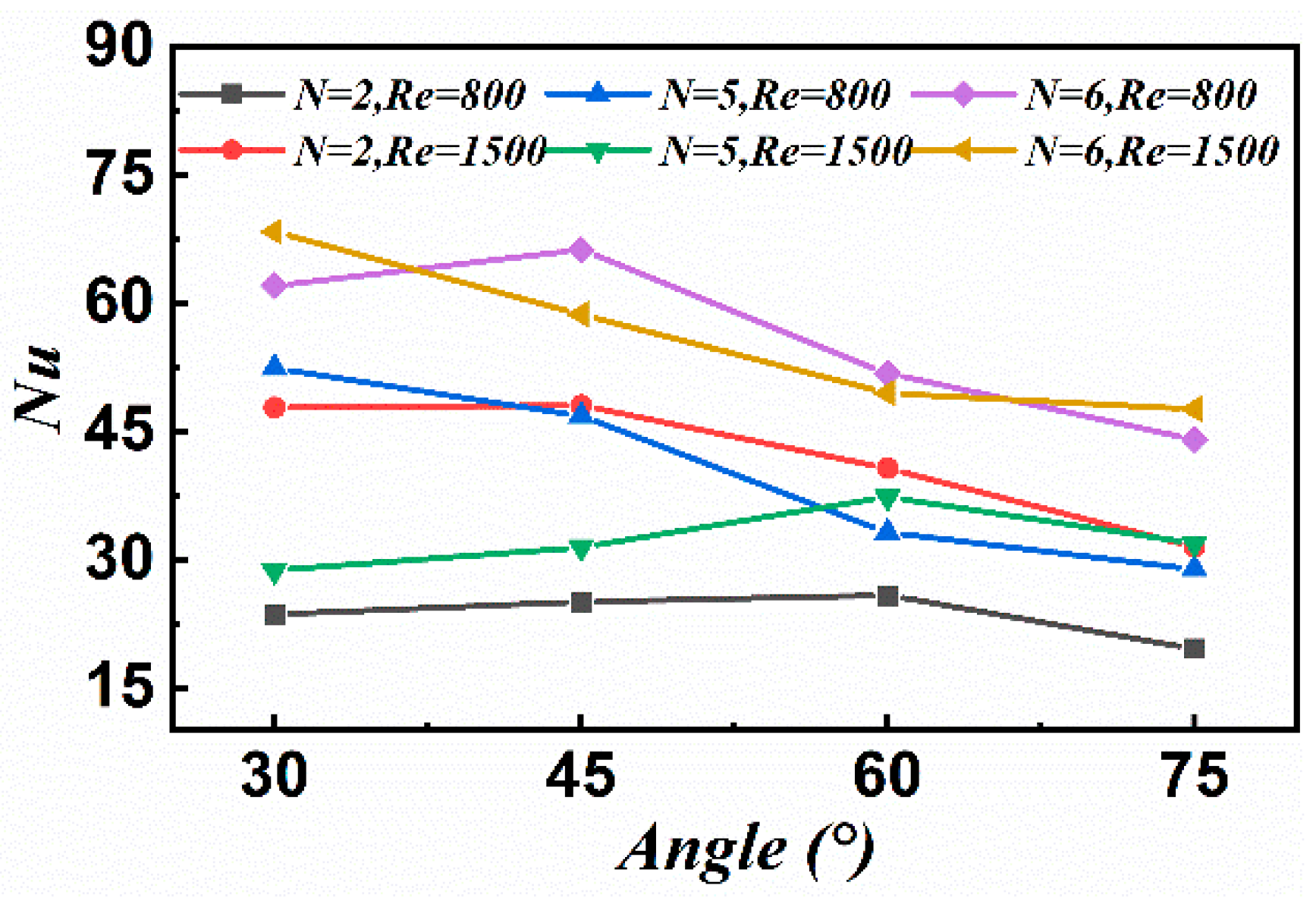
3.1.2. Effect of Geometric Parameters
Number of Blades
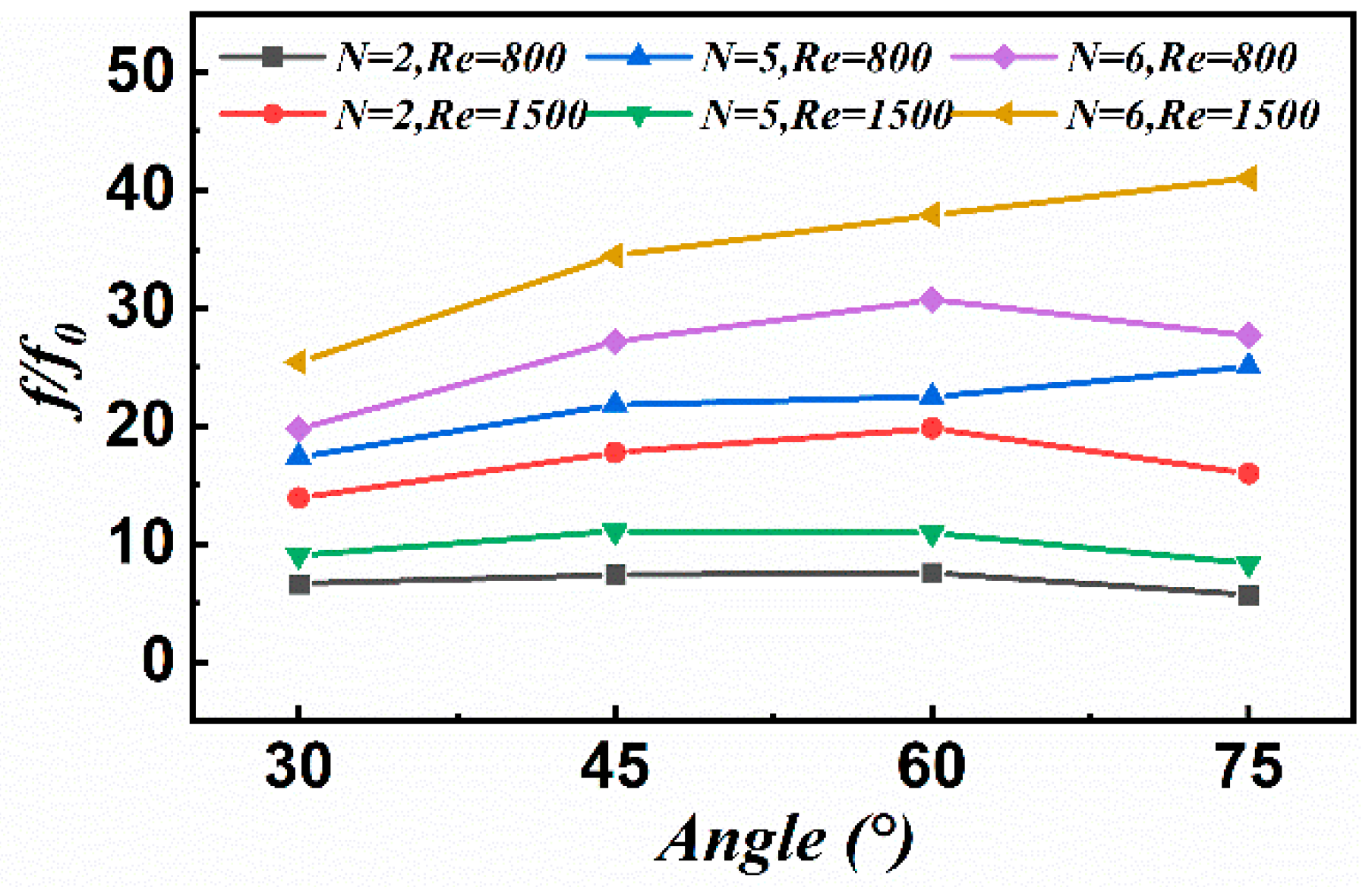
Angle of Inclination
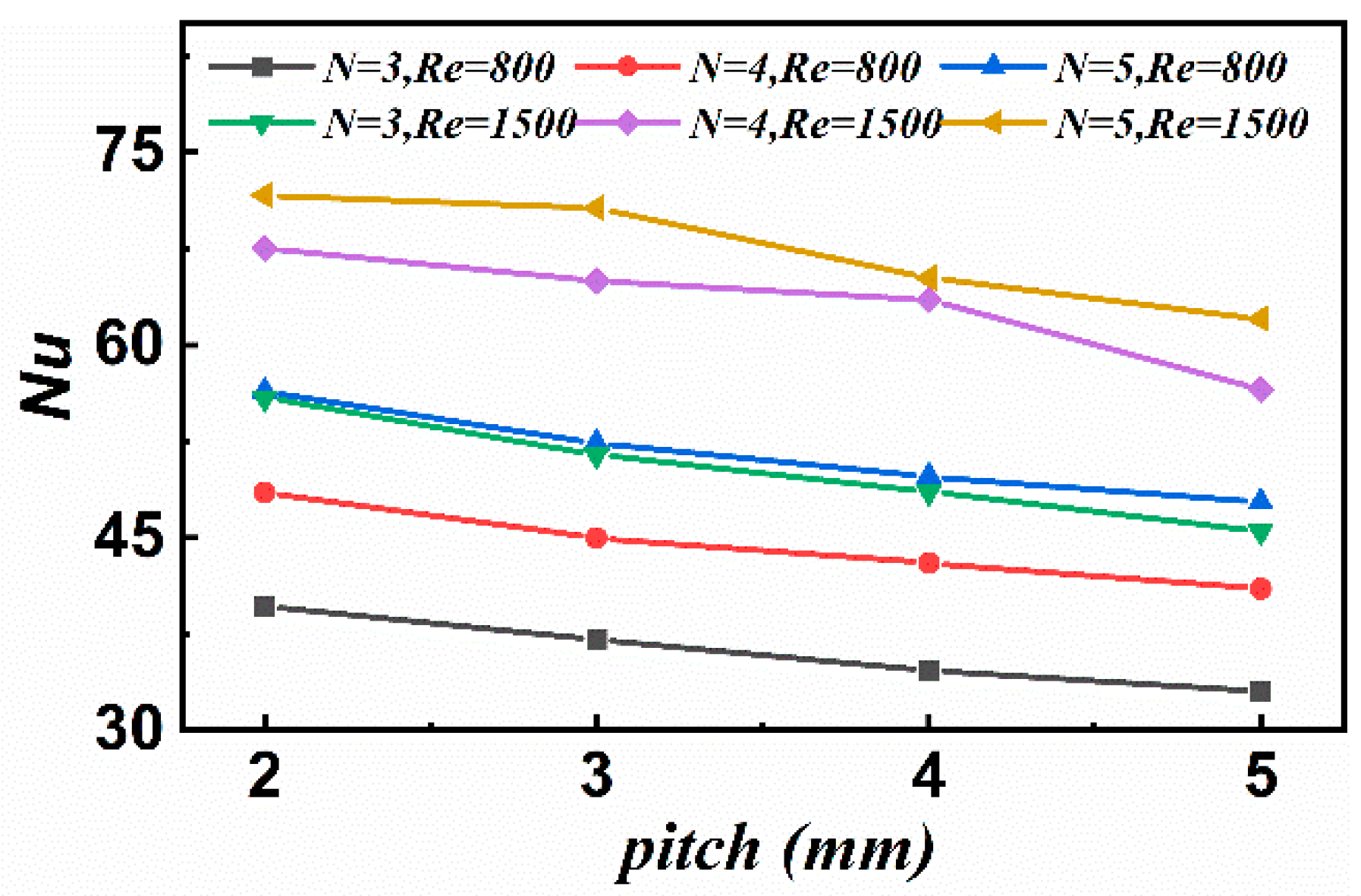
Blade Pitch
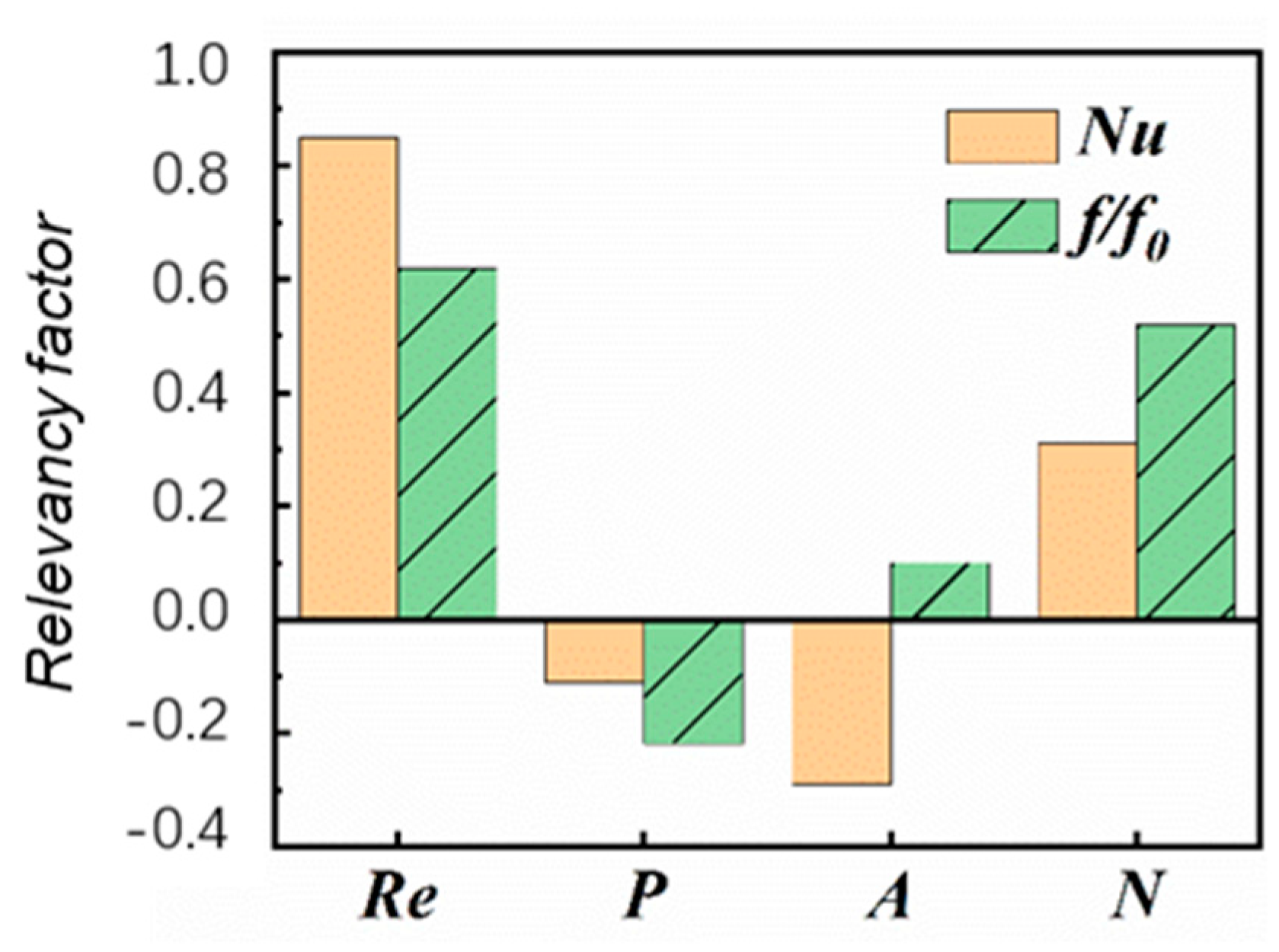
Significance Comparison of Influencing Factors
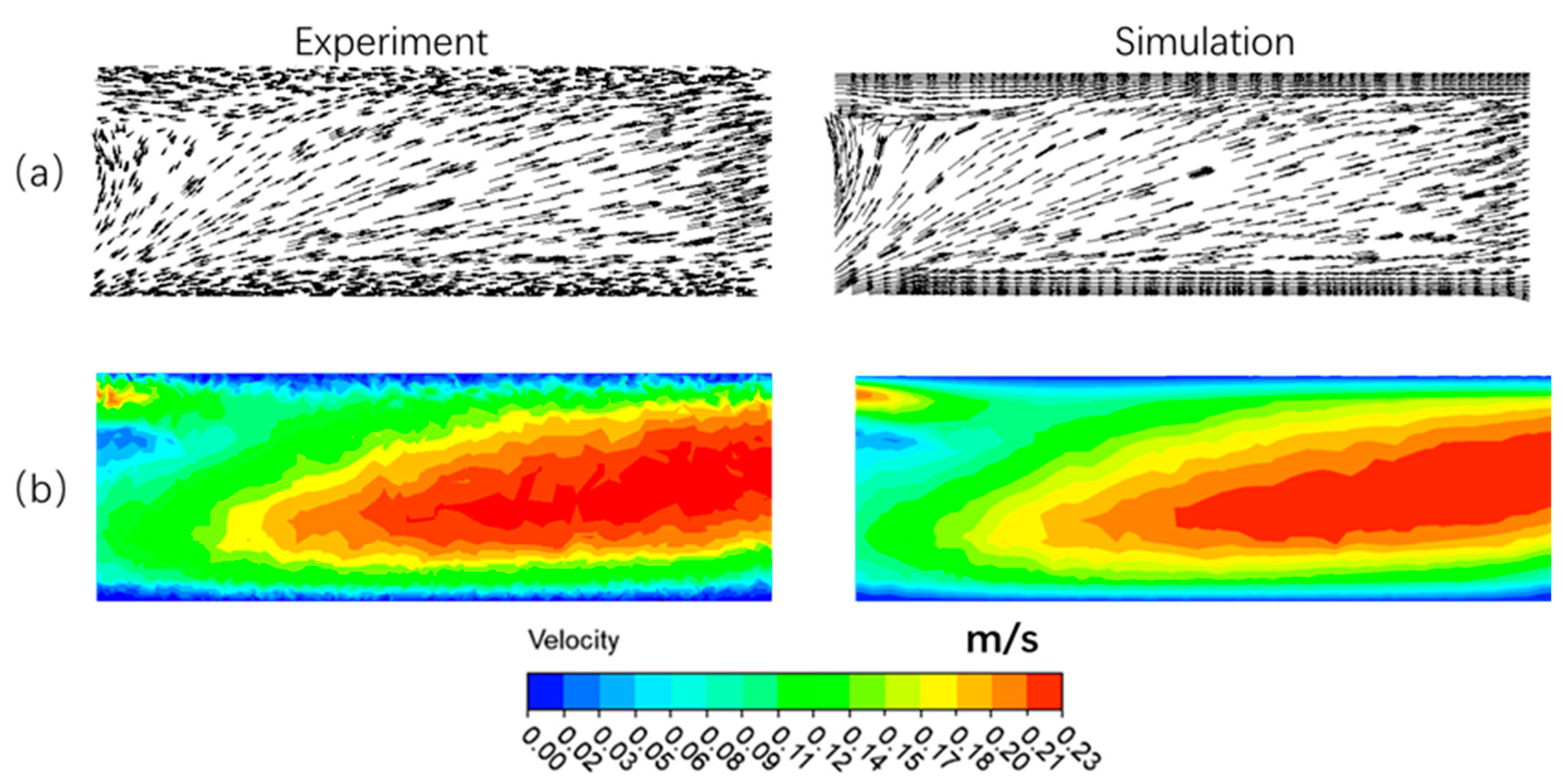
3.2. Comparison between Results from PIV and CFD
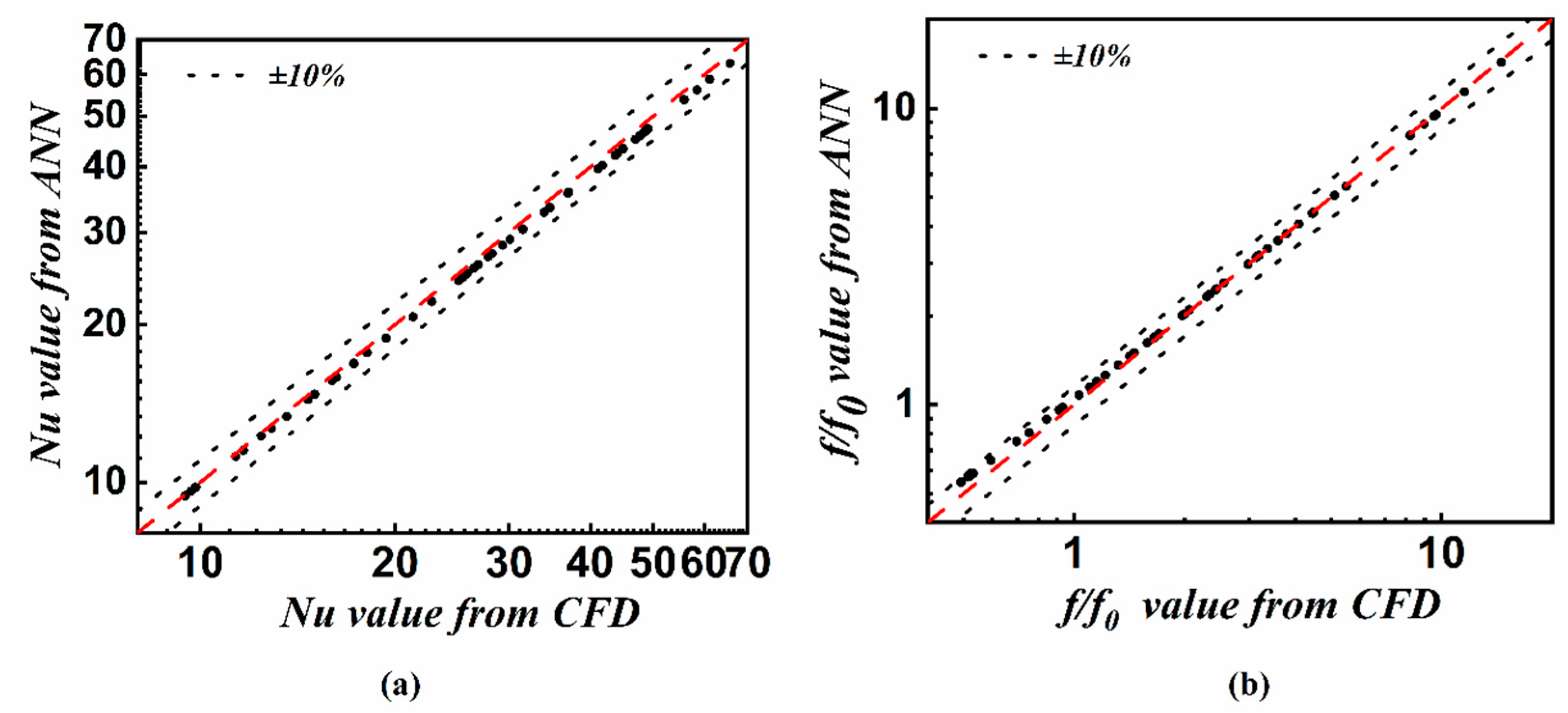
3.3. Neural Network Results
3.4. Model Reaction Case
4. Conclusions and Prospects
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
List of Symbols
| Nomenclature | |
| a | correction factor |
| A | blade angle (°) |
| B | coefficient |
| Bc0 | parameter |
| CA | concentration of key component (mol m−3) |
| Cv | heat capacity (J kg−1 K−1) |
| D | hydraulic diameter (m) |
| DaI | Damköhler number |
| Ea | activation energy (J mol−1) |
| f | friction coefficient |
| hm | overall average heat transfer coefficient (W m−2 K−1) |
| k | reaction rate coefficient (s−1) |
| k0 | reaction rate coefficient at T0 (s−1) |
| L | channel length (m) |
| m | reaction order |
| N | blade number |
| Nu | Nusselt number |
| critical Nusselt number | |
| P | blade spacing (mm) |
| Pr | Prandtl number |
| r | radius (m) |
| RT | gas constant |
| St | Stanton number |
| T | temperature (K) |
| T0 | temperature at reactor inlet (K) |
| Tc | temperature of cooling medium (K) |
| tR | reaction time scale (s) |
| um | mean fluid velocity (m s−1) |
| V | volume (m3) |
| Δp | pressure difference (Pa) |
| (−ΔHr) | reaction enthalpy (J mol−1) |
| Greek Symbols | |
| γ | Arrhenius parameter |
| δ | thickness of blade |
| θc | dimensionless critical temperature |
| critical temperature of the adiabatic reactor | |
| ν | kinematic viscosity (m2s−1) |
| ρ | density (kgm−3) |
| ψ | dimensionless reaction number |
| μ | Viscosity (Pa s) |
References
- Wang, X.; Wang, Y.; Li, F.; Li, L.; Ge, X.; Zhang, S.; Qiu, T. Scale-up of microreactor: Effects of hydrodynamic diameter on liquid–liquid flow and mass transfer. Chem. Eng. Sci. 2020, 226, 115838. [Google Scholar] [CrossRef]
- Trojanowicz, M. Flow Chemistry in Contemporary Chemical Sciences: A Real Variety of Its Applications. Molecules 2020, 25, 1434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wegner, J.; Ceylan, S.; Kirschning, A. Flow Chemistry—A Key Enabling Technology for (Multistep) Organic Synthesis. Adv. Synth. Catal. 2012, 354, 17–57. [Google Scholar] [CrossRef]
- Suryawanshi, P.L.; Gumfekar, S.P.; Bhanvase, B.A.; Sonawane, S.H.; Pimplapure, M.S. A review on microreactors: Reactor fabrication, design, and cutting-edge applications. Chem. Eng. Sci. 2018, 189, 431–448. [Google Scholar] [CrossRef]
- Mason, B.P.; Price, K.E.; Steinbacher, J.L.; Bogdan, A.R.; McQuade, D.T. Greener approaches to organic synthesis using microreactor technology. Chem. Rev. 2007, 107, 2300–2318. [Google Scholar] [CrossRef] [PubMed]
- Wiles, C.; Watts, P. Continuous flow reactors: A perspective. Green Chem. 2012, 14, 38–54. [Google Scholar] [CrossRef]
- Jose Nieves-Remacha, M.; Torres, M.; Ruiz-Abad, M.; Rincon, J.A.; Cumming, G.R.; Garcia-Losada, P. Scale-up of N-alkylation reaction using phase-transfer catalysis with integrated separation in flow. React. Chem. Eng. 2019, 4, 334–345. [Google Scholar] [CrossRef]
- Penverne, C.; Hazard, B.; Rolando, C.; Penhoat, M. Scale-up Study of Benzoic Acid Alkylation in Flow: From Microflow Capillary Reactor to a Milliflow Reactor. Org. Process Res. Dev. 2017, 21, 1864–1868. [Google Scholar] [CrossRef]
- Cherkasov, N.; Al-Rawashdeh, M.M.; Ibhadon, A.O.; Rebrov, E.V. Scale up study of capillary microreactors in solvent-free semihydrogenation of 2-methyl-3-butyn-2-ol. Catal. Today 2016, 273, 205–212. [Google Scholar] [CrossRef] [Green Version]
- Kockmann, N.; Roberge, D.M. Scale-up concept for modular microstructured reactors based on mixing, heat transfer, and reactor safety. Chem. Eng. Process.-Process Intensif. 2011, 50, 1017–1026. [Google Scholar] [CrossRef]
- Zhang, F.; Cerato-Noyerie, C.; Woehl, P.; Lavric, E.D. Intensified liquid/liquid mass transfer in corning® advanced-flow ™reactors. Chem. Eng. Trans. 2011, 24, 1369–1374. [Google Scholar]
- Santana, H.S.; Rodrigues, A.C.; Lopes, M.G.M.; Russo, F.N.; Silva, J.L., Jr.; Taranto, O.P. 3D printed millireactors for process intensification. Chin. J. Chem. Eng. 2020, 28, 180–190. [Google Scholar] [CrossRef]
- Potdar, A.; Thomassen, L.C.J.; Kuhn, S. Scalability of 3D printed structured porous milli-scale reactors. Chem. Eng. J. 2019, 363, 337–348. [Google Scholar] [CrossRef]
- Zhang, C.; Ferrell, A.R.; Nandakumar, K. Study of a toroidal-helical pipe as an innovative static mixer in laminar flows. Chem. Eng. J. 2019, 359, 446–458. [Google Scholar] [CrossRef]
- Santana, H.S.; Silva, J.L., Jr.; da Silva, A.G.P.; Rodrigues, A.C.; Amaral, R.d.L.; Noriler, D.; Taranto, O.P. Development of a New Micromixer “Elis” for Fluid Mixing and Organic Reactions in Millidevices. Ind. Eng. Chem. Res. 2021, 60, 9216–9230. [Google Scholar] [CrossRef]
- Parra-Cabrera, C.; Achille, C.; Kuhn, S.; Ameloot, R. 3D printing in chemical engineering and catalytic technology: Structured catalysts, mixers and reactors. Chem. Soc. Rev. 2018, 47, 209–230. [Google Scholar] [CrossRef] [PubMed]
- Nagy, Z.K.; El Hagrasy, A.; Litster, J. Continuous Pharmaceutical Processing; Springer International Publishing: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Westermann, T.; Mleczko, L. Heat Management in Microreactors for Fast Exothermic Organic Syntheses-First Design Principles. Org. Process Res. Dev. 2016, 20, 487–494. [Google Scholar] [CrossRef]
- Kummer, A.; Varga, T. Completion of thermal runaway criteria: Two new criteria to define runaway limits. Chem. Eng. Sci. 2019, 196, 277–290. [Google Scholar] [CrossRef]
- Jiang, J.J.; Jiang, J.C.; Wang, Z.R.; Pan, Y. Thermal runaway criterion for chemical reaction systems: A modified divergence method. J. Loss Prev. Process Ind. 2016, 40, 199–206. [Google Scholar] [CrossRef]
- Haber, J.; Kashid, M.N.; Renken, A.; Kiwi-Minsker, L. Heat Management in Single and Multi-injection Microstructured Reactors: Scaling Effects, Stability Analysis, and Role of Mixing. Ind. Eng. Chem. Res. 2012, 51, 1474–1489. [Google Scholar] [CrossRef]
- Ni, L.; Cui, J.; Jiang, J.; Pan, Y.; Wu, H.; Shu, C.-M.; Wang, Z.; Mou, S.; Shi, N. Runaway inhibition of styrene polymerization: A simulation study by chaos divergence theory. Process Saf. Environ. Prot. 2020, 135, 294–300. [Google Scholar] [CrossRef]
- Maestri, F.; Copelli, S.; Barozzi, M.; Rota, R. Kinetic-free discontinuous to continuous transformation of fine chemical reactions: A general experimental procedure. Chem. Eng. J. 2020, 395, 125061. [Google Scholar] [CrossRef]
- Jiang, X.; Feng, W.; Guo, Z.; Chen, W. Investigation into maximum temperature of synthesis reaction for single kinetically controlled liquid-liquid semibatch reactions with arbitrary reaction order. J. Therm. Anal. Calorim. 2020, 143, 3793–3804. [Google Scholar] [CrossRef]
- Kummer, A.; Varga, T.; Nagy, L. Semi-batch reactor control with NMPC avoiding thermal runaway. Comput. Chem. Eng. 2020, 134, 106694. [Google Scholar] [CrossRef]
- Kockmann, N.; Gottsponer, M.; Roberge, D.M. Scale-up concept of single-channel microreactors from process development to industrial production. Chem. Eng. J. 2011, 167, 718–726. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R. Closed-Loop Turbulence Control: Progress and Challenges. Appl. Mech. Rev. 2015, 67, 050801. [Google Scholar] [CrossRef]
- Lv, J.Y.; Liu, Z.C.; Liu, W. Active design for the tube insert of center-connected deflectors based on the principle of exergy destruction minimization. Int. J. Heat Mass Transf. 2020, 150, 119260. [Google Scholar] [CrossRef]
- Kockmann, N. Scalable Equipment for Process Development. Chem. Ing. Tech. 2012, 84, 646–659. [Google Scholar] [CrossRef]
- Roberge, D.M.; Gottsponer, M.; Eyholzer, M.; Kockmann, N. Industrial design, scale-up, and use of microreactors. Chim. Oggi-Chem. Today 2009, 27, 8–11. [Google Scholar]
- Kucherov, F.A.; Romashov, L.V.; Ananikov, V.P. Development of 3D+G printing for the design of customizable flow reactors. Chem. Eng. J. 2022, 430. [Google Scholar] [CrossRef]
- Varma, A.; Morbidelli, M.; Wu, H. Parametric Sensitivity in Chemical Systems; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Zhu, H.; Tang, T.; Zhao, H.; Gao, Y. Control of vortex-induced vibration of a circular cylinder using a pair of air jets at low Reynolds number. Phys. Fluids 2019, 31. [Google Scholar] [CrossRef]
- Habchi, C.; Russeil, S.; Bougeard, D.; Harion, J.-L.; Lemenand, T.; Della Valle, D.; Peerhossaini, H. Enhancing heat transfer in vortex generator-type multifunctional heat exchangers. Appl. Therm. Eng. 2012, 38, 14–25. [Google Scholar] [CrossRef]
- Zhai, C.; Islam, M.D.; Simmons, R.; Barsoum, I. Heat transfer augmentation in a circular tube with delta winglet vortex generator pairs. Int. J. Therm. Sci. 2019, 140, 480–490. [Google Scholar] [CrossRef]
- Xiao, H.; Wang, X.; Liu, Z.; Liu, W. Optimization of turbulent heat transfer based on exergy destruction minimization principle. In Proceedings of the 4th Thermal and Fluids Engineering Conference, TFEC 2019, Las Vegas, NV, USA, 14–17 April 2019; Begell House Inc.: Danbury, CT, USA, 2019; pp. 1107–1114. [Google Scholar]
- Xiao, H.; Wang, J.; Liu, Z.; Liu, W. Turbulent heat transfer optimization for solar air heater with variation method based on exergy destruction minimization principle. Int. J. Heat Mass Transf. 2019, 136, 1096–1105. [Google Scholar] [CrossRef]
- Wold, S.; Sjöström, M.; Eriksson, L. PLS-regression: A basic tool of chemometrics. Chemom. Intell. Lab. Syst. 2001, 58, 109–130. [Google Scholar] [CrossRef]
- Tian, Z.; Gu, B.; Yang, L.; Lu, Y. Hybrid ANN–PLS approach to scroll compressor thermodynamic performance prediction. Appl. Therm. Eng. 2015, 77, 113–120. [Google Scholar] [CrossRef]
- Lee, G.; Han, C.; Yoon, E.S. Multiple-fault diagnosis of the Tennessee Eastman process based on system decomposition and dynamic PLS. Ind. Eng. Chem. Res. 2004, 43, 8037–8048. [Google Scholar] [CrossRef]
- Zhu, Q.-X.; Luo, Y.; He, Y.-L. Novel Distributed Alarm Visual Analysis Using Multicorrelation Block-Based PLS and Its Application to Online Root Cause Analysis. Ind. Eng. Chem. Res. 2019, 58, 20655–20666. [Google Scholar] [CrossRef]
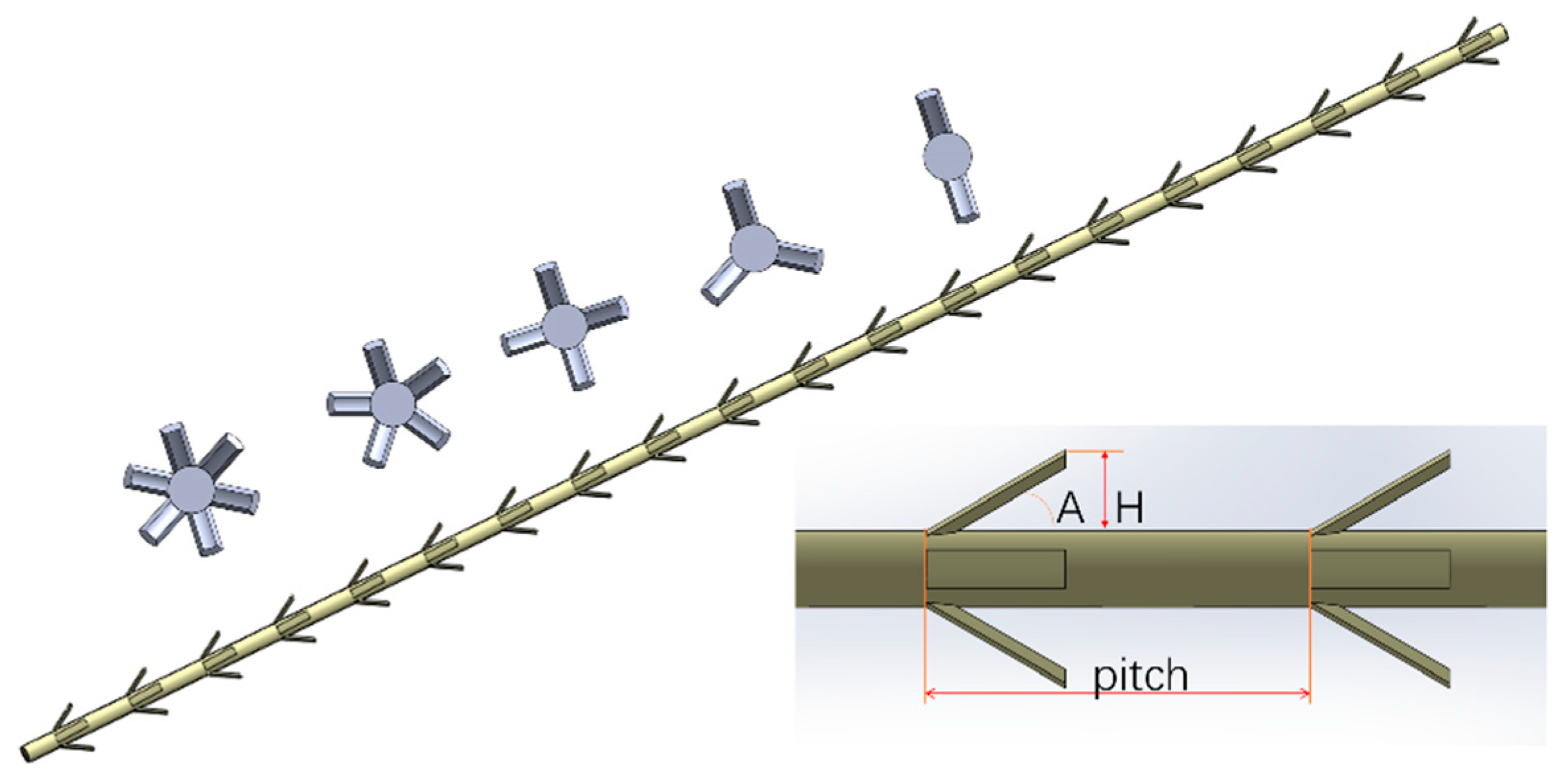



| Number of Blades (N) | 2, 3, 4, 5, 6 |
|---|---|
| Angle (A) with the central rod | 30°, 45°, 60°, 75° |
| Blade spacing (P), mm | 2, 3, 4, 5 |
| Cells | Nu | ΔP/Pa | Error—Nu | Error—ΔP | |
|---|---|---|---|---|---|
| Grid 1 | 9653794 | 48.5 | 5559.7 | −5.96% | 2.60% |
| Grid 2 | 12208773 | 51.5 | 5445.4 | −0.10% | 0.49% |
| Grid 3 | 25818325 | 51.5 | 5418.8 | —— | —— |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Wang, C.; Wang, R.; Yang, X. Design, Heat Transfer, and Visualization of the Milli-Reactor by CFD and ANN. Processes 2022, 10, 2329. https://doi.org/10.3390/pr10112329
Liu H, Wang C, Wang R, Yang X. Design, Heat Transfer, and Visualization of the Milli-Reactor by CFD and ANN. Processes. 2022; 10(11):2329. https://doi.org/10.3390/pr10112329
Chicago/Turabian StyleLiu, Hanyang, Chenfeng Wang, Rijie Wang, and Xiaoxia Yang. 2022. "Design, Heat Transfer, and Visualization of the Milli-Reactor by CFD and ANN" Processes 10, no. 11: 2329. https://doi.org/10.3390/pr10112329
APA StyleLiu, H., Wang, C., Wang, R., & Yang, X. (2022). Design, Heat Transfer, and Visualization of the Milli-Reactor by CFD and ANN. Processes, 10(11), 2329. https://doi.org/10.3390/pr10112329






