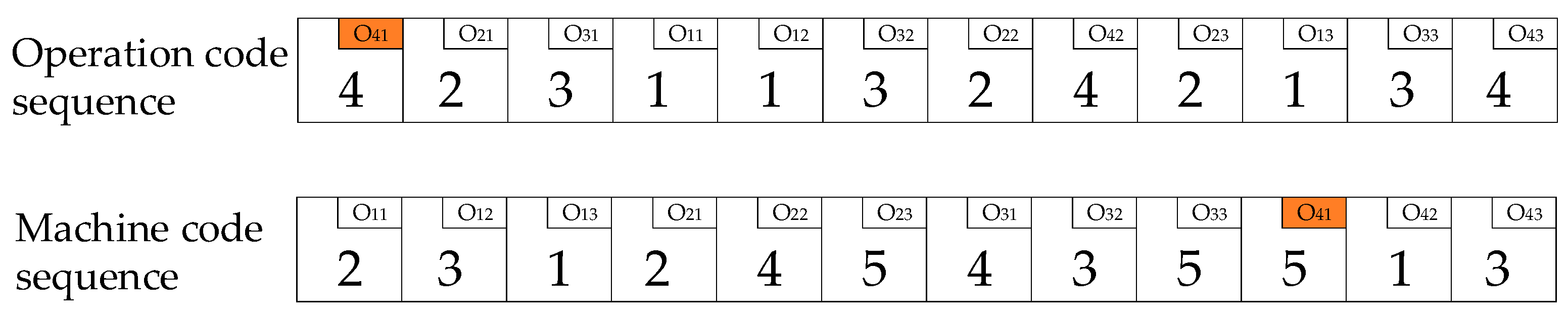Abstract
The optimal configuration of flexible workshop resources is critical to production efficiency, while disturbances pose significant challenges to the effectiveness of the configuration. Therefore, this paper proposes a hybrid-driven resource dynamic configuration model and an improved Imperialist Competitive Algorithm hybrid Neighborhood Search (IICA-NS) that incorporates domain knowledge to allocate resources in flexible workshops. First, a hybrid-driven configuration framework is proposed to optimize resource configuration strategies. Then, in the revolutionary step of the Imperialist Competitive Algorithm (ICA), the bottleneck heuristic neighborhood structure is adopted to retain the excellent genes in the imperial so that the updated imperial is closer to the optimal solution; And a population invasion strategy is proposed further to improve the searchability of the ICA algorithm. Finally, the simulation experiments are carried out through production examples on flexible workshop production cases, and the proposed algorithm is applied. Compared with traditional ICA, genetic algorithm (GA), particle swarm optimization algorithm (PSO), moth-flame optimization (MFO) and sparrow search algorithm (SSA), the proposed method and algorithm effectively solve flexible workshops’ resource dynamic configuration problems.
1. Introduction
As one of the pillars of industrialization, manufacturing occupies an essential position in the national economy. As well, for a long time, the optimal configuration of job shop resources has received extensive attention as a standard and essential problem in manufacturing [1]. The general situation of the issues, similar to real-world scheduling problems, is NP-hard [2]. In particular, various disturbances in the authentic processing environment will directly or indirectly lead to abnormal production processes. The change in real-time working conditions dramatically increases the difficulty of efficient resource configuration [3]. In addition, the raging new crown epidemic has largely damaged the productivity of the global manufacturing industry, and there is an urgent need to improve the efficiency of resource configuration to increase throughput. Therefore, the research on the dynamic configuration of flexible workshop resources has important scientific theoretical significance and practical application value.
The flexible job shop scheduling problem (FJSP) is an abstract model of resource configuration problems in many manufacturing enterprises and service industries. Engin et al. [4] studied the no-waiting job shop, and a scheduling model was used for the no-waiting job shop; Wu [5], Xiao [6], and Zhang et al. [7] studied the FJSP problem targeting energy consumption. At the same time, Su [8] et al. believe that bottlenecks, as critical resources, should be focused on in the configuration process. Berkhout et al. [9] proposed a short-term production scheduling method based on shifting production bottlenecks. Tonke et al. [10] proposed a round-robin scheduling strategy to solve the resource configuration problem in multi-bottleneck systems.
However, the production process is complex and changeable, and many unexpected situations hinder the completion of production goals [11,12,13]. Production exception-driven rescheduling is often used to adjust the configuration of resources in the manufacturing process to reduce losses. Nouiri [14,15] and Sun et al. [16] solved the rescheduling issue under machine failure conditions using a two-stage algorithm; Considering the states of each machine, Zhang et al. [17,18,19] proposed a multi-agent-based rescheduling method; Salido [20] and Zakaria [21] improved the adaptability and effectiveness of the rescheduling model by researching the rescheduling algorithm. Sun et al. [22] believed that a data-driven approach could respond to dynamic systems and proposed a control strategy to suppress the effects of disturbances. Qiu et al. [3] further use thresholds to increase the accuracy of rescheduling drives. It can be seen that the optimal dynamic configuration of resources is of great significance to the production goal achievement. However, the dynamic configuration method research is still in its infancy, so it needs further study.
Effectively solving resource configuration problems has also attracted widespread attention. Among them, the meta-heuristic algorithms have an excellent ability to solve NP-hard problems, such as GA [23] and its improved algorithm [24], ant colony optimization (ACO) [25], PSO [26] and its improved algorithm [27], the ICA [28,29]. The ICA algorithm has been studied due to its novel mechanism and superiority in large-scale combinatorial optimization problems. The ICA and its improved algorithm have been successful in solving resource configuration problems, including multi-objective optimization, single machine [30], parallel machine [31], assembly shop scheduling [32], and flexible job shop scheduling problem (FJSP) [33], etc. However, the issue of insufficient local search ability widely exists in random search algorithms. Karimi [34] et al. calibrated various operators and parameters using the Taguchi method. Many scholars have studied local search algorithms, such as simulated annealing(SA) [35], tabu search algorithm (TS) [36,37], neighborhood search algorithm (NS) [28,38,39], and so on. The neighborhood search algorithm is widely combined with other global search algorithms. Marichelvam et al. [38] improved the speed of solving shop-floor scheduling optimal solutions by PSO optimization with VNS. LEI et al. [28] designed a two-stage metaheuristic algorithm based on the ICA and the VNS for MOFJSP with total energy consumption constraints. In addition, biological evolutionary algorithms have also been used to solve shop floor resource allocation problems in recent years [40,41], such as the whale optimization algorithm (WOA), moth-flame optimization (MFO), and sparrow search algorithm (SSA). The above algorithms are mainly solved and optimized for standard cases. They are not combined with the production situation and are difficult to use directly in the workshop resource configuration process.
In conclusion, most current research on configuration methods is based on idealized mathematical models divorced from actual production situations. When there are abnormal situations in the production process, such as emergency order insertion, tool wear, machine tool failure, etc., the configuration method often fails. Therefore, this paper proposes a state-based hybrid-driven dynamic resource configuration framework considering the actual production situation and designs a hybrid evolutionary algorithm integrating manufacturing domain knowledge to embed the framework. The main contributions of this paper are as follows:
- A state-based hybrid driven resource configuration method is proposed and combined with the traditional cycle-driven method to form a new resource dynamic configuration framework.
- To realize the dynamic configuration of resources driven by the real-time state of the workshop, two novel bottleneck heuristic neighborhood structures are designed and integrated into the ICA optimization algorithm to enhance the algorithm’s optimization ability.
- Introducing the invasion strategy to improve the ICA to avoid the algorithm falling into local optimum.
The rest of this paper is organized as follows. In Section 2, a dynamic resource configuration framework is proposed, and its problem description and modeling are carried out; The hybrid evolutionary algorithm IICA-NS is proposed in Section 3; In Section 4, the superiority of the IICA-NS algorithm is verified by comparing it with different algorithms. As well, the effectiveness of the resource dynamic configuration framework is verified through the workshop case; The summary of the full text is presented in Section 5.
2. Resource Dynamic Configuration Framework and Problem Description
2.1. Resource Dynamic Configuration Framework
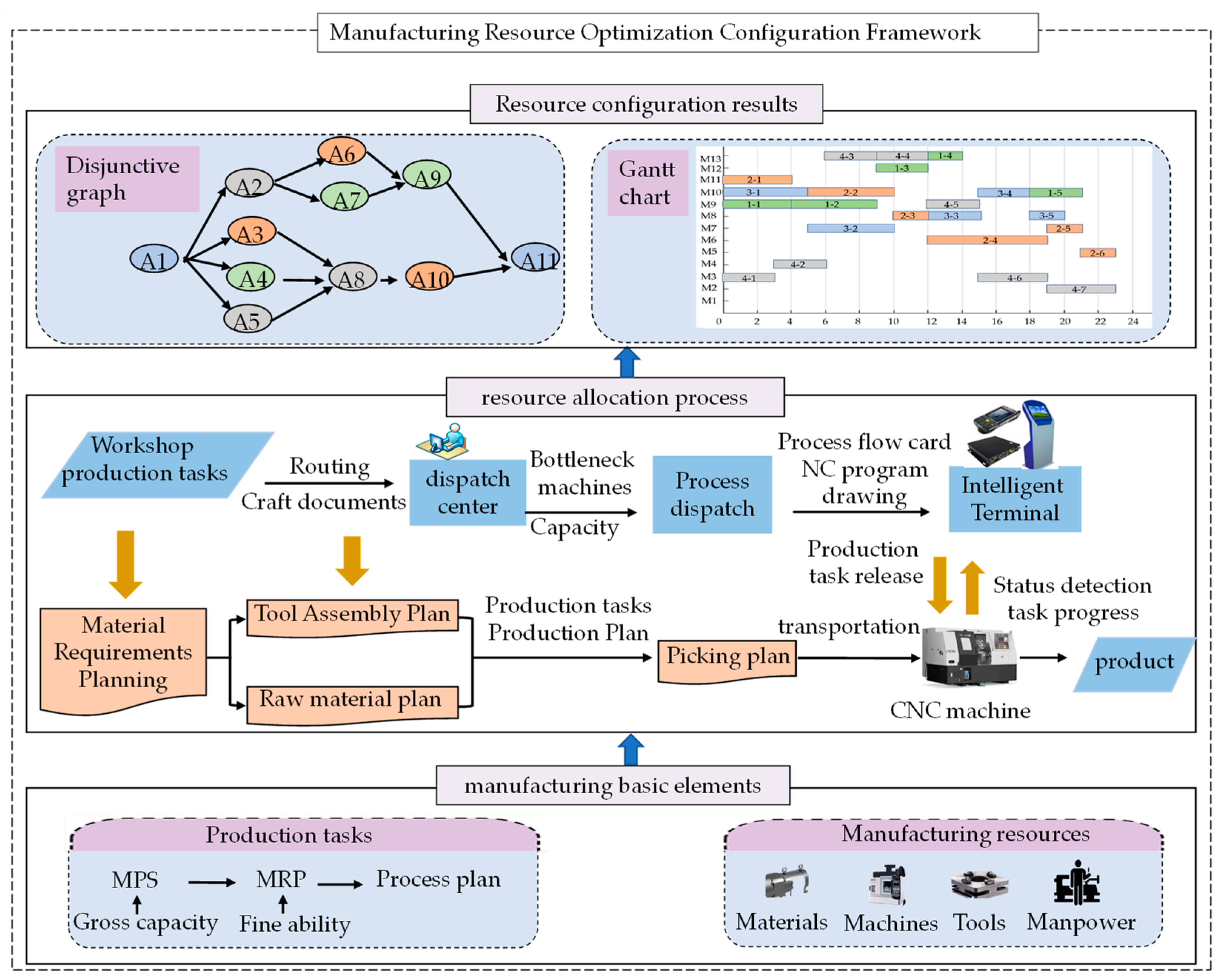
The ultimate goal of resource optimal configuration is to formulate a clear process plan to satisfy the constraints of the production process, coordinate and organize the production activities among resources, and ensure that the manufacturing system’s production efficiency or production cost is optimized. Wang et al. [27] proposed a digital twin-based resource configuration framework. But this framework aims to coordinate the configuration of resources across organizations and cannot guide the dynamic configuration of manufacturing resources in the production process. Therefore, this paper proposes a framework for the optimal configuration of manufacturing resources, as shown in Figure 1. The resources mainly include manufacturing resources and raw material resources. The dynamic configuration process is driven by both tasks and constraints. First, the material requirement plan is prepared according to the master production plan, and the gross capacity and the acceptable ability plan are ready simultaneously; The scheduling center then assigns tasks to the machining center, and each team formulates detailed process plans; Finally, the resource configuration results are presented as a disjunctive graph and Gantt charts. The dispatch center must monitor production execution in real-time during the configuration process. When delayed delivery or bottleneck drift occurs, resources should be reconfigured immediately to ensure smooth production.
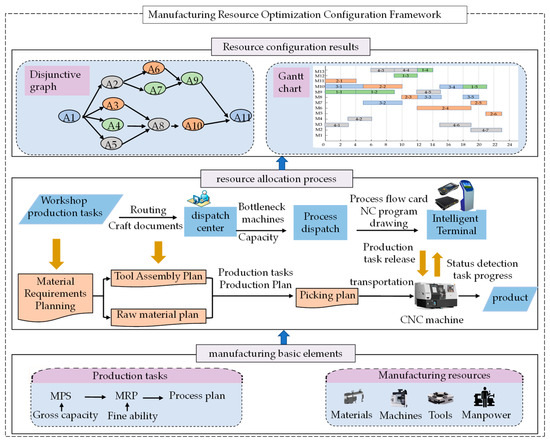
Figure 1.
Flexible Workshop Resource Configuration Framework.
2.2. Problem Description and Mathematical Model
The problem of resource configuration in the manufacturing process emphasizes how to rationally use the multi-attribute resources of the job shop to achieve the established production goals. According to product manufacturing needs and the process route, the processing equipment is reasonably selected, and the processing tasks are allocated. The general workshop resource configuration problem can be summarized as follows: n tasks need to be assigned to m available resources within a specified time, and the configuration process needs to meet constraints such as industrial routes and processing time. For the convenience of discussion, the description of the symbols involved in the model is shown in Table 1.

Table 1.
The symbols involved in the mathematical model and their definitions.
The objective function of minimizing the maximum makespan time is given based on the above definition, as shown in Formula (1).
And satisfies the following constraints:
Among them, Equation (2) indicates that a workpiece can only be processed on one machine at the same time; Equations (3) and (4) indicate that each process needs to be processed in order according to the process route; Equations (5) and (6) indicate that one machine can only process one workpiece at the same time; Equation (7) indicates the limited machinability of equipment r; Equation (8) indicates that the start processing time of all operations is greater than 0;
Equation (9) represents the collection of optional processing equipment for a process; Equation (10) represents the optional processing time of the process on different machines; Equation (11) represents the dynamic bottleneck state of the manufacturing system; Equation (12) is the bottleneck degree calculation formula.
3. Hybrid Evolutionary Algorithm IICA-NS
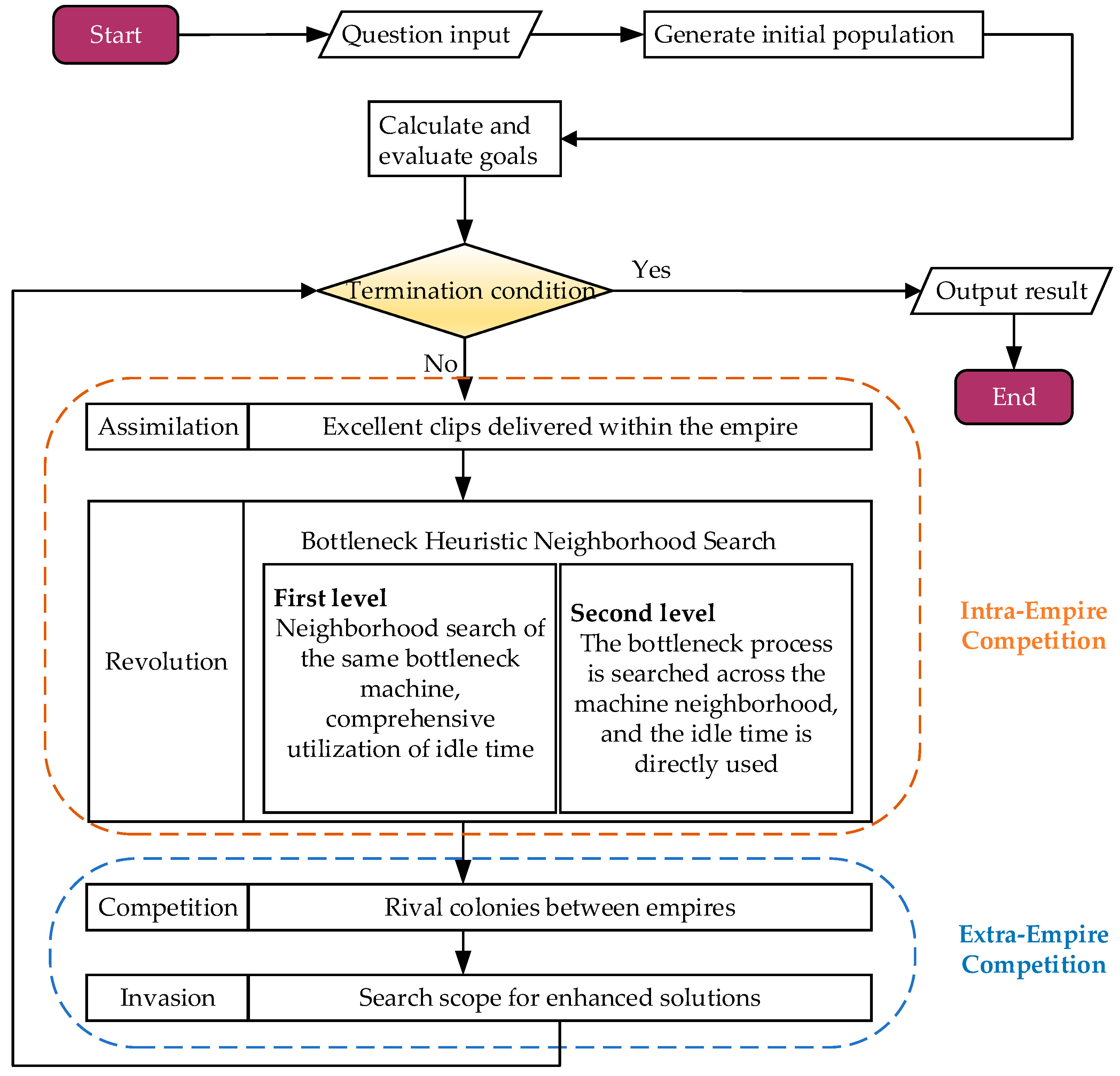
Because the ICA algorithm has a fast convergence speed, flexible structure, and robust searchability, it is always used to optimize single-objective or multi-objective problems [28]. This paper proposed two neighborhood structures to improve the local optimization ability of the ICA. The improved hybrid evolutionary algorithm IICA-NS process is shown in Figure 2.
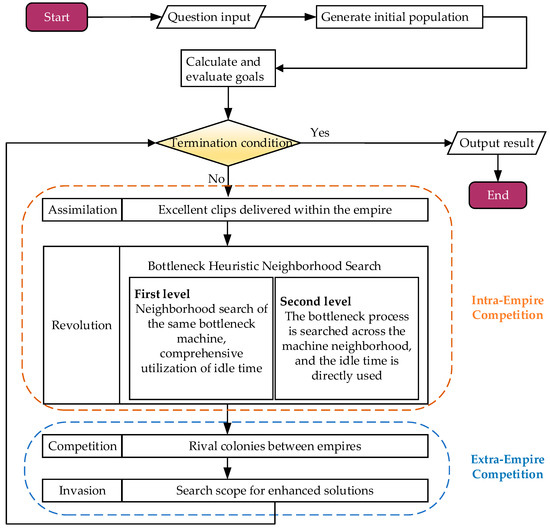
Figure 2.
The framework of the hybrid algorithm.
3.1. Encoding and Decoding
Four workpieces processed on five machines is taken as an example to introduce the encoding and decoding method proposed in this paper, in which each workpiece has three processes to be processed. In the IICA-NS, each country is a feasible solution, which is composed of machine code and operation code. The resource configuration problem should not only consider the workpiece’s processing sequence, but also select the corresponding processing equipment for the process. Therefore, the process sequences and machine sequences are placed in two dimensions, and two-stage coding is used. The process code and machine code are shown in Figure 3. The operation code composed of the workpiece number records the order in which the operation is processed. The process number of the workpiece is represented by the number of times the workpiece appears. The first number, 4, in the process code in Figure 3, illustrates the first operation O41 of workpiece 4. The machine code represents the processing machine of each process. Each digit is arranged from the first workpiece’s first process to the last workpiece’s last process. In particular, machine sets are introduced to avoid generating infeasible solutions when encoding machine codes. The number in the machine code represents the sequence number of the processing machine in the optional processing machine set. The first integer 2 is the second machine of the optional machine set {M2, M3, M4} in the process O11, that is, M3.

Figure 3.
Encoding format.
Operate the machine code after operating the process code when decoding. The process code is decoded into the sequence of process processing; When the machine code is decoded, the processing machine is found by querying the machine set corresponding to the process in turn, and then the processing start and end time of each process are calculated, and finally decoded into activity scheduling.
3.2. Imperial Creation and Initialization
First, among the initialized α countries, the β countries with the shortest maximum completion time are selected as imperialist countries: imp, and the remaining α-β countries are used as colonial countries: col. They are allocated to β imperialist countries according to a certain probability.
Usually, at least one of the colonial countries will have a normalized cost of zero and a power of zero, so these colonial countries cannot be assigned to any colonies. The corresponding initial imperial is difficult to assimilate and revolutionize because it has no settlements, affecting ICA’s search efficiency. To this end, a new calculation formula for the normalized cost is given, as shown in Equation (13).
The standardized sphere of influence Limp of an imperialist country is shown in Equation (14).
Finally, calculate the number of colonies for the first β-1 colonizing countries and randomly assign territories to each colonizing country. The initial number of colonies owned by the n-th colonizing country is NCimp, as shown in Formula (15).
3.3. Intra-Empire Competition
3.3.1. Assimilation Mechanism
Assimilation is a process in which colonial countries gradually tend to become imperialist countries. It is achieved by copying the excellent genetic fragments of the imperialist countries to the colonial countries. The assimilation process is divided into process sequence assimilation and machine sequence assimilation. Multipoint crossover mutation is used to select machines. The specific process is: randomly select r positions, replace the information of the r positions of the colonial country with the corresponding places in the colony, and keep the rest of the position information unchanged; the process sorting part adopts the method of workpiece exchange, the processing part of the colony is exchanged with the processing part of the colonial country, and the processing part of the colony is updated.
3.3.2. Revolutionary Mechanism Based on Neighborhood Search
The revolution consists of two parts: the selection of machines and the sequencing of processes. The former replaces the bottleneck machine with other machines in the machine set; The latter exchange the position information of the two bottleneck processes in the process sequence part. The revolution of the original ICA algorithm is carried out randomly, and it is improved using the bottleneck heuristic neighborhood structure to make the solution approach the optimal solution efficiently.
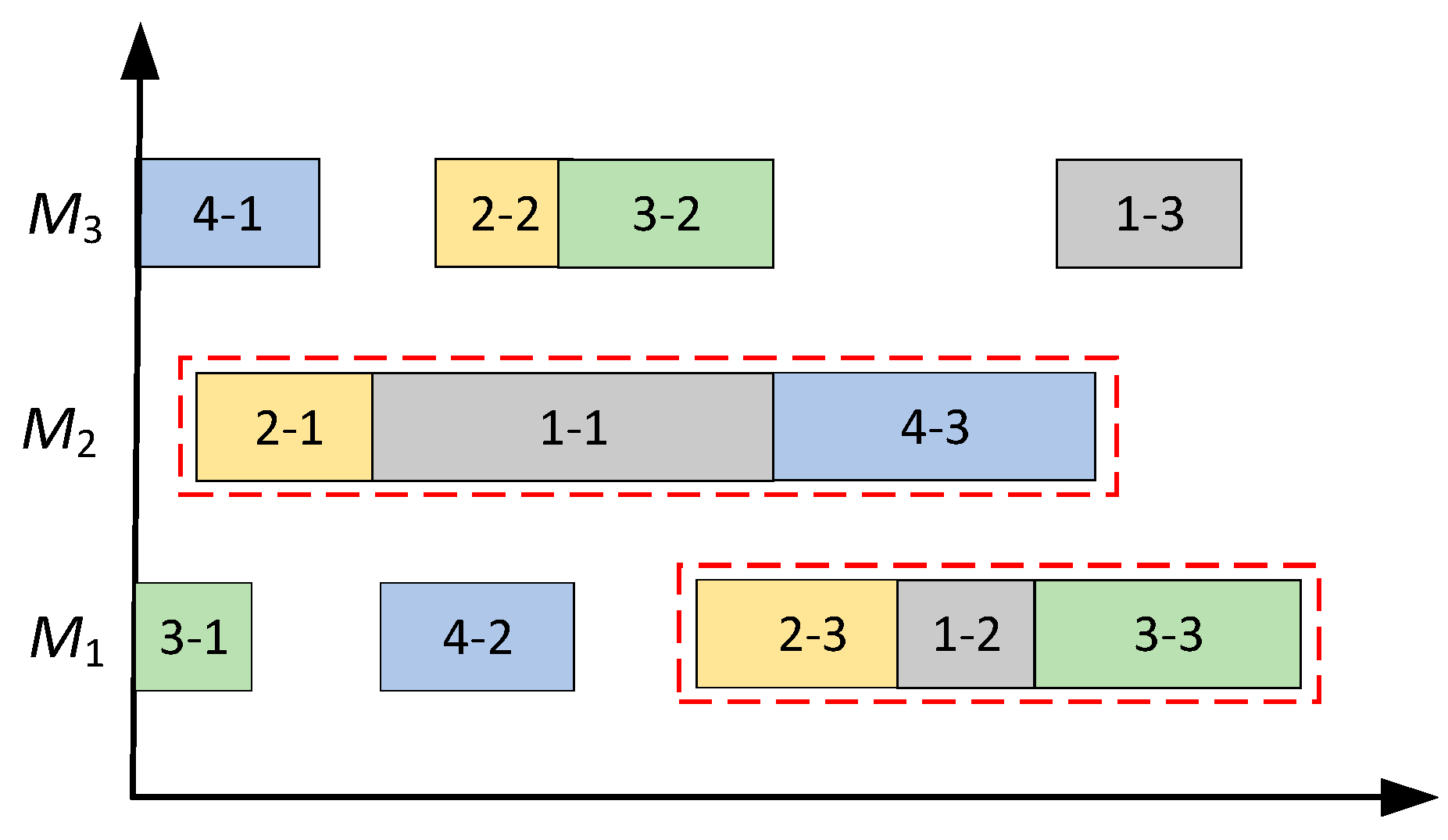
There are generally multiple bottleneck processes in workshop resource configuration that limit the system’s throughput. Among them, the length of the bottleneck process determines the completion time of the entire scheduling. Therefore, changing the bottleneck process can change the completion time to the greatest extent possible. The domain structure can effectively explore the local solution space. Usually, the bottleneck process continuously processed by the same machine is called the process block, the first process in the process block is called the blockhead process, and the last process is called the block tail process. The process with the red frame in Figure 4 is the bottleneck process. For the identification method of the bottleneck process, see the literature [8,42,43]. Taking the bottleneck process on machine 2 as an example, [O21, O11, O43] are process blocks, and O21 is the first process of the block. O43 is the block-end process.
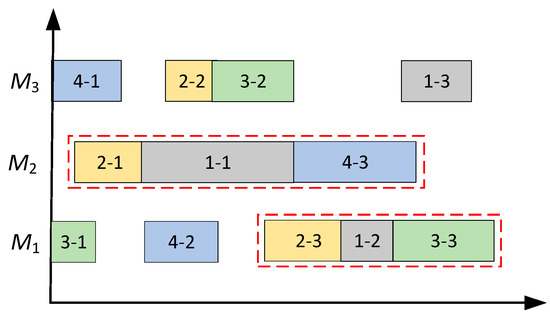
Figure 4.
Resource configuration diagram of the earliest start time.
Based on the above definition, the bottleneck heuristic neighborhood algorithm uses two effective neighborhood structures: exchanging the processing order of two adjacent processes on the bottleneck machine (exact machine neighborhood search), and assigning new equipment to operations on the bottleneck process block (cross-machine neighborhood search). These two types of neighborhoods only include those new solutions that are likely to be improved and exclude the scheduling that is impossible to improve, thus significantly improving the efficiency of the search.
The meanings of the symbols involved in the neighborhood structure are shown in Table 2.

Table 2.
Symbols in neighborhood structure and their interpretations.
- (1)
- Neighborhood search for the same bottleneck machine
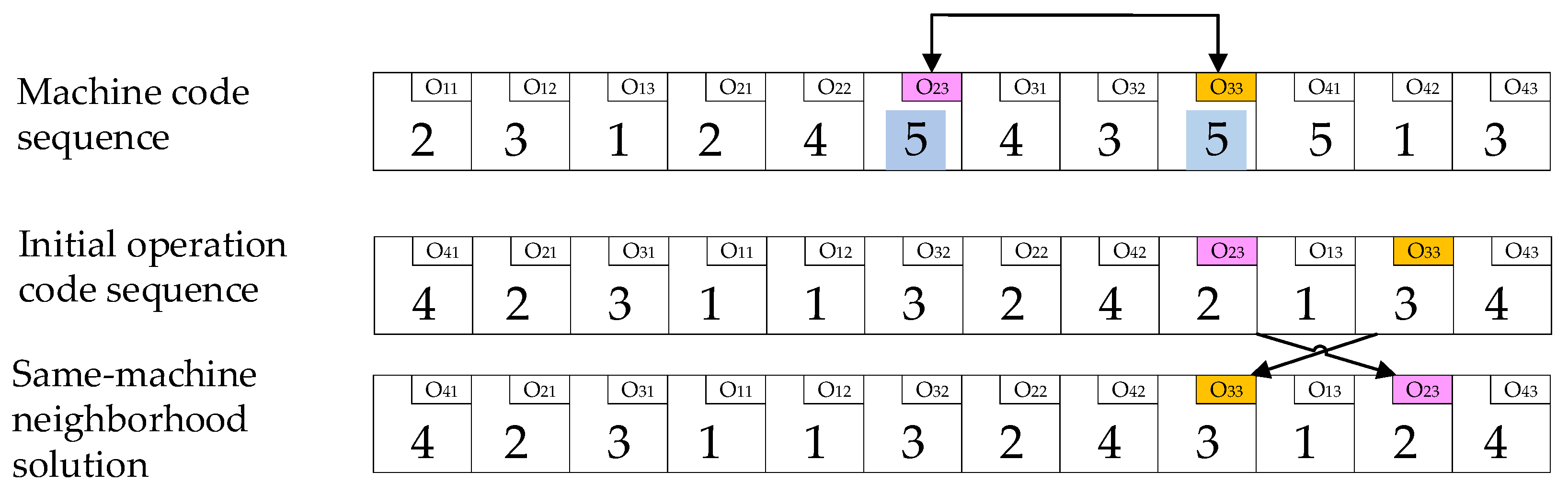
The same machine neighborhood search process is shown in Figure 5. The first line’s two numerical fives in the machine code sequence represent the first and second processes processed by the fifth machine in the optional equipment set. The index O23 and the index O33 locate the two processes to the second initial process code sequence and exchange the two processes for obtaining the third same-machine neighborhood solution.
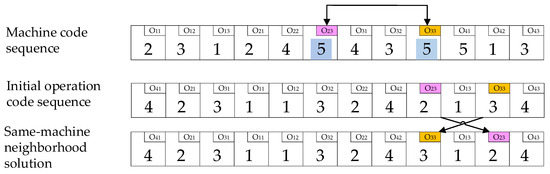
Figure 5.
Schematic diagram of the same-bottleneck machine neighborhood search.
For the same-bottleneck equipment neighborhood search problem, refer to the related neighborhood structures designed for the resource configuration, such as N2, N3, N4, N5, N6, and N7 [44]. Since the number of scales of the neighborhood mentioned above design, the moving process is too small, and its searchability is limited, carrying a more significant number of processes simultaneously is the key to further improving the performance of the neighborhood structure. Based on the neighborhood structures N2 and N5, this paper proposes a new neighborhood search structure with the multi-process linkage of the same bottleneck equipment, as shown in Algorithm 1. The core operation of this structure is to exchange the bottleneck process block with two blockhead and two block tail processes. At the same time, move JP[v] to the idle time slot of other machinable machines (or swap JP[v] and MP[JP[v]]), and move JS[u] to the idle time slot of other machinable machines (or swap JS[u] with MS[JS[u]]). Then, consider the following situation:
- If the earliest completion time of JP[v] is later than the earliest start time of process u, the earliest start time of process v must be later than the earliest start time of process u after exchanging process u and process v. Then the whole solution time extends.
- If the earliest start time of JP[v] is equal to the earliest completion time of JP[JP[v]], then exchanging JP[v] and MP[JP[v]] will not shorten the start time of JP[v]. The same is true for the post-shifting process. Based on the above situation, the algorithm of the same-bottleneck machine neighborhood search designed in this paper is as follows:
| Algorithm 1: neighborhood search in the same bottleneck machine |
|
- (2)
- Neighborhood search across bottleneck machines
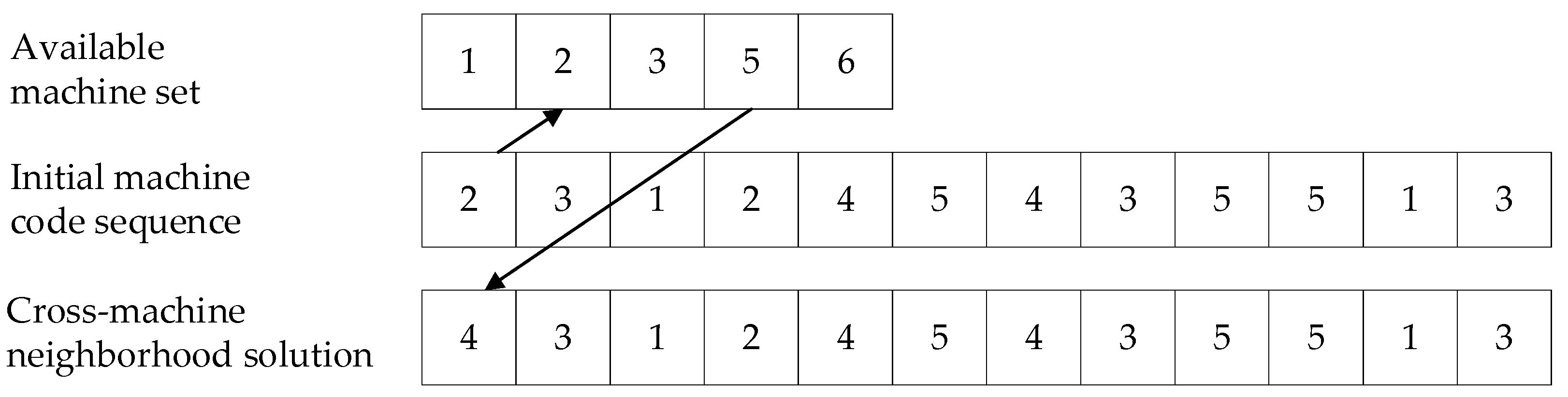
The core idea of the cross-bottleneck machine neighborhood search is to shorten the critical path and reducing the maximum completion time by moving the bottleneck process to the idle time of other machinable machines without extending the latest completion time of different processes. The cross-machine neighborhood search process is shown in Figure 6 and Algorithm 2. The first digital 2 in the second initial machine code sequence represents the second machine in the optional device set. The cross-machine neighborhood solution is obtained by changing selection machine 2 to selection machine 5, as shown in the third line. The expression for judging whether to move is:
where O is the critical process; x is a process processed on the candidate machine of the essential process O; to is the processing time of the crucial process O. The algorithm of the neighborhood search across the machines designed in this paper is as follows:
| Algorithm 2: neighborhood search across the machines |
|
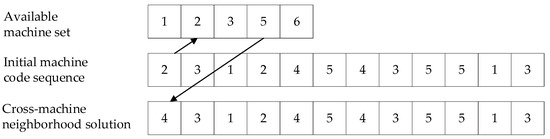
Figure 6.
Schematic diagram of cross-machine neighborhood search for bottleneck process.
When the colony has been assimilated and revolutionized, compare the cost of all the colonies with the imperialist country. The colony replaces the imperialist country as the new imperialist country within the imperial if its cost is lower than that of the imperialist country; Otherwise, the colonial state does not change.
3.4. Extra-Empire Competition
3.4.1. Invasion Mechanism
The original algorithm only iterates in randomly generated initial countries. The algorithm falls into the local optimum if the initial solutions developed are not uniformly distributed in the solution space. Referring to real society, the invasion of solid external forces will aggravate the evolution of conflicts. The surviving parties will rapidly become stronger through the survival of the fittest. Based on this phenomenon, an invasion strategy of foreign imperial groups is proposed to enhance the search breadth of solutions and bring the results closer to optimal.
Step 1: Generate a random country group to form a group of foreign invasion imperial groups.
Step 2: In a binary tournament, the original imperial group and the invading imperial group run for the victorious country.
Step 3: The victorious nation will select outstanding colonies with the same number of colonies as the original imperial to form a victorious nation group and enter the original imperial group to compete.
3.4.2. Country Competition Extra-Empire
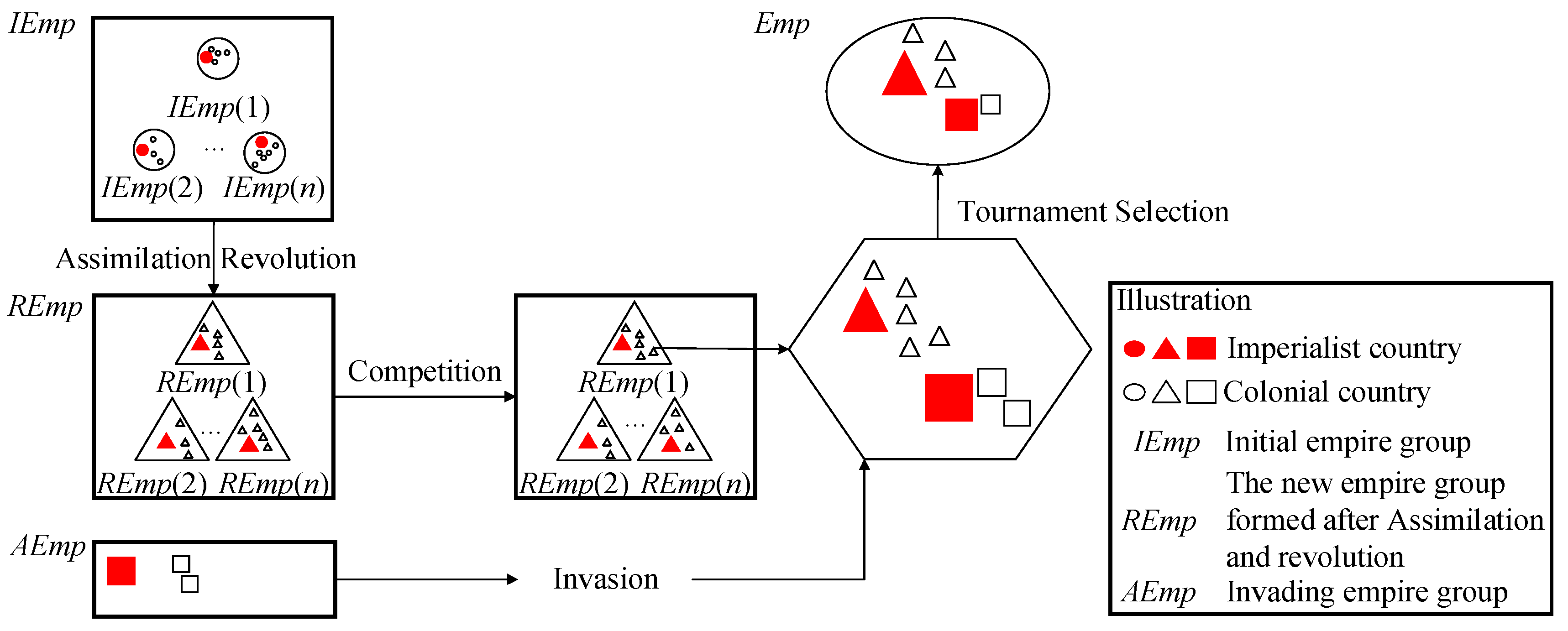
In the algorithm iteration process, extra imperials can acquire weaker colonies in the imperial (the high-cost colonies in this case) with a certain probability through competition. When the number of colonies owned by an imperial is less than or equal to the specified threshold (the threshold in this paper is zero), the imperial is destroyed. The overlord in that imperial was demoted to the colony, and other imperials will complete it. As the iteration progresses, weak imperials are continuously deleted, and eventually, only one imperial remains, or the specified number of iterations has been reached. Use the imperialist country in the most potent imperial as the optimal output of the algorithm. The evolution diagram of the improved ICA is shown in Figure 7.
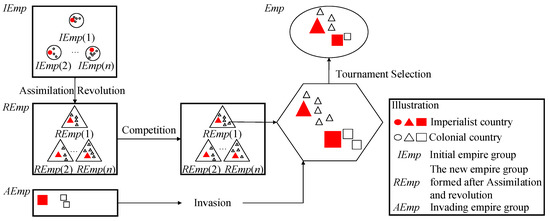
Figure 7.
Schematic diagram of the evolution of the improved imperial competition algorithm.
Release the most expensive colony among the weakest imperials and compete. Generally, the stronger the imperial, the higher the probability of acquiring the colony. The competition process is as follows:
Step 1: Calculate the total cost of the imperial, as shown in Equation (15), and normalize it, as shown in Equation (16).
where τ represents the number of colonies owned by imperialist countries, α is the colony impact factor, 0 < α < 1, and ETCn represents the normalized cost of the nth imperial.
Step 2: Calculate the probability that each imperial occupies a weak colony, as shown in Equation (17).
where γ represents the number of imperials.
Step 3: The strongest imperialist country attains the freed colonies.
4. Case Study
This section verifies the effectiveness of the proposed IICA-NS algorithm in solving the optimal configuration of flexible workshop resources through simulation experiments.
4.1. Basic Data Preparation and Parameter Setting
The workshop of a manufacturing enterprise mainly produces elevator parts, which have the characteristics of flexible manufacturing. The information on the processed workpieces and the processing machines used are shown in Table 3 and Table 4 respectively. The simulation environment for algorithm verification is established based on the discrete manufacturing process data of the workshop. Its parts process route, machine tool processing parameters, master production plan, and material demand plan are used for algorithm parameters. The problem of optimal configuration of flexible workshop resources is simplified as 9 13, as shown in Table 5. The values in the table are all dimensionless quantities, indicating the processing time of each process on the corresponding machine. “-” in the table shows that the operation cannot be processed on the related machine in this column.

Table 3.
Processing parts information.

Table 4.
Processing machine information.

Table 5.
9 13 problem example.
To verify the effectiveness of IICA-NS, the production task set PTS1-PTS9 with different scales is solved. The task set is composed of nine different combinations at three scale levels, and each workpiece appears four times to ensure uniform distribution of data and reduce contingency. The processing tasks included in each production task set are shown in Table 6. [P1, P5, P8] represent part 1 (brake disc), part 5 (brake arm), and part 8 (pin shaft) respectively. The classical imperial competition algorithm (ICA), genetic algorithm (GA), particle swarm optimization (PSO), Moth-flame optimization (MFO), and sparrow search algorithm (SSA) are used as comparison algorithms The larger the population size is, the better the algorithm performance is, but the computational cost also increases. In this paper, the maximum iteration number of 300 and the population size of 200 are selected as the parameter combination of the algorithm. The remaining characteristic parameters of each algorithm are shown in Table 7.

Table 6.
Set of production tasks at different levels.

Table 7.
Details of algorithm parameters.
4.2. Experimental Results and Discussion
The above hybrid algorithm is implemented by Matlab programming. The central frequency of the test computer CPU is 1.90 GHz, and 2.11 GHz, and the memory is 16 GB. Numerical simulation experiments are carried out under the same conditions. Four algorithms were used to solve nine production task sets, and each algorithm was run independently 30 times. The optimal value (Best), relative deviation (RE), and average convergence speed (AV (CPU)) of each algorithm are shown in Table 8, Table 9 and Table 10 respectively.

Table 8.
The Best value comparison of sixalgorithms.

Table 9.
The RE value comparison of six algorithms.

Table 10.
The AV (CPU) value comparison of six algorithms.
RE is the relative deviation between the solution result and the optimal value, and the calculation result is shown in the Formula (20).
The analysis of the RE value shows that the approximate optimal solution obtained by PSO is worse than other algorithms when solving the smaller scale PTS1-PTS3; When solving the slightly larger scale PTS4-PTS6, the performance of GA, MFO and SSA decreases similarly to PSO. The performance of ICA and IICA-NS is similar and better than them; when solving the largest PTS7-PTS9, the performance of GA degrades and the performance gap between SSA, MFO and ICA, IICA-NS increases. In terms of solution speed, regardless of the scale, GA and PSO are better than the ICA algorithm; with the increase of scale, the solution speed of the IICA-NS algorithm exceeds ICA and approaches GA and PSO. To sum up, GA and PSO are faster to solve, SSA and MFO come next, but their solved results worsen with the increase of the problem size. Although the solution speed of the ICA algorithm is not as good as GA and PSO, its solution effect is not lost with the problem size increase. IICA-NS improves the operation speed to ensure the quality of the solution.
To further understand the reasons for the above results, we discussed them from the perspective of the algorithm mechanism. First, the computational complexity is slight in terms of solution speed since GA, MFO, SSA, and PSO are single-structure algorithms. But ICA and IICA-NS are multi-structure algorithms, and the computational complexity is enormous. Therefore, the computational speed of GA and PSO is faster than that of ICA and IICA-NS. In particular, since IICA-NS uses the bottleneck heuristic neighborhood structure, it speeds up the solution while ensuring its quality. Second, in terms of solution quality, compared with the single-structure algorithm, the multi-structure algorithm has a more uniform distribution in the solution space, which gives the multi-structure algorithm a greater probability of approaching the optimal solution. When the scale of the problem is small, the difference between the algorithms of the two structures is not apparent because the distance between the initial solution and the optimal solution is relatively small. However, the advantages of multi-structure algorithms gradually become more prominent as the problem scale increases. In addition, PSO, SSA, and MFO have insufficient population diversity in the late stage and are easy to fall into local optimum. They cannot jump out of the optimal local solution due to the lack of mutation mechanism in the optimization direction; GA and ICA avoid falling into the optimal local solution through mutation and revolution, respectively.
Only the average value and standard deviation of 30 independent operations cannot fully explain the advantages of ISSA, and statistical tests are required. In order to reflect fairness, this paper uses the Wilcoxon rank sum test to verify whether ICA-NS results are significantly different from other algorithms at the significance level of p = 5%. When p < 5%, it can be considered as rejecting the H0 assumption, indicating that there is a significant difference between the two algorithms; when p > 5%, it can be considered to accept the H0 assumption, which indicates that the difference between the two algorithms is not obvious, that is, the optimization performance of the two algorithms is equivalent.
Table 11 shows the results of ICA-NS and ICA, GA, PSO, MFO, and SSA at a significance level p = 5%. When solving small-scale task sets, ICA-NS has significant differences with ICA and PSO, but no significant differences with GA (PTS2, PTS3), MFO (PTS1-PTS3) and SSA (PTS3). When the size of the task set is expanded, ICA-NS is significantly different from all comparison algorithms. In particular, ICA-NS and ICA have significant differences in all scales, indicating that bottleneck heuristic neighborhood structure and population intrusion strategy can effectively improve the solving performance of ICA.

Table 11.
The Wilcoxon rank sum test p values.
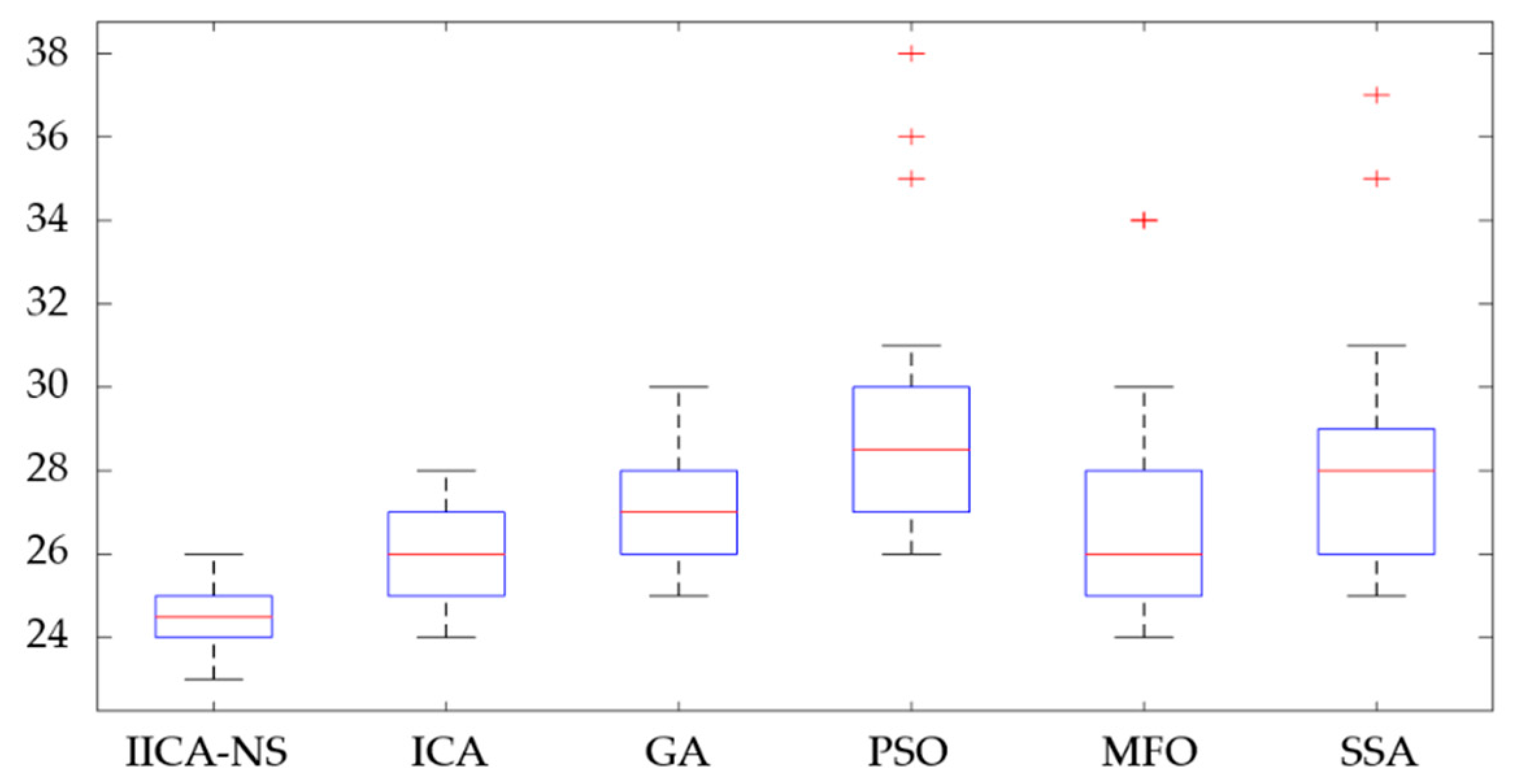
The box-plot can not only show the distribution, abnormal value, fluctuation, and stability of data, but also compare the differences in the distribution of different types of data. Therefore, the box-plot of six algorithms for TPS8 is given, as shown in Figure 8. The median of box-plot produced by the ICA-NS is 25, and other medians of box-plot produced by other algorithms are 26, 27, 28, 26, and 28, respectively. Therefore, the box-plot of the ICA-NS algorithm is in the lowest position, which indicates that the overall quality of the solution generated by the IICA-NS is better than the other five algorithms. As well, the PSO (35, 36, 38), MFO (34), and SSA (35, 37) generate large outliers in the 30 running times of the algorithm, indicating that the PSO, MFO and SSA easily fall into the local extremum. Besides, the IQR of the box-plot generated by the ICA-NS algorithm is 1, and the IQR of the box-plot generated by the other three algorithms are 2, 2, 3, 3, and 3, respectively, indicating that the IICA-NS produces the smallest discrete degree, and the stability of the scheduling results under large-scale data was optimal among the four algorithms. Based on the above analysis, the IICA-NS is better than the ICA, GA, PSO, MFO and SSA.
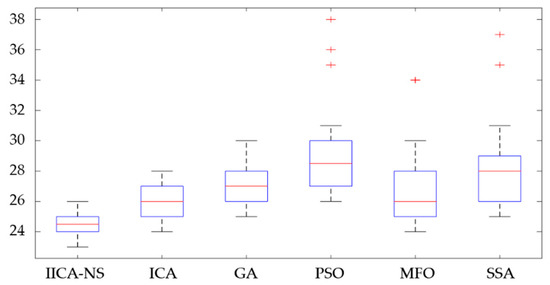
Figure 8.
Box-plot of four algorithms for large-scale TPS8.
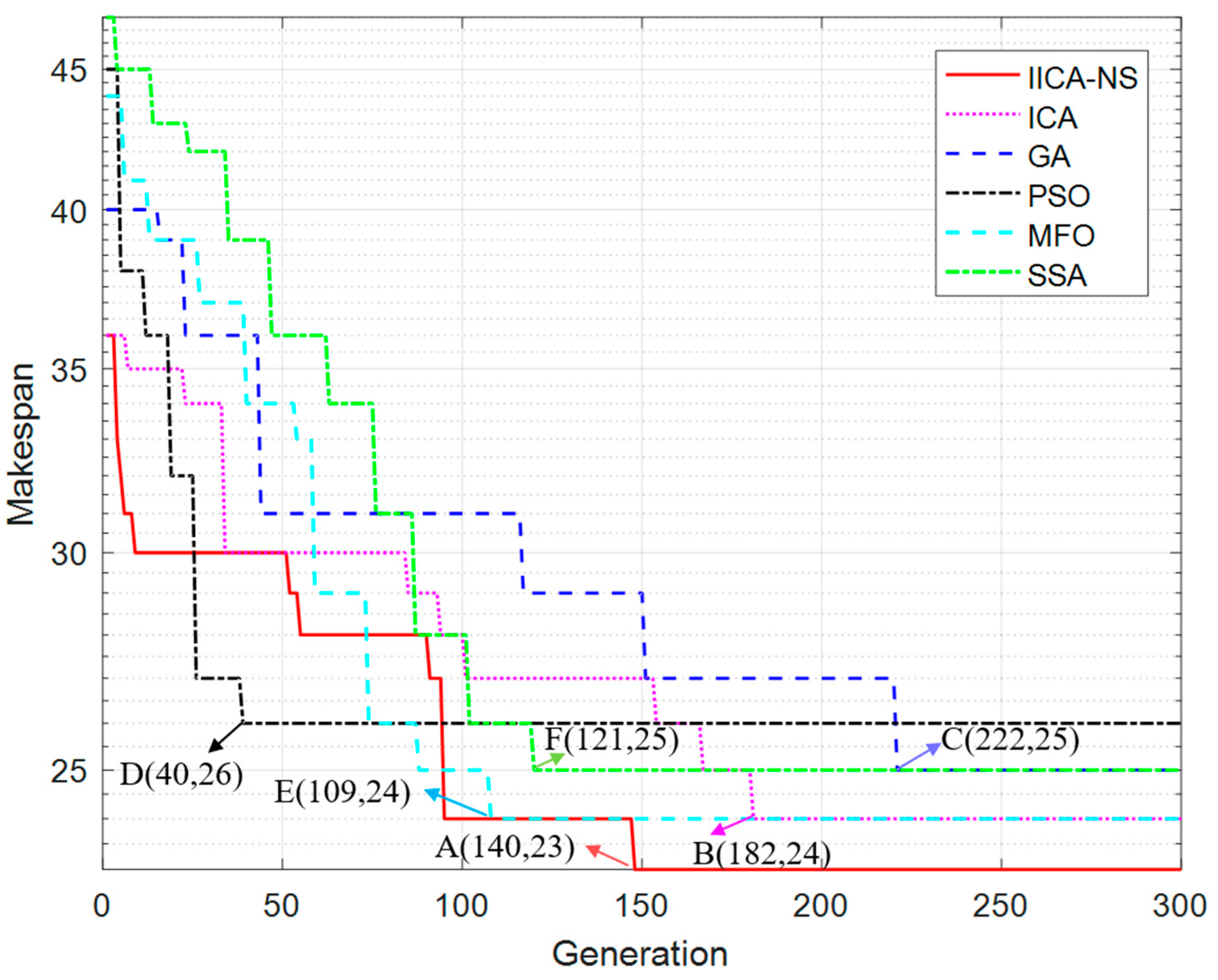
Figure 9 shows the iterative population process of solving the results of TPS8 by the four algorithms, respectively. It can be seen that the PSO algorithm finds the current optimal value 26 in the 40th generation (point D); the GA algorithm finds the current optimal value 25 in the 222nd generation (point C); the ICA algorithm finds the current optimal value 25 in the 182nd generation (B point) point) to find the optimal value 24; the IICA-NS algorithm finds the optimal value 23 at the 149th generation (point A). The MFO found the current optimal value 24 at the 109th generation (point E); the SSM found the current optimal value 25 at the 121st generation (point F). In particular, The PSO, SSA and MFO algorithm have only one convergence stage because it cannot jump out of the optimal local solution. The other three algorithms have multiple convergence stages, proving that they can jump out of local optima. In addition, the IICA-NS algorithm outperforms different algorithms in the solution obtained. The improvement is more significant compared with the PSO which is 11.538%; Compared with the traditional ICA and MFO, the improvement is minor, which is 4.167%. The above results show that the IICA-NS algorithm proposed in this paper is excellent. Because a new neighborhood structure with efficient local search capability is integrated into the ICA algorithm, the intrusion mechanism can further search for promising areas around the individual population when the algorithm falls into a local optimum. It may immediately obtain a higher solution. Even if the quality solution cannot improve the current optimal solution, it can effectively enhance the diversity of the current population and lay the foundation for obtaining higher quality solutions in subsequent operations.
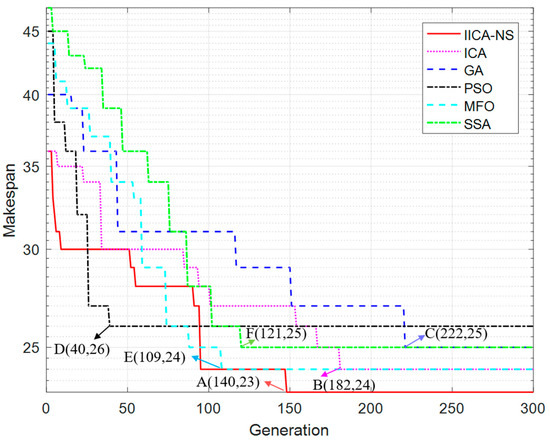
Figure 9.
Comparison of six algorithms convergence curves for large-scale TPS8.
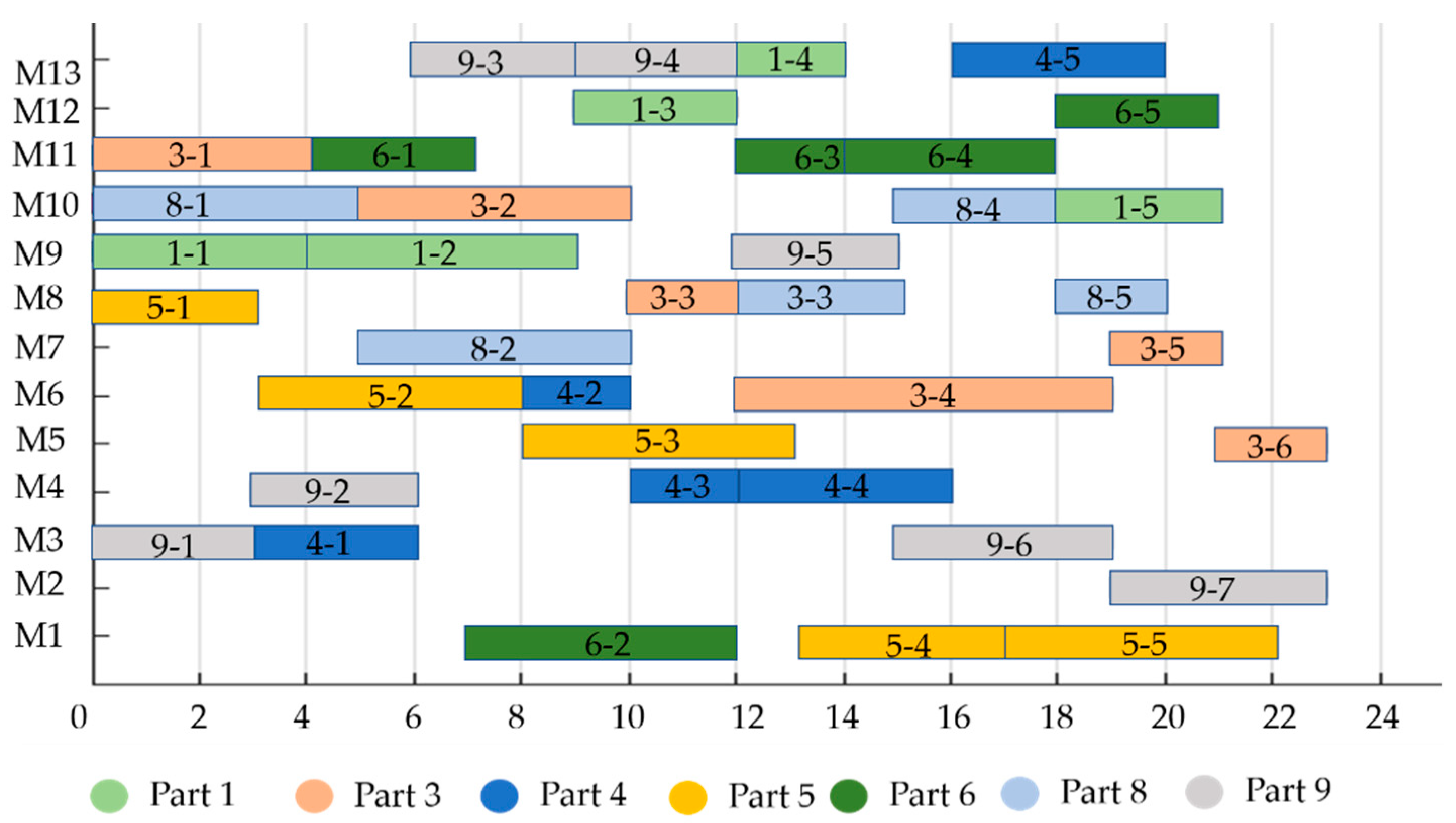
Figure 10 shows the Gantt chart of resource configuration obtained by the IICA-NS algorithm. There are 13 machines that process nine workpieces in this case. The “3-1” represents the 1st operation of the 3rd workpiece. The maximum completion time is 23s, and the maximum completion time is controlled within a reasonable range, which meets the actual production requirements.
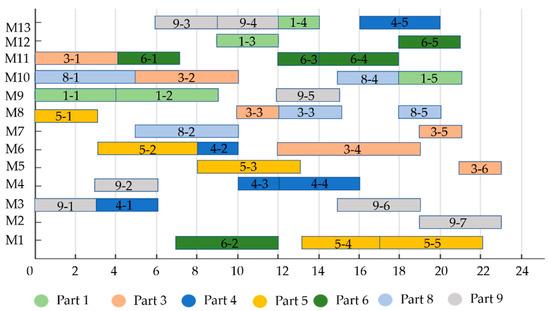
Figure 10.
Resource Configuration Gantt charts obtained by IICA-NS algorithms.
5. Conclusions
This paper aims to optimize the maximum completion time and dynamically optimize the configuration of resources for the flexible workshop. A state-driven dynamic resource configuration framework is proposed to deal with the problem of invalid configuration results due to environmental changes. As well, a hybrid algorithm that integrates the manufacturing domain knowledge is proposed to solve the resource configuration problem. Finally, taking a flexible production workshop as an example, the effectiveness of the proposed algorithm is verified by numerical simulation experiments, and the improved IICA-NS is compared with five different algorithms to verify the effectiveness and feasibility of the algorithm. The main contributions of this paper include:
- (1)
- The impact of disturbance on resource configuration is clarified, and a state-driven dynamic resource configuration framework is proposed.
- (2)
- Integrating the knowledge in the manufacturing field, from the perspective of the critical path, the revolutionary link of the imperial competition algorithm is improved through the bottleneck heuristic neighborhood structure, and the optimization efficiency of the algorithm is effectively improved. Compared with PSO, the optimal solution is improved by 8.695%.
- (3)
- Aiming at the problem that the ICA algorithm is easy to fall into the local optimum, a foreign population invasion strategy is proposed to improve the original algorithm to strengthen its optimization ability of the algorithm. Compared with ICA, the optimal solution is improved by 4.348%.
This paper studies the optimal configuration of work-in-progress and machine resources. In the next step, workers and maintenance equipment can also be considered (the machine resources are further subdivided into the tool, worker, and maintenance resources (accessories, etc.)). It is also considered to establish a workshop full resource configuration model to study the optimal configuration of all workshop resources.
Author Contributions
Conceptualization, X.S.; methodology, X.S. and C.Z.; software, X.S.; validation, C.C. and C.Z.; formal analysis, L.F. and C.C.; investigation, L.F. and X.S.; resources, W.J.; data curation, X.S.; writing—original draft preparation, X.S.; writing—review and editing, W.J. and C.Z.; funding acquisition, W.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Major Scientific and Technological Innovation Project of Shandong Province, grant number 2019JZZY020111 and the National Natural Science Foundation of China, grant number 51805213.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, G.; Zhang, G.; Guo, X.; Zhang, Y. Digital twin-driven service model and optimal allocation of manufacturing resources in shared manufacturing. J. Manuf. Syst. 2021, 59, 165–179. [Google Scholar] [CrossRef]
- Pereira, M.T.; Santoro, M.C. An integrative heuristic method for detailed operations scheduling in assembly job shop systems. Int. J. Prod. Res. 2011, 49, 6089–6105. [Google Scholar] [CrossRef]
- Qiu, Y.; Ji, W.; Zhang, C. A hybrid machine learning and population knowledge mining method to minimize makespan and total tardiness of multi-variety products. Appl. Sci. 2019, 9, 5286. [Google Scholar] [CrossRef]
- Engin, O.; Güçlü, A. A new hybrid ant colony optimization algorithm for solving the no-wait flow shop scheduling problems. Appl. Soft Comput. 2018, 72, 166–176. [Google Scholar] [CrossRef]
- Wu, X.; Sun, Y. A green scheduling algorithm for flexible job shop with energy-saving measures. J. Clean. Prod. 2018, 172, 3249–3264. [Google Scholar] [CrossRef]
- Xiao, H.; Sun, K.; Pan, J.; Li, Y.; Liu, Y. Review of hybrid HVDC systems combining line communicated converter and voltage source converter. Int. J. Electr. Power Energy Syst. 2021, 129, 106713. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, P. RFID-driven energy-efficient control approach of CNC machine tools using deep belief networks. IEEE Trans. Autom. Sci. Eng. 2019, 17, 129–141. [Google Scholar] [CrossRef]
- Su, X.; Lu, J.; Chen, C.; Yu, J.; Ji, W. Dynamic Bottleneck Identification of Manufacturing Resources in Complex Manufacturing System. Appl. Sci. 2022, 12, 4195. [Google Scholar] [CrossRef]
- Berkhout, J.; Pauwels, E.; van der Mei, R.; Stolze, J.; Broersen, S. Short-term production scheduling with non-triangular sequence-dependent setup times and shifting production bottlenecks. Int. J. Prod. Res. 2021, 59, 727–751. [Google Scholar] [CrossRef]
- Tonke, D.; Grunow, M.; Akkerman, R. Robotic-cell scheduling with pick-up constraints and uncertain processing times. IISE Trans. 2019, 51, 1217–1235. [Google Scholar] [CrossRef]
- Dong, Y.; Ma, J.; Wang, S.; Liu, T.; Chen, X.; Huang, H. An Accurate Small Signal Dynamic Model for LCC-HVDC. IEEE Trans. Appl. Supercon. 2021, 31, 0603606. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Z.; Ding, K.; Chan, F.T.; Ji, W. An energy-aware cyber physical system for energy Big data analysis and recessive production anomalies detection in discrete manufacturing workshops. Int. J. Prod. Res. 2020, 58, 7059–7077. [Google Scholar] [CrossRef]
- Dong, Y.; Sun, K.; Wang, J.; Wang, S.; Huang, H.; Liu, T.; Liu, Y. A time-delay correction control strategy for HVDC frequency regulation service. CSEE J. Power Energy Syst. 2022, 1–11. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Jemai, A.; Trentesaux, D.; Ammari, A.C.; Niar, S. Two stage particle swarm optimization to solve the flexible job shop predictive scheduling problem considering possible machine breakdowns. Comput. Ind. Eng. 2017, 112, 595–606. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Trentesaux, D. Towards energy efficient scheduling and rescheduling for dynamic flexible job shop problem. IFAC PapersOnLine 2018, 51, 1275–1280. [Google Scholar] [CrossRef]
- Sun, K.; Xiao, H.; Pan, J.; Liu, Y. VSC-HVDC interties for urban power grid enhancement. IEEE Trans. Power Syst. 2021, 36, 4745–4753. [Google Scholar] [CrossRef]
- Zhang, Y.; Huang, G.Q.; Sun, S.; Yang, T. Multi-agent based real-time production scheduling method for radio frequency identification enabled ubiquitous shopfloor environment. Comput. Ind. Eng. 2014, 76, 89–97. [Google Scholar] [CrossRef]
- Zhang, C.; Ji, W. Big data analysis approach for real-time carbon efficiency evaluation of discrete manufacturing workshops. IEEE Access 2019, 7, 107730–107743. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, P. Sustainability Evaluation of Process Planning for Single CNC Machine Tool under the Consideration of Energy-Efficient Control Strategies Using Random Forests. Sustainability 2019, 11, 3060. [Google Scholar] [CrossRef]
- Salido, M.A.; Escamilla, J.; Barber, F.; Giret, A. Rescheduling in job-shop problems for sustainable manufacturing systems. J. Clean. Prod. 2017, 162, S121–S132. [Google Scholar] [CrossRef]
- Zakaria, Z.; Petrovic, S. Genetic algorithms for match-up rescheduling of the flexible manufacturing systems. Comput. Ind. Eng. 2012, 62, 670–686. [Google Scholar] [CrossRef]
- Sun, K.; Qiu, W.; Yao, W.; You, S.; Yin, H.; Liu, Y. Frequency injection based hvdc attack-defense control via squeeze-excitation double cnn. IEEE Trans. Power Syst. 2021, 36, 5305–5316. [Google Scholar] [CrossRef]
- Li, X.; Gao, L. An effective hybrid genetic algorithm and tabu search for flexible job shop scheduling problem. Int. J. Prod. Econ. 2016, 174, 93–110. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, Y.; Sun, J.; Zhang, W. An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints. Swarm Evol. Comput. 2020, 54, 100664. [Google Scholar] [CrossRef]
- Chaouch, I.; Driss, O.B.; Ghedira, K. A modified ant colony optimization algorithm for the distributed job shop scheduling problem. Procedia Comput. Sci. 2017, 112, 296–305. [Google Scholar] [CrossRef]
- Nouiri, M.; Bekrar, A.; Jemai, A.; Niar, S.; Ammari, A.C. An effective and distributed particle swarm optimization algorithm for flexible job-shop scheduling problem. J. Intell. Manuf. 2018, 29, 603–615. [Google Scholar] [CrossRef]
- Ding, H.; Gu, X. Hybrid of human learning optimization algorithm and particle swarm optimization algorithm with scheduling strategies for the flexible job-shop scheduling problem. Neurocomputing 2020, 414, 313–332. [Google Scholar] [CrossRef]
- Lei, D.; Li, M.; Wang, L. A two-phase meta-heuristic for multiobjective flexible job shop scheduling problem with total energy consumption threshold. IEEE Trans. Cybern. 2018, 49, 1097–1109. [Google Scholar] [CrossRef]
- Majid, K.; Asadollah, A.; Javad, B.; Fatemeh, M.R.; Zahra, S.; Wing, C.K.; Ashkan, N.P. Multi-objective optimization of energy use and environmental emissions for walnut production using imperialist competitive algorithm. Appl. Energy 2020, 284, 116342. [Google Scholar]
- Ahmadizar, F.; Farhadi, S. Single-machine batch delivery scheduling with job release dates, due windows and earliness, tardiness, holding and delivery costs. Comput. Oper. Res. 2015, 53, 194–205. [Google Scholar] [CrossRef]
- Yazdani, M.; Khalili, S.M.; Jolai, F. A parallel machine scheduling problem with two-agent and tool change activities: An efficient hybrid metaheuristic algorithm. Int. J. Comput. Integ. Manuf. 2016, 29, 1075–1088. [Google Scholar] [CrossRef]
- Seidgar, H.; Kiani, M.; Abedi, M.; Fazlollahtabar, H. An efficient imperialist competitive algorithm for scheduling in the two-stage assembly flow shop problem. Int. J. Prod. Res. 2014, 52, 1240–1256. [Google Scholar] [CrossRef]
- Zandieh, M.; Khatami, A.R.; Rahmati, S.H.A. Flexible job shop scheduling under condition-based maintenance: Improved version of imperialist competitive algorithm. Appl. Soft Comput. 2017, 58, 449–464. [Google Scholar] [CrossRef]
- Karimi, S.; Ardalan, Z.; Naderi, B.; Mohammadi, M. Scheduling flexible job-shops with transportation times: Mathematical models and a hybrid imperialist competitive algorithm. Appl. Math. Model. 2017, 41, 667–682. [Google Scholar] [CrossRef]
- Cruz Chávez, M.A.; Martínez Rangel, M.G.; Cruz Rosales, M.H. Accelerated simulated annealing algorithm applied to the flexible job shop scheduling problem. Int. Trans. Oper. Res. 2017, 24, 1119–1137. [Google Scholar] [CrossRef]
- Shen, L.; Dauzère-Pérès, S.; Neufeld, J.S. Solving the flexible job shop scheduling problem with sequence-dependent setup times. Eur. J. Oper. Res. 2018, 265, 503–516. [Google Scholar] [CrossRef]
- Palacios, J.J.; González, M.A.; Vela, C.R.; González-Rodríguez, I.; Puente, J. Genetic tabu search for the fuzzy flexible job shop problem. Comput. Oper. Res. 2015, 54, 74–89. [Google Scholar] [CrossRef]
- Marichelvam, M.K.; Geetha, M.; Tosun, Ö. An improved particle swarm optimization algorithm to solve hybrid flowshop scheduling problems with the effect of human factors—A case study. Comput. Oper. Res. 2020, 114, 104812. [Google Scholar] [CrossRef]
- Shi, F.; Zhao, S.; Meng, Y. Hybrid algorithm based on improved extended shifting bottleneck procedure and GA for assembly job shop scheduling problem. Int. J. Prod. Res. 2020, 58, 2604–2625. [Google Scholar] [CrossRef]
- Duan, J.; Feng, M.; Zhang, Q. Energy-efficient collaborative scheduling of heterogeneous multi-stage hybrid flowshop for large metallic component manufacturing. J. Clean Prod. 2022, 375, 134148. [Google Scholar] [CrossRef]
- Yang, W.; Su, J.; Yao, Y.; Yang, Z.; Yuan, Y. A novel hybrid whale optimization algorithm for flexible job-shop scheduling problem. Machines 2022, 10, 618. [Google Scholar] [CrossRef]
- Subramaniyan, M.; Skoogh, A.; Muhammad, A.S.; Bokrantz, J.; Johansson, B.; Roser, C. A generic hierarchical clustering approach for detecting bottlenecks in manufacturing. J. Manuf. Syst. 2020, 55, 143–158. [Google Scholar] [CrossRef]
- Subramaniyan, M.; Skoogh, A.; Salomonsson, H.; Bangalore, P.; Gopalakrishnan, M.; Sheikh Muhammad, A. Data-driven algorithm for throughput bottleneck analysis of production systems. Prod. Manuf. Res. 2018, 6, 225–246. [Google Scholar] [CrossRef]
- Peng, B.; Lü, Z.; Cheng, T.C.E. A tabu search/path relinking algorithm to solve the job shop scheduling problem. Comput. Oper. Res. 2015, 53, 154–164. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).