A Feedforward Model Predictive Controller for Optimal Hydrocracker Operation
Abstract
1. Introduction
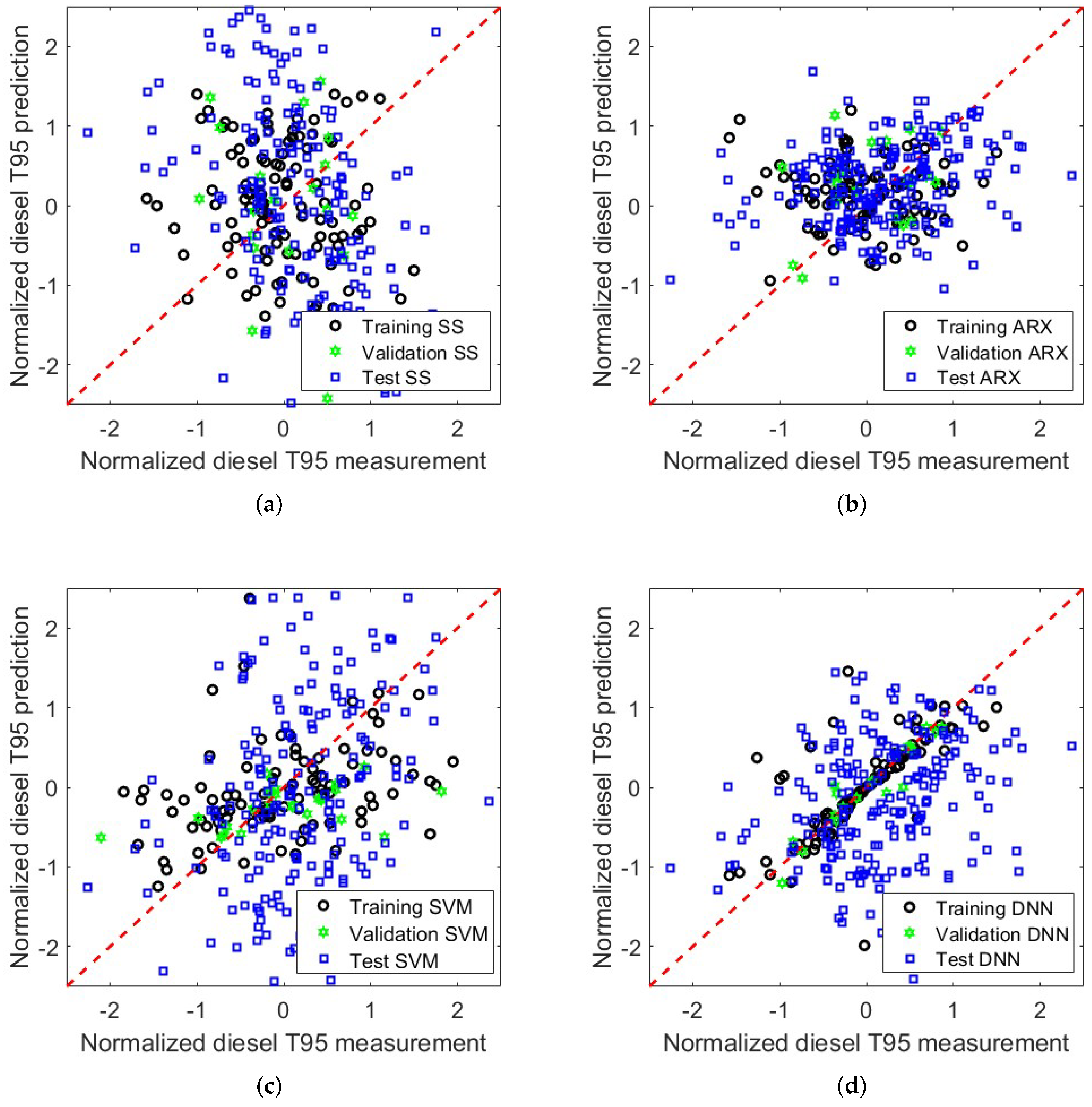
- A first-order state-space model;
- An autoregressive exogenous (ARX) model;
- A support vector machine (SVM) regression model;
- A deep neural network (DNN) model.
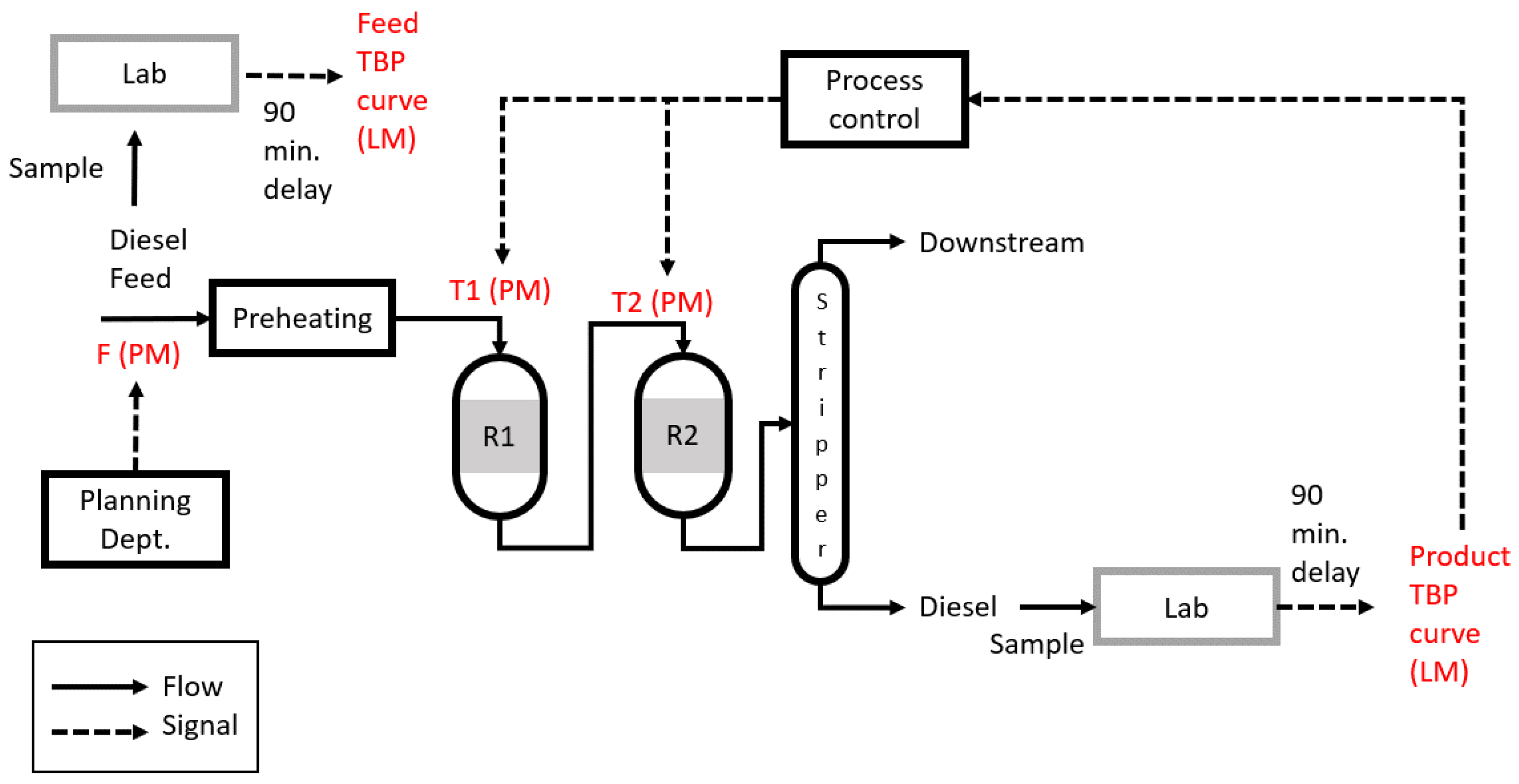
2. Materials and Methods
3. Results and Discussion
3.1. Data-Driven Model Training and Validation
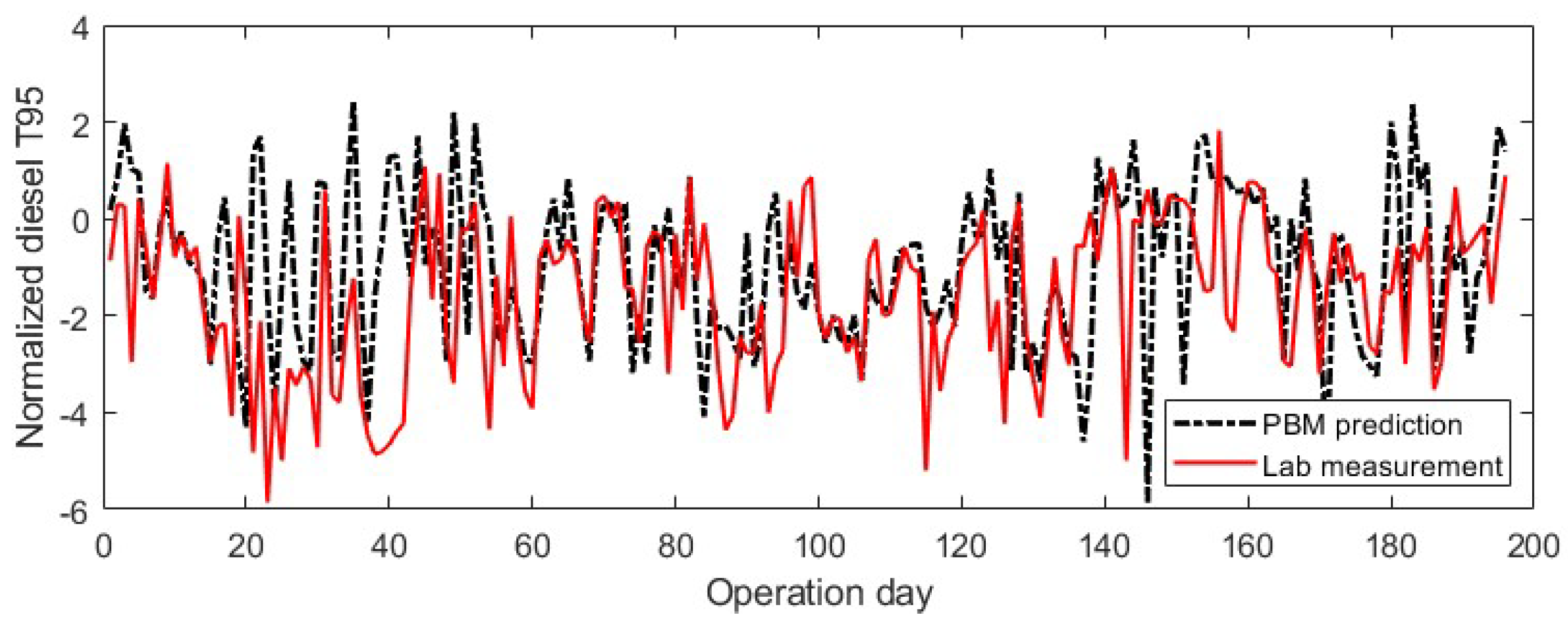
3.2. Simulator Response
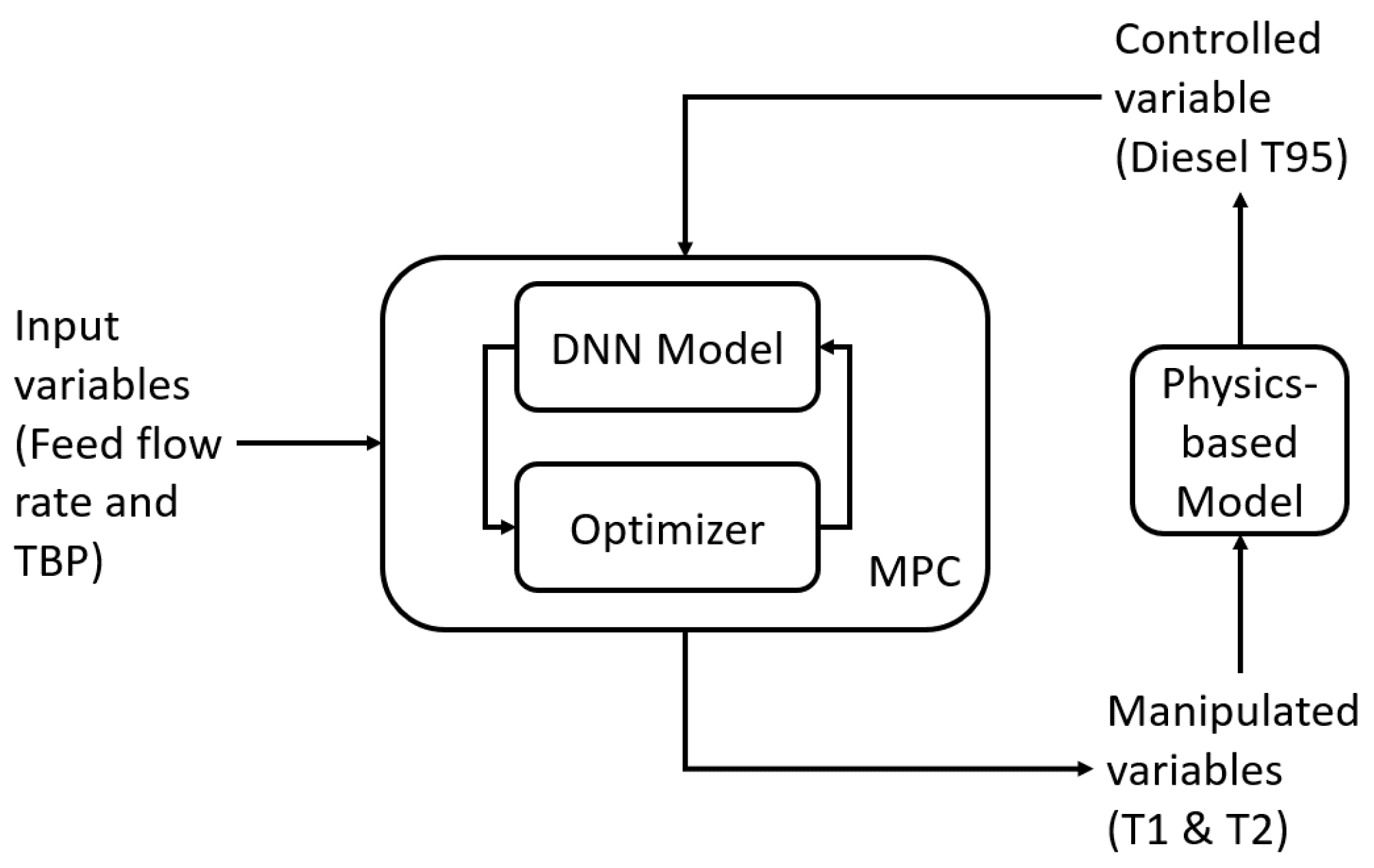
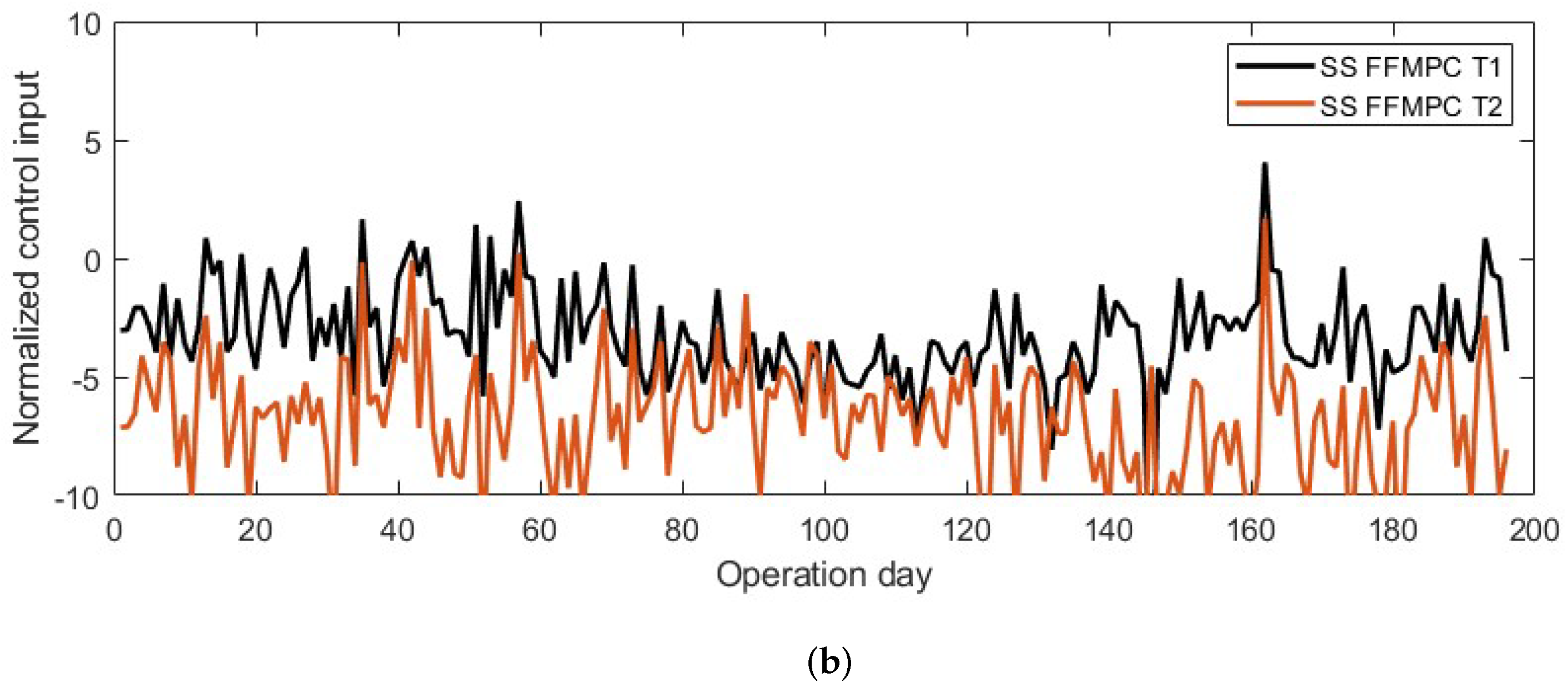
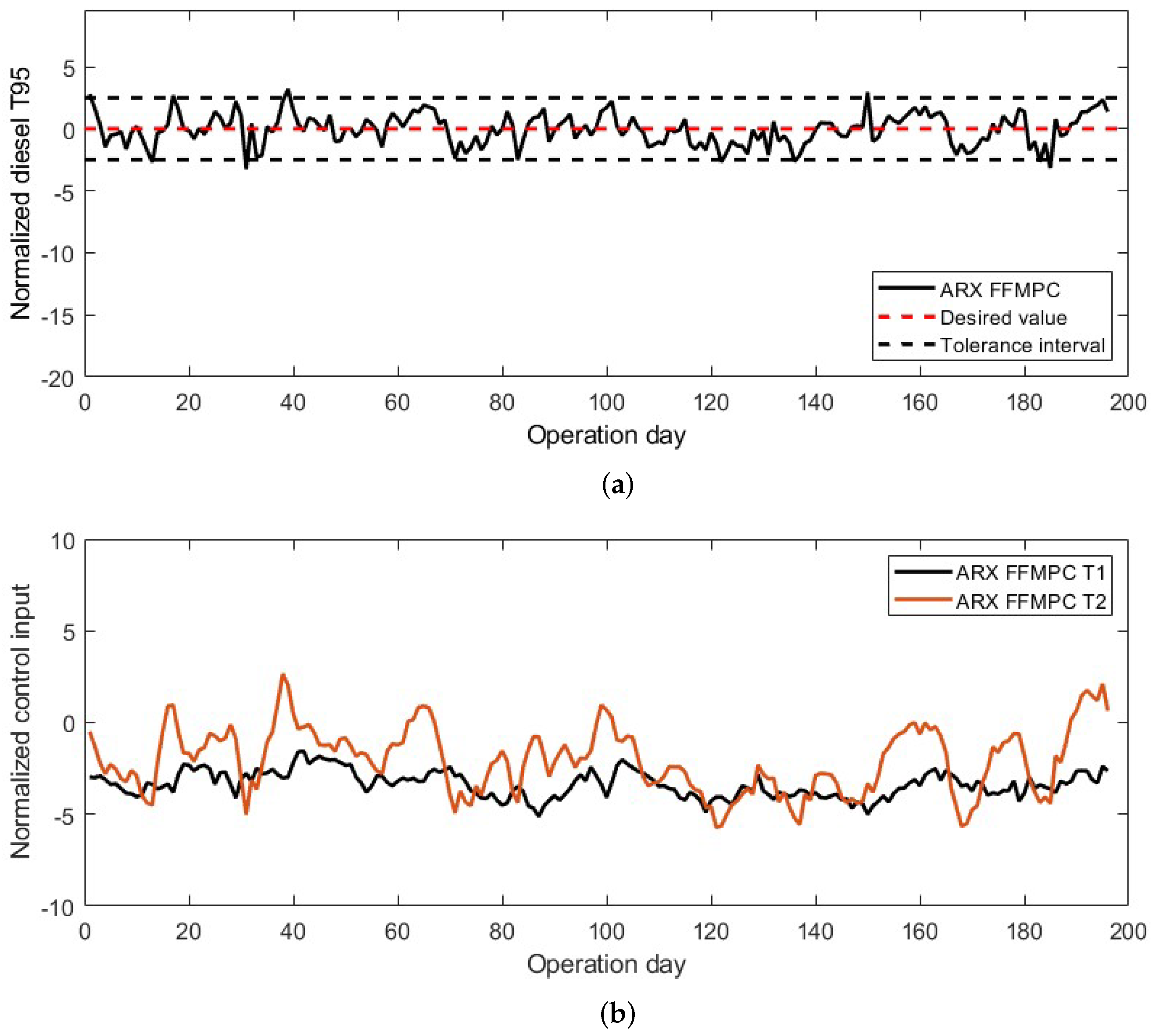
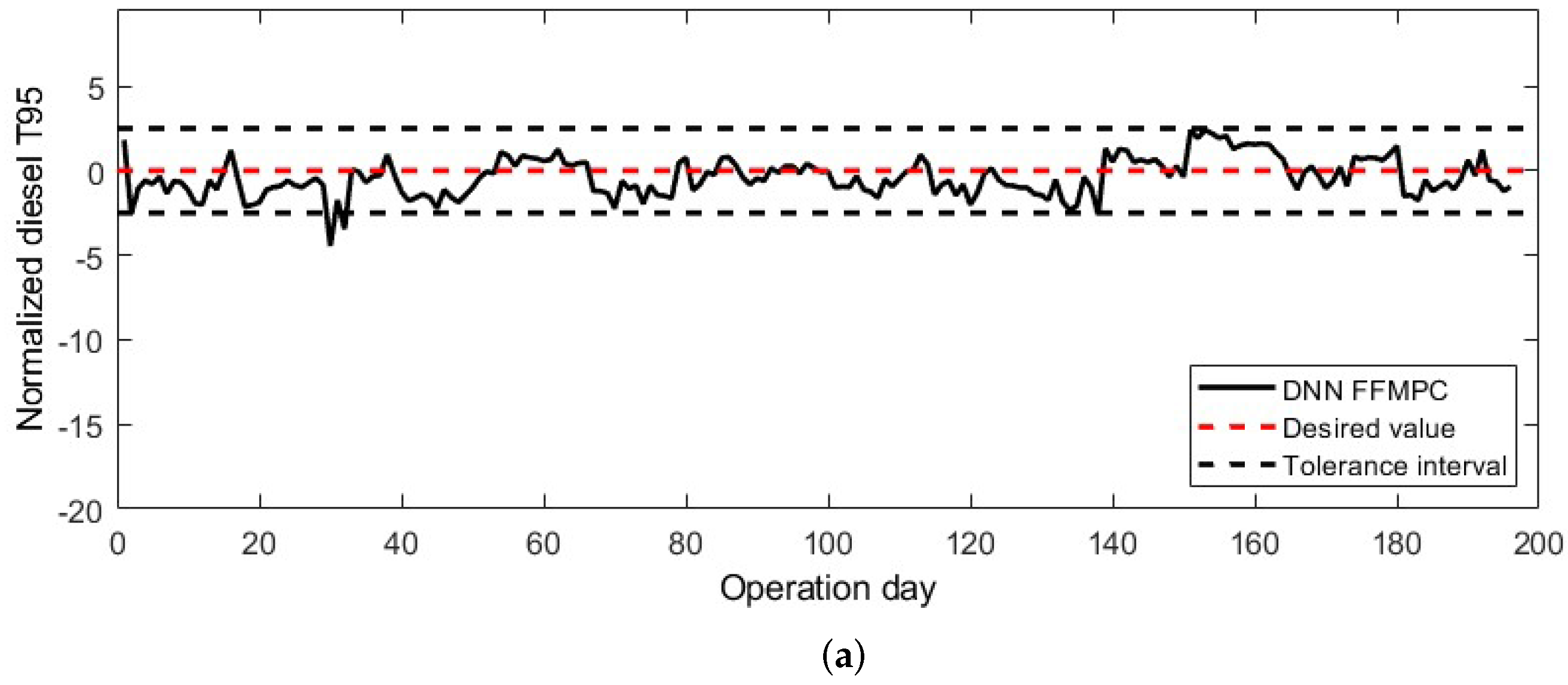
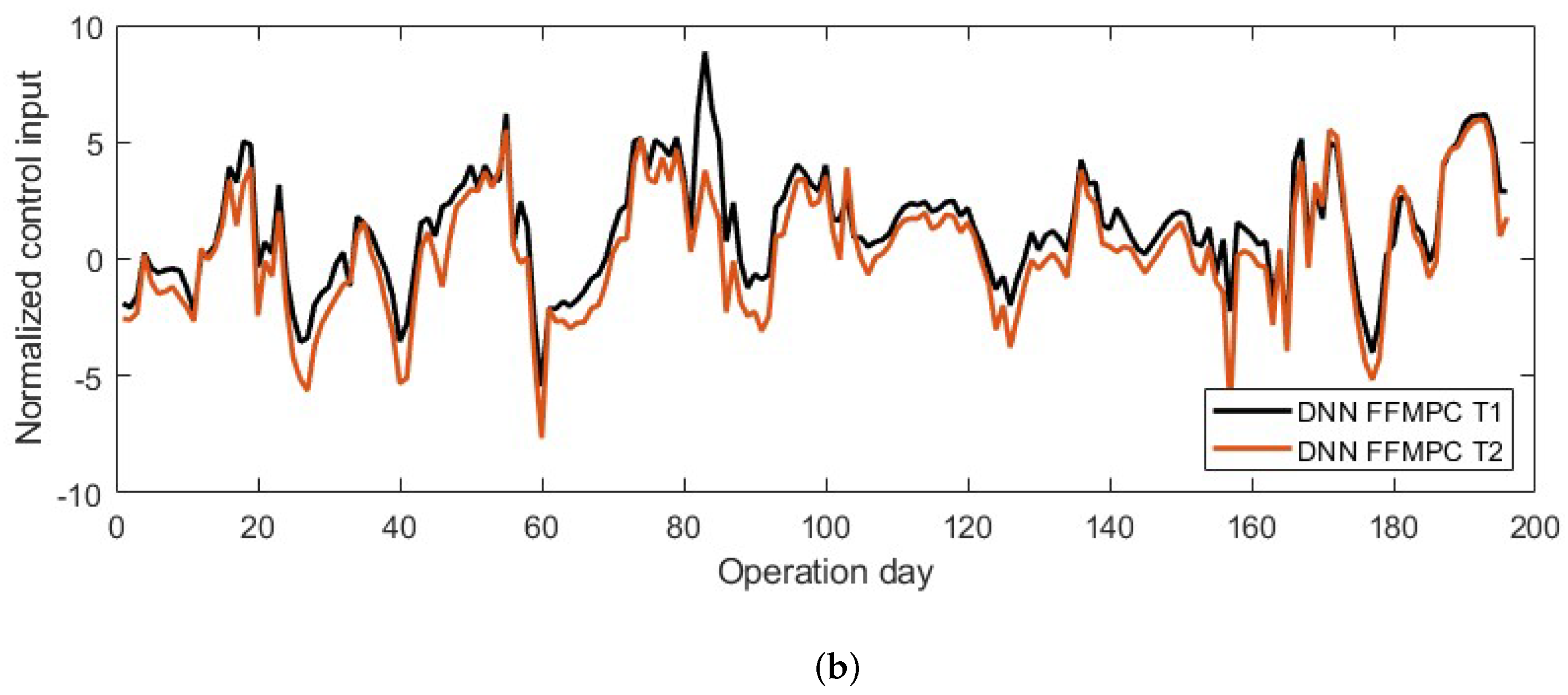
3.3. Control Response
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ebrahimi, S.B.; Bagheri, E. Optimizing profit and reliability using a bi-objective mathematical model for oil and gas supply chain under disruption risks. Comput. Ind. Eng. 2022, 163, 107849. [Google Scholar] [CrossRef]
- Abdellaoui, W.; Souier, M.; Sahnoun, M.; Abdelaziz, F.B. Multi-period optimal schedule of a multi-product pipeline: A case study in Algeria. Comput. Ind. Eng. 2021, 159, 107483. [Google Scholar] [CrossRef]
- Ryzhova, A.; Emelyanov, I.; Ziyatdinov, N.; Khalirakhmanov, Z. Optimal heat integration of large-scale cyber-physical oil refining systems. In Cyber-Physical Systems: Design and Application for Industry 4.0; Springer: Cham, Switzerland, 2021; pp. 335–345. [Google Scholar] [CrossRef]
- Li, F.; Qian, F.; Yang, M.; Du, W.; Mahalec, V. Product tri-section based crude distillation unit model for refinery production planning and refinery optimization. AIChE J. 2021, 67, e17115. [Google Scholar] [CrossRef]
- Chen, X.; Wu, K.; Bai, A.; Masuku, C.M.; Niederberger, J.; Liporace, F.S.; Biegler, L.T. Real-time refinery optimization with reduced-order fluidized catalytic cracker model and surrogate-based trust region filter method. Comput. Chem. Eng. 2021, 153, 107455. [Google Scholar] [CrossRef]
- Rana, M.S.; Sámano, V.; Ancheyta, J.; Diaz, J. A review of recent advances on process technologies for upgrading of heavy oils and residua. Fuel 2007, 86, 1216–1231. [Google Scholar] [CrossRef]
- Wijaya, K.; Nadia, A.; Dinana, A.; Pratiwi, A.F.; Tikoalu, A.D.; Wibowo, A.C. Catalytic hydrocracking of fresh and waste frying oil over Ni-and Mo-based catalysts supported on sulfated silica for biogasoline production. Catalysts 2021, 11, 1150. [Google Scholar] [CrossRef]
- Al-Shathr, A.; Shakor, Z.M.; Majdi, H.S.; AbdulRazak, A.A.; Albayati, T.M. Comparison between Artificial Neural Network and Rigorous Mathematical Model in Simulation of Industrial Heavy Naphtha Reforming Process. Catalysts 2021, 11, 1034. [Google Scholar] [CrossRef]
- Song, W.; Mahalec, V.; Long, J.; Yang, M.; Qian, F. Modeling the hydrocracking process with deep neural networks. Ind. Eng. Chem. Res. 2020, 59, 3077–3090. [Google Scholar] [CrossRef]
- Oh, D.H.; Adams, D.; Vo, N.D.; Gbadago, D.Q.; Lee, C.H.; Oh, M. Actor-critic reinforcement learning to estimate the optimal operating conditions of the hydrocracking process. Comput. Chem. Eng. 2021, 149, 107280. [Google Scholar] [CrossRef]
- Wang, Y.; Li, L.; Wang, K. An online operating performance evaluation approach using probabilistic fuzzy theory for chemical processes with uncertainties. Comput. Chem. Eng. 2021, 144, 107156. [Google Scholar] [CrossRef]
- Yuan, X.; Rao, J.; Gu, Y.; Ye, L.; Wang, K.; Wang, Y. Online Adaptive Modeling Framework for Deep Belief Network-Based Quality Prediction in Industrial Processes. Ind. Eng. Chem. Res. 2021, 60, 15208–15218. [Google Scholar] [CrossRef]
- Santos, F.D.; Vianna, S.G.; Cunha, P.H.; Folli, G.S.; de Paulo, E.H.; Moro, M.K.; Romão, W.; de Oliveira, E.C.; Filgueiras, P.R. Characterization of crude oils with a portable NIR spectrometer. Microchem. J. 2022, 181, 107696. [Google Scholar] [CrossRef]
- Pasadakis, N.; Sourligas, S.; Foteinopoulos, C. Prediction of the distillation profile and cold properties of diesel fuels using mid-IR spectroscopy and neural networks. Fuel 2006, 85, 1131–1137. [Google Scholar] [CrossRef]
- Santos, V.O., Jr.; Oliveira, F.C.; Lima, D.G.; Petry, A.C.; Garcia, E.; Suarez, P.A.; Rubim, J.C. A comparative study of diesel analysis by FTIR, FTNIR and FT-Raman spectroscopy using PLS and artificial neural network analysis. Anal. Chim. Acta 2005, 547, 188–196. [Google Scholar] [CrossRef]
- Filgueiras, P.R.; Terra, L.A.; Castro, E.V.; Oliveira, L.M.; Dias, J.C.; Poppi, R.J. Prediction of the distillation temperatures of crude oils using 1H NMR and support vector regression with estimated confidence intervals. Talanta 2015, 142, 197–205. [Google Scholar] [CrossRef]
- Iplik, E.; Aslanidou, I.; Kyprianidis, K. Hydrocracking: A perspective towards digitalization. Sustainability 2020, 12, 7058. [Google Scholar] [CrossRef]
- Yuan, H.; Tsukuda, T.; Yang, Y.; Shibata, G.; Kobashi, Y.; Ogawa, H. Effects of Chemical Compositions and Cetane Number of Fischer–Tropsch Fuels on Diesel Engine Performance. Energies 2022, 15, 4047. [Google Scholar] [CrossRef]
- Vapnik, V. The Nature of Statistical Learning Theory; Springer Science & Business Media: New York, NY, USA, 1999. [Google Scholar]
- Feng, S.; Zhou, H.; Dong, H. Using deep neural network with small dataset to predict material defects. Mater. Des. 2019, 162, 300–310. [Google Scholar] [CrossRef]
- Gupta, V.; Demirer, M.; Bigelow, M.; Little, K.J.; Candemir, S.; Prevedello, L.M.; White, R.D.; O’Donnell, T.P.; Wels, M.; Erdal, B.S. Performance of a deep neural network algorithm based on a small medical image dataset: Incremental impact of 3D-to-2D reformation combined with novel data augmentation, photometric conversion, or transfer learning. J. Digit. Imaging 2020, 33, 431–438. [Google Scholar] [CrossRef]
- Sone, K.; Nakashika, T. DNN-based Speech Synthesis for Small Data Sets Considering Bidirectional Speech-Text Conversion. In Proceedings of the Interspeech 2018, Hyderabad, India, 2–6 September 2018; pp. 2519–2523. [Google Scholar]
- ASTM-D86-19; Standard Test Method for Distillation of Petroleum Products and Liquid Fuels at Atmospheric Pressure. ASTM International: West Conshohocken, PA, USA, 2019.
- Laxminarasimhan, C.; Verma, R.; Ramachandran, P. Continuous lumping model for simulation of hydrocracking. AIChE J. 1996, 42, 2645–2653. [Google Scholar] [CrossRef]
- Govindhakannan, J.; Riggs, J.B. On the Construction of a Continuous Concentration- Reactivity Function for the Continuum Lumping Approach. Ind. Eng. Chem. Res. 2007, 46, 1653–1656. [Google Scholar] [CrossRef]
- Zhang, L.; Yin, R.; Wang, J.; Li, X. Numerical Investigations on the Molecular Reaction Model for Thermal Cracking of n-Decane at Supercritical Pressures. ACS Omega 2022, 7, 22351–22362. [Google Scholar] [CrossRef] [PubMed]
- Quann, R.J.; Jaffe, S.B. Structure-oriented lumping: Describing the chemistry of complex hydrocarbon mixtures. Ind. Eng. Chem. Res. 1992, 31, 2483–2497. [Google Scholar] [CrossRef]
- Becker, P.J.; Serrand, N.; Celse, B.; Guillaume, D.; Dulot, H. A single events microkinetic model for hydrocracking of vacuum gas oil. Comput. Chem. Eng. 2017, 98, 70–79. [Google Scholar] [CrossRef]
- Lababidi, H.; Alatiqi, I.; Ali, Y. Constrained model predictive control for a pilot hydrotreating plant. Chem. Eng. Res. Des. 2004, 82, 1293–1304. [Google Scholar] [CrossRef]
- Boldyryev, S.; Gil, T. Debottlenecking of existing hydrocracking unit by improved heat recovery for energy and carbon dioxide savings. Energy Convers. Manag. 2021, 238, 114164. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| 6 | |
| 1 | |
| 3 | |
| Sampling time | 3 |
| Control horizon | 15 |
| SS Model | ARX Model | SVMR Model | DNN Model | |
|---|---|---|---|---|
| T1 mean | −3.21 | −3.36 | 4.18 | 1.29 |
| T1 variance | 4.74 | 0.50 | 9.66 | 5.79 |
| T2 mean | −6.73 | −2.07 | 4.55 | 0.33 |
| T2 variance | 6.50 | 3.20 | 5.91 | 6.88 |
| Diesel T95 mean | −0.19 | −0.06 | 0.62 | −0.31 |
| Diesel T95 variance | 10.51 | 1.59 | 1.02 | 2.66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Iplik, E.; Aslanidou, I.; Kyprianidis, K. A Feedforward Model Predictive Controller for Optimal Hydrocracker Operation. Processes 2022, 10, 2583. https://doi.org/10.3390/pr10122583
Iplik E, Aslanidou I, Kyprianidis K. A Feedforward Model Predictive Controller for Optimal Hydrocracker Operation. Processes. 2022; 10(12):2583. https://doi.org/10.3390/pr10122583
Chicago/Turabian StyleIplik, Esin, Ioanna Aslanidou, and Konstantinos Kyprianidis. 2022. "A Feedforward Model Predictive Controller for Optimal Hydrocracker Operation" Processes 10, no. 12: 2583. https://doi.org/10.3390/pr10122583
APA StyleIplik, E., Aslanidou, I., & Kyprianidis, K. (2022). A Feedforward Model Predictive Controller for Optimal Hydrocracker Operation. Processes, 10(12), 2583. https://doi.org/10.3390/pr10122583








