The Influence of Size Effect to Deformation Mechanism of C5131 Bronze Structures of Negative Poisson’s Ratio
Abstract
:1. Introduction
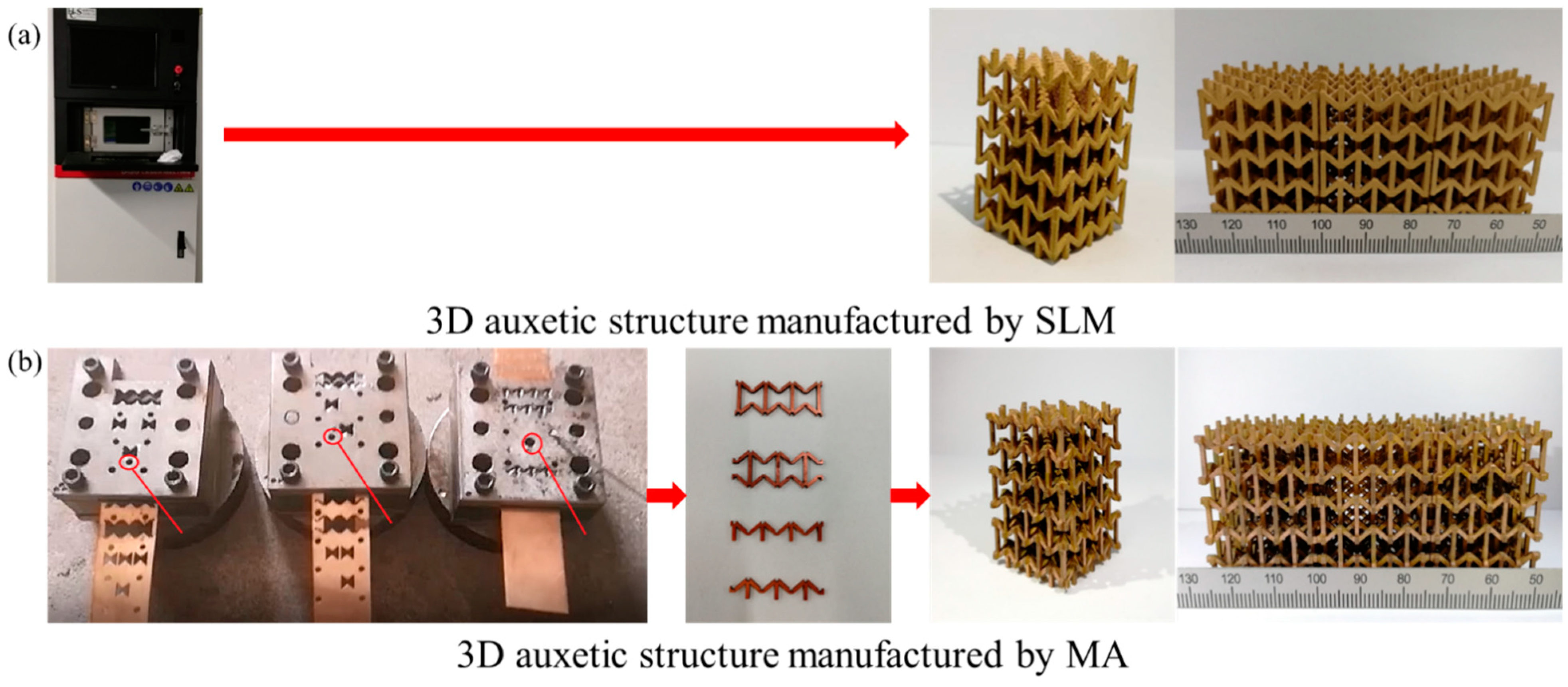
2. Experiment
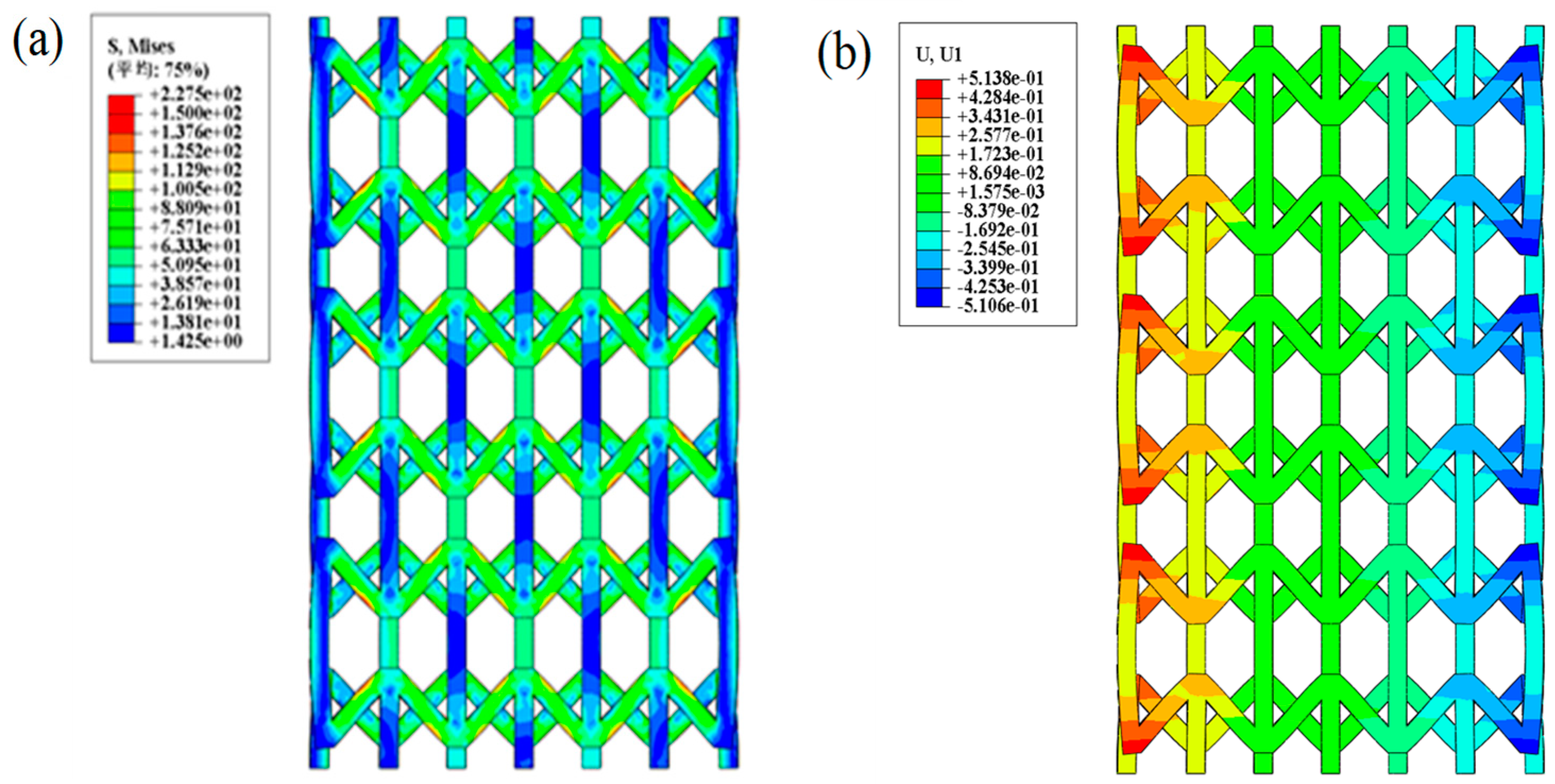
3. Result Analysis
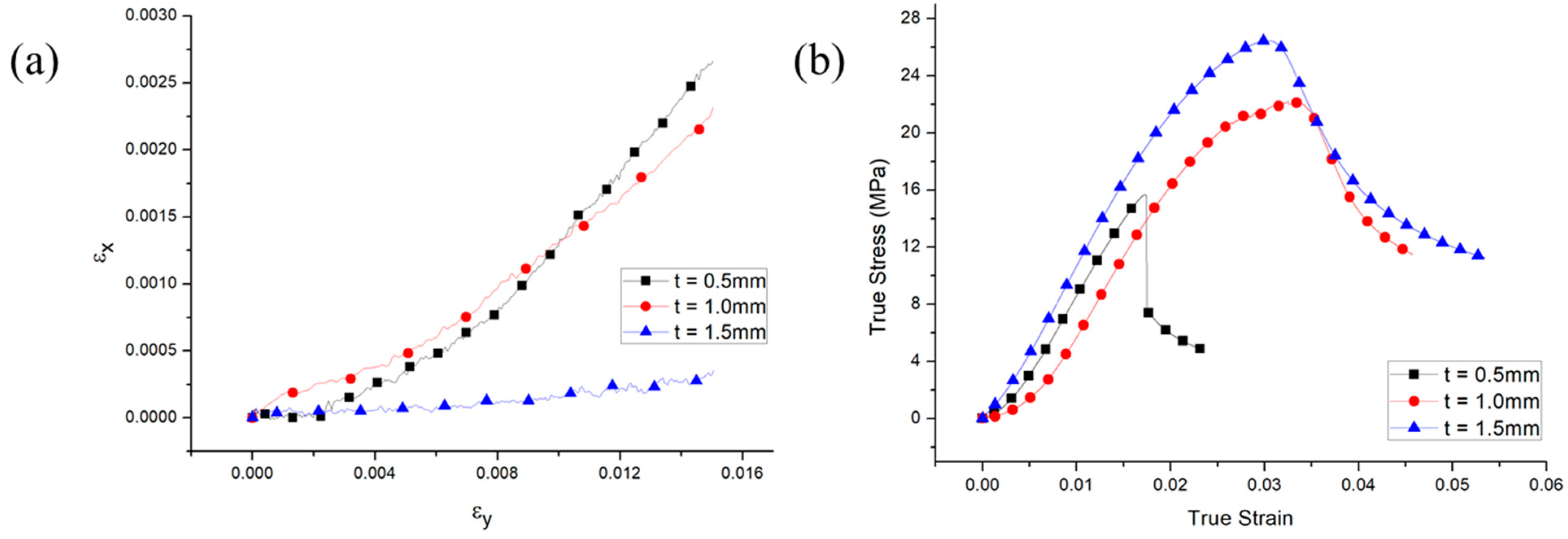
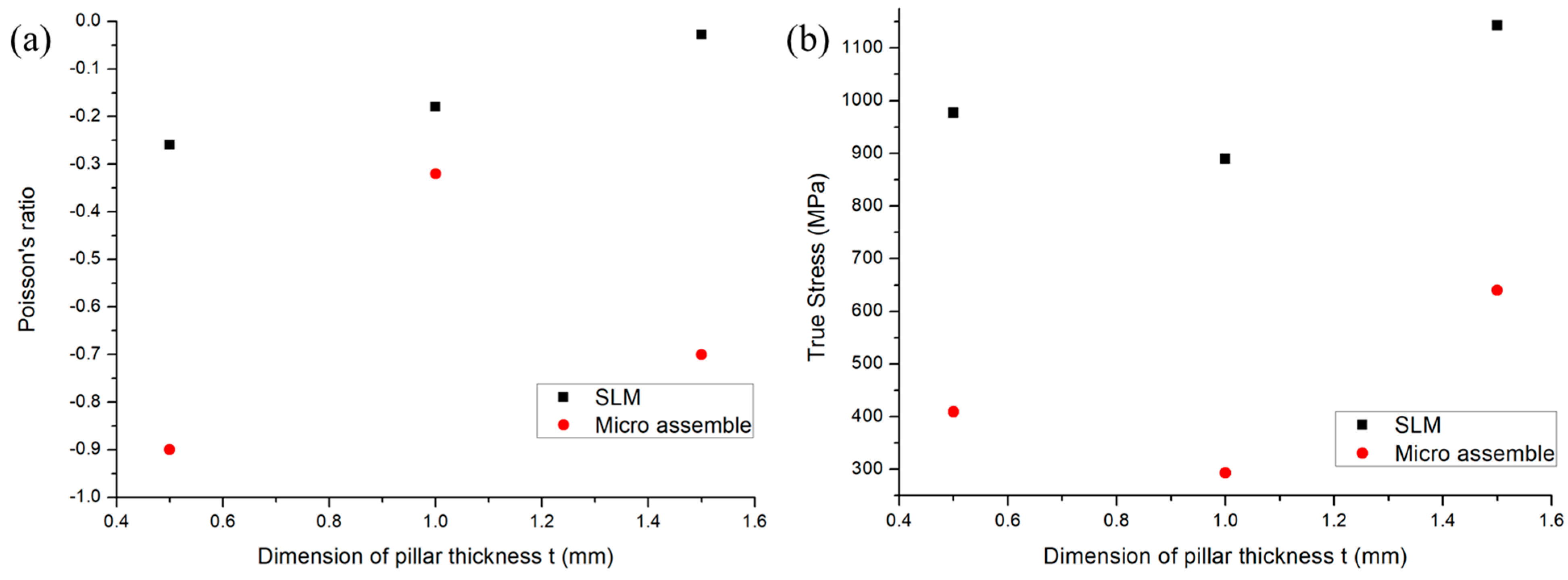
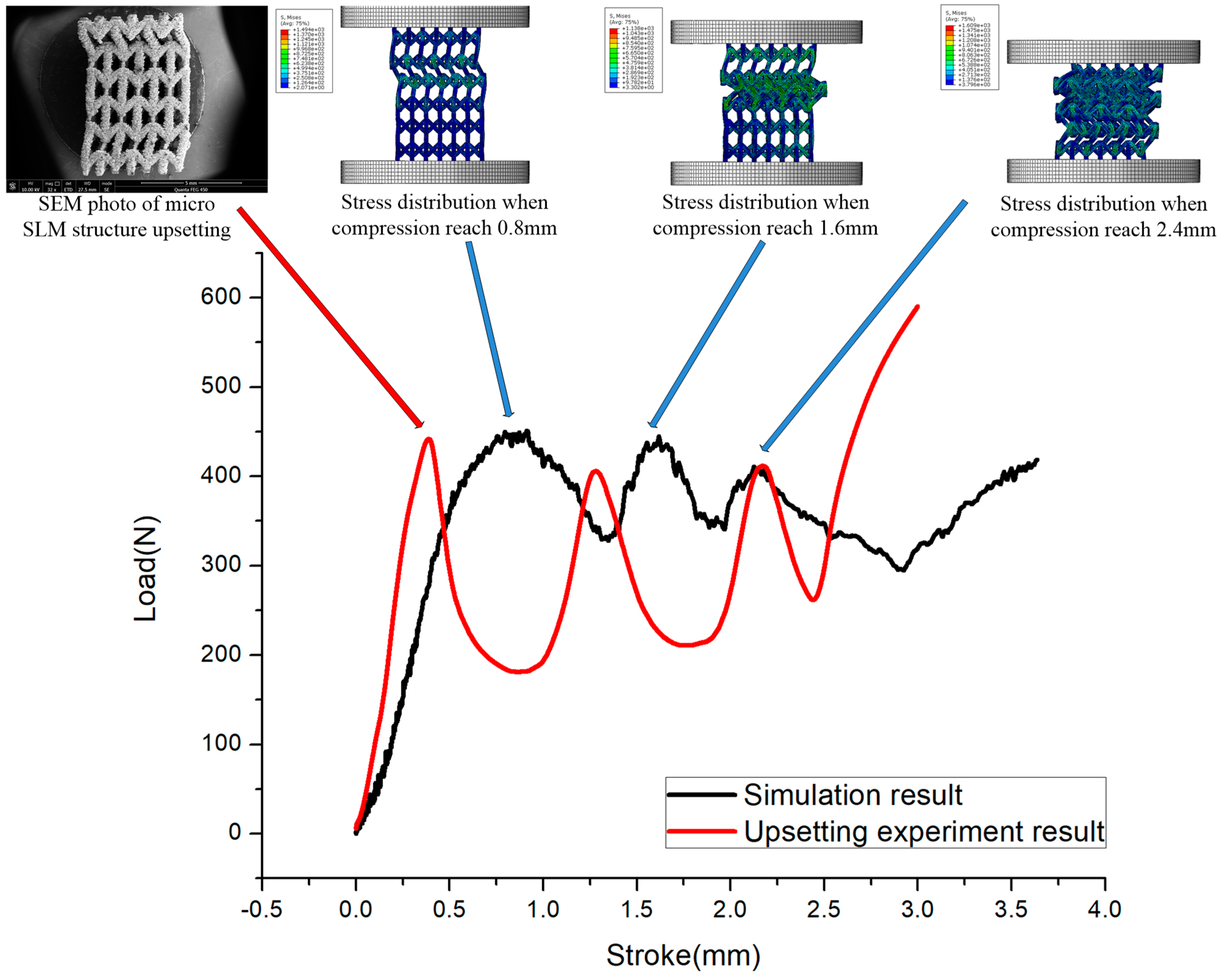
3.1. Comparison of SLM and MA Structure
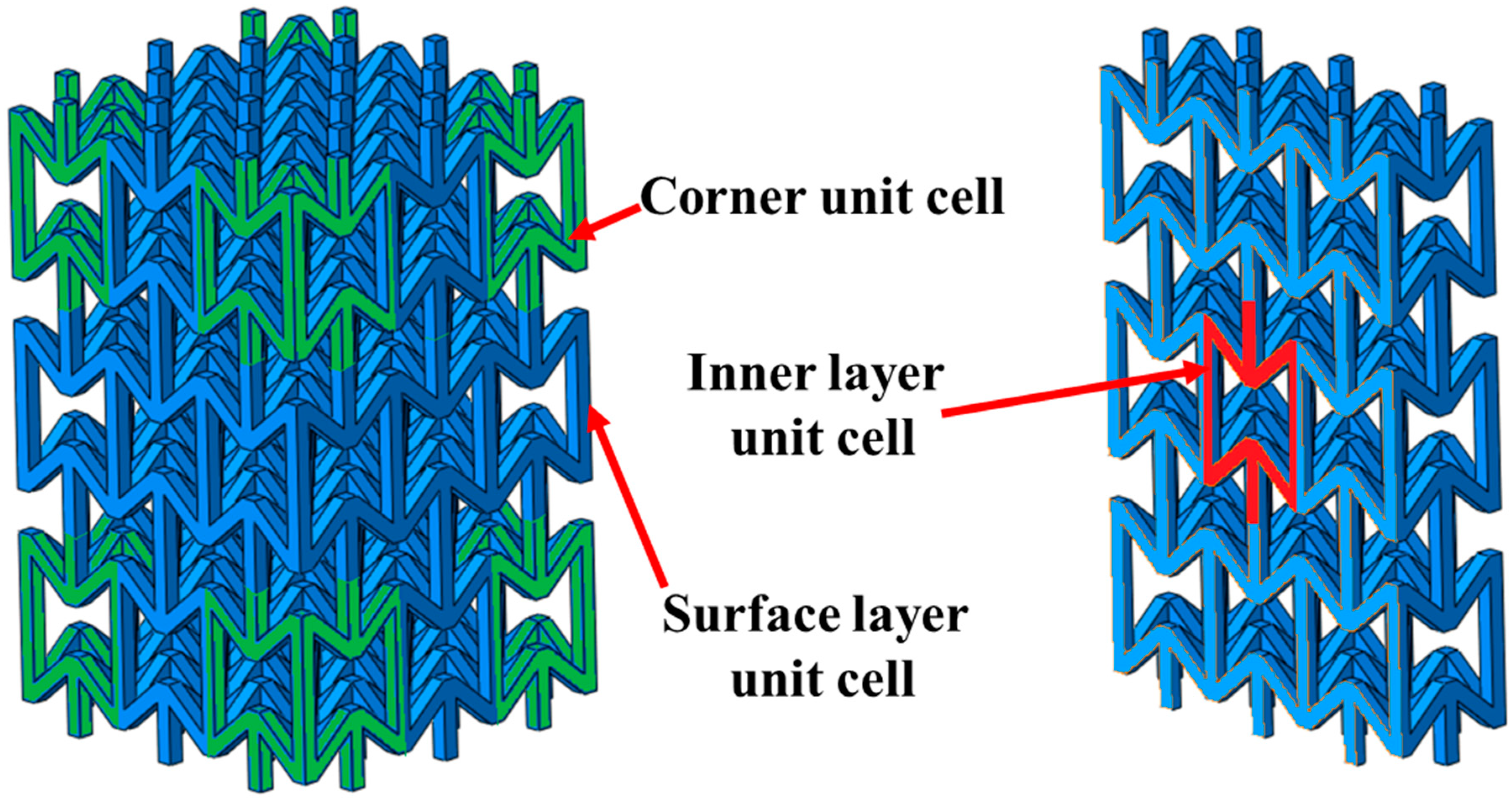
3.2. Structural Size Effect and Structural Surface Layer Model
3.3. Model Application
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gunton, D.J.; Saunders, G.A. The Young’s modulus and Poisson’s ratio of arsenic, antimony and bismuth. J. Mater. Sci. 1972, 7, 1061–1068. [Google Scholar] [CrossRef]
- Lakes, R. Foam structures with a negative Poisson’s ratio. Science 1987, 23, 1038–1040. [Google Scholar] [CrossRef]
- Evans, K.E.; Caddock, B.D. Microporous materials with negative Poisson’s ratios: II. Mechanisms and interpretation. J. Phys. D: Appl. Phys. 1989, 22, 1883–1887. [Google Scholar] [CrossRef]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J.; Rogers, S.C. Molecular network design. Nature 1991, 353, 124. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Constant thermodynamic tension Monte Carlo studies of elastic properties of a two-dimensional system of hard cyclic hexamers. Mol. Phys. 1987, 61, 1247–1258. [Google Scholar] [CrossRef]
- Wojciechowski, K.W. Two-dimensional isotropic system with a negative Poisson ratio. Phys. Lett. A 1989, 137, 60–64. [Google Scholar] [CrossRef]
- Wojciechowski, K.W.; Brańka, A.C. Negative Poisson ratio in a two-dimensional “isotropic” solid. Phys. Rev. A Gen. Phys. 1989, 40, 7222. [Google Scholar] [CrossRef] [PubMed]
- Kolpakov, A.G. Determination of the average characteristics of elastic frameworks. J. Appl. Math. Mech. 1985, 49, 739–745. [Google Scholar] [CrossRef]
- Hoover, W.G.; Hoover, C.G. Searching for auxetics with DYNA3D and ParaDyn. Phys. Status Solidi B 2005, 242, 585–594. [Google Scholar] [CrossRef] [Green Version]
- Pozniak, A.A.; Wojciechowski, K.W. Poisson’s ratio of rectangular anti-chiral structures with size dispersion of circular nodes. Phys. Status Solidi 2014, 251, 367–374. [Google Scholar] [CrossRef]
- Bilski, M.; Pigłowski, P.M.; Wojciechowski, K.W. Extreme Poisson’s Ratios of Honeycomb, Re-Entrant, and Zig-Zag Crystals of Binary Hard Discs. Symmetry 2021, 13, 1127. [Google Scholar] [CrossRef]
- Smardzewski, J.; Maslej, M.; Wojciechowski, K.W. Compression and low velocity impact response of wood-based sandwich panels with auxetic lattice core. Eur. J. Wood Wood Prod. 2021, 79, 797–810. [Google Scholar] [CrossRef]
- Baughman, R.H.; Shacklette, J.M.; Zakhidov, A.A.; Stafstrom, S. Negative Poisson’s ratios as a common feature of cubic metals. Nature 1998, 392, 362–365. [Google Scholar] [CrossRef]
- Piglowski, P.M.; Narojczyk, J.W.; Wojciechowski, K.W.; Tretiakov, K.V. Auxeticity enhancement due to size polydispersity in fcc crystals of hard-core repulsive Yukawa particles. Soft Matter. 2017, 13, 7916–7921. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Narojczyk, J.W.; Wojciechowski, K.W. Elastic properties of the fcc crystals of soft spheres with size dispersion at zero temperature. Phys. Status Solidi B 2008, 245, 606–613. [Google Scholar] [CrossRef]
- Narojczyk, J.W.; Wojciechowski, K.W. Poisson’s Ratio of the f.c.c. Hard Sphere Crystals with Periodically Stacked (001)-Nanolayers of Hard Spheres of Another Diameter. Materials 2019, 12, 700. [Google Scholar] [CrossRef] [Green Version]
- Almgren, R. An isotropic three-dimensional structure with Poisson’s ratio. J. Elast. 1985, 15, 427–430. [Google Scholar]
- Larsen, U.D.; Sigmund, O.; Bouwstra, S. Design and Fabrication of Compliant Micromechanisms and Structures with Negative Poisson’s Ratio. J. Microelectromechanical Syst. 1997, 6, 99–106. [Google Scholar] [CrossRef] [Green Version]
- Grima, J.N.; Gatt, R.; Alderson, A.; Evans, K.E. On the potential of connected stars as auxetic systems. Mol. Simul. 2005, 31, 925–935. [Google Scholar] [CrossRef] [Green Version]
- Shokri, R.M.; Prawoto, Y.; Ahmad, Z. Analytical solution and finite element approach to the 3D re-entrant structures of auxetic materials. Mech. Mater. 2014, 74, 76–87. [Google Scholar] [CrossRef]
- Hengsbach, S.; Lantada, A.D. Direct laser writing of auxetic structures: Present capabilities and challenges. Smart Mater. Struct. 2014, 23, 085033. [Google Scholar] [CrossRef]
- Wang, X.; Li, X.; Ma, L. Interlocking assembled 3D auxetic cellular structures. Mater. Des. 2016, 99, 467–476. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Cormier, D.; West, H.; Harrysson, O.L.A.; Knowlson, K. Non-stochastic Ti–6Al–4V foam structures with negative Poisson’s ratio. Mater. Sci. Eng. A 2012, 558, 579–585. [Google Scholar]
- Evans, K.E.; Nkansah, M.A.; Hutchinson, I.J. Auxetic foams: Modelling negative Poisson’s ratios. Acta Metall. Mater. 1994, 42, 1289–1294. [Google Scholar] [CrossRef]
- Schwerdtfeger, J.; Schury, F.; Stingl, M.; Wein, F.; Singer, R.F.; Körner, C. Mechanical characterisation of a periodic auxetic structure produced by SEBM. Phys. Status Solidi B 2012, 249, 1347–1352. [Google Scholar] [CrossRef]
- Ran, J.Q.; Fu, M.W.; Chan, W.L. The influence of size effect on the ductile fracture in micro-scaled plastic deformation. Int. J. Plast. 2013, 41, 65–81. [Google Scholar] [CrossRef]
- Lemaitre, J. A continuous damage mechanics model for ductile fracture. Trans. Asme J. Eng. Mater. Technol. 1985, 107, 83–89. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, J.; Chen, G.; Zhong, F.; Xu, L.; Xu, T.; Gong, F. The Influence of Size Effect to Deformation Mechanism of C5131 Bronze Structures of Negative Poisson’s Ratio. Processes 2022, 10, 652. https://doi.org/10.3390/pr10040652
Ran J, Chen G, Zhong F, Xu L, Xu T, Gong F. The Influence of Size Effect to Deformation Mechanism of C5131 Bronze Structures of Negative Poisson’s Ratio. Processes. 2022; 10(4):652. https://doi.org/10.3390/pr10040652
Chicago/Turabian StyleRan, Jiaqi, Gangping Chen, Fuxing Zhong, Li Xu, Teng Xu, and Feng Gong. 2022. "The Influence of Size Effect to Deformation Mechanism of C5131 Bronze Structures of Negative Poisson’s Ratio" Processes 10, no. 4: 652. https://doi.org/10.3390/pr10040652




