Transient Stability Analysis of Direct Drive Wind Turbine in DC-Link Voltage Control Timescale during Grid Fault
Abstract
:1. Introduction
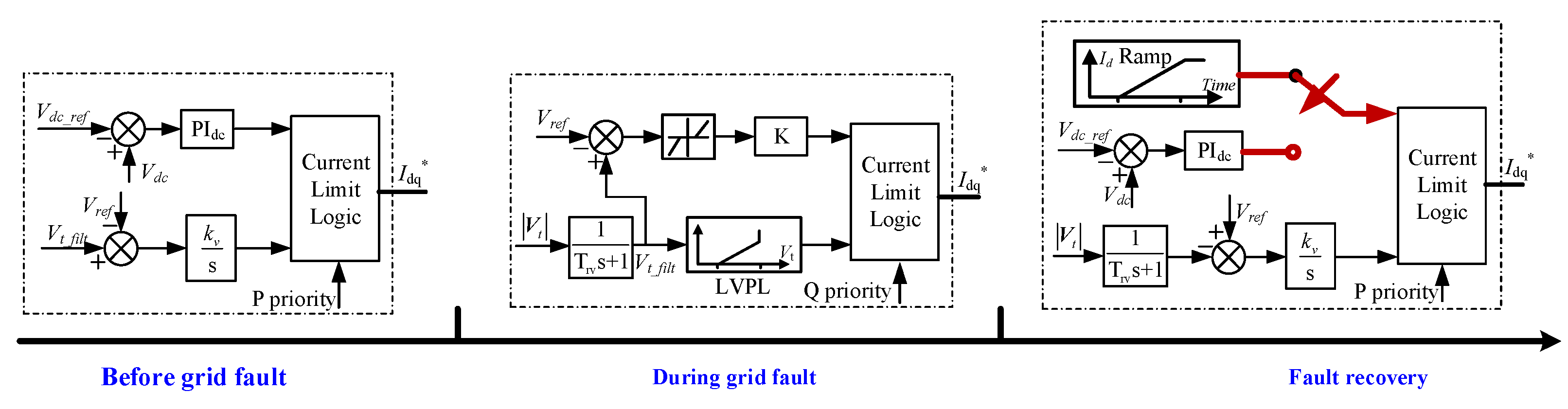
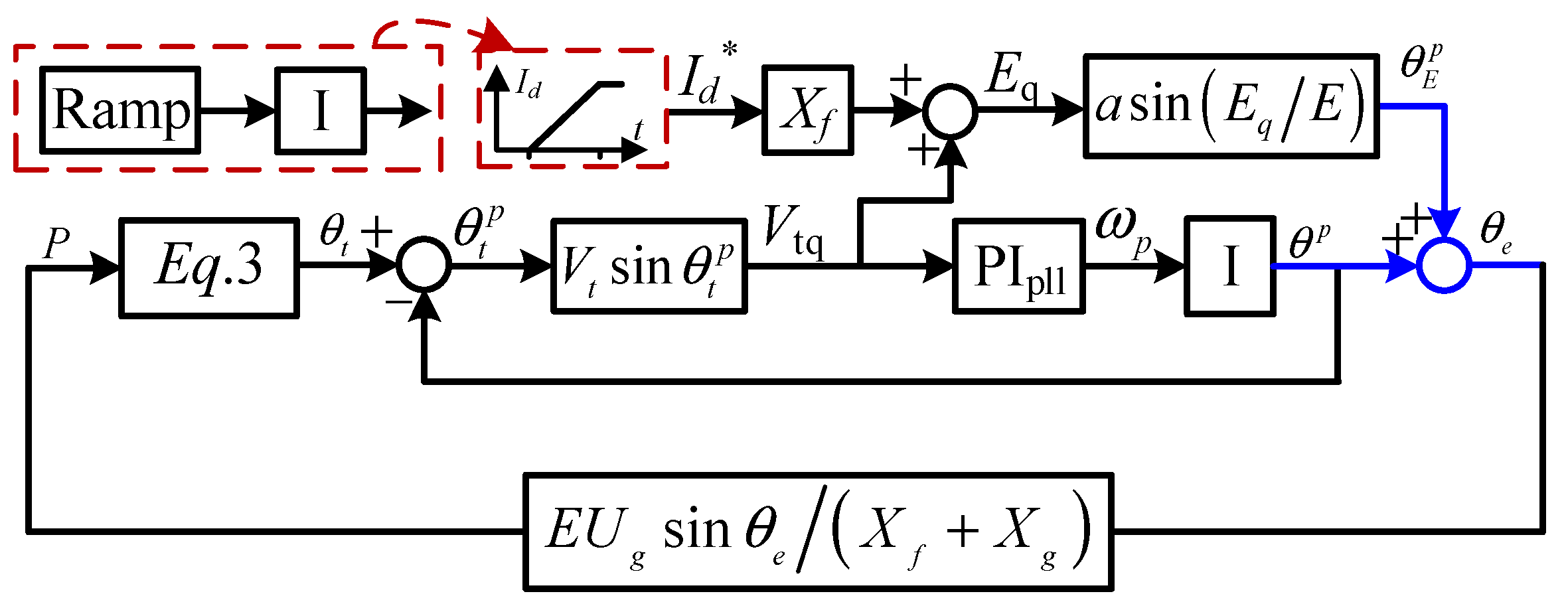
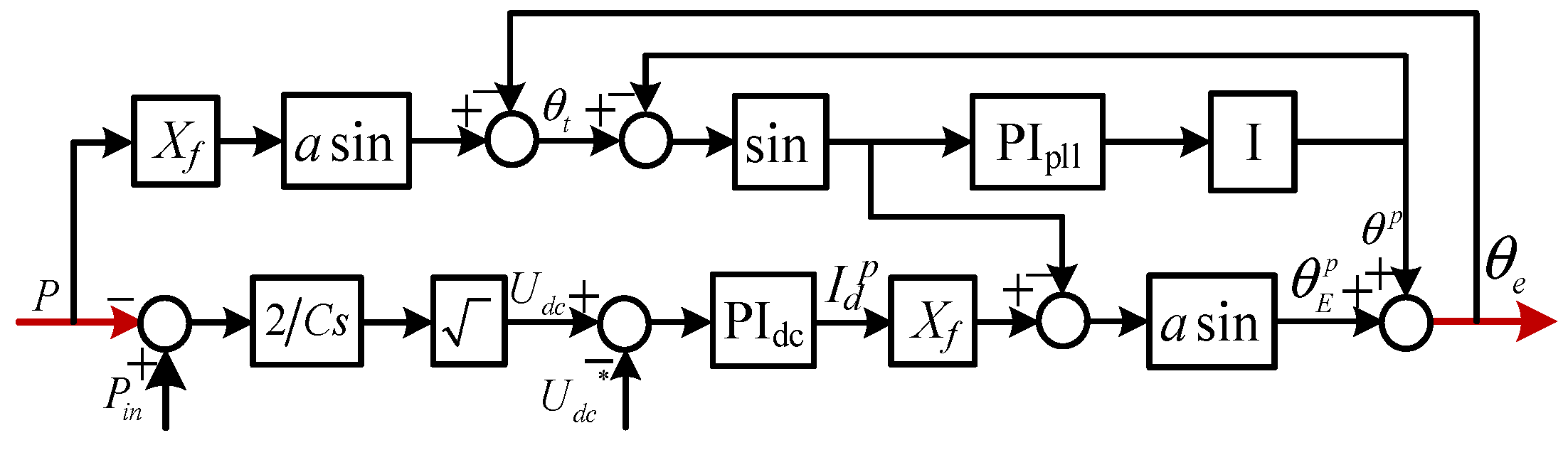
2. Transient Switch Control of Direct Drive Wind Turbine
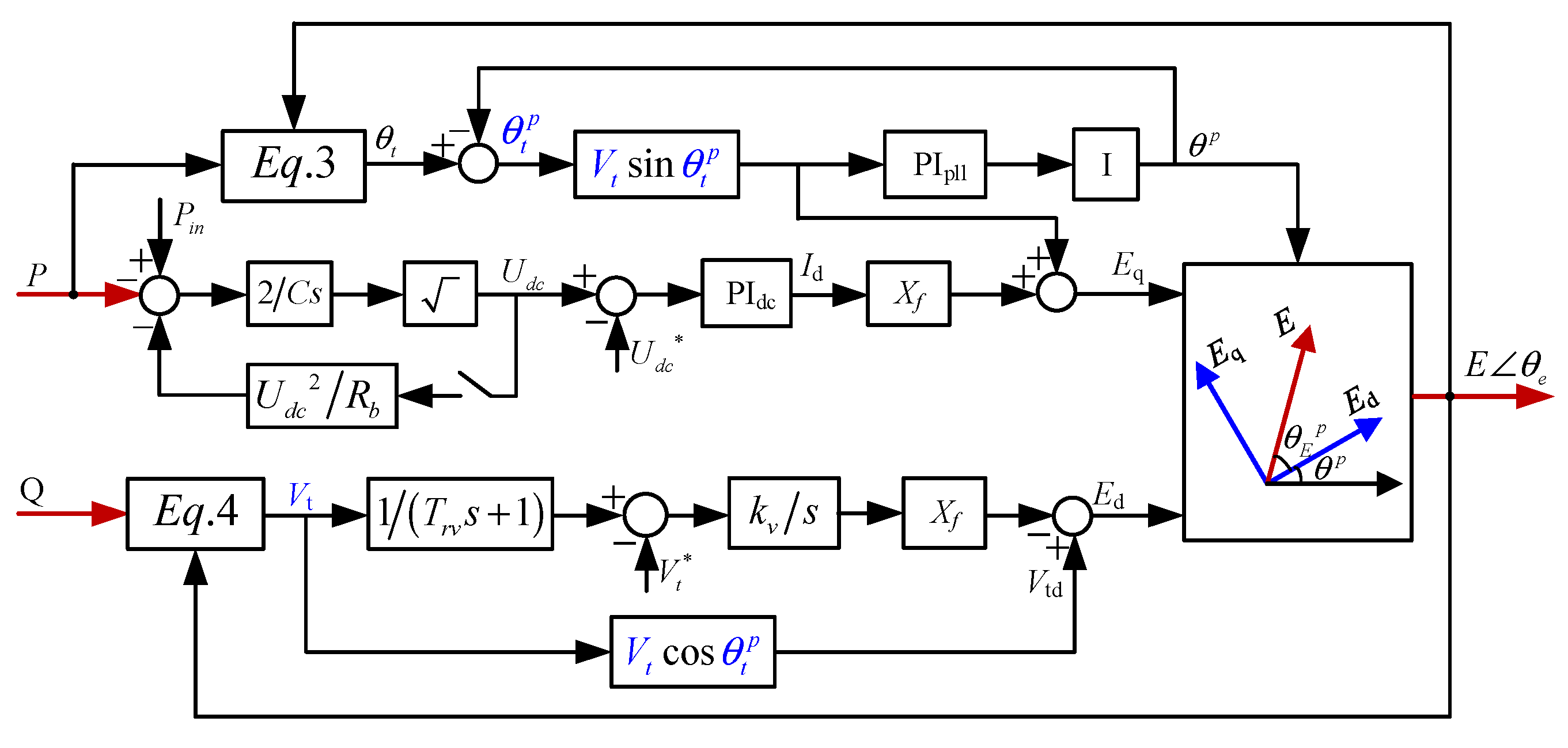
3. Developed Motion Equation Model
3.1. Motion Equation Model in Stage of Active Power Climbing
3.2. Motion Equation Model after Active Power Climbing
3.3. Equipment’s Transient Characteristic Analysis
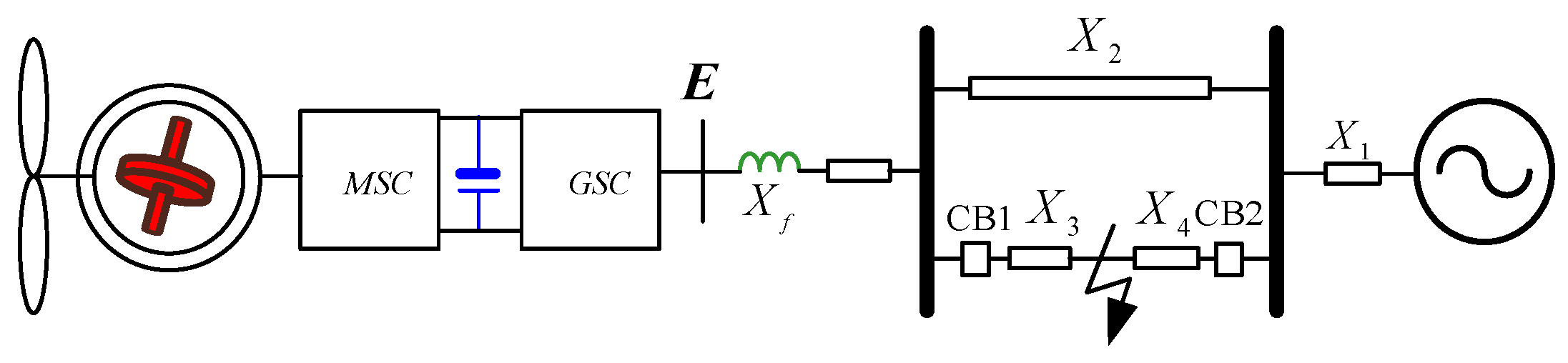
4. Transient Analysis in Single-Machine Infinite-Bus System
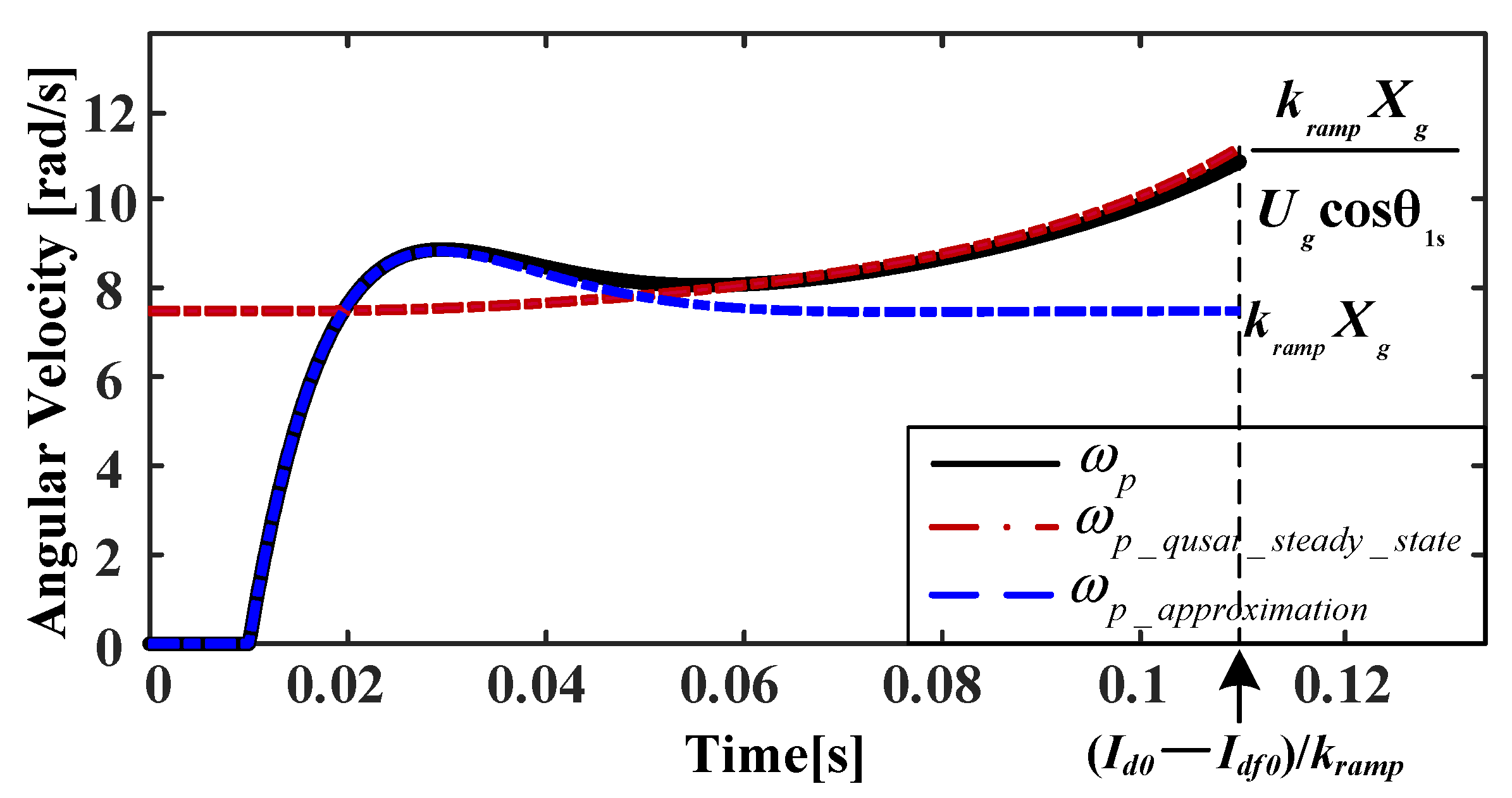
4.1. Transient Analysis in Stage of Active Power Climbing
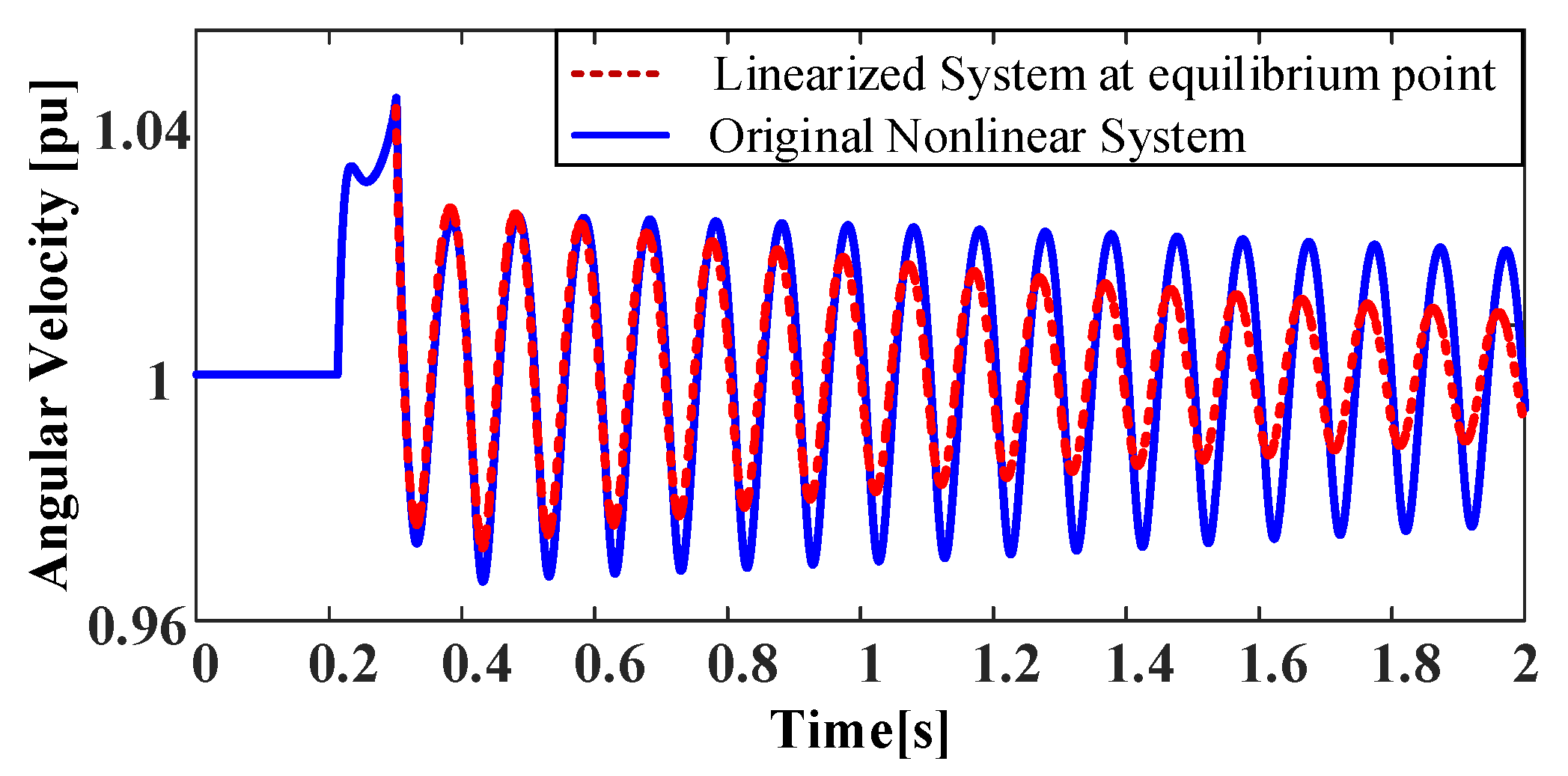
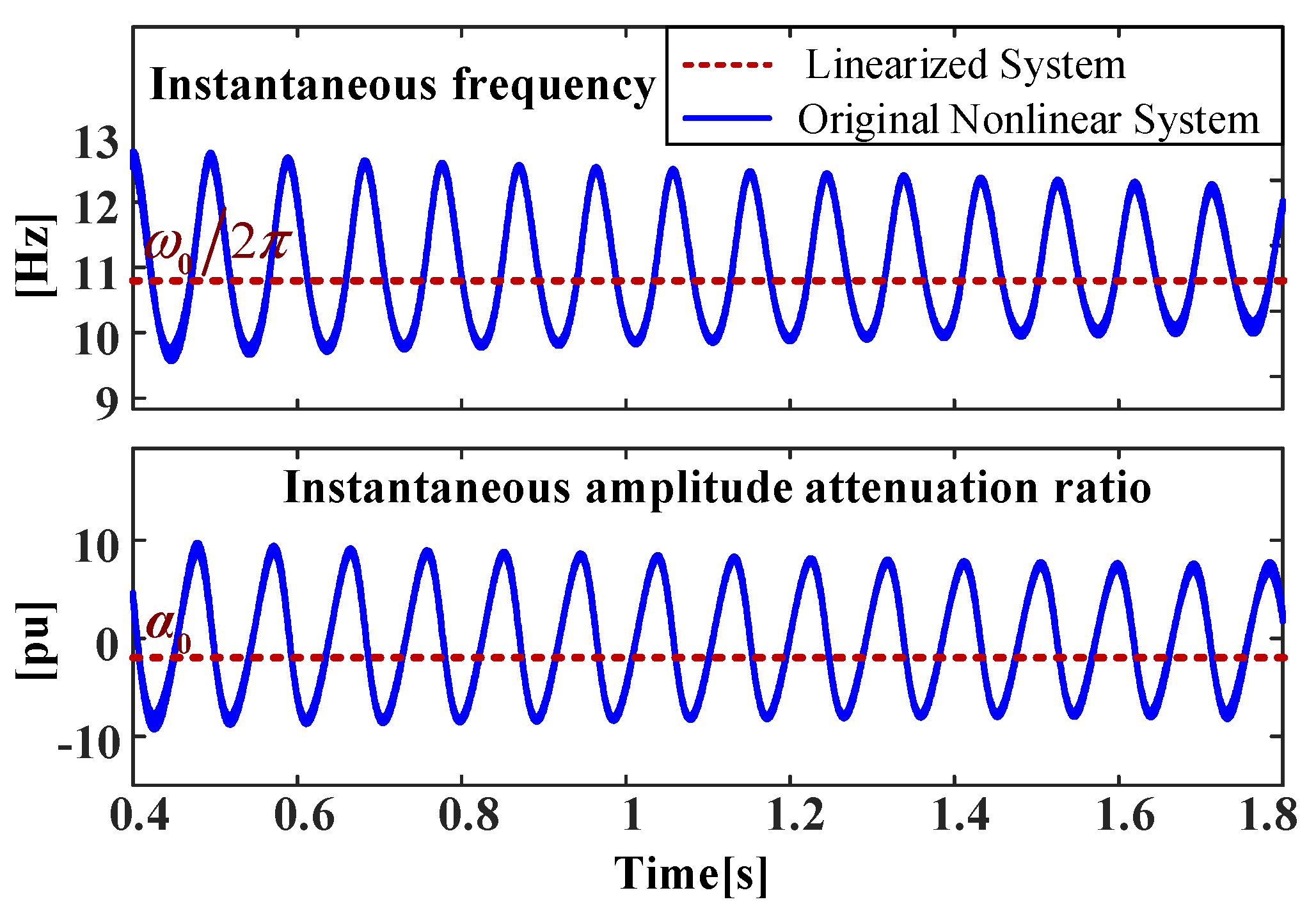
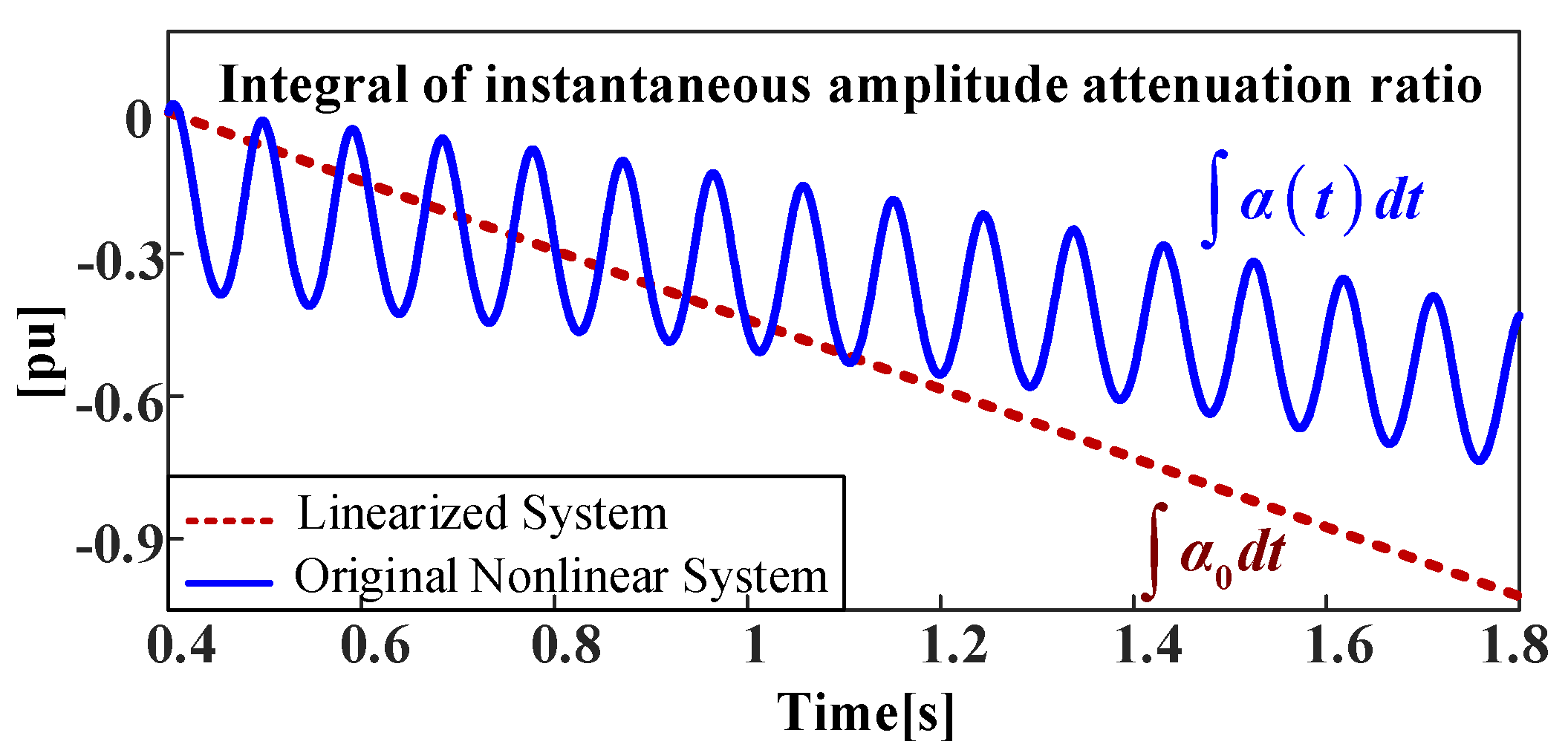
4.2. Nonlinear Oscillation Analysis after Active Power Climbing
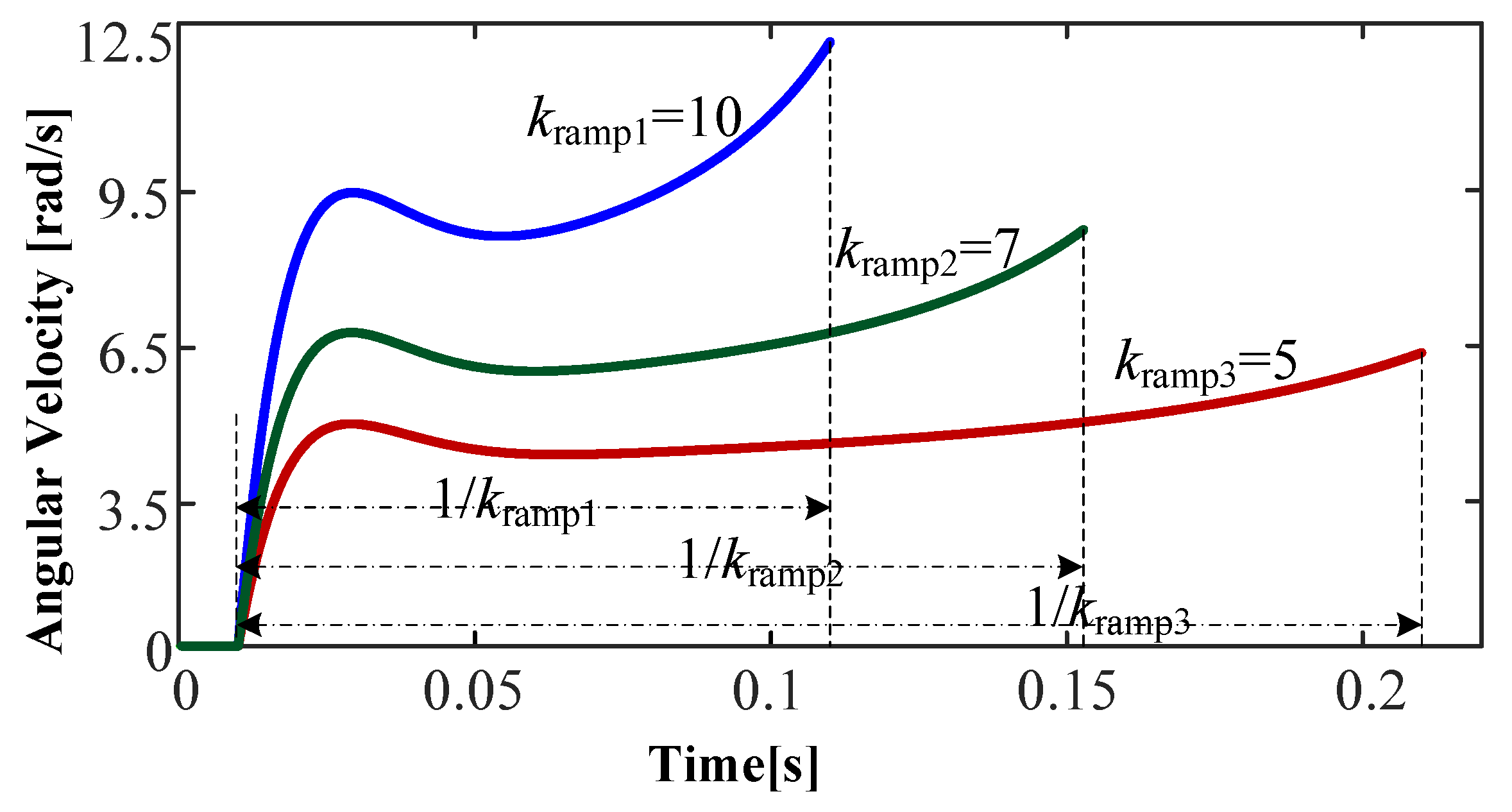
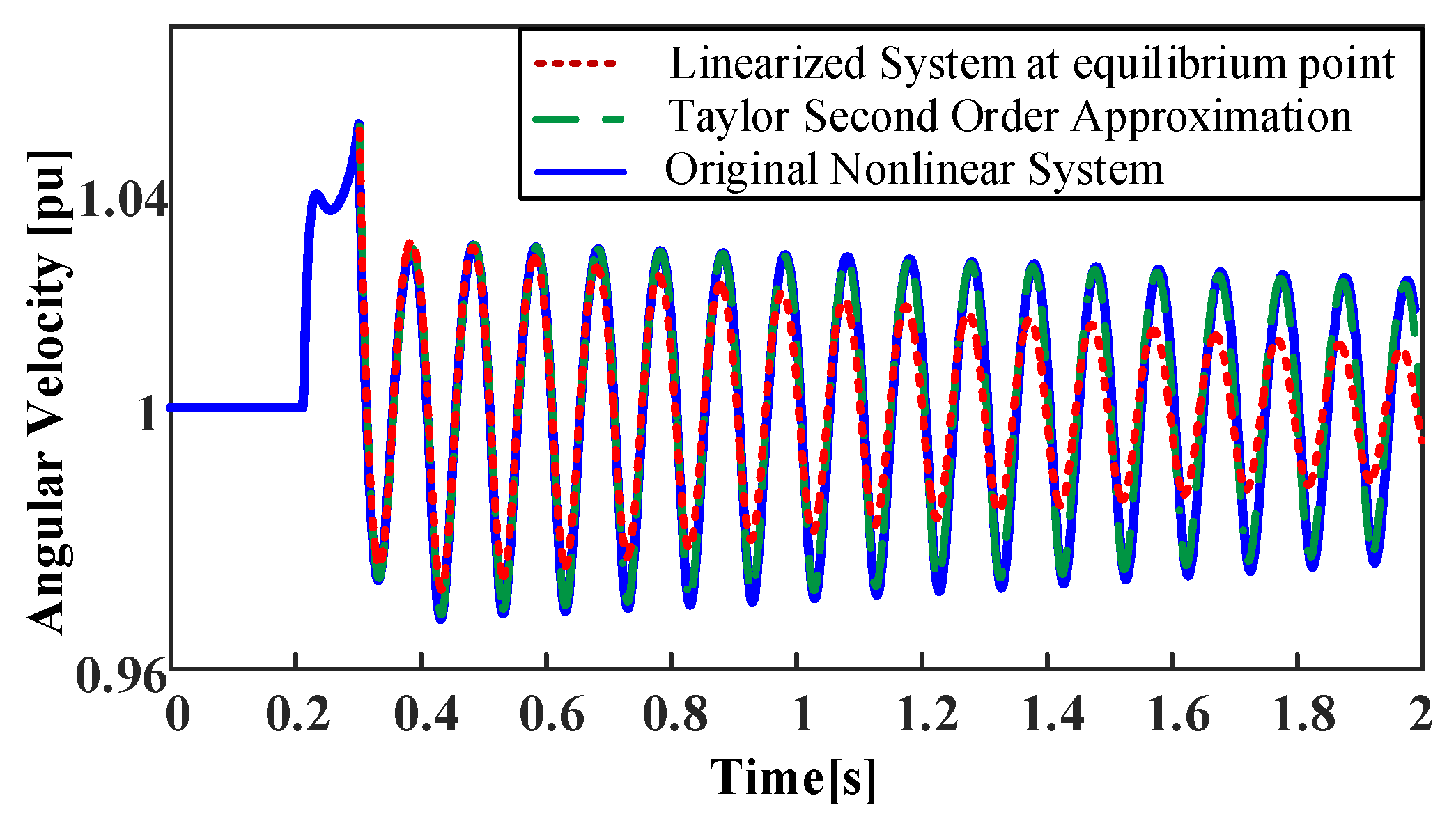
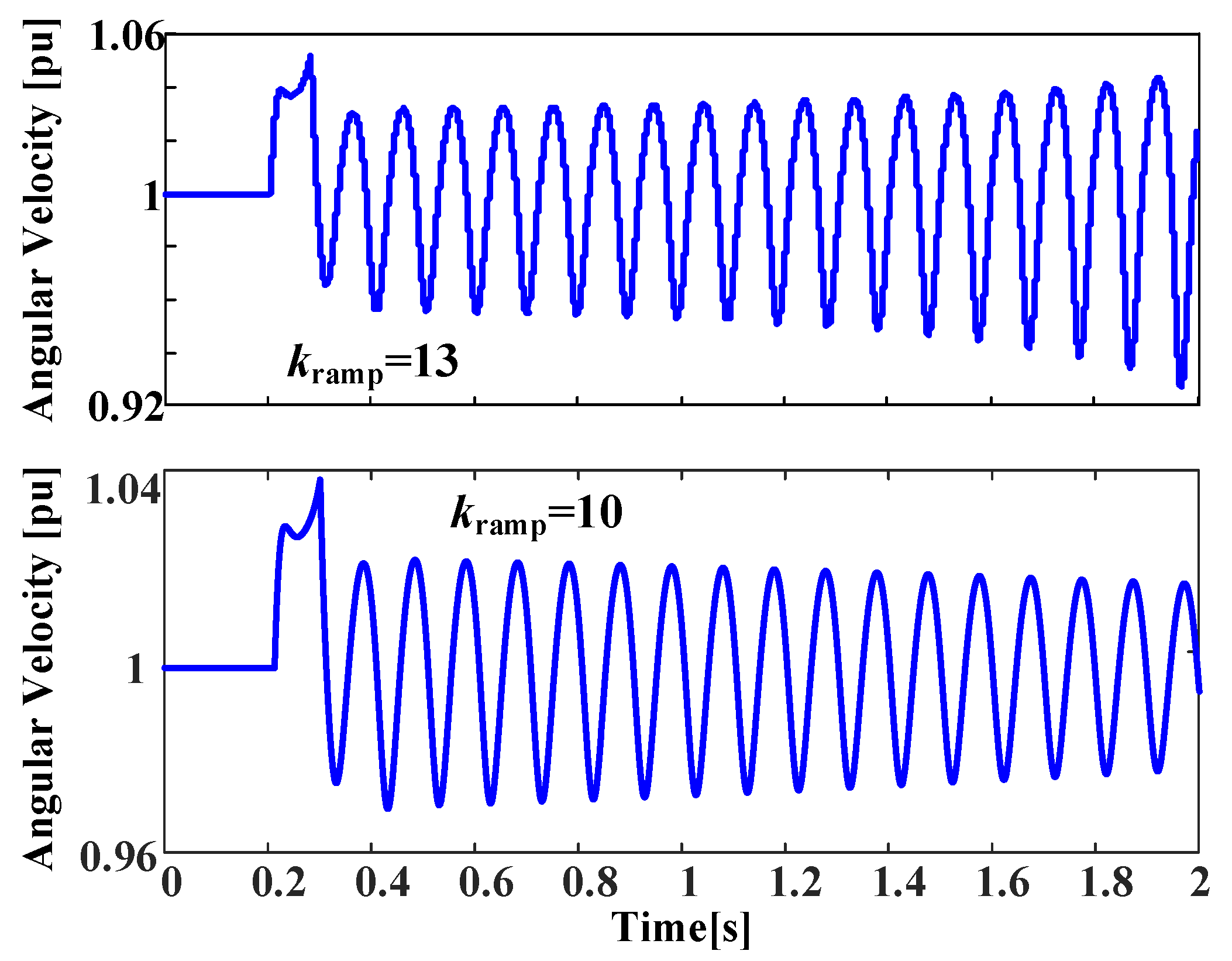
4.3. Influence of Ramp Rate Limit in First Stage on Oscillation Behavior in Second Stage
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbol | Explanation |
| E | GSC internal voltage vector |
| Vt | Terminal voltage vector |
| Ug | Equivalent grid voltage vector |
| I | Current vector across filter inductor |
| P,Q | Active and reactive power output of GSC |
| Xg | Equivalent grid inductor |
| Xf | Grid-side filter inductor |
| θp | PLL output angle relative to grid voltage |
| ωp | Angular velocity of PLL relative to grid voltage |
| kramp | Ramp rate limit |
| Trv, kv | Parameters of AVC’s controller |
| kp_dc, ki_dc | Parameters of DVC’s PI controller |
| kp_pll, ki_pll | Parameters of PLL’s PI controller |
| Subscripts: dq | components in PLL reference frame |
References
- Wang, X.; Taul, M.G.; Wu, H.; Liao, Y.; Blaabjerg, F.; Harnefors, L. Grid-Synchronization Stability of Converter-Based Resources—An Overview. IEEE Open J. Ind. Appl. 2020, 1, 115–134. [Google Scholar] [CrossRef]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F.; Zhang, Y.; Wang, G. Small Signal Synchronizing Stability Analysis of PLL-based VSC Connected to Weak AC Grid. Proc. CSEE 2021, 41, 98–108. (In Chinese) [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, X.; Hu, J.; Yan, Y. Voltage Dynamics of Current Control Time-Scale in a VSC-Connected Weak Grid. IEEE Trans. Power Syst. 2016, 31, 2925–2937. [Google Scholar] [CrossRef]
- Hu, J.; Hu, Q.; Wang, B.; Tang, H.; Chi, Y. Small Signal Instability of PLL-Synchronized Type-4 Wind Turbines Connected to High-Impedance AC Grid During LVRT. IEEE Trans. Energy Convers. 2016, 31, 1676–1687. [Google Scholar] [CrossRef]
- Harnefors, L.; Bongiorno, M.; Lundberg, S. Input-Admittance Calculation and Shaping for Controlled Voltage-Source Converters. IEEE Trans. Ind. Electron. 2007, 54, 3323–3334. [Google Scholar] [CrossRef]
- Chen, X.; Du, W.; Wang, H. Analysis on Wide-range-Frequency Oscillations of Power Systems Integrated with PMSGs Under the Condition of Open-loop Modal Resonance. Proc. CSEE 2019, 39, 2625–2635. (In Chinese) [Google Scholar] [CrossRef]
- Wu, W.; Pu, T.; Chen, Y.; Luo, A.; Zhou, L.; Zhou, X.; Yang, L.; He, Z. Megawatt Wide-bandwidth Impedance Measurement Device Design and its Control Method. Proc. CSEE 2018, 38, 4096–4106. (In Chinese) [Google Scholar] [CrossRef]
- Hu, J.; Yuan, H.; Yuan, X. Modeling of DFIG-Based WTs for Small-Signal Stability Analysis in DVC Timescale in Power Electronized Power Systems. IEEE Trans. Energy Convers. 2017, 32, 1151–1165. [Google Scholar] [CrossRef]
- Gao, Z.; Liu, X. An Overview on Fault Diagnosis, Prognosis and Resilient Control for Wind Turbine Systems. Processes 2021, 9, 300. [Google Scholar] [CrossRef]
- Fu, Y.; Gao, Z.; Liu, Y.; Zhang, A.; Yin, X. Actuator and Sensor Fault Classification for Wind Turbine Systems Based on Fast Fourier Transform and Uncorrelated Multi-Linear Principal Component Analysis Techniques. Processes 2020, 8, 1066. [Google Scholar] [CrossRef]
- Ying, J.; Yuan, X.; Hu, J. Inertia Characteristic of DFIG-Based WT Under Transient Control and Its Impact on the First-Swing Stability of SGs. IEEE Trans. Energy Convers. 2017, 32, 1502–1511. [Google Scholar] [CrossRef]
- Taul, M.G.; Wang, X.; Davari, P.; Blaabjerg, F. An Overview of Assessment Methods for Synchronization Stability of Grid-Connected Converters Under Severe Symmetrical Grid Faults. IEEE Trans. Power Electron. 2019, 34, 9655–9670. [Google Scholar] [CrossRef] [Green Version]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F. Large Signal Synchronizing Instability of PLL-Based VSC Connected to Weak AC Grid. IEEE Trans. Power Syst. 2019, 34, 3220–3229. [Google Scholar] [CrossRef]
- Hu, Q.; Fu, L.; Ma, F.; Ji, F.; Zhang, Y. Analogized Synchronous-Generator Model of PLL-Based VSC and Transient Synchronizing Stability of Converter Dominated Power System. IEEE Trans. Sustain. Energy 2021, 12, 1174–1185. [Google Scholar] [CrossRef]
- Ma, S.; Geng, H.; Liu, L.; Yang, G.; Pal, B.C. Grid-Synchronization Stability Improvement of Large Scale Wind Farm During Severe Grid Fault. IEEE Trans. Power Syst. 2018, 33, 216–226. [Google Scholar] [CrossRef] [Green Version]
- He, X.; Geng, H.; Li, R.; Pal, B.C. Transient Stability Analysis and Enhancement of Renewable Energy Conversion System During LVRT. IEEE Trans. Sustain. Energy 2020, 11, 1612–1623. [Google Scholar] [CrossRef]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of PLL-Synchronized Voltage-Source Converters. IEEE Trans. Power Electron. 2020, 35, 3573–3589. [Google Scholar] [CrossRef] [Green Version]
- Sun, J. Small-Signal Methods for AC Distributed Power Systems–A Review. IEEE Trans. Power Electron. 2009, 24, 2545–2554. [Google Scholar] [CrossRef]
- Zhou, J.Z.; Ding, H.; Fan, S.; Zhang, Y.; Gole, A.M. Impact of Short-Circuit Ratio and Phase-Locked-Loop Parameters on the Small-Signal Behavior of a VSC-HVDC Converter. IEEE Trans. Power Deliv. 2014, 29, 2287–2296. [Google Scholar] [CrossRef]
- Zhao, M.; Yuan, X.; Hu, J. Modeling of DFIG Wind Turbine Based on Internal Voltage Motion Equation in Power Systems Phase-Amplitude Dynamics Analysis. IEEE Trans. Power Syst. 2018, 33, 1484–1495. [Google Scholar] [CrossRef]
- Lu, J.; Yuan, X.; Hu, J.; Zhang, M.; Yuan, H. Motion Equation Modeling of LCC-HVDC Stations for Analyzing DC and AC Network Interactions. IEEE Trans. Power Deliv. 2020, 35, 1563–1574. [Google Scholar] [CrossRef]
- Wang, X.; Harnefors, L.; Blaabjerg, F. Unified Impedance Model of Grid-Connected Voltage-Source Converters. IEEE Trans. Power Electron. 2018, 33, 1775–1787. [Google Scholar] [CrossRef] [Green Version]
- Wen, B.; Boroyevich, D.; Burgos, R.; Mattavelli, P.; Shen, Z. Analysis of D-Q Small-Signal Impedance of Grid-Tied Inverters. IEEE Trans. Power Electron. 2016, 31, 675–687. [Google Scholar] [CrossRef]
- Liao, Y.; Wang, X. Impedance-Based Stability Analysis for Interconnected Converter Systems with Open-Loop RHP Poles. IEEE Trans. Power Electron. 2020, 35, 4388–4397. [Google Scholar] [CrossRef] [Green Version]
- Tavoosi, J.; Mohammadzadeh, A.; Pahlevanzadeh, B.; Kasmani, M.B.; Band, S.S.; Safdar, R.; Mosavi, A.H. A Machine Learning Approach for Active/Reactive Power Control of Grid-Connected Doubly-Fed Induction Generators. Ain Shams Eng. J. 2022, 13, 101564. [Google Scholar] [CrossRef]
- Cao, H.; Yu, T.; Zhang, X.; Yang, B.; Wu, Y. Reactive Power Optimization of Large-Scale Power Systems: A Transfer Bees Optimizer Application. Processes 2019, 7, 321. [Google Scholar] [CrossRef] [Green Version]
- Mohammadi Moghadam, H.; Mohammadzadeh, A.; Hadjiaghaie Vafaie, R.; Tavoosi, J.; Khooban, M.-H. A Type-2 Fuzzy Control for Active/Reactive Power Control and Energy Storage Management. Trans. Inst. Meas. Control 2022, 44, 1014–1028. [Google Scholar] [CrossRef]
- Messina, A.R.; Vittal, V. Nonlinear, Non-Stationary Analysis of Interarea Oscillations via Hilbert Spectral Analysis. IEEE Trans. Power Syst. 2006, 21, 1234–1241. [Google Scholar] [CrossRef]
- Andrade, M.A.; Messina, A.R.; Rivera, C.A.; Olguin, D. Identification of Instantaneous Attributes of Torsional Shaft Signals Using the Hilbert Transform. IEEE Trans. Power Syst. 2004, 19, 1422–1429. [Google Scholar] [CrossRef]
- Sanchez-Gasca, J.J.; Vittal, V.; Gibbard, M.J.; Messina, A.R.; Vowles, D.J.; Liu, S.; Annakkage, U.D. Inclusion of Higher Order Terms for Small-Signal (Modal) Analysis: Committee Report-Task Force on Assessing the Need to Include Higher Order Terms for Small-Signal (Modal) Analysis. IEEE Trans. Power Syst. 2005, 20, 1886–1904. [Google Scholar] [CrossRef] [Green Version]
- Lin, C.-M.; Vittal, V.; Kliemann, W.; Fouad, A.A. Investigation of Modal Interaction and Its Effects on Control Performance in Stressed Power Systems Using Normal Forms of Vector Fields. IEEE Trans. Power Syst. 1996, 11, 781–787. [Google Scholar] [CrossRef]
- Liu, S.; Messina, A.R.; Vittal, V. Characterization of Nonlinear Modal Interaction Using Normal Forms and Hilbert Analysis. In Proceedings of the IEEE PES Power Systems Conference and Exposition, New York, NY, USA, 10–13 October 2004; Volume 2, pp. 1113–1118. [Google Scholar] [CrossRef]
- Tsili, M.; Papathanassiou, S. A Review of Grid Code Technical Requirements for Wind Farms. IET Renew. Power Gener. 2009, 3, 308–332. [Google Scholar] [CrossRef]
- Western Electricity Coordinating Council. WECC Second Generation Wind Turbine Models. Available online: https://www.wecc.org/Reliability/WECC%20Second%20Generation%20Wind%20Turbine%20Models%20012314.pdf (accessed on 3 June 2021).




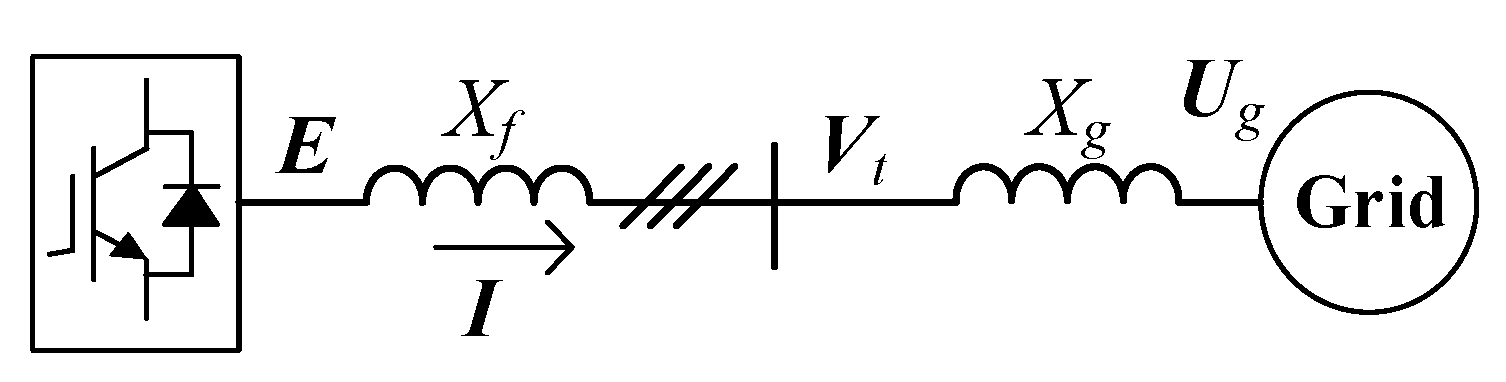

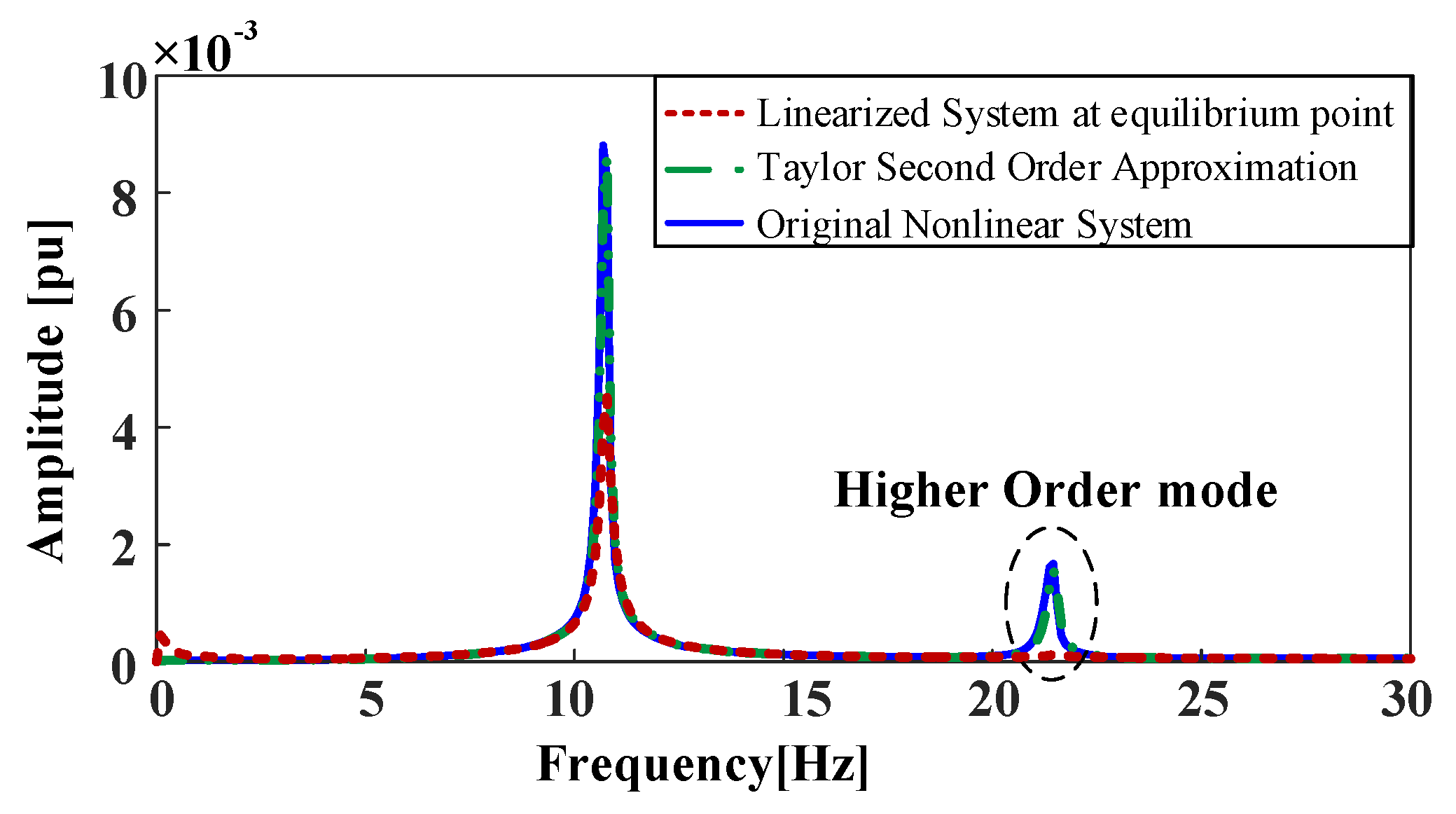
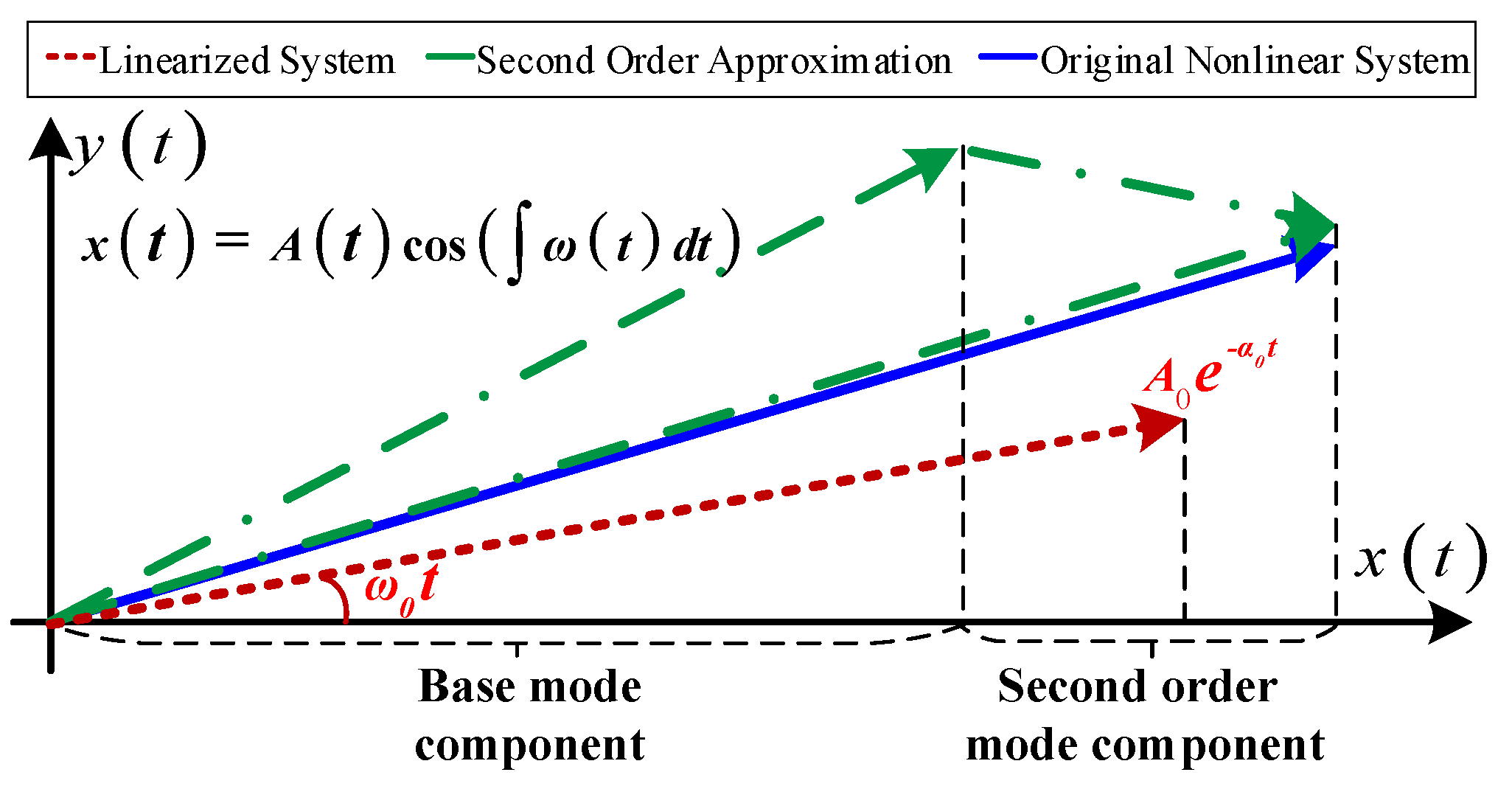
| Mode | Eigenvalue | Freq.(Hz) | Damping Ratio |
|---|---|---|---|
| 1 | −100 ± 99j | 15.8 | 71% |
| 2 | −29.4 ± 35j | 5.6 | 64% |
| 3 | −0.6 ± 67.9j | 10.8 | 1.3% |
| Mode | Eigenvalue | Freq.(Hz) | Damping Ratio |
|---|---|---|---|
| 3 | −0.32 ± 60j | 10 | 0.53% |
| 3,3 | −0.75 ± 127j | 21 | 0.59% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Xiong, Y.; Liu, C.; Wang, G.; Ma, Y. Transient Stability Analysis of Direct Drive Wind Turbine in DC-Link Voltage Control Timescale during Grid Fault. Processes 2022, 10, 774. https://doi.org/10.3390/pr10040774
Hu Q, Xiong Y, Liu C, Wang G, Ma Y. Transient Stability Analysis of Direct Drive Wind Turbine in DC-Link Voltage Control Timescale during Grid Fault. Processes. 2022; 10(4):774. https://doi.org/10.3390/pr10040774
Chicago/Turabian StyleHu, Qi, Yiyong Xiong, Chenruiyang Liu, Guangyu Wang, and Yanhong Ma. 2022. "Transient Stability Analysis of Direct Drive Wind Turbine in DC-Link Voltage Control Timescale during Grid Fault" Processes 10, no. 4: 774. https://doi.org/10.3390/pr10040774
APA StyleHu, Q., Xiong, Y., Liu, C., Wang, G., & Ma, Y. (2022). Transient Stability Analysis of Direct Drive Wind Turbine in DC-Link Voltage Control Timescale during Grid Fault. Processes, 10(4), 774. https://doi.org/10.3390/pr10040774






