Performance Optimization on 3D Diffuser of Volute Pump Using Kriging Model
Abstract
:1. Introduction
2. Numerical Calculation of Hydraulic Model and Experimental Verification
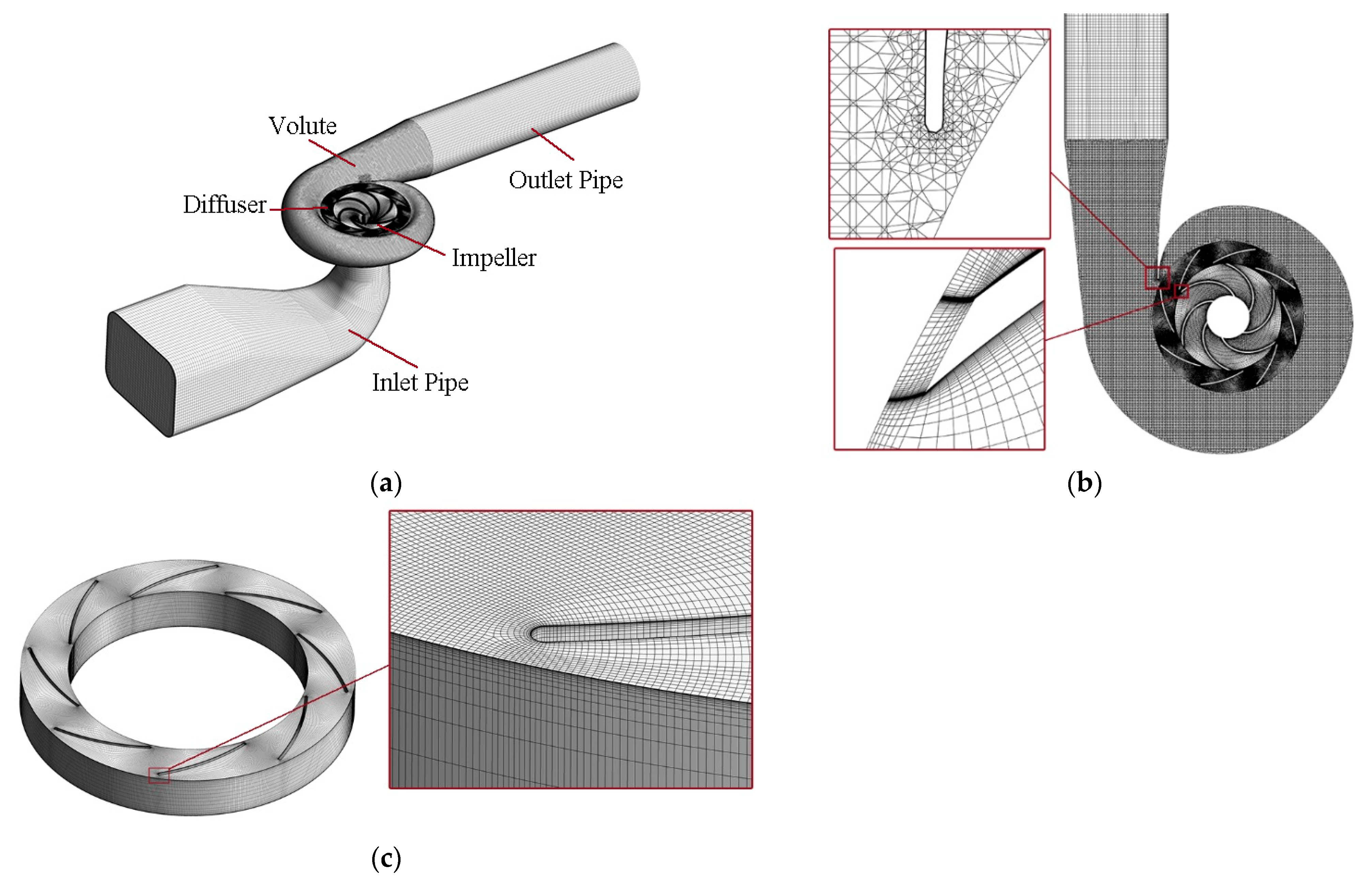
2.1. Hydraulic Model
2.2. Grid Sensitivity Analysis and Numerical Calculation
2.3. Experimental Verification
3. Optimization Process and Setting
3.1. The Kriging Model and Optimization Process
3.2. Optimization Objectives, Design Variables, and Ranges
3.3. Samples and Optimization of Process Parameter Setting
4. Discussion of Results
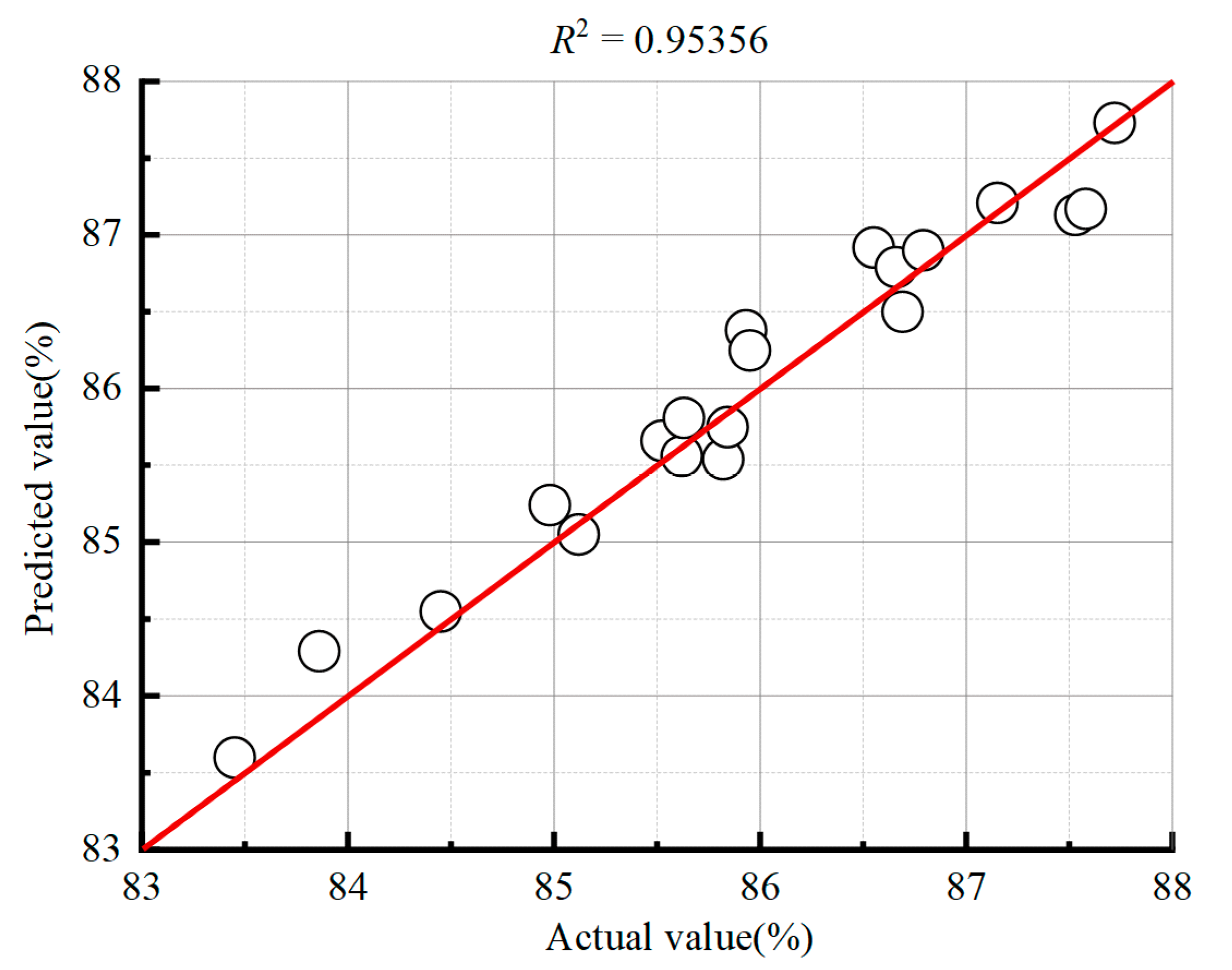
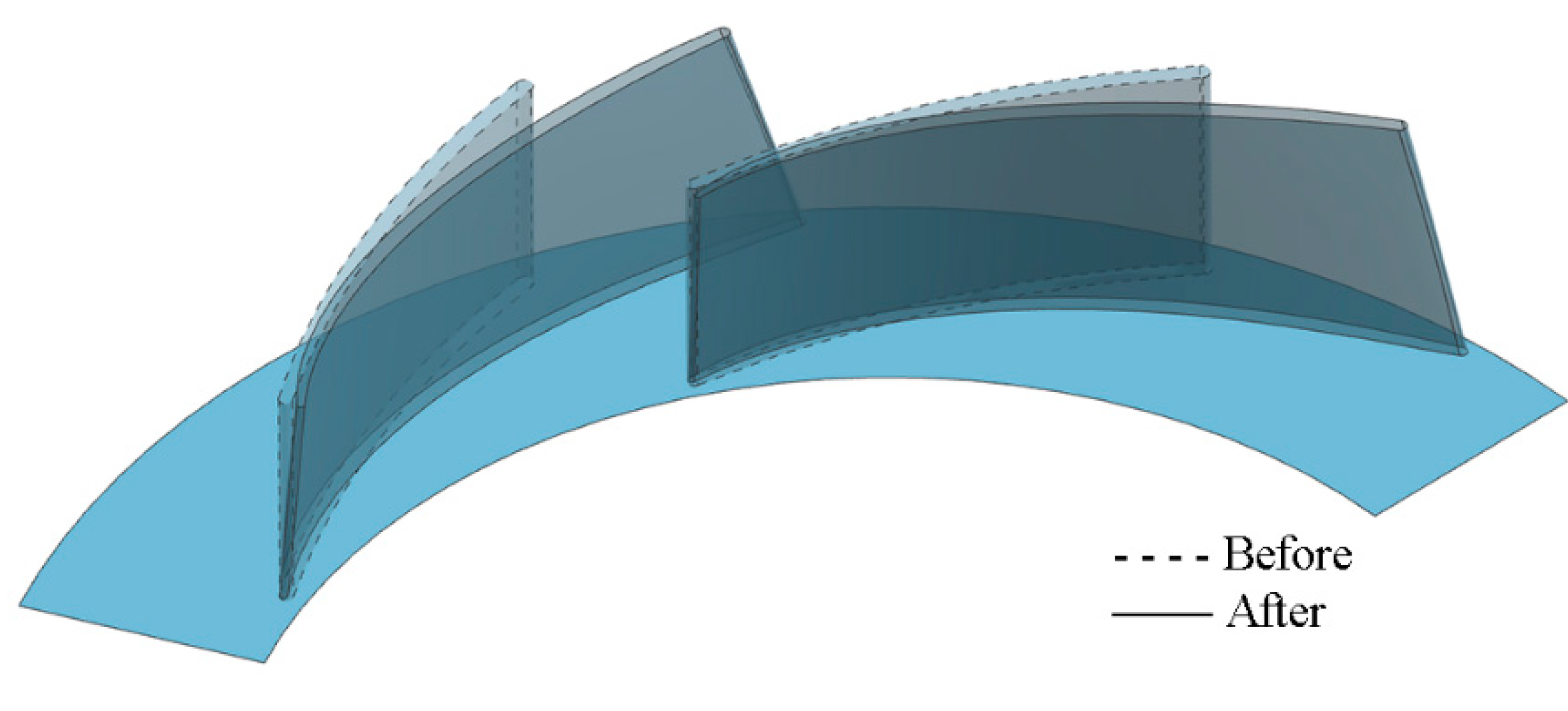
4.1. Surrogate Model Check and Comparison of Diffuser Vane Geometry
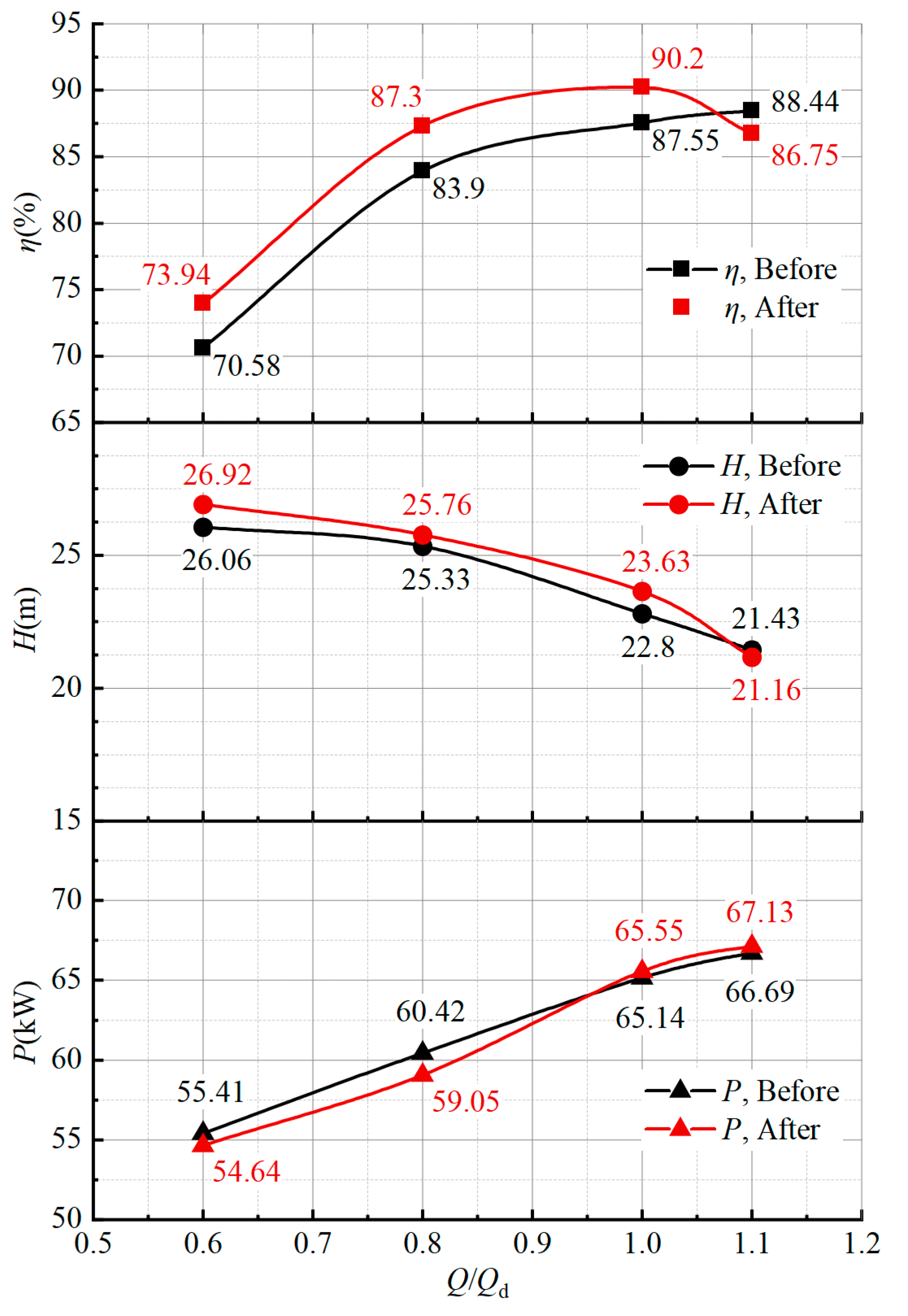
4.2. Hydraulic Performance Curve Analysis
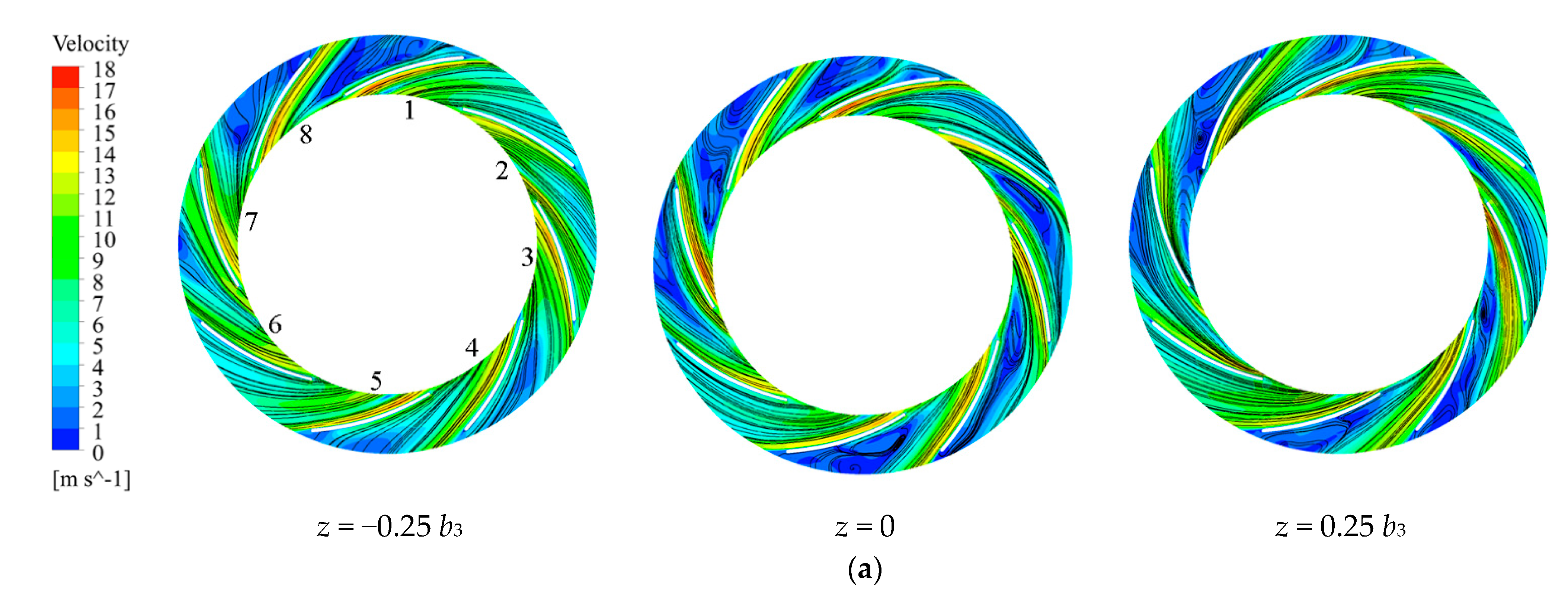
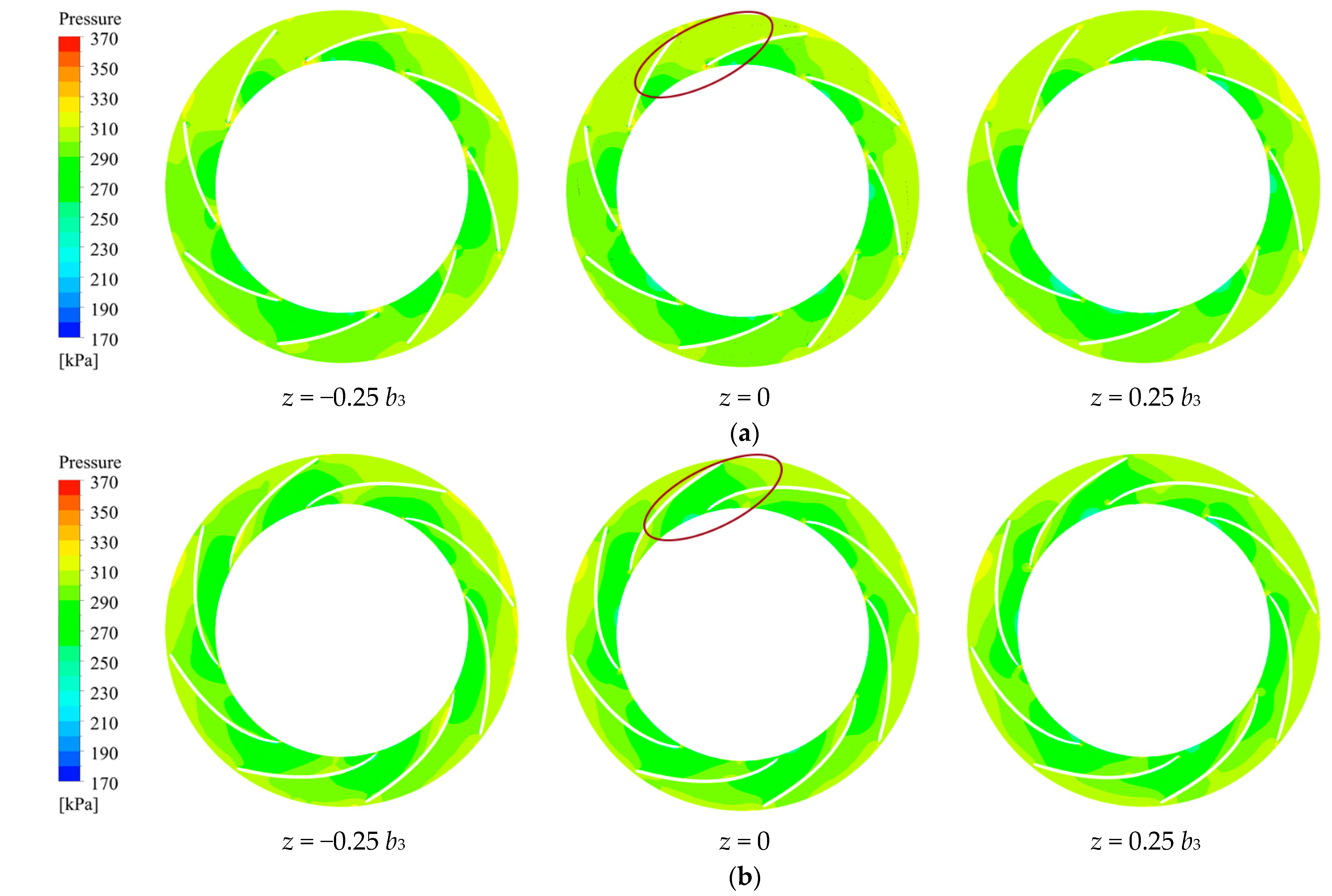
4.3. Inner Flow Analysis
5. Conclusions
- (1)
- The Kriging model can effectively establish the high-precision nonlinear mathematical relationship between the selected 14 design variables and the optimization objectives with an R2 value of 0.95356, which can meet the engineering needs.
- (2)
- The hydraulic performance of the optimized model under design conditions and part-load conditions was greatly improved, the efficiency under design conditions was increased by 2.65%, and the head was increased by 0.83m under the premise that the power was relatively the same.
- (3)
- The inner flow of the optimized model was significantly improved under the design condition, the large low-speed area and vortex area disappeared, and the pressure gradient change was reduced, which reduced the energy loss.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Qd (m3/h) | Design flow rate |
| H (m) | Pump head |
| H (%) | Pump efficiency |
| n (r/min) | Rotational speed |
| ns | Specific speed |
| Zim | Number of impeller blades |
| Zdi | Number of diffuser vanes |
| Dj (mm) | Impeller inlet diameter |
| D2 (mm) | Impeller outlet diameter |
| b2 (mm) | Impeller outlet width |
| β1 (degree) | Impeller inlet blade angle |
| β2 (degree) | Impeller outlet blade angle |
| φ (degree) | Wrap angle of impeller blade |
| D3 (mm) | Diffuser inlet diameter |
| D4 (mm) | Diffuser outlet diameter |
| b3 (mm) | Diffuser width |
| b5 (mm) | Volute inlet width |
| D5 (mm) | Volute base circle diameter |
| D6 (mm) | Volute outlet diameter |
| T (N) | Impeller torque |
| Ω (rad/s) | Impeller angular velocity |
| ρ (kg/m3) | Water density |
| p1tot (Pa) | Total pressure at inlet of the pump |
| p2tot (Pa) | Total pressure at outlet of the pump |
References
- Sakran, H.K.; Abdul Aziz, M.S.; Abdullah, M.Z.; Khor, C.Y. Effects of Blade Number on the Centrifugal Pump Performance: A Review. Arab. J. Sci. Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Arun Shankar, V.K.; Umashankar, S.; Paramasivam, S.; Hanigovszki, N. A Comprehensive Review on Energy Efficiency Enhancement Initiatives in Centrifugal Pumping System. Appl. Energy 2016, 181, 495–513. [Google Scholar] [CrossRef]
- Liu, M.; Tan, L.; Cao, S. Performance Prediction and Geometry Optimization for Application of Pump as Turbine: A Review. Front. Energy Res. 2022, 9, 818118. [Google Scholar] [CrossRef]
- Al-Obaidi, A.R. Influence of Guide Vanes on the Flow Fields and Performance of Axial Pump under Unsteady Flow Conditions: Numerical Study. JMES 2020, 14, 6570–6593. [Google Scholar] [CrossRef]
- Bai, L.; Zhou, L.; Han, C.; Zhu, Y.; Shi, W. Numerical Study of Pressure Fluctuation and Unsteady Flow in a Centrifugal Pump. Processes 2019, 7, 354. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Pavesi, G.; Liu, X.; Xie, T.; Liu, J. Unsteady Flow Characteristics Regarding Hump Instability in the First Stage of a Multistage Pump-Turbine in Pump Mode. Renew. Energy 2018, 127, 377–385. [Google Scholar] [CrossRef]
- Li, Z.; Zheng, X. Review of Design Optimization Methods for Turbomachinery Aerodynamics. Prog. Aerosp. Sci. 2017, 93, 1–23. [Google Scholar] [CrossRef]
- Cho, S.; Kim, M.; Lyu, B.; Moon, I. Optimization of an Explosive Waste Incinerator via an Artificial Neural Network Surrogate Model. Chem. Eng. J. 2021, 407, 126659. [Google Scholar] [CrossRef]
- Zhang, X.; Xie, F.; Ji, T.; Zhu, Z.; Zheng, Y. Multi-Fidelity Deep Neural Network Surrogate Model for Aerodynamic Shape Optimization. Comput. Methods Appl. Mech. Eng. 2021, 373, 113485. [Google Scholar] [CrossRef]
- Keshtegar, B.; Mert, C.; Kisi, O. Comparison of Four Heuristic Regression Techniques in Solar Radiation Modeling: Kriging Method vs RSM, MARS and M5 Model Tree. Renew. Sustain. Energy Rev. 2018, 81, 330–341. [Google Scholar] [CrossRef]
- Ren, C.; Aoues, Y.; Lemosse, D.; Souza De Cursi, E. Ensemble of Surrogates Combining Kriging and Artificial Neural Networks for Reliability Analysis with Local Goodness Measurement. Struct. Saf. 2022, 96, 102186. [Google Scholar] [CrossRef]
- Hasanipanah, M.; Meng, D.; Keshtegar, B.; Trung, N.-T.; Thai, D.-K. Nonlinear Models Based on Enhanced Kriging Interpolation for Prediction of Rock Joint Shear Strength. Neural Comput. Appl. 2021, 33, 4205–4215. [Google Scholar] [CrossRef]
- Tong, S.; Zhao, H.; Liu, H.; Yu, Y.; Li, J.; Cong, F. Multi-Objective Optimization of Multistage Centrifugal Pump Based on Surrogate Model. J. Fluids Eng. 2019, 142, 011101. [Google Scholar] [CrossRef]
- De Donno, R.; Ghidoni, A.; Noventa, G.; Rebay, S. Shape Optimization of the ERCOFTAC Centrifugal Pump Impeller Using Open-Source Software. Optim. Eng. 2019, 20, 929–953. [Google Scholar] [CrossRef]
- Ma, S.-B.; Kim, S.; Kim, J.-H. Optimization Design of a Two-Vane Pump for Wastewater Treatment Using Machine-Learning-Based Surrogate Modeling. Processes 2020, 8, 1170. [Google Scholar] [CrossRef]
- Jaiswal, A.K.; Siddique, M.H.; Paul, A.R.; Samad, A. Surrogate-Based Design Optimization of a Centrifugal Pump Impeller. Eng. Optim. 2021, 1–18. [Google Scholar] [CrossRef]
- Chen, X.B.; Zhang, R.H.; Yang, W.F. Inverse Design and Optimization of Low Specific Speed Centrifugal Pump Blade Based on Adaptive POD Hybrid Model. J. Appl. Fluid Mech. 2022, 15, 453–464. [Google Scholar] [CrossRef]
- Gan, X.; Pei, J.; Yuan, S.; Wang, W.; Tang, Y. Multi-Objective Optimization on Inlet Pipe of a Vertical Inline Pump Based on Genetic Algorithm and Artificial Neural Network. In Proceedings of the Volume 1: Flow Manipulation and Active Control; Bio-Inspired Fluid Mechanics; Boundary Layer and High-Speed Flows; Fluids Engineering Education; Transport Phenomena in Energy Conversion and Mixing; Turbulent Flows; Vortex Dynamics; DNS/LES and Hybrid RANS/LES Methods; Fluid Structure Interaction; Fluid Dynamics of Wind Energy; Bubble, Droplet, and Aerosol Dynamics, Montreal, QC, Canada, 15–20 July 2018; American Society of Mechanical Engineers: New York, NY, USA, 2018; p. V001T06A003. [Google Scholar]
- Posa, A.; Lippolis, A. Effect of Working Conditions and Diffuser Setting Angle on Pressure Fluctuations within a Centrifugal Pump. Int. J. Heat Fluid Flow 2019, 75, 44–60. [Google Scholar] [CrossRef]
- Yang, G.; Zhao, X.; Zhang, D.; Geng, L.; Yang, X.; Gao, X. Hydraulic Components’ Matching Optimization Design and Entropy Production Analysis in a Large Vertical Centrifugal Pump. J. Mech. Sci. Technol. 2021, 35, 5033–5048. [Google Scholar] [CrossRef]
- Lai, F.; Zhu, X.; Li, G.; Zhu, L.; Wang, F. Numerical Research on the Energy Loss of a Single-Stage Centrifugal Pump with Different Vaned Diffuser Outlet Diameters. Energy Procedia 2019, 158, 5523–5528. [Google Scholar] [CrossRef]
- Wang, W.; Pei, J.; Yuan, S.; Yin, T. Experimental Investigation on Clocking Effect of Vaned Diffuser on Performance Characteristics and Pressure Pulsations in a Centrifugal Pump. Exp. Therm. Fluid Sci. 2018, 90, 286–298. [Google Scholar] [CrossRef]
- Krige, D.G. A Statistical Approach to Some Basic Mine Valuation Problems on the Witwatersrand. J. Chem. Metall. Min. Eng. Soc. S. Afr. 1951, 52, 119–139. [Google Scholar]
- Sacks, J.; Welch, W.J.; Mitchell, T.J.; Wynn, H.P. Design and Analysisi of Computer Experiments. Stat. Sci. 1989, 4, 409–423. [Google Scholar]






| Methods | Contents | Advantages | Disadvantages |
|---|---|---|---|
| Design of experiments | Taguchi experimental design | Short optimization period, easy to obtain optimal solution | The design parameters are limited and the resulting solution is not optimal |
| Surrogate models | Artificial neural network Kriging model Response surface method | Short optimization period and low consumption of computational resources | There are errors between the surrogate model and the actual |
| Intelligent algorithms | Genetic algorithms Particle swarm algorithms Gravitational search algorithms | Multiple design parameters | Long optimization period and high consumption of computational resources |
| Design Parameters | Symbol | Value |
|---|---|---|
| Impeller inlet diameter | Dj (mm) | 270 |
| Impeller outlet diameter | D2 (mm) | 360 |
| Impeller outlet width | b2 (mm) | 70.5 |
| Impeller inlet blade angle | β1 (degree) | 24 |
| Impeller outlet blade angle | β2 (degree) | 22 |
| Wrap angle of impeller blade | φ (degree) | 136 |
| Diffuser inlet diameter | D3 (mm) | 365 |
| Diffuser outlet diameter | D4 (mm) | 505 |
| Diffuser width | b3 (mm) | 72 |
| Volute inlet width | b5 (mm) | 72 |
| Volute base circle diameter | D5 (mm) | 440 |
| Volute outlet diameter | D6 (mm) | 350 |
| Domain | Number of Elements (×104) |
|---|---|
| Inlet pipe | 36.5 |
| Impeller | 217.3 |
| Diffuser | 207.7 |
| Volute | 189.3 |
| Outlet pipe | 25.5 |
| Variables | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Upper Bound | 0.19 | 0.19 | 0.252 | 0.252 | 30 | 40 | 40 | 40 | 30 | 30 | 40 | 40 | 40 | 30 |
| Lower Bounds | 0.184 | 0.184 | 0.242 | 0.242 | 15 | 10 | 10 | 10 | 22 | 15 | 10 | 10 | 10 | 22 |
| No. | 1 | 2 | 3 | 4 | 5 | … | 66 | 67 | 68 | 69 | 70 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x0 | 0.1887 | 0.1863 | 0.1895 | 0.1875 | 0.1899 | … | 0.18708 | 0.18499 | 0.18587 | 0.18733 | 0.18673 |
| x1 | 0.1853 | 0.1869 | 0.1865 | 0.18743 | 0.1859 | … | 0.18681 | 0.1874 | 0.18775 | 0.18738 | 0.1873 |
| x2 | 0.2495 | 0.2515 | 0.24417 | 0.252 | 0.24883 | … | 0.2505 | 0.252 | 0.252 | 0.25117 | 0.24917 |
| x3 | 0.24417 | 0.25183 | 0.25083 | 0.24956 | 0.24683 | … | 0.252 | 0.24963 | 0.2487 | 0.252 | 0.25066 |
| x4 | 23.25 | 28.25 | 26.75 | 30 | 15.25 | … | 22.25 | 26.75 | 30 | 27.25 | 30 |
| x5 | 24.5 | 12.5 | 15.5 | 11.93 | 26.5 | … | 12.75 | 15.41 | 10.34 | 17.15 | 13 |
| x6 | 35.5 | 14.5 | 12.5 | 11.5 | 22.5 | … | 26.5 | 14.5 | 10 | 11.3 | 18.5 |
| x7 | 34.5 | 10.5 | 26.5 | 10.5 | 30.5 | … | 13.5 | 21.5 | 10 | 18.5 | 10 |
| x8 | 22.4 | 22.13 | 25.33 | 24.5 | 26.13 | … | 22 | 25.73 | 23.73 | 23.31 | 23.66 |
| x9 | 28.75 | 19.25 | 15.25 | 22.75 | 17.75 | … | 22.25 | 20.25 | 21.29 | 21.44 | 19.5 |
| x10 | 26.5 | 28.5 | 21.5 | 14.76 | 19.5 | … | 26.75 | 20.91 | 21.37 | 25.13 | 21.79 |
| x11 | 10.5 | 26.5 | 14.5 | 17.43 | 25.5 | … | 29.52 | 24.86 | 16.5 | 21.76 | 18.96 |
| x12 | 29.5 | 15.5 | 37.5 | 17.22 | 19.5 | … | 16.64 | 14.82 | 15.99 | 21.5 | 13.53 |
| x13 | 24.27 | 29.87 | 29.33 | 28.26 | 23.73 | … | 29.07 | 27.32 | 26.8 | 28 | 28.27 |
| η (%) | 84.7 | 86.49 | 84.82 | 87.5 | 84.65 | … | 84.98 | 85.63 | 87.72 | 85.84 | 86.55 |
| Variables | x0 | x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | x9 | x10 | x11 | x12 | x13 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before | 0.18774 | 0.18774 | 0.2484 | 0.2484 | 15.53 | 19.97 | 24.24 | 23.2 | 27.15 | 15.53 | 19.97 | 24.24 | 23.2 | 27.15 |
| After | 0.18426 | 0.18986 | 0.25171 | 0.25169 | 16.15 | 11.28 | 11.56 | 10.14 | 22.17 | 29.59 | 11.86 | 10.31 | 23.35 | 22.58 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, Z.; Wang, W.; Huang, C.; Pei, J. Performance Optimization on 3D Diffuser of Volute Pump Using Kriging Model. Processes 2022, 10, 1076. https://doi.org/10.3390/pr10061076
Han Z, Wang W, Huang C, Pei J. Performance Optimization on 3D Diffuser of Volute Pump Using Kriging Model. Processes. 2022; 10(6):1076. https://doi.org/10.3390/pr10061076
Chicago/Turabian StyleHan, Zhenhua, Wenjie Wang, Congbing Huang, and Ji Pei. 2022. "Performance Optimization on 3D Diffuser of Volute Pump Using Kriging Model" Processes 10, no. 6: 1076. https://doi.org/10.3390/pr10061076
APA StyleHan, Z., Wang, W., Huang, C., & Pei, J. (2022). Performance Optimization on 3D Diffuser of Volute Pump Using Kriging Model. Processes, 10(6), 1076. https://doi.org/10.3390/pr10061076








