Hydraulic Optimization of Closed Transformation of Open Sump for the Water Treatment Pumping Station

Abstract

Taking the closed modification of an open sump of a water treatment pump station as the research background, the hydraulic design criteria for the closed modification of the sump are put forward by combining numerical simulation, model test. Based on CFD technology, a water pumping station including closed sump, bellmouth, impeller, guide vane, elbow and outlet sump is simulated, and the hydraulic performance of the schemes under different parameters is analyzed and compared. The top floor clearance, width, back wall distance, and floor clearance of the sump are optimized hydraulically, and the hydraulic design criteria of the closed sump are obtained. The results show that when the recommended optimization parameters of the closed sump in this study are that the top floor height H_D is 0.9 D_L, the width B is 3.0 D_L, the back wall distance T is from 0.4 D_L, and the floor clearance C is 0.75 D_L, the internal flow pattern and hydraulic of the closed sump is better. (D_L is the diameter of bellmouth of water pumping station). The model test was set up to compare the hydraulic performance of the pumping station between CFD and the test. The results showed that the CFD data is in good agreement with the experimental data.

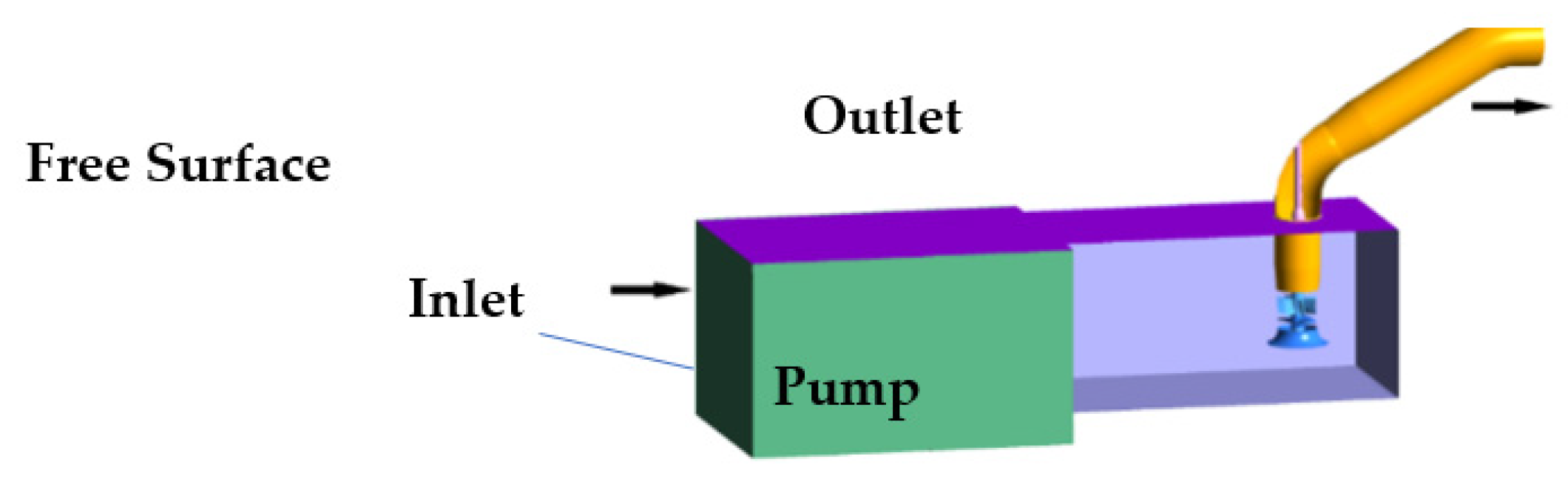
1. Introduction

Small and medium-sized vertical water pumping stations for water treatment mostly use a wet-chamber pump house (Figure 1). The open sump of the wet-chamber pump house is arranged under the pump house to form a wet chamber. The water pump absorbs water from the wet chamber. The sump’s water level varies greatly, and surface vortices, bottom vortices and wall vortices are often formed. Additional structures such as pump beam and overhaul platform are often required in open sump, which will have a negative effect on the flow in the sump [1]. Therefore, to prevent the whirl sump from occurring, and considering the convenience of installation and maintenance of the pump unit, a concrete cover is set at the position of the pump beam to close the open sump, reduce the free water surface, avoid setting the structure of sump, reduce flow interference in the sump and form a closed sump (Figure 2). Closed sump is a newly proposed modification form of the sump, and its geometric parameters have not been referenced yet.

In recent years, domestic and foreign scholars have carried out a lot of experimental research and optimized design for the pump sump, which has made breakthrough progress in the research of sumps. Iversen et al. [2], Japan Agricultural Engineering Association [3], Paterson [4], U.S. Army Engineering Corps [5], Pan et al. [6], Qian et al. [7], and Liu et al. [1] provide reference ranges for essential dimensions of sumps such as floor clearance, submergence depth, back wall distance, sump width and length based on a large number of experiments. Padmanabhan et al. [8] analyzed the scale effect in the flow pattern experiment of the sump, and it is pointed out that the scale effect is not shown in a scale model. Therefore, it is not necessary to use a flow rate scale higher than Fr criterion to test in the experiment. Constantinescu et al. [9,10] and Rajendran et al. [11] predicted the position, number, and structure of vortices in the sump by numerical simulation combined with PIV measurement test. Anwar [12], Fraser [13], Ansar et al. [14], Li et al. [15] and Cheng [16,17] carried out a lot of experiments and numerical simulation studies on the eddy problems existing in the sump. They elaborated the formation mechanism of the eddy, simulated the formation and evolution process of the free water surface vortex, and proposed relevant elimination measures. Guo et al. [18] employed PIV to investigate the influence of back-wall clearance, CWL(Critical Water Level), and air content in water on flow patterns in a pump intake and gave the relationship between free surface vortex and back-wall clearance experimentally and theoretically. Song et al. [19] studied the influence of the floor-attached vortex on the pressure pulsation at the pump sump by combining experimental analysis and eddy current dynamics theory.

In summary, there are many research achievements on pump sumps at home and abroad, but most of them focused on open sumps. There are few studies on closed sumps with more complex flow patterns, especially the hydraulic parameter design of closed sumps is not perfect in some respects, and the structure size has not been well optimized. In this essay, the optimization of geometric parameters of the closed sump and a proposal of the criteria for engineering design and application were studied. The study is based on CFD technology [20,21,22] and model test; take the renovation of a water pumping station as an example.

2. Numerical Simulation

2.1. Calculation Model

The calculation model is a vertical axial flow pump system with a closed sump. The diameter of the pump impeller is 120 mm. The diameter of bellmouth is 188 mm. The speed n is 2500 rpm. There are three impeller blades and 7 guide vanes. UG NX software is used for modeling. The calculation model of the pump system mainly includes inlet forebay, closed sump, impeller, guide vane, and outlet elbow (Figure 3).

2.2. Calculation Method and Grid Meshing

In this paper, the commercial CFD software ANSYS CFX is used for numerical simulation based on the continuity equation of incompressible fluid and the regular time-average Reynolds equation (RANS equation). RNG k-ε used for 3D steady calculation of turbulence model of pump system ε model. According to previous research, the RNG k-ε model can well predict rotational flow and swirl flow and has good applicability in the flow field of axial flow pump. As the fluid is considered incompressible, the heat exchange can be neglected. Thus, the energy conservation equation is not considered since its influence is trivial.

The forebay, closed sump, outlet elbow, guide vane, and impeller have meshed separately. ICEM CFD software and Turbo grid in ANSYS software are used to divide the grid. Impellers and guide vanes are divided into hexahedron grids based on Turbo grid software, while others are based on CFD software to divide hexahedron grids. To ensure the accuracy of calculation, O-block, local encryption, and other methods are used in grid partition. In addition, it is computationally required that the grid determinant be more significant than 0.3 and a minimum angle greater than 18 degrees. The calculation requirements are met by grid quality check. As different turbulence models require different y⁺ values in the grid, RNG k-ε used in this paper limits the y⁺ value between 30 and 100 [14,15]. The model involves the impeller, the grid quality that exerts a significant influence on the result. The y⁺ value of the grid at the impeller is analyzed. The y⁺ value of the grid at the impeller is between 35.46 and 52.25. The y⁺ value in the whole calculation domain should be between 30 and 100, which satisfies the RNG k-ε model requirement.

To verify the rationality of grid partition, an independent analysis of the overall grid of the pump system is performed (Figure 4a). The research shows that when the whole pump system grid number hits 1.82 million and the number of sump grid is 900,000, the head of the pump system tends to stabilize. At this time, the number of the grid has little influence on the calculation results. After careful consideration, 1.82 million whole pump system grids are selected. Figure 4 is a sketch of grid independence verification and grid of sump.

2.3. Parameters and Boundary Condition Setting

Pump impeller diameter D is 120 mm, and speed n is set 2400 r/min to study hydraulic optimization of geometric parameters of the closed sump. The optimum operating condition (Q_BEP = 35 L/s) is taken as the calculation operating condition analysis. The calculation area includes inlet forebay, sump, impeller, guide vane, and outlet elbow. The boundary conditions are set as in

Table 1. Calculation parameter settings.

Main Parameters	CFX Settings	Main Parameters	CFX Settings
Rotational speed	2400 rev/min	Static-static interface	GGI
Simulation type	Transient	Dynamic-static interface	Transient Rotor Stator
Turbulent intensity	5%	Wall condition	Non-slip
Inlet boundary conditions	Mass flow, Q = 35 L/s	Wall function	Scalable wall function
Outlet boundary conditions	1 atm	Convergence accuracy	10−5

.

3. Hydraulic Optimization of Geometric Parameters

Institutions and schools at home and abroad have conducted research on the parameter value range of the open sump through experiments and concrete engineering examples. However, these parameters have discrepancy between experiments and reality. The reason may be the difference in experimental standards under experimental conditions.

Table 2. Recommended geometric parameters of the open sump in different countries.

Geometric Parameters	Japan (JSME)	UK (BHRA)	USA (NI)	China (Design Code for Pumping Station)
Width B	2~2.5 DL	2~3 DL	2 DL	3 DL
Floor Clearance C	0.5~1.0 DL	0.33~0.5 DL	0.52~0.59 DL	0.6~0.8 DL
Back Wall Distance T	0.25~0.5 DL	0.1~0.25 DL	0.25~0.68 DL	0.3~0.5 DL
Length L	5~8 DL	4~6 DL	3.0~5.3 DL	>4 DL

Note: D_L is diameter of bellmouth.

shows the recommended values of geometric parameters of open sump given by different countries.

Based on the recommended values of the geometric parameters of the sump in Table 1 and considering the structure of the closed sump, the single factor analysis method was used to study the effects of the four geometric parameters of the closed sump on the hydraulic performance of the pump system (Figure 5).

Table 3. Research schemes.

No.	Width B/DL	Back Wall Distance T/DL	Floor Clearance C/DL	Top Floor Height HD/DL	Note
Case 1	2.5	0.4	0.5	0.5	Different top floor height
Case 2	2.5	0.4	0.5	0.7
Case 3	2.5	0.4	0.5	0.9
Case 4	2.5	0.4	0.5	1.1
Case 5	2.0	0.4	0.5	0.9	Different width
Case 3	2.5	0.4	0.5	0.9
Case 6	3.0	0.4	0.5	0.9
Case 7	3.5	0.4	0.5	0.9
Case 8	3.0	0.2	0.5	0.9	Different back wall distance
Case 6	3.0	0.4	0.5	0.9
Case 9	3.0	0.6	0.5	0.9
Case 10	3.0	0.8	0.5	0.9
Case 11	3.0	0.4	0.25	0.9	Different floor clearance
Case 6	3.0	0.4	0.5	0.9
Case 12	3.0	0.4	0.75	0.9
Case 13	3.0	0.4	1	0.9

shows the specific research schemes. Case 1 to 4 are to study the influence of top floor height on the hydraulic performance of the closed sump. Case 3 and Case 5 to 7 are to study the impact of width on the hydraulic performance of closed sump. Case 6 and Case 8 to 10 are to study the influence of back wall distance on the hydraulic performance of closed sump. Case 6 and Case 11 to 13 are to study the effect of floor clearance on the hydraulic performance of closed sump.

To obtain the law of the influence of various geometric parameters on hydraulic performance under the change of single factor, four indicators, including pump system efficiency ƞ, hydraulic loss h of the sump, uniformity of flow velocity $\overline{V}$ at the inlet of the bell mouth, and velocity-weighted average angle $\overline{\theta }$, were used as the hydraulic performance evaluation indicators. The formula of each evaluation is as follows.

Equation (1) is the formula for calculating the efficiency of the pump system in a numerical simulation.

$$\eta =\frac{P_{\mathrm{B}}{-P}_{\mathrm{A}}}{{nT}_{\mathrm{P}}/9550}$$

(1)

Among them, $P_{\mathsf{A}}$ is the inlet section pressure of the forebay, kPa. $P_{\mathrm{B}}$ is the pressure of the outlet pipe, kPa. $n$ is the speed of the impeller, r/min. T_P is the torque, $\mathrm{N}·\mathrm{m}$. In the experiment, the efficiency of the pump device is calculated according to the following formula:

$$\eta =\frac{\rho gQH}{N}\times 100\%$$

(2)

Here, N is the shaft power, $\rho$ is the water density (in kg/m³), g is the gravitational acceleration (in m/s²), Q is the flow rate (in m³/s), and H is the pump head.

Equation (2) is the formula of weighted average angle of impeller inlet velocity.

$$\overline{\theta }=\frac{\sum \left[{90}^{\circ }-\arctan \frac{u_{ti}}{u_{ai}}\right]}{\sum u_{ai}}$$

(3)

Among them, $u_{ti}$ is the lateral velocity of each unit at the inlet section of the impeller chamber, m/s. $u_{ai}$ is the axial velocity of each unit at the inlet section of the impeller chamber, m/s.

Equation (3) is the formula for the uniformity of the impeller inlet flow velocity $\overline{V}$

$$\overline{V}=\left[1-\frac{1}{\overline{u_a}}\sqrt{\frac{\sum {\left(u_{ai}-\overline{u_a}\right)}^2}{m}}\right]\times 100\%$$

(4)

$u_{ai}$ is the axial velocity of each unit at the inlet section of the impeller chamber, m/s; $\overline{u_a}$ is the average axial velocity of the inlet section of the impeller chamber, m/s; $m$ is the number of cells in this section for numerical calculations of the flow field.

3.1. Top Floor Height H_D

Four cases were set up to analyze the influence of top floor height H_D change on the hydraulic performance of the closed sump. Four cases set the same width 2.5 D_L, the same back wall distance 0.4 D_L, the same floor clearance 0.5 D_L, the top floor height is from 0.5 D_L to 1.1 D_L.

3.1.1. Velocity and Pressure Distribution

To study the change of hydraulic characteristics of the closed sump with the height of the top roof, sections 1-1 and 2-2 are set (Figure 6). Section 1-1 is the vertical section of the sump center. Section 2-2 is the horizontal section below the bell mouth.

Figure 7 shows the velocity distribution in sections 1-1 of different top floor heights. When the size is 0.5 D_L, the low-velocity zone at the back wall extends from below the bellmouth to the top floor, when the top floor height is 0.5 D_L, 0.7 D_L, and 1.1 D_L, the velocity gradient in the high-velocity area changes faster than that in 0.9 D_L, especially in 0.7 D_L.

Figure 8 shows the pressure distribution of each top floor in 2-2 sections. When the top floor height is 0.5 D_L and 0.7 D_L, the streamlines on both sides of the back wall have obvious whirls, especially in the crescent low-pressure area under the bellmouth. High pressure zones appear at the corners of the back wall and the center of the back wall when the top floor height is 1.1 D_L high. This indicates that the velocity here is low and has a poor flow pattern. By contrast, the pressure is much more well-distributed at 0.9 D_L.

3.1.2. Velocity and Pressure Distribution

The pressure measuring surfaces A, and inlet pressure measuring surface B of impeller chamber were set (Figure 9). Hydraulic loss h of the closed sump can be calculated by the difference between pressure measuring surface A and pressure measuring surface at impeller chamber inlet. Pump system head and efficiency can be obtained from pressure measuring surface A, pressure surface B and impeller torque. Through the velocity data derived from the inlet surface of the impeller chamber, the velocity uniformity and velocity-weighted average angle at the inlet of the impeller chamber can be obtained.

Figure 10a showed the pump system efficiency and hydraulic loss curve with different top floor height. The efficiency of pump system η changes little when the top floor height is 0.5 D_L, 0.7 D_L and 0.9 D_L. It decreased significantly at 1.1 D_L. The efficiency was the highest at 0.9 D_L. The hydraulic loss h is larger when the top floor is low, as the flow area becomes smaller, the velocity increases, and the hydraulic loss increases. When the top floor height is 0.9 D_L, the hydraulic loss is the smallest.

Figure 10b showed the velocity uniformity and weighted average angle of exit velocity curve with different top floor. The flow velocity uniformity at the outlet of the sump reaches a peak at 0.9 D_L. The weighted average angle of outlet velocity decreases gradually with the increase of top floor height. As the height of the top floor increases, the water flow on the upper layer of the sump needs to be adjusted at a larger angle before it can enter the bell mouth. However, when the top floor is low, there is no such water body in the closed sump. Most of the water flows into the bell mouth below the impeller elevation.

The change of velocity, pressure distribution and hydraulic characteristics are thus comprehensively analyzed. 0.9 D_L top floor height is selected for subsequent single factor geometric parameter analysis.

3.2. Width B

Four cases are set to analyze the influence of width B variation on hydraulic performance of the closed sump. Four cases set the same top floor height 0.9 D_L, the same back wall distance 0.4 D_L, the same floor clearance 0.5 D_L. The width is changed from 2 D_L to 3.5 D_L.

3.2.1. Velocity and Pressure Distribution

Figure 11 shows the pressure distribution of section 2-2 with different widths. The variation of width changes the distribution of pressure and flow pattern in the horizontal direction. It is observed that severe streamline cycles occur on both sides of the back wall when the width is 2 D_L. The pressure distribution is not uniform near the inlet of the sump and under the bell mouth. When the width is 2.5 D_L and 3 D_L, the flow pattern and pressure distribution are more uniform. When the width is 3 D_L, smaller whirls in streamlines on both sides of the back wall is observed. When the width is 3.5 D_L, the low-pressure area under the bellmouth enlarges, whirls of other widths do not appear at both corners of the back wall, and the direction is opposite to that of inner whirls of other widths. Bad flow pattern is easy to form here.

Figure 12 shows the velocity distribution of section 3-3 with different widths. When the width is 2 D_L, the velocity gradient changes rapidly in the sump. When the width is 3.5 D_L, there is a wide range of low velocity zone at both corners of the back wall, which is easy to form an undesirable flow pattern. When the width is 2.5 D_L and 3 D_L, the velocity is relatively uniform, and the range of low velocity zone and high velocity zone is smaller. In general, when the width is between 2 D_L and 3 D_L, the streamlines on both sides of the back wall and behind the bell mouth form a whirl due to the direction in which the rectangular back wall does not fit the streamlines.

3.2.2. Hydraulic Performance

The hydraulic performance of the closed sump is analyzed as the width changes (Figure 13). It is found that the efficiency of the pump gradually increases with the increase of width. It shows that the closed sump may need a wider width than the open sump. The hydraulic loss decreases with the increase of width due to the increase of overflow area, the decrease of flow rate and the decrease of hydraulic loss.

Figure 14 shows the velocity uniformity and weighted average angle of outlet velocity curve with different width. The uniformity of flow velocity at the outlet of the sump is the highest when the width is 2.5 D_L, the lowest when the width is 2 D_L and the smaller when the width is 3 D_L and 3.5 D_L. The weighted average angle of velocity at the outlet of the sump increases with the increase of the width. The reason may be that the water flow in the horizontal direction has more space to adjust the angle entering the bellmouth with the increase of the width.

After comprehensively analyzing the flow pattern, pressure distribution and hydraulic performance, the width B of 3.0 D_L for subsequent single factor geometric parameter analysis were selected.

3.3. Back Wall Distance T

Four cases are set up to analyze the influence of the change of back wall distance T on the hydraulic performance of closed sump. The four cases set the same top floor height of 0.9 D_L, the same width of 3.0 D_L, the same floor clearance of 0.5 D_L, and change the back wall distance from 0.2 D_L to 0.8 D_L.

3.3.1. Velocity and Pressure Distribution

Figure 15 shows the velocity distribution of the section with each back wall distance on section 1-1. The change of the back wall distance has little impact on the whole section, but has a certain impact on the velocity gradient near the back wall of the bellmouth. A smaller back wall reduces the range of the low velocity area at the back wall, and the angle of the streamline also changes greatly.

Figure 16 shows the pressure distribution of section 2-2 at each back wall distance. The pressure division of section 2-2 is analyzed. When the back wall distance is greater than 0.6 D_L, the pressure at the back wall of this section is less than the overall pressure of the sump. However, the streamline has a certain degree of gyration at the back wall. In general, the back wall distance has little effect on the flow pattern.

3.3.2. Velocity and Pressure Distribution

Figure 17a showed the pump system efficiency and hydraulic loss curve with different back wall distance. The efficiency of the pump system decreases with the increase of the back wall distance. When the back wall distance reaches 0.6 D_L, the efficiency changes little. The hydraulic loss of the sump is small under the small back wall distance.

Figure 17b showed the velocity uniformity and weighted average angle curve with different back wall distance. The uniformity of flow velocity at the outlet of the sump increases with the increase of the back wall distance, because there is a large water flow space after the increase of the back wall distance, and the water can enter the horn pipe more evenly from all around. With the increase of back wall distance, the weighted average angle of inlet and outlet velocity first decreases and then increases.

Comprehensively analyze the section velocity, pressure distribution and hydraulic performance, and select the back wall distance of 0.4 D_L for subsequent single factor analysis.

3.4. Floor Clearance C

Four cases are set up to analyze the influence of floor clearance C change on the hydraulic performance of closed sump. The four schemes set the same top floor height, back wall distance and width 3 D_L, and change the floor clearance from 0.25 D_L to 1 D_L.

3.4.1. Velocity and Pressure Distribution

Figure 18 shows the velocity distribution of section 1-1 of each floor clearance. It is found that the influence of floor clearance on flow pattern is obvious, which is mainly reflected in that when the floor clearance is 0.25 D_L, the velocity gradient changes rapidly, and the high velocity area in front of the bellmouth and the low velocity area at the back of the bellmouth are directly connected with the bottom floor. The streamline bending angle is large. When the floor clearance rises to 0.5 D_L, there are still some high velocity areas and low velocity areas connected with the bottom floor, but the streamline bending angle has been improved. With the continuous increase of floor clearance, the two shell shaped high velocity and low velocity areas gradually separate from the bottom floor, and the streamline angle is more smooth.

Figure 19 shows the pressure distribution of sections 2-2 at each floor clearance. When the floor clearance is 0.25 D_L high, there are two gyrations on both sides of the inlet of the sump, and the high-pressure area at the back wall is very large. The pressure distribution under the bellmouth is extremely uneven. Most of the streamline at the back wall enters this section from the upper and lower sides rather than from the horizontal direction. With the increase of the floor clearance, the pressure distribution gradually tends to be uniform, and when the floor clearance reaches 0.75 D_L, the gyration of the streamline at the back wall disappears and is replaced by the smoother streamline in the horizontal direction.

3.4.2. Hydraulic Performance

Figure 20 showed the pump system efficiency and hydraulic loss curve with different floor clearance. The change of hydraulic performance of the sump with the floor clearance were observed. It is found that the efficiency of the pump system gradually increases with the increase of the floor clearance. It changes rapidly from 0.25 D_L to 0.5 D_L and slowly after 0.5 D_L, indicating that the floor clearance cannot be too low, otherwise it will have a great impact on the efficiency of the pump system. The hydraulic loss is larger at lower floor clearance, and gradually decreases after reaching 0.5 D_L, but changes little.

Figure 21 showed the velocity uniformity and weighted average angle curve with different floor clearance. The variation law of flow velocity uniformity at the outlet of the sump is the same as that of the efficiency of the pump system. It changes rapidly from 0.25 D_L to 0.5 D_L, and gradually increases after 0.5 D_L, but it is not obvious. When the floor clearance is from 0.25 D_L to 0.5 D_L, the velocity weighted average angle is poor. The two-shell shaped high velocity and low velocity areas separate from the bottom floor after 0.75 D_L, which improves the velocity weighted average angle.

4. Experimental Verification

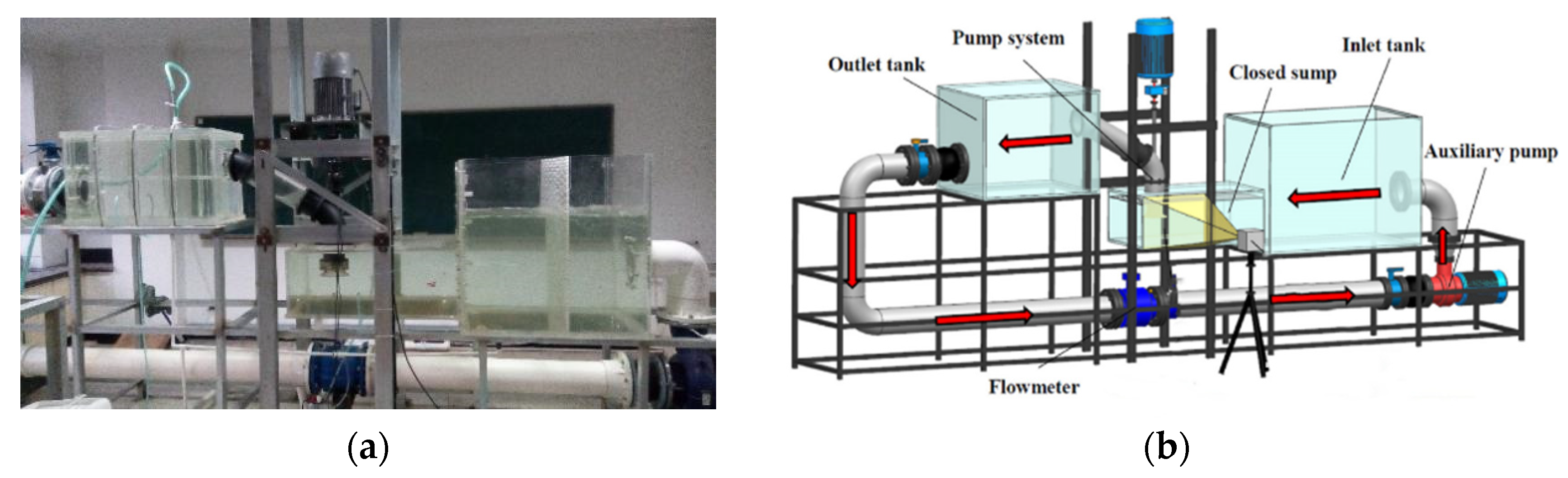
In order to verify the CFD optimization of geometric parameters of closed sump, a circular experimental system of transparent closed sump model was built. The loop length of the whole experimental system is 12 m, which is composed of closed sump model and circulating test system, as shown in Figure 22. The length of the closed sump model is 3.3 m, and its components include sump, closed sump, water pump system and pressure tank. The circulating test system is 8.7 m, and its components include auxiliary pump, electromagnetic flowmeter and connecting pipeline. The whole system runs stably and has good repeatability. The comprehensive error of efficiency measurement is ±1.73%.

The geometric parameters of the closed sump in the experimental model are as follows: Sump length L is 5.37 D_L, sump width B is 3.58 D_L, top floor height H_D is 2.88 D_L, floor clearance C = 1.01 D_L, and back wall distance T is 0.85 D_L, as shown in Figure 23. In order to facilitate observation, the transparent plexiglass plate is used to make the closed sump. In the test, different diaphragms are added into the closed sump to simulate the influence of changing the height, width, back wall distance and floor clearance on the hydraulic performance of the closed sump.

Figure 24 showed the comparison of Case 12 hydraulic performance of pumping station between CFD and test. Comparing the performance data of the prototype pump obtained by conversion with the performance curve of the device obtained by CFD, the overall trend is similar, but the difference is obvious when the flow coefficient Q/Q_BEP, the ratio of calculated flow to design flow, is greater than 100%. When Q/Q_BEP is less than 100%, the two values are similar and the error is small. As the prototype pump station often operates under ultra-low head conditions such as zero head or even negative head, when the calculated flow reaches 1.4 times the design flow, the pumping station head H_st (difference between the upstream and downstream pumping station water levels) is 0.01 m, so it is used as the ultra-low head condition for calculation and analysis, and the data is reliable.

5. Conclusions

Taking the closed modification of an open sump of a water pump station as the research background, the hydraulic design criteria for the closed modification of sump are put forward by combining numerical simulation, model test and field test methods.

Based on CFD technology, a pump station including closed sump, bellmouth, impeller, guide vane, elbow and outlet sump is simulated, and the hydraulic performance of the schemes under different parameters are analyzed and compared. The top floor clearance, width, back wall distance, and floor clearance of the sump are optimized hydraulically, and the hydraulic design criteria of the closed sump are obtained.

The hydraulic efficiency changes little when the top floor clearance is from 0.5 D_L to 0.9 D_L, but decreases significantly at 1.1 D_L. The hydraulic loss is larger when the top floor clearance is low. When the top floor clearance is 0.9 D_L, the hydraulic loss is the smallest. The flow velocity uniformity at the outlet of the inlet sump reaches a peak at 0.9 D_L. The weighted average angle of outlet velocity decreases gradually with the increase of top floor clearance.

With the increase of the sump width, the hydraulic efficiency also increases. If the closed sump width is too small, the flow velocity in the sump will speed up, the head loss will increase, and the streamline curvature when the flow converges to the horizontal direction of the bell mouth will be increased, which is easy to induce vortex. However, the width of the closed sump is too large, which is easy to form bias current and reflux in the sump and produce vortex. The uniformity of flow velocity at the outlet of the sump is the highest when the width is 2.5 D_L, the lowest when the width is 2 D_L, and the change is small when the width is 3 D_L and 3.5 D_L. The weighted average angle of inlet and outlet velocity increases with the increase of width.

The hydraulic efficiency decreases with the increase of back wall distance. When the back wall distance reaches 0.6 D_L, the efficiency changes little. The hydraulic loss of the closed sump is small under the small back wall distance. The uniformity of flow velocity at the outlet of sump increases with the increase of back wall distance. With the increase of back wall distance, the weighted average angle of inlet and outlet velocity first decreases and then increases.

The hydraulic efficiency increases gradually with the increase of floor clearance, changes rapidly from 0.25 D_L to 0.5 D_L, and changes slowly after 0.5 D_L. The hydraulic loss is larger at lower floor clearance, and gradually decreases after reaching 0.5 D_L, but changes little. The uniformity of flow velocity at the outlet of the closed sump changes rapidly from 0.25 D_L to 0.5 D_L, and then increases gradually after 0.5 D_L. When the floor clearance is 0.25 D_L–0.5 D_L, the velocity weighted average angle is small.

The recommended parameters of closed sump in this study is that the top floor height H_D is 0.9 D_L, the width B is 3.0 D_L, the back wall distance T is from 0.4 D_L, and the floor clearance C is 0.75 D_L.

The model test was set up to comparing hydraulic performance of pumping station between CFD and test. The results showed that the CFD data is in good agreement with the experimental data.