Performance Improvement of H8 Transformerless Grid-Tied Inverter Using Model Predictive Control Considering a Weak Grid
Abstract
:1. Introduction
- Apply the MPC algorithm to the H8 transformerless inverter.
- Investigate the system discrete model including the LCL filter.
- Discuss the effects of the grid weakness on the system response.
- Study the system response, under the disturbances in the insolation level.
- Test the robustness of the system performance against the parameter variations.
- Implement the proposed system using the HIL validation technique.
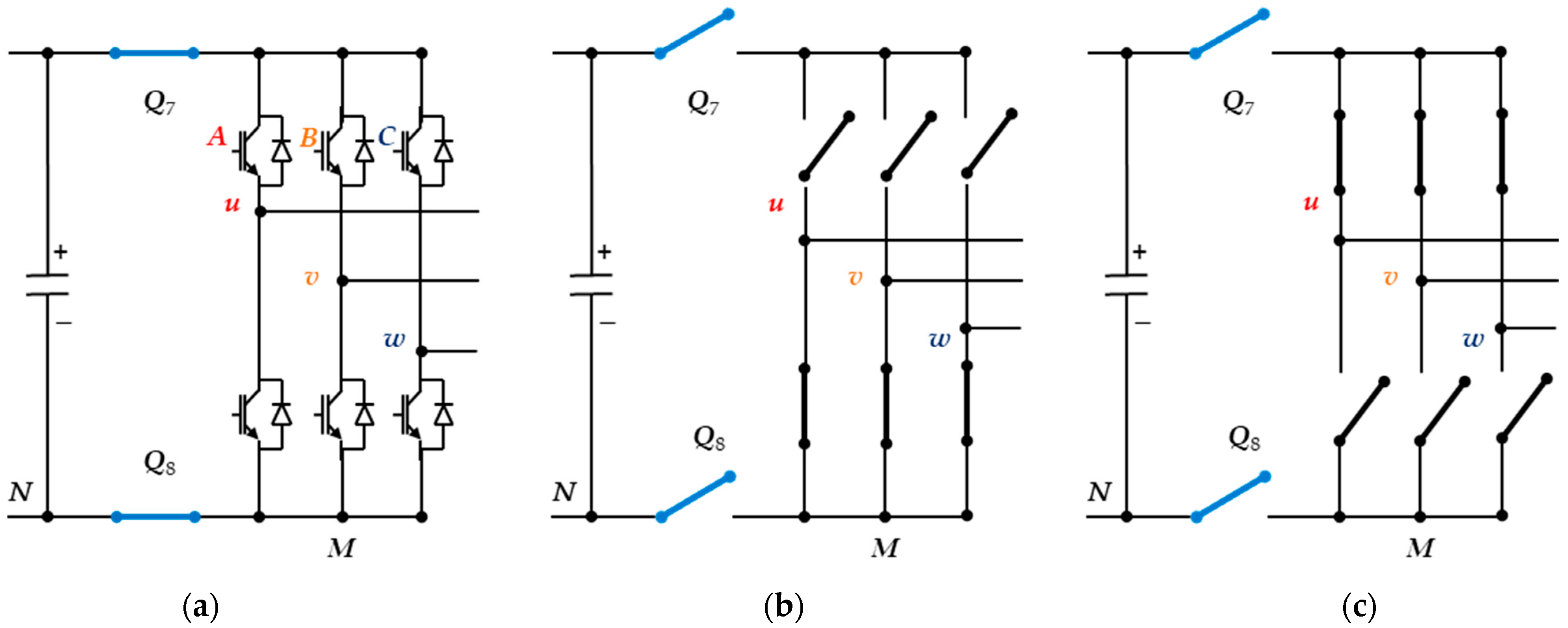
2. H8 Transformerless Inverter Structure and Operation
2.1. CMV Model of the H8 Transformerless Inverter
- For the active voltage vectors (), the switches Q7 and Q8 are on. Hence, the voltage VMN is zero. Hence, the CMV is Vdc/3.
- For the active voltage vectors (), the switches Q7 and Q8 are on. Hence, the voltage VMN is zero. Hence, the CMV is 2Vdc/3.
- For the zero voltage vectors (), the switches Q7 and Q8 are off. Hence, the voltage VMN is not zero and can be determined for each case. Finally, the CMV equals 2Vdc/3 for and it equals Vdc/3 for .
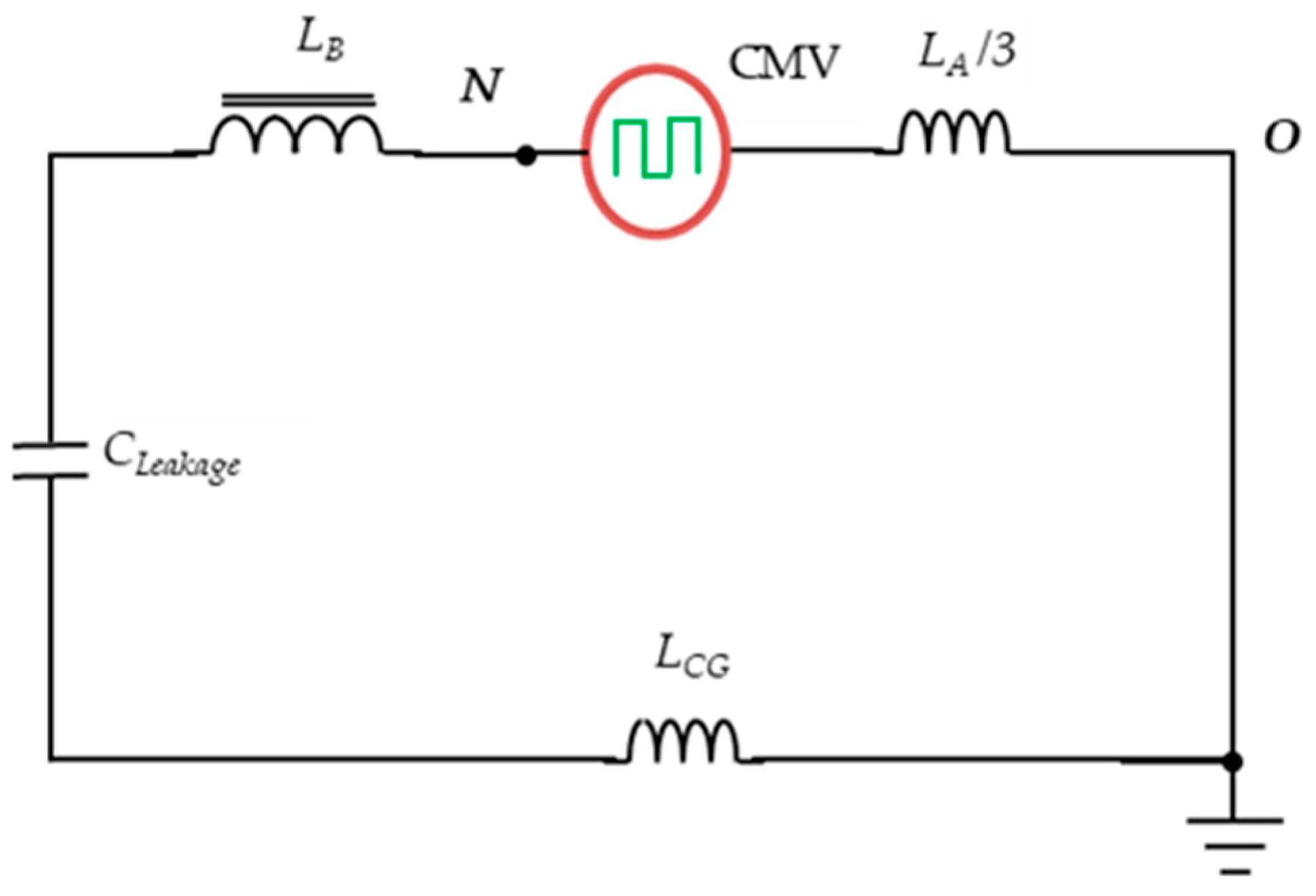
2.2. Earth Leakage Current Path of the H8 Transformerless Inverter
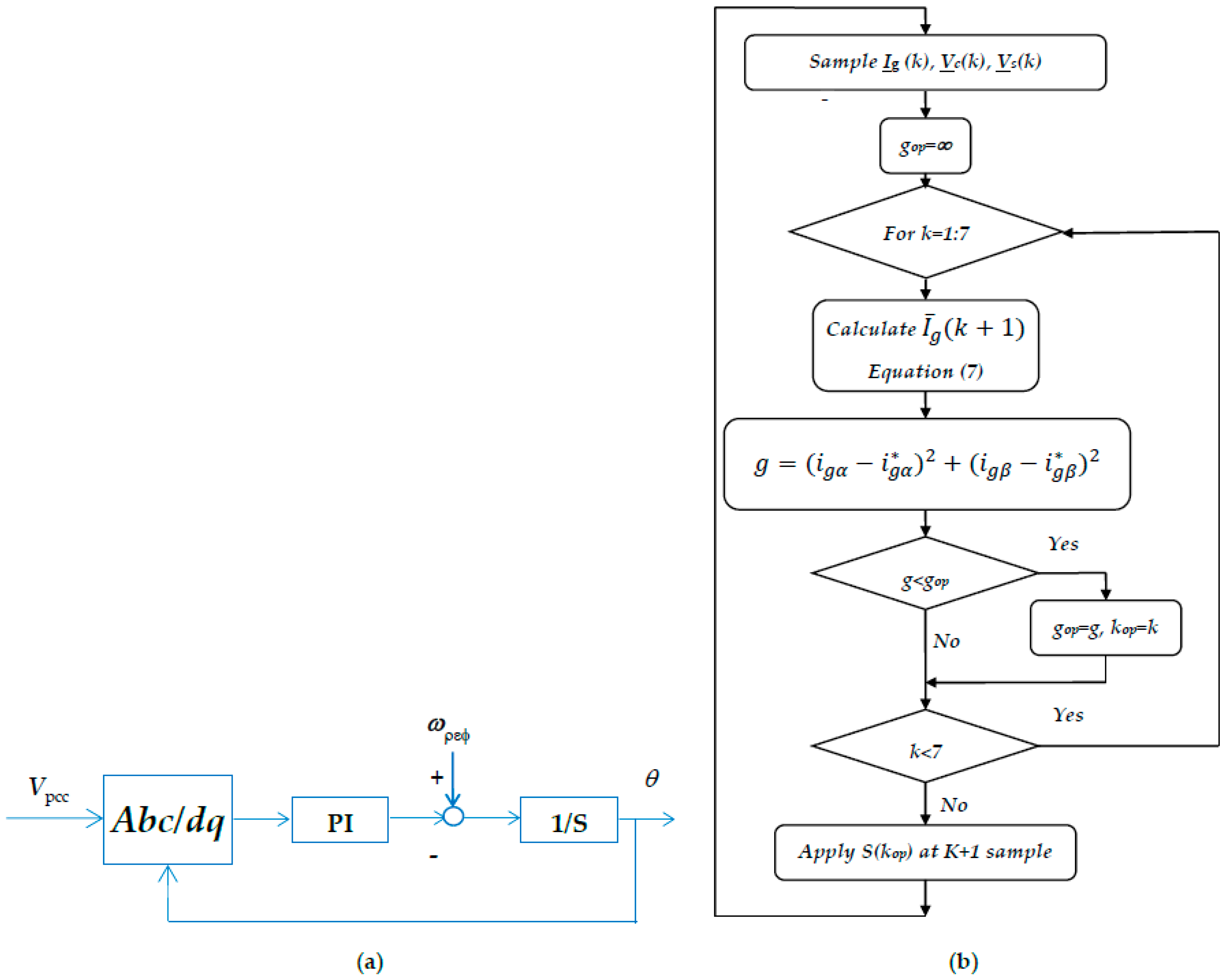
3. Model Predictive Control of the H8 Transformerless Inverter
4. System Controllers
4.1. Power Controller
- Let the integral part be zero and decrease the proportional part to a very small value.
- Increase the proportional part until the output oscillates.
- Measure the period of oscillation (Ts) and the corresponding proportional gain (Kcp). Hence, the PI controller gains are calculated using:
4.2. H8 Transformerless Inverter Controller
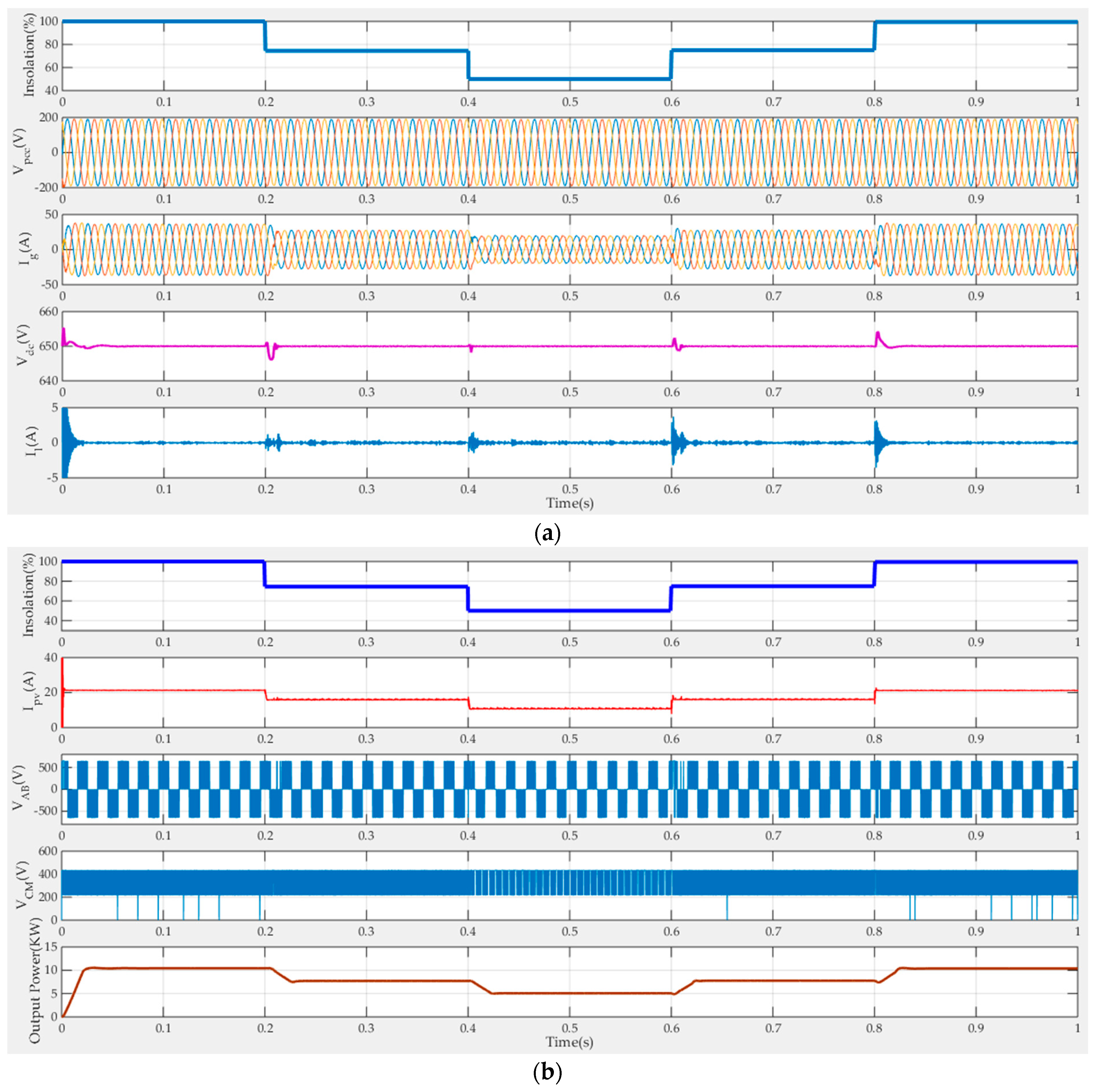
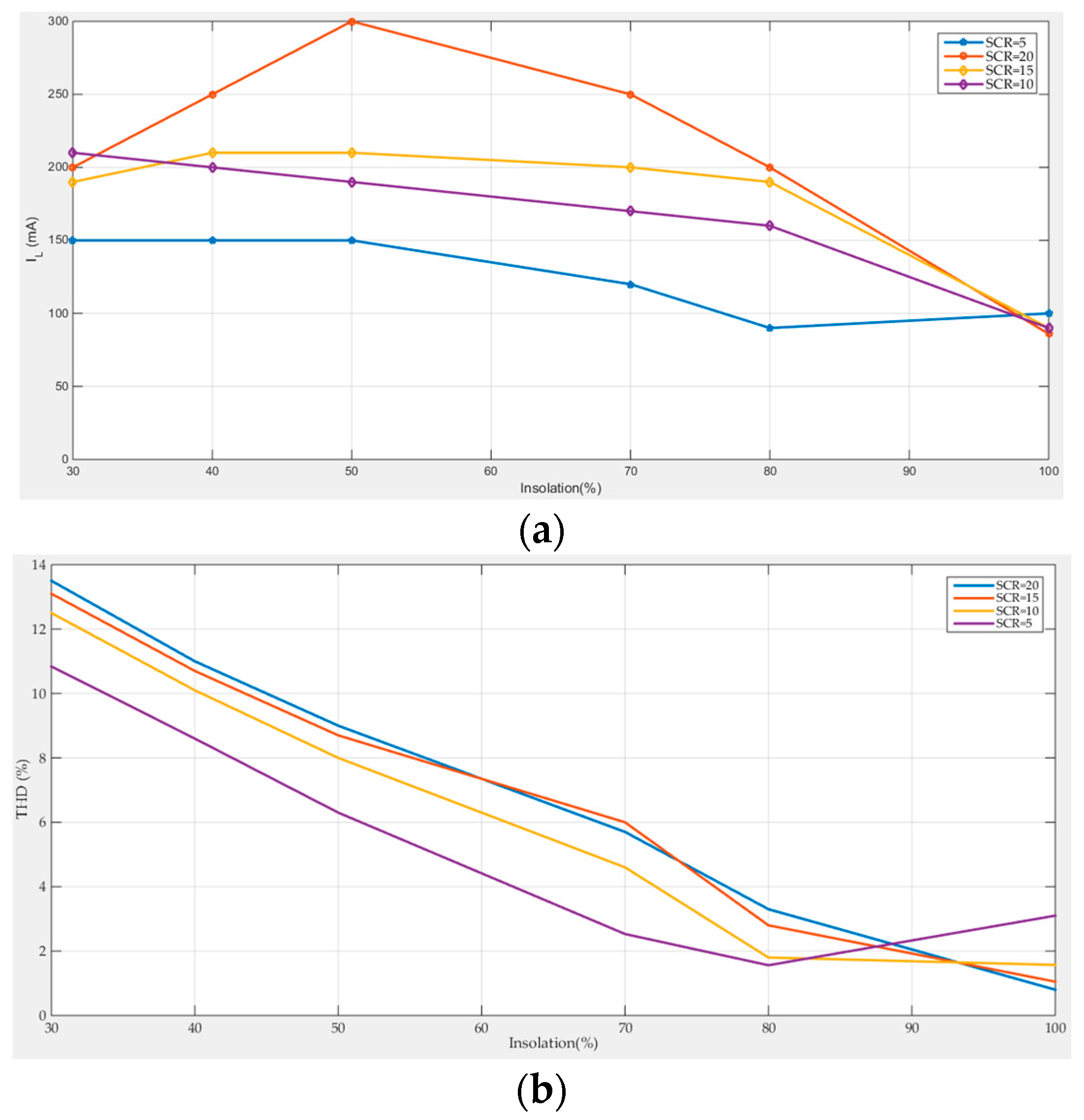
5. Weak Grid Operation of the H8 Transformerless Inverter
6. Simulation Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ronanki, D.; Sang, P.H.; Sood, V.; Williamson, S.S. Comparative assessment of three-phase transformerless grid-connected solar inverters. In Proceedings of the 2017 IEEE International Conference on Industrial Technology (ICIT), Toronto, ON, Canada, 22–25 March 2017; pp. 66–71. [Google Scholar] [CrossRef]
- Atawi, I.E.; Hendawi, E.; Zaid, S.A. Analysis and Design of a Standalone Electric Vehicle Charging Station Supplied by Photovoltaic Energy. Processes 2021, 9, 1246. [Google Scholar] [CrossRef]
- Zaid, S.A.; Kassem, A.M. Review, analysis and improving the utilization factor of a PV-grid connected system via HERIC transformerless approach. Renew. Sustain. Energy Rev. 2017, 73, 1061–1069. [Google Scholar] [CrossRef]
- Petrone, G.; Spagnuolo, G.; Teodorescu, R.; Veerachary, M.; Vitelli, M. Reliability issues in photovoltaic power processing systems. IEEE Trans. Ind. Electron. 2008, 55, 2569–2580. [Google Scholar] [CrossRef]
- Xiao, H.; Xie, S.; Chen, Y.; Huang, R. An Optimized Transformerless Photovoltaic Grid-Connected Inverter. IEEE Trans. Ind. Electron. 2011, 58, 1887–1895. [Google Scholar] [CrossRef]
- Meneses, D.; Blaabjerg, F.; García, Ó.; Cobos, J.A. Review and Comparison of Step-Up Transformerless Topologies for Photovoltaic AC-Module Application. IEEE Trans. Power Electron. 2013, 28, 2649–2663. [Google Scholar] [CrossRef] [Green Version]
- VDE 0126-1-1-2006; Automatic Disconnection Device between a Generator and the Public Low-Voltage Grid. DIN_VDE Normo: Berlin, Germany, 2011.
- Gonzalez, R.; Lopez, J.; Sanchis, P.; Marroyo, L. Transformerless inverter for single-phase photovoltaic systems. IEEE Trans. Power Electron. 2007, 22, 693–697. [Google Scholar] [CrossRef]
- Kerekes, T.; Teodorescu, R.; Rodríguez, P.; Vázquez, G.; Aldabas, E. A new high-efficiency single-phase transformerless PV inverter topology. IEEE Trans. Ind. Electron. 2011, 58, 184–191. [Google Scholar] [CrossRef] [Green Version]
- Freddy, T.K.S.; Rahim, N.A.; Hew, W.; Che, H.S. Comparison and analysis of single-phase transformerless grid-connected PV inverters. IEEE Trans. Power Electron. 2014, 29, 5358–5369. [Google Scholar] [CrossRef]
- Elbalawi, H.; Zaid, S.A. H5 transformerless inverter for grid-connected pv system with improved utilization factor and simple maximum power point algorithm. Energies 2018, 11, 2912. [Google Scholar] [CrossRef] [Green Version]
- Hou, C.; Shih, C.; Cheng, P.; Hava, A.M. Common-Mode voltage reduction pulsewidth modulation techniques for three-phase grid-connected converters. IEEE Trans. Power Electron. 2013, 28, 1971–1979. [Google Scholar] [CrossRef]
- Kerekes, T.; Teodorescu, R.; Liserre, M.; Klumpner, C.; Sumner, M. Evaluation of three-phase transformerless photovoltaic inverter topologies. IEEE Trans. Power Electron. 2009, 24, 2202–2211. [Google Scholar] [CrossRef]
- Guo, X.; He, R.; Jian, J.; Lu, Z.; Sun, X.; Guerrero, J.M. leakage current elimination of four-leg inverter for transformerless three-phase pv systems. IEEE Trans. Power Electron. 2016, 31, 1841–1846. [Google Scholar] [CrossRef] [Green Version]
- Hasanzad, F.; Rastegar, H.; Pichan, M. Performance evaluation of space vector modulation techniques for reducing leakage current of a three-phase four-leg PV inverter. In Proceedings of the 17th Iranian Conference on Electrical Engineering (ICEE), Tehran, Iran, 12–14 May 2009; pp. 1026–1031. [Google Scholar]
- Albalawi, H.; Zaid, S.A. Performance Improvement of a Grid-Tied Neutral-Point-Clamped 3-φ Transformerless Inverter Using Model Predictive Control. Processes 2019, 7, 856. [Google Scholar] [CrossRef] [Green Version]
- Morris, C.T.; Han, D.; Sarlioglu, B. Reduction of common mode voltage and conducted EMI through three-phase inverter topology. IEEE Trans. Power Electron. 2017, 32, 1720–1724. [Google Scholar] [CrossRef]
- Lorenzani, E.; Migliazza, G.; Immovilli, F.; Gerada, C.; Zhang, H.; Buticchi, G. Internal current return path for ground leakage current mitigation in current source inverters. IEEE Access 2019, 7, 96540–96548. [Google Scholar] [CrossRef]
- Wang, W.; Gao, F.; Yang, Y.; Blaabjerg, F. Operation and modulation of h7 current-source inverter with hybrid sic and si semiconductor switches. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 387–399. [Google Scholar] [CrossRef]
- Atawi, I.; Zaid, S. Model Predictive Control of H7 Transformerless Inverter Powered by PV. Intell. Autom. Soft Comput. 2022, 31, 449–469. [Google Scholar] [CrossRef]
- Concari, L.; Barater, D.; Buticchi, G.; Concari, C.; Liserre, M. H8 inverter for common-mode voltage reduction in electric drives. IEEE Trans. Ind. Appl. 2016, 52, 4010–4019. [Google Scholar] [CrossRef] [Green Version]
- Jeong, W.-S.; Kim, S.-H.; Yi, J.; Won, C.-Y. Finite Control Set–Model Predictive Control of H8 Inverter Considering Dead-Time Effect for PMSM Drive Systems with Reduced Conducted Common-Mode EMI and Current Distortions. IEEE Trans. Power Electron. 2022, 37, 5342–5356. [Google Scholar] [CrossRef]
- Gupta, A.K.; Agrawal, H.; Agarwal, V. A novel three-phase transformerless H-8 topology with reduced leakage current for grid-tied solar pv applications. IEEE Trans. Ind. Appl. 2019, 55, 1765–1774. [Google Scholar] [CrossRef]
- Rahimi, R.; Farhangi, S.; Farhangi, B.; Moradi, G.R.; Afshari, E.; Blaabjerg, F. H8 Inverter to Reduce Leakage Current in Transformerless Three-Phase Grid-Connected Photovoltaic systems. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 910–918. [Google Scholar] [CrossRef]
- Guo, X.; Wang, N.; Wang, B.; Lu, Z.; Blaabjerg, F. Evaluation of Three-Phase Transformerless DC-Bypass PV Inverters for Leakage Current Reduction. IEEE Trans. Power Electron. 2020, 35, 5918–5927. [Google Scholar] [CrossRef]
- Xiang, Y.; Pei, X.; Wang, M.; Shi, P.; Kang, Y. An Improved H8 Topology for Common-Mode Voltage Reduction. IEEE Trans. Power Electron. 2019, 34, 5352–5361. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Guo, Z.; Wang, J.; Wang, Y.; Li, F.; Zhao, W. The Control Strategy for the Grid-Connected Inverter Through Impedance Reshaping in q-Axis and its Stability Analysis Under a Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 3229–3242. [Google Scholar] [CrossRef]
- Lasseter, R.H.; Chen, Z.; Pattabiraman, D. Grid-forming inverters: A critical asset for the power grid. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 925–935. [Google Scholar] [CrossRef]
- IEEE Standards Board. IEEE Standard for Interconnecting Distributed Resources with Electric Power Systems:1547-2003; IEEE: Piscataway, NJ, USA, 2003; pp. 1–28. [Google Scholar]
- Yang, D.; Ruan, X.; Wu, H. Impedance Shaping of the Grid-Connected Inverter with LCL Filter to Improve Its Adaptability to the Weak Grid Condition. IEEE Trans. Power Electron. 2014, 29, 5795–5805. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Zaid, S.A.; Abu-Elyazeed, M.F.; Elsayed, H.M. Improved model predictive control for three-phase inverter with output LC filter. Int. J. Model. Identif. Control. 2015, 23, 371–379. [Google Scholar] [CrossRef]
- Mohamed, I.S.; Zaid, S.A.; Elsayed, H.M.; Abu-Elyazeed, M.F. Implementation of model predictive control for a three-phase inverter with output LC filter on eZdsp F28335 Kit using HIL simulation. Int. J. Model. Identif. Control 2016, 25, 301–312. [Google Scholar]
- Zaid, S.A.; Mohamed, I.S.; Bakeer, A.; Liu, L.; Albalawi, H.; Tawfiq, M.E.; Kassem, A.M. From MPC Based to End-to-End (E2E) Learning-Based Control Policy for Grid-Tied 3L-NPC Transformerless Inverter. IEEE Access 2022, 10, 57309–57326. [Google Scholar] [CrossRef]
- Zaid, S.A.; Albalawi, H. Application of model predictive control to ultra-sparse matrix rectifier. Int. Rev. Electr. Eng. 2018, 13, 357–364. [Google Scholar] [CrossRef]
- Huang, Z.; Li, H.; Li, W.; Liu, J.; Huang, C.; Yang, Z.; Fang, W. A New Trajectory Tracking Algorithm for Autonomous Vehicles Based on Model Predictive Control. Sensors 2021, 21, 7165. [Google Scholar] [CrossRef]
- Tan, N.; Kaya, I.; Yeroglu, C.; Atherton, D.P. Computation of stabilizing PI and PID controllers using the stability boundary locus. Energy Convers. Manag. 2006, 47, 3045–3058. [Google Scholar] [CrossRef]
- Gao, R.; Gao, Z. Pitch control for wind turbine systems using optimization, estimation and compensation. Renew. Energy 2016, 91, 501–515. [Google Scholar]







| Switching state | (1001) | (0101) | (0011) | (1101) | (0111) | (1011) | (0000) | (1110) |
| VuM/Vdc | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 1 |
| VvM/Vdc | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 |
| VwM/Vdc | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 |
| VCMV/Vdc | 1/3 | 2/3 | 1/3 | 2/3 | 1/3 | 2/3 | 1/3 | 2/3 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| (ISC,VOC) of the PV | 24.53 A, 633 V | Vdc | 650 V |
| Power | 11 KW | DC-link capacitor | 2000 µF |
| CLeakage | 400 nF | Utility voltage | 230 V |
| Cf | 2 µF | Utility frequency | 50 Hz |
| Lfmmm | 3 mH | Sampling period | 33 µs |
| Weak grid (Rg, Lg) | 74.8 mΩ, 238 µH | SCR | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zaid, S.A.; Albalawi, H.; AbdelMeguid, H.; Alhmiedat, T.A.; Bakeer, A. Performance Improvement of H8 Transformerless Grid-Tied Inverter Using Model Predictive Control Considering a Weak Grid. Processes 2022, 10, 1243. https://doi.org/10.3390/pr10071243
Zaid SA, Albalawi H, AbdelMeguid H, Alhmiedat TA, Bakeer A. Performance Improvement of H8 Transformerless Grid-Tied Inverter Using Model Predictive Control Considering a Weak Grid. Processes. 2022; 10(7):1243. https://doi.org/10.3390/pr10071243
Chicago/Turabian StyleZaid, Sherif A., Hani Albalawi, Hossam AbdelMeguid, Tareq A. Alhmiedat, and Abualkasim Bakeer. 2022. "Performance Improvement of H8 Transformerless Grid-Tied Inverter Using Model Predictive Control Considering a Weak Grid" Processes 10, no. 7: 1243. https://doi.org/10.3390/pr10071243
APA StyleZaid, S. A., Albalawi, H., AbdelMeguid, H., Alhmiedat, T. A., & Bakeer, A. (2022). Performance Improvement of H8 Transformerless Grid-Tied Inverter Using Model Predictive Control Considering a Weak Grid. Processes, 10(7), 1243. https://doi.org/10.3390/pr10071243






