Multi-Objective Optimization of a Crude Oil Hydrotreating Process with a Crude Distillation Unit Based on Bootstrap Aggregated Neural Network Models
Abstract
:1. Introduction
2. A Crude Oil HDT Process with CDU
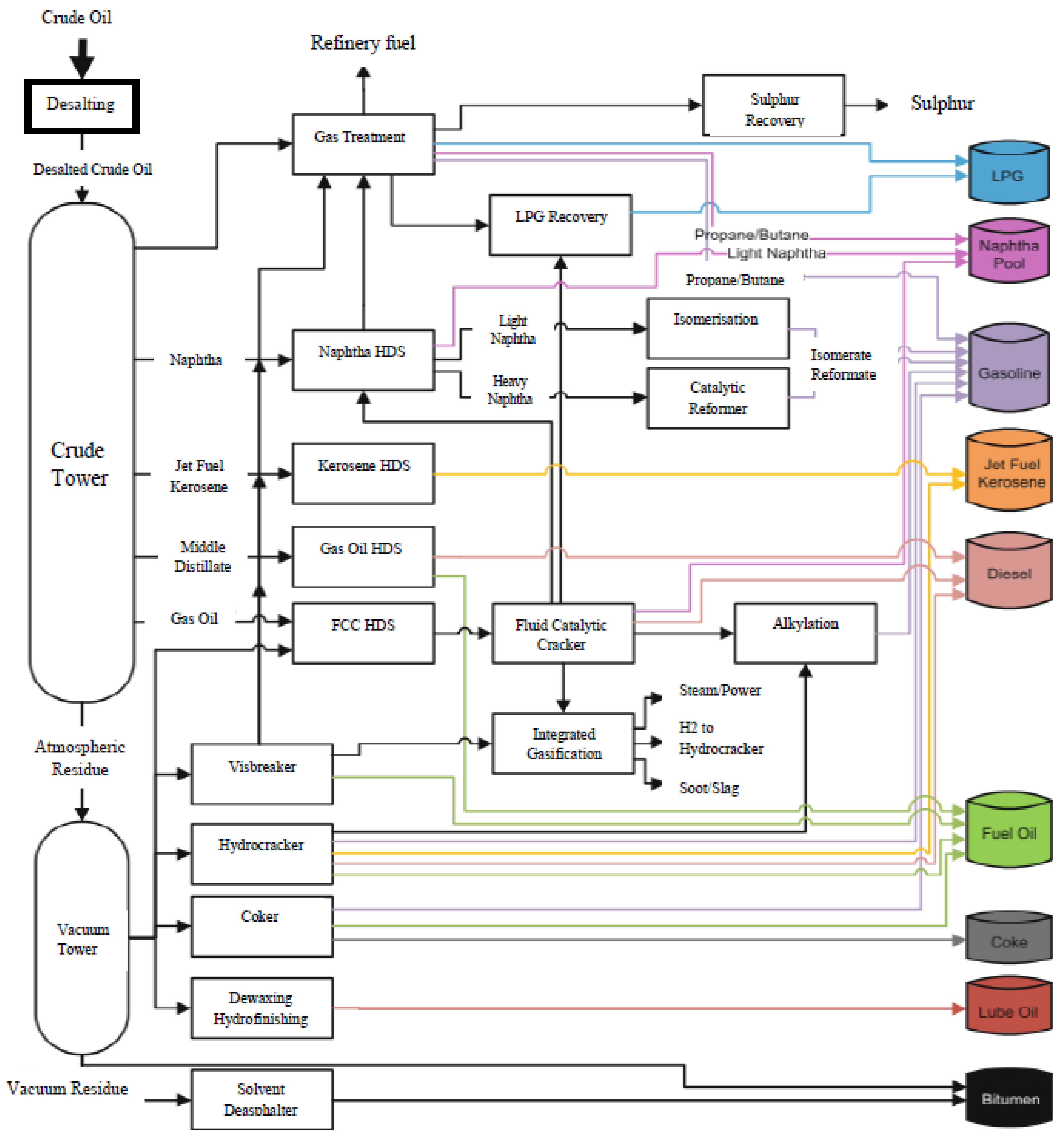
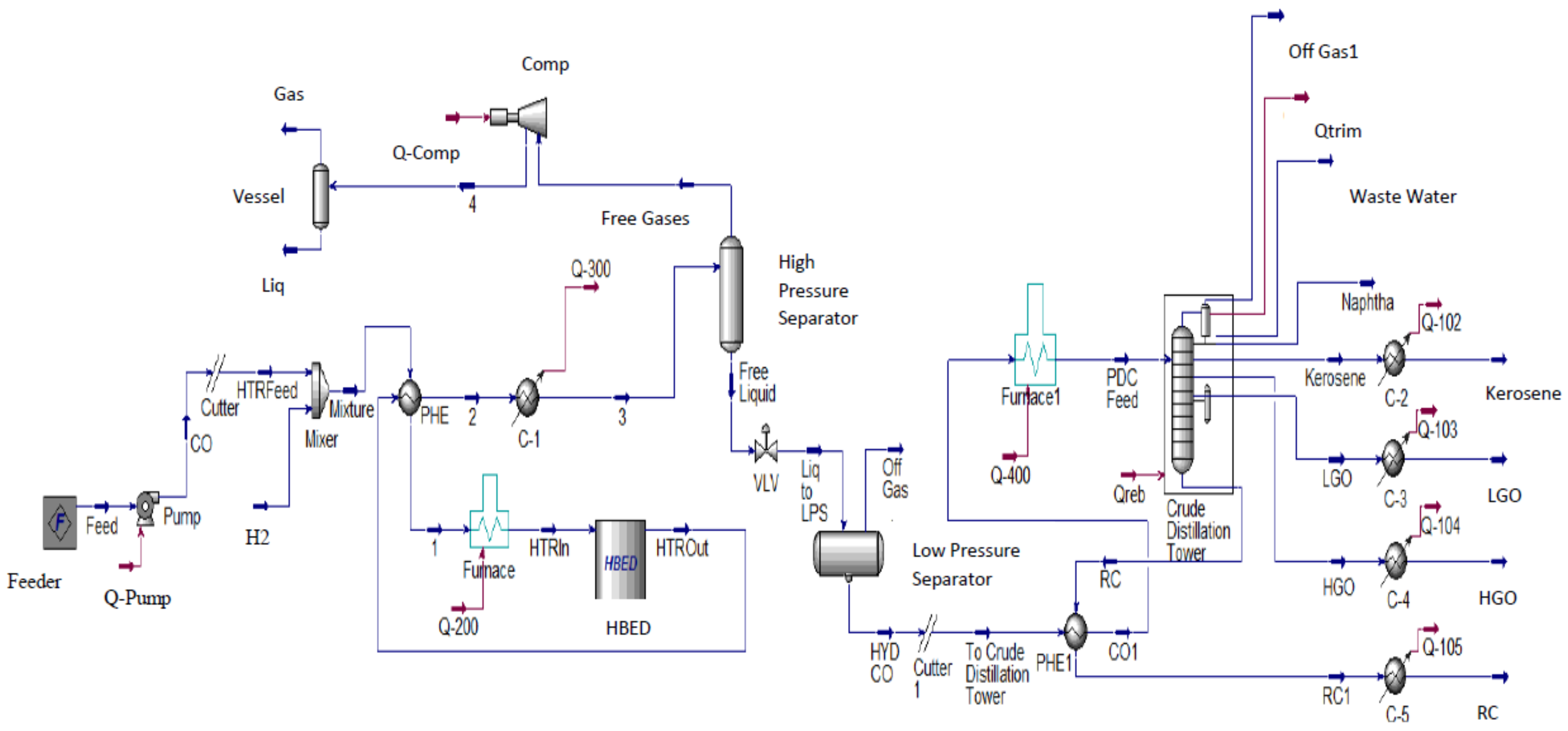
2.1. Process Description
2.2. Feed and Products Specifications
3. Modelling of the Crude Oil HDT Process with CDU Using Bootstrap Aggregated Neural Networks
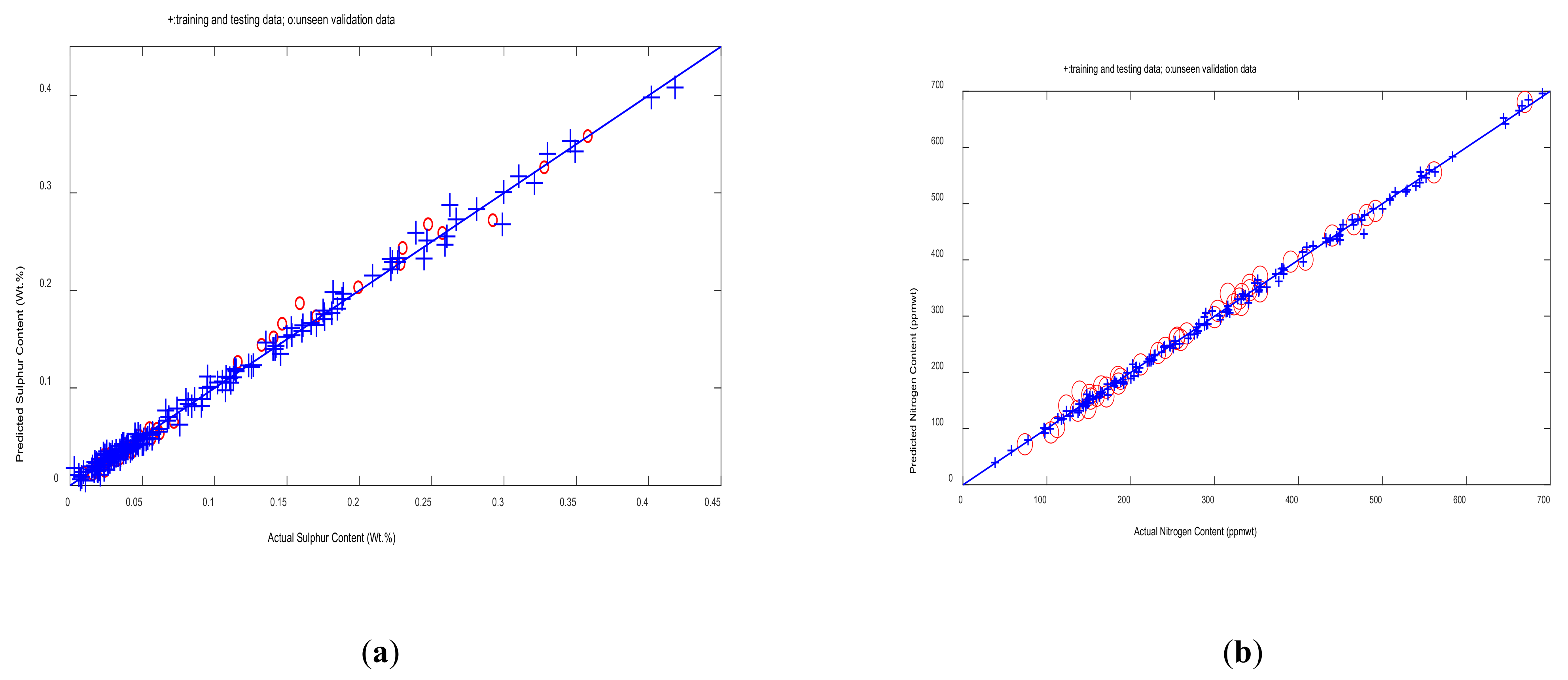
3.1. Single Neural Network Models
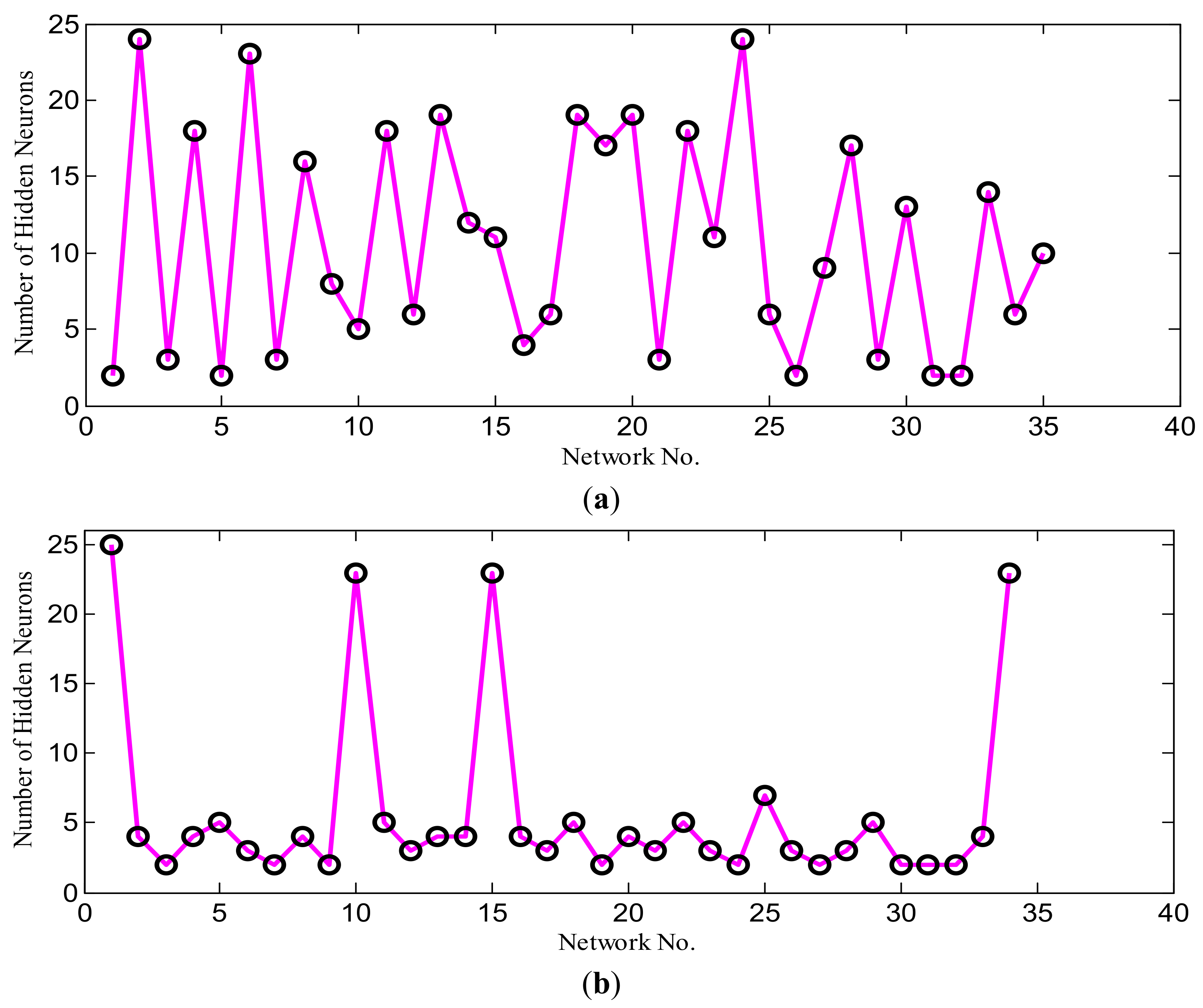
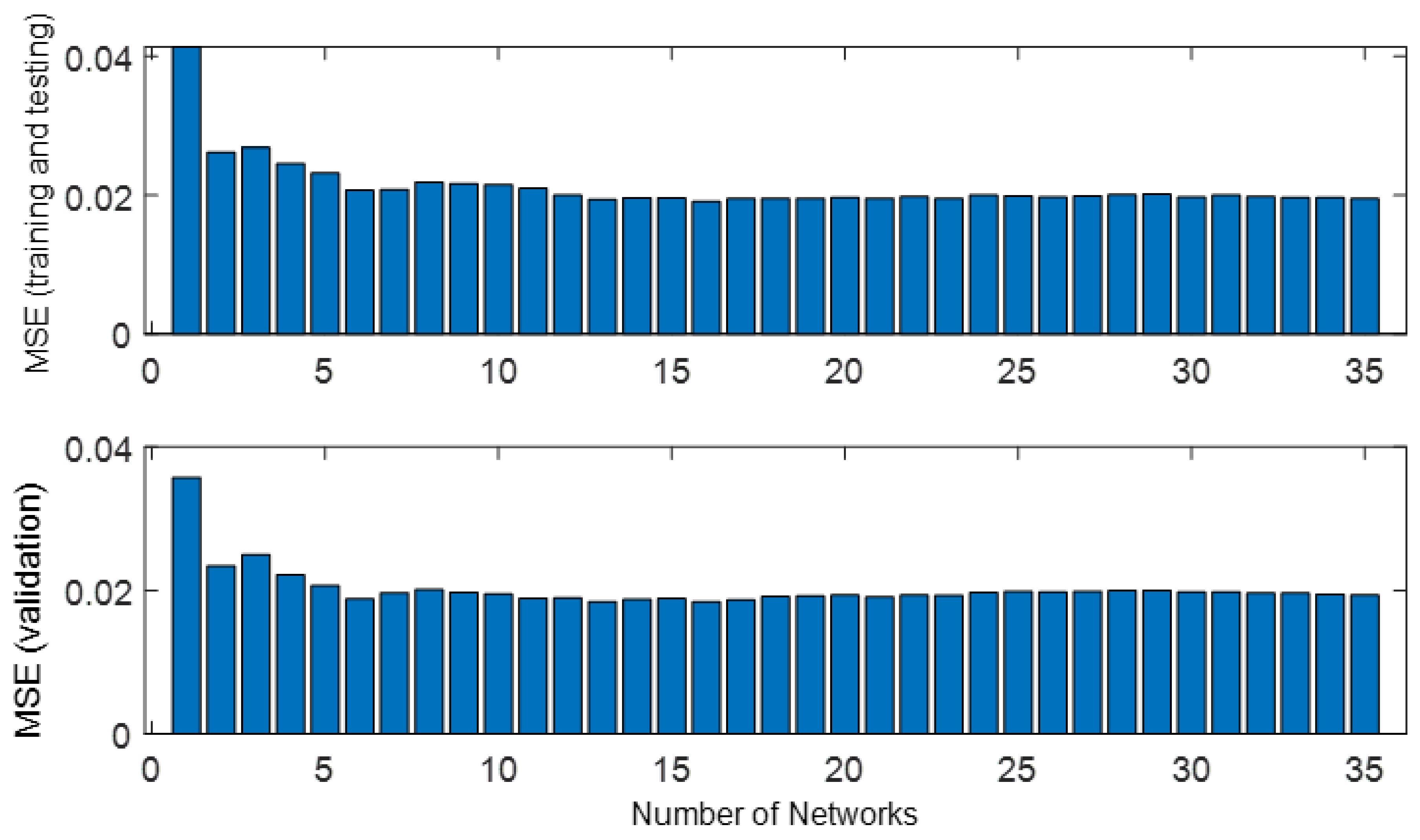
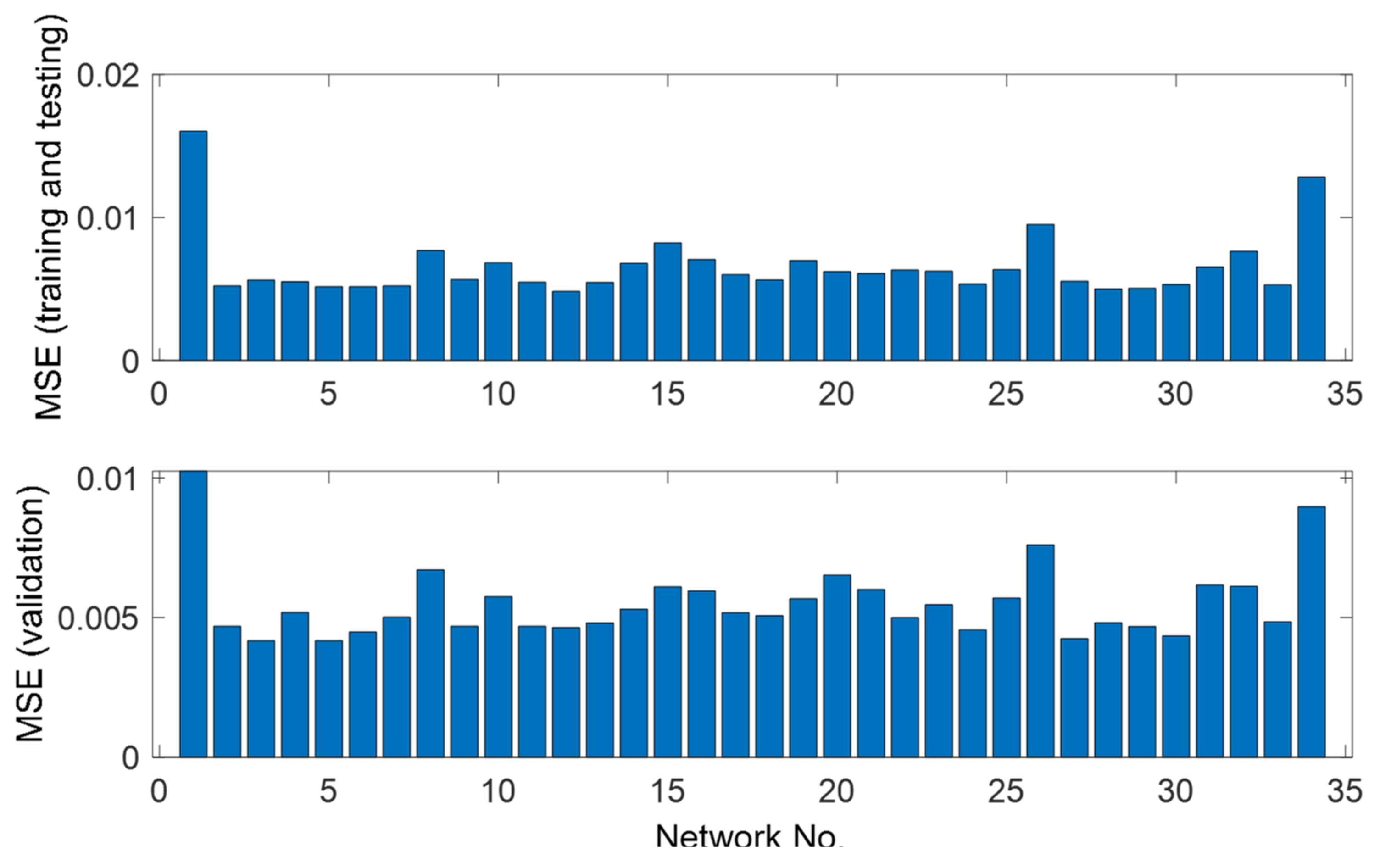
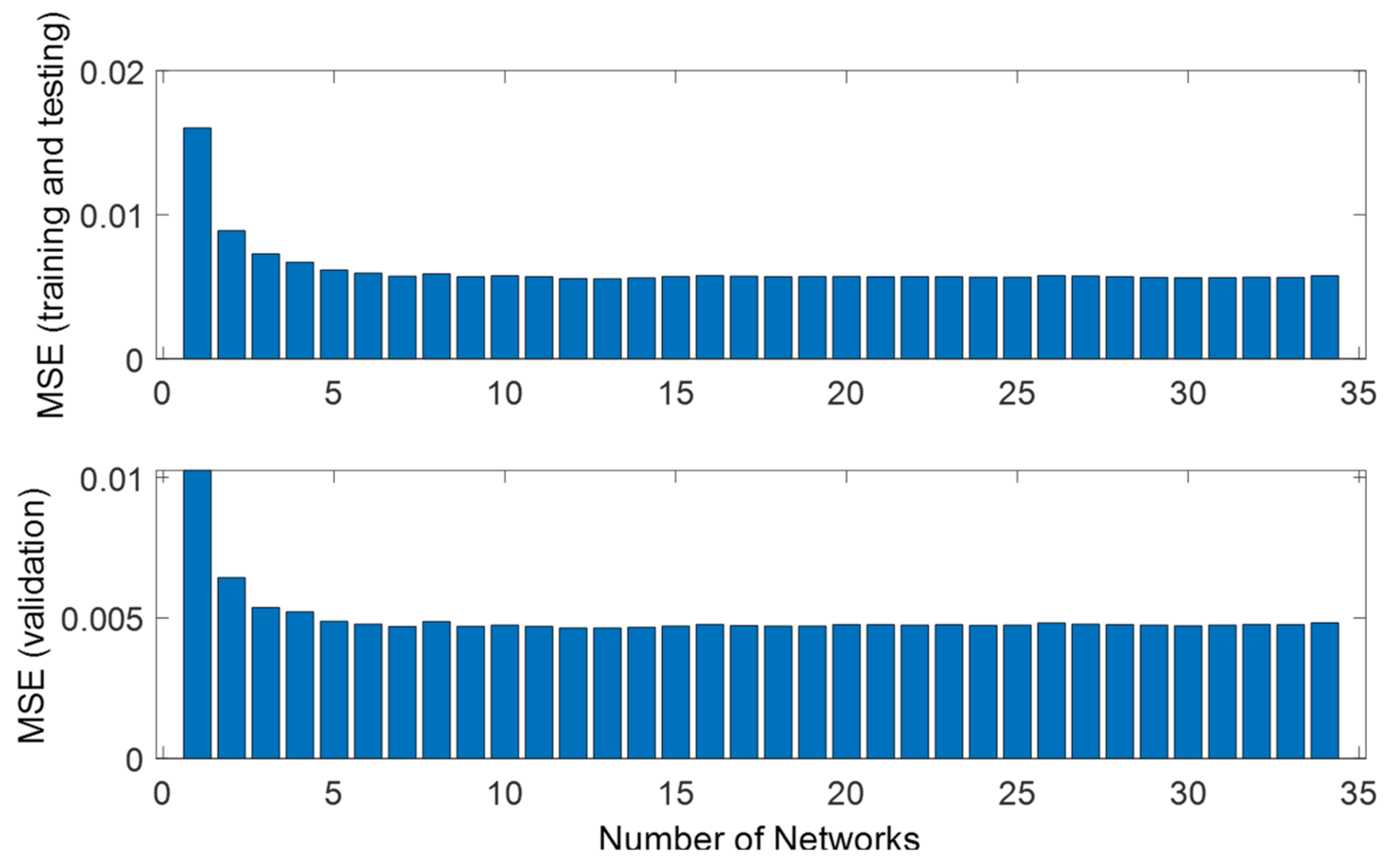
3.2. Bootstrap Aggregated Neural Networks
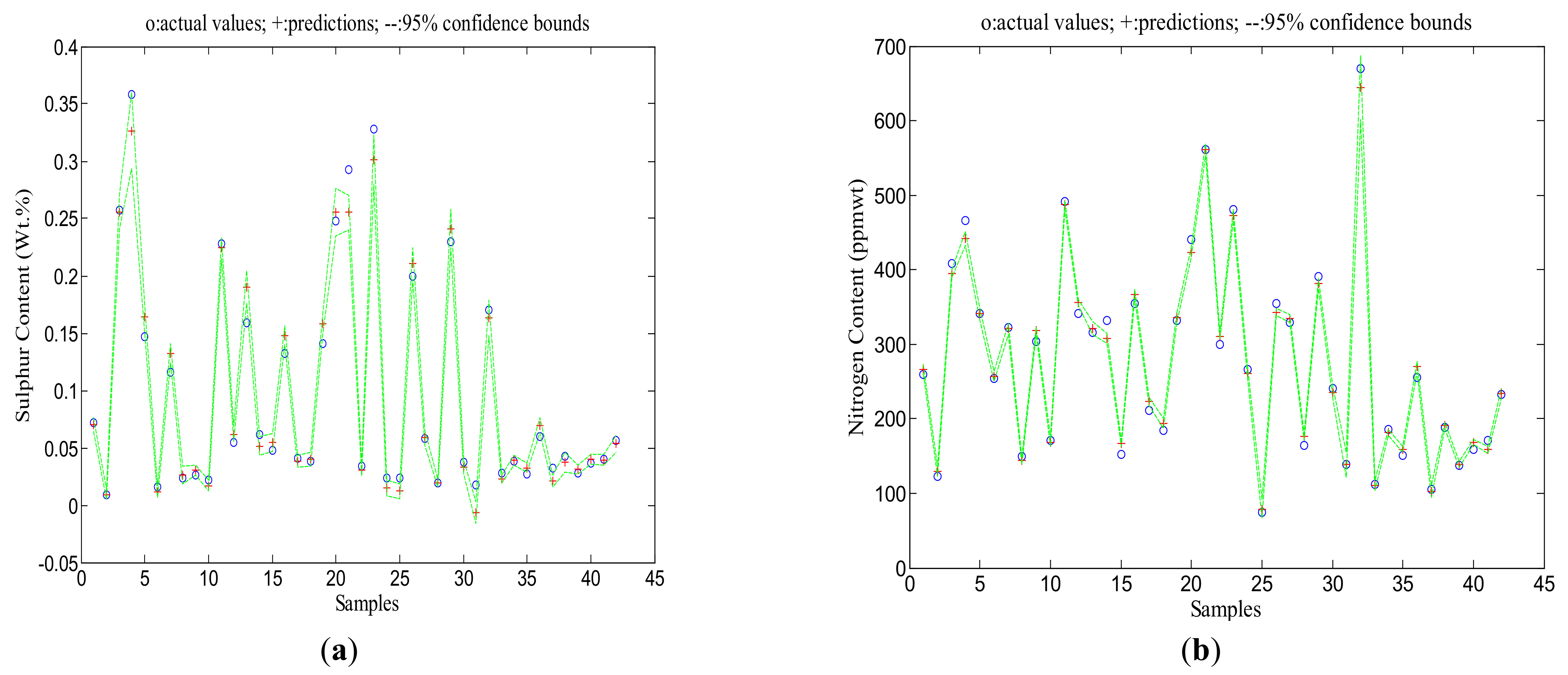
3.3. Neural Network Model Prediction Confidence Bounds
4. Multi-Objective Optimization of the Process Using the Goal-Attainment Technique
4.1. Goal-Attainment Method
4.2. Reliable Multi-Objective Optimization through Incorporating Model Prediction Confidence Bounds
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Speight, J.G. The Chemistry and Technology of Petroleum, 5th ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gary, J.H.; Kaiser, M.J. Petroleum Refining: Technology and Economics, 5th ed.; Taylor & Francis: Boca Raton, FL, USA, 2007. [Google Scholar]
- Orszulik, S.T. Environmental Technology in the Oil Industry, 3rd ed.; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Muhsin, W.A.S.; Zhang, J.; Lee, J. Modelling and optimisation of a crude oil hydrotreating process using neural networks. Chem. Eng. Trans. 2016, 52, 211–216. [Google Scholar]
- Rodriguez, M.A.; Ancheyta, J. Modeling of hydrodesulfurization (HDS), hydrodenitrogenation (HDN), and the hydrogenation of aromatics (HDA) in a vacuum gas oil hydrotreater. Energy Fuels 2004, 18, 789–794. [Google Scholar] [CrossRef]
- Jarullah, A.T.; Mujtaba, I.M.; Wood, A.S. Kinetic parameter estimation and simulation of trickle-bed reactor for hydrodesulfurization of crude oil. Chem. Eng. Sci. 2011, 66, 859–871. [Google Scholar] [CrossRef]
- Jarullah, A.T.; Mujtaba, I.M.; Wood, A.S. Whole crude oil hydrotreating from small-scale laboratory pilot plant to large-scale trickle-bed reactor: Analysis of operational issues through modeling. Energy Fuels 2012, 26, 629–641. [Google Scholar] [CrossRef]
- Muhsin, W.; Zhang, J. Modelling and optimal operation of a crude oil hydrotreating process with atmospheric distillation unit utilising stacked neural networks. In Computer Aided Chemical Engineering; Antonio Espuña, M.G., Luis, P., Eds.; Elsevier: Amsterdam, The Netherlands, 2017; pp. 2479–2484. [Google Scholar]
- Ancheyta, J. Modeling of Processes and Reactors for Upgrading of Heavy Petroleum; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Shang, C.; Yang, F.; Huang, D.; Lyu, W. Data-driven soft sensor development based on deep learning technique. J. Process Control 2014, 24, 223–233. [Google Scholar] [CrossRef]
- Chang, H.; Su, Z.; Lu, S.; Zhang, G. Application of deep learning network in bumper warpage quality improvement. Processes 2022, 10, 1006. [Google Scholar] [CrossRef]
- Li, F.; Zhang, J.; Shang, C.; Huang, D.; Oko, E.; Wang, M. Modelling of a post-combustion CO2 capture process using deep belief network. Appl. Therm. Eng. 2018, 130, 997–1003. [Google Scholar] [CrossRef] [Green Version]
- Zhu, C.; Zhang, J. Developing soft sensors for polymer melt index in an industrial polymerization process using deep belief networks. Int. J. Autom. Comput. 2020, 17, 44–54. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Huang, P.; Zhou, J.; Li, M. An enhanced stacking ensemble method for granule moisture prediction in fluidized bed granulation. Processes 2022, 10, 725. [Google Scholar] [CrossRef]
- Ibrahim, D.; Jobson, M.; Li, J.; Guillén-Gosálbez, G. Optimization-based design of crude oil distillation units using surrogate column models and a support vector machine. Chem. Eng. Res. Des. 2018, 134, 212–225. [Google Scholar] [CrossRef] [Green Version]
- Brambilla, A.; Vaccari, M.; Pannocchia, G. Analytical RTO for a critical distillation process based on offline rigorous simulation. In Proceedings of the 13th IFAC Symposium on Dynamics and Control of Process Systems, Including Biosystems (DYCOPS), Busan, Korea, 14–17 June 2022. [Google Scholar]
- Aspen Technology. Assay Management in Aspen HYSYS®Petroleum Refining; Aspen Technology: Houston, TX, USA, 2015. [Google Scholar]
- Aspen Technology. Kirkuk Crude Oil Assay; Assay Library: Houston, TX, USA, 2011. [Google Scholar]
- Fahim, M.A.; Alsahhaf, T.A.; Elkilani, A. Refinery feedstocks and products. In Fundamentals of Petroleum Refining; Elsevier: Amsterdam, The Netherlands, 2010; pp. 11–31. [Google Scholar]
- Thrampoulidis, E.; Mavromatidis, G.; Lucchi, A.; Orehounig, K. A machine learning-based surrogate model to approximate optimal building retrofit solutions. Appl. Energy 2021, 281, 116024. [Google Scholar] [CrossRef]
- Vaccari, M.; Pannocchia, G.; Tognotti, L.; Paci, M.; Bonciani, R. A rigorous simulation model of geothermal power plants for emission control. Appl. Energy 2020, 263, 114563. [Google Scholar] [CrossRef]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Herrera, F.; Zhang, J. Optimal control of batch processes using particle swam optimisation with stacked neural network models. Comput. Chem. Eng. 2009, 33, 1593–1601. [Google Scholar] [CrossRef]
- Bishop, C. Improving the generalization properties of radial basis function neural networks. Neural Comput. 1991, 3, 579–588. [Google Scholar] [CrossRef] [PubMed]
- MacKay, D.J.C. Bayesian interpolation. Neural Comput. 1992, 4, 415–447. [Google Scholar] [CrossRef]
- Wolpert, D.H. Stacked generalization. Neural Netw. 1992, 5, 241–259. [Google Scholar] [CrossRef]
- Sridhar, D.V.; Seagrave, R.C.; Bartlett, E.B. Process modeling using stacked neural networks. AIChE J. 1996, 42, 2529–2539. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Martin, E.B.; Morris, A.J.; Kiparissides, C. Inferential estimation of polymer quality using stacked neural networks. Comput. Chem. Eng. 1997, 21, S1025–S1030. [Google Scholar] [CrossRef]
- Zhang, J. Batch-to-batch optimal control of a batch polymerisation process based on stacked neural network models. Chem. Eng. Sci. 2008, 63, 1273–1281. [Google Scholar] [CrossRef]
- Khaouane, L.; Ammi, Y.; Hanini, S. Modeling the retention of organic compounds by nanofiltration and reverse osmosis membranes using bootstrap aggregated neural networks. Arab. J. Sci. Eng. 2017, 42, 1443–1453. [Google Scholar] [CrossRef]
- Zhang, J. Developing robust non-linear models through bootstrap aggregated neural networks. Neurocomputing 1999, 25, 93–113. [Google Scholar] [CrossRef]
- Li, F.; Zhang, J.; Oko, E.; Wang, M. Modelling of a post-combustion CO2 capture process using extreme learning machine. Int. J. Coal Sci. Technol. 2017, 4, 33–40. [Google Scholar] [CrossRef] [Green Version]
- Koziel, S.; Bekasiewicz, A. Multi-Objective Design of Antennas Using Surrogate Models; World Scientific: Singapore, 2016. [Google Scholar]
- Vaccari, M.; Capaci, R.B.; Brunazzi, E.; Tognotti, L.; Pierno, P.; Vagheggi, R.; Pannocchia, G. Optimally Managing Chemical Plant Operations: An Example Oriented by Industry 4.0 Paradigms. Ind. Eng. Chem. Res. 2021, 60, 7853–7867. [Google Scholar] [CrossRef]
- Miettinen, K. Nonlinear Multiobjective Optimization; Kluwer Academic Publishers: Boston, MA, USA, 1998. [Google Scholar]
- Haimes, Y.Y.; Hall, W.A.; Freedman, H.T. Multiobjective Optimization in Water Resources Systems: The Surrogate Worth Trade-off Method; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Osuolale, F.N.; Zhang, J. Multi-objective optimisation of atmospheric crude distillation system operations based on bootstrap aggregated neural network models. Comput. Aided Chem. Eng. 2015, 37, 671–676. [Google Scholar]





| Hydrotreating Process | T (°C) | PH2 (MPa) | LHSV (h−1) | H2/Oil (Nm3/m3) |
|---|---|---|---|---|
| Naphtha | 320 | 1–2 | 3–8 | 60 |
| Kerosene | 330 | 2–3 | 2–5 | 80 |
| Gasoil | 340 | 2.5–4 | 1.5–4 | 140 |
| VGO | 360 | 5–9 | 1–2 | 210 |
| Atmospheric Residue | 370–410 | 8–13 | 0.2–0.5 | ˃525 |
| Hydrocracking VGO | 380–430 | 9–20 | 0.5–1.5 | 1000–2000 |
| Vacuum Residue | 400–440 | 12–21 | 0.1–0.5 | 1000–2000 |
| No. | Property | Bulk Value |
|---|---|---|
| 1 | Sulphur By (Wt.%) | 2.63 |
| 2 | Std Liquid Density (kg/m3) | 867.5162 |
| 3 | Watson K | 11.4279 |
| 4 | Pour Point (°C) | 21.8696 |
| 5 | Total Acid Number (mg KOH/g) | 0.171 |
| 6 | Kinematic Viscosity (cSt)@ 20 (°C) | 13.0798 |
| 7 | Kinematic Viscosity (cSt)@ 37.78 (°C) | 7.7831 |
| 8 | Kinematic Viscosity (cSt)@ 37.78 (°C) | 7.7831 |
| 9 | Kinematic Viscosity (cSt)@ 50 (°C) | 5.697 |
| 10 | Kinematic Viscosity (cSt)@ 60 (°C) | 4.5238 |
| 11 | Kinematic Viscosity (cSt)@ 80 (°C) | 2.9883 |
| 12 | Kinematic Viscosity (cSt)@ 100 (°C) | 2.0967 |
| 13 | NaCl By (Wt.%) | 0.002 |
| 14 | Mercaptan Sulphur By (Wt.%) | 0.0217 |
| 15 | Conradson Carbon By (Wt.%) | 6.0699 |
| 16 | Asphaltene By (Wt.%) | 2.3412 |
| 17 | Nickel By (Wt.%) | 0.0008 |
| 18 | Vanadium By (Wt.%) | 0.0037 |
| 19 | Iron By (Wt.%) | 0.0001 |
| 20 | Gross Heating Value (kJ/kg) | 44,157.58 |
| 21 | Net Heating Value (kJ/kg) | 41,482.25 |
| 22 | Cut Yield By (Wt.%) | 100 |
| 23 | Cut Yield By (Vol.%) | 100 |
| 24 | Nitrogen By (Wt.%) | 0.1113 |
| 25 | Paraffins By (Vol.%) | 30.5540 |
| 26 | Naphthenes By (Vol.%) | 40.8213 |
| 27 | Arom By (Vol.%) | 28.6245 |
| 28 | N + 2A (%) | 98.0705 |
| 29 | Smoke Pt (m) | 0.0156 |
| 30 | Freeze Point (°C) | 79.3312 |
| 31 | Basic Nitrogen By (Wt.%) | 0.0378 |
| 32 | Cloud Point (°C) | 38.6010 |
| 33 | CtoH Ratio By Wt | 6.6651 |
| Cut Oils | Yield (Wt.%) | Specific Gravity at 15 °C | Flash Point (°C) | Color | TBP (°C) |
|---|---|---|---|---|---|
| Fuel gases | 0.01 | – | – | – | – |
| LPG | 0.12 | – | – | – | – |
| LN | 8.98 | 0.665–0.680 | – | – | 35–120 |
| HN | 12.40 | 0.735–0.750 | – | – | 90–178 |
| Ker | 10.80 | 0.785–0.800 | 40 min. | 30 min. | 135–250 |
| LGO | 17.70 | 0.825–0.840 | 70 min. | 0.5 max. | 200–350 |
| HGO | 3.68 | 0.880–0.890 | 90 min. | 2.5 max. | 335–355 |
| RC | 46.31 | 0.965–0.980 | 120 min. | – | 355+ |
| Petroleum Products | Carbon Range |
|---|---|
| Fuel gases | C1–C2 |
| LPG | C3–C4 |
| LN and HN | C5–C12 |
| Ker | C12–C16 |
| LGO and HGO | C12–C20 |
| Lubricating oil | C20–C50 |
| RC | >C50 |
| Variables | Units | Lower Bounds | Upper Bounds |
|---|---|---|---|
| crude oil flow rate | m3/h | 40 | 70 |
| hydrogen flow rate | kgmole/h | 700 | 1000 |
| reactor pressure | bar | 70 | 130 |
| reactor temperature | °C | 330 | 380 |
| Case | Goals | Cb(S) | Cb(N) | W | x | Stacked Network | HYSYS | Absolute Error |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.0177 | 0.0149 | S: 0.0329 N: 140.0000 | S: 0.0300 N: 143.0000 | 0.0029 3.0000 | |||
| 2 | 0.0168 | 0.0171 | S: 0.0292 N: 130.0000 | S: 0.0300 N: 134.5000 | 0.0008 4.5000 |
| Run | Goals | W | x | Stacked Network | HYSYS | Absolute Error |
|---|---|---|---|---|---|---|
| 1 | S: 0.0294 N: 132.6498 Cb(S): 0.0165 Cb(N): 0.0165 | S: 0.0300 N: 137.7000 | 0.0006 5.0502 | |||
| 2 | S: 0.0294 N: 132.6510 Cb(S): 0.0165 Cb(N): 0.0165 | S: 0.0300 N: 137.7000 | 0.0006 5.0490 | |||
| 3 | S: 0.0322 N: 139.5789 Cb(S): 0.0139 Cb(N): 0.0139 | S: 0.0300 N: 132.6000 | 0.0022 6.9789 |
| Run | Goals | W | x | Stacked Network | HYSYS | Absolute Error |
|---|---|---|---|---|---|---|
| 1 | S: 0.0294 N: 132.0352 Cb(S): 0.0170 Cb(N): 0.0170 | S: 0.0300 N: 134.1000 | 0.0006 4.0648 | |||
| 2 | S: 0.0294 N: 130.0704 Cb(S): 0.0170 Cb(N): 0.0170 | S: 0.0300 N: 137.7000 | 0.0006 4.0296 | |||
| 3 | S: 0.0304 N: 130.6100 Cb(S): 0.0160 Cb(N): 0.0160 | S: 0.0300 N: 127.0000 | 0.0004 3.6100 |
| Cases | Feed (m3/h) | H2 Molar Flow (kgmole/h) | Pressure (bar) | Temperature (°C) | S Removal (Wt.%) | N Removal (Wt.%) |
|---|---|---|---|---|---|---|
| Base | 55.00 | 800.00 | 90.00 | 375.00 | 85.32 | 88.08 |
| Optimum 1 | 69.65 | 865.01 | 120.78 | 376.42 | 88.63 | 88.18 |
| Optimum 2 | 69.99 | 836.62 | 122.27 | 378.00 | 88.64 | 88.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Muhsin, W.; Zhang, J. Multi-Objective Optimization of a Crude Oil Hydrotreating Process with a Crude Distillation Unit Based on Bootstrap Aggregated Neural Network Models. Processes 2022, 10, 1438. https://doi.org/10.3390/pr10081438
Muhsin W, Zhang J. Multi-Objective Optimization of a Crude Oil Hydrotreating Process with a Crude Distillation Unit Based on Bootstrap Aggregated Neural Network Models. Processes. 2022; 10(8):1438. https://doi.org/10.3390/pr10081438
Chicago/Turabian StyleMuhsin, Wissam, and Jie Zhang. 2022. "Multi-Objective Optimization of a Crude Oil Hydrotreating Process with a Crude Distillation Unit Based on Bootstrap Aggregated Neural Network Models" Processes 10, no. 8: 1438. https://doi.org/10.3390/pr10081438
APA StyleMuhsin, W., & Zhang, J. (2022). Multi-Objective Optimization of a Crude Oil Hydrotreating Process with a Crude Distillation Unit Based on Bootstrap Aggregated Neural Network Models. Processes, 10(8), 1438. https://doi.org/10.3390/pr10081438







