Multiphysics Numerical Simulation Model and Hydraulic Model Experiments in the Argon-Stirred Ladle
Abstract
:1. Introduction
2. Experimental Methods
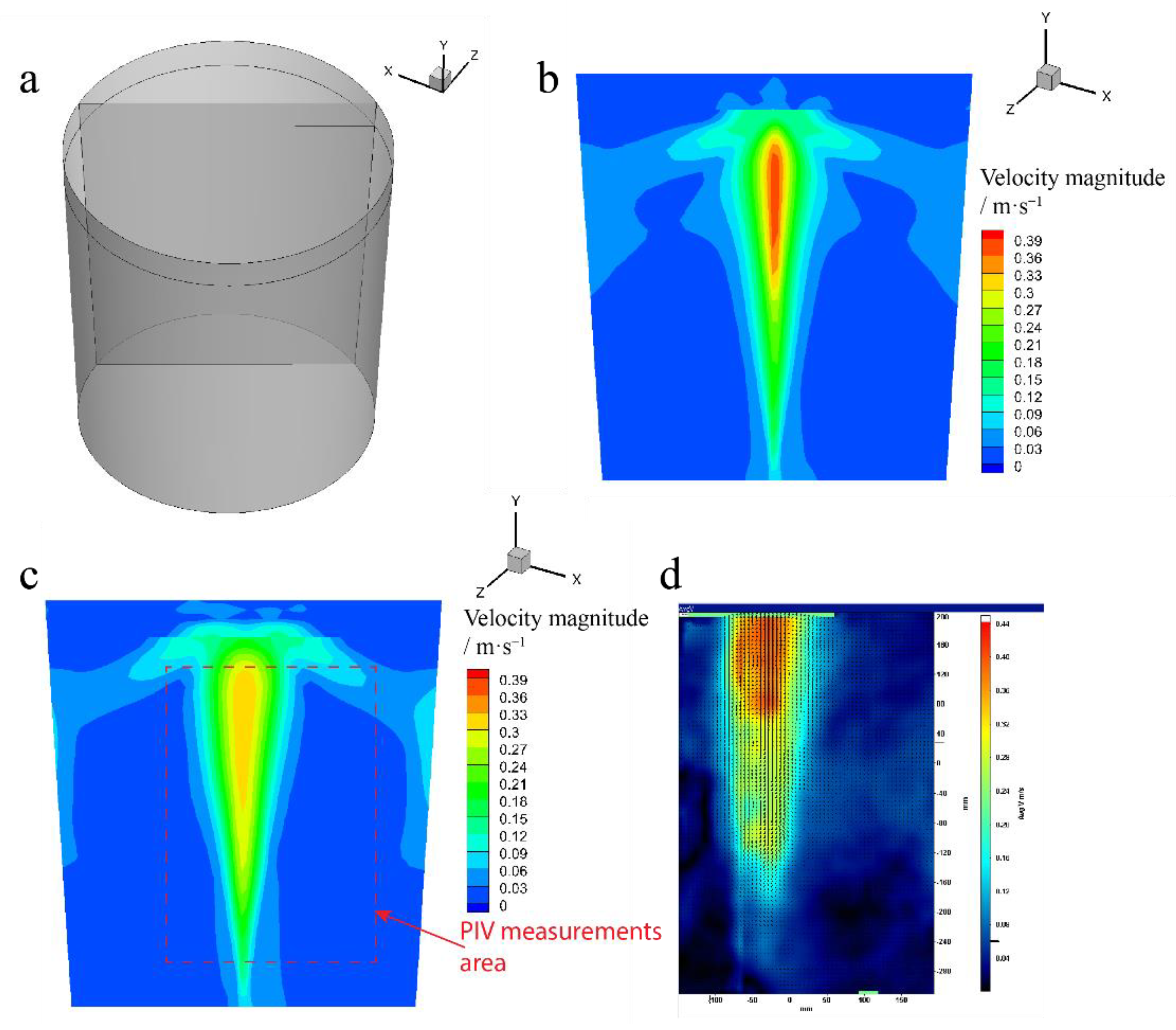
2.1. The measurement of the Fluid Flow in the Ladle Water Model
2.2. Numerical Simulation Models
2.2.1. Fluid Flow and VOF Model
2.2.2. Bubble and Alloy Transport Model
2.2.3. Energy Conservation and Bubble Heat Exchange Model
2.2.4. Alloy Melting and Alloy Concentration Diffusion Model
2.3. Boundary Condition and Solution Strategy
3. Results and Discussion
3.1. Model Validation
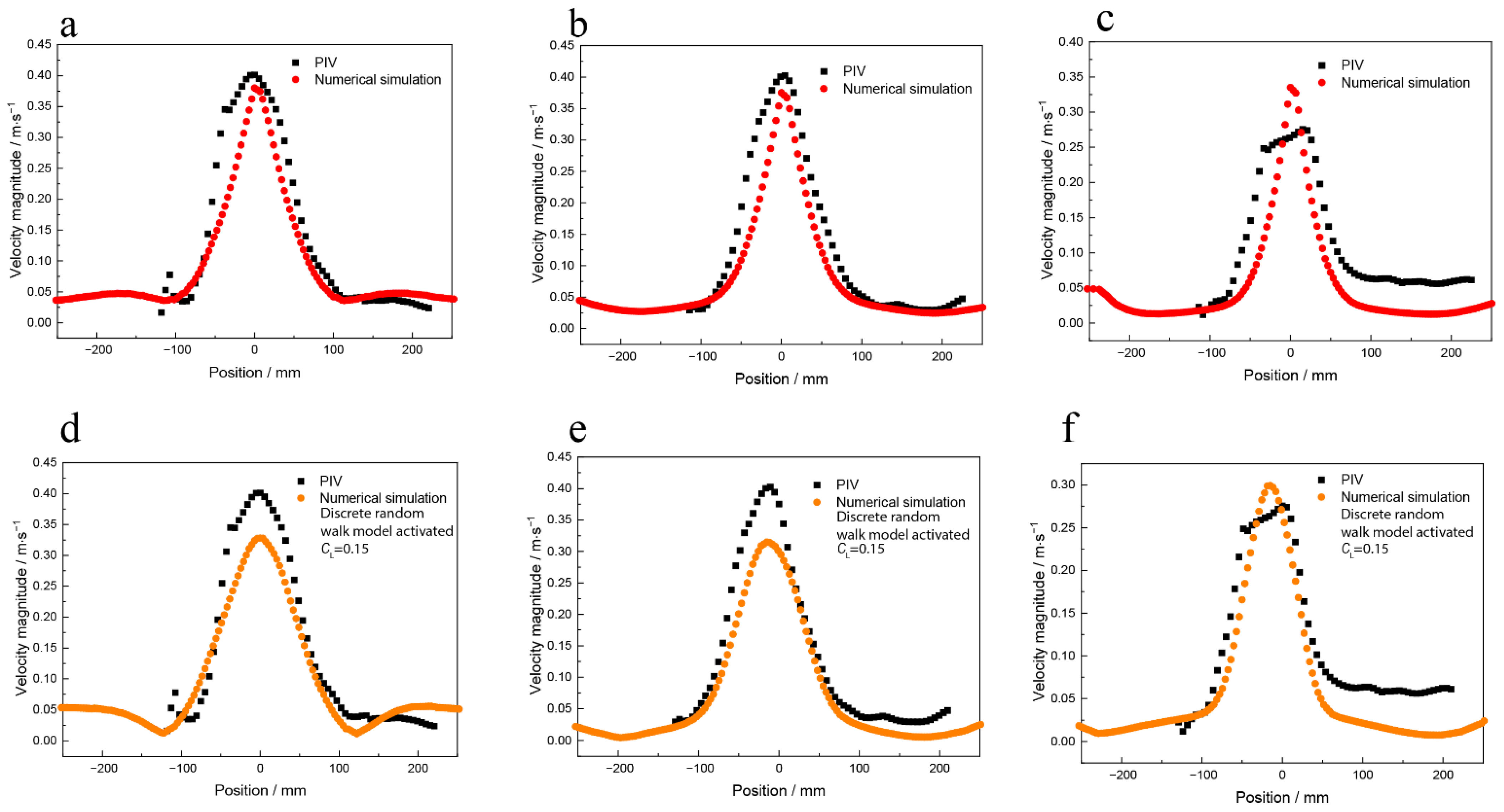
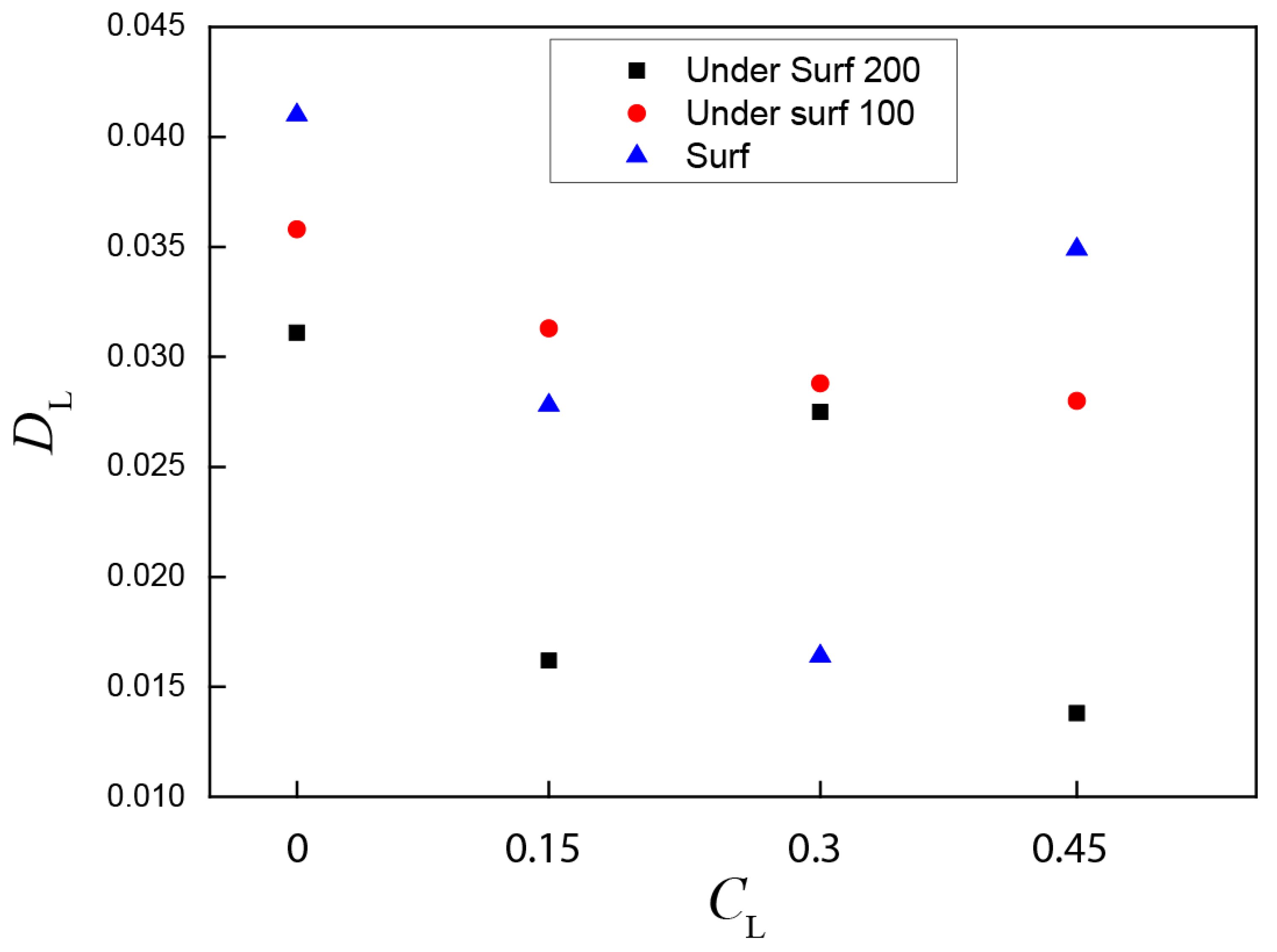
3.1.1. Effect of Discrete Random walk Model on the Simulation Results
3.1.2. Effect of Time Scale Factor on the Simulation Results
3.2. Model Application of the Prototype Argon-Stirred Ladle
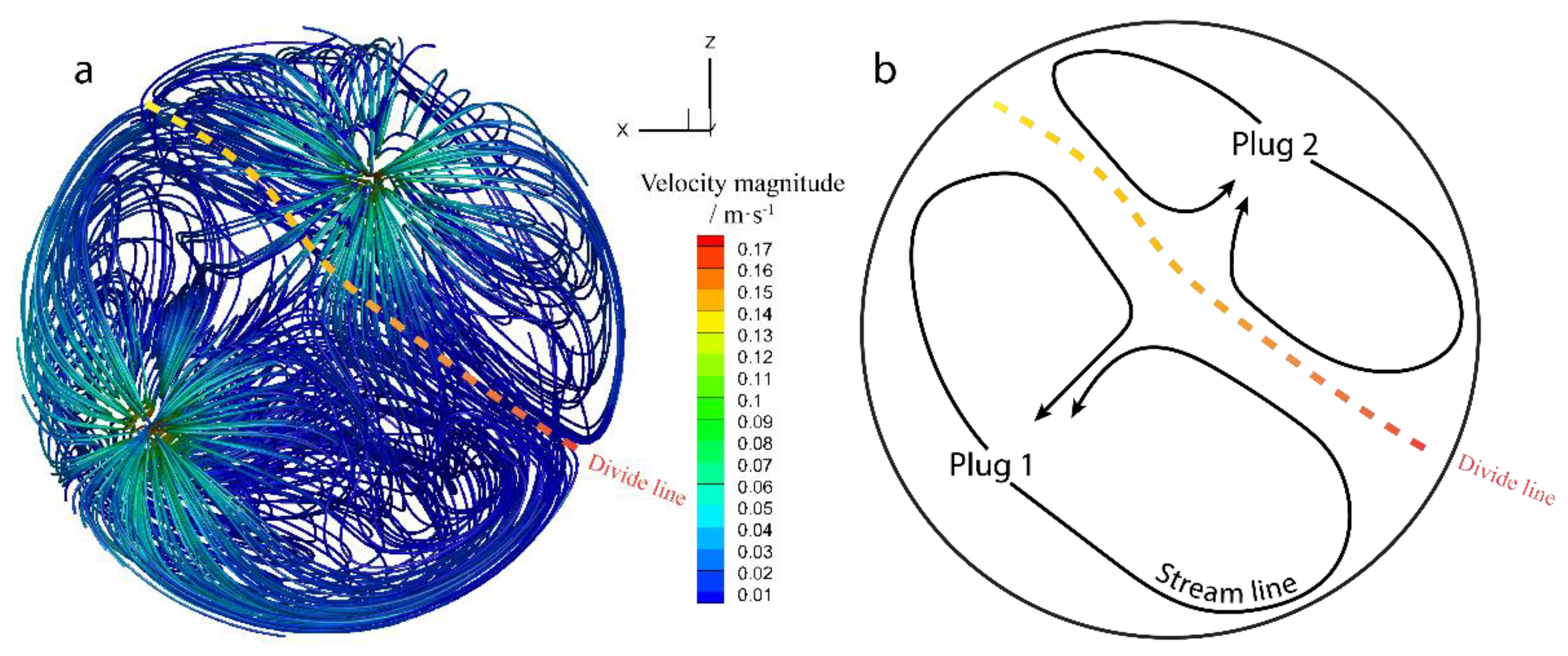
3.2.1. The Fluid Flows
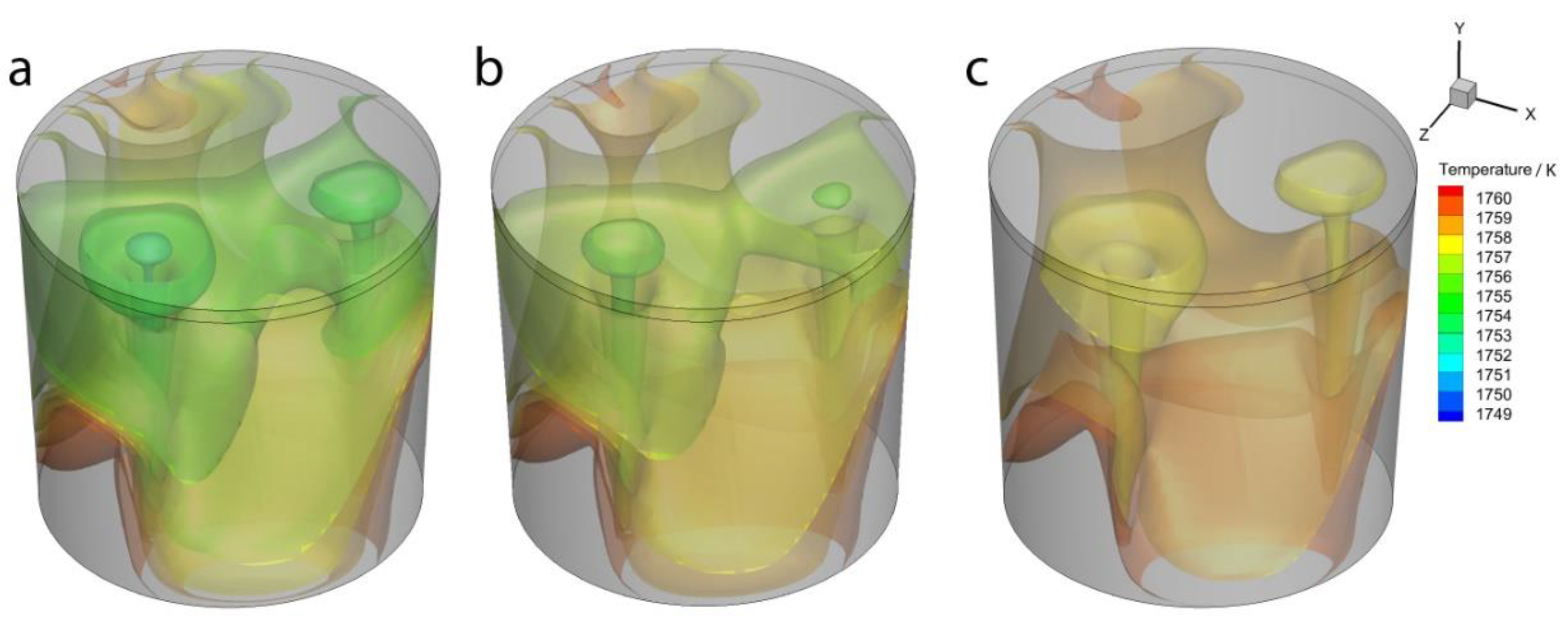
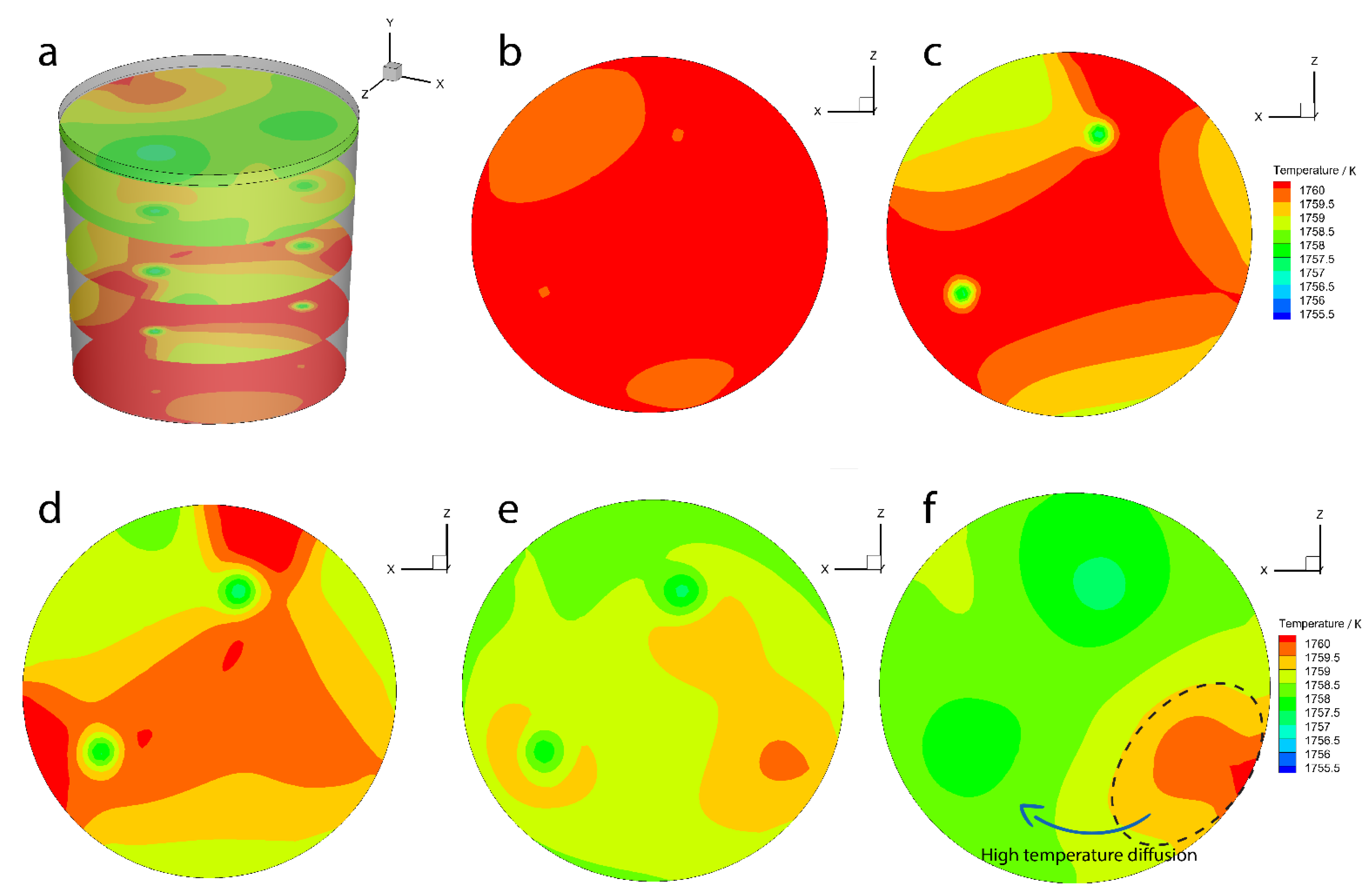
3.2.2. The Temperature Fields
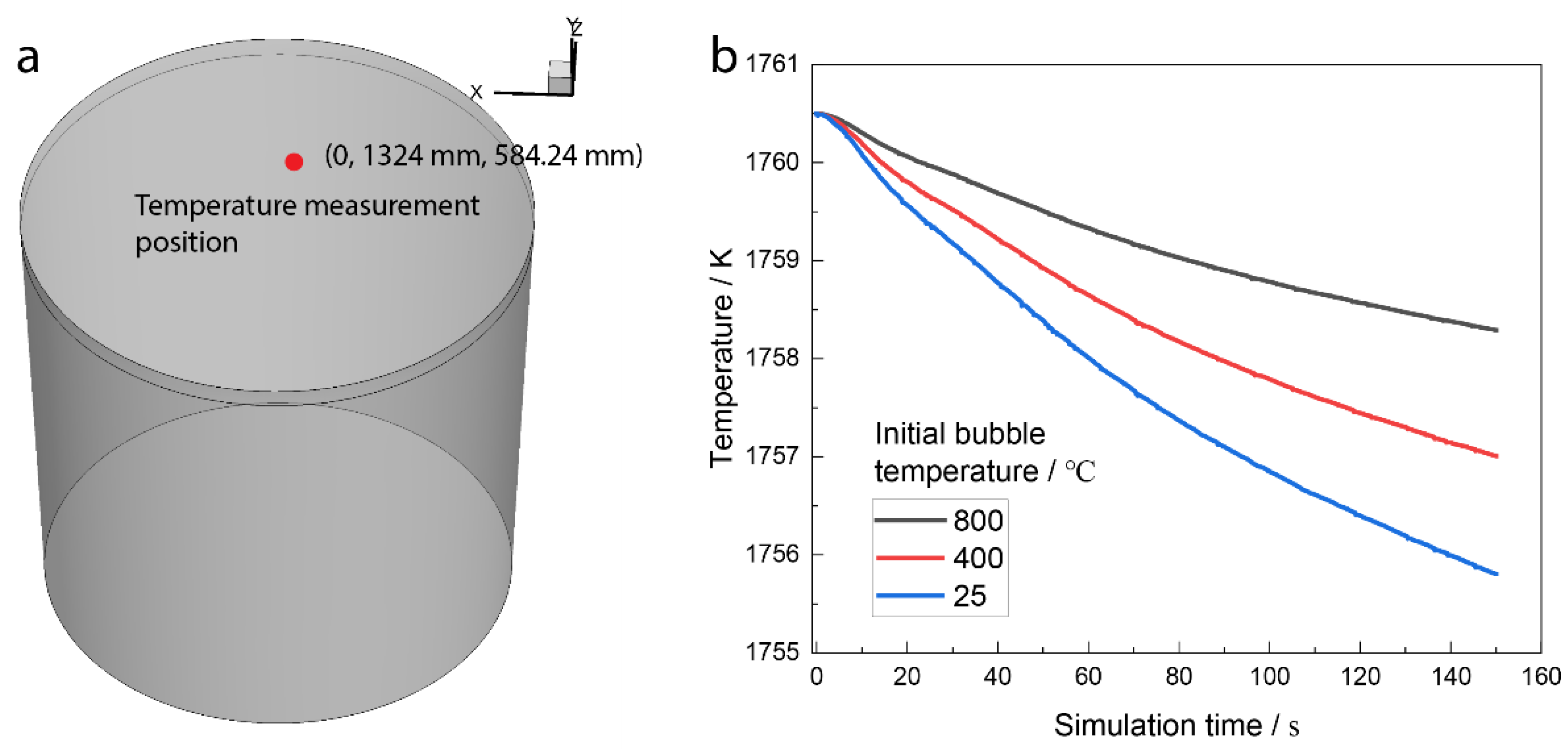
Effect of Initial Bubble Temperature on the Temperature Filed
3.2.3. The Steel–Slag Interface Shape
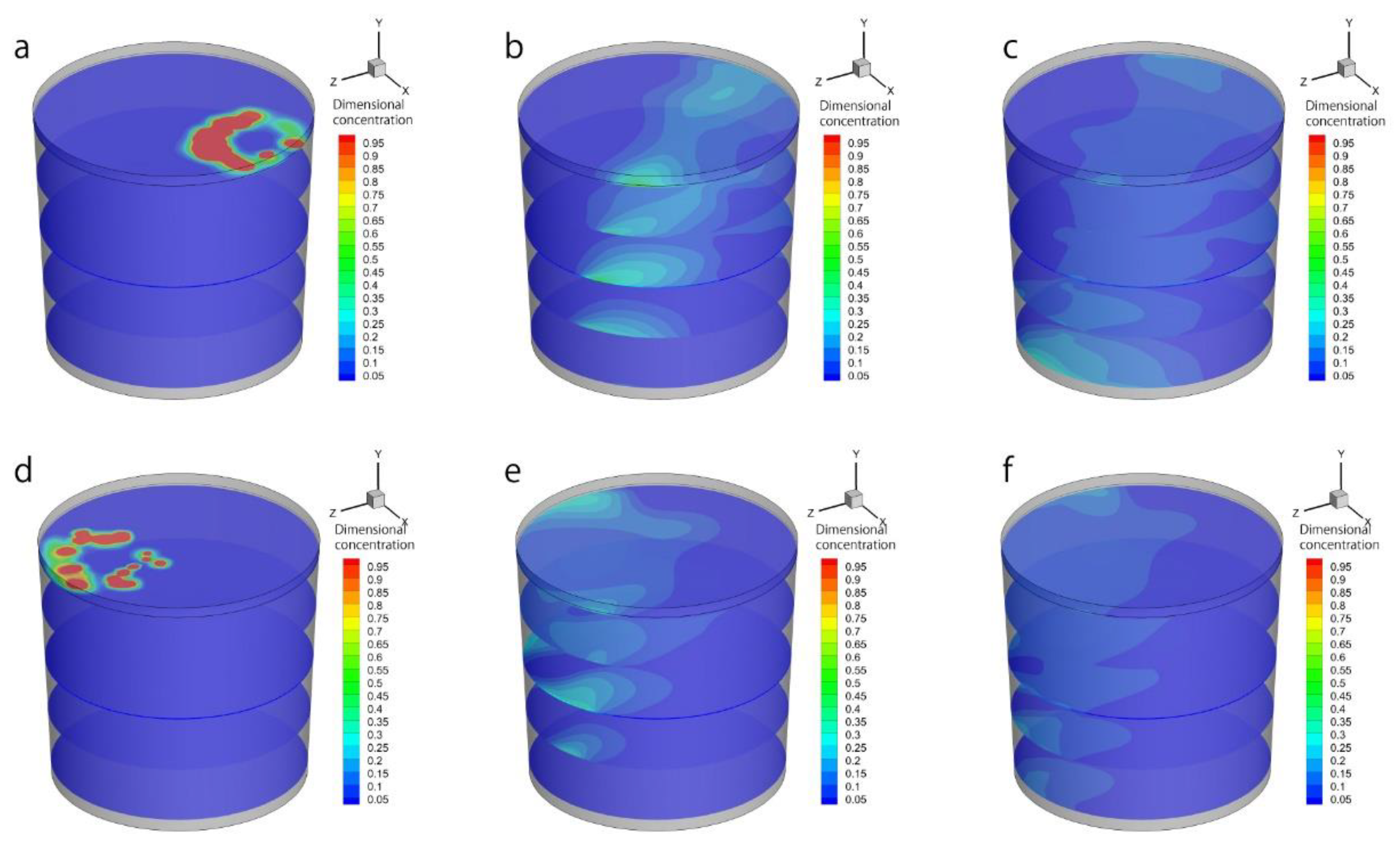
3.2.4. Alloy Melting and Alloy Species Diffusion
4. Conclusions
- (1)
- The random walk model needs to be applied to the bubble transport model. The velocity difference between the numerical simulation and the hydraulic model decreases when the CL decreases from 0 to 0.3 and increases when the CL increases from 0.3 to 0.45. The velocity difference between the numerical simulation and the hydraulic model is minimum when the CL is 0.3.
- (2)
- There are two circulations of fluid flow in the prototype. The velocity is higher in the center of the plume. The velocity is smaller near the steel–slag interface. The maximum velocity is 0.172 m·s−1.
- (3)
- The molten steel temperature will decrease when the argon bubbles are injected into the molten steel from the plugs. The temperature decrease rate will increase when the initial bubble temperature decreases. The temperature decrease rate in industrial practice is 0.0144 K/s. The numerical simulation results of the temperature decrease rate are 0.0147 K/s when the initial bubble temperature is 800 °C.
- (4)
- The steel–slag interface position is higher above the plugs. The maximum height of the steel–slag interface is 7.95 mm.
- (5)
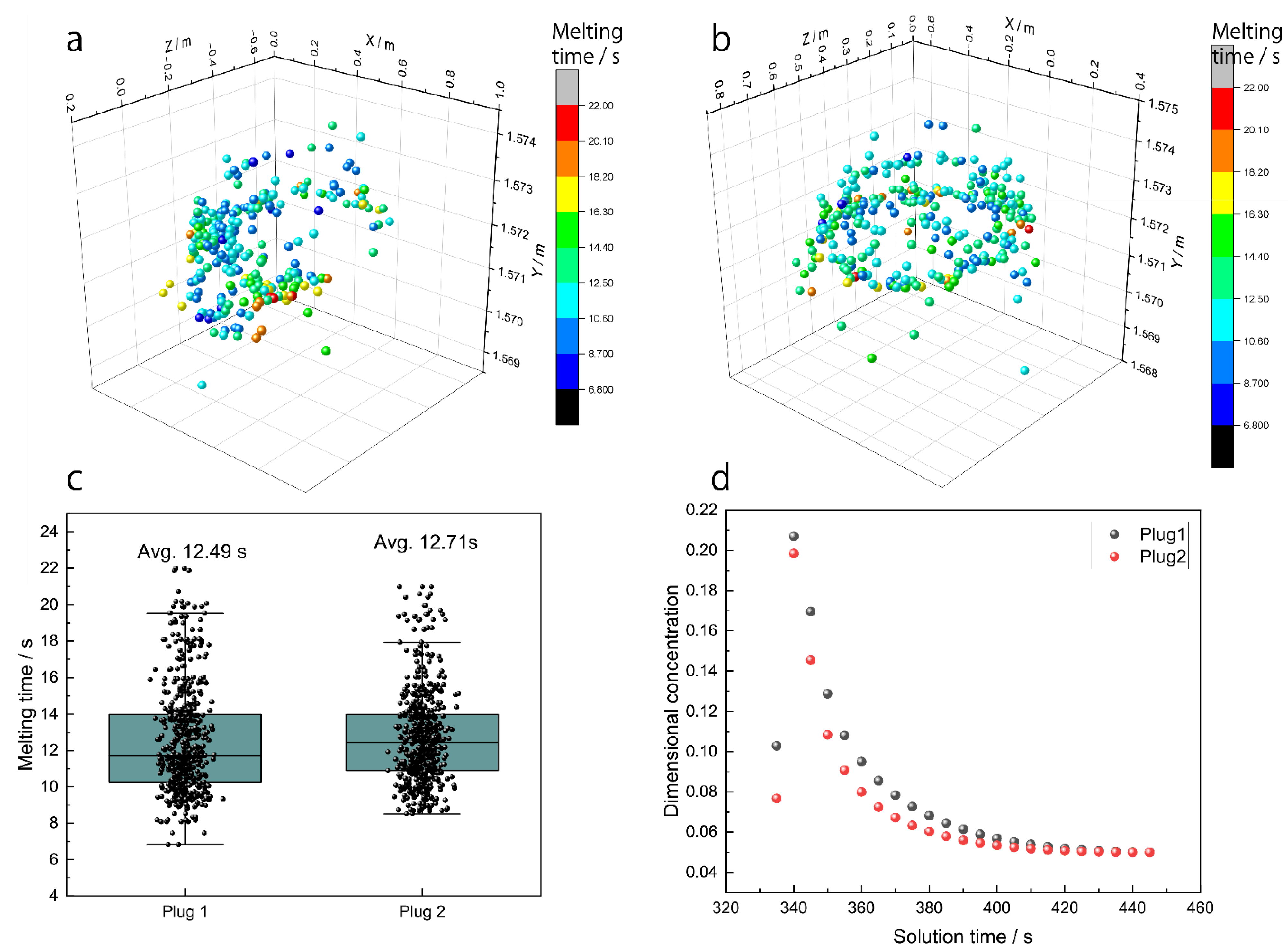
- The average alloy melting time is 12.49 s or 12.71 s when the alloy is added on the two slag eyes separately. The alloy melting time has a little difference because the molten steel temperature has little difference in the two slag eyes. The average alloy concentration in the ladle is increased when the alloy is added to the molten steel in 20 s, and the average alloy concentration decreases during the alloy species diffusion. The alloy concentration has fewer changes when the alloy is added to the molten steel after 100 s.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| velocity | |
| fluid vector | |
| Gravitational acceleration | |
| particle vector | |
| source term of the bubble-driven flow | |
| C | mass concentration of alloy |
| Cb.i | heat capacity of the bubble |
| CD,i | coefficient of drag force |
| CL | integral time-scale constant |
| Cp | heat capacity of the fluid |
| CP,A | heat capacity of the alloy |
| dA | diameter of the alloy |
| db,i | diameter of the bubble |
| DL | variance in the velocity magnitude difference between the numerical simulation and the PIV measurements |
| Estep | energy exchange in each timestep |
| ET | total energy of the bubble |
| Gb | generation of turbulence kinetic energy due to buoyancy |
| Gk | generation of turbulence kinetic energy due to the mean velocity gradient |
| h | sensible enthalpy |
| hc | coefficient of the heat transfer |
| I | unit tensor |
| k | turbulent kinetic energy |
| km | fluid thermal conductivity |
| malloy | mass of the melted alloy |
| mb.i | bubble mass |
| mcell | mass of the cell where the alloy melting |
| N | bubble count in the cell |
| n | phase count |
| Nper | bubble injection count in 1 s |
| Nu | Nusselt number |
| Q | flow rate of the argon |
| r | random Gaussian number |
| Rei | Reynolds number of bubble |
| Rm | the radius in the hydraulic model |
| Rp | the radius in the prototype(ladle) |
| Sc | source term of the alloy melting |
| T0 | initial alloy temperature |
| Tb, pre.temp | bubble temperature in the previous timestep |
| Tb.init | initial bubble temperature |
| Tcell | cell’s temperature where the bubble is injected into the fluid domain |
| TE | eddy lifetime |
| TL | integral time scale |
| TM | temperature of molten steel |
| tmelt | alloy solid crust melting time |
| Ts | solidification temperature of molten steel |
| ub,i | velocity of the bubble |
| ul | velocity of the fluid |
| vb,init | initial velocity when the bubble is injected into the fluid zone |
| αl | volume fraction of liquid phase |
| αq | volume fraction of qth phase in the fluid |
| Δt | time step |
| ΔVcell | volume of the cell |
| ε | turbulent kinetic energy dissipation |
| μ | molecular viscosity |
| ρ | density of the fluid |
| ρA | alloy density |
| ρb,i | density of the bubble |
| ρf | fluid density |
| ρp | particle density |
| ρq | density of qth phase in the fluid |
References
- Conejo, A.N.; Kitamura, S.; Maruoka, N.; Kim, S.J. Effects of Top Layer, Nozzle Arrangement, and Gas Flow Rate on Mixing Time in Agitated Ladles by Bottom Gas Injection. Metall. Mater. Trans. B 2013, 44, 914–923. [Google Scholar] [CrossRef]
- Liu, Z.; Li, L.; Li, B. Modeling of Gas-Steel-Slag Three-Phase Flow in Ladle Metallurgy: Part I. Physical Modeling. ISIJ Int. 2017, 57, 1971–1979. [Google Scholar] [CrossRef] [Green Version]
- Manuel Amaro-Villeda, A.; Aurelio Ramirez-Argaez, M.; Conejo, A.N. Effect of Slag Properties on Mixing Phenomena in Gas-stirred Ladles by Physical Modeling. ISIJ Int. 2014, 54, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Mazumdar, D.; Dhandapani, P.; Sarvanakumar, R. Modeling and Optimisation of Gas Stirred Ladle Systems. ISIJ Int. 2017, 57, 286–295. [Google Scholar] [CrossRef] [Green Version]
- Szekely, J.; Wang, H.J.; Kiser, K.M. Flow Pattern Velocity and Turbulence Energy Measurements and Predictions in a Water Model of an Argon-Stirred Ladle. Metall. Trans. B 1976, 7, 287–295. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, H.; Wang, R.; Ren, Z.; He, Y. Bubble behavior and evolution characteristics in the RH riser tube-vacuum chamber. Int. J. Chem. React. Eng. 2022. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, H.; Wang, R.; Ren, Z.; Lin, L. Prediction of two phase flow behavior and mixing degree of liquid steel under reduced pressure. Vacuum 2021, 192, 110480. [Google Scholar] [CrossRef]
- Pan, Q.; Johansen, S.T.; Olsen, J.E.; Reed, M.; Sætran, L.R. On the turbulence modelling of bubble plumes. Chem. Eng. Sci. 2021, 229, 116059. [Google Scholar] [CrossRef]
- Mantripragada, V.T.; Sahu, S.; Sarkar, S. Morphology and flow behavior of buoyant bubble plumes. Chem. Eng. Sci. 2021, 229, 116098. [Google Scholar] [CrossRef]
- Xu, Y.; Ersson, M.; Jonsson, P.G. A Numerical Study about the Influence of a Bubble Wake Flow on the Removal of Inclusions. ISIJ Int. 2016, 56, 1982–1988. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.-H.; Bao, Y.-P.; Wang, R.; Ma, L.-F.; Liu, J.-S. Modeling study on the flow patterns of gas-liquid flow for fast decarburization during the RH process. Int. J. Miner. Metall. Mater. 2018, 25, 153–163. [Google Scholar] [CrossRef]
- Yuan, F.; Xu, A.-J.; Gu, M.-Q. Development of an improved CBR model for predicting steel temperature in ladle furnace refining. Int. J. Miner. Metall. Mater. 2021, 28, 1321–1331. [Google Scholar] [CrossRef]
- Gu, C.; Liu, W.-Q.; Lian, J.-H.; Bao, Y.-P. In-depth analysis of the fatigue mechanism induced by inclusions for high-strength bearing steels. Int. J. Miner. Metall. Mater. 2021, 28, 826–834. [Google Scholar] [CrossRef]
- Xiao, W.; Bao, Y.-Q.; Gu, C.; Wang, M.; Liu, Y.; Huang, Y.-S.; Sun, G.-T. Ultrahigh cycle fatigue fracture mechanism of high-quality bearing steel obtained through different deoxidation methods. Int. J. Miner. Metall. Mater. 2021, 28, 804–815. [Google Scholar] [CrossRef]
- Li, Y.; He, Y.; Ren, Z.; Bao, Y.; Wang, R. Comparative Study of the Cleanliness of Interstitial-Free Steel with Low and High Phosphorus Contents. Steel Res. Int. 2021, 92, 2000581. [Google Scholar] [CrossRef]
- Guo, X.; Godinez, J.; Walla, N.J.; Silaen, A.K.; Oltmann, H.; Thapliyal, V.; Bhansali, A.; Pretorius, E.; Zhou, C.Q. Computational Investigation of Inclusion Removal in the Steel-Refining Ladle Process. Processes 2021, 9, 1048. [Google Scholar] [CrossRef]
- Krishnapisharody, K.; Irons, G.A. A Model for Slag Eyes in Steel Refining Ladles Covered with Thick Slag. Metall. Mater. Trans. B 2015, 46, 191–198. [Google Scholar] [CrossRef]
- Patil, S.P.; Satish, D.; Peranandhanathan, M.; Mazumdar, D. Mixing Models for Slag Covered, Argon Stirred Ladles. ISIJ Int. 2010, 50, 1117–1124. [Google Scholar] [CrossRef] [Green Version]
- Peranandhanthan, M.; Mazumdar, D. Modeling of Slag Eye Area in Argon Stirred Ladles. ISIJ Int. 2010, 50, 1622–1631. [Google Scholar] [CrossRef] [Green Version]
- Conejo, A.N. Physical and Mathematical Modelling of Mass Transfer in Ladles due to Bottom Gas Stirring: A Review. Processes 2020, 8, 750. [Google Scholar] [CrossRef]
- Hua, J.; Wang, C.-H. Numerical simulation of bubble-driven liquid flows. Chem. Eng. Sci. 2000, 55, 4159–4173. [Google Scholar] [CrossRef]
- Chen, C.; Jonsson, L.T.I.; Tilliander, A.; Cheng, G.; Jönsson, P.G. A mathematical modeling study of the influence of small amounts of KCl solution tracers on mixing in water and residence time distribution of tracers in a continuous flow reactor-metallurgical tundish. Chem. Eng. Sci. 2015, 137, 914–937. [Google Scholar] [CrossRef]
- Geng, D.-Q.; Lei, H.; He, J.-C. Optimization of mixing time in a ladle with dual plugs. Int. J. Miner. Metall. Mater. 2010, 17, 709–714. [Google Scholar] [CrossRef]
- Li, L.; Liu, Z.; Li, B.; Matsuura, H.; Tsukihashi, F. Water Model and CFD-PBM Coupled Model of Gas-Liquid-Slag Three-Phase Flow in Ladle Metallurgy. ISIJ Int. 2015, 55, 1337–1346. [Google Scholar] [CrossRef] [Green Version]
- Uriostegui-Hernandez, A.; Garnica-Gonzalez, P.; Angel Ramos-Banderas, J.; Alberto Hernandez-Bocanegra, C.; Solorio-Diaz, G. Multiphasic Study of Fluid-Dynamics and the Thermal Behavior of a Steel Ladle during Bottom Gas Injection Using the Eulerian Model. Metals 2021, 11, 1082. [Google Scholar] [CrossRef]
- Mazumdar, D.; Guthrie, R.I.L. Modeling Energy Dissipation in Slag-Covered Steel Baths in Steelmaking Ladles. Metall. Mater. Trans. B 2010, 41, 976–989. [Google Scholar] [CrossRef]
- Zhu, M.Y.; Inomoto, T.; Sawada, I.; Hsiao, T.C. Fluid-Flow and Mixing Phenomena in the Ladle Stirred by Argon through Multi-Tuyere. ISIJ Int. 1995, 35, 472–479. [Google Scholar] [CrossRef]
- Liu, H.; Qi, Z.; Xu, M. Numerical Simulation of Fluid Flow and Interfacial Behavior in Three-phase Argon-Stirred Ladles with One Plug and Dual Plugs. Steel Res. Int. 2011, 82, 440–458. [Google Scholar] [CrossRef]
- Llanos, C.A.; Garcia-Hernandez, S.; Ramos-Banderas, J.A.; Barret, J.D.J.; Solorio-Diaz, G. Multiphase Modeling of the Fluidynamics of Bottom Argon Bubbling during Ladle Operations. ISIJ Int. 2010, 50, 396–402. [Google Scholar] [CrossRef] [Green Version]
- Tang, H.; Guo, X.; Wu, G.; Wang, Y. Effect of Gas Blown Modes on Mixing Phenomena in a Bottom Stirring Ladle with Dual Plugs. ISIJ Int. 2016, 56, 2161–2170. [Google Scholar]
- Huang, A.; Gu, H.; Zhang, M.; Wang, N.; Wang, T.; Zou, Y. Mathematical Modeling on Erosion Characteristics of Refining Ladle Lining with Application of Purging Plug. Metall. Mater. Trans. B 2013, 44, 744–749. [Google Scholar] [CrossRef]
- Li, L.; Li, B. Investigation of Bubble-Slag Layer Behaviors with Hybrid Eulerian-Lagrangian Modeling and Large Eddy Simulation. JOM 2016, 68, 2160–2169. [Google Scholar] [CrossRef]
- Liu, W.; Tang, H.; Yang, S.; Wang, M.; Li, J.; Liu, Q.; Liu, J. Numerical Simulation of Slag Eye Formation and Slag Entrapment in a Bottom-Blown Argon-Stirred Ladle. Metall. Mater. Trans. B 2018, 49, 2681–2691. [Google Scholar] [CrossRef]
- Xue, Z.L.; Wang, Y.F.; Wang, L.T.; Li, Z.B.; Zhang, J.W. Inclusion removal from molten steel by attachment small bubbles. Acta Metall. Sin. 2003, 39, 431–434. [Google Scholar]
- Zhu, M.Y.; Zheng, S.G.; Huang, Z.Z.; Gu, W.P. Numerical simulation of nonmetallic inclusions behaviour in gas-stirred ladies. Steel Res. Int. 2005, 76, 718–722. [Google Scholar] [CrossRef]
- Mantripragada, V.T.; Sarkar, S. Multi-Objective Optimization of Bottom Purged Steelmaking Ladles. Trans. Indian Inst. Met. 2022, 1–10. [Google Scholar] [CrossRef]
- Cheng, R.; Zhang, L.; Yin, Y.; Ma, H.; Zhang, J. Influence of Argon Gas Flow Parameters in the Slot Plug on the Flow Behavior of Molten Steel in a Gas-Stirred Ladle. Trans. Indian Inst. Met. 2021, 74, 1827–1837. [Google Scholar] [CrossRef]
- Bhattacharjee, A.; Mazumdar, D. Mathematical-Modeling of Fluid-Flow, Alloy Dissolution and Mixing in Industrial Argon Stirred Ladles. Trans. Indian Inst. Met. 1992, 45, 153–161. [Google Scholar]
- Kwon, Y.-J.; Zhang, J.; Lee, H.-G. A CFD-based nucleation-growth-removal model for inclusion behavior in a gas-agitated ladle during molten steel deoxidation. ISIJ Int. 2008, 48, 891–900. [Google Scholar] [CrossRef] [Green Version]
- Lachmund, H.; Xie, Y.K.; Buhles, T.; Pluschkell, W. Slag emulsification during liquid steel desulphurisation by gas injection into the ladle. Steel Res. Int. 2003, 74, 77–85. [Google Scholar] [CrossRef]
- Singh, U.; Anapagaddi, R.; Mangal, S.; Padmanabhan, K.A.; Singh, A.K. Multiphase Modeling of Bottom-Stirred Ladle for Prediction of Slag-Steel Interface and Estimation of Desulfurization Behavior. Metall. Mater. Trans. B 2016, 47, 1804–1816. [Google Scholar] [CrossRef]
- Wondrak, T.; Timmel, K.; Bruch, C.; Gardin, P.; Hackl, G.; Lachmund, H.; Lungen, H.B.; Odenthal, H.-J.; Eckert, S. Large-Scale Test Facility for Modeling Bubble Behavior and Liquid Metal Two-Phase Flows in a Steel Ladle. Metall. Mater. Trans. B 2022, 53, 1703–1720. [Google Scholar] [CrossRef]
- Uriostegui-Hernandez, A.; Garnica-Gonzalez, P.; Hernandez-Bocanegra, C.-A.; Ramos-Banderas, J.-A.; Montes-Rodriguez, J.-J.; Ortiz-Castillo, J.-R. Study of fluid dynamics and sulfar mass transfer between steel and slag in a ladle furnace considering drag and non-drag forces. Dyna 2022, 97, 176–183. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, C.; Pan, L.; He, Z.; Li, G. Numerical Understanding on Refractory Flow-Induced Erosion and Reaction-Induced Corrosion Patterns in Ladle Refining Process. Metall. Mater. Trans. B 2022, 53, 1617–1630. [Google Scholar] [CrossRef]
- Joubert, N.; Gardin, P.; Popinet, S.; Zaleski, S. Experimental and numerical modelling of mass transfer in a refining ladle. Metall. Res. Technol. 2022, 119, 109. [Google Scholar] [CrossRef]
- Riabov, D.; Gain, M.M.; Kargul, T.; Volkova, O. Influence of Gas Density and Plug Diameter on Plume Characteristics by Ladle Stirring. Crystals 2021, 11, 475. [Google Scholar] [CrossRef]
- Li, Q.; Pistorius, P.C. Interface-Resolved Simulation of Bubbles-Metal-Slag Multiphase System in a Gas-Stirred Ladle. Metall. Mater. Trans. B 2021, 52, 1532–1549. [Google Scholar] [CrossRef]





| Item | Parameters |
|---|---|
| The bottom diameter of the hydraulic model/mm | 661.75 |
| Top diameter of the hydraulic model/mm | 752 |
| Height of the hydraulic model/mm | 910.5 |
| Height of water/mm | 716.5 |
| Position of argon plug in the hydraulic model | 0.6 Rm |
| The bottom diameter of the prototype ladle/mm | 1612 |
| Top diameter of prototype ladle/mm | 1848 |
| Height of the prototype ladle/mm | 2374 |
| Hight of molten steel/mm | 1574 |
| Position of argon plugs in prototype | 0.6 Rp and 0.67 Rp |
| Item | Parameters |
|---|---|
| Water density (25 °C)/kg·m−3 | 997.04 |
| Water viscosity (25 °C)/Pa·s | 0.8949 × 10−3 |
| Air phase density (25 °C)/kg·m−3 | 1.185 |
| Air phase viscosity (25 °C)/Pa·s | 1.8315 × 10−5 |
| Water surface tension/N·m−1 | 0.07197 |
| Argon bubble flow rate in hydraulic model/L·min−1 | 6 |
| Molten steel density/kg·m−3 | 7000 |
| Molten steel viscosity/Pa·s | 0.0067 |
| Molten slag density/kg·m−3 | 3500 |
| Molten slag viscosity/Pa·s | 0.06 |
| Argon density/kg·m−3 | 1.784 |
| Argon viscosity/Pa·s | 2.2624 × 10−5 |
| Molten steel–slag interface surface tension/N·m−1 | 1.6 |
| Molten steel specific heat/J·kg−1·K−1 | 680 |
| Molten slag specific heat/J·kg−1·K−1 | 1100 |
| Argon specific heat/J·kg−1·K−1 | 1006.43 |
| Molten steel thermal conductivity/W·m−1·K−1 | 40.3 |
| Molten slag thermal conductivity/W·m−1·K−1 | 34 |
| Argon thermal conductivity/W·m−1·K−1 | 0.0242 |
| Alloy density/kg·m−3 | 5780 |
| Alloy specific heat/J·kg−1·K−1 | 364 |
| Alloy diameter/mm | 50 |
| Alloy thermal conductivity/W·m−1·K−1 | 26.32 |
| Initial alloy temperature/°C | 25 |
| Initial bubble temperature/°C | 25, 400, 800 |
| Alloy concentration diffusion coefficient/m2·s−1 | 1.566 × 10−14 |
| Argon bubble flow rate in prototype/L·min−1 | 5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hua, C.; Bao, Y.; Wang, M. Multiphysics Numerical Simulation Model and Hydraulic Model Experiments in the Argon-Stirred Ladle. Processes 2022, 10, 1563. https://doi.org/10.3390/pr10081563
Hua C, Bao Y, Wang M. Multiphysics Numerical Simulation Model and Hydraulic Model Experiments in the Argon-Stirred Ladle. Processes. 2022; 10(8):1563. https://doi.org/10.3390/pr10081563
Chicago/Turabian StyleHua, Chengjian, Yanping Bao, and Min Wang. 2022. "Multiphysics Numerical Simulation Model and Hydraulic Model Experiments in the Argon-Stirred Ladle" Processes 10, no. 8: 1563. https://doi.org/10.3390/pr10081563
APA StyleHua, C., Bao, Y., & Wang, M. (2022). Multiphysics Numerical Simulation Model and Hydraulic Model Experiments in the Argon-Stirred Ladle. Processes, 10(8), 1563. https://doi.org/10.3390/pr10081563







