Online Pyrometry Calibration for Industrial Combustion Process Monitoring
Abstract
:1. Introduction
- 1.
- Indirect methods: camera spectral response calibration
- 2.
- Direct methods: estimating model parameters with reference temperature
- 1.
- An experimental procedure for online pyrometry calibration of the camera in use is proposed.
- 2.
- Experimentally, it is found that there are two peaks in the flame temperature distribution, and the temperature corresponding to the peak remains unchanged in a short period. Based on this phenomenon, a digital camera-based pyrometry calibration algorithm is developed.
- 3.
- The procedure and algorithm are tested in an industrial-scale MSWI. The calibration was successfully completed without affecting normal operation of the plant. The calibrated pyrometer meets the accuracy requirements of combustion control and monitoring.
2. Digital Camera-Based Pyrometry Model
2.1. Principle of Thermal Radiation Temperature Measurement
2.2. Digital Camera-Based Pyrometry
2.3. Revision of Radio Pyrometry
3. Procedure of Online Pyrometer Calibration
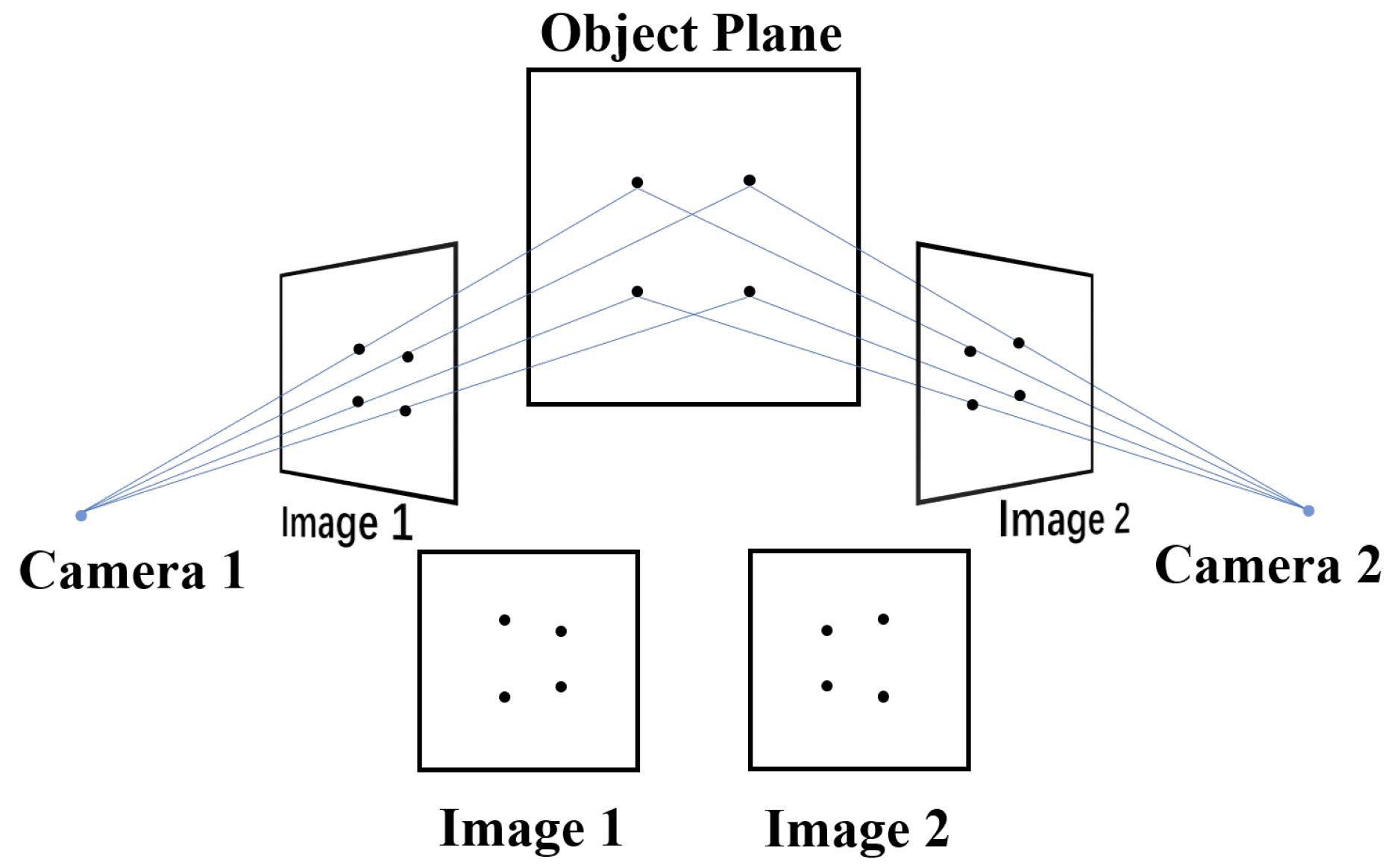
3.1. Physical Model of Camera Sensor
3.2. Offline Calibration of Digital Camera for Pyrometry
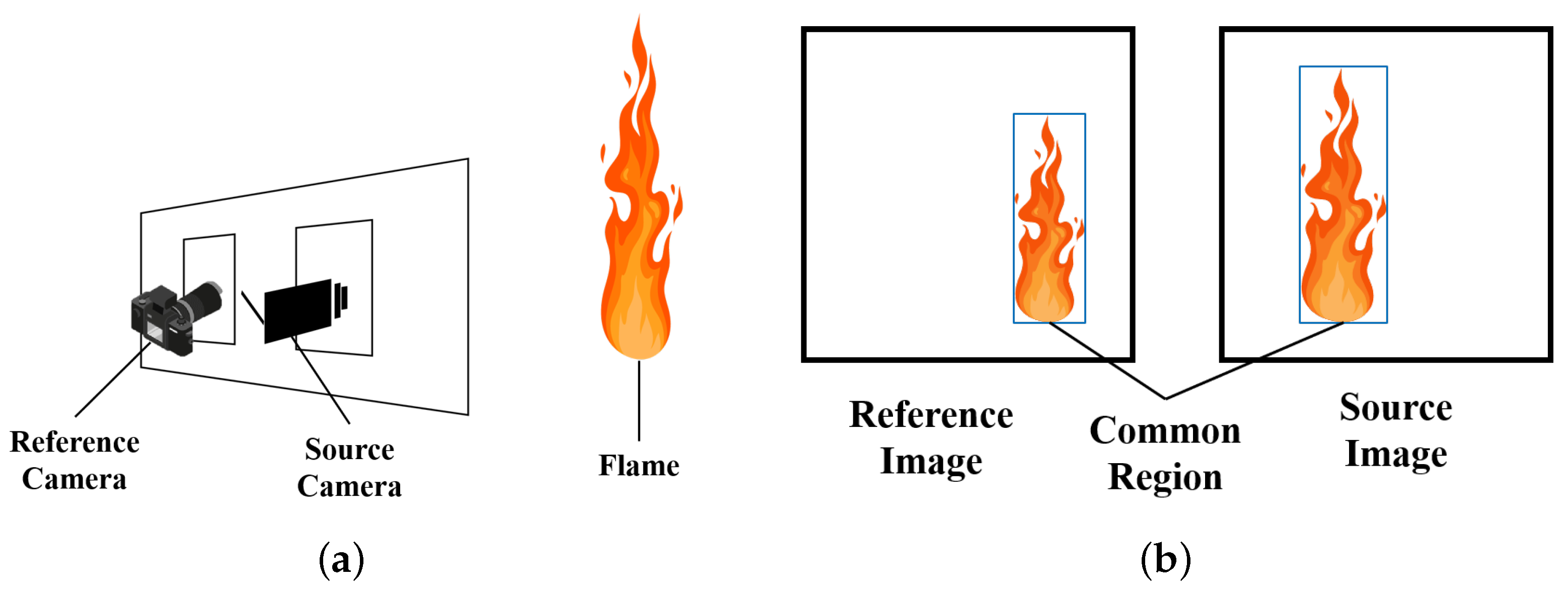
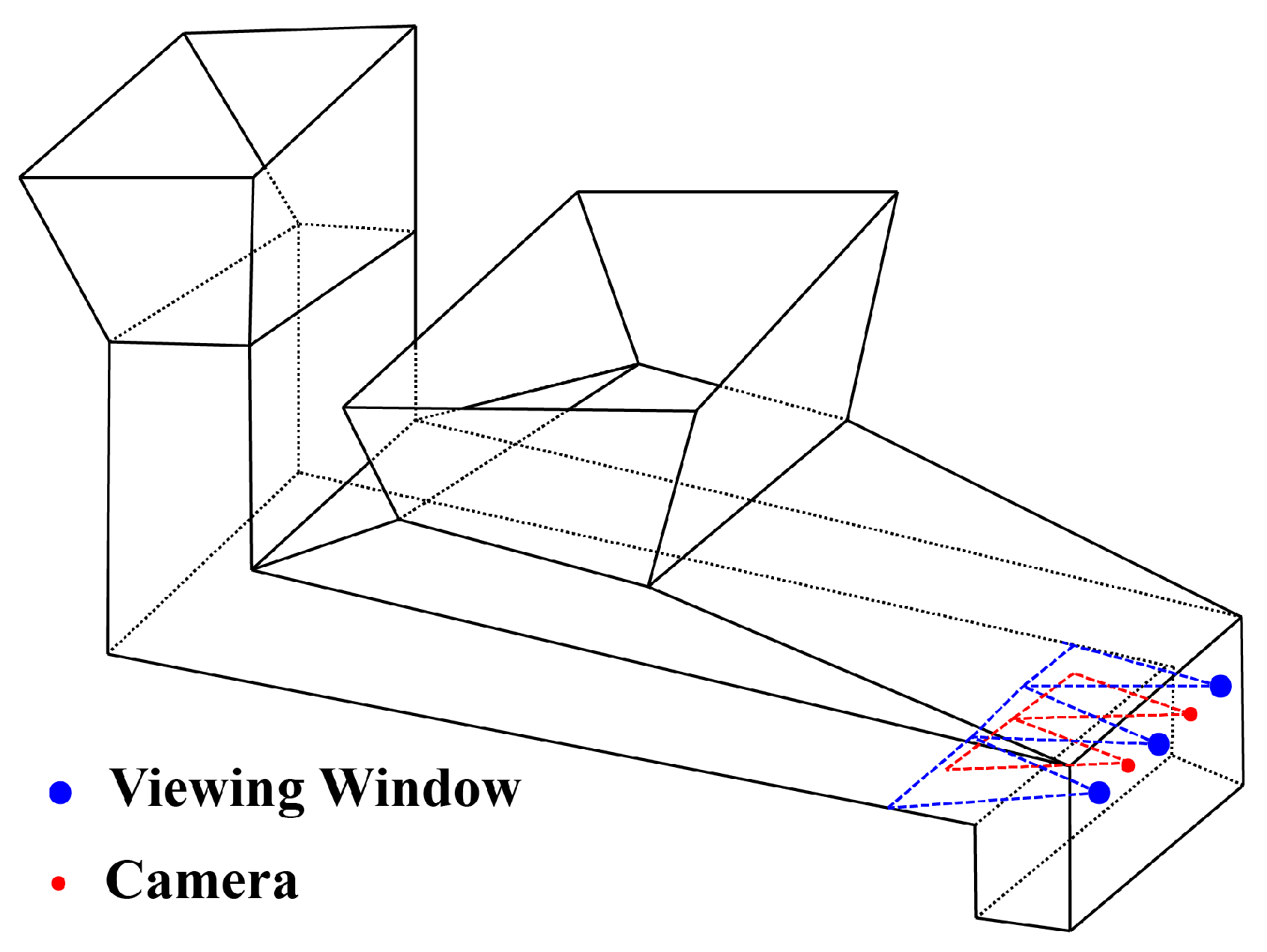
3.3. Online Calibration Setup of Digital Camera for Pyrometry
4. Online Pyrometer Calibration Algorithm Based on Flame Temperature Distribution Matching
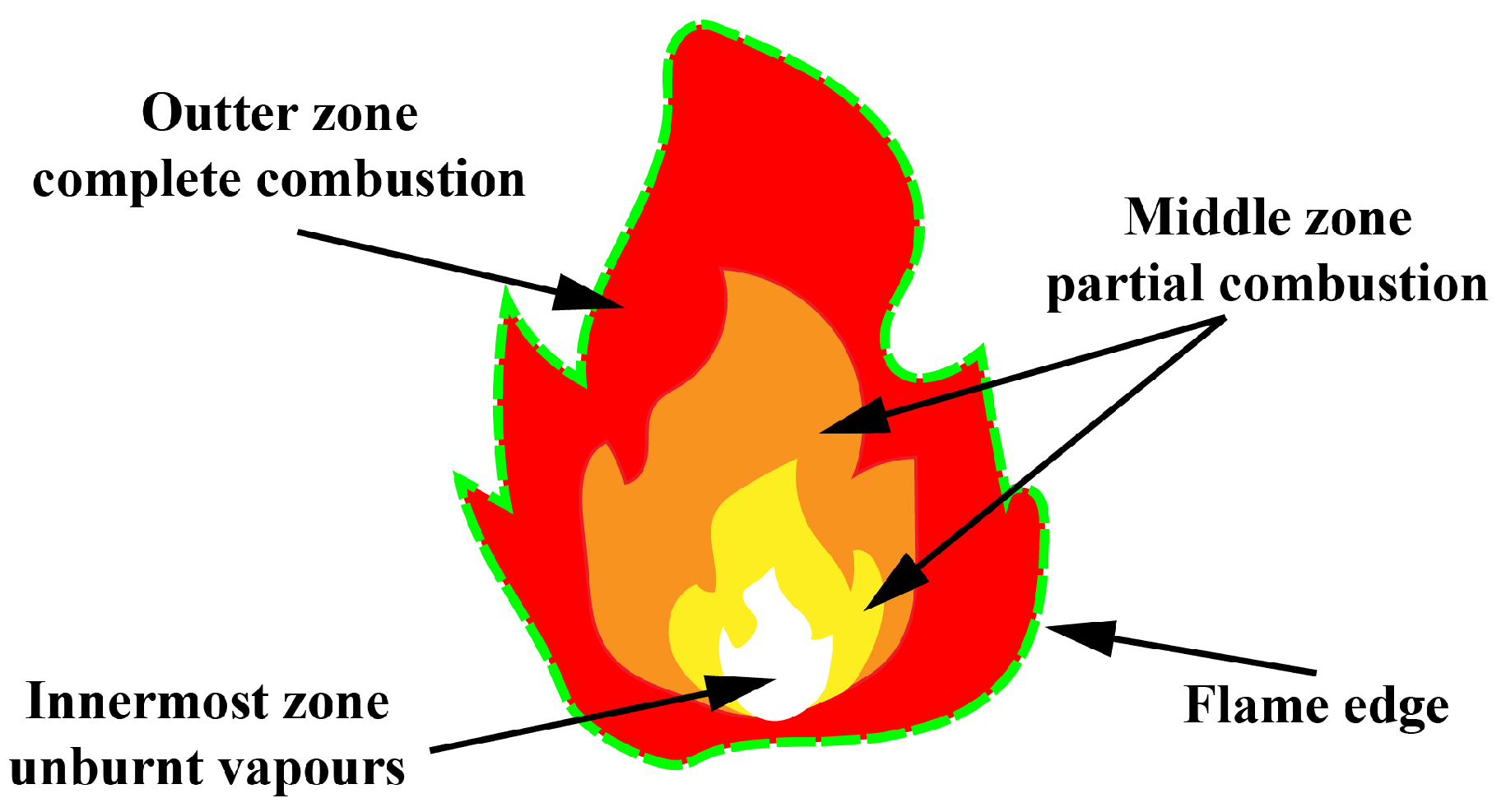
4.1. Flame Temperature Distribution and Flame Zones
- 1.
- 2.
- The edge of the flame is the hottest zone of the flame, and the highest temperature of a flame is always similar at the same combustion condition too [25].
4.2. Innermost Flame Segmentation Algorithm
- 1:
- Transform the original colour image I into the greyscale image ;
- 2:
- 3:
- Get the binary image using the maximum threshold calculated in step 2;
- 4:
- Morphologically open the binary image in order to reduce misclassification.
4.3. Temperature Distribution Matching Based Calibration Algorithm
5. Experiment and Validations
5.1. Offline Preparation—Convert a Digital Camera into a Pyrometer in Laboratory
5.2. Online Calibration Experiment—A Real Industrial Experiment of MSWI Flame Temperature Measurement
6. Conclusions
- 1.
- Only taking one photo by a calibrated pyrometer at a close position to the video camera being used, the calibration can be accomplished.
- 2.
- It significantly reduces the cost and difficulty of pyrometer calibration.
- 3.
- This method can enhance the ability of combustion state diagnosis in a very convenient and cheap way.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, B.; Xu, C.; Tan, H.; Qi, H.; Sun, J.; Hossain, M.M.; Wang, S. Three-dimensional temperature field measurement of flame using a single light field camera. Opt. Express 2016, 24, 1118–1132. [Google Scholar] [CrossRef]
- Ballester, J.; García-Armingol, T. Diagnostic techniques for the monitoring and control of practical flames. Prog. Energy Combust. Sci. 2010, 36, 375–411. [Google Scholar] [CrossRef]
- Docquier, N.; Candel, S. Combustion control and sensors: A review. Prog. Energy Combust. Sci. 2002, 28, 107–150. [Google Scholar] [CrossRef]
- Sun, J.; Hossain, M.M.; Xu, C.; Zhang, B. Investigation of flame radiation sampling and temperature measurement through light field camera. Int. J. Heat Mass Transf. 2018, 121, 1281–1296. [Google Scholar] [CrossRef]
- Alaruri, S.D.; Brewington, A.J.; Thomas, M.A.; Miller, J.A. High-Temperature Remote Thermometry Using Laser-Induced Fluorescence Decay Lifetime Measurements of Y2O3: Eu and YAG: Tb Thermographic Phosphors. IEEE Trans. Instrum. Meas. 1993, 42, 735–739. [Google Scholar] [CrossRef]
- Gassino, R.; Perrone, G.; Vallan, A. Temperature monitoring with fiber bragg grating sensors in nonuniform conditions. IEEE Trans. Instrum. Meas. 2020, 69, 1336–1343. [Google Scholar] [CrossRef]
- Cao, H.; Yan, X.; Yang, S.; Ren, H.; Ge, S.S. Low-Cost Pyrometry System with Nonlinear Multisense Partial Least Squares. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1029–1038. [Google Scholar] [CrossRef]
- Zhao, W.; Zhang, B.; Xu, C.; Duan, L.; Wang, S. Optical sectioning tomographic reconstruction of three-dimensional flame temperature distribution using single light field camera. IEEE Sens. J. 2018, 18, 528–539. [Google Scholar] [CrossRef]
- Hernández, R.; Ballester, J. Flame imaging as a diagnostic tool for industrial combustion. Combust. Flame 2008, 155, 509–528. [Google Scholar] [CrossRef]
- Gibbins, J.; Lin, Y.M.; Bowden, S.; Cameron, S. Video Observations of Full-Size Pulverised Coal Flames. Combust. Sci. Technol. 2007, 162, 263–280. [Google Scholar] [CrossRef]
- Han, Z.; Hossain, M.M.; Wang, Y.; Li, J.; Xu, C. Combustion stability monitoring through flame imaging and stacked sparse autoencoder based deep neural network. Appl. Energy 2020, 259, 114159. [Google Scholar] [CrossRef]
- Tóth, P.; Garami, A.; Csordás, B. Image-based deep neural network prediction of the heat output of a step-grate biomass boiler. Appl. Energy 2017, 200, 155–169. [Google Scholar] [CrossRef]
- González-Cencerrado, A.; Peña, B.; Gil, A. Coal flame characterization by means of digital image processing in a semi-industrial scale PF swirl burner. Appl. Energy 2012, 94, 375–384. [Google Scholar] [CrossRef]
- Chen, J.; Chan, L.L.T.; Cheng, Y.C. Gaussian process regression based optimal design of combustion systems using flame images. Appl. Energy 2013, 111, 153–160. [Google Scholar] [CrossRef]
- Chen, J.; Chang, Y.H.; Cheng, Y.C.; Hsu, C.K. Design of image-based control loops for industrial combustion processes. Appl. Energy 2012, 94, 13–21. [Google Scholar] [CrossRef]
- Lu, C.; Wang, Z.; Zhou, B. Intelligent fault diagnosis of rolling bearing using hierarchical convolutional network based health state classification. Adv. Eng. Inform. 2017, 32, 139–151. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Aphale, S.S.; DesJardin, P.E. Development of a non-intrusive radiative heat flux measurement for upward flame spread using DSLR camera based two-color pyrometry. Combust. Flame 2019, 210, 262–278. [Google Scholar] [CrossRef]
- Zhao, H.; Feng, H.; Xu, Z.; Li, Q. Research on temperature distribution of combustion flames based on high dynamic range imaging. Opt. & Laser Technol. 2007, 39, 1351–1359. [Google Scholar] [CrossRef]
- Khan, M.A.; Allemand, C.; Eagar, T.W. Noncontact temperature measurement. I. Interpolation based techniques. Rev. Sci. Instrum. 1998, 62, 392. [Google Scholar] [CrossRef]
- Magunov, A. Spectral pyrometry. Instrum. Exp. Tech. 2009, 52, 451–472. [Google Scholar] [CrossRef]
- Yan, W.; Zhou, H.; Jiang, Z.; Lou, C.; Zhang, X.; Chen, D. Experiments on Measurement of Temperature and Emissivity of Municipal Solid Waste (MSW) Combustion by Spectral Analysis and Image Processing in Visible Spectrum. Energy Fuels 2013, 27, 6754–6762. [Google Scholar] [CrossRef]
- Zitová, B.; Flusser, J. Image registration methods: A survey. Image Vis. Comput. 2003, 21, 977–1000. [Google Scholar] [CrossRef]
- Dixon-Lewis G, N. Flame structure and flame reaction kinetics II. Transport phenomena in multicomponent systems. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1968, 307, 111–135. [Google Scholar] [CrossRef]
- Yu, M.; Lin, J.; Chan, T. Numerical simulation of nanoparticle synthesis in diffusion flame reactor. Powder Technol. 2008, 181, 9–20. [Google Scholar] [CrossRef]
- Otsu, N. Threshold selection method from gray-level histograms. IEEE Trans Syst Man Cybern 1979. [Google Scholar] [CrossRef]
- Aziz, M.A.E.; Ewees, A.A.; Hassanien, A.E. Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- Hill, P.D. Kernel Estimation of a Distribution Function. Commun. Stat.—Theory Methods 1985, 14, 605–620. [Google Scholar] [CrossRef]
- Kafadar, K.; Bowman, A.W.; Azzalini, A. Applied Smoothing Techniques for Data Analysis: The Kernel Approach with S-PLUS Illustrations. J. Am. Stat. Assoc. 1999, 94, 982. [Google Scholar] [CrossRef] [Green Version]
- Shen, X.; Agrawal, S. Kernel density estimation for an anomaly based intrusion detection system. In Proceedings of the International Conference on Machine Learning; Models, Technologies and Applications, Las Vegas, NV, USA, 26–29 June 2006; pp. 161–167. [Google Scholar]
- Byrd, R.H.; Hribar, M.E.; Nocedal, J. An interior point algorithm for large-scale nonlinear programming. SIAM J. Optim. 1999, 9, 877–900. [Google Scholar] [CrossRef]








| ISO | Aperture | MSE | MSE |
|---|---|---|---|
| Time (s) | (Linear) | (Quadratic) | |
| 200 | 1/1000 | 20.89 | 8.41 |
| 200 | 1/800 | 78.95 | 5.61 |
| 200 | 1/600 | 87.52 | 13.85 |
| 250 | 1/1000 | 81.11 | 8.43 |
| 250 | 1/800 | 91.10 | 17.39 |
| 250 | 1/600 | 44.71 | 18.95 |
| 320 | 1/1000 | 95.33 | 16.55 |
| 320 | 1/800 | 44.62 | 20.89 |
| 320 | 1/600 | 44.65 | 11.60 |
| 500 | 1/1000 | 45.64 | 12.88 |
| 500 | 1/800 | 35.52 | 27.48 |
| 500 | 1/600 | 41.87 | 17.55 |
| 800 | 1/1000 | 42.54 | 19.23 |
| 800 | 1/800 | 40.51 | 24.39 |
| 800 | 1/600 | 32.92 | 33.82 |
| Blackbody Temp. (K) | Temp. Calculate (K) | Errors (%) |
|---|---|---|
| 1123.15 | 1141.67 | 1.62 |
| 1173.15 | 1164.65 | 0.70 |
| 1223.15 | 1222.64 | 0.04 |
| 1273.15 | 1275.54 | 0.19 |
| 1323.15 | 1328.40 | 0.40 |
| 1373.15 | 1375.05 | 0.14 |
| 1423.15 | 1415.90 | 0.51 |
| 1473.15 | 1473.70 | 0.04 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, C.; Wang, S.; Cao, Y.; Yang, S.-H.; Bai, B. Online Pyrometry Calibration for Industrial Combustion Process Monitoring. Processes 2022, 10, 1694. https://doi.org/10.3390/pr10091694
Zhou C, Wang S, Cao Y, Yang S-H, Bai B. Online Pyrometry Calibration for Industrial Combustion Process Monitoring. Processes. 2022; 10(9):1694. https://doi.org/10.3390/pr10091694
Chicago/Turabian StyleZhou, Chenchen, Shaoqi Wang, Yi Cao, Shuang-Hua Yang, and Bin Bai. 2022. "Online Pyrometry Calibration for Industrial Combustion Process Monitoring" Processes 10, no. 9: 1694. https://doi.org/10.3390/pr10091694
APA StyleZhou, C., Wang, S., Cao, Y., Yang, S.-H., & Bai, B. (2022). Online Pyrometry Calibration for Industrial Combustion Process Monitoring. Processes, 10(9), 1694. https://doi.org/10.3390/pr10091694






