Review of Latest Advances in Nature-Inspired Algorithms for Optimization of Activated Sludge Processes

Abstract

The activated sludge process (ASP) is the most widely used biological wastewater treatment system. Advances in research have led to the adoption of Artificial Intelligence (AI), in particular, Nature-Inspired Algorithm (NIA) techniques such as Genetic Algorithms (GAs) and Particle Swarm Optimization (PSO) to optimize treatment systems. This has aided in reducing the complexity and computational time of ASP modelling. This paper covers the latest NIAs used in ASP and discusses the advantages and limitations of each algorithm compared to more traditional algorithms that have been utilized over the last few decades. Algorithms were assessed based on whether they looked at real/ideal treatment plant (WWTP) data (and efficiency) and whether they outperformed the traditional algorithms in optimizing the ASP. While conventional algorithms such as Genetic Algorithms (GAs), Particle Swarm Optimization (PSO), and Ant Colony Optimization (ACO) were found to be successfully employed in optimization techniques, newer algorithms such as Whale Optimization Algorithm (WOA), Bat Algorithm (BA), and Intensive Weed Optimization Algorithm (IWO) achieved similar results in the optimization of the ASP, while also having certain unique advantages.

1. Introduction

The design and operation of wastewater treatment plants must consider quite a few uncertain factors, such as the physical and chemical composition of wastewater and the biological composition of organisms used to treat the wastewater. There are increasing concerns about the environmental impacts of wastewater, in terms of safe treatment, safe disposal, and safe reuse [1,2,3]. Over the years, this has led to Artificial Intelligence techniques, predominantly nature-inspired Artificial Intelligence techniques, being used for process control within treatment plants to maximize the efficiency of treatment and decrease energy consumption [4]. This paper will attempt to provide an overview of the recent advances in nature-inspired techniques used in wastewater treatment processes.

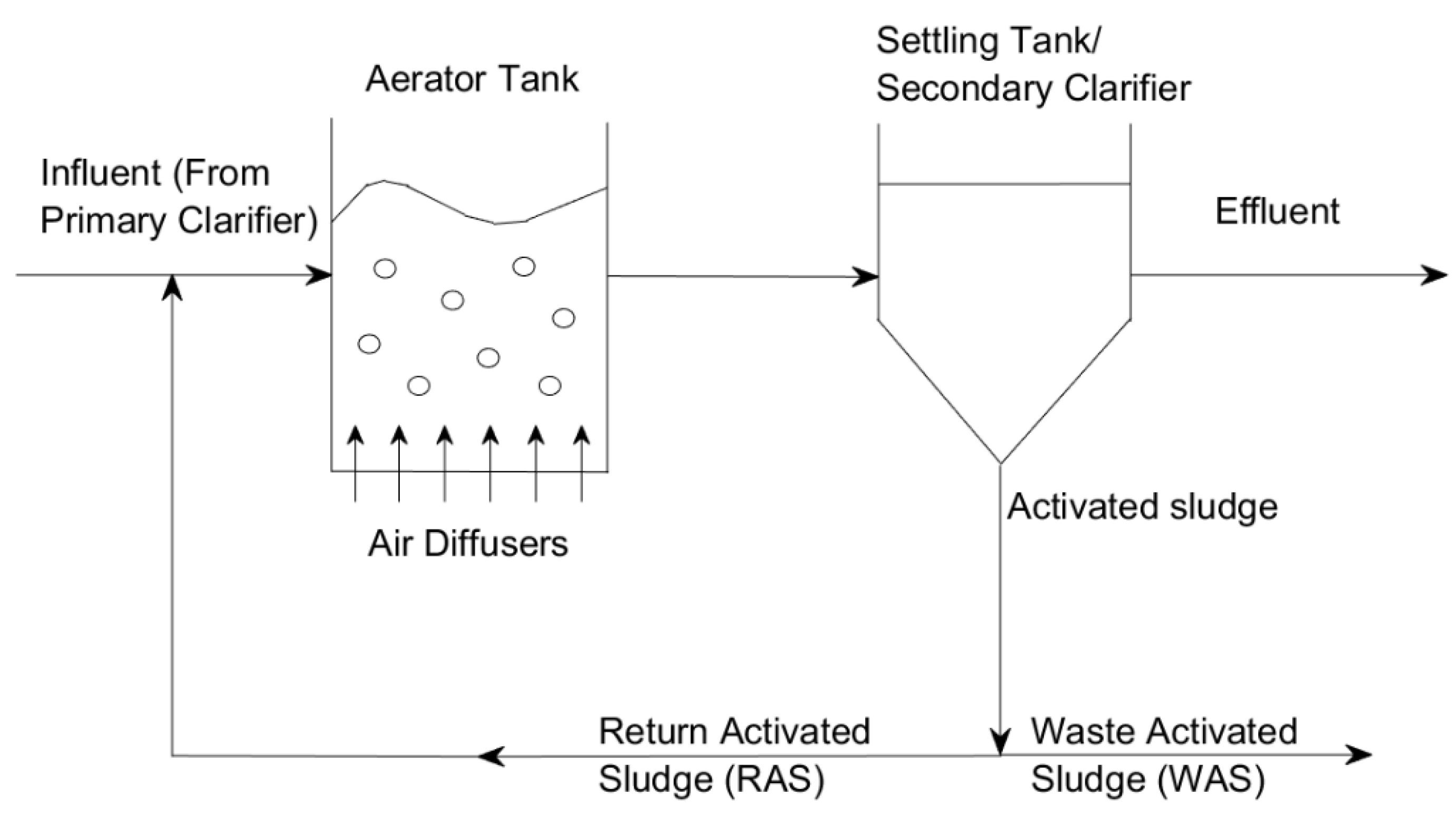
The most common type of biological wastewater treatment is the activated sludge process (ASP). Activated sludge is a mix of wastewater that contains a population of bacteria that focus on removing biological nitrogen, biological phosphorous, and organic carbon substances from the wastewater [5]. A basic process diagram for ASP is shown in Figure 1.

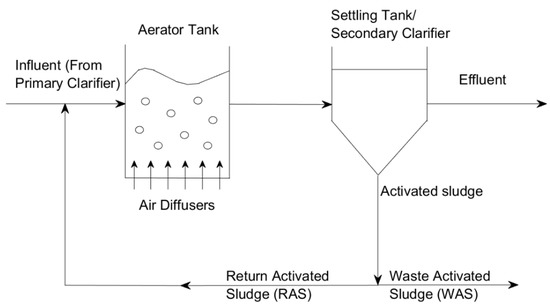
Figure 1. Schematic of a conventional activated sludge system with basic processes shown.

2. Modelling of Activated Sludge Process

A typical model that would simulate the ASP operation will have the following steps: a model objective, data collection, mathematical equations or models for each ASP as mentioned above, model calibration, and model validation [6].

Mathematical modelling has become an integral part of the design and operation of wastewater treatment processes, particularly the ASP. Simulations conducted with the models created have been a great source of value for ASP operators, designers, and even the wider scientific community. The main benefits of these models are the wide range of system functions and conditions that can be simulated and tested and solutions that can be found in a short time with low associated costs [7]. There are three main types of modelling that have been historically used for the ASP: deterministic or mechanistic modelling, stochastic modelling, and hybrid models combining the two approaches. The most efficient models use hybrid models where stochastic modelling is used for the hard-to-define parameters and variables in the treatment process. Deterministic modelling is used for the parts of the process that are both better understood and can be validated using the biological, physical, and chemical laws of the ASP [8].

Historically, deterministic models were the earliest type of work on activated sludge plants. Experimental data were taken and used to generate mathematical equations that depicted the relationship between variables in the various stages of the ASP. The most used mathematical model of the ASP was created by the International Association on Water Pollution Research and Control (IAWPRC) Task Group [9]—the Activated Sludge Model No. 1 (ASM1). Even though it was developed in 1987, researchers still widely use it for their work, albeit with modified versions.

The main processes involved in the traditional ASM1 model were the microorganisms’ growth, maintenance, and decay. Nitrification and denitrification were also included in some models along the way. It was accepted that this simplified approach has some demerits due to considering only these few processes and components [8]. Over the years, many modifications have been made to the traditional model approach. For example, Eckhoff et al. [10] used COD instead of BOD as a parameter to calculate the inert fraction of the substrate. Models based on COD are generally preferred over BOD in academic/research models because they are better at conserving the mass oxygen balance. However, BOD models are used to better characterize influent wastewater [11].

There are a few drawbacks to the ASM1 model. The International Water Association (IWA) has only given reference values for the dynamic or stoichiometric parameters of the model and its application to a real-life WWTP; the parameters will have to be corrected [12]. Different calibration data sets can produce the same results. Some variables used cannot be measured in the real-time process, making it hard to verify the model. Certain factors are not considered, such as the dependency of temperature and pH on the constants used. Calibration and model verification can be difficult and highly sensitive—sometimes, extensive lab equipment is required. Phosphorous removal was also not considered in this model, which created issues in practical application [13].

In 1995, a modified version of the ASM1 called the Activated Sludge Model No. 2 (ASM2) was developed, which included phosphorous removal in addition to carbonaceous and nitrogenous material. However, phosphorous removal is complex, thereby complicating the calibration and verification of the ASM2 model. The ASM1 and ASM2 were further improved by creating two models, Activated Sludge Model No. 2d (ASM2d) and Activated Sludge Model No. 3 (ASM3). ASM2d builds upon ASM2 by adding denitrifying activity of Polysulphate Accumulating Organisms that show better relation between phosphorous and nitrate. ASM3 was developed similar to ASM1 but considering the effect of storage polymers in heterotrophic activated sludge conversion [14].

To summarize, ASM1 can be used to simulate both carbon removal and denitrification, ASM2 simulates phosphorous removal in addition to decarbonization and denitrification, ASM2d further improved the relationship between phosphorous and nitrate in ASM2, and ASM3 improved upon ASM1 adding the effect of storage polymers. All the ASM models are mechanistic models where differential equations are used to describe and restore the dynamic changes in the wastewater treatment system. The models ASM1 and ASM2, ASM2d use the theoretical basis of death–regeneration and maintenance, whereas ASM3 utilizes the theoretical basis of endogenous microbial respiration [13].

Due to the many processes, variables, and parameters involved, activated sludge models are often validated and calibrated by trial and error with no standard procedure [8,15]. For example, Siegrist and Tschui [16] created several models with different sets of parameters for partial and sequential calibration. Calibration for COD removal was undertaken by considering the oxygen consumption rate when other parameters were held constant. The model was validated by comparing it with full-scale treatment plant data, where an example would be [17]. They created a dynamic model for carbon and nitrogen removal and validated it with data obtained from 10 days of monitoring Norwich Sewage Works in England. Côté et al. [18] used a hybrid model, which improved upon previous work by using a neural network to predict and reduce error in mechanistic model variables such as effluent suspended solids, effluent COD, and volatile solids in return sludge, etc. The mechanistic model was validated with data from Norwich Sewage Works.

2.1. Artificial Intelligence Used in Modelling of WWTP

The traditional mechanistic models, such as ASM1, have reached a limit when considering the complexity and accuracy of application to the ASP, with some of the issues mentioned in Section 2. Thus, Artificial Intelligence can be used as a modelling tool to minimize the complexities and reduce computing time [19].

There are several different types of AI modelling tools adapted for different fields and functions. Of these are feedforward Artificial Neural Networks (ANNs); radial basis functions (RBFs); recurrent neural networks (RNNs); multilayer perceptron (MLP) using backpropagation learning; hybrid models such as adaptive neuro-fuzzy inference (ANFIS). More recently, deep neural networks (DNNs) contain multiple hidden layers and require significant computational power [20,21]. The traditional ANN has a few limitations such as poor generalization due to incorrectly chosen network structure, hard-to-interpret system information stored in neuron weights, and a large amount of data required for accuracy. ANFIS tends to overcome a few of these limitations [21]. Additionally, Feedforward Artificial Neural Networks (FANNs)—MLPs and RBFs—are commonly used in wastewater treatment operations. MLPs have been found to be better than regression models for wastewater treatment [8], whilst RBFs are useful because they can easily predict system behavior from past observations [22]. DNNs vary from typical feedforward neural networks (ANNs) because DNNs contain more neurons, complexity in connecting layers, more computing power required to train the network due to having more neurons/connections, and automatic feature extraction [22]. Some of these tools, along with applications in wastewater treatment, particularly the ASP, are discussed below.

2.2. Artificial Neural Network (ANN)

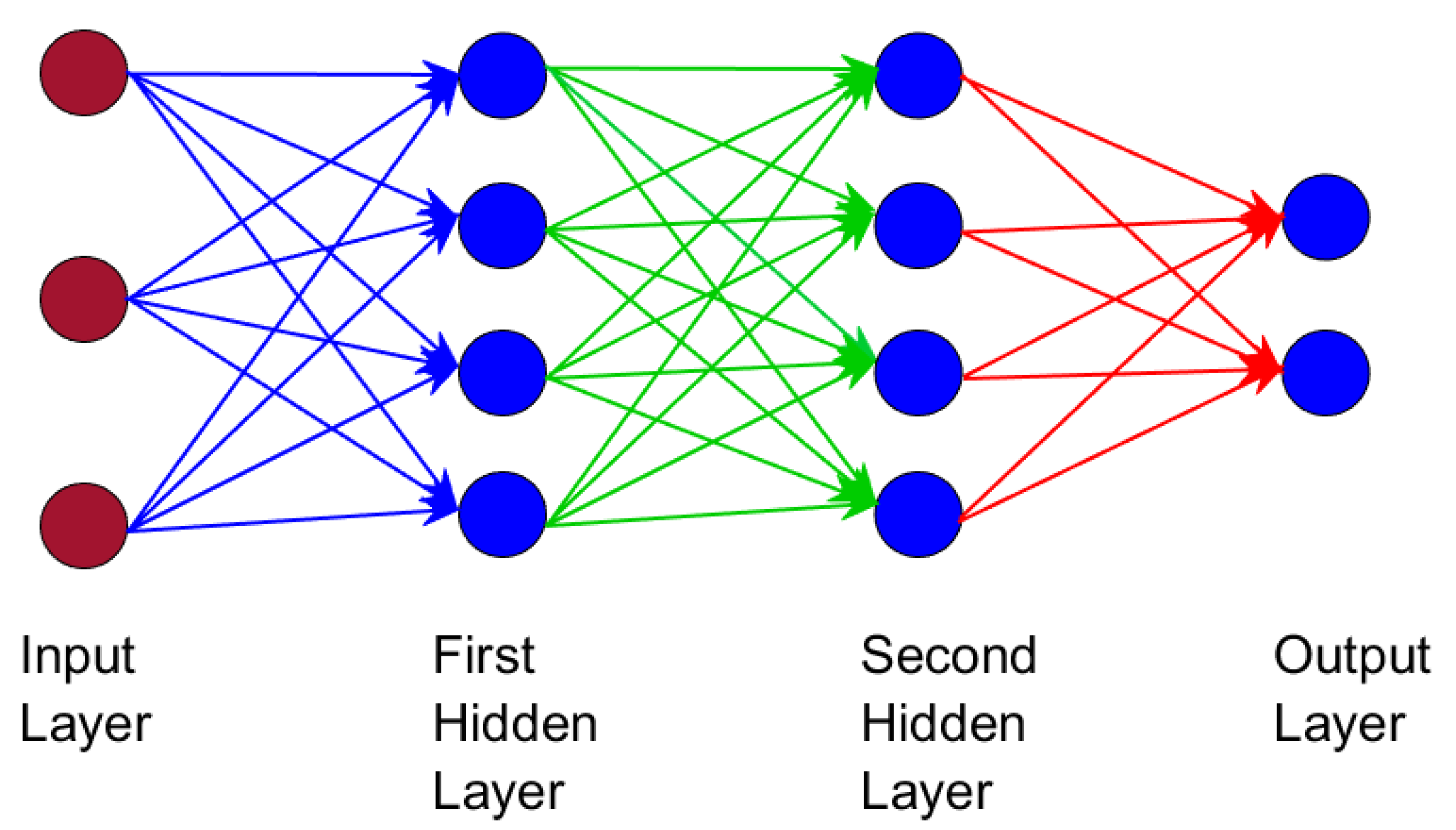
ANN is designed as a simplified version of the human brain, where inputted neurons generate output signals. The general structure of a neural network is shown in Figure 2, where there are layers of interconnected neurons. There are several layers: the input layer, where inputs are given as weights to input neurons; the output layer, where output neurons do processing based on the input using an activation function and generate output; and single/multiple hidden layers, where intermediary neurons process the weighted sums of the inputs. Sometimes, output neurons can also be connected to each other and not just to the previous inputs, but this is complex and uncommon [20,23].

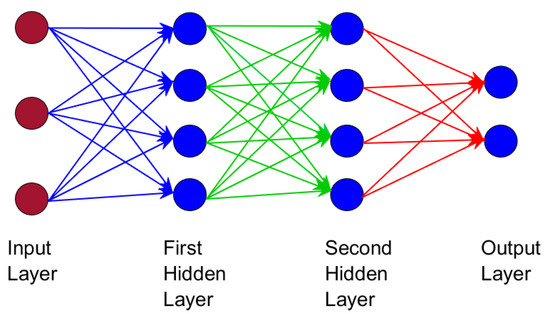
Figure 2. A depiction of a simplified artificial neural network with input–output layer and interconnecting hidden layers shown [8] [Reproduced with permission from Rustum, R. Modelling Activated Sludge Wastewater Treatment Plants Using Artificial Intelligence Techniques (Fuzzy Logic and Neural Networks). Doctor of Philosophy. Heriot-Watt University. April 2009.].

The neuron weights are determined using multiple data sets’ training and validation processes. This is achieved by introducing various data sets of inputs and corresponding outputs (real experimental results) to the neural network. Weights will be continuously adjusted to minimize errors. These training data sets will also help identify the number of hidden neurons; more data points used means more hidden neurons are required. Validation or verification using separate datasets should be conducted at the end of the training process to ensure it was achieved correctly [23]. A few examples of ANN used in WWTP modelling are given below.

Plonka [23] used a layered ANN to create a virtual sensor that measures nitrate–nitrogen in the activated sludge reactor tank. The predicted readings from the ANN were then compared to the actual probe in the reactor. Cascade training was used to form a layered ANN wherein more neurons are added, each creating another network layer. There has not been an exact method of calculating the size of an ANN, so this type of training is beneficial. The training was conducted using ‘FannTool’ graphical interface [23]. ANNs require large samples of inputs and outputs to train the network, in this case, the measuring probes. The input needed was obtained by computer simulation via the STOAT (Sewage Treatment Operation and Analysis over Time) application with the BSM1 (Benchmark Simulation Model No. 1) mathematical model. STOAT works with both COD and BOD measurements. The ANN was run with two sets of data—one obtained from the simulation and another set of distorted data where artificial random noise of ±2% of each individual value was introduced into the simulation data. Values of average error found for both sets of data were found to be well below the sensitivity of the actual measuring probes. The distortion had a negligible effect on the accuracy of the calculations.

Messaoud et al. [24] used a standard feedforward neural network to predict the performance of the wastewater treatment process. The ANN used had one hidden layer and one output layer, with training conducted for a different number of iterations and a number of hidden layer neurons. Training and validation were conducted with different data sets taken from a WWTP in Ain Beida, Algeria, designed for 16,000 m³/day flow and 300,000 equivalent population. Sensitivity analysis was conducted to determine input parameters. Results showed the ANN model is a good tool for reliability prediction and can help plant operators predict parameters, especially BOD, which usually has a five-day determination period.

2.3. Multilayer Perceptron Neural Network (MLP)

MLPs are a class of feedforward ANNs, especially with backpropagation (MLPBPNN) which minimizes the error function of MLP by using a gradient descent method to change the value of the weights. Kusiak and Wei [25] used a multilayer perceptron (MLP) neural network to build and validate an ASP model. Data used were from an industrial Wastewater Reclamation Authority (WRA) in Des Moines, Iowa, US. Dissolved oxygen (DO) concentration was used as a control variable. The MLP neural network was used to build three prediction models for minimizing three parameters: airflow rate, effluent CBOD, and TSS concentration. Two hundred networks were trained for each model, each with one hidden layer and neurons between three and ten. All airflow rates and TSS rates were predicted accurately; however, CBOD values obviously differed. The correlation coefficient was 0.99, indicating an accurate model.

2.4. Adaptive-Network-Based Fuzzy Inference System (ANFIS)

ANFIS joins fuzzy logic and ANN to form a combined system that extracts fuzzy rules from data to a rule-base and feeds it to the ANN [21]. A few examples of ANFIS used in WWTP are summarized below.

Araromi et al. [21] used an adaptive neuro-fuzzy inference system (ANFIS) for non-linear dynamic system identification of the wastewater treatment process. The study used ANFIS and GLM (Generalized Linear Model Regression). Brute force exhaustive search was used for the ANFIS model wherein all elements of the search space are tested iteratively, and LASSO (least absolute shrinkage and selection operator) was used as penalized regression method in GLM. Outliers were removed from the data and smoothed out. For both training and validation datasets, ANFIS predicted values better than GLM regression models. It was also found that ANFIS can be used to estimate the time required to reach an adequate performance level, as the model indicated that there are time lags in the treatment process.

Rustum [8] used an improvised ANFIS using the Kohonen Self-Organizing Map (Hybrid KSOM-ANFIS) to model an ASP and predict effluent Biological Oxygen Demand (BOD₅) and Suspended Solids (SS) concentration. Results showed the hybrid model outperformed the ANFIS model in predicting the necessary values [8]. KSOM was used to extract features from noisy data and fill in missing values [26,27,28,29]. Three years of data were taken from a WWTP in Edinburgh, UK, and two models were tested, one with ANFIS alone and another with the hybrid KSOM-ANFIS [27]. Du et al. also [30] used ANFIS to predict and have a heuristic understanding of sludge age in ASP. The combined fuzzy logic with the neural network was able to not only understand the complex relationships within the data, but also perform rule extraction. Additionally, Rustum and Forrest [31] developed a model for fault detection in the activated sludge process using the Kohonen self-organizing Map. Rustum and Adeloye [26] developed a model for knowledge discovery from activated sludge processes using unsupervised neural networks (Kohonen Self-Organizing Map).

2.5. Deep Learning Neural Network (DNN)

DNNs are a form of ANN where there is higher complexity in the number of layers and connections between layers. It is the latest development in the field of ANNs, and an example used in WWTP is given below.

Oulebsir [32] used a deep neural network (DNN) to optimize the energy conservation of WWTP. It is estimated that energy costs consume 28% of the total costs of wastewater treatment. This paper proposed a methodology to select the best methods of energy consumption based on Key Performance Indicators (KPI) at a conventional activated sludge WWTP located in Boumerdes, Algeria. Daily data for entry/exit pollution parameters—[BOD5, COD, SS, NH4], total flow, total energy consumed, influent temperature, and recirculated sludge flow—were collected from the treatment plant and cleaned of missing data and outliers. Two types of data selection were performed; effluent quality values that were near design values corresponding to environmental standards were selected. KPIs used here were Treatment Yield, Global Treatment Yield, and Standardized Global Treatment Yield. The second selection was made to find the best energy consumption according to certain KPIs: the Pollution Index, Abatement Degree of Pollution, Global Degree of Abatement of Pollution, and Water Quality Index. The selected data were then used to train (80% of data) and test (20% of data). DNN used for this study had four inputs, and six hidden layers, each having 200 neurons. Trial and error were used for the number of neurons/hidden layers. Results showed good performance for all models. A model trained with Global Degree of Abatement of Pollution (GPAB) selected data was best; however, Root Mean Squared Error observations standard deviation ratio (RSR) in the testing period, and Percentage Bias (PBIAS) values indicated overfitting. The model trained with Pollution Index PI (Water Quality Index, WQI) also had R² close to the GPAB model; however, PBIAS showed underfitting. It was concluded from the values of the KPIs that pollution entering the WWTP had more effect on energy consumption than effluent parameters and removal efficiency. The study states that limited data might restrict the applicability of their model to other WWTP and that more criteria might be applied in selecting the data to train and test the DNN for better understanding.

3. Optimization of Operation and Control of Activated Sludge Process (ASP)

Wastewater requires comprehensive treatment before being disposed of safely or reused for specific applications. Therefore, many locally and globally standards are imposed on the effluent before it is approved for its end purpose. Given the strict criteria, optimizing the operational and control process is the only way to reduce costs since stinting on quality is impossible [5].

For optimal performance of ASP, there must be a balance maintained between available organic matter for bacteria to break down, the available number of bacteria (activated sludge), and dissolved oxygen necessary for effective breakdown. In terms of parameters to be controlled, these balance factors translate to aeration rate, dissolved oxygen concentration (DO), rate of recirculation of activated sludge (RAS), and amount of excess sludge disposed of from the secondary clarifier (WAS). Further secondary parameters include Mixed Liquor Suspended Solids (MLSS) concentration, Food to Microorganism Ratio (F:M), and sludge age [8]. Some common operational problems in the operation of ASP are sludge bulking and foaming caused by non-degradable surfactants or overgrowth of filamentous bacteria in the sludge. It can cause poor settling of sludge, resulting in lower effluent quality, loss of active bacteria, and increased costs. Therefore, ASP operators need to avoid this issue for a successful treatment process, usually by predicting the Sludge Volume Index (SVI) [22].

Optimization of the ASP would balance operation and energy consumption while also considering safety and other environmental factors. For example, the aeration process included in activated sludge treatment within WWTP, although very important for mixing the influent with enough oxygen for the proliferation of bacteria, and mixing sludge with wastewater influent, consumes around 60% of energy consumption [5,32]. Then, the secondary clarifier collects treated water from the activated sludge reactor and purifies it further using sedimentation [5]. Nitrification is another process where dissolved oxygen (DO) content is crucial to the effective removal of nitrogen (in the form of nitrate, ammonia, nitrite, etc.), which is difficult to remove. Generally, WWTPs are a necessary component in society, and, therefore, energy conservation is not the primary focus. However, even though WWTPs are relatively inefficient in energy consumption, there is potential for improvement. A possibility here is to utilize electricity generated from biomass for a part of the WWTP’s energy demand [20,32].

As seen above, the process of ASP optimization involves a balancing act of many factors, usually achieved by an optimization algorithm. Any such algorithm must have the following components: an objective function that should either be minimized or maximized for best performance, state variables of the process, decision variables which are the values that should be manipulated to maximize or minimize the objective function, and constraints placed on the decision variables to avoid generating unfeasible or undesirable solutions [32]. If one single objective is to be fulfilled, the algorithm is called Single Objective Optimization (SOO). However, the typical ASP will have several objectives to optimize, for example, maximizing the dissolved oxygen (DO) concentration within the aerator while minimizing energy output and costs, which may end up contradicting each other. So, a single solution cannot be found that satisfies all the objectives. The algorithms that deal with these multiple conflicting objectives and associated restraints are multiobjective optimization (MOO) algorithms. Utilizing the algorithms will provide a set of non-dominated solutions called a Pareto set rather than one single solution. These solutions can then be judged based on trade-offs, and the final solution can be selected [33]. In addition, a common issue in MOOs is that of local optima being found, which means the algorithm will often identify a solution that is the best within its neighborhood of possible solutions but not the best solution within the entire population space of possible solutions [34].

The objective function plays an essential role in any optimization algorithm. It allows the algorithm to search and find the possible solutions by evaluating its fitness against the objective function, i.e., how well each solution satisfies the objective function. A typical MOO would contain an objective function similar to the form in Equation (1):

Min_u,tf J(x, u, t_f) = [J₁, J₂,……..J_n]^T

(1)

where J is the objective function to be minimized, J₁, J₂,……..J_n represents the multiple objectives, t is time, t_f is the time horizon, x is the set of process state variables, u is the set of decision variables, T is a transpose, and n is the number of objectives.

The above equation is usually subject to certain initial conditions, for example, x(t₀ = x₀), equality or inequality constraints, for example, h(x,u) = 0 or g(x,u) ≤ 0, and boundaries for decision variables, for example, u_lowerbound ≤ u ≤ u_upperbound [35,36].

Choosing the proper objective function, decision variables, and especially the constraints to avoid local optima and achieve the global optimum solution is the challenge faced in optimizing the ASP. The history of optimization of the ASP began with SOO algorithms being conducted, especially for DO concentration. However, once MOOs were used, they were usually linearized into separate SOOs to reach feasible solutions. The following sections show how a newer branch of Artificial-Intelligence-based algorithms has helped solve optimization problems with multiple objectives within the ASP.

4. Nature-Inspired Computing (NIC)

NIC is an umbrella term for Artificial Intelligence techniques that can be used to optimize processes, including the ASP. It is based primarily on the principle of how various species evolve to survive in nature. These techniques are focused on metaheuristic algorithms. Metaheuristic comes from the Greek terms ‘meta’, meaning beyond, and ‘heuristic’, meaning to discover. These algorithms intelligently use heuristics (rules learned from evolutionary processes) to identify a set of near-optimal solutions that can be sorted based on trade-offs with desired outcomes [32]. The reason for the success of such metaheuristic techniques, as stated by Yang [37], is based on three factors—the algorithms are simplistic, easy to implement, and generate diverse solutions.

NIAs can be written in several software packages such as C/C++, FORTRAN, R, PYTHON, and MATLAB; these packages can even support multiple algorithms, if necessary, based on computational power and available time [34]. The demanding part is maintaining a balance between computational speed and diversity in solutions. The greater the number of solutions considered, the greater the time to reach a solution. This is called the balance between local exploitation and global exploration. While it is essential to attain this balance, this question is still under research, mainly because of the wide variety of algorithms that exist under the NIC approach [37].

One advantage of NIAs is that they can be classified, to a certain extent, as Artificial Intelligence (AI) since the algorithms can continually adjust themselves based on the results that it obtains from the analysis. Admittedly, it is still not possible to have a truly intelligent algorithm (the perfect balance); however, current research is moving in the right direction.

One of the critical challenges this spectrum faces is the gap between theory and practical applications [37]. Most algorithms work within a small range or on one specific application, and they would have issues if applied widely. This is typical because there is no fixed mathematical framework for these analyses. Most algorithms are created based on trial and error, operating within a set of restraints that do not imitate real life with great precision [37].

5. Classification of NIC Algorithms

It is estimated that there are more than 100 NIAs currently available and classified for use in the literature. Currently, there is not a singular accepted categorization of these algorithms; however, the generally accepted classification is that all NIAs are stochastic in nature and can be divided into heuristic techniques such as Genetic Algorithm (GA) and metaheuristic techniques, which can be further subdivided into swarm-intelligence (SI)-based algorithms and bio-inspired (non-SI-based) algorithms. In addition, there is a third subset, physics or chemistry-based, rather than bio-based, but it is not considered herein [2,32].

SI-based algorithms utilize ‘swarm behavior’, which is the phenomenon in nature wherein multiple social creatures collectively function using some rules. Hence, the system has collective intelligence due to these rules, which can be described using an algorithm to generate solutions. Common examples include Ant Colony Optimization (ACO), Artificial Bee Colony (ABC), Bat Algorithm (BA), Cuckoo Search (CS), Firefly algorithm (FA), and Particle Swarm Optimization (PSO) [38].

While bio-inspired algorithms do not use swarm behavior, they still use biological concepts such as evolution and genetics. Examples are Differential Evolution (DE), Invasive Weed Optimization (IWO), Non-Invasive Weed Optimization Algorithm (NAIWO), Shuffled Frog Leaping Algorithm (SFLA), and Flower Pollination Algorithm (FPA) [37].

6. Application of NIC to Wastewater Treatment Plants

6.1. Genetic Algorithm (GA)

Genetic Algorithms are based on the principle of natural selection in nature—the base of evolution in organisms depends on a ‘survival of the fittest’ policy. GAs use pseudo-organisms in a constant-size population; they represent possible solutions and imitate the natural processes of chromosome transfer, reproduction, and mutation principles. Each pseudo-organism comprises a series of chromosome bits (0 s and 1 s) collectively representing a gene. For the algorithm to check which pseudo-organisms to ‘let live’ and which to ‘kill off’, there should be an objective function defined, which will give a measure of fitness for the pseudo-organisms. This function will differ from algorithm to algorithm and depends on the problem to be solved. A common fitness function used in several algorithms is the Mean Square Error (MSE) between the solutions generated by the algorithm and the actual or laboratory values of the process [32,39].

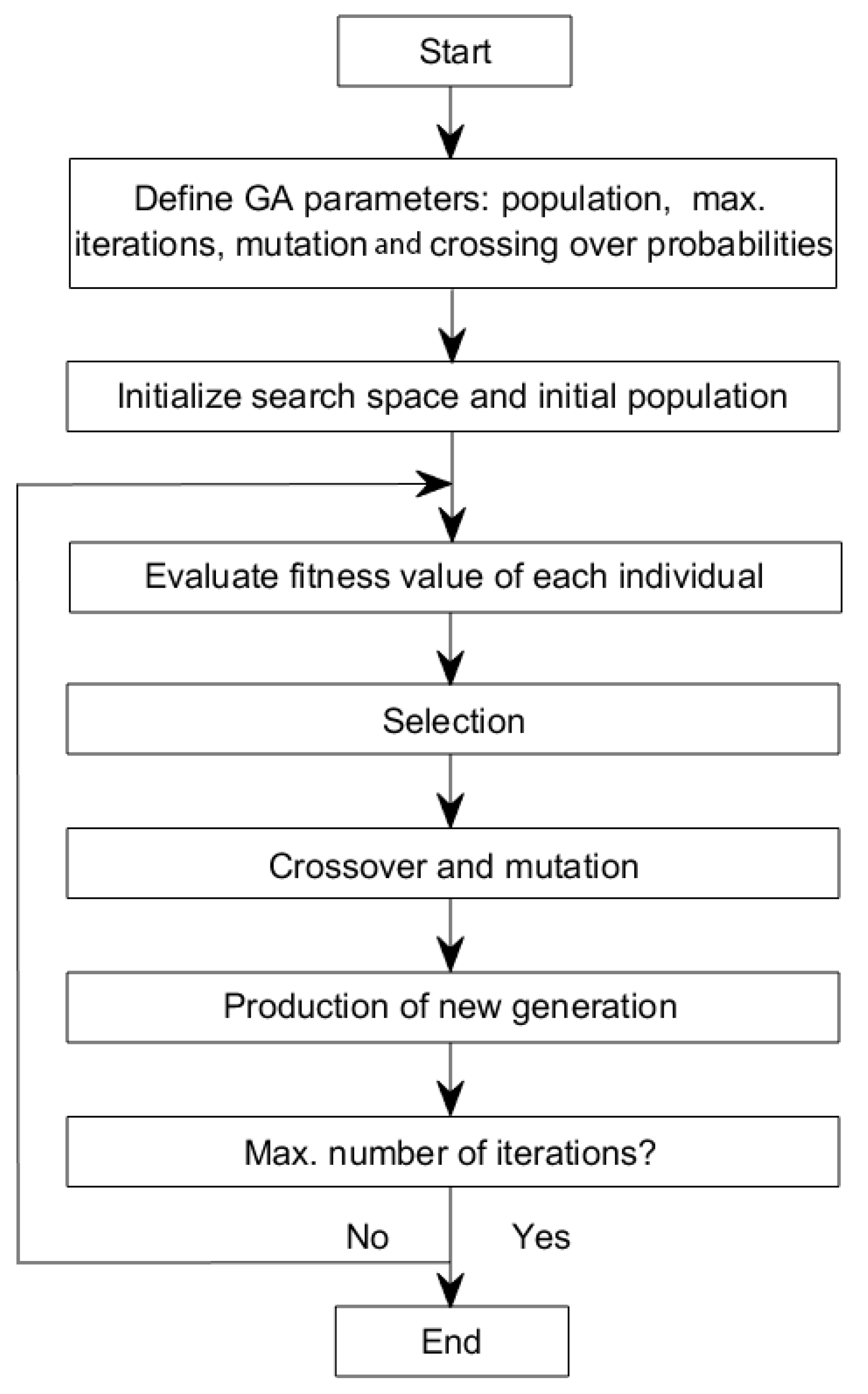
Once the initial population has been checked for fitness, evolutionary operators are used to moving to the next generations. Selection of where the best solution in the considered population will always move to the next generation, Crossover, where genetic information of two organisms in a population will be transferred and combined to make up the next generation, and Mutation, where random modifications are made to the genetic information of some organisms in the population to generate diversity and ensure that the algorithm does not converge to local optima [39]. A flowchart of a basic steady-state GA is shown in Figure 3.

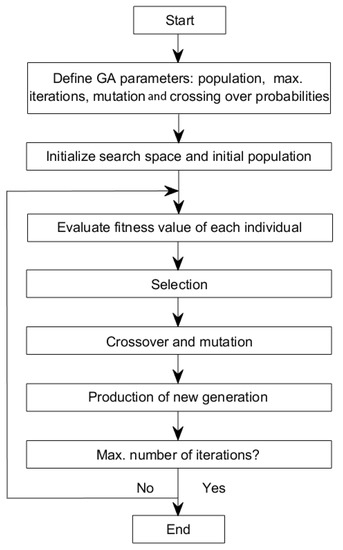
Figure 3. A flowchart depicting the steps involved in a typical Genetic Algorithm.

GA benefits are that it can handle discontinuous data and has a good chance of reaching global optimum because the whole population of solutions is being considered simultaneously. However, this increases the time required for the analysis and takes up a lot of computing power. Therefore, calibrating the model should ensure that the minimum number of iterations is used to obtain the solution from the GA. This would also mean there will be a limit to the number of parameters that can be chosen [34]. Genetic Algorithms (GAs) are also used extensively in wastewater treatment, as they have less potential to become trapped in local minima [33]. Some applications of GA in wastewater treatment are summarized in Table 1.

Table 1. Research in ASP optimization using Genetic Algorithm (GA).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Intissar Khoja, Taoufik Ladhari, Anis Sakly, Faouzi Msahli [39]	Use GA to identify parameters of an activated sludge process.	Readily biodegradable substrate concentration (SS), nitrate (SNO3), ammonia (SNH4), dissolved oxygen (SO2), external carbon concentration (Ssc), soluble substrate (Ssin), ammoniacal nitrogen (SNH4in)	Offline data from the pilot unit installed in the Engineering Laboratory of Environmental Processes (ELEP) of the National Institution of Applied Sciences (NIAS) in Toulouse, France	Mean Square Error (MSE)	Not specified	Compared to Simplex method, GA was able to identify model parameters with similar values to laboratory data
Fang Fang, Bing-Jie Ni, Han-Qing Yu [40]	Use accelerating GA (AGA) to estimate kinetic parameters of the activated sludge process	Microbial yield, the coefficient for growth on the substrate (YH), maximum specific growth rate (µH), substrate half-saturation constant (Ks), a fraction of substrate diverted to storage product formation (kSTO)	Online data from a laboratory-scale sequencing batch reactor (SBR)	Minimizing the sum of the squared weighted errors (SSWE)	Not specified	AGA could find values of parameters with a good fit to values in the literature. Compared to the Monte Carlo method and PSO, GA converged to the solution more rapidly.
Jawed Iqbal, Chandan Guria [33]	Binary-coded elitist non-dominated sorting GA is used for: estimating kinetic parameters determining optimal operation conditions such that throughput is maximized, and effluent BOD and plant operating cost is minimized	The maximum growth rate constant (ko), half-saturation constant (Ks), a decimal fraction of food mass converted to biomass (Y), endogenous decay rate constant (kd) Mean cell residence time (θc), MLSS concentration in reactor (X), underflow MLSS concentration (Xu), food to microorganism ratio (F/M), oxygen demand (OD), sludge production rate (Qw)	Online data from an operating domestic wastewater treatment unit located in Rajrappa (CCL, India)	Normalized weighted sum of square errors (E) between operating plant and computed values Maximize influent flow rate. Then, the influent flow is maximized, and effluent BOD is minimized simultaneously. Then, plant operating cost (OC) is minimized while maximizing influent flow rate. Then, OC and effluent BOD is minimized. Then, flow rate is maximized, and effluent BOD and OC are minimized simultaneously.	Not specified	All the objectives are performed successfully using the GA.
S. Revollar, M. Francisco, P. Vega, R. Lamanna [41]	Use a real-coded GA for integrated synthesis and design of the activated sludge process	Reactor volumes (v1, v2), a cross-sectional area of settler (A), aeration factors for each reactor (Fk1, Fk2), overall recycle flow (q2)	Offline data from a model developed by Moreno et al. (1992) based on the wastewater treatment process of the Manresa plant (Spain)	Minimize a cost function based on Integral Square Error (ISE)	Not specified	GA gives smaller relative error compared to Simulated Annealing (SA) and deterministic Branch and Bound algorithm (B&B).

6.2. Particle Swarm Optimization (PSO)

Particle Swarm Optimization (PSO) is an evolutionary algorithm that emulates social behavior within a swarm. The algorithm uses a random set of data with a certain population size, including the candidate solutions or particles. The particles move or fly with a certain assigned velocity through the search space to locate the best solution based on a mathematical fitness function. The particles communicate with each other; thereby, each particle will contain the memory of its best solution so far (local optimum) and the best solution of the entire population so far (global optimum). Depending on the information sharing between particles, the particles will ultimately move from their local optima and converge at a single global optimum (problem-solution). The movement of a particle from one point to the next depends on three components. An inertial component means they tend to go in the current direction of movement, a memory component means they will revisit their best solutions, and a social component means they will visit the best solutions achieved by their neighboring particles. The algorithm applies certain mathematical equations until a pre-specified rule is achieved, usually the maximum number of iterations [40,42].

PSO is known for quickly converging to an optimum solution because of not having any evolutional operators and utilizing simple mathematical operations for updating each iteration [43]. Some applications in ASP are given in Table 2.

Table 2. Research in ASP optimization using Particle Swarm Optimization (PSO).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
R.R. Wang, L.L. Cao, M.D. Liu [44]	Use multiobjective particle swarm optimization (MOPSO) to calibrate parameters of an activated sludge process model	Chemical oxygen demand (COD), total nitrogen (TN), ammoniacal nitrogen (SNH)	Offline data based on ASM3 model	Minimize relative average error between monitoring value of effluent and simulation value of the model	Not specified	Errors of the parameters were reduced by a significant margin after calibration with MOPSO, especially for COD and SNH
Mina Rafati, Mohammad Pazouki, Hossein Ghadamian, Azarmidokht Hossein nia, Ali Jalilzadeh [45]	Use PSO to calibrate and validate activated sludge model parameters	Return activated sludge (RAS), internal recycle rate (IRR), oxygen transfer coefficient (kLa)	Online data from South WWTP of Tehran	Minimize percentage difference between simulated and data values based on RMSE, Pearson correlation, and MAPE	MATLAB/Simulink	PSO was able to calibrate parameter values to minimize energy consumption and enhance plant efficiency
N.A. Selamat, N.A. Wahab, S. Sahlan [46]	Tuning of MPID controller using PSO	Biomass concentration (X), substrate concentration (S), dissolved oxygen (C), recycled biomass (Xr)	Four PID methods were chosen—Davison, Penttinen-Koivo, Maciejowki, and a proposed combined method similar to Maciejowki method	Integral Time Square Error (ITSE)	MATLAB and Simulink	PSO was used successfully with reduced time consumption and complexity to tune the parameters for the four PIDs
Huong Pei Choo [47]	Optimize a self-tuning PID controller using PSO	Dissolved oxygen and nitrate concentration, Kp, Kl, KD—parameters of tuning controller	Offline ASP model obtained using Prediction Error Estimation of Linear or Non-Linear (PEM) method	Minimize a cost function based on ISE, IAE, ITAE, ITSE	System Identification MATLAB	PSO was used to tune the PID controller automatically with a minimum ITSE value

6.3. Differential Evolution (DE)

DE is a population-based algorithm proposed by Storn and Price [43]. The algorithm begins with a uniformly random set of possible solutions from the search space and then uses the same principles as any evolutionary algorithm (EAs). The difference from other EA is that DE uses self-referential Mutation wherein Mutation of the second generation is performed using a scaled difference of each member of the population. This helps the searching of the algorithm be easier across iterations as the scaled differences adapt to the natural scaling of the population in each iteration. Basic DEs only require four basic steps—initialization of decision variables, Mutation with difference vectors, Crossover, and selection [48]. Some applications in ASP are given in Table 3.

Table 3. Research in ASP optimization using Differential Evolution (DE).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Jun-Fei Qiao, Ying Hou, Lu Zhang, Hong-Gui Han [49]	Use an adaptive multiobjective differential evolution algorithm (AMODE) with an adaptive fuzzy neural network (AFNN) controller to optimize BSM1 for standard effluent quality and low energy consumption	Nitrogen nitrate concentration in the second anoxic tank (SNO2), dissolved oxygen in the fifth tank (SO5)	Offline data from BSM1	Aeration energy (AE), pumping energy (PE), effluent quality (EQ), Integral Absolute Error (IAE)	MATLAB 2012	AMODE algorithm can optimize SO5 and SNO2 in three weather conditions—dry weather, rainy weather, and stormy weather. Additionally, AMODE with AFNN controller was able to reduce AE by 7%, PE by 8%, EQ by 1%, and IAE by 4% in dry weather conditions compared to other controllers.
Jukka Keskitalo, Kauko Leiviskä [48]	Use DE for ASM model calibration	Ammonium nitrogen (NH4-N), nitrate–nitrogen (NO3-N), COD, total phosphorous (P), total nitrogen (N)	Online data from municipal WWTP and pulp mill WWTP	The weighted sum of squares functions with RMSE, mean, and standard deviation	Not specified	DE method required much less computation time for model calibration compared to GA- and Monte-Carlo-based methods.
Wei Zhang, Jiao-long Zhang [50]	Use Crossover and Mutation of DE to improve non dominated sorting genetic algorithm (NSGA-II) in optimizing WWTP	Dissolved oxygen concentration, nitrate concentration	Offline BSM1 model	Minimize the test functions for two multiobjective problems—CONSTR and SRN	Not specified	The improved NSGA-II with DE shows much more uniform Pareto solutions with better performance index (SP) values
Hongbiao Zhou, Junfei Qiao [51]	Develop an optimal control strategy for WWTP based on an adaptive DE strategy introduced to an adaptive multiobjective evolutionary algorithm based on decomposition (AMOEA/D)	Nitrogen nitrate concentration in the second anoxic tank (SNO2), dissolved oxygen in the fifth tank (SO5), effluent suspended solids (SSe), effluent COD (CODe), effluent Kjeldahl nitrogen (SNK,e), effluent nitrate–nitrogen (SNO,e), effluent BOD (BODe), effluent flow rate (Qe)	Offline BSM1 model	Minimize energy consumption and effluent quality based on Inverted Generational Distance (IGD) and Hypervolume (HV)	Not specified	DE strategy was found to enhance search performance of AMOEA/D with more boundary solutions found, and EC is also found to be lower.

6.4. Ant Colony Optimization (ACO)

The ACO algorithm aims to imitate the foraging behavior of ants, where virtual ants move through the solution space, tending towards the areas where more ‘pheromones’ are deposited. All repetitions have the same amount of pheromone at the beginning with some maximum and minimum limits. The pheromones are usually updated according to the MAX-MIN Ant system, wherein at the end of each iteration, a new amount of pheromone is added along the edges of the path, followed by the ant achieving the best solution [52]. There is a tendency for multiple ants to produce similar solutions in one iteration, this can be overcome by using a local pheromone update in addition to the usual pheromone update in the MAX-MIN system. The local pheromone update reduces the pheromones along paths that have already been covered so remaining ants will choose different paths. This will diversify the solution space, thereby increasing the chance of finding the necessary solution. This system is referred to as Ant Colony System (ACS) [53]. ACO is useful in problems containing discrete-continuous optimization which is the case in the ASP [20]. Some applications of ACO in the ASP are given in Table 4.

Table 4. Research in ASP optimization using Ant Colony Optimization (ACO).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Martin Schlüter, Jose A. Egea, Luis T. Antelo, Antonio A. Alonso, Julio R. Banga [54]	Use extended ACO for integrated design and control of multiple WWTP problems	Dissolved oxygen based on oxygen transfer rate and nitrate level based on internal recycle flow rate Addition of aeration factors of aerated tanks (KLa3, KLa4), external recycling flow rate (Qr), sludge purge flow rate (Qw) Proportional gain O2 controller (KO), integral time O2 controller (τiO), anti-windup constant O2 controller (τtO), proportional gain N controller (KN), integral time N controller (τiN), anti-windup constant N controller (τtN), aeration factor ASU1 (KLa1), aeration factor ASU2 (KLa2), aeration factor ASU3 (KLa3), aeration factor ASU4 (KLa4), Qr, Qw, settler input layer (Lfeed) Purge flow, recycled flow, A + C feed (largest gaseous feed)	Offline data from benchmark by Dr. Ulf Jeppsson Same as above Same as above Offline data from Tennessee Eastman Process by Downs and Vogel	Integral Square Error (ISE) Same as above Same as above Minimize cost function based on total operating cost, purge costs, purge flow rate, product stream cost, compressor and steam cost	Simulink (r) Same as above Same as above Not specified	ACO gave the best overall and mean objective function value compared to SSm, CMAES, MITS ACO had a better overall objective function value while SSm had a slightly better mean objective function value ACO had the best overall and mean objective function value Using two different oracle penalty methods (ACOΩ1 and ACOΩ2), the mean objective function value of ACOΩ1 is better, but the overall value was worse than others.
Marta Verdaguer, Narcís Clara, Manel Poch [55]	Optimize influent classes based on wastewater volumes and/or pollutant loads using ACO	Total suspended solids (TSS), BOD, COD, total nitrogen (TN), total phosphorous (TP), admissible volume of influent to plant (V)	Offline case study data from a WWTP that receives wastewater from 25 industrial activities with different wastewater compositions	Global cost function based on volumetric discharge and pollutant loads to obtain maximum overall volume and pollutant loads not exceeding plant capacity	Not specified	Two versions of ACO with different penalties—sP and gP were used—both providing optimal cost solutions, with gP showing better performance in influents with large fluctuations in pollutant loads.
M. Verdaguer, N. Clara, O. Gutiérrez, M. Poch [52]	Optimize a sequence for discharge of retention tanks to prevent first flush effects	The volume of stormwater, TSS, BOD, COD, TN, TP	Offline case study based on BSM1 of a WWTP receiving domestic wastewater and stormwater runoff from nine retention tanks	Maximize global cost function based on volumetric discharge and pollutant loads	Java language	ACO optimized the total volume of each discharge to reach a maximum acceptable volume of WWTP while taking into account the storage capacity of retention tanks for each time interval
Xu Chao, Li Jinhua, Yu Zhongqing, Yang Xixin [56]	Optimize an ANFIS system using ACO and GA to model a relationship between energy consumption of WWTP pumping station and internal variables	time (t), time interval (Δt), pump unit energy consumption (E), total flow rate (F), liquid level (CL), pump operating frequency (×1, ×2, ×3, ×4, ×5)	Online data from Wuchang City WWTP	Minimize pump energy consumption based on Mean Absolute Error (MAE), absolute error standard deviation (SdAE), mean absolute percentage error (MAPE), absolute percentage error standard deviation (SdAPE)	Not specified	ACO-ANFIS model was able to reduce energy consumption of pumping station by 24%.

6.5. Cuckoo Search Algorithm (CSA)

The CSA is based on breeding patterns of cuckoo birds and the Lévy flights of some fruit flies and birds. It is commonly observed that the female cuckoo bird lays her eggs in other birds’ nests and ensures the survival of her spawn by consuming some of the host bird’s eggs that were already present in those nests. Some host birds may abandon the nest if they discover foreign eggs, and to prevent this, some cuckoo birds have learnt to imitate the shape and size of the host bird eggs. In nature, they use an almost random method to search for the nests; however, the Lévy flight mechanism is used, which is like the way many birds fly [57,58]. Lévy flights are mathematical models for random walks characterized by step lengths that follow the power law [58]. The conventional CSA uses a step size that is small enough that it will readily converge to the local optimum. If the size is larger, it will move out of the local optimum, but search precision and speed will be affected [57]. The success of the cuckoo’s nest search depends on finding a suitable host nest. Generally, it is seen that flight behavior and search of many birds and insects are like the characteristics of Lévy flights wherein they take small random steps followed by large jumps. This flight behavior, combined with the cuckoo breeding patterns, forms the basis of the CSA. There are certain rules enforced in a typical CSA, such as that each cuckoo bird lays one egg at a time in a randomly chosen nest, the best nest with the highest egg qualities passes onto the next generation, the number of host nests is fixed, and hosts can discover the cuckoo eggs based on randomized probability. If the cuckoo egg is discovered, then the host can either destroy the nest or abandon them, in which case, a new nest will be created [58] when the estimated parameters in the model are encoded as the location of the bird’s nest, with an objective function for the nest. To obtain a minimum/maximum value for the function, the CSA is used to adjust each nest position, effectively determining the value of the parameters [57]. Most important in CSA is the switching parameter probability, which controls the randomization, elitism, and local search. This gives CSA the ability to efficiently search the space. Additionally, the long jumps of the Lévy flights allow the CSA to avoid local optima [59]. Some research on applying CSA in ASP is given in Table 5.

Table 5. Research in ASP optimization using Cuckoo Search Algorithm (CSA).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Intissar Khoja, Taoufik Ladhari, Faouzi M’sahli, Anis Sakly [58]	Optimize error between simulated and experimental data for WWTP	Nitrate, ammonium, and oxygen concentrations	Offline data from the pilot unit in the Engineering Laboratory of Environmental Processes (ELEP) of the National Institution of Applied Sciences (NIAS) inToulouse, France	Mean Square Error (MSE)	Not specified	CSA provided reduced MSE compared to NM (Nelder Mead Method), GA, PSO. CSA also requires fewer algorithm parameters to be fine-tuned to the problem, so it is faster.
Xianjun Du, Junlu Wang, Veeriah Jegatheesan, Guohua Shi [57]	Estimate parameters of ASM1 using improved CSA (ICSA)	Heterotrophic yield (YH), heterotrophic decay rate (bH), maximum heterotrophic growth rate (µmH), maximum autotrophic growth rate (µmA), oxygen half-saturation coefficient for autotrophic growth (KOA), ammonia half-saturation coefficient for autotrophic growth (KNH), substrate half-saturation coefficient for heterotrophic growth (KS)	Offline data based on ASM1 from Pingliang Wastewater Treatment Plant, Gansu Province, China	Least squares error	Not specified	When there are large disturbances in the system, ICSA was able to predict the values better than CSA, and GA with minimum errors.
Taoufik Ladhari, Intissar Khoja, Faouzi Msahli, Anis Sakly [59]	Estimate parameters of ASM1 using CSA	Biodegradable substrate (SS) nitrate, ammonium, and oxygen concentrations	Offline data from the pilot unit in the Engineering Laboratory of Environmental Processes (ELEP) of the National Institution of Applied Sciences (NIAS) in Toulouse, France	MSE and SD (Standard Deviation)	Not specified	CSA compared with NM method, GA and PSO give minimum values of MSE and maximum SD value.
Ping Yu, Jie Cao, Veeriah Jegatheesan, Xianjun Du [60]	Optimize an Extreme Learning Machine (ELM) using Improved CSA (ICSA) for measuring BOD in WWTP	Biological Oxygen Demand (BOD)	Offline simulation on benchmark simulation model (BSM1)	MSE	Not specified	MSE from ICSA is much smaller than CSA, RVM (Relevance Vector Machine), LS-SVM (Least squares Support Vector Machine), BP (Back Propagation Neural Network)

6.6. Firefly Algorithm (FA)

The Firefly Algorithm (FA) is based on the flashing patterns of fireflies. These patterns are produced by bioluminescence and form a sort of signal system by which the fireflies can attract mates or prey and even act as a warning system. The flashing pattern has a rhythm that can be formulated into an objective function to be optimized. A few rules for the basic FA can be as follows: fireflies are attracted to each other regardless of sex, the landscape of objective function determines the brightness of the firefly, and the brightness determines the attractiveness of a firefly. Each firefly in an FA can work almost independently, so it can be used for parallel implementation and can even outperform the PSO in this situation. The fireflies also tend to aggregate around each optimum instead of jumping from one to the other, so FA can be more accurate in finding the global optimum as well as local optima [61]. FA has been used in the field of ASP optimization, as discussed in Table 6.

Table 6. Research in ASP optimization using Firefly Algorithm (FA).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
S. Saravana Kumar, K. Latha, V. Rajinikanth [62]	Optimize a PI controller for the aerobic reactor of WWTP using FA	Dissolved oxygen (DO) based on Oxygen Transfer Coefficient (KLa)	Offline data based on model equations in ASM1	Integral Absolute Error (IAE)	Not specified	FA-based tuning method outperforms BSM1 (Benchmark Simulation Model 1) and IMC (Internal Model Control) with minimum IAE, fast settling time, less overshoot, and small undershoot of DO concentration
Norul Ashikin Norzain, Shafishuhaza Sahlan [63]	Optimize a Model Order Reduction (MOR) for WWTP using FA	Model coefficients A, B, C, and D are based on Suspended Solids input and pH output	Online data from Bunus Regional Sewage Treatment Plant	Integral Square Error (ISE)	Not specified	Compared to GSA (Gravitational Search Algorithm), the FA provided a slightly greater error; however, the difference is too small, so both methods are suitable
Javad Alavi, Ahmed A. Ewees, Sepideh Ansari, Shamsuddin Shahid, Zaher Mundher Yaseen [64]	Optimize inlet COD prediction of kernel-based extreme learning machines (KELMs) with FA	Chemical oxygen demand (COD) based on flow rate, NH4, pH, EC (electric conductivity), temperature	Online data from a modified Ludzack–Ettinger (MLE) ASP WWTP in Mashhad, Iran	RMSE, MAE, MAPE, NSE (Nash–Sutcliffe efficiency, WI (Wilmot Index of Agreement), r2 (coefficient of determination)	MATLAB 9.2	FA model and SSA (Salp swarm algorithm) simulated standard deviation better than other models (PSO, GA, GWO, SCA-Sine cosine algorithm), leading to smaller RMSE.

6.7. Whale Optimization Algorithm (WOA)

This algorithm is based on the bubble-net feeding behavior of the whale. When they hunt for nutrients close to the water surface, whales exhibit a spiral movement around their prey characterized by distinctive bubbles along an Archimedean path. The algorithm consists of two phases—prey and encircling. The whales will update their position based on the best location with respect to the prey, which is called encircling behavior. There is a 50% probability of whether the whale will continue moving around prey in shrinking circles or if they will update their position randomly [5]. The advantage of WOA is the exploration where search space is randomly explored and intensive exploitation wherein current top solutions are searched intensively until the best solution is found. The main issues with WOA are the tendency to end in local optima and slow convergence speed compared to other algorithms [65]. Some applications of WOA in ASP are given in Table 7.

Table 7. Research in ASP optimization using Whale Optimization Algorithm (WOA).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Ahmed M. Anter, Deepak Gupta, Oscar Castillo [66]	A binary version of WOA, with chaos theory and fuzzy logic (CF-WOA) used to create a model for feature selection and to detect sensor process faults in WWTP		Online data from an urban WWTP in Manresa, Barcelona	Fast fuzzy c-means clustering algorithm (FCM), checked with mean fitness value, standard deviation (SD), best score value (BS), worst score value (WS), average feature selection size (ASS), Wilcoxon’s rank-sum test, average accuracy (AC), and RMSE	Not specified	CF-WOA model provides the optimal estimated parameters, higher convergence speed, shorter execution time and better accuracy compared to WOA, Chaotic Ant Lion Optimization (CALO), Ant Lion Optimization (ALO), Chaotic Binary Crow Search Algorithm (BCCSA), Grey Wolf Optimizer (GWO), and BA
Bayram Arda Kuş, Tolgay Kara [5]	Use WOA to optimize diffuser location for a Unified Tank Model (UTM) in a WWTP	Dissolved oxygen (DO) Concentration	Online data from Oğuzeli WWTP in Giaziantep province, Turkey	RMSE	Not specified	The time duration of aeration and the accuracy of DO variation in the UTM with WOA are significantly improved compared to the UTM model.
Roxana Recio-Colmenares, Kelly Joel Gurubel-Tun, Virgilio Zúñiga-Grajeda [67]	Use WOA for optimizing parameters of a Recurrent High Order Neural Network (RHONN) for WWTP	Total chemical oxygen demand (COD) is controlled by oxygen transfer rate (KLA)	Offline ASM1 model	Mean square tracking error between neural model state and given trajectory reference	MATLAB R2016a	WOA is compared with Harris Hawks Optimizations (HHO), Ant Lion Optimization (ALO), and Grey Wolf Optimization (GWO). ALO showed a better tracking trajectory, WOA showed a more stable KLA, and HHO showed better convergence for neural states.
Akey Sungheetha, Rajesh Sharma R [65]	Combine WOA with fuzzy logic, chaos theory, BA to create a novel model for WWTP parameter estimation and process fault detection	Not specified	Online dataset of an urban WWTP from UCI repository	Not specified	Not specified	The fuzzy combination weights (FCW-BAT) algorithm was able to overcome the local minima during feature selection of the Whale Optimization Algorithm (WOA).

6.8. Bat Algorithm (BA)

Bat Algorithm (BA) is based on the echolocation behavior of bats for their foraging needs. Bats use echolocation for multiple purposes—to estimate distances and to differentiate between food, prey, and obstacles. They do this by the varying wavelength of their sound emissions and by adjusting the emissions rate as they come into proximity to their target. The BA imitates this behavior by the following: create an initial bat population from the search space, and set the initial parameters—sound pulse frequency, rate, and loudness. The algorithm will then generate the position and velocity for each bat. Now each bat is ranked for pulse rate, loudness, and minimum frequency depending on the random number generated (rand > pulse, rand > loudness), and the best solutions are selected [68]. The loudness and pulse rate provides a mechanism for automatic control, allowing the algorithm to balance between exploration and exploitation [69]. The process continues until the stopping criteria are met [68]. BA has been used in the field of ASP optimization, as summarized in Table 8.

Table 8. Research in ASP optimization using Bat Algorithm (BA).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Nur Atikah Nor’Azlan, Nur Asmiza Selamat [68]	Optimize parameters of multivariate PID controller	Scalar tuning parameters—Epsilon (ε), Alpha (α), and Rho ($\rho$)	Offline WWTP simulation benchmark model by COST Action 624 and 682 Research Group	Integral Time Square Error (ITSE)	MATLAB/Simulink	The BA algorithm with the proposed tuning methods gave optimum results for the parameters.
Veri Julianto, Kuntjoro A. Sidarto [70]	Solve five single and multiple objective optimization problems on WWTP operation and performance monitoring	Mean cell residence time (θc), MLSS concentration in reactor (X), under flow MLSS concentration (Xu)	Domestic WWTP in Rajarappa, CGL, India	Direct Maximization/ Minimization of parameters with respect to constraints. A use penalty method for Pareto solutions.	Software not specified—used processor AMD A8-4555M APU Radeon, 8 GB RAM, 1.6 GHz	All single/multiobjective problems are solved successfully using BA.
Akey Sungheetha, Rajesh Sharma R [65]	Combine BA with fuzzy logic, chaos theory, Whale Optimization Algorithm (WOA) to create a novel model for WWTP parameter estimation and process fault detection	Not specified	Online dataset of an urban WWTP from UCI repository	Not specified	Not specified	The fuzzy combination weights (FCW-BAT) algorithm was able to overcome the local minima during feature selection of the Whale Optimization Algorithm (WOA).
Bin Zhao, Hao Chen, Diankui Gao, Lizhi Xu, Yuanyuan Zhang [71]	An improved BA is used to optimize parameters of Bandelet Neural Network to predict membrane flux and recovery rate for a Membrane Bioreactor (MBR) in ASP.	Specific membrane flux (J), a recovery rate of specific membrane flux (γ)	History data from test and industrial production in an MBR sewage treatment plant	Mean Square Error (MSE)	Not specified	The improved BA (BNN-IBA) showed the highest performance and efficiency compared to traditional BA and Linear Size History Adaptive Differential Evolution Algorithm (LSHADE-RSP)

6.9. Invasive Weed Optimization Algorithm (IWO)

The Invasive Weed Optimization (IWO) algorithm imitates field weeds’ growth, reproduction, diffusion, and competition. Weeds generally show a strong pattern of dominance in their behavior. With successive iterations, the IWO algorithm depicts a narrowing spatial distribution of the next generation of seeds, which gives the algorithm better global searchability at the beginning and better localized searchability in the later iterations. However, this may end up hindering the results, so the IWO must be improved [12]. Possible solutions (weeds) are generated randomly in the D-dimension solution space, and the seeds grow and bloom. The new generation of seeds in the next iteration is based on parent fitness. Spatial diffusion is represented by the standard deviation of the normal distribution of seeds in the search space. The maximum population is pre-set, and when it is reached, the parents will reproduce and then the adaptive value is used to eliminate unfit parents/children [12]. The advantage of IWO is that it allows all possible candidates to participate in the reproduction process to form the next generation. This contrasts with GA, where less-fitted individuals would not be allowed to reproduce. Additionally, compared to PSO, which has a heavy computational burden due to multiple updates (position, velocity, etc.) in every iteration, IWO is straightforward and, therefore, less computationally heavy [72]. IWO has been used in the field of ASP optimization, as discussed in Table 9.

Table 9. Research in ASP optimization using Invasive Weed Optimization Algorithm (IWO).

Authors	Optimization Problem	Parameters	Location of Case Study	Fitness Function	Software	Major Findings
Xianjun Du, Yue Ma, Zueqin Wei, Veeriah Jegatheesan [12]	Optimize kinetic parameters of ASM1 model	Heterotrophic yield coefficient (YH), the attenuation coefficient of heterotrophic bacteria (bH), maximum specific growth rate coefficient of heterotrophic bacteria (µH), maximum specific growth rate of autotrophic bacteria (µA), oxygen half-saturation coefficient of autotrophic bacteria (KOA), ammonium half-saturation coefficient of autotrophic bacteria (KNH), half-saturation coefficient of heterotrophic bacteria (KS)	Online data measured from sensors at Pingliang City Wastewater Treatment Plant in Gansu Province, China (large full-scale) and Wushan County Wastewater Treatment Plant in Tianshui City, Gansu Province, China (small scale)	Sum of squares of relative errors	Not specified	ASM1 model with Niche Adaptive Intensive Weed Optimization Algorithm (NAIWO) optimized parameters agreed with measured data compared to IWA recommendations. Niche-based IWO had higher convergence accuracy and faster convergence speed than IWO, Genetic Algorithm (GA), and Bat Algorithm (BA).
Taher Abunama, Mozafar Ansari, Oluyemi Olatunji Awolusi, Khalid Muzamil Gani, Sheena Kumari, Faizal Bux [73]	Integrate IWO with Fussy Inference Systems (FIS) to enhance the modelling accuracy of WWTP parameters	Alkalinity (ALK), sulphate (SLP), phosphate (PHS), total Kjeldahl nitrogen (TKN), total suspended solids (TSS), Chemical oxygen demand (COD)	Online data from full-scale domestic WWTP in Gauteng Province of South Africa	Root Mean Square Error (RMSE) as the main criterion; also coefficient of determination (R2), Nash–Sutcliffe coefficient of efficiency (NSE), Mean Absolute Error (MAE)	MATLAB	Mutating Invasive Weed Optimization Algorithm (M-IWO) did not predict any parameter with sufficient accuracy, R2 and NSE values were low and RMSE values were high.
Macarena Céspedes, Mónica Contreras, Joaquín Cordero, Gustavo Montoya, Karen Valverde, José David Rojas [74]	Optimal tuning of industrial WWTP Proportional Integral Derivative (PID) controllers	Controller parameters—proportional gain (Kp), integral time constant (Ti), derivative time constant (Td)	Offline data—An industrial PID with a Second Order Plus Time Delay (SOPTD) plant	Integral of Absolute Value of Error (IAE)	MATLAB	IWO and PSO both found the minimum value of IAE followed by GA, Linear Biogeography-based optimization (LBBO), and ACO. IWO, along with GA also had the least number of mean iterations.
Mohamadreza Ahmadi, Hamed Mojallali, Roozbeh Izadi-Zamanabadi [72]	Optimize Particle Filtering (PF) Algorithm for state estimation of WWTP	Biodegradable substrate (S), slowly biodegradable substrate (R), heterotrophic biomass (X), inert material (P)	Offline—Mathematical model of a batch reactor	Sampling step of PF algorithm—fitness of ith particle (Fi); checked with mean of absolute percentage error (MAPE) and RMSE	Not specified	The PF-IWO can be used for state estimation of highly non-linear WWTP. It was found to solve the shortcoming of the PF, its sampling step, and accurately determine sampling step.

7. Conclusions

Optimization of wastewater treatment remains a widely researched topic, and nature-inspired techniques are some of the quicker and more efficient ways to go about it. This paper analyzed the latest algorithms developed and applied in wastewater treatment research and discussed the advantages and limitations of each technique that can be applied to the ASP. Most applications dealt with the NIAs being used to improve and optimize the models—such as finding the number of neurons needed for an ANN-based model. NIAs can have their own possible issues, as mentioned in the sections above. A short comparison of the methods reviewed here are shown below in Table 10.

Table 10. List of some benefits and advantages of reviewed nature inspired algorithms.

Algorithm	Benefits	Drawbacks
GA	Can handle discontinuous data, considers entire population space so can reach global optimum [34]	Requires long computing time; limited number of model parameters can be used [34].
PSO	Does not have evolutional operators so converges quickly; simple mathematical equations for updating iterations [43]	If size of swarm is too small or parameter selection is not conducted carefully, algorithm can become trapped in local minima [75].
DE	Simplicity of code makes implementation easier than other NIAs. The searching of the algorithm is easier across iterations as scaled differences are used to adapt to the natural scaling of the population in each iteration [76]	DE is not suited to discrete optimization problems as using different settings of control parameters can give differing results [76]
ACO	ACO is useful in problems containing discrete–continuous optimization [20].	Can become trapped in local minima. For large problems, can be time consuming to lay pheromones on the ant trails [77].
CSA	The switching parameter probability gives CSA the ability to efficiently search the space. Additionally, the long jumps of the Lévy flights allow the CSA to avoid local optima [59].	Performs best on continuous problems; can struggle with discrete problems. If step size is not chosen carefully, cannot obtain solution [78].
FA	Each firefly in an FA can work almost independently, so it can be used for parallel implementation. The fireflies also tend to aggregate around each optimum instead of jumping from one to the other, so FA can be more accurate in finding the global optimum as well as local optima [72].	Firefly always goes in one direction which can lead to low exploration capability and not reaching a solution [79].
WOA	The advantage of WOA is the exploration where search space is randomly explored and intensive exploitation wherein current top solutions are searched intensively until the best solution is found [65].	The tendency to end in local optima and slow convergence speed [65].
BA	The BA can converge quickly by transferring from exploration stage to exploitation stage at the correct time. It can deal with highly non-linear problems efficiently [80].	If exploitation stage is reached too fast, algorithm may stagnate and not reach the solution [80].
IWO	With successive iterations, the algorithm depicts a narrowing spatial distribution of the next generation of seeds, which gives the algorithm better global searchability at the beginning and better localized searchability in the later iterations. It also allows all possible candidates to participate in the reproduction process to form the next generation [80].	Improper selection of control parameters affects search ability of algorithm leading to not finding a solution or becoming trapped in local optima [80].

These NIA improved models can be of great significance in the field of wastewater treatment going into the future. Currently, lot of research has been conducted in this field; however, successful implementation in the industry remains to be achieved. This is mainly because most models are not reproducible—standardization is yet to be achieved in this aspect [81]. While there are numerous algorithms being created, there is no single framework model on which to compare efficiency of using any algorithm. Limited academic transparency is also another issue wherein code used for building a model is not available in research papers, making it harder for other researchers to improve upon it or even for treatment plant operators to utilize it [81].

Hybridization of the models, wherein multiple algorithms can be utilized within one model, might help to balance out some of the drawbacks of each algorithm while making use of individual advantages [82]. For example, ref. [83] utilized both PSO and GA within a back propagation neural network creating a hybrid model. The combination was able to use the global optimization ability of the PSO as well as the parallel computing ability of the GA to improve the model. More research conducted on hybrid models might also lead to an eventual framework model. Most research models also utilize small size data with a narrow range limiting the applicability of the models to real-life WWTP [82]. An additional step to increase the accuracy of these algorithms can be to utilize large and varied data sets, as limited data can affect model applicability across WWTPs. Further work would be to develop a descriptive model for ASP with data taken from a real-life treatment plant using an AI modelling tool such as DNN and then optimize the models using some NIAs as appropriate. Such a model could then be used to research the future applications mentioned above and ultimately lead to widespread application in treatment plants.