RETRACTED: Power Cable Status Evaluation Method Based on Electrical Tree Growth and Data Association Rules
Abstract
:1. Introduction
2. Power Cable Status Evaluation Method Based on Electrical Tree Growth
2.1. Partial Discharge and Electrical Trees
2.2. Calculation Model for the Length of Electrical Tree Growth in PD
2.3. Evaluation of the Probability of PD Faults in XLPE Cables
2.3.1. Stress–Strength Interference Model
2.3.2. Estimation of the Probability of PD Faults
3. Power Cable Status Evaluation Method Based on Data Association Rules
3.1. Comprehensive State Parameters for Power Cables
- (A)
- Key parameter preprocessing
- (B)
- Construction of state model
3.2. Calculation of Weight Coefficients
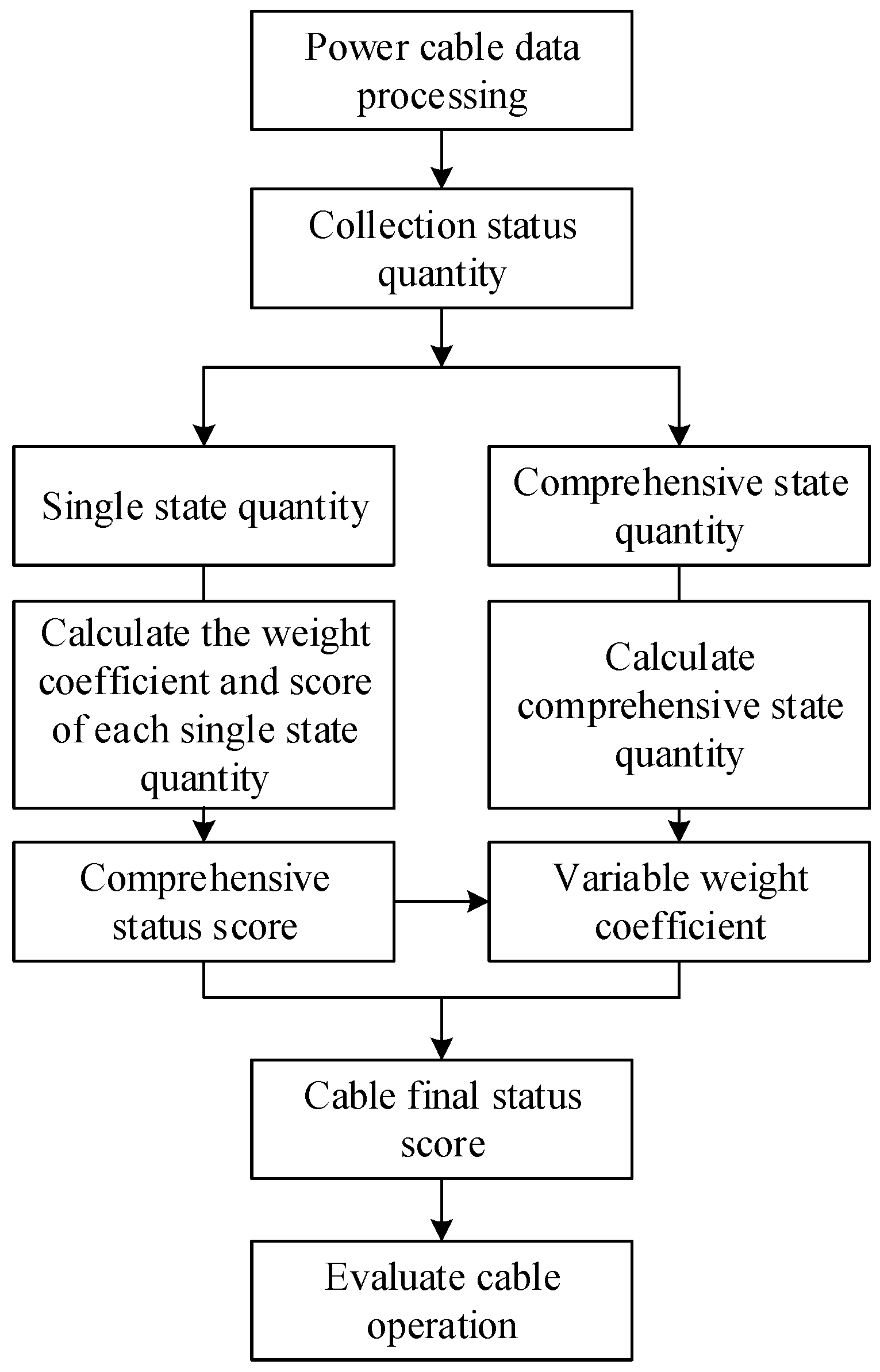
3.3. Power Cable Condition Assessment Process
4. Case Study
4.1. Example Simulation and Analysis for the Power Cable Status Evaluation Method Based on Electrical Tree Growth
4.2. Example Simulation and Analysis for the Power Cable Status Evaluation Method Based on Data Association Rules
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Zhang, Y.; Qian, K.; Wu, J.; Yin, Y. Assessment of 10kV HVAC cable under different aging modes by pulsed electro-acoustic method. In Proceedings of the 2016 International Conference on Condition Monitoring and Diagnosis (CMD), Xi’an, China, 25–28 September 2016; pp. 964–967. [Google Scholar]
- Chang, C.-K.; Boyanapalli, B.K. Assessment of the Insulation Status Aging in Power Cable Joints Using Support Vector Machine. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 2170–2177. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, S.; Wu, S.; Liu, D.; Guan, A.; Zhong, A. Analysis of Electrical Tree Growth and Partial Discharge Stagnation in Epoxy Resin. In Proceedings of the 2021 International Conference on Advanced Electrical Equipment and Reliable Operation (AEERO), Beijing, China, 15–17 October 2021; pp. 1–4. [Google Scholar]
- Peng, S.; Zhu, X.; Wu, J.; Yin, Y. Characteristics of Partial Discharge in XLPE during Electrical Tree Initiation Process under Different Temperatures. In Proceedings of the 2020 International Symposium on Electrical Insulating Materials (ISEIM), Tokyo, Japan, 13–17 September 2020; pp. 561–564. [Google Scholar]
- Chang, C.-K.; Lai, C.-S.; Wu, R.-N. Decision tree rules for insulation condition assessment of pre-molded power cable joints with artificial defects. IEEE Trans. Dielectr. Electr. Insul. 2019, 26, 1636–1644. [Google Scholar] [CrossRef]
- Zhang, Q.; Xia, X.; Yang, Z.; Yuan, C. Research on insulation condition assessment of XLPE cble based on fuzzy theory. Insul. Mater. 2014, 2, 84–88. [Google Scholar]
- Lee, C.-K.; Kwon, G.-Y.; Shin, Y.-J. Condition Assessment of I&C Cables in Nuclear Power Plants via Stepped-Frequency Waveform Reflectometry. IEEE Trans. Instrum. Meas. 2019, 68, 215–224. [Google Scholar]
- Wang, J.; Stone, P.E.C.; Coats, D.; Shin, Y.-J.; Dougal, R.A. Health Monitoring of Power Cable via Joint Time-Frequency Domain Reflectometry. IEEE Trans. Instrum. Meas. 2011, 60, 1047–1053. [Google Scholar] [CrossRef]
- Xie, L. Basic Theory and Method of Mechanical Reliability; Science Press: Beijing, China, 2009. [Google Scholar]
- Chang, C.-K.; Boyanapalli, B.-K. Application of Convolutional Neural Networks on Insulation Status Prediction Using Partial discharges for Underground Cable Joints. In Proceedings of the 2022 International Conference on Computing, Communication and Power Technology (IC3P), Visakhapatnam, India, 7–8 January 2022; pp. 297–302. [Google Scholar]
- Lei, Y.; Qi, L.; Lei, W.; Guo, K.; Tong, J. Study for the Condition Monitoring and Status Assessment of Optical fiber composite low-voltage cable. In Proceedings of the 2018 IEEE International Conference on Electronics and Communication Engineering (ICECE), Xi’an, China, 10–12 December 2018; pp. 125–129. [Google Scholar]
- Chang, C.-K.; Boyanapalli, B.-K. The Detection of Change-Point of Partial Discharges on Power Cable Joints. In Proceedings of the 2021 International Conference on Fuzzy Theory and Its Applications (iFUZZY), Taitung, Taiwan, 5–8 October 2021; pp. 1–6. [Google Scholar]
- Bindi, M.; Luchetta, A.; Scarpino, P.A.; Piccirilli, M.C.; Grasso, F.; Sturchio, A. Assessment of the health status of Medium Voltage lines through a complex neural network. In Proceedings of the 2021 AEIT International Annual Conference (AEIT), Milan, Italy, 4–8 October 2021; pp. 1–6. [Google Scholar]
- Meng, H.; Wu, X.; Zhang, K.; Liu, H.; Mao, H.; Gao, F.; Gao, Y.; Li, L.; Su, G.; Zhang, H.; et al. Aging Evaluation of 10kV overhead Cables Based on Frequency Domain Spectroscopy. In Proceedings of the 2020 IEEE 1st China International Youth Conference on Electrical Engineering (CIYCEE), Wuhan, China, 1–4 November 2020; pp. 1–5. [Google Scholar]
- Alotaibi, N.H.; Alotaibi, A.M.; Alshaiban, A.H. Usability Testing and Cognitive Walkthrough for Evaluate USB Cable (SMART Universal Serial Bus (USB)). In Proceedings of the 2019 2nd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 1–3 May 2019; pp. 1–6. [Google Scholar]
- Dong, M.; Li, W.; Nassif, A.B. Long-Term Health Index Prediction for Power Asset Classes Based on Sequence Learning. IEEE Trans. Power Deliv. 2022, 37, 197–207. [Google Scholar] [CrossRef]
- Chang, C.-K.; Chang, H.-H. Learning entirely unknown classes in time-series data using convolutional neural networks for insulation status assessment of partial discharges in power cable joints. IEEE Trans. Dielectr. Electr. Insul. 2023. [Google Scholar] [CrossRef]
- Ou, X.; Liu, S.; Chen, J.; Wang, Y.; Li, L.; Qiu, H. Insulation condition assessment of cable intermediate joint based topsis method with variable weight. In Proceedings of the 2022 Tsinghua-IET Electrical Engineering Academic Forum, Online, Beijing, China, 28–29 May 2022; pp. 75–80. [Google Scholar]
- Bai, W.; Chu, G.; Li, J.; Li, T.; Qu, Q.; Wang, S.; Fu, Y. Evaluation of the Dielectric Response Characteristics and Insulation State of Cables Under Impulse Voltage. In Proceedings of the 2022 4th International Conference on Electrical Engineering and Control Technologies (CEECT), Shanghai, China, 16–18 December 2022; pp. 635–641. [Google Scholar]
- Chu, F.; Xu, M.; Jia, S.; Hou, J.; Qian, Y.; Peng, X. Dynamic characteristics of partial discharge from typical defects of high voltage cables. In Proceedings of the 18th International Conference on AC and DC Power Transmission (ACDC 2022), Online Conference, China, 2–3 July 2022; pp. 708–711. [Google Scholar]
- Zhou, L.A.; Tang, W.Z.; Cui, X.H. Nonlinear fuzzy comprehensive evaluation model for power cable operation safety. J. Shandong Univ. Eng. Ed. 2013, 83–88. [Google Scholar]
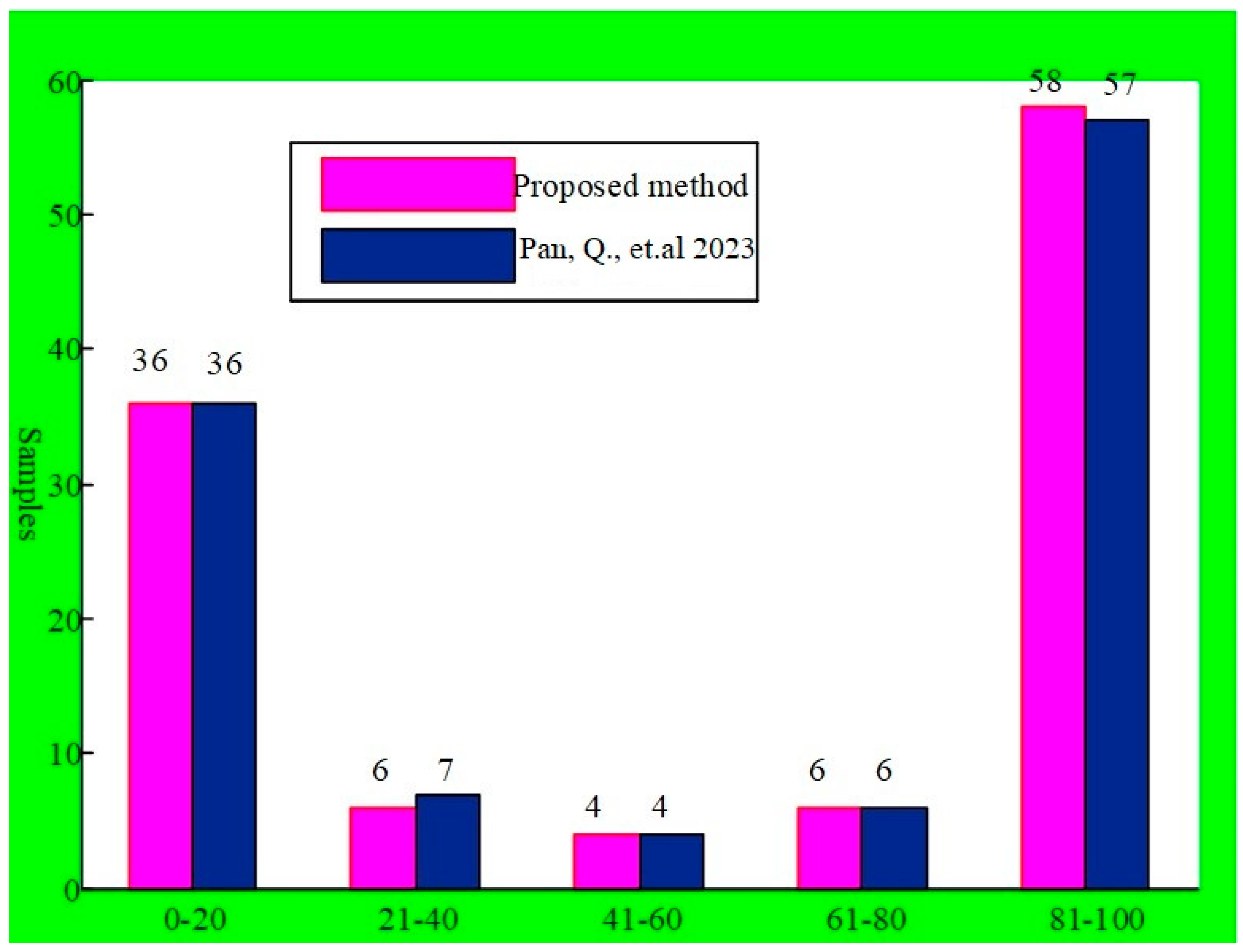
- Pan, Q.; Zhang, C.; Wei, X.; Wan, A.; Wei, Z. Assessment of MV XLPE cable aging state based on PSO-XGBoost algorithm. Electr. Power Syst. Res. 2023, 221, 109427. [Google Scholar] [CrossRef]


| Indicators | Status |
|---|---|
| Online | dielectric loss |
| core temperature | |
| grounding current | |
| Offline | voltage test |
| Groups | PD | Temperature | Groups | PD | Temperature |
|---|---|---|---|---|---|
| 1 | 820 | 30.1 | 26 | 1035 | 30.1 |
| 2 | 870 | 30.1 | 27 | 885 | 30.3 |
| 3 | 810 | 30.3 | 28 | 925 | 30.1 |
| 4 | 970 | 30.4 | 29 | 1035 | 30.3 |
| 5 | 770 | 30.3 | 30 | 915 | 30.0 |
| 6 | 1010 | 30.1 | 31 | 785 | 30.1 |
| 7 | 860 | 30.2 | 32 | 725 | 30.0 |
| 8 | 760 | 30.2 | 33 | 1045 | 30.3 |
| 9 | 940 | 30.3 | 34 | 895 | 30.1 |
| 10 | 1040 | 30.4 | 35 | 975 | 30.2 |
| 11 | 1140 | 30.3 | 36 | 1075 | 30.3 |
| 12 | 890 | 30.1 | 37 | 985 | 30.2 |
| 13 | 940 | 30.3 | 38 | 835 | 30.0 |
| 14 | 990 | 30.2 | 39 | 915 | 30.1 |
| 15 | 1050 | 30.0 | 40 | 865 | 30.0 |
| 16 | 1110 | 30.2 | 41 | 1095 | 30.3 |
| 17 | 750 | 30.1 | 42 | 1075 | 30.4 |
| 18 | 830 | 30.1 | 43 | 955 | 30.1 |
| 19 | 980 | 30.4 | 44 | 855 | 30.2 |
| 20 | 1070 | 30.5 | 45 | 935 | 30.2 |
| 21 | 1030 | 30.2 | 46 | 1065 | 30.4 |
| 22 | 960 | 30.2 | 47 | 1025 | 30.2 |
| 23 | 950 | 30.3 | 48 | 815 | 30.0 |
| 24 | 850 | 30.2 | 49 | 945 | 30.3 |
| 25 | 1000 | 30.2 | 50 | 995 | 30.4 |
| Parameter | Value |
|---|---|
| Comprehensive Indicators | Fault Cases | Number of Single Fault | Single Fault Cases | Support | Confidence | Weight Coefficient |
|---|---|---|---|---|---|---|
| Online monitoring | 112 | 130 | 110 | 0.9831 | 0.7692 | 0.2541 |
| 145 | 99 | 0.8991 | 0.6827 | 0.2267 | ||
| 133 | 106 | 0.9473 | 0.7969 | 0.2638 | ||
| 134 | 105 | 0.9473 | 0.7835 | 0.2681 | ||
| Offline detection | 110 | 156 | 95 | 0.9523 | 0.6089 | 0.3130 |
| 135 | 93 | 0.9334 | 0.6889 | 0.3243 | ||
| 120 | 85 | 0.8567 | 0.7083 | 0.3331 | ||
| Equipment | 72 | 62 | 60 | 0.8329 | 0.9677 | 0.3295 |
| 60 | 52 | 0.7235 | 0.8667 | 0.3122 | ||
| 63 | 54 | 0.7560 | 0.8571 | 0.3173 | ||
| Routine inspection | 84 | 120 | 76 | 0.9022 | 0.6333 | 0.3247 |
| 110 | 79 | 0.9418 | 0.7181 | 0.3763 | ||
| 132 | 80 | 0.9537 | 0.6061 | 0.3291 |
| Indicators | Score | Coefficient |
|---|---|---|
| Online | 14.39 | 0.5337 |
| Offline | 64.75 | 0.2461 |
| Equipment | 87.62 | 0.1377 |
| Routine inspection | 86.37 | 0.1578 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Wang, B.; Ma, H.; Zhang, J.; He, Y.; Wang, H.; Zhang, H. RETRACTED: Power Cable Status Evaluation Method Based on Electrical Tree Growth and Data Association Rules. Processes 2023, 11, 2900. https://doi.org/10.3390/pr11102900
Wang L, Wang B, Ma H, Zhang J, He Y, Wang H, Zhang H. RETRACTED: Power Cable Status Evaluation Method Based on Electrical Tree Growth and Data Association Rules. Processes. 2023; 11(10):2900. https://doi.org/10.3390/pr11102900
Chicago/Turabian StyleWang, Leixiong, Bo Wang, Hengrui Ma, Jiaxing Zhang, Yifan He, Hongxia Wang, and Hanqi Zhang. 2023. "RETRACTED: Power Cable Status Evaluation Method Based on Electrical Tree Growth and Data Association Rules" Processes 11, no. 10: 2900. https://doi.org/10.3390/pr11102900
APA StyleWang, L., Wang, B., Ma, H., Zhang, J., He, Y., Wang, H., & Zhang, H. (2023). RETRACTED: Power Cable Status Evaluation Method Based on Electrical Tree Growth and Data Association Rules. Processes, 11(10), 2900. https://doi.org/10.3390/pr11102900







