Linear Quadratic Optimal Control of Discrete-Time Stochastic Systems Driven by Homogeneous Markov Processes
Abstract
:1. Introduction
2. Preliminaries
3. LQ Problem of the Discrete-Time Linear Stochastic Systems Driven by a Homogeneous Markovian Process
3.1. Well-Posedness
- (i)
- (ii)
- (iii)
- (i)
- for any random variable x.
- (ii)
- There exists a symmetric matrix , such that for any random variable x.
- (iii)
- and .
- (iv)
- There exists a symmetric matrix , such that
3.2. Attainability
- (i)
- (ii)
- (iii)
- The LMI condition (6) is feasible.
- (iv)
- The GDRE (9) is solvable.
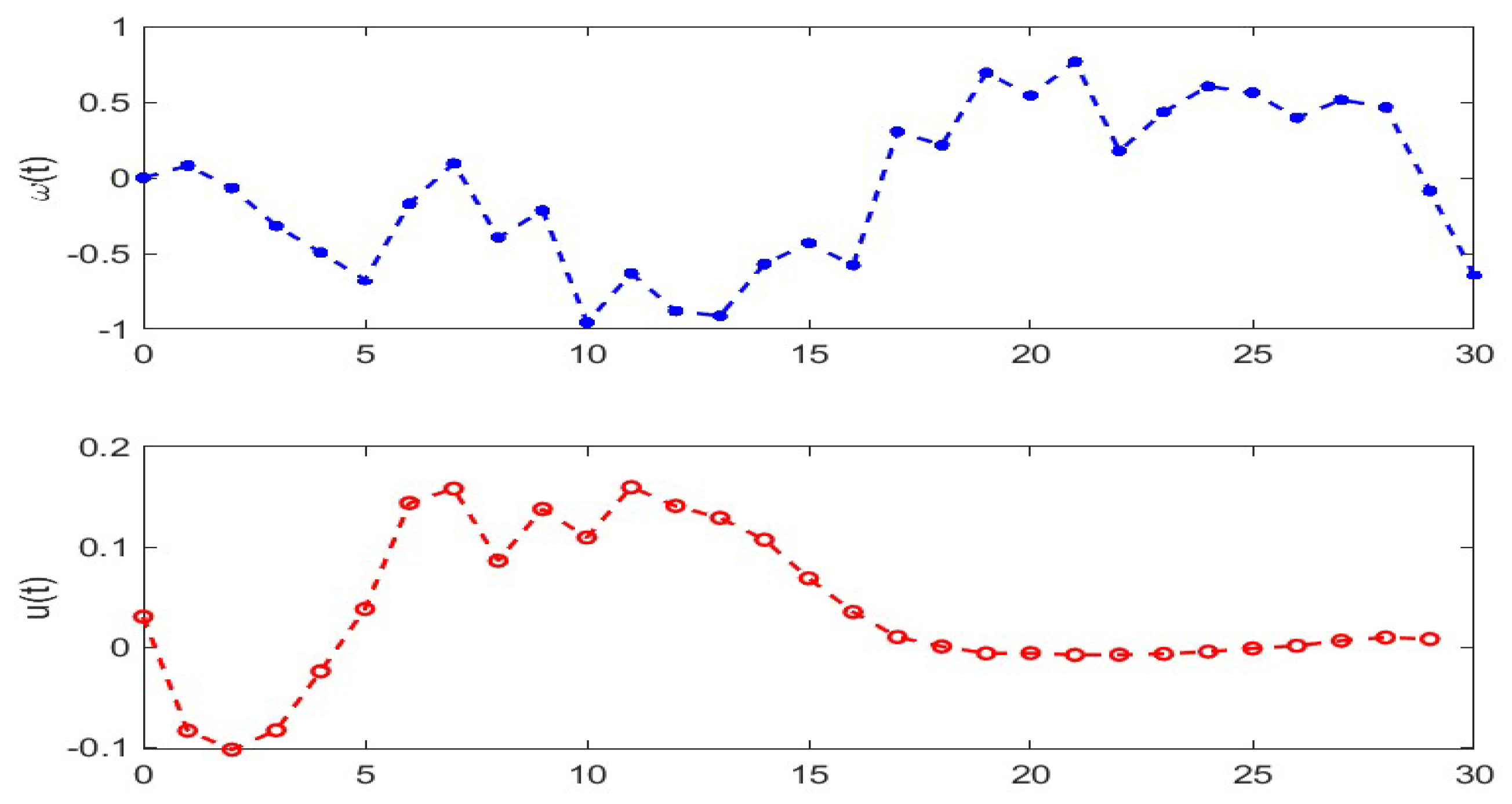
4. Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kalman, R.E. Contributions to the theory of optimal control. Bol. Soc. Mex. 1960, 5, 102–119. [Google Scholar]
- Lewis, F.L. Optimal Control; John Wiley & Sons: New York, NY, USA, 1986. [Google Scholar]
- Wonham, W.M. On a matrix Riccati equation of stochastic control. SIAM J. Control. Optim. 1968, 6, 312–326. [Google Scholar] [CrossRef]
- Luenberger, D.G. Linear and Nonlinear Programming, 2nd ed.; Addision-Wesley: Reading, MA, USA, 1984. [Google Scholar]
- De Souza, C.E.; Fragoso, M.D. On the existence of maximal solution for generalized algebraic Riccati equations arising in stochastic control. Syst. Control. Lett. 1990, 14, 233–239. [Google Scholar] [CrossRef]
- Chen, S.P.; Zhou, X.Y. Stochastic linear quadratic regulators with indefinite control weight costs. SIAM J. Control Optim. 2000, 39, 1065–1081. [Google Scholar] [CrossRef]
- Rami, M.A.; Zhou, X.Y. Linear matrix inequalities, Riccati equations, and indefinite stochastic linear quadratic controls. IEEE Trans. Autom. Control 2000, 45, 1131–1143. [Google Scholar] [CrossRef]
- Yao, D.D.; Zhang, S.Z.; Zhou, X.Y. Stochastic linear quadratic control via semidefinite programming. SIAM J. Control Optim. 2001, 40, 801–823. [Google Scholar] [CrossRef]
- Rami, M.A.; Moore, J.B.; Zhou, X.Y. Indefinite stochastic linear quadratic control and generalized differential Riccati equation. SIAM J. Control Optim. 2001, 40, 1296–1311. [Google Scholar] [CrossRef]
- Rami, M.A.; Chen, X.; Zhou, X.Y. Discrete-time indefinite LQ control with state and control dependent noises. J. Glob. Optim. 2002, 23, 245–265. [Google Scholar] [CrossRef]
- Zhang, W. Study on generalized algebraic Riccati equation and optimal regulators. Control. Theory Appl. 2003, 20, 637–640. [Google Scholar]
- Zhang, W.; Chen, B.S. On stabilizability and exact observability of stochastic systems with their applications. Automatica 2004, 40, 87–94. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, W.; Zhang, H. Infinite horizon LQ optimal control for discrete-time stochastic systems. Asian J. Control 2008, 10, 608–615. [Google Scholar] [CrossRef]
- Li, G.; Zhang, W. Discrete-time indefinite stochastic linear quadratic optimal control: Inequality constraint case. In Proceedings of the 32nd Chinese Control Conference, Xi’an, China, 26 July 2013; pp. 2327–2332. [Google Scholar]
- Huang, H.; Wang, X. LQ stochastic optimal control of forward-backward stochastic control system driven by Lévy process. In Proceedings of the IEEE Advanced Information Management, Communicates, Electronic and Automation Control Conference, Xi’an, China, 3 October 2016; pp. 1939–1943. [Google Scholar]
- Tan, C.; Zhang, H.; Wong, W. Delay-dependent algebraic Riccati equation to stabilization of networked control systems: Continuous-time case. IEEE Trans. Cybern. 2018, 48, 2783–2794. [Google Scholar] [CrossRef]
- Tan, C.; Yang, L.; Zhang, F.; Zhang, Z.; Wong, W. Stabilization of discrete time stochastic system with input delay and control dependent noise. Syst. Control Lett. 2019, 123, 62–68. [Google Scholar] [CrossRef]
- Zhang, T.; Deng, F.; Sun, Y.; Shi, P. Fault estimation and fault-tolerant control for linear discrete time-varying stochastic systems. Sci. China Inf. Sci. 2021, 64, 200201. [Google Scholar] [CrossRef]
- Jiang, X.; Zhao, D. Event-triggered fault detection for nonlinear discrete-time switched stochastic systems: A convex function method. Sci. China Inf. Sci. 2021, 64, 200204. [Google Scholar] [CrossRef]
- Dashtdar, M.; Rubanenko, O.; Rubanenko, O.; Hosseinimoghadam, S.M.S.; Belkhier, Y.; Baiai, M. Improving the Differential Protection of Power Transformers Based on Fuzzy Systems. In Proceedings of the 2021 IEEE 2nd KhPI Week on Advanced Technology (KhPIWeek), Kharkiv, Ukraine, 13 September 2021; pp. 16–21. [Google Scholar]
- Belkhier, Y.; Nath Shaw, R.; Bures, M.; Islam, M.R.; Bajaj, M.; Albalawi, F.; Alqurashi, A.; Ghoneim, S.S.M. Robust interconnection and damping assignment energy-based control for a permanent magnet synchronous motor using high order sliding mode approach and nonlinear observer. Energy Rep. 2022, 8, 1731–1740. [Google Scholar] [CrossRef]
- Djouadi, H.; Ouari, K.; Belkhier, Y.; Lehouche, H.; Ibaouene, C.; Bajaj, M.; AboRas, K.M.; Khan, B.; Kamel, S. Non-linear multivariable permanent magnet synchronous machine control: A robust non-linear generalized predictive controller approach. IET Control Theory Appl. 2023, 2023, 1–15. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, T.; Zhang, W.; Chen, B.S. New Approach to General Nonlinear Discrete-Time Stochastic H∞ Control. IEEE Trans. Autom. Control 2019, 64, 1472–1486. [Google Scholar] [CrossRef]
- Lv, Q. Well-posedness of stochastic Riccati equations and closed-loop solvability for stochastic linear quadratic optimal control problems. J. Differ. Equ. 2019, 267, 180–227. [Google Scholar]
- Tang, C.; Li, X.Q.; Huang, T.M. Solvability for indefinite mean-field stochastic linear quadratic optimal control with random jumps and its applications. Optim. Control Appl. Methods 2020, 41, 2320–2348. [Google Scholar] [CrossRef]
- Chen, X.; Zhu, Y.G. Multistage uncertain random linear quadratic optimal control. J. Syst. Sci. Complex. 2020, 33, 1–26. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.Q. A BSDE approach to stochastic linear quadratic control problem. Optim. Control Appl. Methods 2021, 42, 1206–1224. [Google Scholar] [CrossRef]
- Meng, W.J.; Shi, J.T. Linear quadratic optimal control problems of delayed backward stochastic differential equations. Appl. Math. Optim. 2021, 84, 1–37. [Google Scholar] [CrossRef]
- Li, Y.B.; Wahlberg, B.; Hu, X.M. Identifiability and solvability in inverse linear quadratic optimal control problems. J. Syst. Sci. Complex. 2021, 34, 1840–1857. [Google Scholar] [CrossRef]
- Li, Y.C.; Ma, S.P. Finite and infinite horizon indefinite linear quadratic optimal control for discrete-time singular Markov jump systems. J. Frankl. Inst. 2021, 358, 8993–9022. [Google Scholar]
- Tan, C.; Zhang, S.; Wong, W.; Zhang, Z. Feedback stabilization of uncertain networked control systems over delayed and fading channels. IEEE Trans. Control Netw. Syst. 2021, 8, 260–268. [Google Scholar] [CrossRef]
- Tan, C.; Yang, L.; Wong, W. Learning based control policy and regret analysis for online quadratic optimization with asymmetric information structure. IEEE Trans. Cybern. 2022, 52, 4797–4810. [Google Scholar] [CrossRef]
- Bolzern, P.; Colaneri, P.; Nicolao, G.D. Almost sure stability of Markov jump linear systems with deterministic switching. IEEE Trans. Autom. Control 2013, 58, 209–214. [Google Scholar] [CrossRef]
- Dong, S.; Chen, G.; Liu, M.; Wu, Z.G. Cooperative adaptive H∞ output regulation of continuous-time heterogeneous multi-agent Markov jump systems. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 3261–3265. [Google Scholar]
- Wu, X.; Shi, P.; Tang, Y.; Mao, S.; Qian, F. Stability analysis of aemi-Markov jump atochastic nonlinear systems. IEEE Trans. Autom. Control 2022, 67, 2084–2091. [Google Scholar] [CrossRef]
- Øksendal, B. Stochastic Differential Equations: An Introduction with Applications; Springer: New York, NY, USA, 2005. [Google Scholar]
- Bertoin, J. Lévy Processes; Cambridge University Process: New York, NY, USA, 1996. [Google Scholar]
- Han, Y.; Li, Z. Maximum Principle of Discrete Stochastic Control System Driven by Both Fractional Noise and White Noise. Discret. Dyn. Nat. Soc. 2020, 2020, 1959050. [Google Scholar] [CrossRef]
- Ni, Y.H.; Li, X.; Zhang, J.F. Mean-field stochastic linear-quadratic optimal control with Markov jump parameters. Syst. Control Lett. 2016, 93, 69–76. [Google Scholar] [CrossRef]
- Rami, M.A.; Chen, X.; Moore, J.B.; Zhou, X.Y. Solvability and asymptotic behavior of generalized Riccati equations arising in indefinite stochastic LQ controls. IEEE Trans. Autom. Control 2001, 46, 428–440. [Google Scholar] [CrossRef]
- Albert, A. Conditions for positive and nonnegative definiteness in terms of pseudo-inverse. SIAM J. Appl. Math. 1969, 17, 434–440. [Google Scholar] [CrossRef]
- Yu, X.; Yin, J.; Khoo, S. Generalized Lyapunov criteria on finite-time stability of stochastic nonlinear systems. Automatica 2019, 107, 183–189. [Google Scholar] [CrossRef]
- Yin, J.; Khoo, S.; Man, Z.; Yu, X. Finite-time stability and instability of stochastic nonlinear systems. Automatica 2011, 47, 2671–2677. [Google Scholar] [CrossRef]
- Bu, X.F.; Xie, Y.H. Study on characteristics of electromagnetic hybrid active vehicle suspension based on mixed H2/H∞ control. J. Manuf. Autom. 2018, 40, 129–133. [Google Scholar]
- Chen, M.; Long, H.Y.; Ju, L.Y.; Li, Y.G. Stochastic road roughness modeling and simulation in time domain. Mech. Eng. Autom. Chin. 2017, 201, 40–41. [Google Scholar]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, X.; Song, L.; Rong, D.; Zhang, R.; Zhang, W. Linear Quadratic Optimal Control of Discrete-Time Stochastic Systems Driven by Homogeneous Markov Processes. Processes 2023, 11, 2933. https://doi.org/10.3390/pr11102933
Lin X, Song L, Rong D, Zhang R, Zhang W. Linear Quadratic Optimal Control of Discrete-Time Stochastic Systems Driven by Homogeneous Markov Processes. Processes. 2023; 11(10):2933. https://doi.org/10.3390/pr11102933
Chicago/Turabian StyleLin, Xiangyun, Lifeng Song, Dehu Rong, Rui Zhang, and Weihai Zhang. 2023. "Linear Quadratic Optimal Control of Discrete-Time Stochastic Systems Driven by Homogeneous Markov Processes" Processes 11, no. 10: 2933. https://doi.org/10.3390/pr11102933





