Enhancing Response Surface Methodology through Coefficient Clipping Based on Prior Knowledge
Abstract
:1. Introduction
2. Materials and Methods
3. Result and Discussion
3.1. Case 1: One-Variable Experiment with a Factorial Design
3.2. Case 2: Two-Variable RSM Using Vehicle Miles per Gallon (MPG) Data
3.3. Case 3: Searching Optimal Experimental Conditions for Antibiotics Adsorption Using Thermal Treated Activated Carbon
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tian, J.; Yu, L.; Xue, R.; Zhuang, S.; Shan, Y. Global low-carbon energy transition in the post-COVID-19 era. Appl. Energy 2022, 307, 118205. [Google Scholar] [CrossRef]
- Kovač, A.; Paranos, M.; Marciuš, D. Hydrogen in energy transition: A review. Int. J. Hydrogen Energy 2021, 46, 10016–10035. [Google Scholar] [CrossRef]
- Kamyab, H.; Klemeš, J.J.; Van Fan, Y.; Lee, C.T. Transition to sustainable energy system for smart cities and industries. Energy 2020, 207, 118104. [Google Scholar] [CrossRef]
- Wang, S.; Sun, L.; Iqbal, S. Green financing role on renewable energy dependence and energy transition in E7 economies. Renew. Energy 2022, 200, 1561–1572. [Google Scholar] [CrossRef]
- Muntasir, M.; Zahoor, A.; Shabbir, A.M.; Haider, M.; Rehman, A.; Vishal, D. Reinvigorating the role of clean energy transition for achieving a low-carbon economy: Evidence from Bangladesh. Environ. Sci. Pollut. Res. 2021, 28, 67689–67710. [Google Scholar]
- Zagho, M.M.; Hassan, M.K.; Khraisheh, M.; Al-Maadeed, M.A.A.; Nazarenko, S. A review on recent advances in CO2 separation using zeolite and zeolite-like materials as adsorbents and fillers in mixed matrix membranes (MMMs). Chem. Eng. J. Adv. 2021, 6, 100091. [Google Scholar] [CrossRef]
- Al-Mamoori, A.; Krishnamurthy, A.; Rownaghi, A.A.; Rezaei, F. Carbon capture and utilization update. Energy Technol. 2017, 5, 834–849. [Google Scholar] [CrossRef]
- Lee, J.; Lee, W.; Ryu, K.H.; Park, J.; Lee, H.; Lee, J.H.; Park, K.T. Catholyte-free electroreduction of CO2 for sustainable production of CO: Concept, process development, techno-economic analysis, and CO2 reduction assessment. Green Chem. 2021, 23, 2397–2410. [Google Scholar] [CrossRef]
- Gür, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large-scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. [Google Scholar] [CrossRef]
- Wilcox, J.; Psarras, P.C.; Liguori, S. Assessment of reasonable opportunities for direct air capture. Environ. Res. Lett. 2017, 12, 065001. [Google Scholar] [CrossRef]
- Dieterich, V.; Buttler, A.; Hanel, A.; Spliethoff, H.; Fendt, S. Power-to-liquid via synthesis of methanol, DME or Fischer–Tropsch-fuels: A review. Energy Environ. Sci. 2020, 13, 3207–3252. [Google Scholar] [CrossRef]
- Lee, W.J.; Li, C.; Prajitno, H.; Yoo, J.; Patel, J.; Yang, Y.; Lim, S. Recent trend in thermal catalytic low temperature CO2 methanation: A critical review. Catal. Today 2021, 368, 2–19. [Google Scholar] [CrossRef]
- Olabi, A.; Onumaegbu, C.; Wilberforce, T.; Ramadan, M.; Abdelkareem, M.A.; Al-Alami, A.H. Critical review of energy storage systems. Energy 2021, 214, 118987. [Google Scholar] [CrossRef]
- IEA. World Energy Outlook 2022; IEA: Paris, France, 2022. [Google Scholar]
- Fisher, R.A. Design of experiments. Br. Med. J. 1936, 1, 554. [Google Scholar] [CrossRef]
- Durakovic, B. Design of experiments application, concepts, examples: State of the art. Period. Eng. Nat. Sci. 2017, 5, 421–439. [Google Scholar] [CrossRef]
- Kim, B.; Ryu, K.H.; Heo, S. Mean squared error criterion for model-based design of experiments with subset selection. Comput. Chem. Eng. 2022, 159, 107667. [Google Scholar] [CrossRef]
- Frey, D.D.; Engelhardt, F.; Greitzer, E.M. A role for “one-factor-at-a-time” experimentation in parameter design. Res. Eng. Des. 2003, 14, 65–74. [Google Scholar] [CrossRef]
- Karacan, F.; Ozden, U.; Karacan, S. Optimization of manufacturing conditions for activated carbon from Turkish lignite by chemical activation using response surface methodology. Appl. Therm. Eng. 2007, 27, 1212–1218. [Google Scholar] [CrossRef]
- Saari, N.; Lamaming, J.; Hashim, R.; Sulaiman, O.; Sato, M.; Arai, T.; Kosugi, A.; Nadhari, W.N.A.W. Optimization of binderless compressed veneer panel manufacturing process from oil palm trunk using response surface methodology. J. Clean. Prod. 2020, 265, 121757. [Google Scholar] [CrossRef]
- Geng, H.; Xiong, J.; Huang, D.; Lin, X.; Li, J. A prediction model of layer geometrical size in wire and arc additive manufacture using response surface methodology. Int. J. Adv. Manuf. Technol. 2017, 93, 175–186. [Google Scholar] [CrossRef]
- Jiang, N.; Zhao, Y.; Qiu, C.; Shang, K.; Lu, N.; Li, J.; Wu, Y.; Zhang, Y. Enhanced catalytic performance of CoOx-CeO2 for synergetic degradation of toluene in multistage sliding plasma system through response surface methodology (RSM). Appl. Catal. B Environ. 2019, 259, 118061. [Google Scholar] [CrossRef]
- Shah, S.N.H.; Asghar, S.; Choudhry, M.A.; Akash, M.S.H.; Rehman, N.u.; Baksh, S. Formulation and evaluation of natural gum-based sustained release matrix tablets of flurbiprofen using response surface methodology. Drug Dev. Ind. Pharm. 2009, 35, 1470–1478. [Google Scholar] [CrossRef]
- Bhattacharya, S. Central composite design for response surface methodology and its application in pharmacy. In Response Surface Methodology in Engineering Science; IntechOpen: London, UK, 2021. [Google Scholar]
- Gengec, E.; Kobya, M.; Demirbas, E.; Akyol, A.; Oktor, K. Optimization of baker’s yeast wastewater using response surface methodology by electrocoagulation. Desalination 2012, 286, 200–209. [Google Scholar] [CrossRef]
- Salah Al-Shati, A.; Alabboodi, K.O.; Shamkhi, H.A.; Abd, Z.N.; Emeen, S.I.M. The Treatment of Hospital Wastewater Using Electrocoagulation Process—Analysis by Response Surface Methodology. J. Ecol. Eng. 2023, 24, 260–276. [Google Scholar] [CrossRef]
- Zhdanova, L.; Lucas, T. Justice beliefs, personal well-being and harsh social attitudes: Initial demonstration of a polynomial regression and response surface methodology. Curr. Psychol. 2016, 35, 615–624. [Google Scholar] [CrossRef]
- Humberg, S.; Nestler, S.; Back, M.D. Response surface analysis in personality and social psychology: Checklist and clarifications for the case of congruence hypotheses. Soc. Psychol. Personal. Sci. 2019, 10, 409–419. [Google Scholar] [CrossRef]
- Askari, M.; Abbaspour-Gilandeh, Y.; Taghinezhad, E.; El Shal, A.M.; Hegazy, R.; Okasha, M. Applying the response surface methodology (RSM) approach to predict the tractive performance of an agricultural tractor during semi-deep tillage. Agriculture 2021, 11, 1043. [Google Scholar] [CrossRef]
- Yolmeh, M.; Jafari, S.M. Applications of response surface methodology in the food industry processes. Food Bioprocess Technol. 2017, 10, 413–433. [Google Scholar] [CrossRef]
- Myers, R.H.; Montgomery, D.C.; Anderson-Cook, C.M. Response Surface Methodology: Process and Product Optimization Using Designed Experiments; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Hamzaoui, A.H.; Jamoussi, B.; M’nif, A. Lithium recovery from highly concentrated solutions: Response surface methodology (RSM) process parameters optimization. Hydrometallurgy 2008, 90, 1–7. [Google Scholar] [CrossRef]
- Wong, Y.; Tan, Y.; Taufiq-Yap, Y.; Ramli, I. An optimization study for transesterification of palm oil using response surface methodology (RSM). Sains Malays. 2015, 44, 281–290. [Google Scholar] [CrossRef]
- Aktaş, N. Optimization of biopolymerization rate by response surface methodology (RSM). Enzym. Microb. Technol. 2005, 37, 441–447. [Google Scholar] [CrossRef]
- Šumić, Z.; Vakula, A.; Tepić, A.; Čakarević, J.; Vitas, J.; Pavlić, B. Modeling and optimization of red currants vacuum drying process by response surface methodology (RSM). Food Chem. 2016, 203, 465–475. [Google Scholar] [CrossRef] [PubMed]
- Pereira, L.M.S.; Milan, T.M.; Tapia-Blácido, D.R. Using Response Surface Methodology (RSM) to optimize 2G bioethanol production: A review. Biomass Bioenergy 2021, 151, 106166. [Google Scholar] [CrossRef]
- Mahapatra, A.P.K.; Saraswat, R.; Botre, M.; Paul, B.; Prasad, N. Application of response surface methodology (RSM) in statistical optimization and pharmaceutical characterization of a patient compliance effervescent tablet formulation of an antiepileptic drug levetiracetam. Future J. Pharm. Sci. 2020, 6, 82. [Google Scholar] [CrossRef]
- Bashir, M.J.; Amr, S.A.; Aziz, S.Q.; Aun, N.C.; Sethupathi, S. Wastewater treatment processes optimization using response surface methodology (RSM) compared with conventional methods: Review and comparative study. Middle-East J. Sci. Res. 2015, 23, 244–252. [Google Scholar]
- Quinlan, J.R. Combining instance-based and model-based learning. In Proceedings of the Tenth International Conference on Machine Learning, Amherst, MA, USA, 27–29 July 1993; pp. 236–243. [Google Scholar]

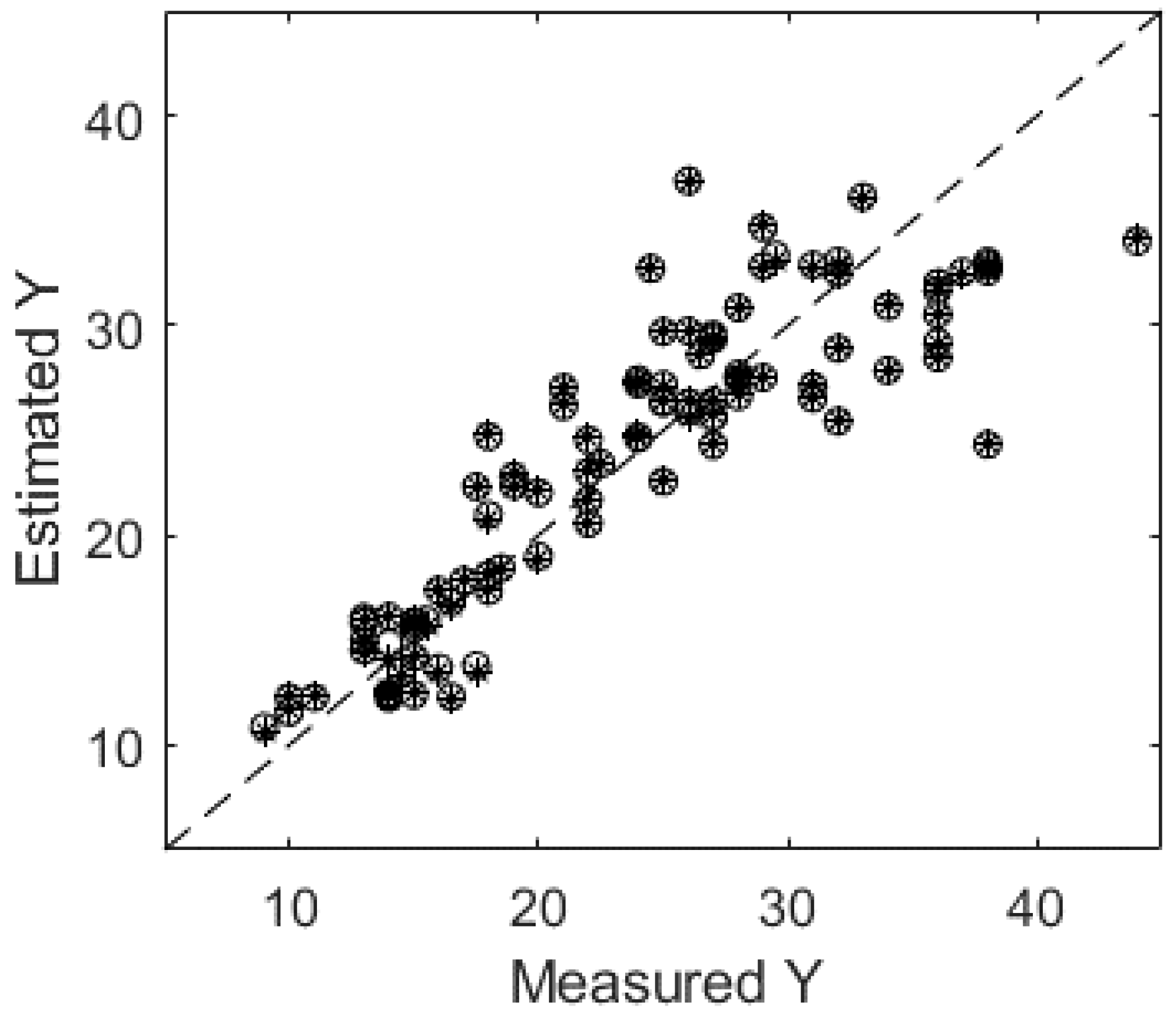

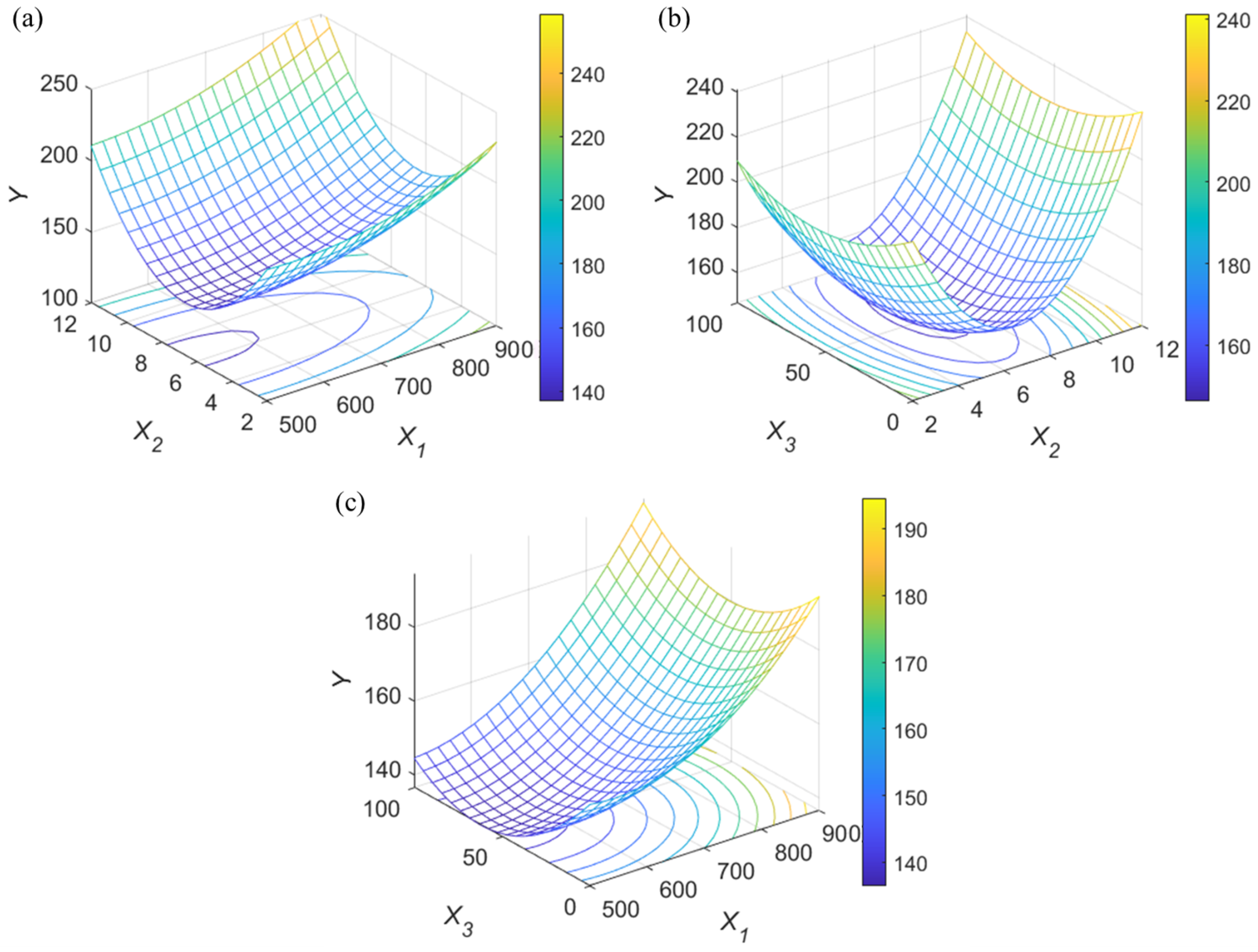
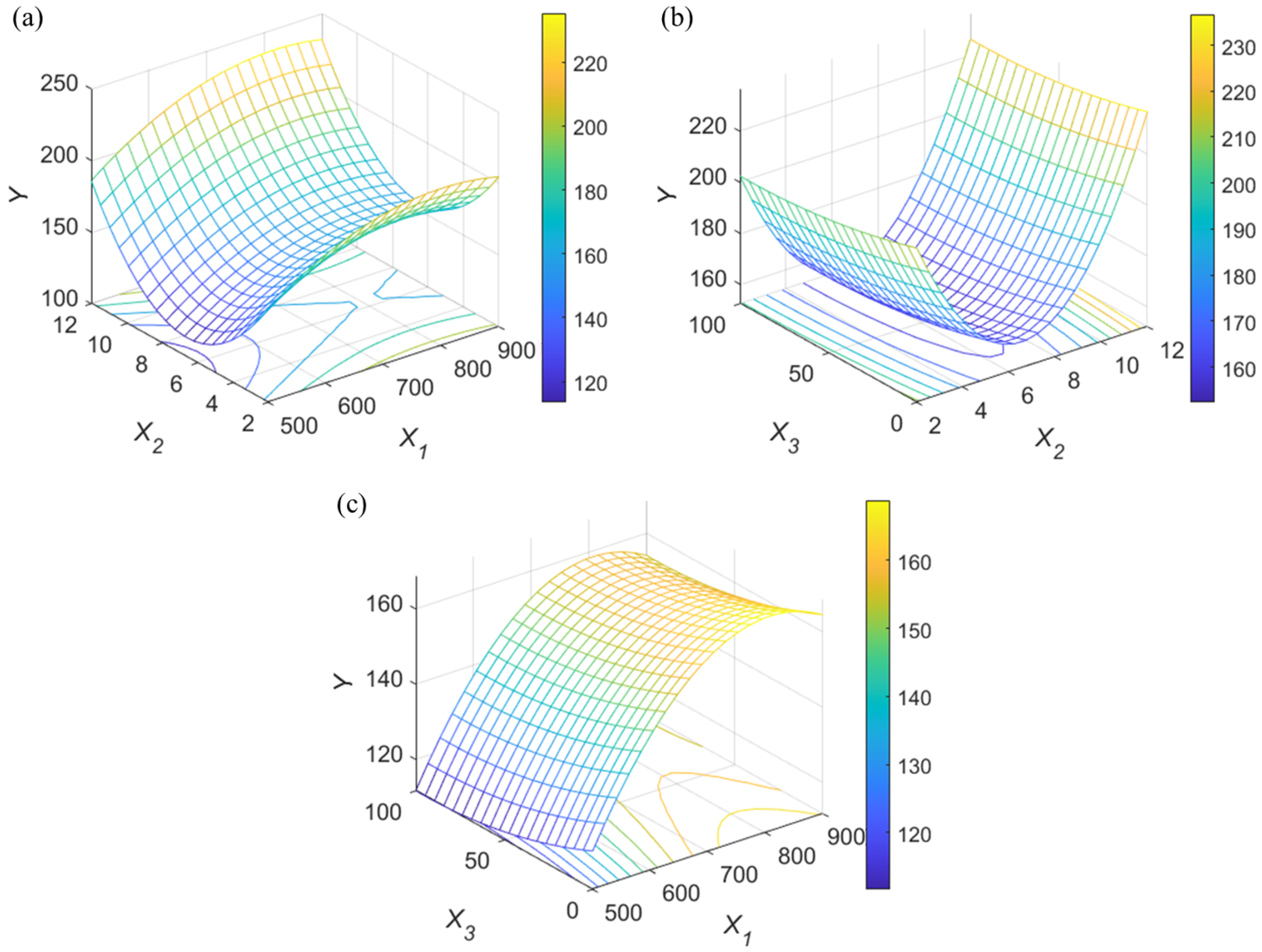
| Sample Point | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|
| Wrong behavior (%) | ||||||
| 5% | Previous | 0.72 | 0.74 | 0.38 | 0.35 | 0.18 |
| 10% | 14.9 | 12.8 | 11.5 | 10.2 | 9.1 | |
| 20% | 31.0 | 29.0 | 28.7 | 26.7 | 25.7 | |
| MSE | ||||||
| 5% | Previous | |||||
| Proposed | ||||||
| 10% | Previous | |||||
| Proposed | ||||||
| 20% | Previous | |||||
| Proposed |
| Variables | Units | Variable Level | |
|---|---|---|---|
| −1 | 1 | ||
| PAC thermal treatment temperature () | C | 500 | 900 |
| pH () | - | 2 | 12 |
| Ionic strength () | mM | 0 | 100 |
| Run | Coded Variable | Response * | ||
|---|---|---|---|---|
| 1 | 0 | 0 | 1 | 150.65 |
| 2 | 0.5 | 0.59 | 0.59 | 196.93 |
| 3 | 0.5 | −0.59 | 0.59 | 195.73 |
| 4 | −0.5 | 0.59 | 0.59 | 161.82 |
| 5 | −0.5 | −0.59 | 0.59 | 168.20 |
| 6 | 1 | 0 | 0 | 166.21 |
| 7 | 0 | 1 | 0 | 235.63 |
| 8 | 0 | 0 | 0 | 148.25 |
| 9 | 0 | −1 | 0 | 171.40 |
| 10 | −1 | 0 | 0 | 140.27 |
| 11 | 0.5 | 0.59 | −0.59 | 198.13 |
| 12 | 0.5 | −0.59 | −0.59 | 200.92 |
| 13 | −0.5 | 0.59 | −0.59 | 171.00 |
| 14 | −0.5 | −0.59 | −0.59 | 172.99 |
| 15 | 0 | 0 | −1 | 157.03 |
| 16 | 0 | 0 | 0 | 144.21 |
| 17 | 0 | 0 | 0 | 153.49 |
| 18 | 0 | 0 | 0 | 138.94 |
| 19 | 0 | 0 | 0 | 142.44 |
| 20 | 0 | 0 | 0 | 132.83 |
| 21 | 0 | 0 | 0 | 148.30 |
| 22 | 0 | 0 | 0 | 132.66 |
| 23 | 0 | 0 | 0 | 177.43 |
| 24 | 0 | 0 | 0 | 157.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, J.; Kim, D.-G.; Ryu, K.H. Enhancing Response Surface Methodology through Coefficient Clipping Based on Prior Knowledge. Processes 2023, 11, 3392. https://doi.org/10.3390/pr11123392
Kim J, Kim D-G, Ryu KH. Enhancing Response Surface Methodology through Coefficient Clipping Based on Prior Knowledge. Processes. 2023; 11(12):3392. https://doi.org/10.3390/pr11123392
Chicago/Turabian StyleKim, Jiyun, Do-Gun Kim, and Kyung Hwan Ryu. 2023. "Enhancing Response Surface Methodology through Coefficient Clipping Based on Prior Knowledge" Processes 11, no. 12: 3392. https://doi.org/10.3390/pr11123392
APA StyleKim, J., Kim, D.-G., & Ryu, K. H. (2023). Enhancing Response Surface Methodology through Coefficient Clipping Based on Prior Knowledge. Processes, 11(12), 3392. https://doi.org/10.3390/pr11123392





