Investigation of Formation Process and Intensity of Coal and Gas Outburst Shockwave
Abstract
:1. Introduction
2. The Relationship between Outburst Shock Wave and General Shock Wave
2.1. The Formation of General Shock Waves
2.2. Coal and Gas Outburst Formation Characteristics
3. Coal and Gas Outburst Shock Wave Theory
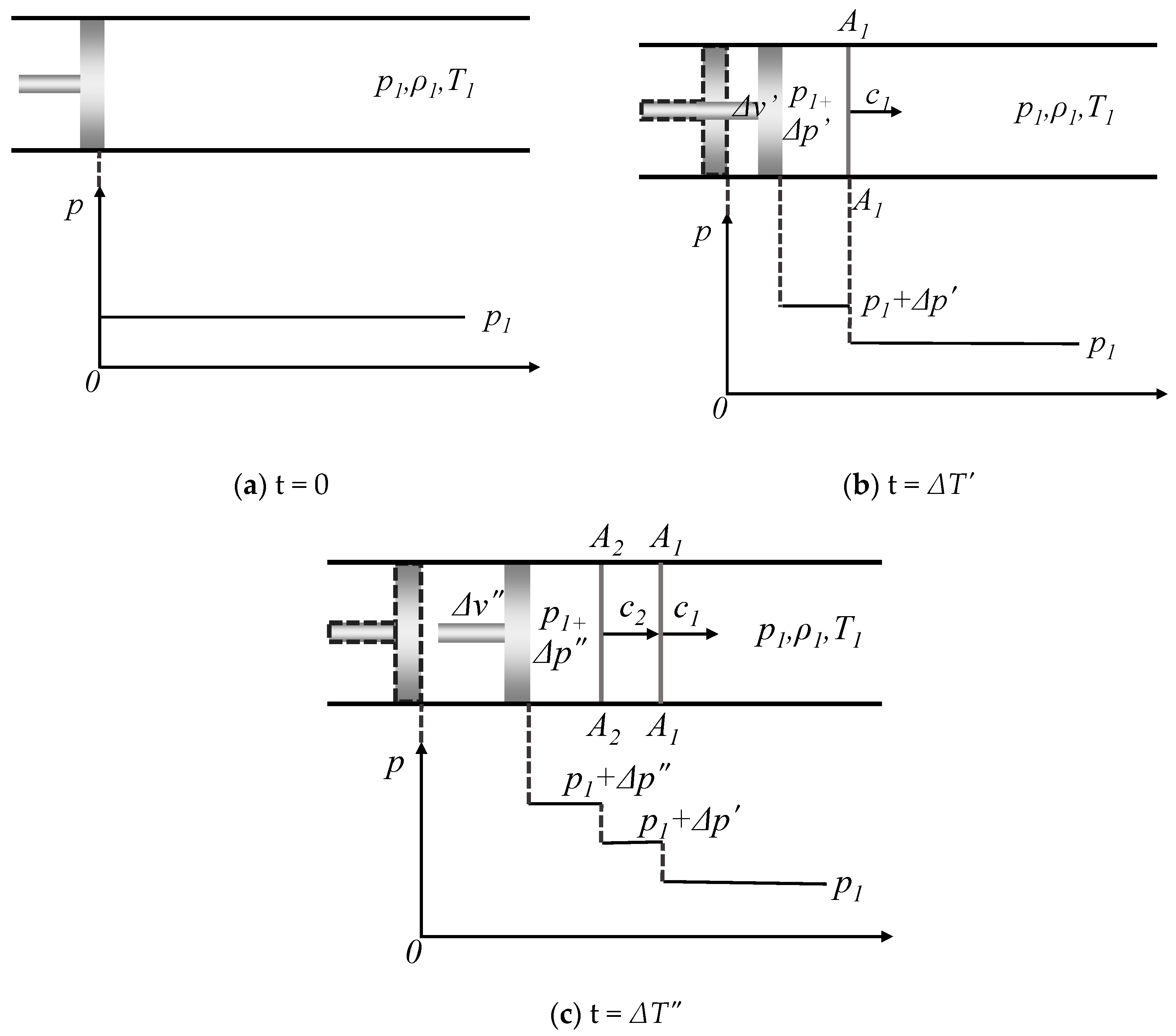
3.1. Overview of Shock Tube
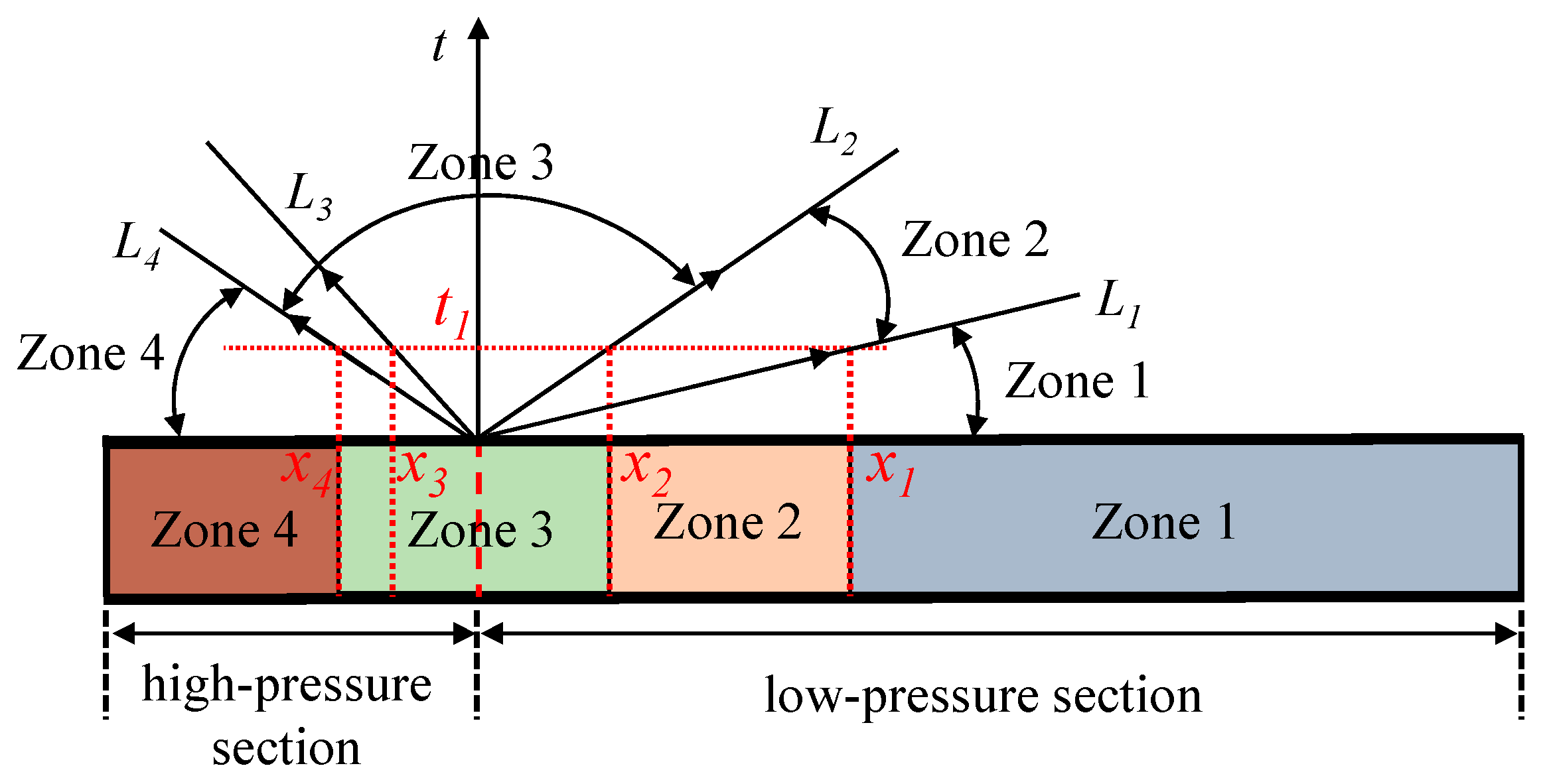
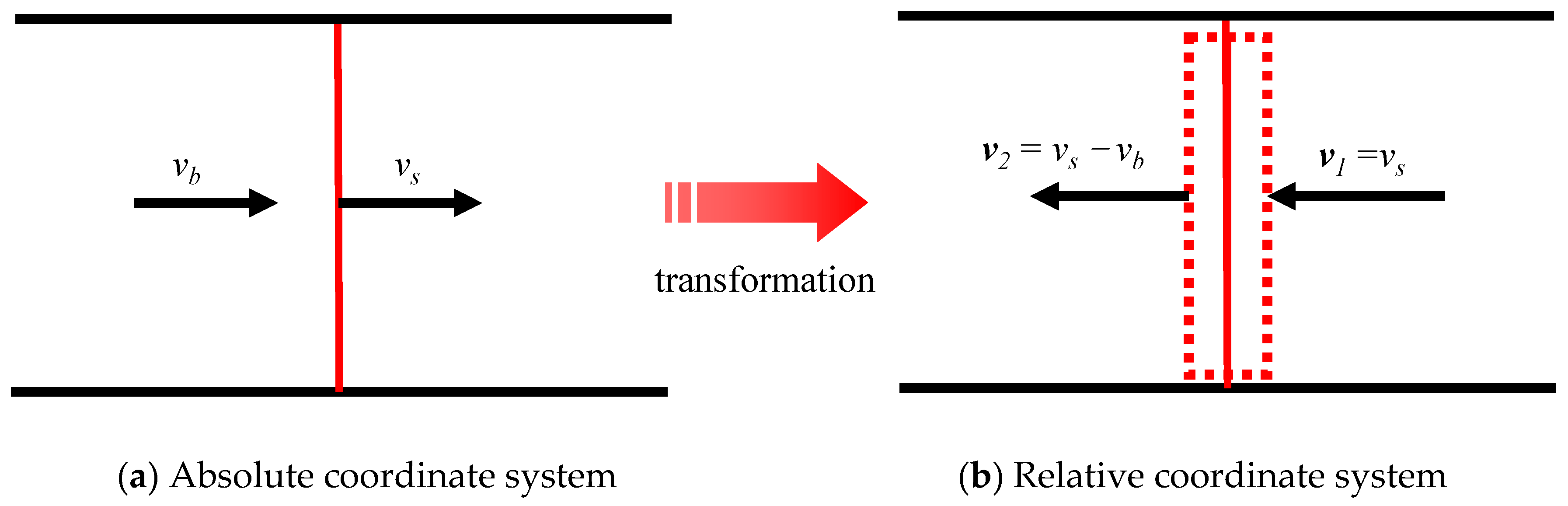
3.2. Derivation of Outburst Shock Wave Parameters
3.3. The Attenuation of Outburst Shock Wave Intensity
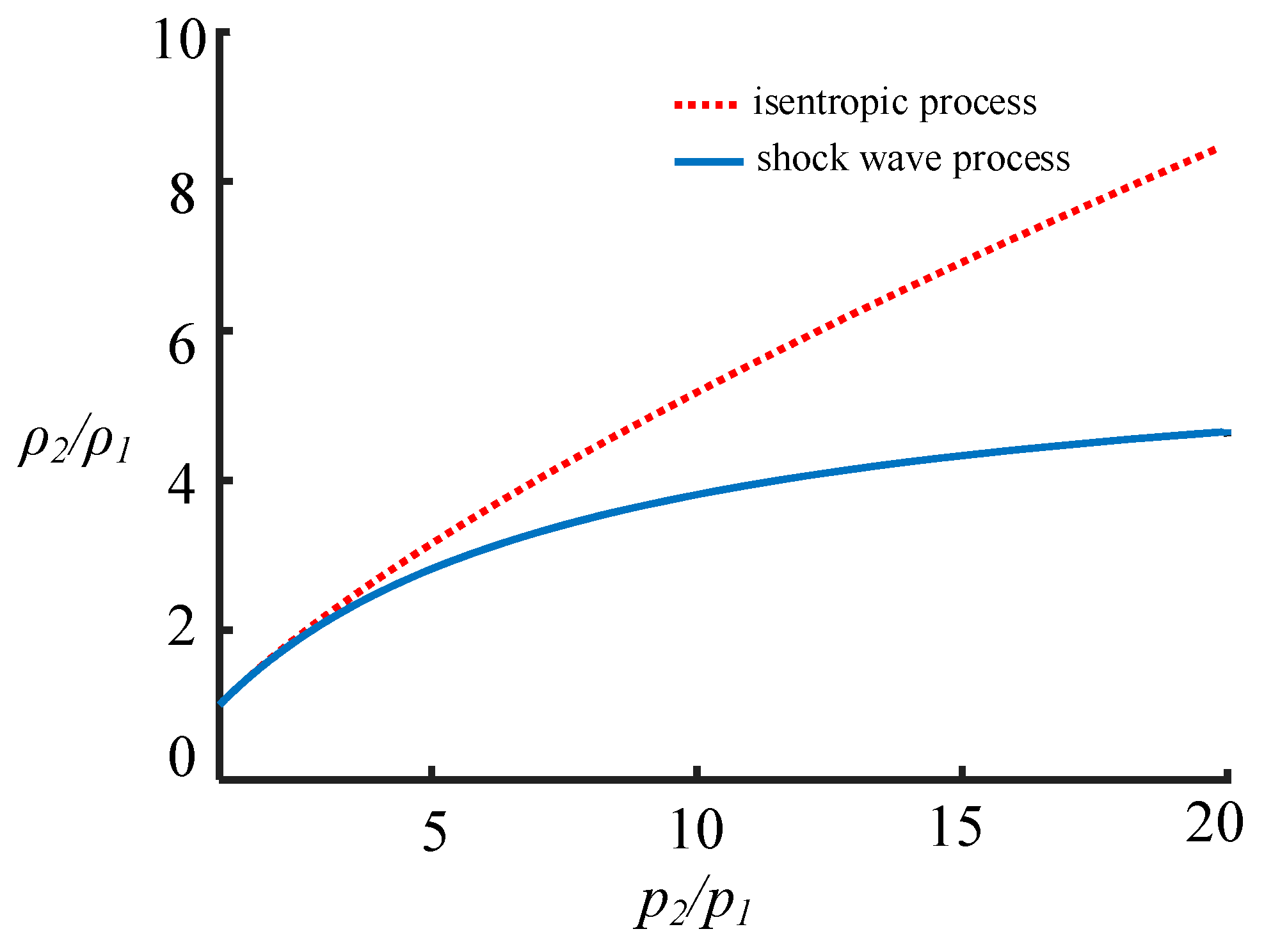
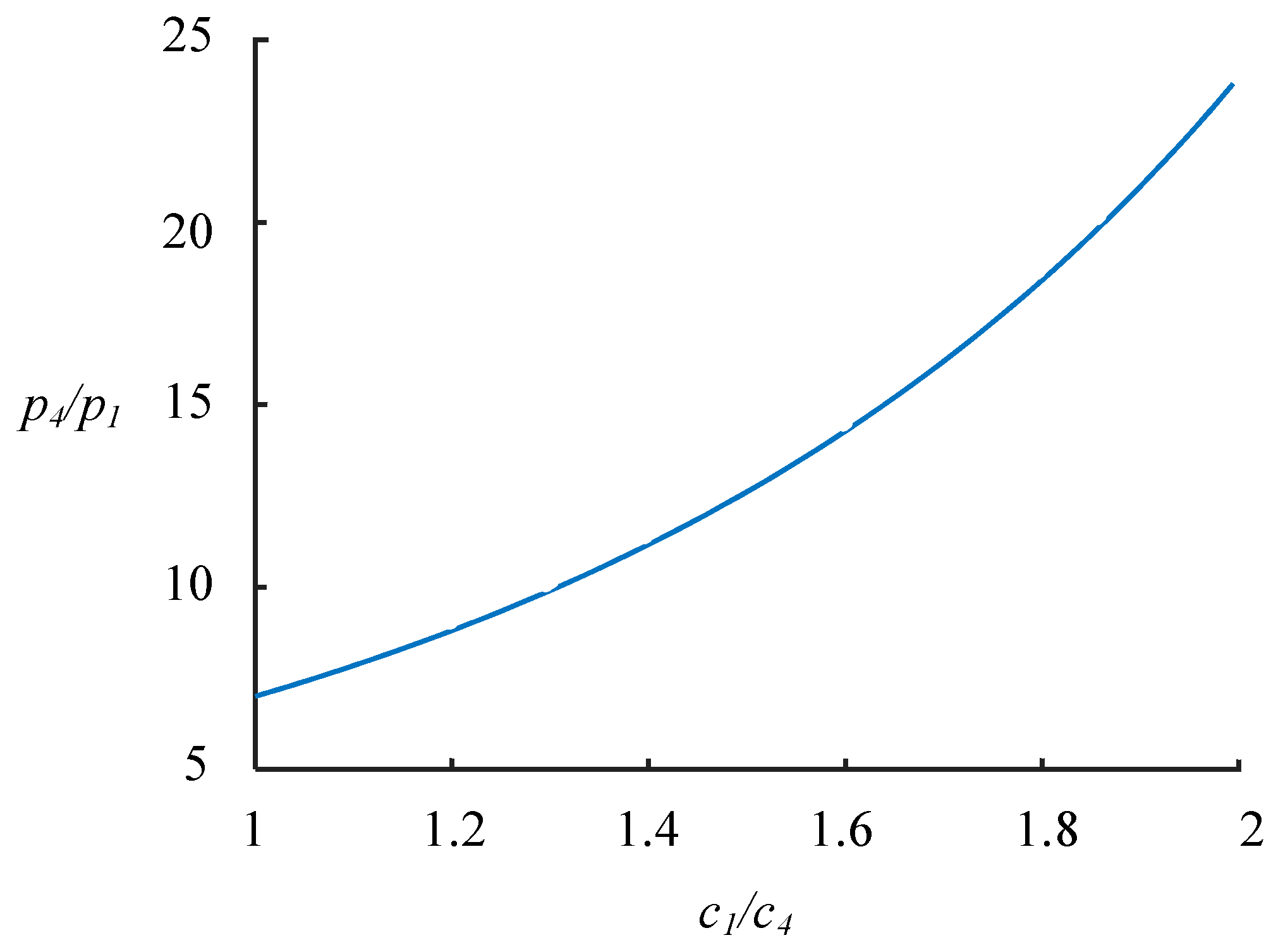
4. Relationship between Gas Pressure and Outburst Shock Wave Intensity
5. Conclusions
- (1)
- When outburst occurs, a large amount of broken coal and gas migrates from the coal seam to the roadway under the action of ground stress and gas pressure. It can be divided into stable coal seam area, coal-gas flow area, air compression area and roadway unaffected area. The location of these zones will change with the development of the outburst, and the internal of each region is uneven. The outburst energy accumulates continuously at the interface between the air compression zone and the unaffected zone of the roadway, forming an outburst wave front, and its formation and propagation satisfies the aerodynamic theory;
- (2)
- Based on the shock wave theory, the shock wave of a coal and gas outburst is studied, and the theoretical model of the shock wave of a coal and gas outburst is established. The propagation velocity of an outburst shock wave is greater than the speed of sound, and much larger than the velocity of airflow. After the outburst shock wave passes through, the pressure, temperature and density of the roadway air will change suddenly. Due to the viscosity of the moving gas and the heat conduction between the roadway and other factors, the strength of the shock wave gradually decays, and the attenuation speed is slow in the straight roadway. The attenuation of a shock wave in an underground ventilation system mainly depends on the bending of facilities such as anti-burst doors or the roadway itself;
- (3)
- According to the shock wave theory, the expressions of outburst gas pressure and outburst shock wave intensity are derived. In order to facilitate understanding and calculation, the concept of the equivalent sound velocity of coal-gas flow is proposed. Under the condition of determined outburst intensity, the initial gas pressure is very sensitive to the equivalent sound velocity. According to the initial gas pressure and the intensity of the outburst shock wave, the equivalent sound velocity can be calculated. Or, under the condition of the known equivalent sound velocity, the intensity of the outburst shock wave can be directly calculated according to the initial gas pressure.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yuan, L. Deep coal and gas mining strategic thinking in China. J. China Coal Soc. 2016, 41, 1–6. [Google Scholar]
- Wang, K.; Du, F. Coal-gas compound dynamic disasters in China: A review. Process Saf. Environ. Prot. 2020, 133, 1–17. [Google Scholar] [CrossRef]
- Du, F.; Wang, K.; Zhang, X.; Xin, C.P.; Shu, L.Y.; Wang, G.D. Experimental Study of Coal-gas Outburst: Insights from Coal–Rock Structure, Gas Pressure and Adsorptivity. Nat. Resour. Res. 2020, 29, 1–13. [Google Scholar] [CrossRef]
- Ding, Y.; Yue, Z.Q. Outburst characteristics of CO2 gas-coal mixture with tunnel outburst simulator in deep mining. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 1–23. [Google Scholar] [CrossRef]
- Zhang, C.L.; Wang, Y.B.; Wang, E.Y.; Zhou, X.F.; Wang, P.Z.; Zeng, W. Influence of coal seam gas pressure on the propagation mechanism of outburst two-phase flow in visual roadway. Fuel 2022, 322, 124296. [Google Scholar] [CrossRef]
- Zhao, X.S.; Cao, J.; Wang, B.; Yang, X.L. Experiment Study of Outburst Pulverized Coal-Gas Two-Phase Flow and Characteristic Analysis of Outburst Wave. Geofluids 2021, 2021, 8186230. [Google Scholar] [CrossRef]
- Savonko, C.K.; Jilin, A.A., II. Underground Air Shock Wave; Metallurgical Industry Press: Beijing, China, 1979. [Google Scholar]
- Zhang, J.F.; Wang, K.; Wei, C.P. Formation and Propagation of Shock Waves During Coal and Gas Outburst. J. Min. Saf. Eng. 2010, 27, 67–71. [Google Scholar]
- Sun, D.L.; Cao, J.; Miao, F.T.; Sun, H.T.; Zhao, X.S.; Dai, L.C.; Wang, B. Migration law of outburst coal and gas in roadway. J. China Coal Soc. 2018, 43, 2773–2779. [Google Scholar] [CrossRef]
- Cheng, W.Y.; Liu, X.Y.; Wang, K.J.; Li, X. Study on regulation about shock-wave-front propagating for coal and gas outburst. J. China Coal Soc. 2004, 29, 57–60. [Google Scholar]
- Zhang, S.Z.; Zhang, R.L. Research on Injuries Due to Shock Wave and Gas Flow from Coal and Gas Outburst. China Saf. Sci. J. 2012, 22, 62–66. [Google Scholar] [CrossRef]
- Tang, J.P.; Yu, N.; Chen, S. Impact of the gas pressure on the jet outburst energy of coal and gas. J. Saf. Environ. 2017, 17, 943–948. [Google Scholar] [CrossRef]
- Miao, F.T.; Sun, D.L.; Hu, Q.T. The formation mechanism of shock waves in the coal and gas outburst process. J. China Coal Soc. 2013, 38, 367–372. [Google Scholar] [CrossRef]
- Hu, W.J. Theoretical and Experimental Research for Gas-Pulverized Coal Impactive Dynamic Effect after Outburst; University of Mining and Technology: Beijing, China, 2013. [Google Scholar]
- Zhou, A.T.; Wang, K.; Wu, Z.Q. Propagation law of shock waves and gas flow in cross roadway caused by coal and gas outburst. Int. J. Min. Sci. Technol. 2014, 24, 23–29. [Google Scholar] [CrossRef]
- Zhou, A.T.; Wang, K. Airflow stabilization in airways induced by gas flows following an outburst. J. Nat. Gas Sci. Eng. 2016, 35, 720–725. [Google Scholar] [CrossRef]
- Zhou, A.T.; Zhang, M.; Wang, K.; Elsworth, D.; Wang, J.W.; Fan, L.P. Airflow disturbance induced by coal mine outburst shock waves: A case study of a gas outburst disaster in China. Int. J. Rock Mech. Min. Sci. 2020, 128, 104262. [Google Scholar] [CrossRef]
- Li, W.X. One-Dimensional Unsteady Flow and Shock Wave; National Defense Industry Press: Beijing, China, 2003. [Google Scholar]
- Tan, H. Physical Guidance of Experimental Shock Wave; National Defense Industry Press: Beijing, China, 2007. [Google Scholar]
- Cheng, B.Q. Gas Dynamics; National Defense Industry Press: Beijing, China, 2009. [Google Scholar]
- John, D.; Anderson, J. Fundamentals of Aerodynamics; University of Maryland: College Park, MD, USA, 2009. [Google Scholar]
- Wang, G.F. A Shock Tube Study of Methane Combustion Chemical Kinetics Mechanism; University of Science and Technology of China: Hefei, China, 2008. [Google Scholar]
- Cui, H.T.; Liu, Q.M. Dynamic calibration of shock wave pressure measurement system. Exp. Meas. Fluid Mech. 2004, 18, 92–96. [Google Scholar]
- Zhang, D.Y. The Application of Shock tube in Testing and Calibrating the Performance of Pressure Sensor. J. Astronaut. Metrol. Meas. 2004, 24, 24–27. [Google Scholar]
- Xu, L.; Sun, J.S. SPH Simulation of One-dimensional Shock Tube Problems. Chin. J. Comput. Phys. 2003, 20, 153–156. [Google Scholar] [CrossRef]
- Li, J.P.; Feng, H.; Jiang, Z.L.; Yu, H.R. Numerical computation on the tailored shock Mach numbers for a hydrogen-oxygen detonation shock tube. Acta Aerodyn. Sin. 2008, 112, 291–296. [Google Scholar]
- Davidson, D.; Hanson, R. Interpreting shock tube ignition data. Int. J. Chem. Kinet. 2004, 36, 510–523. [Google Scholar] [CrossRef]
- Gauthier, B.; Davidson, D.F.; Hanson, R.K. Shock tube determination of ignition delay times in full-blend and surrogate fuel mixtures. Combust. Flame 2004, 139, 300–311. [Google Scholar] [CrossRef]
- Duff, R.E. Shock-tube performance at low initial pressure. Phys. Fluids 1959, 2, 207–216. [Google Scholar] [CrossRef]
- Chen, Q. Theory and Experimental Technique of Shock Tube Flow; China University of Science and Technology Press: Hefei, China, 1979. [Google Scholar]
- Chen, F.; Quan, X.B.; Song, Y.P. Aerodynamic Basis; Harbin Institute of Technology Press: Harbin, China, 2015. [Google Scholar]
- Mirels, H. Attenuation in a Shock Tube due to Unsteady-Boundary-Layer Action; National Advisory Committee for Aeronautics Collection: Washington, DC, USA, 1957. [Google Scholar]
- Kitagawa, K.; Yasuhara, M.; Takayama, K. Attenuation of shock waves propagating in polyurethane foams. Shock Waves 2006, 15, 437–445. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Cao, J.; Dai, L.; Li, R.; Liu, Y. Investigation of Formation Process and Intensity of Coal and Gas Outburst Shockwave. Processes 2023, 11, 659. https://doi.org/10.3390/pr11030659
Sun D, Cao J, Dai L, Li R, Liu Y. Investigation of Formation Process and Intensity of Coal and Gas Outburst Shockwave. Processes. 2023; 11(3):659. https://doi.org/10.3390/pr11030659
Chicago/Turabian StyleSun, Dongling, Jie Cao, Linchao Dai, Rifu Li, and Yanbao Liu. 2023. "Investigation of Formation Process and Intensity of Coal and Gas Outburst Shockwave" Processes 11, no. 3: 659. https://doi.org/10.3390/pr11030659
APA StyleSun, D., Cao, J., Dai, L., Li, R., & Liu, Y. (2023). Investigation of Formation Process and Intensity of Coal and Gas Outburst Shockwave. Processes, 11(3), 659. https://doi.org/10.3390/pr11030659







