Structural Optimization of High-Pressure Polyethylene Cyclone Separator Based on Energy Efficiency Parameters
Abstract
:1. Introduction
2. Numerical Simulation
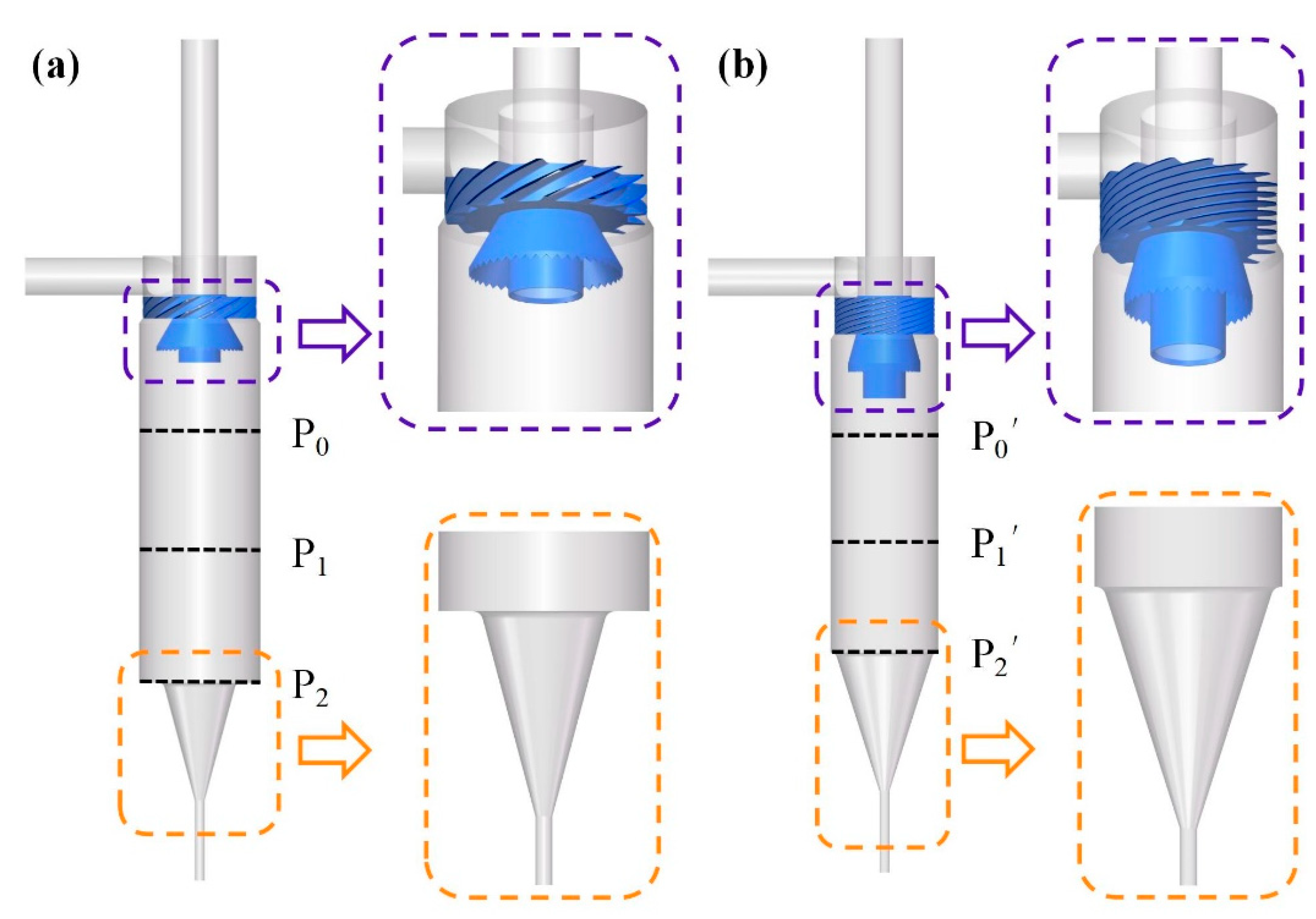
2.1. Cyclone Geometry
2.2. The Governing Equations
2.3. Boundary Conditions
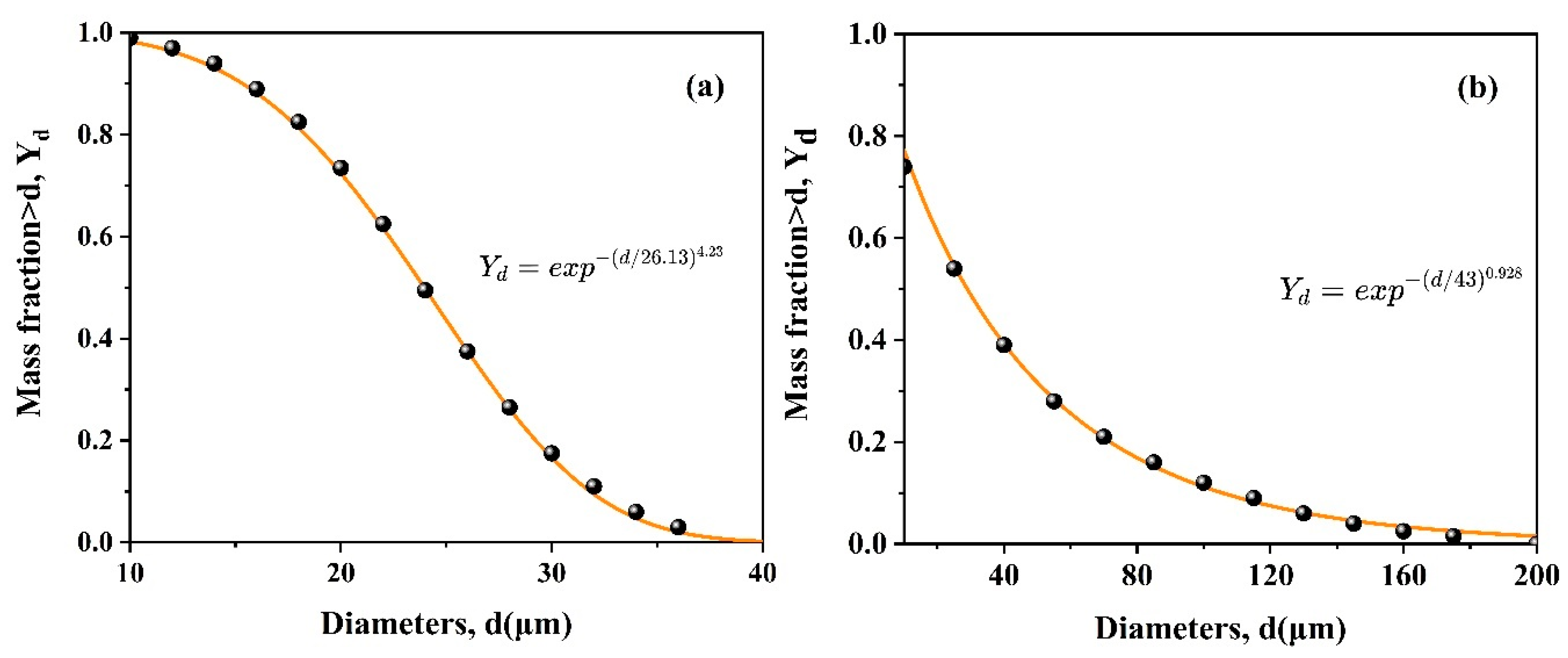
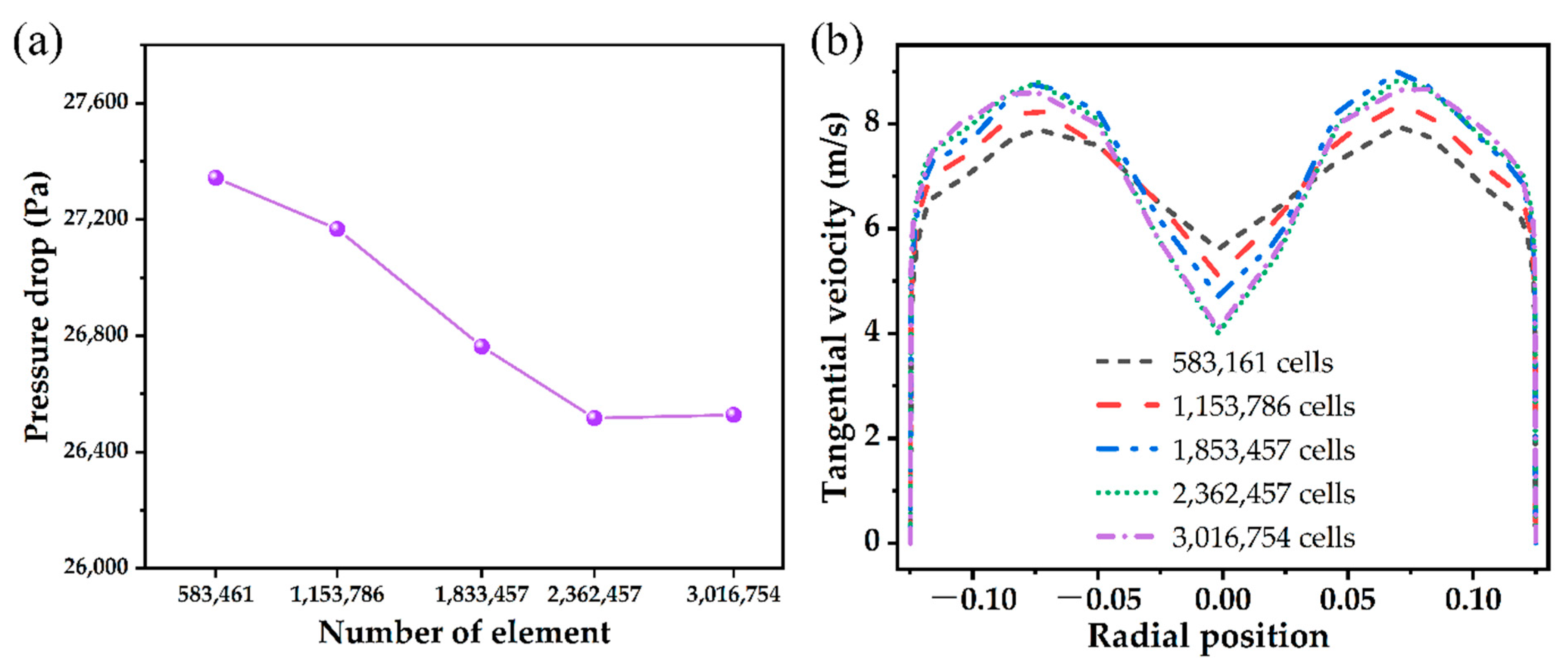
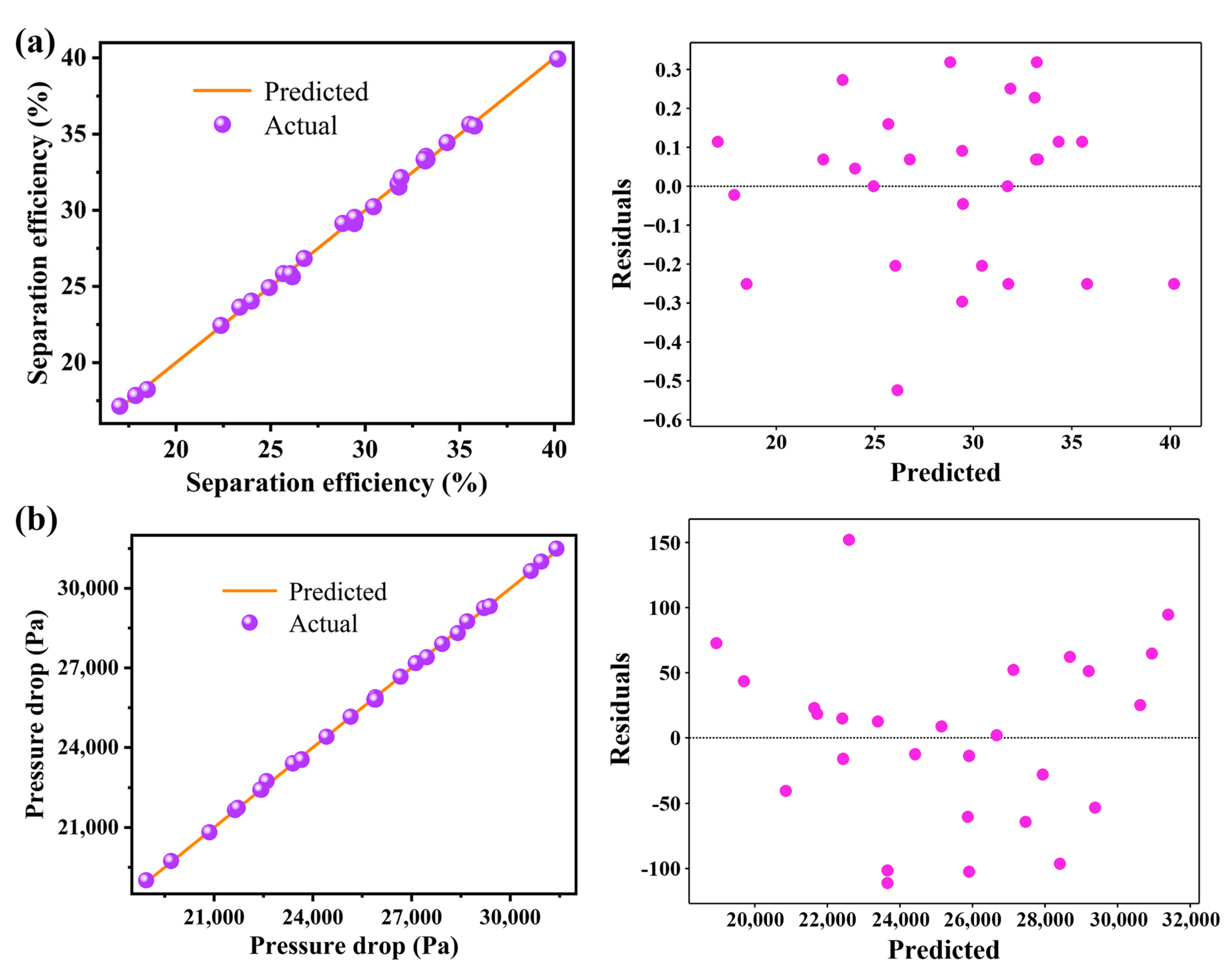
2.4. Verification of Simulation
3. Experimental Design
4. Results and Discussion
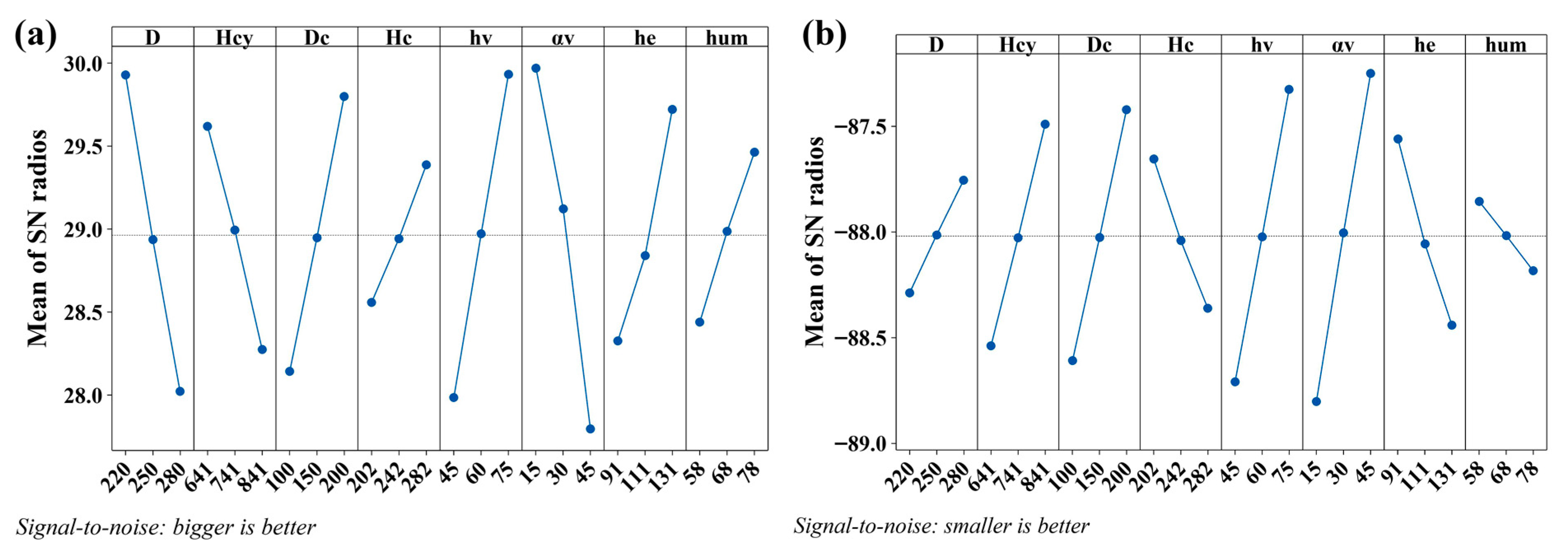
4.1. Analysis of the Control Factors
4.2. Analysis of Variance
4.3. Regression Analysis
4.4. Multi-Objective Optimization
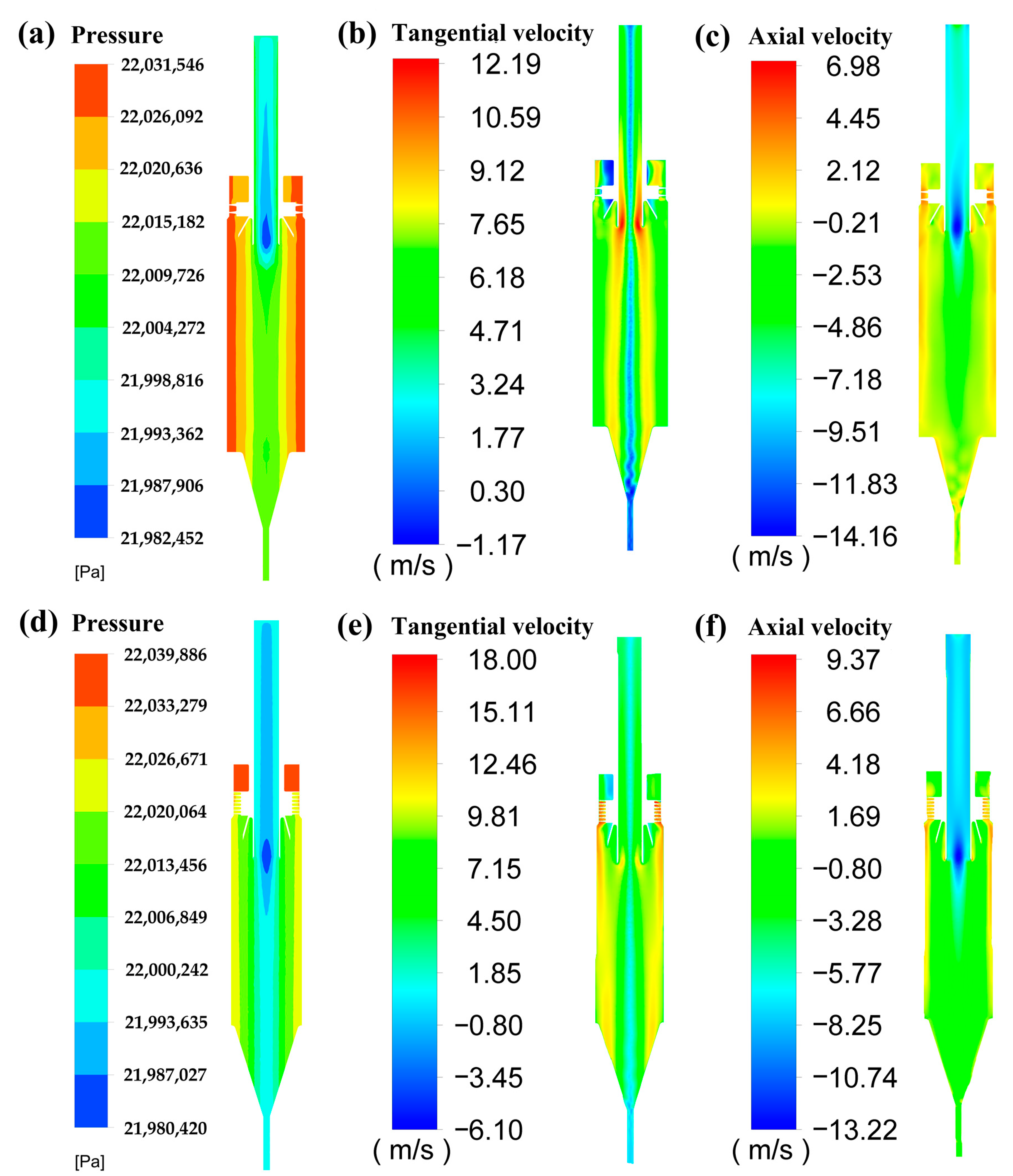
4.5. Improved and Original Structure Comparison
5. Conclusions
- (1)
- For the separation efficiency, the influencing factors were, in order of priority: guide vane angle > guide vane height > cone diameter > cylinder diameter > exhaust pipe extension length > cylinder height > umbrella structure height > cone height. The optimal parameter levels for separation efficiency were taken as: cylinder diameter at 220 mm, cylinder height at 641 mm, cone diameter at 200 mm, cone height at 282 mm, guide vane height at 75 mm, guide vane angle at 15°, exhaust pipe extension length at 131 mm, and umbrella structure height at 78 mm. The optimal combination for separation efficiency improved the separation efficiency by 98.7% compared with that of the original structure. The mathematical equations for separation efficiency and the eight parameters were also obtained and predicted with a maximum error of 3.1%.
- (2)
- For the pressure drop, the influencing factors were, in order of priority: guide vane angle > guide vane height > cone diameter > cylinder length > exhaust pipe extension length > cone height > cylinder diameter > umbrella structure height. The optimal parameter levels for pressure drop were taken as: cylinder diameter at 280 mm, cylinder height at 841 mm, cone diameter at 200 mm, cone height at 202 mm, guide vane height at 75 mm, guide vane angle at 45°, exhaust pipe extension length at 91 mm, and umbrella structure height at 58 mm. The optimal pressure drop combination reduced the pressure drop by 42.8% compared with that of the original structure. The mathematical equations for pressure drop and the eight parameters were also obtained and predicted, and the maximum error of the predicted value was 3.6%.
- (3)
- An energy-efficiency factor was defined and used to reduce the multi-objective optimization problem and achieve a higher separation efficiency and lower pressure drop. The guide vane height, cone diameter, and cylinder diameter had the greatest influence on the comprehensive performance of the cyclone separator and the comprehensive optimal combination was the same as the optimal separation efficiency combination. The improved structure increased the separation efficiency by 98.7% compared to the original structure, while the pressure drop increased by only 8.2%. When the improved structure was applied in the high-pressure polyethylene process, the separation efficiency reached 91.1%, which was 17.7% higher than that of the original structure, which could thus effectively reduce the frequency of filter cleaning and greatly improve the production efficiency. The mathematical equations of the energy-efficiency factor and the eight parameters were also obtained and predicted, and the simulated values of the improved structure were in good agreement with the predicted values, with a relative error within 5.5%.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| General symbols | |
| d | Inlet diameter (mm) |
| D | Cylinder diameter (mm) |
| Db | Bottom flow pipe diameter (mm) |
| Dc | Cone diameter (mm) |
| De | Exhaust pipe diameter (mm) |
| Dij | Stress diffusion |
| dk | Particle diameter (μm) |
| H | Total height of the cyclone separator (mm) |
| Hb | Bottom flow pipe height (mm) |
| Hc | Cone height (mm) |
| Hcy | Cylinder height (mm) |
| he | Exhaust pipe extension length (mm) |
| hum | Umbrella structure height (mm) |
| hv | Guide vane height (mm) |
| mk | Mass flow rate of k-sized oligomers in the feed |
| nk | Number of k-sized particles captured per unit of time |
| Pij | Shear production |
| Qm | Mass flow rate of oligomers |
| Qv | Volume flow rate of oligomers |
| R | Cylinder radius of the corresponding structure |
| r | Radial position |
| ui | Time-averaged fluid velocity i (m/s) |
| u′i | Fluctuating velocity to direction i (m/s) |
| Sub-grid scale velocity (m/s) | |
| Y | Response variable |
| Greek symbols | |
| αv | Guide vane angle (°) |
| βum | Umbrella structure angle (mm) |
| δij | Kronecker delta |
| ΔP | Pressure drop (Pa) |
| ΔP′ | Relative pressure drop (Pa) |
| εij | Source term |
| η | Separation efficiency |
| η′ | Relative separation efficiency |
| μ | Viscosity (kg/m.s) |
| ρ | Gas density (kg/m3) |
| ρo | Oligomer density (kg/m3) |
| σ | Energy-efficiency factor |
| μt | Eddy viscosity (kg/m.s) |
| Φij | Pressure-strain |
References
- Mazyan, W.I.; Ahmadi, A.; Brinkerhoff, J.; Ahmed, H.; Hoorfar, M. Enhancement of Cyclone Solid Particle Separation Performance Based on Geometrical Modification: Numerical Analysis. Sep. Purif. Technol. 2018, 191, 276–285. [Google Scholar] [CrossRef]
- Vieira, L.G.M.; Silva, D.O.; Barrozo, M.A.S. Effect of Inlet Diameter on the Performance of a Filtering Hydrocyclone Separator. Chem. Eng. Technol. 2016, 39, 1406–1412. [Google Scholar] [CrossRef]
- Chi, Y.; Meng, X.; Zhang, R.; Liu, H.; Liu, Z. Progress in numerical simulation of liquid-liquid cyclone separator. Chin. J. Process Eng. 2021, 21, 1132–1141. [Google Scholar]
- El-Emam, M.A.; Shi, W.; Zhou, L. CFD-DEM Simulation and Optimization of Gas-Cyclone Performance with Realistic Macroscopic Particulate Matter. Adv. Powder Technol. 2019, 30, 2686–2702. [Google Scholar] [CrossRef]
- Yang, L.; Zhang, J.; Ma, Y.; Xu, J.; Wang, J. Experimental and Numerical Study of Separation Characteristics in Gas-Liquid Cylindrical Cyclone. Chem. Eng. Sci. 2020, 214, 115362. [Google Scholar] [CrossRef]
- Katare, P.; Krupan, A.; Dewasthale, A.; Datar, A.; Dalkilic, A.S. CFD Analysis of Cyclone Separator Used for Fine Filtration in Separation Industry. Case Stud. Therm. Eng. 2021, 28, 101384. [Google Scholar] [CrossRef]
- Bymaster, A.; Olson, M.; Grave, E.; Svedeman, S.J.; Viana, F.; Akdim, M.R.; Mikkelsen, R. High Pressure Gas-Liquid Separation: An Experimental Study on Separator Performance of Natural Gas Streams at Elevated Pressures. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 2–5 May 2011. [Google Scholar]
- Dueck, J.; Farghaly, M.; Neesse, T. The Theoretical Partition Curve of the Hydrocyclone. Miner. Eng. 2014, 62, 25–30. [Google Scholar] [CrossRef]
- He, F.; Wang, H.; Wang, J.; Li, S.; Fan, Y.; Xu, X. Experimental Study of Mini-Hydrocyclones with Different Vortex Finder Depths Using Particle Imaging Velocimetry. Sep. Purif. Technol. 2020, 236, 116296. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, P.; Yang, X.; Zhang, Y.; Li, X.; Zhang, Y.; Wang, H. Experimental Research on the Separation Performance of W-Shaped Hydrocyclone. Powder Technol. 2020, 372, 532–541. [Google Scholar] [CrossRef]
- Kozić, M.; Ristic, S.; Puharic, M.; Linic, S. CFD Analysis of the Influence of Centrifugal Separator Geometry Modification on the Pulverized Coal Distribution at the Burners. Trans. FAMENA 2014, 38, 25–36. [Google Scholar]
- Ye, J.; Xu, Y.; Song, X.; Yu, J. Novel Conical Section Design for Ultra-Fine Particles Classification by a Hydrocyclone. Chem. Eng. Res. Des. 2019, 144, 135–149. [Google Scholar] [CrossRef]
- Fadaei, M.; Ameri, M.J.; Rafiei, Y.; Ghorbanpour, K. A Modified Semi-Empirical Correlation for Designing Two-Phase Separators. J. Pet. Sci. Eng. 2021, 205, 108782. [Google Scholar] [CrossRef]
- Hwang, K.-J.; Hwang, Y.-W.; Yoshida, H. Design of Novel Hydrocyclone for Improving Fine Particle Separation Using Computational Fluid Dynamics. Chem. Eng. Sci. 2013, 85, 62–68. [Google Scholar] [CrossRef]
- Tian, J.; Ni, L.; Song, T.; Shen, C.; Yao, Y.; Zhao, J. Numerical Study of Foulant-Water Separation Using Hydrocyclones Enhanced by Reflux Device: Effect of Underflow Pipe Diameter. Sep. Purif. Technol. 2019, 215, 10–24. [Google Scholar] [CrossRef]
- Yohana, E.; Tauviqirrahman, M.; Yusuf, B.; Choi, K.-H.; Paramita, V. Effect of Vortex Limiter Position and Metal Rod Insertion on the Flow Field, Heat Rate, and Performance of Cyclone Separator. Powder Technol. 2021, 377, 464–475. [Google Scholar] [CrossRef]
- Chu, K.; Chen, J.; Yu, A.B.; Williams, R.A. Numerical Studies of Multiphase Flow and Separation Performance of Natural Medium Cyclones for Recovering Waste Coal. Powder Technol. 2017, 314, 532–541. [Google Scholar] [CrossRef]
- Pei, B.; Yang, L.; Dong, K.; Jiang, Y.; Du, X.; Wang, B. The Effect of Cross-Shaped Vortex Finder on the Performance of Cyclone Separator. Powder Technol. 2017, 313, 135–144. [Google Scholar] [CrossRef]
- Shukla, S.K.; Shukla, P.; Ghosh, P. The Effect of Modeling of Velocity Fluctuations on Prediction of Collection Efficiency of Cyclone Separators. Appl. Math. Model. 2013, 37, 5774–5789. [Google Scholar] [CrossRef]
- Qiu, S.; Wang, G. Effects of Reservoir Parameters on Separation Behaviors of the Spiral Separator for Purifying Natural Gas Hydrate. Energies 2020, 13, 5346. [Google Scholar] [CrossRef]
- Gao, X.; Chen, J.; Feng, J.; Peng, X. Numerical Investigation of the Effects of the Central Channel on the Flow Field in an Oil–Gas Cyclone Separator. Comput. Fluids 2014, 92, 45–55. [Google Scholar] [CrossRef]
- Kępa, A. The Efficiency Improvement of a Large-Diameter Cyclone—The CFD Calculations. Sep. Purif. Technol. 2013, 118, 105–111. [Google Scholar] [CrossRef]
- Chuah, T.G.; Gimbun, J.; Choong, T.S.Y. A CFD Study of the Effect of Cone Dimensions on Sampling Aerocyclones Performance and Hydrodynamics. Powder Technol. 2006, 162, 126–132. [Google Scholar] [CrossRef]
- Zhang, H.; Dewil, R.; Degrève, J.; Baeyens, J. The Design of Cyclonic Pre-Heaters in Suspension Cement Kilns. Int. J. Sustain. Eng. 2014, 7, 307–312. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Chen, J.; Yang, Y.; Han, M.; Zhou, Y.; Ye, S.; Yan, C.; Yue, T. Experimental and Numerical Performance Study of a Downward Dual-Inlet Gas-Liquid Cylindrical Cyclone (GLCC). Chem. Eng. Sci. 2021, 238, 116595. [Google Scholar] [CrossRef]
- Lim, J.-H.; Oh, S.-H.; Kang, S.; Lee, K.-J.; Yook, S.-J. Development of Cutoff Size Adjustable Omnidirectional Inlet Cyclone Separator. Sep. Purif. Technol. 2021, 276, 119397. [Google Scholar] [CrossRef]
- Safikhani, H.; Mehrabian, P. Numerical Study of Flow Field in New Cyclone Separators. Adv. Powder Technol. 2016, 27, 379–387. [Google Scholar] [CrossRef]
- Liu, L.; Bai, B. Numerical Study on Swirling Flow and Separation Performance of Swirl Vane Separator. Interfacial Phenom. Heat Transf. 2017, 5, 9–21. [Google Scholar] [CrossRef] [Green Version]
- Elsayed, K.; Lacor, C. The Effect of Cyclone Vortex Finder Dimensions on the Flow Pattern and Performance Using LES. Comput. Fluids 2013, 71, 224–239. [Google Scholar] [CrossRef]
- Hamdy, O.; Bassily, M.A.; El-Batsh, H.M.; Mekhail, T.A. Numerical Study of the Effect of Changing the Cyclone Cone Length on the Gas Flow Field. Appl. Math. Model. 2017, 46, 81–97. [Google Scholar] [CrossRef]
- Shastri, R.; Brar, L.S. Numerical Investigations of the Flow-Field inside Cyclone Separators with Different Cylinder-to-Cone Ratios Using Large-Eddy Simulation. Sep. Purif. Technol. 2020, 249, 117149. [Google Scholar] [CrossRef]
- Misiulia, D.; Elsayed, K.; Andersson, A.G. Geometry Optimization of a Deswirler for Cyclone Separator in Terms of Pressure Drop Using CFD and Artificial Neural Network. Sep. Purif. Technol. 2017, 185, 10–23. [Google Scholar] [CrossRef]
- Zhou, F.; Sun, G.; Han, X.; Zhang, Y.; Bi, W. Experimental and CFD Study on Effects of Spiral Guide Vanes on Cyclone Performance. Adv. Powder Technol. 2018, 29, 3394–3403. [Google Scholar] [CrossRef]
- Misiulia, D.I.; Kuz’min, V.V.; Markov, V.A. Developing an Untwisting Device for Cyclones and Estimating Its Parameters. Theor. Found. Chem. Eng. 2013, 47, 274–283. [Google Scholar] [CrossRef]
- Wasilewski, M.; Singh Brar, L.; Ligus, G. Effect of the Central Rod Dimensions on the Performance of Cyclone Separators—Optimization Study. Sep. Purif. Technol. 2021, 274, 119020. [Google Scholar] [CrossRef]
- Ficici, F.; Ari, V. Optimization of the Preheater Cyclone Separators Used in the Cement Industry. Int. J. Green Energy 2013, 10, 12–27. [Google Scholar] [CrossRef]
- Safikhani, H.; Hajiloo, A.; Ranjbar, M.A. Modeling and Multi-Objective Optimization of Cyclone Separators Using CFD and Genetic Algorithms. Comput. Chem. Eng. 2011, 35, 1064–1071. [Google Scholar] [CrossRef]
- Sankar, P.S.; Prasad, R.K. Process Modeling and Particle Flow Simulation of Sand Separation in Cyclone Separator. Part. Sci. Technol. 2015, 33, 385–392. [Google Scholar] [CrossRef]
- Mariani, F.; Risi, F.; Grimaldi, C.N. Separation Efficiency and Heat Exchange Optimization in a Cyclone. Sep. Purif. Technol. 2017, 179, 393–402. [Google Scholar] [CrossRef]
- Venkatesh, S.; Suresh Kumar, R.; Sivapirakasam, S.P.; Sakthivel, M.; Venkatesh, D.; Yasar Arafath, S. Multi-Objective Optimization, Experimental and CFD Approach for Performance Analysis in Square Cyclone Separator. Powder Technol. 2020, 371, 115–129. [Google Scholar] [CrossRef]
- Babaoğlu, N.U.; Hosseini, S.H.; Ahmadi, G.; Elsayed, K. The Effect of Axial Cyclone Inlet Velocity and Geometrical Dimensions on the Flow Pattern, Performance, and Acoustic Noise. Powder Technol. 2022, 407, 117692. [Google Scholar] [CrossRef]
- Shastri, R.; Singh Brar, L.; Elsayed, K. Multi-Objective Optimization of Cyclone Separators Using Mathematical Modelling and Large-Eddy Simulation for a Fixed Total Height Condition. Sep. Purif. Technol. 2022, 291, 120968. [Google Scholar] [CrossRef]
- Elsayed, K.; Parvaz, F.; Hosseini, S.H.; Ahmadi, G. Influence of the Dipleg and Dustbin Dimensions on Performance of Gas Cyclones: An Optimization Study. Sep. Purif. Technol. 2020, 239, 116553. [Google Scholar] [CrossRef]
- Brar, L.S.; Elsayed, K. Analysis and Optimization of Cyclone Separators with Eccentric Vortex Finders Using Large Eddy Simulation and Artificial Neural Network. Sep. Purif. Technol. 2018, 207, 269–283. [Google Scholar] [CrossRef]
- Yao, X.; Zuo, P.; Lu, C.; E, C.; Liu, M. Characteristics of Flow and Liquid Distribution in a Gas–Liquid Vortex Separator with Multi Spiral Arms. Particuology 2022, 68, 101–113. [Google Scholar] [CrossRef]
- Baltrėnas, P.; Chlebnikovas, A. Removal of Fine Solid Particles in Aggressive Gas Flows in a Newly Designed Multi-Channel Cyclone. Powder Technol. 2019, 356, 480–492. [Google Scholar] [CrossRef]
- Zhou, W.; E, C.; Fan, Y.; Wang, K.; Lu, C. Experimental Research on the Separation Characteristics of a Gas-Liquid Cyclone Separator in WGS. Powder Technol. 2020, 372, 438–447. [Google Scholar] [CrossRef]
- Elsayed, K. Optimization of the Cyclone Separator Geometry for Minimum Pressure Drop Using Co-Kriging. Powder Technol. 2015, 269, 409–424. [Google Scholar] [CrossRef]
- Elsayed, K. Design of a Novel Gas Cyclone Vortex Finder Using the Adjoint Method. Sep. Purif. Technol. 2015, 142, 274–286. [Google Scholar] [CrossRef]
- Singh, P.; Couckuyt, I.; Elsayed, K.; Deschrijver, D.; Dhaene, T. Shape Optimization of a Cyclone Separator Using Multi-Objective Surrogate-Based Optimization. Appl. Math. Model. 2016, 40, 4248–4259. [Google Scholar] [CrossRef]
- Cengel, Y.; Cimbala, J. Fluid Mechanics Fundamentals and Applications (Si Units); McGraw-Hill Higher Education: Boston, MA, USA, 2010. [Google Scholar]
- Fathizadeh, N.; Mohebbi, A.; Soltaninejad, S.; Iranmanesh, M. Design and Simulation of High Pressure Cyclones for a Gas City Gate Station Using Semi-Empirical Models, Genetic Algorithm and Computational Fluid Dynamics. J. Nat. Gas Sci. Eng. 2015, 26, 313–329. [Google Scholar] [CrossRef]
- Oh, J.; Choi, S.; Kim, J. Numerical Simulation of an Internal Flow Field in a Uniflow Cyclone Separator. Powder Technol. 2015, 274, 135–145. [Google Scholar] [CrossRef]
- Kui, C. Design of Experiments and Analysis; Tsinghua University Press: Beijing, China, 1996. [Google Scholar]
- Roy, R.K. Design of Experiments Using the Taguchi Approach: 16 Steps to Product and Process Improvement; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
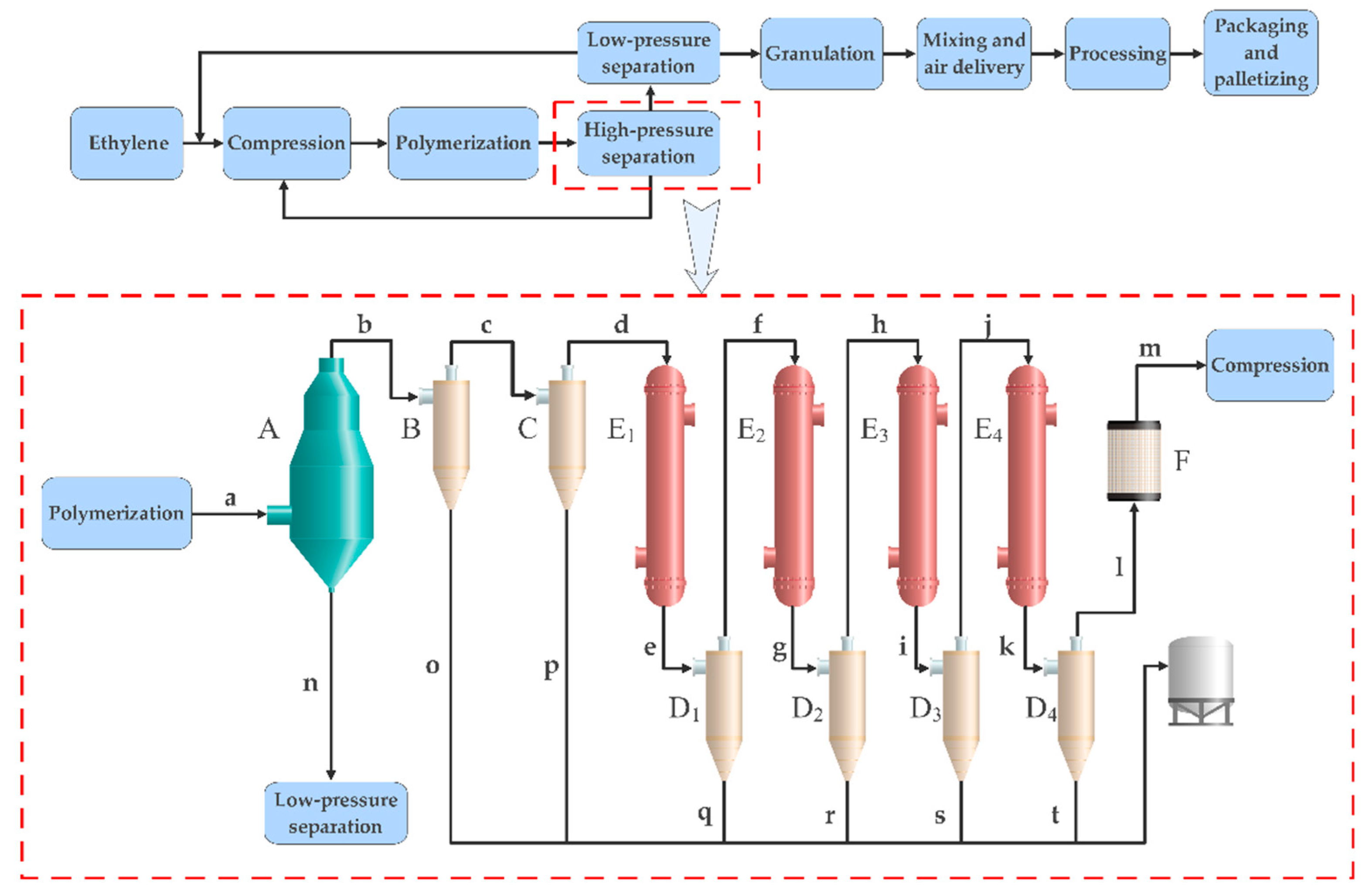






| H (mm) | Hcy (mm) | Hc (mm) | Hb (mm) | D (mm) | Dc (mm) | d (mm) | De (mm) | Db (mm) | hv (mm) | he (mm) | hum (mm) | αv (°) | βum (°) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1750 | 741 | 242 | 169 | 250 | 150 | 77 | 77 | 20 | 45 | 91 | 68 | 30 | 30 |
| Models | B | C | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|
| Inlet velocity (m/s) | 9.05 | 9.05 | 7.32 | 6.86 | 6.52 | 6.37 |
| Working temperature (℃) | 200 | 200 | 110 | 80.0 | 55.0 | 45.0 |
| Gaseous density (g/cm3) | 0.178 | 0.178 | 0.220 | 0.235 | 0.247 | 0.253 |
| Gaseous viscosity (cP) | 0.0150 | 0.0150 | 0.0130 | 0.0130 | 0.0110 | 0.0110 |
| Liquid density (g/cm3) | 0.740 | 0.740 | 0.740 | 0.740 | 0.740 | 0.740 |
| Liquid viscosity (cP) | 290 | 290 | 290 | 290 | 290 | 290 |
| Device Number | B | C | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|
| Separation efficiency (%) | 36.73 | 28.24 | 23.28 | 14.11 | 13.49 | 12.87 |
| Import mass flow rate (kg/s) | 2.48 × 10−4 | 1.57 × 10−4 | 1.12 × 10−4 | 0.86 × 10−4 | 0.74 × 10−4 | 0.64 × 10−4 |
| Separating mass flow rate (kg/s) | 9.09 × 10−5 | 4.42 × 10−5 | 2.62 × 10−5 | 1.22 × 10−5 | 1.00 × 10−5 | 0.82 × 10−5 |
| Separation volume flow (L/h) | 0.44 | 0.22 | 0.13 | 0.06 | 0.05 | 0.04 |
| One quarter’s worth of oligomer content (L) | 2408 | 1523.58 | 1093.35 | 838.82 | 720.44 | 623.23 |
| One quarter’s worth of separation volume (L) | 884.42 | 430.23 | 254.53 | 118.38 | 97.21 | 80.2 |
| No. | D (mm) | Hcy (mm) | Dc (mm) | Hc (mm) | hv (mm) | αv (°) | he (mm) | hum (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 220 | 641 | 100 | 202 | 45 | 15 | 91 | 58 |
| 2 | 250 | 741 | 150 | 242 | 60 | 30 | 111 | 68 |
| 3 | 280 | 841 | 200 | 282 | 75 | 45 | 131 | 78 |
| No. | D (mm) | Hcy (mm) | Dc (mm) | Hc (mm) | hv (mm) | αv (°) | he (mm) | hum (mm) | η (%) | SNR for η | ΔP (Pa) | SNR for ΔP | σ | SNR for σ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 220 | 641 | 100 | 202 | 45 | 15 | 91 | 58 | 25.84 | 28.25 | 31,007 | −89.83 | 0.83 | −1.58 |
| 2 | 220 | 641 | 100 | 202 | 60 | 30 | 111 | 68 | 29.43 | 29.38 | 28,309 | −89.04 | 1.04 | 0.34 |
| 3 | 220 | 641 | 100 | 202 | 75 | 45 | 131 | 78 | 33.34 | 30.46 | 25,808 | −88.24 | 1.29 | 2.23 |
| 4 | 220 | 741 | 150 | 242 | 45 | 15 | 91 | 68 | 29.13 | 29.29 | 29,254 | −89.32 | 1.00 | −0.03 |
| 5 | 220 | 741 | 150 | 242 | 60 | 30 | 111 | 78 | 33.54 | 30.51 | 26,668 | −88.52 | 1.26 | 2.00 |
| 6 | 220 | 741 | 150 | 242 | 75 | 45 | 131 | 58 | 31.53 | 29.97 | 22,749 | −87.14 | 1.39 | 2.84 |
| 7 | 220 | 841 | 200 | 282 | 45 | 15 | 91 | 78 | 33.24 | 30.43 | 27,399 | −88.75 | 1.21 | 1.68 |
| 8 | 220 | 841 | 200 | 282 | 60 | 30 | 111 | 58 | 31.73 | 30.03 | 23,407 | −87.39 | 1.36 | 2.65 |
| 9 | 220 | 841 | 200 | 282 | 75 | 45 | 131 | 68 | 35.64 | 31.04 | 20,817 | −86.37 | 1.71 | 4.68 |
| 10 | 250 | 641 | 150 | 282 | 45 | 30 | 131 | 58 | 29.53 | 29.41 | 30,653 | −89.73 | 0.96 | −0.32 |
| 11 | 250 | 641 | 150 | 282 | 60 | 45 | 91 | 68 | 26.84 | 28.58 | 24,404 | −87.75 | 1.10 | 0.83 |
| 12 | 250 | 641 | 150 | 282 | 75 | 15 | 111 | 78 | 39.93 | 32.03 | 28,752 | −89.17 | 1.39 | 2.86 |
| 13 | 250 | 741 | 200 | 202 | 45 | 30 | 131 | 68 | 29.14 | 29.29 | 25,893 | −88.26 | 1.13 | 1.03 |
| 14 | 250 | 741 | 200 | 202 | 60 | 45 | 91 | 78 | 25.63 | 28.18 | 19,739 | −85.91 | 1.30 | 2.27 |
| 15 | 250 | 741 | 200 | 202 | 75 | 15 | 111 | 58 | 34.44 | 30.74 | 22,421 | −87.01 | 1.54 | 3.73 |
| 16 | 250 | 841 | 100 | 242 | 45 | 30 | 131 | 78 | 24.93 | 27.93 | 29,324 | −89.34 | 0.85 | −1.40 |
| 17 | 250 | 841 | 100 | 242 | 60 | 45 | 91 | 58 | 17.14 | 24.68 | 21,657 | −86.71 | 0.79 | −2.03 |
| 18 | 250 | 841 | 100 | 242 | 75 | 15 | 111 | 68 | 30.23 | 29.61 | 25,805 | −88.23 | 1.17 | 1.38 |
| 19 | 280 | 641 | 200 | 242 | 45 | 45 | 111 | 58 | 22.44 | 27.02 | 23,556 | −87.44 | 0.95 | −0.42 |
| 20 | 280 | 641 | 200 | 242 | 60 | 15 | 131 | 68 | 35.53 | 31.01 | 27,903 | −88.91 | 1.27 | 2.10 |
| 21 | 280 | 641 | 200 | 242 | 75 | 30 | 91 | 78 | 33.34 | 30.46 | 21,738 | −86.74 | 1.53 | 3.72 |
| 22 | 280 | 741 | 100 | 282 | 45 | 45 | 111 | 68 | 18.23 | 25.22 | 27,180 | −88.69 | 0.67 | −3.46 |
| 23 | 280 | 741 | 100 | 282 | 60 | 15 | 131 | 78 | 32.14 | 30.14 | 31,496 | −89.97 | 1.02 | 0.18 |
| 24 | 280 | 741 | 100 | 282 | 75 | 30 | 91 | 58 | 24.03 | 27.62 | 23,547 | −87.44 | 1.02 | 0.18 |
| 25 | 280 | 841 | 150 | 202 | 45 | 45 | 111 | 78 | 17.84 | 25.03 | 22,422 | −87.01 | 0.80 | −1.98 |
| 26 | 280 | 841 | 150 | 202 | 60 | 15 | 131 | 58 | 25.83 | 28.24 | 25,157 | −88.01 | 1.03 | 0.23 |
| 27 | 280 | 841 | 150 | 202 | 75 | 30 | 91 | 68 | 23.64 | 27.47 | 19,010 | −85.58 | 1.24 | 1.90 |
| Level | D (mm) | Hcy (mm) | Dc (mm) | Hc (mm) | hv (mm) | αv (°) | he (mm) | hum (mm) | |
|---|---|---|---|---|---|---|---|---|---|
| Separation efficiency | 1 | 29.93 | 29.62 | 28.14 | 28.56 | 27.98 | 29.97 | 28.33 | 28.44 |
| 2 | 28.94 | 28.99 | 28.95 | 28.94 | 28.97 | 29.12 | 28.84 | 28.99 | |
| 3 | 28.02 | 28.27 | 29.80 | 29.39 | 29.93 | 27.80 | 29.72 | 29.46 | |
| Delta | 1.91 | 1.35 | 1.66 | 0.83 | 1.95 | 2.17 | 1.39 | 1.02 | |
| Rank | 3 | 6 | 4 | 8 | 2 | 1 | 5 | 7 | |
| Pressure drop | 1 | −88.29 | −88.54 | −88.61 | −87.65 | −88.71 | −88.80 | −87.56 | −87.86 |
| 2 | −88.01 | −88.03 | −88.03 | −88.04 | −88.02 | −88.01 | −88.06 | −88.02 | |
| 3 | −87.75 | −87.49 | −87.42 | −88.36 | −87.33 | −87.25 | −88.44 | −88.18 | |
| Delta | 0.53 | 1.05 | 1.19 | 0.71 | 1.38 | 1.55 | 0.88 | 0.33 | |
| Rank | 7 | 4 | 3 | 6 | 2 | 1 | 5 | 8 |
| Source | DF | SS | MS | F | p | |
|---|---|---|---|---|---|---|
| Separation efficiency | D | 2 | 16.3 | 8.17 | 100 | 2.43 × 10−7 |
| Hcy | 2 | 8.16 | 4.08 | 50.0 | 6.20 × 10−6 | |
| Dc | 2 | 12.4 | 6.19 | 75.8 | 9.06 × 10−7 | |
| Hc | 2 | 3.09 | 1.54 | 18.9 | 3.98 × 10−4 | |
| hv | 2 | 17.1 | 8.54 | 104 | 1.97 × 10−7 | |
| αv | 2 | 21.6 | 10.8 | 132 | 6.34 × 10−8 | |
| he | 2 | 8.96 | 4.48 | 54.9 | 4.05 × 10−6 | |
| hum | 2 | 4.72 | 2.36 | 28.9 | 6.94 × 10−5 | |
| Residual error | 10 | 0.816 | 0.0820 | |||
| Total | 26 | 93.2 | ||||
| Pressure drop | D | 2 | 1.28 | 0.640 | 59.1 | 2.89 × 10−6 |
| Hcy | 2 | 4.96 | 2.48 | 229 | 4.47 × 10−9 | |
| Dc | 2 | 6.35 | 3.17 | 293 | 1.33 × 10−9 | |
| Hc | 2 | 2.25 | 1.13 | 104 | 2.04 × 10−7 | |
| hv | 2 | 8.62 | 4.31 | 398 | 2.94 × 10−10 | |
| αv | 2 | 10.8 | 5.42 | 500 | 9.49 × 10−11 | |
| he | 2 | 3.52 | 1.76 | 162 | 2.39 × 10−8 | |
| hum | 2 | 0.485 | 0.242 | 22.4 | 2.04 × 10−4 | |
| Residual error | 10 | 0.108 | 0.0110 | |||
| Total | 26 | 38.4 |
| Predictor | Coef | SE Coef | T | p | |
|---|---|---|---|---|---|
| Separation efficiency | Constant | 20.6 | 9.89 × 10−1 | 20.8 | 4.90 × 10−14 |
| D | −9.33 × 10−2 | 2.02 × 10−3 | −46.3 | 3.58 × 10−20 | |
| Hcy | −2.00 × 10−2 | 6.05 × 10−4 | −33.1 | 1.42 × 10−17 | |
| Dc | 5.09 × 10−2 | 1.21 × 10−3 | 42.1 | 1.96 × 10−19 | |
| Hc | 3.64 × 10−2 | 1.51 × 10−3 | 24.0 | 3.90 × 10−15 | |
| hv | 0.207 | 4.03 × 10−3 | 51.3 | 5.80 × 10−21 | |
| αv | −0.214 | 4.03 × 10−3 | −53.0 | 3.21 × 10−21 | |
| he | 0.108 | 3.02 × 10−3 | 35.6 | 3.81 × 10−18 | |
| hum | 0.175 | 6.05 × 10−3 | 28.9 | 1.58 × 10−16 | |
| Pressure drop | Constant | 4.43 × 104 | 302 | 146 | 3.83 × 10−29 |
| D | −24.8 | 0.616 | −40.3 | 4.25 × 10−19 | |
| Hcy | −15.1 | 0.185 | −81.6 | 1.41 × 10−24 | |
| Dc | −34.7 | 0.370 | −94.0 | 1.11 × 10−25 | |
| Hc | 24.8 | 0.462 | 53.8 | 2.47 × 10−21 | |
| hv | −133 | 1.23 | −108 | 8.59 × 10−27 | |
| αv | −151 | 1.23 | −123 | 8.99 × 10−28 | |
| he | 61.2 | 0.924 | 66.3 | 5.85 × 10−23 | |
| hum | 51.1 | 1.85 | 27.6 | 3.42 × 10−16 |
| Simulation Value of Separation Efficiency (%) | Prediction Value of Separation Efficiency (%) | Simulation Value of Pressure Drop (Pa) | Prediction Value of Pressure Drop (Pa) | |
|---|---|---|---|---|
| The original structure | 23.28 | 23.42 | 26,157 | 26,188 |
| Optimal structure for separation efficiency | 46.25 | 47.68 | 28,294 | 28,923 |
| Optimal structure for pressure drop | 21.61 | 20.96 | 14,951 | 14,420 |
| Level | D (mm) | Hcy (mm) | Dc (mm) | Hc (mm) | hv (mm) | αv (°) | he (mm) | hum (mm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.646 | 1.086 | −0.462 | 0.910 | −0.720 | 1.174 | 0.773 | 0.589 |
| 2 | 0.929 | 0.972 | 0.926 | 0.907 | 0.954 | 1.122 | 0.789 | 0.975 |
| 3 | 0.274 | 0.790 | 2.384 | 1.031 | 2.613 | 0.552 | 1.286 | 1.285 |
| Delta | 1.372 | 0.296 | 2.846 | 0.124 | 3.333 | 0.622 | 0.513 | 0.696 |
| Rank | 3 | 7 | 2 | 8 | 1 | 5 | 6 | 4 |
| Predictor | Coef | SE Coef | T | p |
|---|---|---|---|---|
| Constant | 1.19 × 10−2 | 1.57 × 10−1 | 0.0757 | 9.40 × 10−1 |
| D | −2.86 × 10−3 | 3.21 × 10−4 | −8.95 | 4.82 × 10−8 |
| Hcy | −1.20 × 10−4 | 9.62 × 10−5 | −1.25 | 2.27 × 10−1 |
| Dc | 3.68 × 10−3 | 1.92 × 10−4 | 19.1 | 2.06 × 10−13 |
| Hc | 3.53 × 10−4 | 2.40 × 10−4 | 1.47 | 1.60 × 10−1 |
| hv | 1.44 × 10−2 | 6.41 × 10−4 | 22.4 | 1.30 × 10−14 |
| αv | −1.71 × 10−3 | 6.41 × 10−4 | −2.66 | 1.59 × 10−2 |
| he | 1.72 × 10−3 | 4.81 × 10−4 | 3.58 | 2.14 × 10−3 |
| hum | 4.36 × 10−3 | 9.62 × 10−4 | 4.53 | 2.58 × 10−4 |
| Device Number | B | C | D1 | D2 | D3 | D4 |
|---|---|---|---|---|---|---|
| Separation efficiency (%) | 36.73 | 28.24 | 47.68 | 33.23 | 26.56 | 23.66 |
| Import mass flow rate (kg/s) | 2.48 × 10−4 | 1.57 × 10−4 | 1.12 × 10−4 | 5.88 × 10−5 | 3.93 × 10−5 | 2.88 × 10−5 |
| Separating mass flow rate (kg/s) | 9.09 × 10−5 | 4.42 × 10−5 | 5.36 × 10−5 | 1.95 × 10−5 | 1.04 × 10−5 | 6.82 × 10−6 |
| Separation volume flow (L/h) | 0.44 | 0.22 | 0.26 | 0.10 | 0.05 | 0.03 |
| One quarter’s worth of oligomer content (L) | 2408 | 1523.58 | 1093.35 | 572.04 | 381.95 | 280.51 |
| One quarter’s worth of separation volume (L) | 884.42 | 430.23 | 521.31 | 190.09 | 101.45 | 66.37 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Liu, S.; Wang, C.; Gao, B. Structural Optimization of High-Pressure Polyethylene Cyclone Separator Based on Energy Efficiency Parameters. Processes 2023, 11, 691. https://doi.org/10.3390/pr11030691
Hu B, Liu S, Wang C, Gao B. Structural Optimization of High-Pressure Polyethylene Cyclone Separator Based on Energy Efficiency Parameters. Processes. 2023; 11(3):691. https://doi.org/10.3390/pr11030691
Chicago/Turabian StyleHu, Baisong, Shuo Liu, Chuanzhi Wang, and Bingjun Gao. 2023. "Structural Optimization of High-Pressure Polyethylene Cyclone Separator Based on Energy Efficiency Parameters" Processes 11, no. 3: 691. https://doi.org/10.3390/pr11030691
APA StyleHu, B., Liu, S., Wang, C., & Gao, B. (2023). Structural Optimization of High-Pressure Polyethylene Cyclone Separator Based on Energy Efficiency Parameters. Processes, 11(3), 691. https://doi.org/10.3390/pr11030691






