On the Importance of Model Selection for CFD Analysis of High Temperature Gas-Solid Reactive Flow; Case Study: Post Combustion Chamber of HIsarna Off-Gas System
Abstract
:1. Introduction
2. Case Study: Off-Gas System of HIsarna Ironmaking
3. Governing Equation
4. Base Model Set Up and Validation
4.1. Computational Grid (Mesh)
4.2. Boundary Conditions
4.3. Reactions and Kinetics
4.4. Model Solution Procedure
4.5. Base Model Validation
5. Result and Discussion
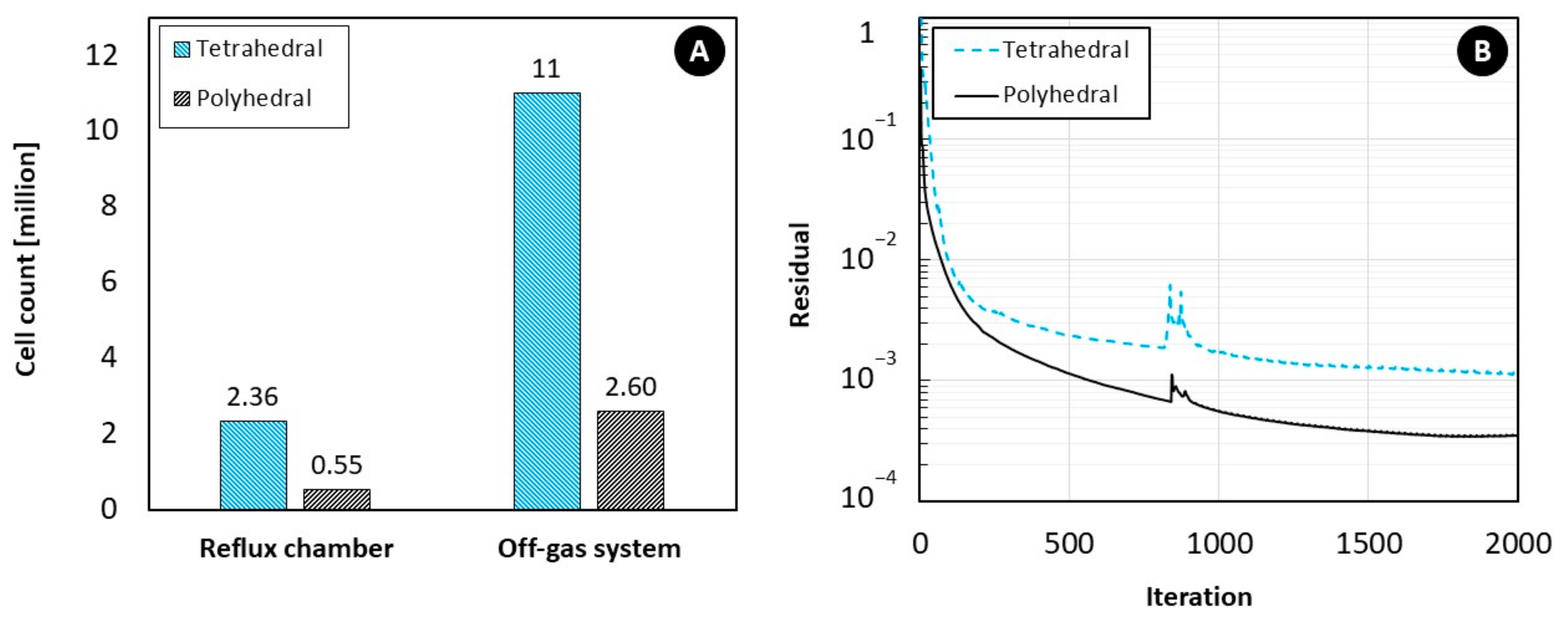
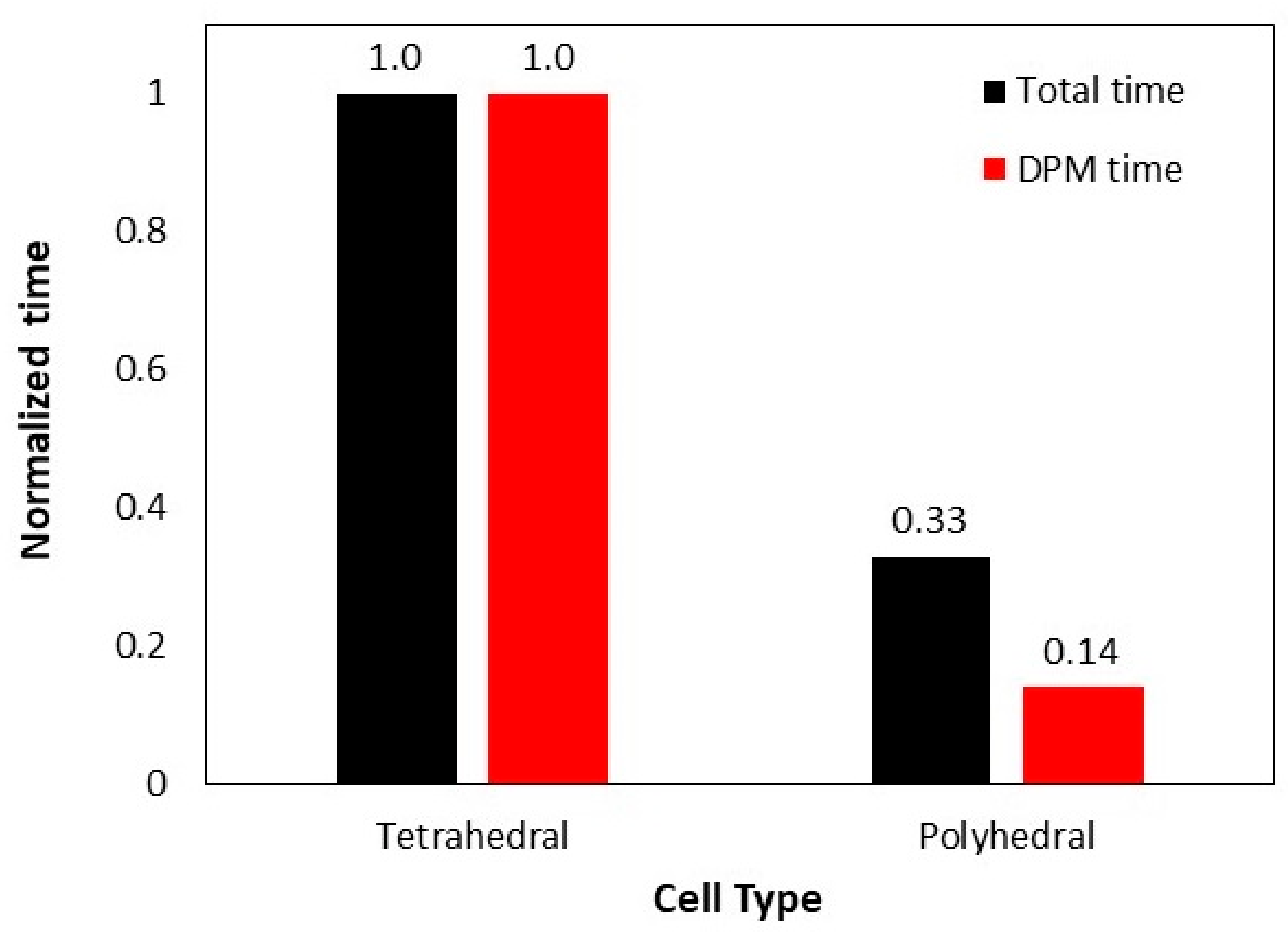
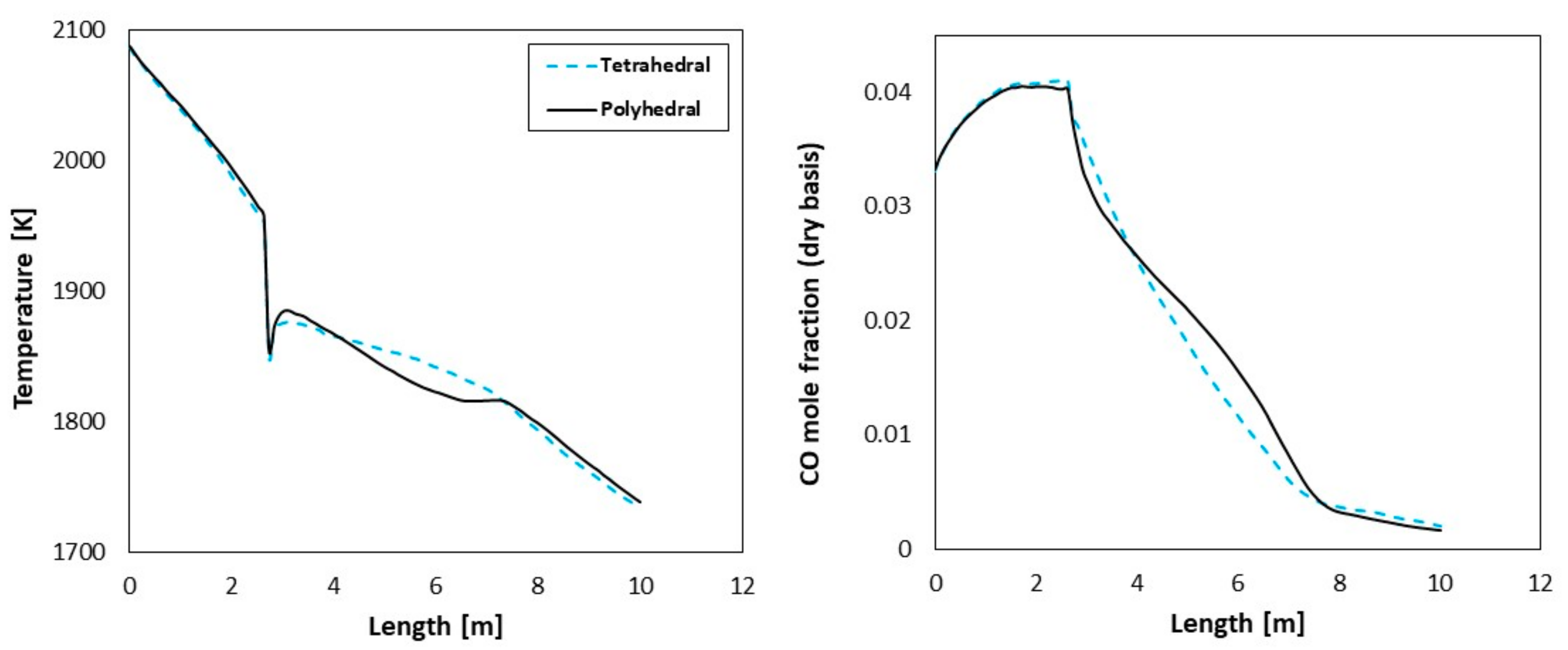
5.1. Effect of Mesh Cell Type
5.2. Effect of Mesh Cell Count (Grid Independency Analysis for Polyhedral Cells)
5.3. Selection of Turbulence Model
5.4. Effect of Reaction Mechanism
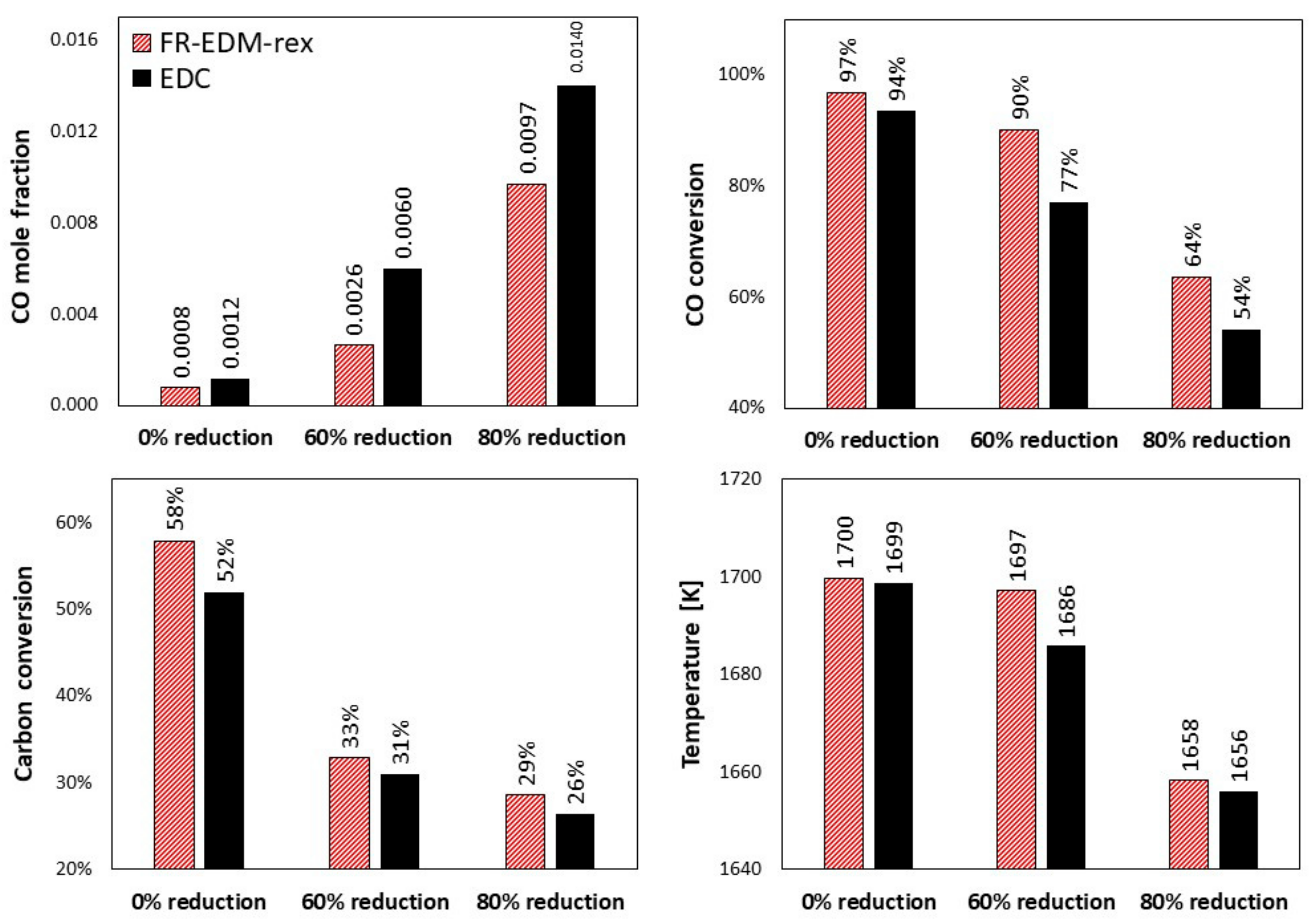
5.5. Effect of Turbulent-Chemistry Interaction Models
- EDM and FR-EDM are better to be used with global mechanism (with few steps) as the mixing rate is considered to be the same for all included reactions.
- FR-EDM takes into the account the effect of finite rate chemistry; however, it still predicts temperature overshoot in fuel-rich zones.
- Using FR-EDM, the ignition of reactions might be poorly predicted and the reactions might not be initiated even at very high temperatures. An artificial ignition source might be required to initiate the reaction chain.
- The performance of FR-EDM can be improved by considering relaxed to equilibrium calculation.
- For fuel lean mixture, FR-EDM-rex and EDC predict similar results with a slight difference. The discrepancies between the two appear for fuel-rich mixtures.
5.6. Effect of Gas-Solid (Carbon Particles) Reaction and Carbon Particle Dispersion
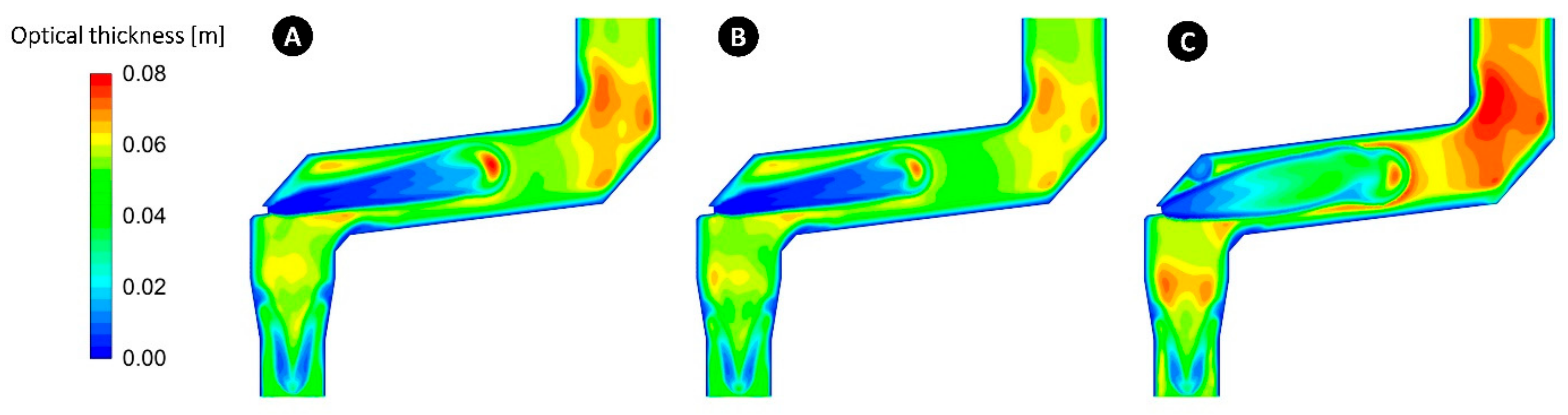
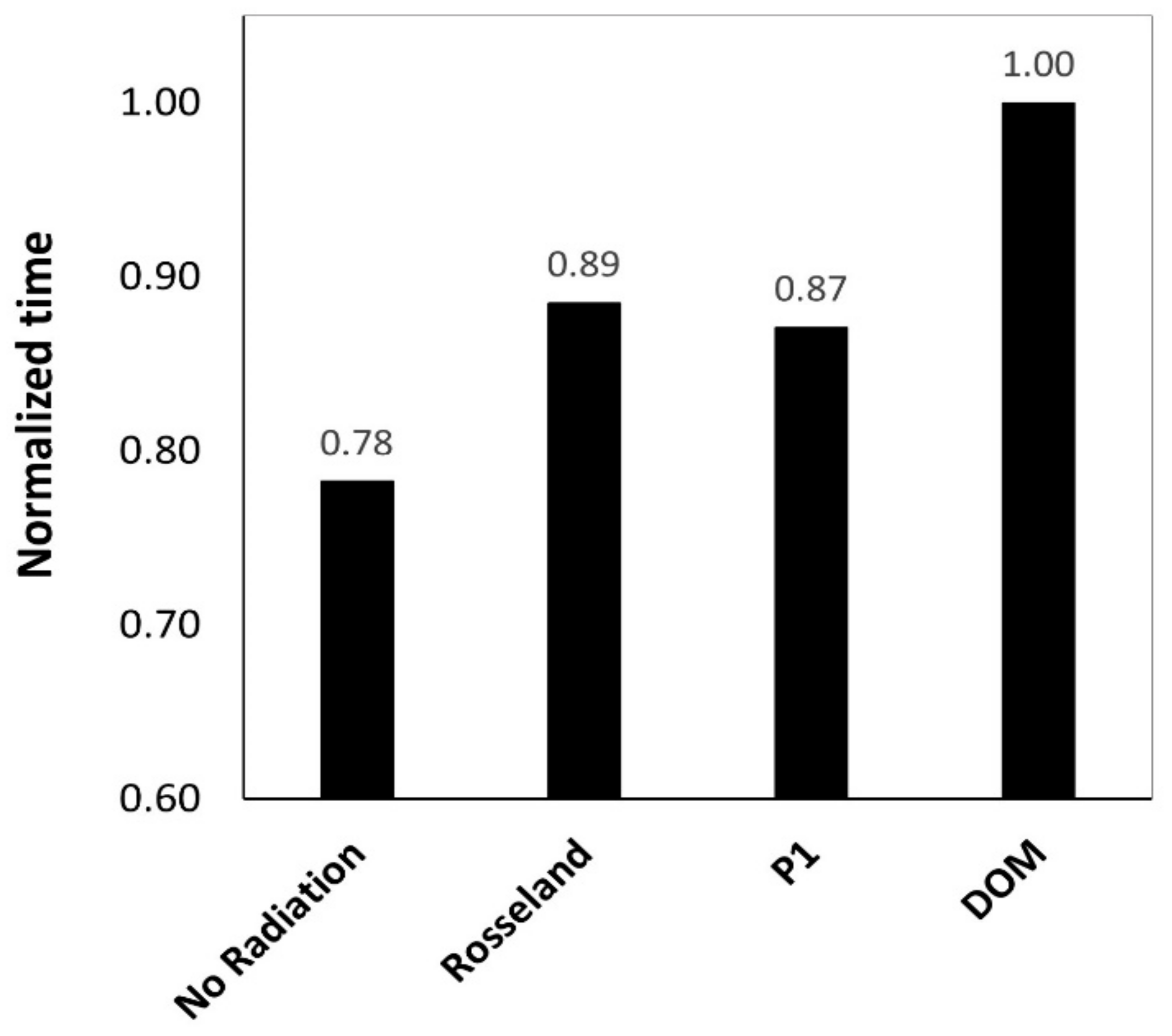
5.7. Effect of Radiation Model
- For systems with combustion process involved or any system where there is a noticeable difference between fluid and solid surfaces, the radiative heat transfer plays an important and sometimes dominant role. The case without radiation model showed unrealistic and deviated predictions from the measured values.
- The Rosseland model must be used for optically thick mediums (>3) and is not suitable for the current case where computed local optical thickness at any point is lower than 0.1.
- P1 can predict and capture the main feature of the flow and very close to the predicted values by DOM; however, there are still discrepancies between P1 predictions and measured values.
- According to the current results and the references [62,84], P1 model is accurate for optically thick media. It will yield inaccurate results for thinner (more transparent) medium, especially near boundaries, and for anisotropic radiation field. It can also fail in cases with complex geometry, such as congested spaces or geometries with many and large openings.
- P1 model is computationally cheaper and lead to lower calculation times compared to DOM.
- Ultimately, based on the obtained results and the literature review, DOM is generally preferred and seems to be very well-suited for radiation modelling in the current post combustion case.
6. Conclusions
- For coarse meshes, cell type plays an important role in predictions accuracy but the cell type effect can be ignored for fine meshes.
- Polyhedral mesh grid is always preferred over other types, especially for large-scale and industrial cases with complex geometries and more importantly when computational resources are limited. This is due to the fact that polyhedral mesh exhibits the same accuracy with much lower mesh count thus higher simulation speed.
- Even though k-ω model is more precise for prediction of turbulent nature of the flow, k-ε model is still preferred in industrial and large-scale cases as it requires lower mesh count.
- TCI model selection and kinetic mechanism are important parts of any reactive flow modelling. Based on the literature review and also performed analysis for HIsarna off-gas system, eddy dissipation concept (EDC) model is the most reliable TCI model to predict correct species and temperature profile in a reactive flow.
- Detailed kinetic mechanism is always preferred over global mechanisms for their higher accuracy. However, using detailed mechanisms come at a higher computational cost.
- Including gas–solid reactions could play a vital role in predicting correct temperature and composition profile, specifically for highly exothermic reactions such as carbon oxidation. A sensitivity analysis is needed to include enough number of particles in the calculations that can properly represent the real particle flowrate in the reactive flow.
- For high temperature application, radiation plays an important even a major role. Including radiation model is necessary to take into account the radiation effects especially for internal flow where there is a high temperature difference between the walls and the main flow stream. It becomes even more important for cases where internal reactive flow includes highly exothermic reactions (in the current case, the combustion of CO-H2 and carbon mixture).
- According to the current results and also the literature reviews, discrete ordinate mode (DOM) is more reliable than the other radiation models (P1 and Rosseland model), which is applicable for all temperature and fluid optical thickness ranges. However, using DOM comes at a higher computational cost relative to the other studied models.
- According to the current case study, it turned out that species composition profile is not as sensitive as temperature profile to sub-model selections, boundary condition, and grid variations. It is suggested to use both temperature profiles and composition profiles for model validation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Parameter | Description and units |
| Pre-exponential factor [consistent units] | |
| Particle surface area | |
| Absorption coefficient | |
| Constant coefficients | |
| Molar concentration of species in reaction [kmol/m3] | |
| Volume fraction constant equal to 2.1377 | |
| Volume fraction constant | |
| Time scale constant equal to 0.4082 | |
| Cross diffusion term | |
| Unreacted core diameter [remaining carbon] [m] | |
| Particle diameter including product [ash] layer [m] | |
| Total energy [J/kg] | |
| Activation ener for the reaction [J/kmol] | |
| Force [N] | |
| Molar fraction of species in the reactions | |
| Gravity constant [m/s2] | |
| Incident radiation | |
| Generation of turbulence kinetic energy due to the mean velocity gradients | |
| Generation of turbulence dissipation energy | |
| Generation of turbulence kinetic energy due to buoyancy | |
| Enthalpy of species [kJ/kg] | |
| Heat transfer coefficient [W/m2-K] | |
| Spectral radiation intensity | |
| Unity matrix | |
| and | Diffusion flux of species |
| Equilibrium constant for the reaction, computed from | |
| Turbulent kinetic energy [m2/s2], | |
| Effective conductivity [W/m-K] | |
| Forward rate constant for reaction | |
| Backward rate constant for reaction | |
| Mass transfer coefficient [m/s] | |
| Kinetic rate constant [kg/m2-s-Pa] | |
| Diffusion rate constant [kg/m2-s-Pa] | |
| Ash diffusion rate constant [kg/m2-s-Pa] | |
| Molecular weight of species [kg/kmol] | |
| Particle mass [kg] | |
| Drag force [N] | |
| Rate of char depletion [kg/s] | |
| Spectral index of refraction of the medium | |
| Pressure [Pa] | |
| Effective pressure [Pa] | |
| Radiative flux [W/m2] | |
| Arrhenius molar rate of creation/destruction of species in reaction [mol/s] | |
| Universal gas constant [J/kmol-K] | |
| Net rate of production/consumption of species by chemical reaction [mol/s] | |
| Overall rate of solid reaction per unit particle surface area [kg/m2-s] | |
| and | User-defined source terms in turbulence equation |
| Strain rate magnitude [1/s] | |
| Source term in species transport | |
| Source term for the reaction heat and other volumetric heat sources | |
| Position vector [m] | |
| Direction vector | |
| Scattering direction vector | |
| Path length [m] | |
| Particle temperature [K] | |
| Fluid temperature [K] | |
| t | Time [s] |
| Fluid fluctuating velocity [m/s] | |
| Fluid mean velocity [m/s] | |
| Fluid phase velocity [m/s] | |
| Particle velocity [m/s] | |
| Contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate | |
| Dissipation of kinetic energy | |
| Dissipation of eddy dissipation frequency | |
| Distance to the next surface | |
| Yi | Local mass fraction of each species |
| Mass fraction of fine-scale species after reacting over the time | |
| Chemical equilibrium mass fraction | |
| Vapor mass fraction at the surface | |
| Vapor mass fraction in the bulk gas | |
| Mass fraction of reactive surface species | |
| σ | Stefan-Boltzmann constant |
| Scattering coefficient | |
| Solid angle | |
| Effective diffusivities [kg/m-s] | |
| Energy dissipation rate [m2/s3] | |
| Turbulent viscosity [m2/s] | |
| Molecular viscosity [kg/m-s] | |
| Density of fluid [kg/m3] | |
| Density of the particle [kg/m3] | |
| Particle relaxation time | |
| Characteristic time-scale | |
| Time scale in EDC | |
| Effective shear stress [Pa] | |
| Eddy dissipation frequency [1/s] | |
| and | Turbulent Prandtl numbers |
| Corresponding stoichiometric coefficient | |
| Rate exponent for reactant species in reaction | |
| Rate exponent for reactant species in reaction | |
| Stoichiometric coefficient for reactant in reaction | |
| Stoichiometric coefficient for product in reaction | |
| Net effect of third bodies on the reaction rate | |
| Third-body efficiency of the species in the reaction | |
| Temperature exponent | |
| Length fraction of the fine scales | |
| Porosity of the ash layer | |
| kinematic viscosity [m2/s] |
Appendix A. List of Literature Review for Sub-Model Sections
| Fuel Mixture | Oxidizer | Pressure [atm] | Mechanism | Number of Species | Number of Reactions | References |
|---|---|---|---|---|---|---|
| CO-H2O | Air | 1–20 atm | Detailed | 13 | 28 | [37] |
| CO-H2-H2O | Air | 1 | Detailed | 8 | 31 | [85] |
| CO/H2/CH4 | Air | 1 | Detailed GRI | 53 | 325 | [86] |
| CO/H2 | Air/O2 | 1 | Detailed | 14 | 30 | [38] |
| CO/H2 | Air | 40–200 | Detailed | 12 | 27 | [87] |
| CO/H2 | 1–20 | Detailed | 14 | 30 | [39] | |
| CH4/CO/H2 | Air | 1 | Detailed GRI | 53 | 325 | [88] |
| CH4/CO/H2 | Air | 1 | Detailed GRI | 53 | 325 | [89] |
| CH4/CO/H2 | Air | 1 | Detailed USC II | 111 | 784 | [89] |
| CO/H2 | Air | 1–5 | Detailed GRI and mechanism from [38] | 53 | 325 | [24] |
| CO/H2 | Air/O2 | 1–10 | Detailed | 14 | 33 | [40] |
| CH4/CO/H2 | 1–40 | Detailed GRI Reduced GRI NUIG [41] Heghes [90] Frenklach [42,91] | [43,44,45] | |||
| CO/H2 | Air/O2 | 1 | Detailed | 14 | 33 | [47,48] |
| CH4/CO | Air | 1 | Global 3 step Westbrook-Dryer | 5 | 3 | [50] |
| CH4/CO/H2 | Air | 1 | Global 4 step Jones-Lindstedt | 6 | 4 | [50] |
| CH4/CO/H2 | Air | 1 | Global 6 step modified Jones-Lindstedt | 9 | 6 | [50] |
| CO/H2 | Air/O2 | 1–20 | Global 5 step | 8 | 5 | [25] |
| Application | Scale | Fuel Mixture | Mechanism | TCI Model | References |
|---|---|---|---|---|---|
| Hydrogen jet | Experimental | H2 | Detailed (16 and 37 reactions) | EDM/EDC | [92] |
| Gas burner | Pilot | C2H6/CH4/CO/H2 | Reduced GRI | EDC | [93] |
| Gas burner | Experimental | CH4/CO/H2 | GRI | EDC | [94,95,96] |
| Wood pellet burner | Domestic | Solid biomass CO-H2 | Global | EDC | [97] |
| Sulfur recovery unit (SRU) | Industrial | H2S/CH4 | Detailed (432 reactions) | EDC | [98] |
| Gas burner | Pilot | CH4/H2 | GRI DRM-22 [99] | EDC | [100,101] |
| Gas burner | Industrial | CH4/H2 | Global DRM-19 [99] GRI | EDC/FR-EDM | [58] |
| Entrained Flow Coal Gasifier | Experimental/pilot | Coal/CO/H2 | Global [14,22,102] GRI CRECK [103] | EDC/FR-EDM | [51] |
| Cyclonic gas burner | Experimental | C3H8 | San Diego [104] | EDC | [105] |
| JHC burner | Experimental | ethylene/H2 | GRI POLIMI [106] | EDC | [107] |
| Gas burner | Experimental | CH4 | GRI DRM 19 global | EDC | [14] |
| Burner | Experimental | CH4/CO | SFM KEE | EDC | [108] |
| burner | Pilot | H2 | EDM | [109] | |
| pulsejet engine | Experimental | C12H23/CH4 | EDM | [110] | |
| Furnace | Experimental | CH4/CO/H2 | DRM19 | EDC | [111] |
| rocket combustion chamber | Experimental | CH4/CO/H2 | detailed (18 reactions) [112] | EDC | [113] |
| Coal burner | Experimental | pulverized coal/CO/H2 | Detailed frank | EDM/EDC | [56] |
| furnace | Industrial | Natural gas | Global 4 step | EDM | [114] |
| Entrained flow gasifier | Pilot | Coal/CO/H2 | Reduced GRI | EDC | [115] |
| Entrained bed gasifier | Pilot | Coal/CO/H2 | Detailed | FR-EDM | [116] |
| high-velocity oxy-fuel | Experimental | H2 | Global 2 step | EDM/EDC | [53] |
| Thermal cracking | Pilot | C2H6/C3H8/C4H10 | Detailed (23 reactions) | FR-EDM | [117] |
| Thermal cracking | Pilot | C3H8 | Detailed (23 reactions) [118] | EDC | [119] |
| Micro mixing | Experimental | Boric acid | Global 3 step | FR-EDM | [120] |
| Solid Fuel Ramjet | Experimental | C2H4 | Global 3 step | EDM/FR-EDM | [52] |
| ethylene cracking furnaces | Pilot | Detailed (22 reactions) | FR-EDM | [121] | |
| Steam methane reforming furnace | Industrial | CH4 | Global (3 step) | FR-EDM | [82] |
| Application | Scale | Temperature Range [K] | Fuel | Radiation Model | Reference |
|---|---|---|---|---|---|
| Steam methane reforming furnace | Pilot | 1100–1400 | CH4 | DOM | [122] |
| Ethylene cracking furnaces | Pilot | 300–2100 | n-Paraffins/i-Paraffins/Olefins | DOM | [121] |
| Post combustion chamber | Pilot | 300–2000 | CO/H2 | P1 | [79] |
| Methane combustor | pilot | 300–2325 | CH4/H2 | P1 | [123] |
| Ethylene furnace | Industrial | 300–2150 | CH4/H2—complex feed | DOM | [124] |
| Sulphur removal unit | Industrial | - | H2S | DOM | [98] |
| hydrogen production reformer | Industrial | 650–2500 | CH4 | P1 | [81] |
| naphtha thermal cracking furnaces | Industrial | 300–1550 | CH4/C2H4/C2H6/C3H8/H2 | DOM | [17] |
| semi-suspension biomass fired industrial | Industrial | 300–1600 | Bagasse | DOM | [125] |
| Steam methane reforming furnace | Industrial | 500–2000 | CH4 | DOM | [82] |
| Mild combustor | Industrial | 300–2519 | CH4/H2 | DOM | [58] |
| Gas burner | Industrial | - | C2H6/CH4/CO/H2 | DOM | [114] |
| entrained-flow gasifier | Industrial | 300–2250 | Coal/CO/H2 | P1 | [115] |
| Gasifier | Industrial | 600–1100 | Wood chips | DOM | [126] |
References
- Tillman, D.A.; Duong, D.N.B.; Harding, N.S. Chapter 7—Modeling and Fuel Blending; Butterworth-Heinemann: Boston, MA, USA, 2012; pp. 271–293. [Google Scholar]
- Vásquez, E.; Eldredge, T. Process modeling for hydrocarbon fuel conversion: Science and Technology. In Advances in Clean Hydrocarbon Fuel Processing; Elsevier: Amsterdam, The Netherlands, 2011; pp. 509–545. Available online: https://www.sciencedirect.com/science/article/pii/B9781845697273500184 (accessed on 1 November 2021).
- Uriz, I.; Arzamendi, G.; Diéguez, P.M.; Gandía, L.M. Chapter 17—Computational Fluid Dynamics as a Tool for Designing Hydrogen Energy Technologies. In Renewable Hydrogen Technologies Production, Purification, Storage, Applications and Safety; Elsevier: Amsterdam, The Netherlands, 2013; pp. 401–435. [Google Scholar]
- Moser, A.; Schäulin, A.; Davidson, L.; Corrado, V.; Dorer, V.; Koschenz, M.; Schälin, A. Design with Modeling Techniques. In Industrial Ventilation Design Guidebook; Academic Press: Cambridge, MA, USA, 2001; pp. 1025–1104. [Google Scholar] [CrossRef]
- Juretić, F.; Gosman, A.D. Error Analysis of the Finite-Volume Method with Respect to Mesh Type. Numer. Heat Transf. Part B Fundam. 2010, 57, 414–439. [Google Scholar] [CrossRef]
- Duan, R.; Liu, W.; Xu, L.; Huang, Y.; Shen, X.; Lin, C.-H.; Liu, J.; Chen, Q.; Sasanapuri, B. Mesh Type and Number for the CFD Simulations of Air Distribution in an Aircraft Cabin. Numer. Heat Transfer Part B Fundam. 2015, 67, 489–506. [Google Scholar] [CrossRef]
- Xie, B.; Xiao, F. A multi-moment constrained finite volume method on arbitrary unstructured grids for incompressible flows. J. Comput. Phys. 2016, 327, 747–778. [Google Scholar] [CrossRef]
- Xie, B.; Deng, X.; Liao, S. High-fidelity solver on polyhedral unstructured grids for low-Mach number compressible viscous flow. Comput. Methods Appl. Mech. Eng. 2019, 357, 112584. [Google Scholar] [CrossRef]
- Yu, G.; Yu, B.; Sun, S.; Tao, W.-Q. Comparative Study on Triangular and Quadrilateral Meshes by a Finite-Volume Method with a Central Difference Scheme. Numer. Heat Transfer Part B Fundam. 2012, 62, 243–263. [Google Scholar] [CrossRef]
- Sosnowski, M.; Krzywanski, J.; Gnatowska, R. Polyhedral meshing as an innovative approach to computational domain discretization of a cyclone in a fluidized bed CLC unit. E3S Web Conf. 2017, 14, 01027. [Google Scholar] [CrossRef] [Green Version]
- Tu, J.; Yeoh, G.H.; Liu, C. Chapter 6—Practical Guidelines for CFD Simulation and Analysis. In Computational Fluid Dynamics-A Practical Approach, 2nd ed.; Butterworth-Heinemann: Amsterdam, The Netherlands, 2013; pp. 219–273. [Google Scholar]
- Sosnowski, M.; Gnatowska, R.; Grabowska, K.; Krzywański, J.; Jamrozik, A. Numerical Analysis of Flow in Building Arrangement: Computational Domain Discretization. Appl. Sci. 2019, 9, 941. [Google Scholar] [CrossRef] [Green Version]
- Zhang, H.; Tang, S.; Yue, H.; Wu, K.; Zhu, Y.; Liu, C.; Liang, B.; Li, C. Comparison of Computational Fluid Dynamic Simulation of a Stirred Tank with Polyhedral and Tetrahedral Meshes. Iran. J. Chem. Chem. Eng. 2020, 39, 311–319. [Google Scholar]
- Westbrook, C.K.; Dryer, F.L. Simplified Reaction Mechanisms for the Oxidation of Hydrocarbon Fuels in Flames. Combust. Sci. Technol. 1981, 27, 31–43. [Google Scholar] [CrossRef]
- Westbrook, C.K.; Dryer, F.L. Chemical kinetics and modeling of combustion processes. Symp. Int. Combust. 1981, 18, 749–767. [Google Scholar] [CrossRef]
- Mulder, M. O2/CH4 Kinetic Mechanisms for Aerospace Applications at Low Pressure and Temperature, Validity Ranges and Comparison. In Aeronautics and Astronautics; IntechOpen: London, UK, 2011; p. 13. [Google Scholar]
- Rezaeimanesh, M.; Ghoreyshi, A.A.; Peyghambarzadeh, S.; Hashemabadi, S.H. A coupled CFD simulation approach for investigating the pyrolysis process in industrial naphtha thermal cracking furnaces. Chin. J. Chem. Eng. 2021, 44, 528–542. [Google Scholar] [CrossRef]
- Castilla, G.M.; Montañés, R.M.; Pallarès, D.; Johnsson, F. Comparison of the Transient Behaviors of Bubbling and Circulating Fluidized Bed Combustors. Heat Transf. Eng. 2022, 44, 303–316. [Google Scholar] [CrossRef]
- Chen, L.; Ghoniem, A.F. Modeling CO2 Chemical Effects on CO Formation in Oxy-Fuel Diffusion Flames Using Detailed, Quasi-Global, and Global Reaction Mechanisms. Combust. Sci. Technol. 2014, 186, 829–848. [Google Scholar] [CrossRef] [Green Version]
- Andersen, J.; Rasmussen, C.L.; Giselsson, T.; Glarborg, P. Global Combustion Mechanisms for Use in CFD Modeling under Oxy-Fuel Conditions. Energy Fuels 2009, 23, 1379–1389. [Google Scholar] [CrossRef]
- Novosselov, I.V.; Malte, P.C. Development and Application of an Eight-Step Global Mechanism for CFD and CRN Simulations of Lean-Premixed Combustors. In Proceedings of the ASME Turbo Expo 2007: Power for Land Sea, and Air, Montreal, QC, Canada, 14–17 May 2007; pp. 769–779. [Google Scholar]
- Jones, W.; Lindstedt, R. Global reaction schemes for hydrocarbon combustion. Combust. Flame 1988, 73, 233–249. [Google Scholar] [CrossRef]
- GRI-Mech. GRI 3.0 Mechanism. Available online: http://combustion.berkeley.edu/gri-mech/overview.html (accessed on 8 April 2022).
- Natarajan, J.; Lieuwen, T.; Seitzman, J. Laminar flame speeds of H2/CO mixtures: Effect of CO2 dilution, preheat temperature, and pressure. Combust. Flame 2007, 151, 104–119. [Google Scholar] [CrossRef]
- Nikolaou, Z.M.; Chen, J.Y.; Swaminathan, N. A 5-step reduced mechanism for combustion of CO/H2/H2O/CH4/CO2 mixtures with low hydrogen/methane and high H2O content. Combust Flame 2013, 160, 56–75. [Google Scholar] [CrossRef] [Green Version]
- Iavarone, S.; Parente, A. NOx Formation in MILD Combustion: Potential and Limitations of Existing Approaches in CFD. Front. Mech. Eng. 2020, 6, 13. [Google Scholar] [CrossRef] [Green Version]
- Dally, B.; Karpetis, A.; Barlow, R. Structure of turbulent non-premixed jet flames in a diluted hot coflow. Proc. Combust. Inst. 2002, 29, 1147–1154. [Google Scholar] [CrossRef]
- Sung, C.; Law, C.; Chen, J.-Y. Augmented reduced mechanisms for NO emission in methane oxidation. Combust. Flame 2001, 125, 906–919. [Google Scholar] [CrossRef]
- Xu, H.; Liu, F.; Wang, Z.; Ren, X.; Chen, J.; Li, Q.; Zhu, Z. A Detailed Numerical Study of NOx Kinetics in Counterflow Methane Diffusion Flames: Effects of Fuel-Side versus Oxidizer-Side Dilution. J. Combust. 2021, 2021, 6642734. [Google Scholar] [CrossRef]
- Weydahl, T.; Ertesvåg, I.; Gran, I.; Magnussen, B.; Kilpinen, P. Prediction of Nitrogen Oxide Formation in Ammonia-Doped Turbulent Syngas Jet Flames. In Proceedings of the 29th International Symposium on Combustion, Sapporo, Japan, 21–26 July 2022. [Google Scholar]
- Zahirović, S.; Scharler, R.; Kilpinen, P.; Obernberger, I. Validation of flow simulation and gas combustion sub-models for the CFD-based prediction of NOx formation in biomass grate furnaces. Combust. Theory Model. 2010, 15, 61–87. [Google Scholar] [CrossRef]
- Hu, X.Z.; Yu, Q.B.; Li, Y.M. Skeletal and Reduced Mechanisms of Methane at O2/CO2 Atmosphere. Chem. J. Chin. Univ. 2018, 39, 95–101. [Google Scholar]
- Wang, W. Studies on the Efficient Reduction Methods for the Combustion Chemical Kinetic Mechanism of Fuel. Ph.D. Thesis, Chongqing University, Chongqing, China, 2016. [Google Scholar]
- Gou, X.L.; Wang, W.; Gui, Y. Methane Reaction Mechanism Reduction Using Paths Flux Analysis of Three Generations Method. J. Eng. Thermophys. 2014, 35, 1870–1873. [Google Scholar]
- Liu, H.; Chen, F.; LIU, H.; Zheng, Z.H.; Yang, S.H. 18-step reduced mechanism for methane/air premixed supersonic combustion. J. Combust. Sci. Technol. 2012, 18, 467–472. [Google Scholar]
- Lu, H.; Liu, F.; Wang, Y.; Fan, X.; Yang, J.; Liu, C.; Xu, G. Mechanism Reduction and Bunsen Burner Flame Verification of Methane. Energies 2018, 12, 97. [Google Scholar] [CrossRef] [Green Version]
- Kim, T.J.; Yetter, R.A.; Dryer, F.L. New results on moist CO oxidation: High pressure, high temperature experiments and comprehensive kinetic modeling. Symp. Int. Combust. 1994, 25, 759–766. [Google Scholar] [CrossRef]
- Davis, S.G.; Joshi, A.V.; Wang, H.; Egolfopoulos, F. An optimized kinetic model of H2/CO combustion. Proc. Combust. Inst. 2005, 30, 1283–1292. [Google Scholar] [CrossRef]
- Saxena, P.; Williams, F.A. Testing a small detailed chemical-kinetic mechanism for the combustion of hydrogen and carbon monoxide. Combust Flame 2006, 145, 316–323. [Google Scholar] [CrossRef]
- Sun, H.; Yang, S.; Jomaas, G.; Law, C. High-pressure laminar flame speeds and kinetic modeling of carbon monoxide/hydrogen combustion. Proc. Combust. Inst. 2007, 31, 439–446. [Google Scholar] [CrossRef]
- Healy, D.; Donato, N.; Aul, C.; Petersen, E.; Zinner, C.; Bourque, G.; Curran, H. Isobutane ignition delay time measurements at high pressure and detailed chemical kinetic simulations. Combust. Flame 2010, 157, 1540–1551. [Google Scholar] [CrossRef]
- Frenklach, M. Reaction mechanism of soot formation in flames. Phys. Chem. Chem. Phys. 2002, 4, 2028–2037. [Google Scholar] [CrossRef]
- Fischer, M.; Jiang, X. An investigation of the chemical kinetics of biogas combustion. Fuel 2015, 150, 711–720. [Google Scholar] [CrossRef]
- Fischer, M.; Jiang, X. An assessment of chemical kinetics for bio-syngas combustion. Fuel 2014, 137, 293–305. [Google Scholar] [CrossRef]
- Fischer, M.; Jiang, X. A chemical kinetic modelling study of the combustion of CH4–CO–H2–CO2 fuel mixtures. Combust Flame 2016, 167, 274–293. [Google Scholar] [CrossRef] [Green Version]
- Maas, U.; Warnatz, J. Ignition processes in carbon-monoxide-hydrogen-oxygen mixtures. Symp. Int. Combust. 1989, 22, 1695–1704. [Google Scholar] [CrossRef]
- Frassoldati, A.; Faravelli, T.; Ranzi, E. The ignition, combustion and flame structure of carbon monoxide/hydrogen mixtures. Note 1: Detailed kinetic modeling of syngas combustion also in presence of nitrogen compounds. Int. J. Hydrog. Energy 2007, 32, 3471–3485. [Google Scholar] [CrossRef]
- Cuoci, A.; Frassoldati, A.; Buzzi Ferraris, G.; Faravelli, T.; Ranzi, E. The ignition, combustion and flame structure of carbon monoxide/hydrogen mixtures. Note 2: Fluid dynamics and kinetic aspects of syngas combustion. Int. J. Hydrog. Energy 2007, 32, 3486–3500. [Google Scholar] [CrossRef]
- Graça, M.; Duarte, A.; Coelho, P.; Costa, M. Numerical simulation of a reversed flow small-scale combustor. Fuel Process. Technol. 2012, 107, 126–137. [Google Scholar] [CrossRef]
- Frassoldati, A.; Cuoci, A.; Faravelli, T.; Ranzi, E.; Candusso, C.; Tolazzi, D. Simplified kinetic schemes for oxy-fuel combustion. In Proceedings of the 1st International Conference on Sustainable Fossil Fuels for Future Energy 2009; Available online: https://www.researchgate.net/profile/Eliseo-Ranzi/publication/237494009_Simplified_kinetic_schemes_for_oxy-fuel_combustion/links/546f61b50cf24af340c08922/Simplified-kinetic-schemes-for-oxy-fuel-combustion.pdf (accessed on 1 November 2021).
- Mularski, J.; Modliński, N. Impact of Chemistry–Turbulence Interaction Modeling Approach on the CFD Simulations of Entrained Flow Coal Gasification. Energies 2020, 13, 6467. [Google Scholar] [CrossRef]
- Musa, O.; Xiong, C.; Changsheng, Z.; Min, Z. Combustion modeling of unsteady reacting swirling flow in solid fuel ramjet. In Proceedingds of the 2017 International Conference on Mechanical, System and Control Engineering (ICMSC), St. Petersburg, Russia, 19–21 May 2017; pp. 115–120. [Google Scholar] [CrossRef]
- Emami, S.; Jafari, H.; Mahmoudi, Y. Effects of Combustion Model and Chemical Kinetics in Numerical Modeling of Hydrogen-Fueled Dual-Stage HVOF System. J. Therm. Spray Technol. 2019, 28, 333–345. [Google Scholar] [CrossRef] [Green Version]
- May, S.; Karl, S.; Bo, O. Development of an Eddy Dissipation Model for the use in Numerical Hybrid Rocket Engine Combustion Simulation. In Proceedings of the 7th European Conference for Aeronautics and Space Sciences (EUCASS), Milan, Italy, 3–6 July 2017. [Google Scholar]
- Elwina; Yunardi; Bindar, Y.; Syukran. Simulation of the Influence of Air Preheat Combustion on the Temperature of Propane Turbulent Flame Using Probability Density Function Approach and Eddy Dissipation Model. Adv. Mat. Res. 2014, 871, 95–100. [Google Scholar] [CrossRef]
- Vascellari, M.; Cau, G. Influence of turbulence–chemical interaction on CFD pulverized coal MILD combustion modeling. Fuel 2012, 101, 90–101. [Google Scholar] [CrossRef]
- Rohani, B.; Wahid, M.A.; Sies, M.M.; Saqr, K.M. Comparison of eddy dissipation model and presumed probability density function model for temperature prediction in a non-premixed turbulent methane flame. In Proceedings of the 4th International Meeting of Advances in Thermofluids (IMAT 2011); AIP Conference Proceedings: Perlis, Malaysia, 2012; Volume 1440, pp. 384–391. [Google Scholar] [CrossRef] [Green Version]
- Parente, A.; Galletti, C.; Tognotti, L. Effect of the combustion model and kinetic mechanism on the MILD combustion in an industrial burner fed with hydrogen enriched fuels. Int. J. Hydrog. Energy 2008, 33, 7553–7564. [Google Scholar] [CrossRef]
- Olivieri, A.; Vegliò, F. Process simulation of natural gas steam reforming: Fuel distribution optimisation in the furnace. Fuel Process. Technol. 2008, 89, 622–632. [Google Scholar] [CrossRef]
- Liesche, G.; Sundmacher, K. Radiation-based model reduction for the optimization of high temperature tube bundle reactors: Synthesis of hydrogen cyanide. Comput. Chem. Eng. 2019, 127, 186–199. [Google Scholar] [CrossRef]
- Yu, Z.; Cao, E.; Wang, Y.; Zhou, Z.; Dai, Z. Simulation of natural gas steam reforming furnace. Fuel Process. Technol. 2006, 87, 695–704. [Google Scholar] [CrossRef]
- Habibi, A.; Merci, B.; Heynderickx, G. Impact of radiation models in CFD simulations of steam cracking furnaces. Comput. Chem. Eng. 2007, 31, 1389–1406. [Google Scholar] [CrossRef]
- Modest, M.F. The Weighted-Sum-of-Gray-Gases Model for Arbitrary Solution Methods in Radiative Transfer. J. Heat Transf. 1991, 113, 650–656. [Google Scholar] [CrossRef]
- Krishnamoorthy, G. A new weighted-sum-of-gray-gases model for CO2–H2O gas mixtures. Int. Commun. Heat Mass Transf. 2010, 37, 1182–1186. [Google Scholar] [CrossRef]
- Cassol, F.; Brittes, R.; França, F.H.; Ezekoye, O.A. Application of the weighted-sum-of-gray-gases model for media composed of arbitrary concentrations of H2O, CO2 and soot. Int. J. Heat Mass Transf. 2014, 79, 796–806. [Google Scholar] [CrossRef]
- Kim, O.J.; Song, T.-H. Implementation of the weighted sum of gray gases model to a narrow band: Application and validity. Numer. Heat Transfer Part B Fundam. 1996, 30, 453–468. [Google Scholar] [CrossRef]
- Levenspiel, O. Chemical Reaction Engineering; Wiley: New York, NY, USA, 1972; Volume 2. [Google Scholar]
- Stapountzis, H.; Tzavellas, P.; Moros, T. Effects of Turbulence on the Mixing and Chemical Reaction for Cross Flow and Coflowing jets BT. In Advances in Turbulence 3; Johansson, A.V., Alfredsson, P.H., Eds.; Springer: Berlin/Heidelberg, Germany, 1991; pp. 300–311. [Google Scholar]
- Glassman, I.; Eberstein, I.J. Turbulence effects in chemical reaction kinetics measurements. AIAA J. 1963, 1, 1424–1426. [Google Scholar] [CrossRef]
- Magnussen, B.; Hjertager, B. On mathematical modeling of turbulent combustion with special emphasis on soot formation and combustion. Symp. Int. Combust. 1977, 16, 719–729. [Google Scholar] [CrossRef]
- Poinsot, T.; Veynante, D. Theoretical and Numerical Combustion; RT Edwards Inc.: Spring Hope, NC, USA, 2005. [Google Scholar]
- Rebola, P.; Coelho, J.; Costa, M. Assessment of the Performance of Several Turbulence and Combustion Models in the Numerical Simulation of a Flameless Combustor. Combust. Sci. Technol. 2013, 185, 600–626. [Google Scholar] [CrossRef]
- Toporov, D.D. Chapter 4—Mathematical Modelling and Model Validations. In Combustion of Pulverised Coal in a Mixture of Oxygen and Recycled Flue Gas; Elsevier: Boston, MA, USA, 2014; pp. 51–97. [Google Scholar]
- Morsi, S.A.; Alexander, A.J. An investigation of particle trajectories in two-phase flow systems. J. Fluid Mech. 1972, 55, 193–208. [Google Scholar] [CrossRef]
- Mofakham, A.A.; Ahmadi, G. Improved Discrete Random Walk Stochastic Model for Simulating Particle Dispersion and Deposition in Inhomogeneous Turbulent Flows. J. Fluids Eng. 2020, 142, 101401. [Google Scholar] [CrossRef]
- Hosseini, A.; Dhiman, V.; Meijer, K.; Zeilstra, C.; Hage, J.; Peeters, T.; Offerman, E.; Yang, Y. CFD modelling of the off-gas system HIsarna iron making process part 2: Reflux chamber geometry modification and effects on flow behaviour. Ironmak. Steelmak. 2022, 49, 783–794. [Google Scholar] [CrossRef]
- Wen, C.Y.; Chaung, T.Z. Entrainment Coal Gasification Modeling. Ind. Eng. Chem. Process Des. Dev. 1979, 18, 684–695. [Google Scholar] [CrossRef]
- Wang, W.; Cao, Y.; Okaze, T. Comparison of hexahedral, tetrahedral and polyhedral cells for reproducing the wind field around an isolated building by LES. Build. Environ. 2021, 195, 107717. [Google Scholar] [CrossRef]
- Sripriya, R.; Peeters, T.; Meijer, K.; Zeilstra, C.; Van Der Plas, D. Computational fluid dynamics and combustion modelling of HIsarna incinerator. Ironmak. Steelmak. 2016, 43, 192–202. [Google Scholar] [CrossRef]
- Labiscsak, L.; Straffelini, G.; Corbetta, C.; Bodino, M. Fluid dynamics of a post-combustion chamber in electric arc steelmaking plants. Comput. Methods Exp. Meas. 2011, 51, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Chen, P.; Du, W.; Zhang, M.; Duan, F.; Zhang, L. Numerical studies on heat coupling and configuration optimization in an industrial hydrogen production reformer. Int. J. Hydrog. Energy 2018, 44, 15704–15720. [Google Scholar] [CrossRef]
- Tran, A.; Aguirre, A.; Durand, H.; Crose, M.; Christofides, P.D. CFD modeling of a industrial-scale steam methane reforming furnace. Chem. Eng. Sci. 2017, 171, 576–598. [Google Scholar] [CrossRef]
- ANSYS Inc. Guide AFU; ANSYS Inc.: Canonsburg, PA, USA, 2013. [Google Scholar]
- Keramida, E.; Liakos, H.; Founti, M.; Boudouvis, A.; Markatos, N. Radiative heat transfer in natural gas-fired furnaces. Int. J. Heat Mass Transf. 2000, 43, 1801–1809. [Google Scholar] [CrossRef]
- Wang, W.; Rogg, B. Reduced kinetic mechanisms and their numerical treatment I: Wet CO flames. Combust. Flame 1993, 94, 271–292. [Google Scholar] [CrossRef]
- Vagelopoulos, C.; Egolfopoulos, F. Laminar flame speeds and extinction strain rates of mixtures of carbon monoxide with hydrogen, methane, and air. Symp. Int. Combust. 1994, 25, 1317–1323. [Google Scholar] [CrossRef]
- Li, W.; Zou, C.; Yao, H.; Lin, Q.; Fu, R.; Luo, J. An optimized kinetic model for H2/CO combustion in CO2 diluent at elevated pressures. Combust Flame 2022, 241, 112093. [Google Scholar] [CrossRef]
- Singh, D.; Nishiie, T.; Tanvir, S.; Qiao, L. An experimental and kinetic study of syngas/air combustion at elevated temperatures and the effect of water addition. Fuel 2012, 94, 448–456. [Google Scholar] [CrossRef]
- He, Y.; Wang, Z.; Yang, L.; Whiddon, R.; Li, Z.; Zhou, J.; Cen, K. Investigation of laminar flame speeds of typical syngas using laser based Bunsen method and kinetic simulation. Fuel 2012, 95, 206–213. [Google Scholar] [CrossRef]
- Heghes, C. Soot Formation Modeling During Hydrocarbon Pyrolysis and Oxidation Behind Shock Waves. Ph.D. Thesis, University of Heidelberg, Heidelberg, Germany, 2006. [Google Scholar]
- Wang, H.; Frenklach, M. A detailed kinetic modeling study of aromatics formation in laminar premixed acetylene and ethylene flames. Combust Flam 1997, 110, 173–221. [Google Scholar] [CrossRef]
- Vankova, O.S. Comparison of Turbulence/Chemistry Interaction Models in the Problem of Ignition a Parallel Hydrogen Jet in a Supersonic Air Flow; AIP Conference Proceedings: Perlis, Malaysia, 2021; Volume 2351. [Google Scholar] [CrossRef]
- Lewandowski, M.T.; Pozorski, J. Assessment of turbulence-chemistry interaction models in the computation of turbulent non-premixed flames. J. Phys. Conf. Ser. 2016, 760, 012015. [Google Scholar] [CrossRef] [Green Version]
- Christo, F.; Dally, B. Modeling turbulent reacting jets issuing into a hot and diluted coflow. Combust. Flame 2005, 142, 117–129. [Google Scholar] [CrossRef]
- De, A.; Oldenhof, E.; Sathiah, P.; Roekaerts, D. Numerical Simulation of Delft-Jet-in-Hot-Coflow (DJHC) Flames Using the Eddy Dissipation Concept Model for Turbulence–Chemistry Interaction. Flow Turbul. Combust. 2011, 87, 537–567. [Google Scholar] [CrossRef] [Green Version]
- De, A.; Dongre, A. Assessment of Turbulence-Chemistry Interaction Models in MILD Combustion Regime. Flow Turbul. Combust. 2015, 94, 439–478. [Google Scholar] [CrossRef]
- Chapela, S.; Porteiro, J.; Costa, M. Effect of the Turbulence–Chemistry Interaction in Packed-Bed Biomass Combustion. Energy Fuels 2017, 31, 9967–9982. [Google Scholar] [CrossRef]
- Mahmoodi, B.; Hosseini, S.H.; Ahmadi, G.; Raj, A. CFD simulation of reactor furnace of sulfur recovery units by considering kinetics of acid gas (H2S and CO2) destruction. Appl. Therm. Eng. 2017, 123, 699–710. [Google Scholar] [CrossRef]
- DRM Mechanism. Available online: http://combustion.berkeley.edu/drm/ (accessed on 1 November 2021).
- Mardani, A. Optimization of the Eddy Dissipation Concept (EDC) model for turbulence-chemistry interactions under hot diluted combustion of CH4/H2. Fuel 2017, 191, 114–219. [Google Scholar] [CrossRef]
- Mardani, A.; Tabejamaat, S.; Mohammadi, M.B. Numerical study of the effect of turbulence on rate of reactions in the MILD combustion regime. Combust. Theory Model. 2011, 15, 753–772. [Google Scholar] [CrossRef]
- Hautman, D.J.; Dryer, F.L.; Schug, K.P.; Glassman, I. A Multiple-step Overall Kinetic Mechanism for the Oxidation of Hydrocarbons. Combust. Sci. Technol. 1981, 25, 219–235. [Google Scholar] [CrossRef]
- Ranzi, E.; Frassoldati, A.; Stagni, A.; Pelucchi, M.; Cuoci, A.; Faravelli, T. Reduced Kinetic Schemes of Complex Reaction Systems: Fossil and Biomass-Derived Transportation Fuels. Int. J. Chem. Kinet. 2014, 46, 512–542. [Google Scholar] [CrossRef]
- San Diego Mechanism. Available online: https://web.eng.ucsd.edu/mae/groups/combustion/mechanism.html (accessed on 2 February 2022).
- Sorrentino, G.; Sabia, P.; de Joannon, M.; Ragucci, R.; Cavaliere, A.; Göktolga, U.; van Oijen, J.; de Goey, P. Development of a Novel Cyclonic Flow Combustion Chamber for Achieving MILD/Flameless Combustion. Energy Procedia 2015, 66, 141–144. [Google Scholar] [CrossRef] [Green Version]
- Ranzi, E.; Frassoldati, A.; Grana, R.; Cuoci, A.; Faravelli, T.; Kelley, A.P.; Law, C.K. Hierarchical and comparative kinetic modeling of laminar flame speeds of hydrocarbon and oxygenated fuels. Prog. Energy Combust. Sci. 2012, 38, 468–501. [Google Scholar] [CrossRef]
- Shabanian, S.R.; Medwell, P.R.; Rahimi, M.; Frassoldati, A.; Cuoci, A. Kinetic and fluid dynamic modeling of ethylene jet flames in diluted and heated oxidant stream combustion conditions. Appl. Therm. Eng. 2013, 52, 538–554. [Google Scholar] [CrossRef]
- Danon, B.; de Jong, W.; Roekaerts, D.J.E.M. Experimental and Numerical Investigation of a FLOX Combustor Firing Low Calorific Value Gases. Combust. Sci. Technol. 2010, 182, 1261–1278. [Google Scholar] [CrossRef]
- Halouane, Y.; Dehbi, A. CFD simulations of premixed hydrogen combustion using the Eddy Dissipation and the Turbulent Flame Closure models. Int. J. Hydrog. Energy 2017, 42, 21990–22004. [Google Scholar] [CrossRef]
- Agarwal, A.; Pitso, I. Modelling & numerical exploration of pulsejet engine using eddy dissipation combustion model. Mater. Today Proc. 2020, 27, 1341–1349. [Google Scholar]
- Romero-Anton, N.; Huang, X.; Bao, H.; Martin-Eskudero, K.; Salazar-Herran, E.; Roekaerts, D. New extended eddy dissipation concept model for flameless combustion in furnaces. Combust. Flame 2020, 220, 49–62. [Google Scholar] [CrossRef]
- Dong, G.; Huang, Y.; Chen, Y. Study of effects of different chemical reaction mechanisms on computation results for methane jet turbulence diffusion flame. J. Fuel Chem. Technol. 2000, 28, 49–54. [Google Scholar]
- Wei, J.; Ye, M.; Zhang, S.; Qin, J.; Haidn, O.J. Modeling of a 7-elements GOX/GCH4 combustion chamber using RANS with Eddy-Dissipation Concept model. Aerosp. Sci. Technol. 2020, 99, 10576. [Google Scholar] [CrossRef]
- Jóźwiak, P.; Hercog, J.; Kiedrzyńska, A.; Badyda, K. CFD analysis of natural gas substitution with syngas in the industrial furnaces. Energy 2019, 179, 593–602. [Google Scholar] [CrossRef]
- Richter, A.; Vascellari, M.; Nikrityuk, P.A.; Hasse, C. Detailed analysis of reacting particles in an entrained-flow gasifier. Fuel Process. Technol. 2016, 144, 95–108. [Google Scholar] [CrossRef]
- Park, S.S.; Jeong, H.J.; Hwang, J. 3-D CFD Modeling for Parametric Study in a 300-MWe One-Stage Oxygen-Blown Entrained-Bed Coal Gasifier. Energies 2015, 8, 4216–4236. [Google Scholar] [CrossRef] [Green Version]
- Zhang, N.; Chen, B.; Qiu, T. CFD simulation of cracking tube with internal twisted slices. In 11th International Symposium on Process Systems Engineering; Karimi, I.A., Srinivasan, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2012; pp. 905–909. [Google Scholar]
- Sundaram, K.M.; Froment, G.F. Modeling of Thermal Cracking Kinetics. 3. Radical Mechanisms for the Pyrolysis of Simple Paraffins, Olefins, and Their Mixtures. Ind. Eng. Chem. Fundam. 1978, 17, 174–182. [Google Scholar] [CrossRef]
- Zhang, N.; Qiu, T.; Chen, B. CFD Simulation of Propane Cracking Tube Using Detailed Radical Kinetic Mechanism. Chin. J. Chem. Eng. 2013, 21, 1319–1331. [Google Scholar] [CrossRef]
- Ouyang, Y.; Xiang, Y.; Zou, H.; Chu, G.; Chen, J. Flow characteristics and micromixing modeling in a microporous tube-in-tube microchannel reactor by CFD. Chem. Eng. J. 2017, 321, 533–545. [Google Scholar] [CrossRef]
- Guihua, H.; Honggang, W.; Feng, Q. Numerical simulation on flow, combustion and heat transfer of ethylene cracking furnaces. Chem. Eng. Sci. 2011, 66, 1600–1611. [Google Scholar] [CrossRef]
- Tutar, M.; Üstün, C.E.; Campillo-Robles, J.M.; Fuente, R.; Cibrián, S.; Arzua, I.; Fernández, A.; López, G.A. Optimized CFD modelling and validation of radiation section of an industrial top-fired steam methane reforming furnace. Comput. Chem. Eng. 2021, 155, 107504. [Google Scholar] [CrossRef]
- Lbas, M.; Yılmaz, İ.; Kaplan, Y. Investigations of hydrogen and hydrogen–hydrocarbon composite fuel combustion and NOx emission characteristics in a model combustor. Int. J. Hydrog. Energy 2005, 30, 1139–1147. [Google Scholar]
- Lan, X.; Gao, J.; Xu, C.; Zhang, H. Numerical Simulation of Transfer and Reaction Processes in Ethylene Furnaces. Chem. Eng. Res. Des. 2007, 85, 1565–1579. [Google Scholar] [CrossRef]
- Laubscher, R.; van der Merwe, S. Heat transfer modelling of semi-suspension biomass fired industrial watertube boiler at full- and part-load using CFD. Therm. Sci. Eng. Prog. 2021, 25, 100969. [Google Scholar] [CrossRef]
- Gruber, T.; Scharler, R.; Obernberger, I. Application of an empirical model in CFD simulations to predict the local high temperature corrosion potential in biomass fired boilers. Biomass Bioenergy 2015, 79, 145–154. [Google Scholar] [CrossRef]













| Main Equation | Sub-Equations and Constants | ||
|---|---|---|---|
| Continuity equation | (1) | ||
| Momentum equation | (2) | ||
| Turbulence models | Realizable k-ε Model | and =1.2 1.44 | |
| Equation for turbulent kinetic energy (k) | |||
| (3) | |||
| Equation for dissipation of turbulent kinetic energy (ε): | |||
| (4) | |||
| SST k-ω model | , | ||
| Equation for turbulent kinetic energy (k) | |||
| (5) | |||
| Equation for turbulent kinetic energy dissipation rate (ω): | |||
| (6) | |||
| Energy equation | (7) | ||
| Radiation models | Discrete ordinate model (DOM) | ||
| (8) | |||
| P1 model: | |||
| (9) | |||
| (10) | |||
| (11) | |||
| Rosseland model: | |||
| (12) | G = 4σn2T4 | ||
| (13) | qr = −16σn2T3 | ||
| Species transport equation | (14) | ||
| Turbulence-chemistry interaction models | Finite rate model (FR): | ||
| (15) | |||
| (16) | |||
| Eddy dissipation model (EDM): | |||
| (17) | |||
| Finite rate eddy dissipation model (FR-EDM) | |||
| (18) | |||
| Finite rate eddy dissipation model—relaxed to equilibrium (FR-EDM-rex): | |||
| (19) | |||
| Eddy dissipation concept (EDC): | |||
| (20) | |||
| (21) | |||
| (22) | |||
| Particle force balance equation—Discrete phase model | (23) | ||
| Particle evaporation model | (24) | ||
| carbon particle reaction rate | (25) | ||
| (26) | |||
| Flue Gas Inlet | Air Quench Inlet | Oxygen Port Inlet | Nitrogen Ports Inlet | Water Spray Injection | |
|---|---|---|---|---|---|
| Temperature [K] | 2086 | 293 | 293 | 293 | 293 |
| Volumetric flowrate [m3/s] | 20.8 | 3.10 | 0.206 | - | |
| Average density [Kg/m3] | 0.208 | 1.19 | 1.31 | 1.25 | 998 |
| mass flowrate [Kg/s] | 4.33 | 3.69 | 0.27 | 0.205 | 0.45 |
| Composition—average mole fraction at inlet | |||||
| CO | 0.0261 | 0 | 0 | 0 | 0 |
| CO2 | 0.61 | 0.0003 | 0 | 0 | 0 |
| H2 | 0.002 | 0 | 0 | 0 | 0 |
| O2 | 0 | 0.21 | 0.995 | 0 | 0 |
| N2 | 0.166 | 0.78 | 0.005 | 1 | 0 |
| H2O | 0.2 | 0.012 | 0 | 0 | 1 |
| Post Combustion Ratio [%] | 96.63 | - | - | - | - |
| Parameters | Refractory | Steel Pipe | ||
|---|---|---|---|---|
| Thermal conductivity [W/m-K] | 3.65 | |||
| Heat Capacity [J/kg-K] | 836 | 461 | ||
| Density [Kg/m3] | 3010 | 7850 | ||
| Thickness [m] | 0.037 | 0.005 | ||
| Cooling water properties | Stack1 | Stack 2 and 3 | Stack 4 | |
| Average Temperature [K] | 314 | 307 | 314.5 | |
| Water side heat transfer coefficient [W/m2-K] | 5000 | 4500 | 4000 | |
| Reaction | A | n | Ea | |
|---|---|---|---|---|
| 1 | H + O2 = OH + O | 2.21 × 1011 | 0 | 16,650 |
| 2 | O + H2 = OH + H | 4.33 × 1010 | 0 | 10,000 |
| 3 | H + O2 + [M] = HO2 + [M] | 4.65 × 109 | −0.8 | 0 |
| 4 | H + O2 + O2 = HO2 + O2 | 8.90 × 108 | 0 | −2822 |
| 5 | OH + HO2 = H2O + O2 | 5.00 × 1010 | 0 | 1000 |
| 6 | H + HO2 = OH + OH | 2.50 × 1011 | 0 | 1900 |
| 7 | O + HO2 = O2 + OH | 3.25 × 1010 | 0 | 0 |
| 8 | OH + OH = O + H2O | 7.36 × 109 | 0 | 1100 |
| 9 | H2 + [M] = H + H + [M] | 2.23 × 1011 | 0 | 96,081 |
| 10 | O2 + [M] = O + O + [M] | 1.55 × 1011 | 0 | 115,120 |
| 11 | H + OH + [M] = H2O + [M] | 4.50 × 1016 | −2 | 0 |
| 12 | H + HO2 = H2 + O2 | 2.50 × 1010 | 0 | 700 |
| 13 | HO2 + HO2 = H2O2 + O2 | 2.11 × 109 | 0 | 0 |
| 14 | OH + OH + [M] = H2O2 + [M] | 7.40 × 1010 | −0.37 | 0 |
| 15 | O + OH + [M] = HO2 + [M] | 1.00 × 1010 | 0 | 0 |
| 16 | H + H2O = H2 + OH | 4.00 × 107 | 1 | 19,000 |
| 17 | H2O2 + H = H2O + OH | 2.41 × 1010 | 0 | 3970 |
| 18 | H2O2 + H = H2 + HO2 | 6.03 × 1010 | 0 | 7950 |
| 19 | HO2 + H2O→H2O2 + OH | 5.39 × 105 | 2 | 28,780 |
| 20 | OH + H2O2→H2O + HO2 | 3.20 × 105 | 2 | −4170 |
| 21 | O + H2O2→OH + HO2 | 1.08 × 106 | 2 | −1657 |
| 22 | CO + O + [M] = CO2 + [M] | 9.64 × 107 | 0 | 3800 |
| 23 | CO + OH = CO2 + H | 9.60 × 108 | 0.14 | 7352 |
| 24 | CO + HO2 = CO2 + OH | 3.01 × 1010 | 0 | 23,000 |
| 25 | CO + H2O = CO2 + H2 | 2.00 × 108 | 0 | 38,000 |
| 26 | O2 + CO = CO2 + O | 2.53 × 109 | 0 | 47,700 |
| 27 | HCO + [M] = CO + H + [M] | 1.20 × 1014 | −1 | 17,000 |
| 28 | HCO + O = CO2 + H | 3.00 × 1010 | 0 | 0 |
| 29 | HCO + H = H2 + CO | 1.00 × 1011 | 0 | 0 |
| 30 | HCO + OH = H2O + CO | 5.00 × 1010 | 0 | 0 |
| 31 | HCO + HO2 = H2O2 + CO | 4.00 × 108 | 0 | 0 |
| 32 | O2 + HCO = HO2 + CO | 1.00 × 109 | 0 | 0 |
| 33 | HCO + HO2⇒H + OH + CO2 | 3.00 × 1010 | 0 | 0 |
| Reaction | A | E [J/kgmol] | Temperature Exponent | Diffusion Rate Constant [] |
|---|---|---|---|---|
| 0.85961 | 1 | |||
| 0.02438 | 0 | |||
| 0.02438 | 0 |
| Sub Models | Model/Algorithm |
|---|---|
| Turbulent flow | Realizable k-ε model Enhanced wall treatment |
| TCI | EDC |
| Radiation | DOM |
| Particle trajectory | DPM model with stochastic tracking |
| Particle dispersion (NTs) | DRW model (20) |
| Gas solid reaction | DPM multiple surface reaction model Field char oxidation |
| Particle evaporation | Convection-diffusion |
| Tetrahedral | Polyhedral | |
|---|---|---|
| Orthogonal quality | 0.7891 | 0.9725 |
| Skewness | 0.21 | - |
| Cell Size [mm] | Cell Count [Million] | |||
|---|---|---|---|---|
| Zone | Reflux Chamber | Air Quench | Up/Down Leg | |
| Very coarse | 65 | 55 | 75 | 0.88 |
| Coarse | 55 | 45 | 65 | 1.05 |
| Medium | 40 | 30 | 50 | 2.69 |
| Fine | 30 | 25 | 40 | 2.3 |
| Very fine | 25 | 20 | 35 | 3.3 |
| Mesh | First Layer Thickness [mm] | Number of Inflation Layers | Mesh Size (Reflux Chamber) | Mesh Size (Off-Gas System) | y+ | Number of Tracked Particles | Incomplete Particles (Average) |
|---|---|---|---|---|---|---|---|
| Mesh 1 | 0.2 | 14 | 880 × 103 | 5.31 × 106 | 0.38 | 9185 | 880 (10%) |
| Mesh 2 | 0.3 | 12 | 840 × 103 | 4.8 × 106 | 0.6 | 8800 | 686 (8%) |
| Mesh 3 | 0.5 | 10 | 750 × 103 | 4.1 × 106 | 0.95 | 7600 | 356 (5%) |
| Mesh 4 | 1 | 8 | 645 × 103 | 3.58 × 106 | 1.9 | 6315 | 230 (4%) |
| Mesh 5 | 2 | 5 | 627 × 103 | 3.12 × 106 | 4.6 | 5900 | 117 (2%) |
| Mesh 6 (base model) | 10 | 4 | 485 × 103 | 2.6 × 106 | 34 | 4516 | 0 |
| Plant Measurement | Calculated | |||||
|---|---|---|---|---|---|---|
| Number of tries [] | - | 1 | 3 | 5 | 10 | 20 |
| Number of injected particles [] | - | 923 | 2769 | 4615 | 9230 | 15,840 |
| Reflux chamber outlet carbon flowrate [kg/s] | - | 0.0141 | 0.0137 | 0.0136 | 0.0135 | 0.0135 |
| Reflux chamber outlet carbon conversion [%] | 50 | 50 | 52 | 52 | 53 | 52 |
| Reflux chamber outlet temperature [K] | 1710 | 1692 | 1698 | 1702 | 1695 | 1702.4 |
| Reflux chamber outlet molar composition (dry basis) | ||||||
| CO | 0.00 | 0.002 | 0.0021 | 0.002 | 0.00192 | 0.002 |
| O2 | 0.054 | 0.0535 | 0.0532 | 0.0534 | 0.0533 | 0.0534 |
| Heat loss | ||||||
| Reflux chamber [MW] | 3.9 | 3.89 | 3.91 | 3.91 | 3.92 | 3.91 |
| Rest of the off-gas system [MW] | 5.4 | 4.87 | 4.85 | 4.87 | 4.83 | 4.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hosseini, A.; Hage, J.L.T.; Meijer, K.; Offerman, E.; Yang, Y. On the Importance of Model Selection for CFD Analysis of High Temperature Gas-Solid Reactive Flow; Case Study: Post Combustion Chamber of HIsarna Off-Gas System. Processes 2023, 11, 839. https://doi.org/10.3390/pr11030839
Hosseini A, Hage JLT, Meijer K, Offerman E, Yang Y. On the Importance of Model Selection for CFD Analysis of High Temperature Gas-Solid Reactive Flow; Case Study: Post Combustion Chamber of HIsarna Off-Gas System. Processes. 2023; 11(3):839. https://doi.org/10.3390/pr11030839
Chicago/Turabian StyleHosseini, Ashkan, Johannes L. T. Hage, Koen Meijer, Erik Offerman, and Yongxiang Yang. 2023. "On the Importance of Model Selection for CFD Analysis of High Temperature Gas-Solid Reactive Flow; Case Study: Post Combustion Chamber of HIsarna Off-Gas System" Processes 11, no. 3: 839. https://doi.org/10.3390/pr11030839
APA StyleHosseini, A., Hage, J. L. T., Meijer, K., Offerman, E., & Yang, Y. (2023). On the Importance of Model Selection for CFD Analysis of High Temperature Gas-Solid Reactive Flow; Case Study: Post Combustion Chamber of HIsarna Off-Gas System. Processes, 11(3), 839. https://doi.org/10.3390/pr11030839





