The Short-Circuit Fault Current Impact Mechanism and Adaptive Control Strategy of an MMC-HVDC
Abstract
:1. Introduction
- The mechanism of the short circuit supplied by the MMC-HVDC system is clarified, and the main impact factors are analyzed.
- To allow for the MMC to adjust its injected fault current, an adaptive reference control and an adaptive limiter control are proposed, which are easy to realize and effective in impacting the short circuits of AC systems.
- To guarantee that the MMC can continuously impact an AC system’s fault current, an adaptive capacitor method is also proposed that can render the system more stable during the fault period.
2. The Structure and Control of an MMC-HVDC
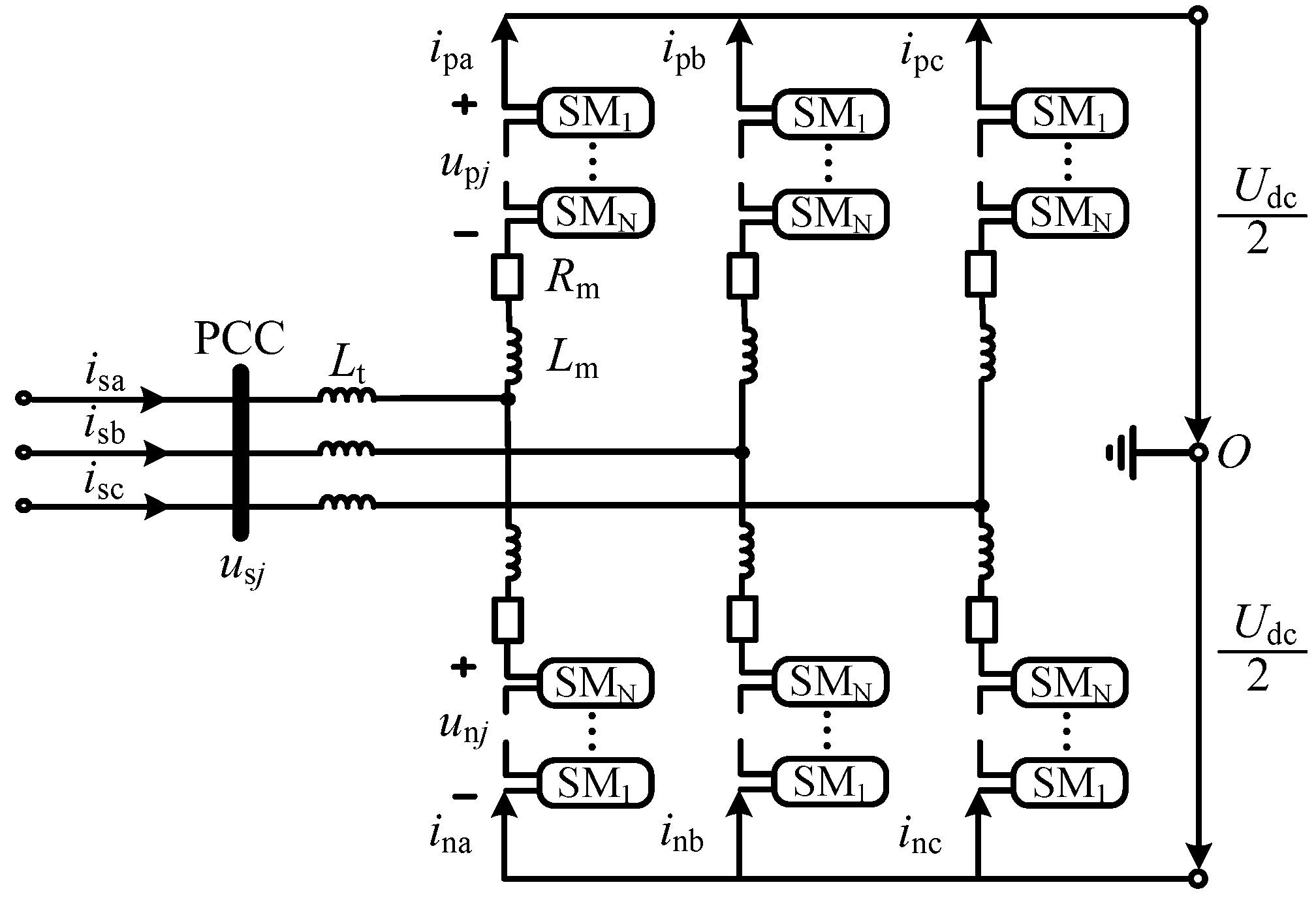
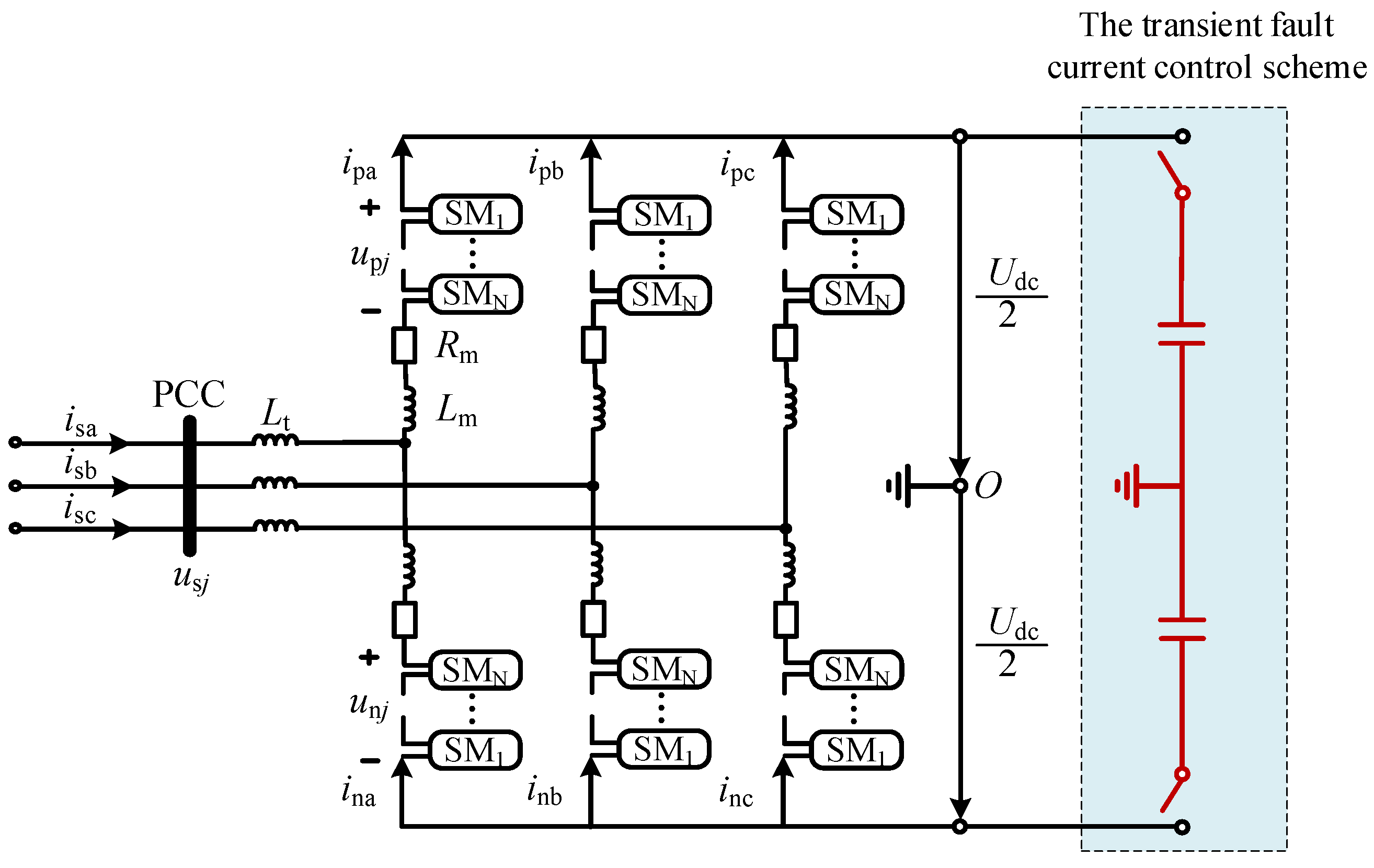
2.1. The Structure of an MMC-HVDC
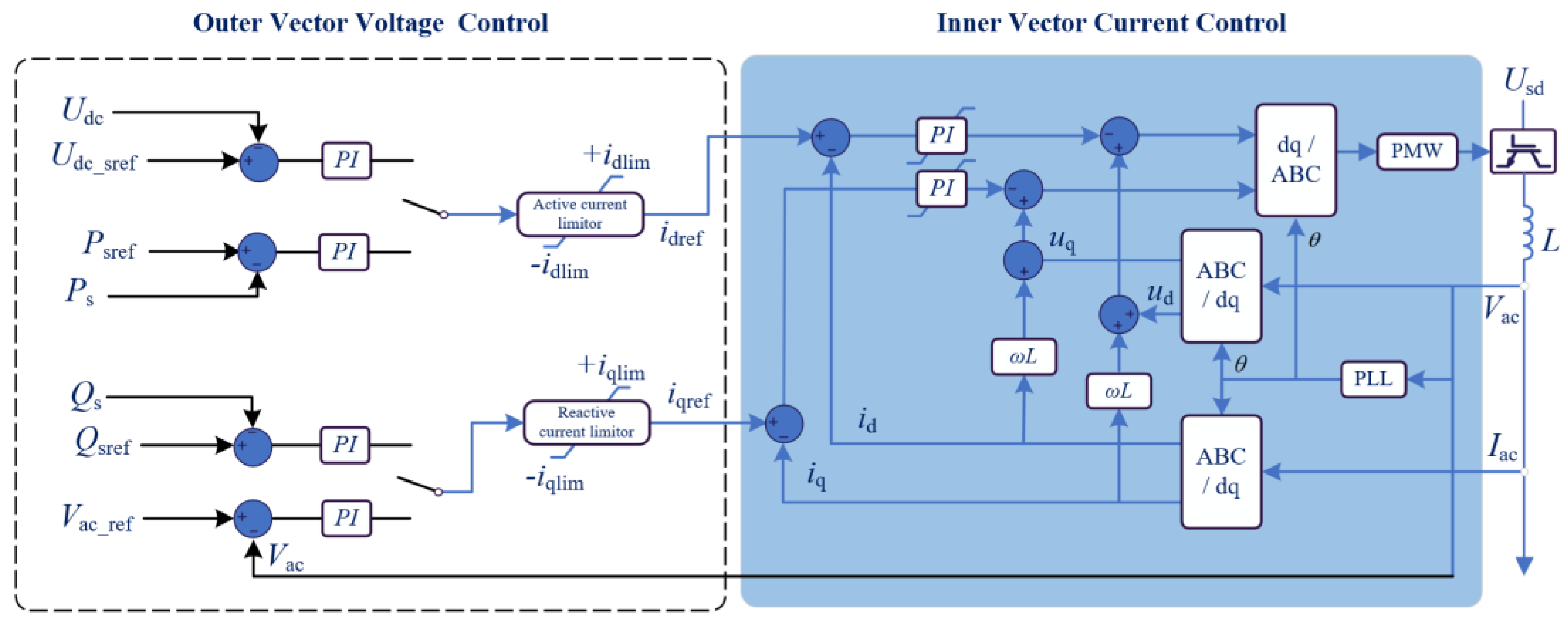
2.2. The Control of an MMC-HVDC
2.3. The Limiter of an MMC-HVDC
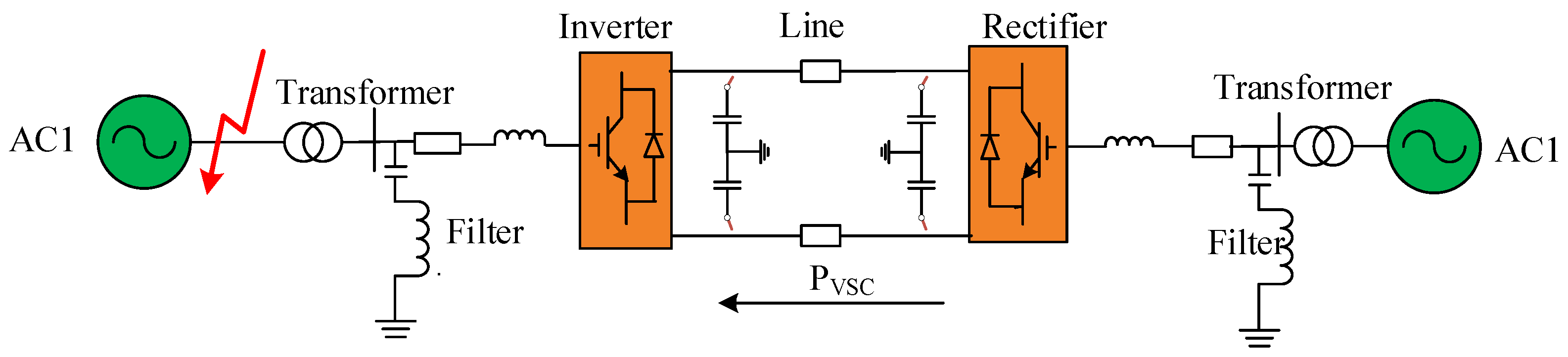
3. The Fault Current Influence Mechanism of the VSC and the Control Strategy
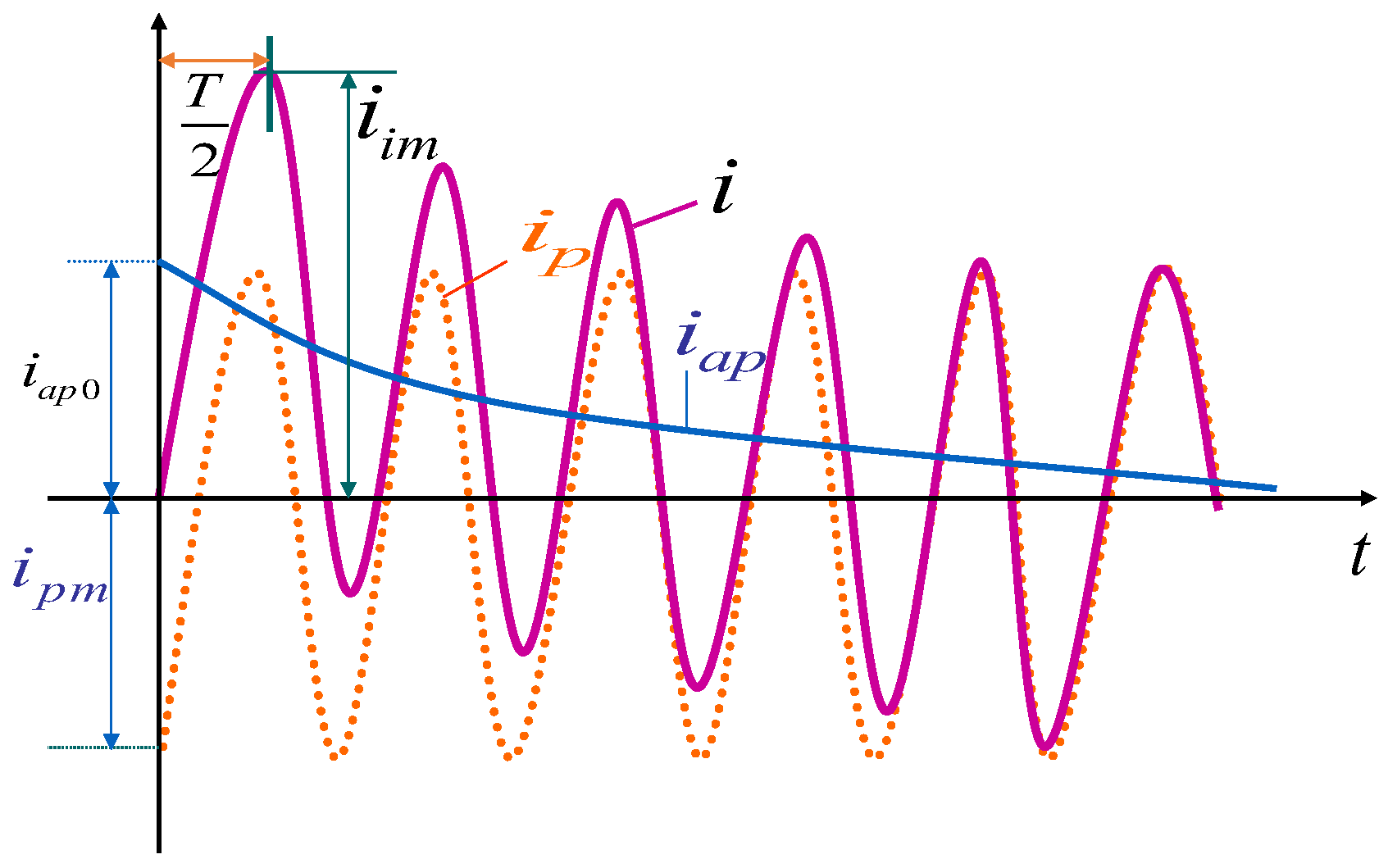
3.1. The Fault Current Influence Mechanism
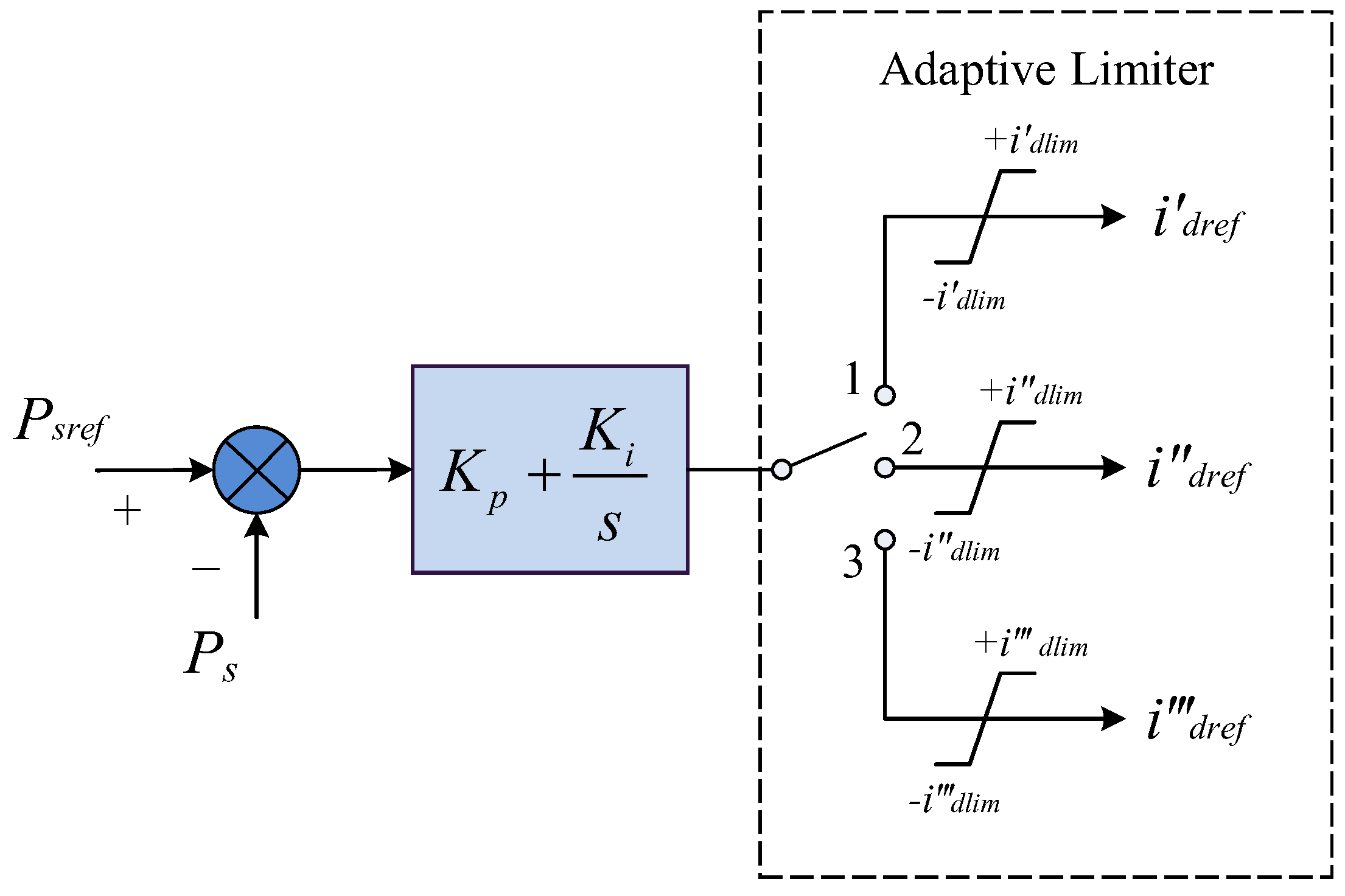
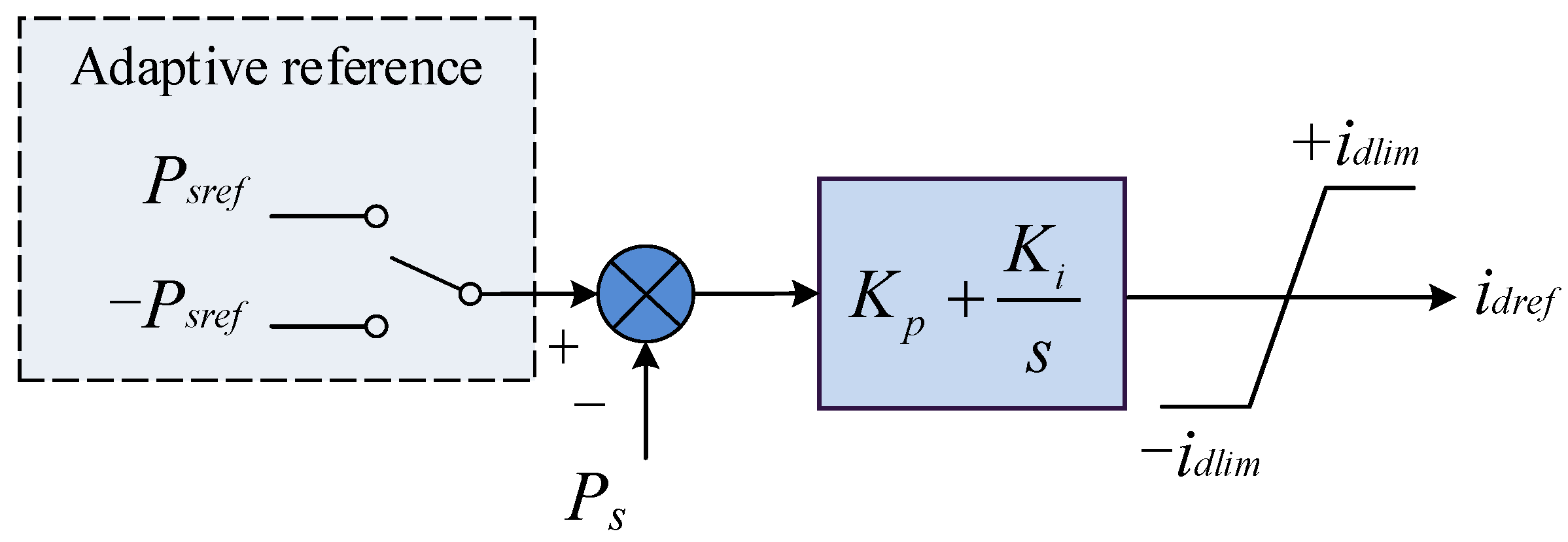
3.2. The Adapative Control Strategy
3.3. The Adapative Capacitor Strategy
4. Simulation Verifications
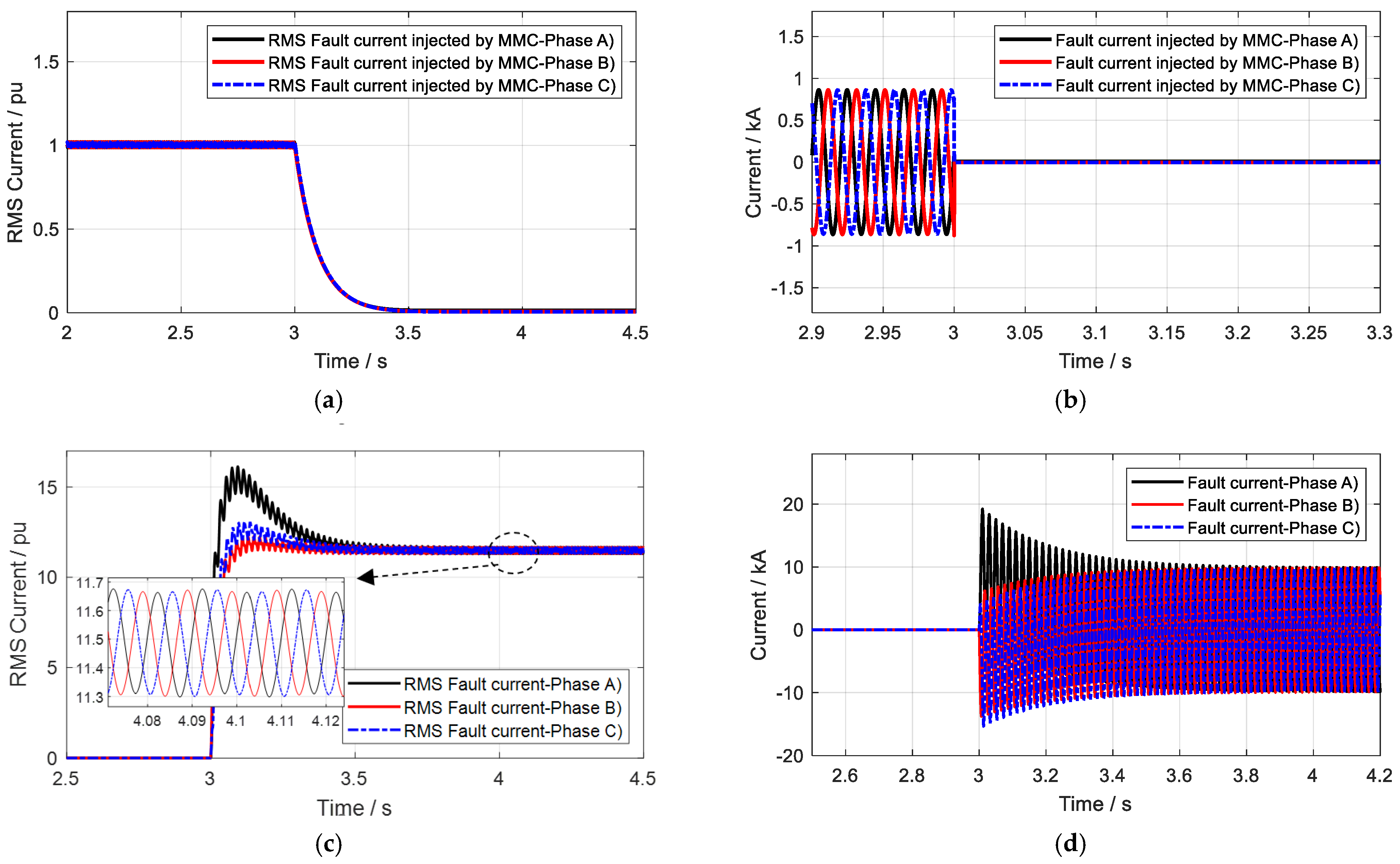
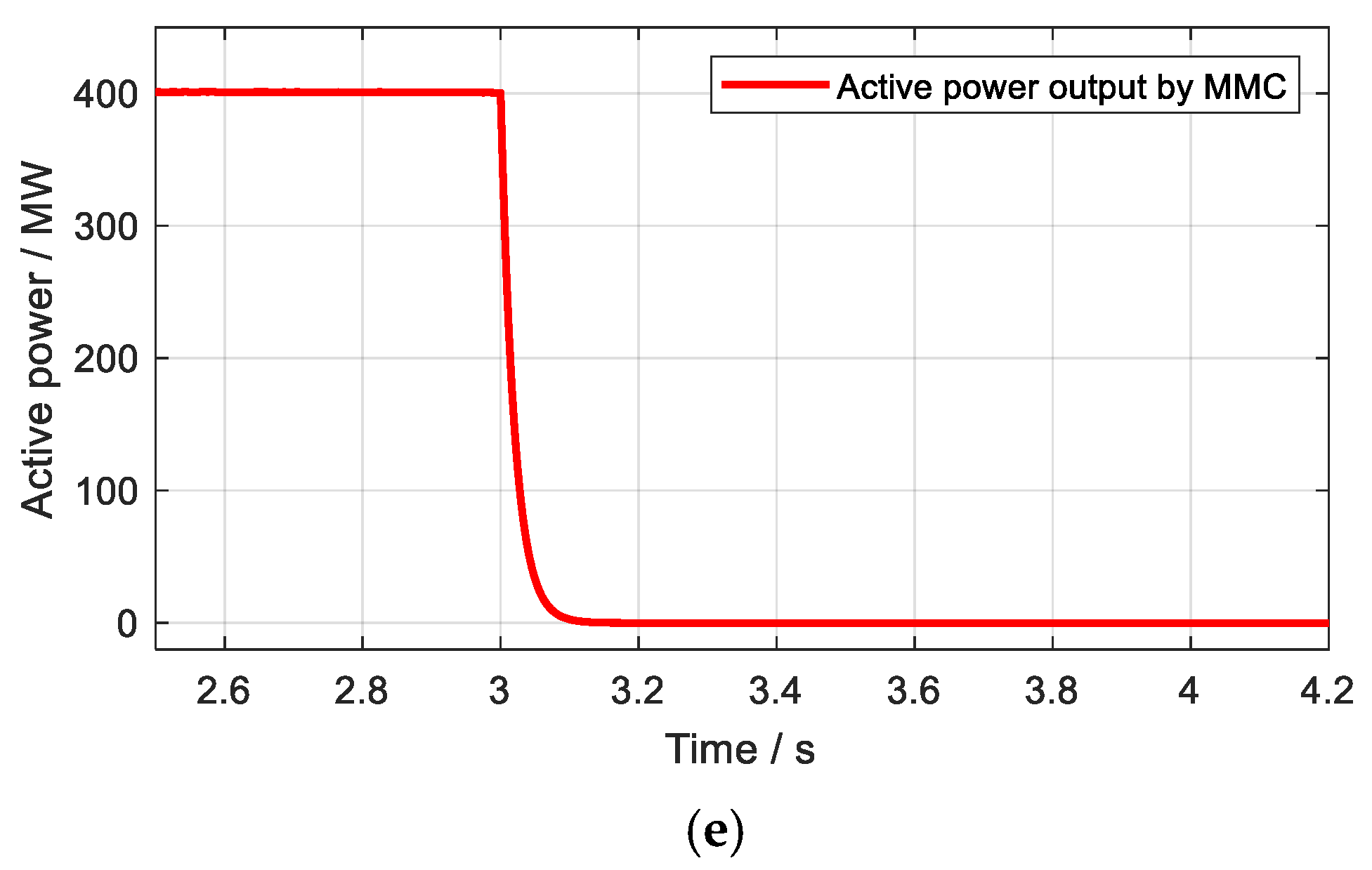
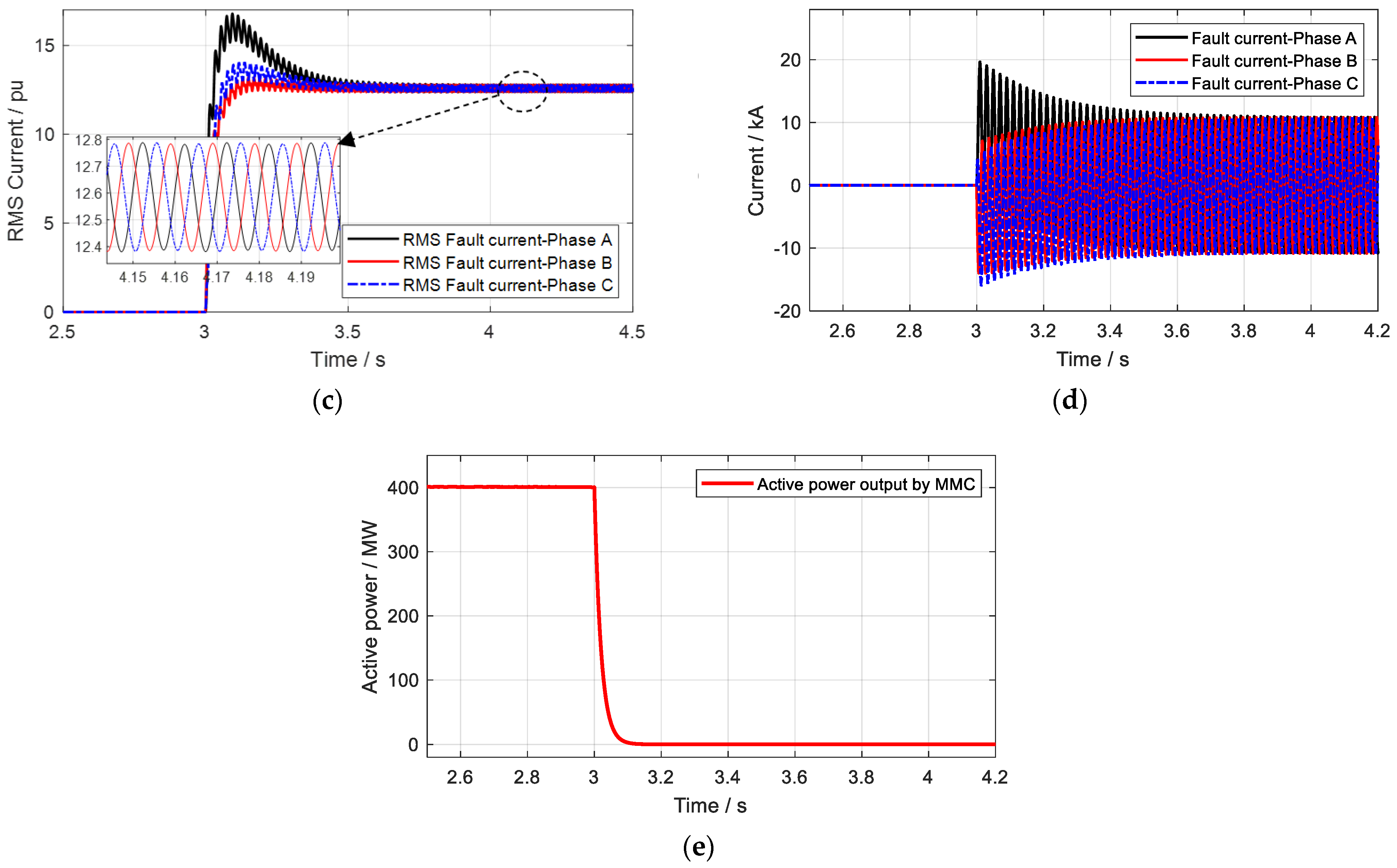
4.1. Case 1 Study: An MMC without Adaptive Control
4.2. Case 2 Study: MMC with a Positive Adaptive Reference Control
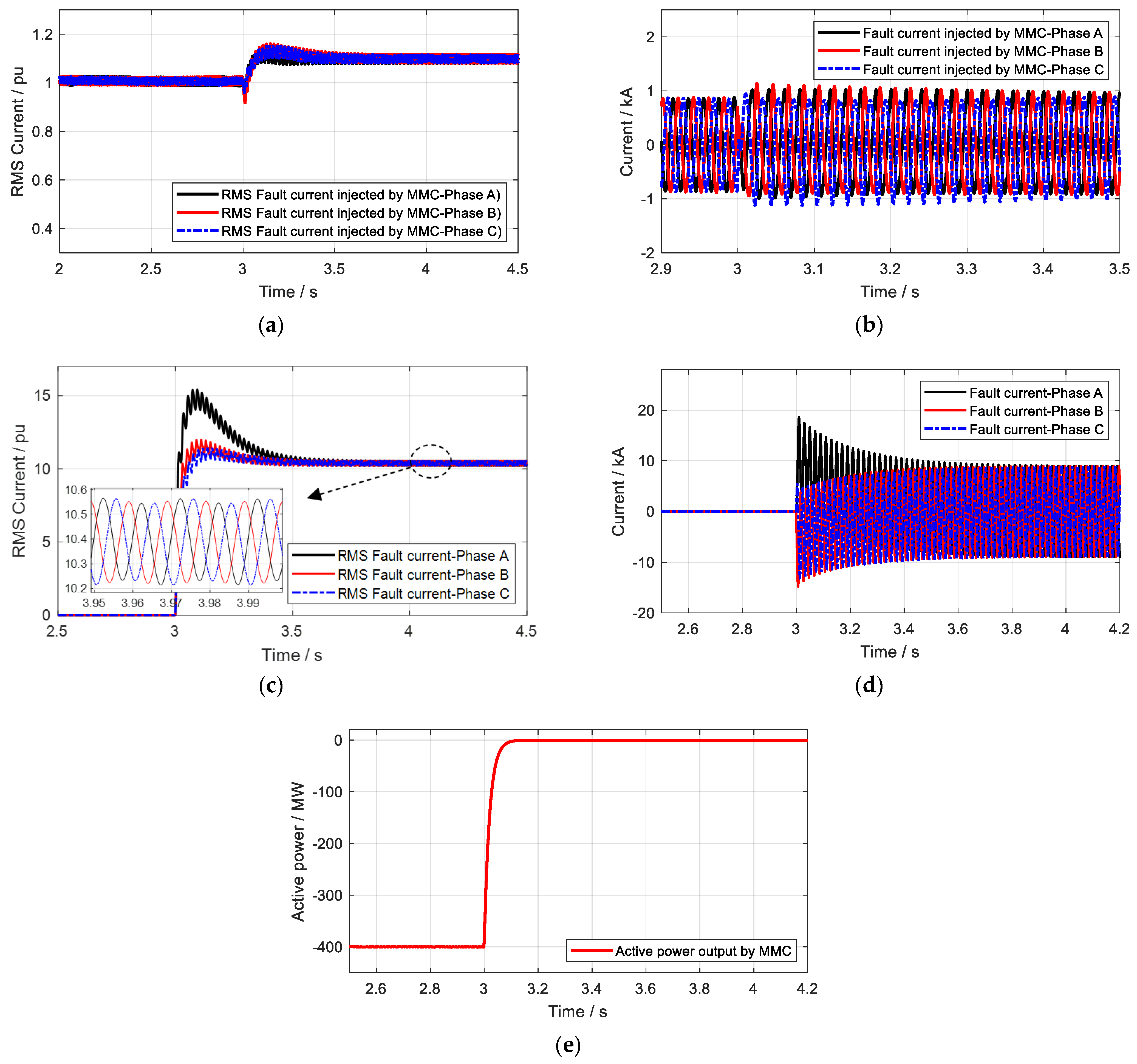
4.3. Case 3 Study: The MMC with a Negative Adaptive Reference Control
4.4. Case 4 Study: The MMC with an Adaptive Limiter Control
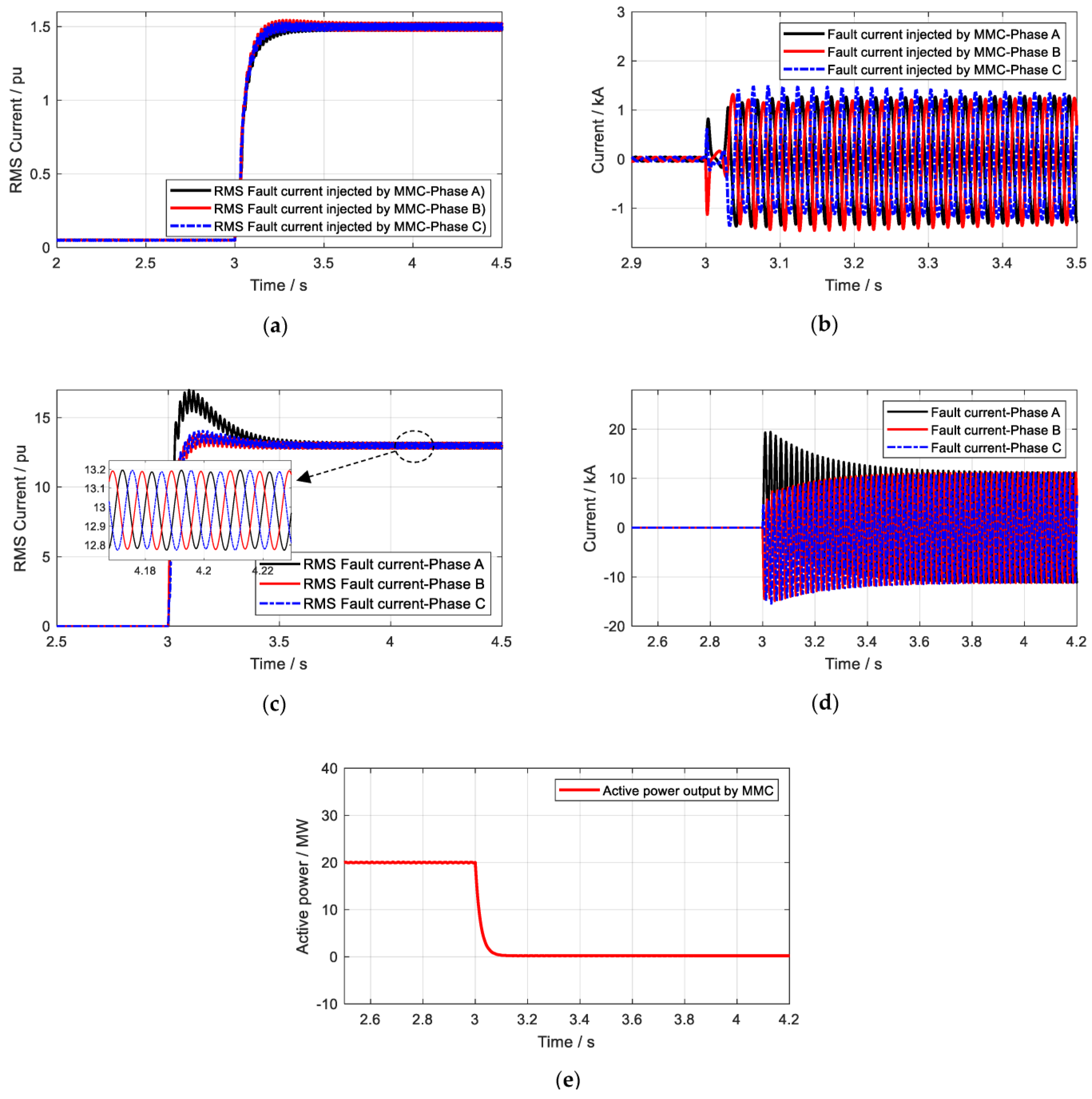
4.5. Case 5 Study: The MMC with an Adaptive Capacitor
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMC | Modular multilevel converter |
| AC | Alternate current |
| HVDC | High-voltage direct current |
| DFIG | Doubly fed induction generator |
| FACTS | Flexible AC transmission systems |
| LCC | Line-commutated converter |
| UPFC | Unified power flow controller |
| PCC | Point of common coupling |
| SM | Submodules |
| RMS | Root mean square |
References
- Jiang, Q.; Zeng, X.; Li, B.; Wang, S.; Liu, T.; Chen, Z.; Wang, T.; Zhang, M. Time-Sharing Frequency Coordinated Control Strategy for PMSG-Based Wind Turbine. IEEE J. Emerg. Sel. Top. Circuits Syst. 2022, 12, 268–278. [Google Scholar] [CrossRef]
- Li, B.; Chen, S.; Liu, T. Theoretical analysis on the VSC instability caused by PLL in weak system. IET Renew. Power Gener. 2020, 14, 1782–1788. [Google Scholar] [CrossRef]
- Ding, Z.; Yuan, K.; Qi, J.; Wang, Y.; Hu, J.; Zhang, K. Robust and Cost-Efficient Coordinated Primary Frequency Control of Wind Power and Demand Response Based on Their Complementary Regulation Characteristics. IEEE Trans. Smart Grid 2022, 13, 4436–4448. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X.; Cui, M.; Zhang, K.; Zhao, J.; Li, F. Stability assessment of secondary frequency control system with dynamic false data injection attacks. IEEE Trans. Ind. Inf. 2022, 18, 3224–3234. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, J.; Zuo, Z.; Han, Q.; Zhang, W. Periodic zero-dynamics attacks for discrete-time second-order multi-agent systems. Int. J. Robust Nonlinear Control 2022, 32, 5619. [Google Scholar] [CrossRef]
- Li, B.; Chen, S.; Liu, T. Improved practical method for Low-inertia VSC-HVDC stability analysis in weak system. IET Gener. Transm. Distrib. 2020, 14, 5072–5079. [Google Scholar] [CrossRef]
- Zhang, B.; Li, G.; Wang, J.; Hao, Z.; Liu, Z.; Bo, Z. Affecting factors of grid-connected wind power on fault current and impact on protection relay. Electr. Power Autom. Equip. 2012, 32, 1–8. [Google Scholar]
- Samaan, N.; Zavadil, R.; Smith, J.C.; Conto, J. Modeling of wind power plants short circuit analysis in the transmission network. In Proceedings of the IEEE PES 2008 Transmission and Distribution Conference and Exposition, Chicago, IL, USA, 21–24 April 2008; pp. 1–7. [Google Scholar]
- Zhao, C.; Qi, L.; Chen, N.; Cui, X.; Ma, J. Research on Producing Mechanism of Healthy Pole Bus Overvoltage for Monopolar Grounding Fault in ±500kV Zhangbei Flexible DC Power Grid. Power Syst. Technol. 2019, 43, 530–536. [Google Scholar]
- Zhou, N.; Zhang, Z.; Liang, T.; Ying, W.; Bo, Y. Short-circuit Current Calculation Method for Near-end Bus of Unified Power Flow Controller. Autom. Electr. Power Syst. 2020, 44, 95–102. [Google Scholar]
- Kong, X.; Yuan, Y.; Huang, H.; Zhu, W.; Li, P.; Wang, Y. Fault Current Transient Features and Its Related Impact Factors of PV Generator. Power Syst. Technol. 2015, 39, 2444–2449. [Google Scholar]
- Tao, Y.; Li, B.; Dragičević, T.; Liu, T.; Blaabjerg, F. HVDC grid fault current limiting method through topology optimization based on genetic algorithm. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 7045–7055. [Google Scholar] [CrossRef]
- Tao, Y.; Li, B.; Liu, T. Pole-to-ground fault current estimation in symmetrical monopole high-voltage direct current grid considering modular multilevel converter control. Electron. Lett. 2020, 56, 392–395. [Google Scholar] [CrossRef]
- Jiang, Q.; Li, B.; Liu, T.; Wang, P. Fault current limiting method based on virtual impedance for hybrid high-voltage direct current with cascaded MMC inverters. Electron. Lett. 2021, 57, 229–231. [Google Scholar] [CrossRef]
- Wang, T.; Wan, L.; Zhang, Y.; Bu, G. Study of the short circuit current contributed by a DC system with a three-phase fault on the AC side of an inverter. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar] [CrossRef]
- Sadeghi, A.; Seyyedbarzegar, S.; Yazdani-Asrami, M. Investigation on the Electrothermal Performance of a High-Temperature Superconducting Cable in an Offshore Wind Farm Integrated Power System: Fault and Islanding Conditions. IEEE Trans. Appl. Supercond. 2022, 32, 5401011. [Google Scholar] [CrossRef]
- Amini, M.; Aliabad, A.D.; Amiri, E. Design and Analysis of Fault Current Limiter Based on Air Core Variable Series Reactor. IEEE Access 2021, 9, 166129–166136. [Google Scholar] [CrossRef]
- Lee, J.I.; Dao, V.Q.; Dinh, M.C.; Lee, S.J.; Kim, C.S.; Park, M. Combined Operation Analysis of a Saturated Iron-Core Superconducting Fault Current Limiter and Circuit Breaker for an HVDC System Protection. Energies 2021, 14, 7993. [Google Scholar] [CrossRef]





| Control Strategy | Inverter | Rectifier |
|---|---|---|
| Active power control mode | Constant active power control | Constant DC voltage control |
| Reactive power control mode | Constant reactive power control | Constant reactive power control |
| Name | Value | |
|---|---|---|
| AC system | Rated AC voltage/kV | 380 |
| MMC Converter | Rated DC voltage/kV | 400 |
| HBSM number | 180 | |
| HBSM capacitance/mF | 15 | |
| Arm reactance/mH | 50 | |
| idlim of inverter/p.u. | 1.1 | |
| iqlim of inverter/p.u. | 0.4 | |
| idlim of rectifier/p.u. | 1.1 | |
| iqlim of rectifier/p.u. | 0.4 | |
| Line Parameter | Resistance/ohm/m | 0.1782 × 10−4 |
| Inductive reactance/ohm/m | 0.3139 × 10−3 | |
| Capacitive reactance/ohm*m | 273.5448 |
| Control Strategy | AC System Supplied Fault Current | MMC Supplied Fault Current | The Total Fault Current |
|---|---|---|---|
| MMC without adaptive control | 11.5 p.u. | 0 p.u. | 11.5 p.u. |
| MMC with positive adaptive reference control | 11.5 p.u. | 1.1 p.u. | 12.6 p.u. |
| MMC with negative adaptive reference control | 11.5 p.u. | −1.1 p.u. | 10.4 p.u. |
| MMC with adaptive limiter control | 11.5 p.u. | 1.5 p.u. | 13.0 p.u. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Chen, Z.; Zhang, Y.; Jiang, Q.; Li, B.; He, Y.; Li, Q. The Short-Circuit Fault Current Impact Mechanism and Adaptive Control Strategy of an MMC-HVDC. Processes 2023, 11, 837. https://doi.org/10.3390/pr11030837
Wang X, Chen Z, Zhang Y, Jiang Q, Li B, He Y, Li Q. The Short-Circuit Fault Current Impact Mechanism and Adaptive Control Strategy of an MMC-HVDC. Processes. 2023; 11(3):837. https://doi.org/10.3390/pr11030837
Chicago/Turabian StyleWang, Xi, Zhen Chen, Yinming Zhang, Qin Jiang, Baohong Li, Yao He, and Qiping Li. 2023. "The Short-Circuit Fault Current Impact Mechanism and Adaptive Control Strategy of an MMC-HVDC" Processes 11, no. 3: 837. https://doi.org/10.3390/pr11030837
APA StyleWang, X., Chen, Z., Zhang, Y., Jiang, Q., Li, B., He, Y., & Li, Q. (2023). The Short-Circuit Fault Current Impact Mechanism and Adaptive Control Strategy of an MMC-HVDC. Processes, 11(3), 837. https://doi.org/10.3390/pr11030837











