An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling
Abstract
:1. Introduction
2. Statistical Properties
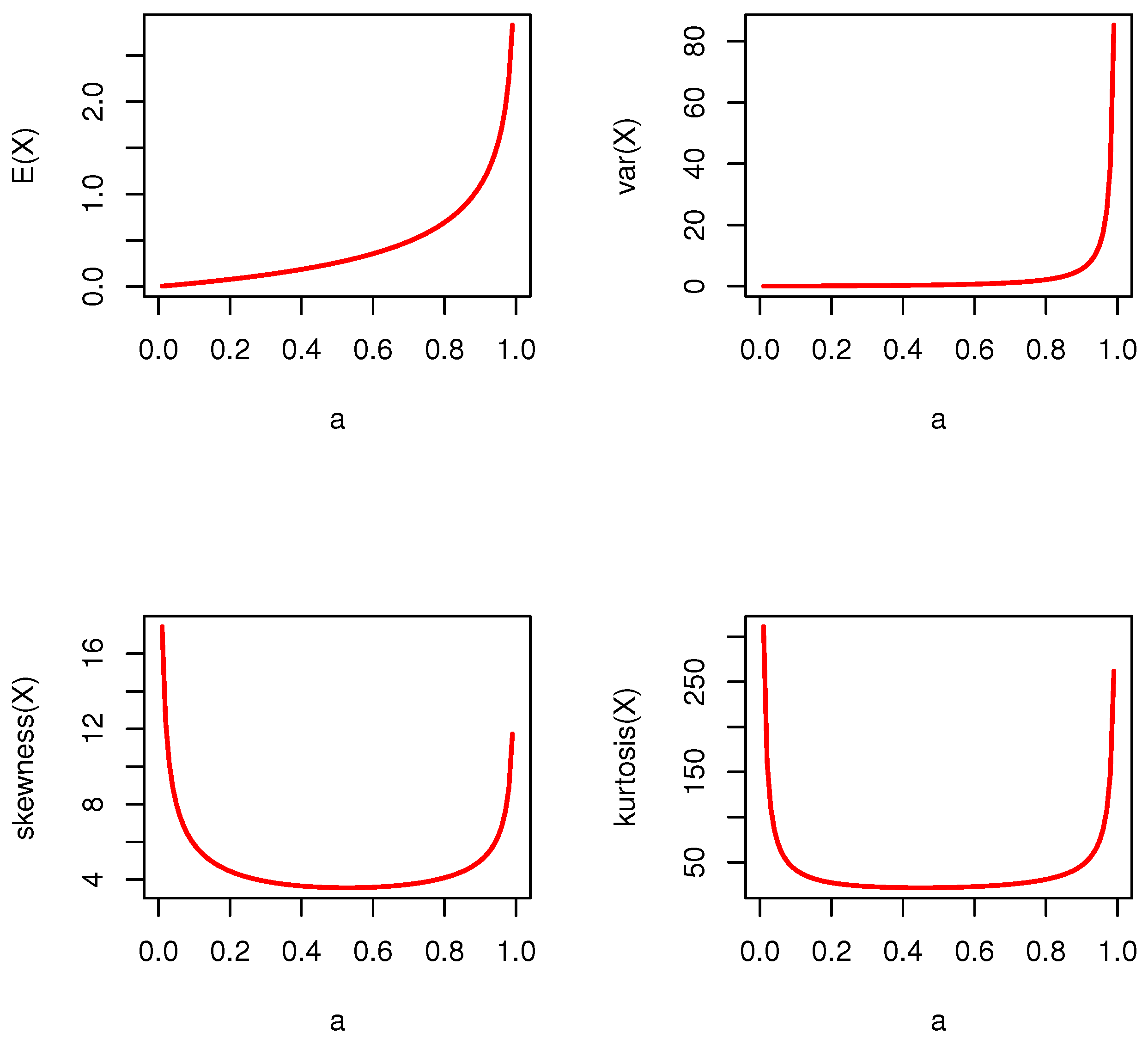
2.1. Moments and Auxiliary Statistical Measures
2.2. Conditional Expectation
2.3. Order Statistic (OrSc)
2.4. Lorenz Curve
3. Estimation Methods: Unbiased and Consistent Estimators
3.1. Maximal Likelihood Estimation
3.2. Moment Estimation
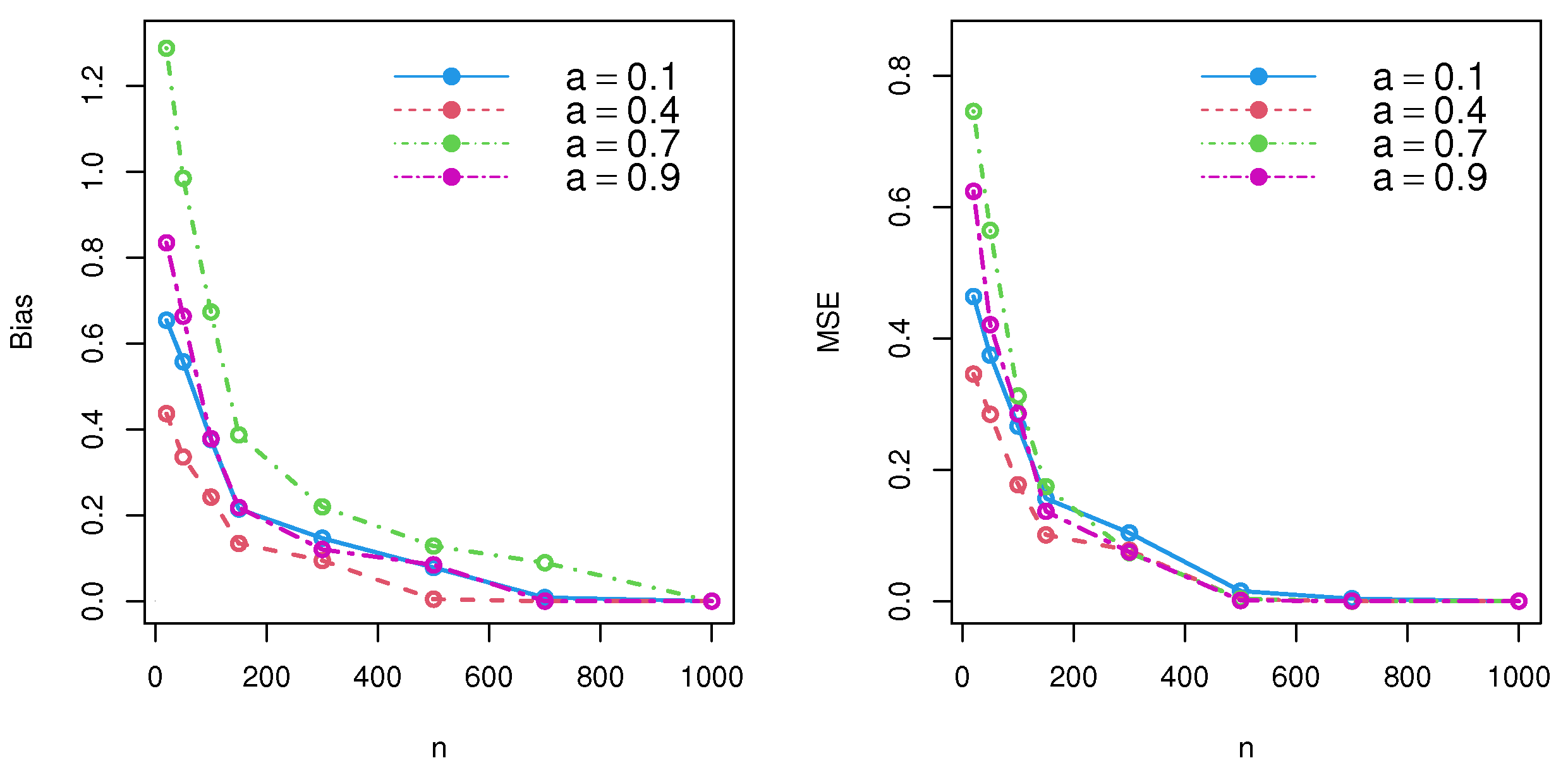
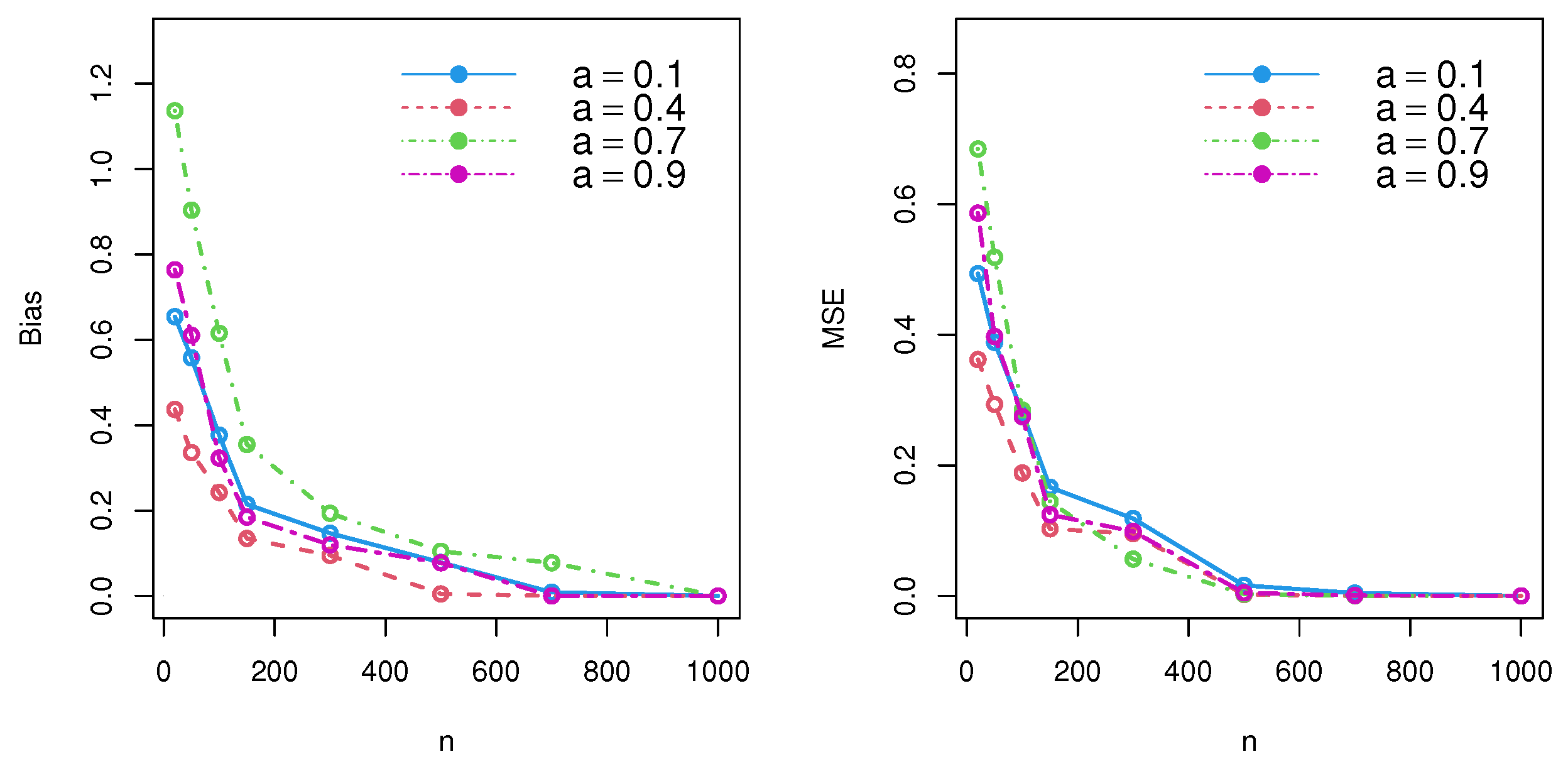
4. Estimator Performance: Simulation Results
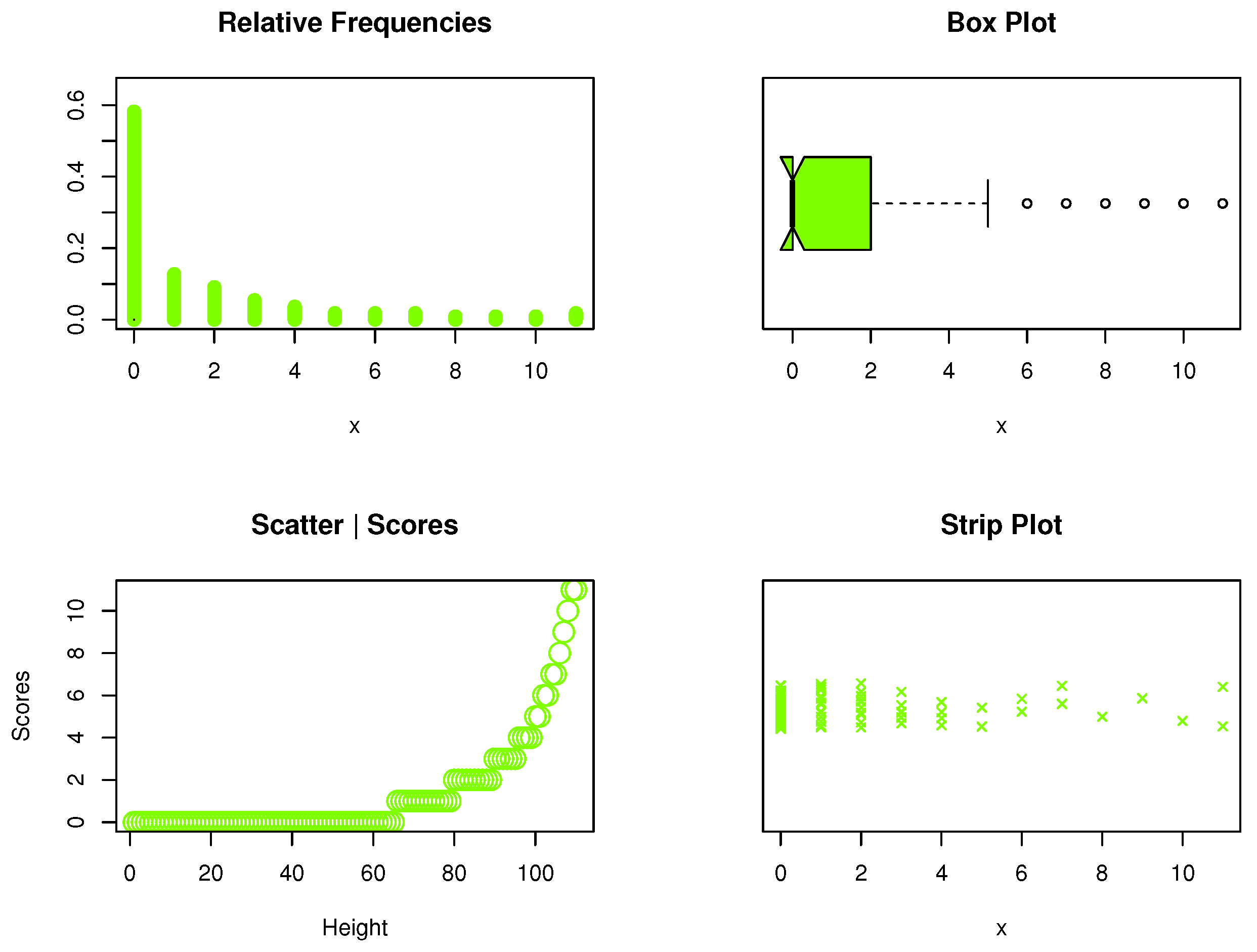
5. Data Analysis: Kidney Dysmorphogenetics
6. Results and Future Work
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yari, G.; Tondpour, Z. Some new discretization methods with application in reliability. Appl. Appl. Math. Int. J. (AAM) 2018, 13, 6. [Google Scholar]
- Roy, D. Discrete Rayleigh distribution. IEEE Trans. Reliab. 2004, 53, 255–260. [Google Scholar] [CrossRef]
- Krishna, H.; Pundir, P.S. Discrete Burr and discrete Pareto distributions. Stat. Methodol. 2009, 6, 177–188. [Google Scholar] [CrossRef]
- Gomez-Déniz, E. Another generalization of the geometric distribution. Test 2010, 19, 399–415. [Google Scholar] [CrossRef]
- Jazi, M.A.; Lai, C.D.; Alamatsaz, M.H. A discrete inverse Weibull distribution and estimation of its parameters. Stat. Methodol. 2010, 7, 121–132. [Google Scholar] [CrossRef]
- Al-Huniti, A.A.; AL-Dayian, G.R. Discrete Burr type III distribution. Am. J. Math. Stat. 2012, 2, 145–152. [Google Scholar] [CrossRef]
- Nekoukhou, V.; Alamatsaz, M.H.; Bidram, H. Discrete generalized exponential distribution of a second type. Statistics 2013, 47, 876–887. [Google Scholar] [CrossRef]
- Hussain, T.; Ahmad, M. Discrete inverse Rayleigh distribution. Pak. J. Stat. 2014, 30. [Google Scholar]
- Hussain, T.; Aslam, M.; Ahmad, M. A two parameter discrete Lindley distribution. Rev. Colomb. Estad. 2016, 39, 45–61. [Google Scholar] [CrossRef]
- Abebe, B.; Shanker, R.A. Discrete Lindley distribution with applications in biological sciences. Biom. Biostat. Int. J. 2018, 7, 48–52. [Google Scholar] [CrossRef]
- Al-Babtain, A.A.; Ahmed, A.H.N.; Afify, A.Z. A new discrete analog of the continuous Lindley distribution, with reliability applications. Entropy 2020, 22, 603. [Google Scholar] [CrossRef]
- Eliwa, M.S.; Altun, E.; El-Dawoody, M.; El-Morshedy, M. A new three-parameter discrete distribution with associated INAR (1) process and applications. IEEE Access 2020, 8, 91150–91162. [Google Scholar] [CrossRef]
- Almazah, M.M.A.; Erbayram, T.; Akdoğan, Y.; Al Sobhi, M.M.; Afify, A.Z. A new extended geometric distribution: Properties, regression model, and actuarial applications. Mathematics 2021, 9, 1336. [Google Scholar] [CrossRef]
- Poisson, S.D. Mémoire sur l’équilibre et le mouvement des corps élastiques. Mém. Acad. R. Sci. Inst. Fr. 1829, 8, 357–570. [Google Scholar]
- Del Castillo, J.; Pérez-Casany, M. Weighted Poisson distributions for overdispersion and underdispersion situations. Ann. Inst. Stat. Math. 1998, 50, 567–585. [Google Scholar] [CrossRef]
- Fisher, R.A. The effect of methods of ascertainment upon the estimation of frequencies. Ann. Eugen. 1934, 6, 13–25. [Google Scholar] [CrossRef]
- Dietz, E.; Bhning, D. On estimation of the Poisson parameter in zero-modified Poisson models. Comput. Stat. Data Anal. 2000, 34, 441–459. [Google Scholar] [CrossRef]
- Kokonendji, C.C.; Mizere, D.; Balakrishnan, N. Connections of the Poisson weight function to overdispersion and underdispersion. J. Stat. Plan. Inference 2008, 138, 1287–1296. [Google Scholar] [CrossRef]
- El-Morshedy, M.; Eliwa, M.S.; Altun, E. Discrete Burr-Hatke distribution with properties, estimation methods and regression model. IEEE Access 2020, 8, 74359–74370. [Google Scholar] [CrossRef]
- Wolfram Research. HurwitzLerchPhi Function. J. Appl. Stat. 2008, 32, 1461–1478. [Google Scholar]
- Altun, E.; El-Morshedy, M.; Eliwa, M.S. A study on discrete Bilal distribution with properties and applications on integervalued autoregressive process. Revstat-Stat. J. 2022, 20, 501–528. [Google Scholar]
- Poisson, S.D. Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilitiés; Bachelier: Paris, France, 1837; Volume 1, p. 1837. [Google Scholar]
- Eliwa, M.S.; El-Morshedy, M. A one-parameter discrete distribution for over-dispersed data: Statistical and reliability properties with applications. J. Appl. Stat. 2022, 49, 2467–2487. [Google Scholar] [CrossRef] [PubMed]
- Para, B.A.; Jan, T.R. Discrete version of log-logistic distribution and its applications in genetics. Int. J. Mod. Math. Sci. 2016, 14, 407–422. [Google Scholar]
- Para, B.A.; Jan, T.R. On discrete three parameter Burr type XII and discrete Lomax distributions and their applications to model count data from medical science. Biom. Biostat. J. 2016, 4, 1–15. [Google Scholar]
- Shanker, R.; Mishra, A. A two-parameter Poisson-Lindley distribution. Int. J. Stat. Syst. 2014, 9, 79–85. [Google Scholar]
- Almazah, M.M.A.; Alnssyan, B.; Ahmed, A.H.N.; Afify, A.Z. Reliability properties of the NDL family of discrete distributions with its inference. Mathematics 2021, 9, 1139. [Google Scholar] [CrossRef]
- Eldeeb, A.S.; Ahsan-Ul-Haq, M.; Babar, A. A discrete analog of inverted Topp-Leone distribution: Properties, estimation and applications. Int. J. Anal. Appl. 2021, 19, 695–708. [Google Scholar]
- El-Morshedy, M.; Altun, E.; Eliwa, M.S. A new statistical approach to model the counts of novel coronavirus cases. Math. Sci. 2022, 16, 37–50. [Google Scholar] [CrossRef]
- Chan, S.K.; Riley, P.R.; Price, K.L.; McElduff, F.; Winyard, P.J.; Welham, S.J.; Long, D.A. Corticosteroid-induced kidney dysmorphogenesis is associated with deregulated expression of known cystogenic molecules, as well as Indian hedgehog. Am. J.-Physiol.-Ren. Physiol. 2010, 298, F346–F356. [Google Scholar] [CrossRef] [PubMed] [Green Version]

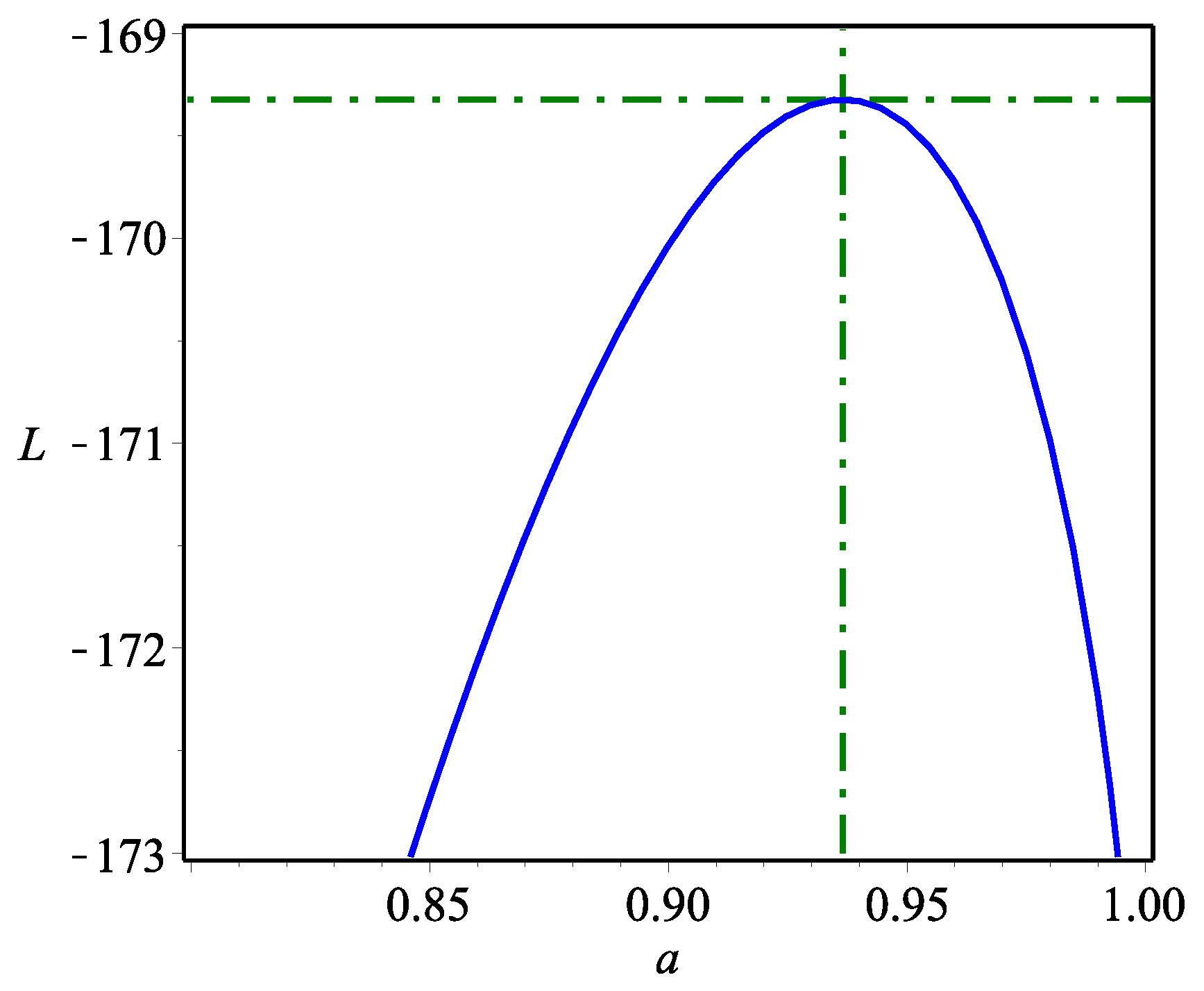
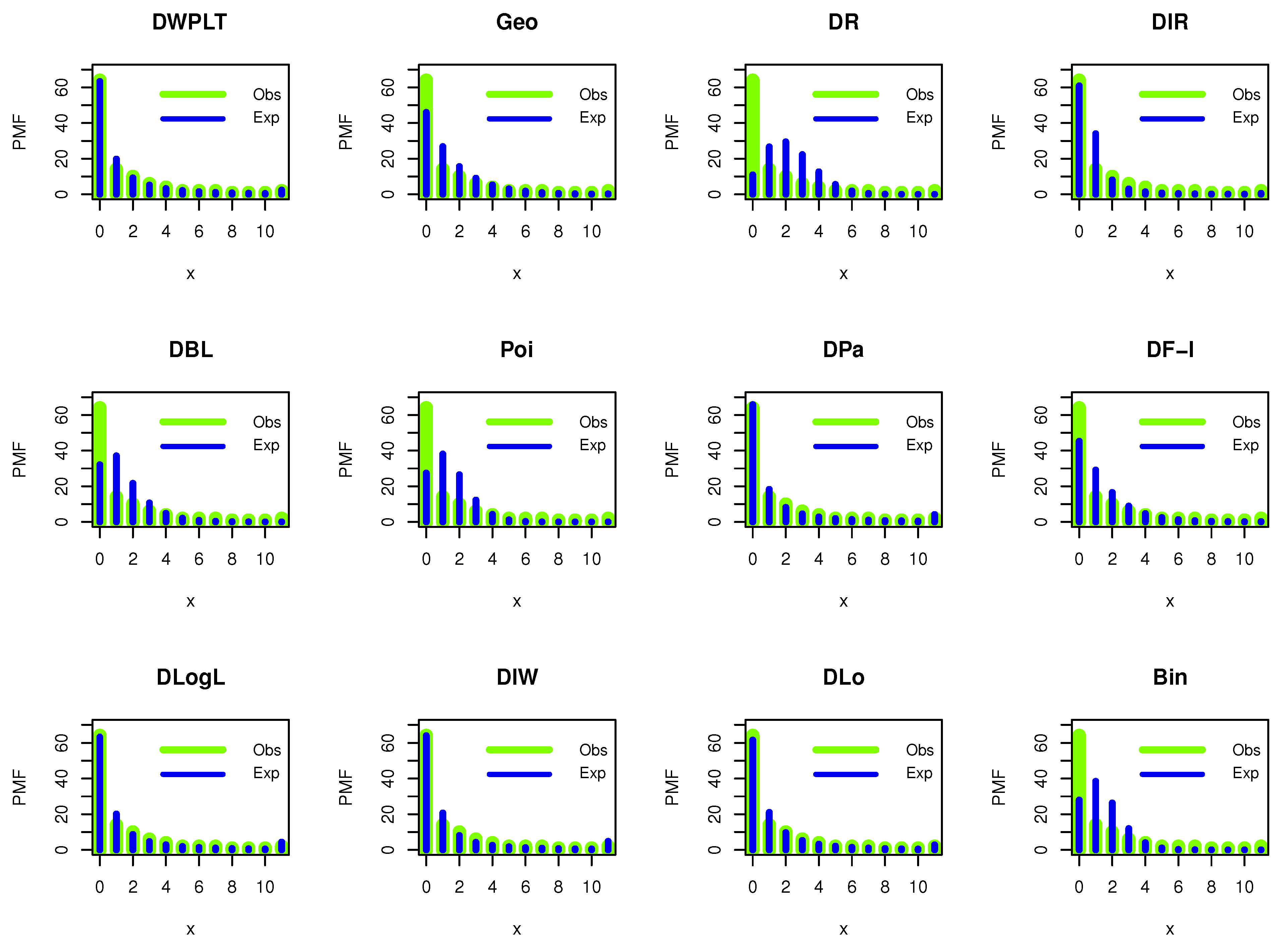

| Scheme I () | Scheme II () | |||
| n | Bias | MSE | Bias | MSE |
| 20 | ||||
| 50 | ||||
| 100 | ||||
| 150 | ||||
| 300 | ||||
| 500 | ||||
| 700 | ||||
| 1000 | ||||
| scheme III () | scheme IV () | |||
| Bias | MSE | Bias | MSE | |
| 20 | ||||
| 50 | ||||
| 100 | ||||
| 150 | ||||
| 300 | ||||
| 500 | ||||
| 700 | ||||
| 1000 | ||||
| Scheme I () | Scheme II () | |||
| n | Bias | MSE | Bias | MSE |
| 20 | ||||
| 50 | ||||
| 100 | ||||
| 150 | ||||
| 300 | ||||
| 500 | ||||
| 700 | ||||
| 1000 | ||||
| scheme III () | scheme IV () | |||
| Bias | MSE | Bias | MSE | |
| 20 | ||||
| 50 | ||||
| 100 | ||||
| 150 | ||||
| 300 | ||||
| 500 | ||||
| 700 | ||||
| 1000 | ||||
| Observed | Expected Frequencies | |||||||
|---|---|---|---|---|---|---|---|---|
| X | Frequencies | DWPLT | Geo | DR | DIR | DBL | Poi | DPa |
| 0 | 65 | |||||||
| 1 | 14 | |||||||
| 2 | 10 | |||||||
| 3 | 6 | |||||||
| 4 | 4 | |||||||
| 5 | 2 | |||||||
| 6 | 2 | |||||||
| 7 | 2 | |||||||
| 8 | 1 | |||||||
| 9 | 1 | |||||||
| 10 | 1 | |||||||
| 11 | 2 | |||||||
| Total | 110 | 110 | 110 | 110 | 110 | 110 | 110 | 110 |
| a | ||||||||
| Ac | ||||||||
| Bc | ||||||||
| CAc | ||||||||
| Hc | ||||||||
| Chi | ||||||||
| Dm | 4 | 4 | 4 | 2 | 3 | 3 | 4 | |
| Pv | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |||
| Observed | Expected Frequencies | |||||||
|---|---|---|---|---|---|---|---|---|
| X | Frequencies | DWPLT | DF-I | DLogL | DIW | DLo | Bin | DB-II |
| 0 | 65 | |||||||
| 1 | 14 | |||||||
| 2 | 10 | |||||||
| 3 | 6 | |||||||
| 4 | 4 | |||||||
| 5 | 2 | |||||||
| 6 | 2 | |||||||
| 7 | 2 | |||||||
| 8 | 1 | |||||||
| 9 | 1 | |||||||
| 10 | 1 | |||||||
| 11 | 2 | |||||||
| Total | 110 | 110 | 110 | 110 | 110 | 110 | 110 | 110 |
| a | ||||||||
| X | Frequencies | DWPLT | DF-I | DLogL | DIW | DLo | Bin | DB-II |
| b | ||||||||
| Ac | ||||||||
| Bc | ||||||||
| CAc | ||||||||
| Hc | ||||||||
| Chi | ||||||||
| Dm | 4 | 4 | 3 | 3 | 3 | 2 | 2 | |
| Pv | <0.001 | <0.001 | ||||||
| Observed | Expected Frequencies | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| X | Frequencies | DWPLT | DL-I | DL-II | DL-III | NDL | PoiL | DITL | DGL |
| 0 | 65 | ||||||||
| 1 | 14 | ||||||||
| 2 | 10 | ||||||||
| 3 | 6 | ||||||||
| 4 | 4 | ||||||||
| 5 | 2 | ||||||||
| 6 | 2 | ||||||||
| 7 | 2 | ||||||||
| 8 | 1 | ||||||||
| 9 | 1 | ||||||||
| 10 | 1 | ||||||||
| 11 | 2 | ||||||||
| Total | 110 | 110 | 110 | 110 | 110 | 110 | 110 | 110 | 110 |
| a | |||||||||
| b | |||||||||
| c | |||||||||
| Ac | |||||||||
| Bc | |||||||||
| CAc | |||||||||
| Hc | |||||||||
| Chi | |||||||||
| Dm | 4 | 4 | 3 | 2 | 4 | 4 | 3 | 4 | |
| Pv | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
El-Dawoody, M.; Eliwa, M.S.; El-Morshedy, M. An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling. Processes 2023, 11, 1195. https://doi.org/10.3390/pr11041195
El-Dawoody M, Eliwa MS, El-Morshedy M. An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling. Processes. 2023; 11(4):1195. https://doi.org/10.3390/pr11041195
Chicago/Turabian StyleEl-Dawoody, Mohamed, Mohamed S. Eliwa, and Mahmoud El-Morshedy. 2023. "An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling" Processes 11, no. 4: 1195. https://doi.org/10.3390/pr11041195
APA StyleEl-Dawoody, M., Eliwa, M. S., & El-Morshedy, M. (2023). An Extension of the Poisson Distribution: Features and Application for Medical Data Modeling. Processes, 11(4), 1195. https://doi.org/10.3390/pr11041195








