Mechanical Behavior and Low-Cycle Fatigue Performance of a Carburized Steel for GTF Engines
Abstract
:1. Introduction
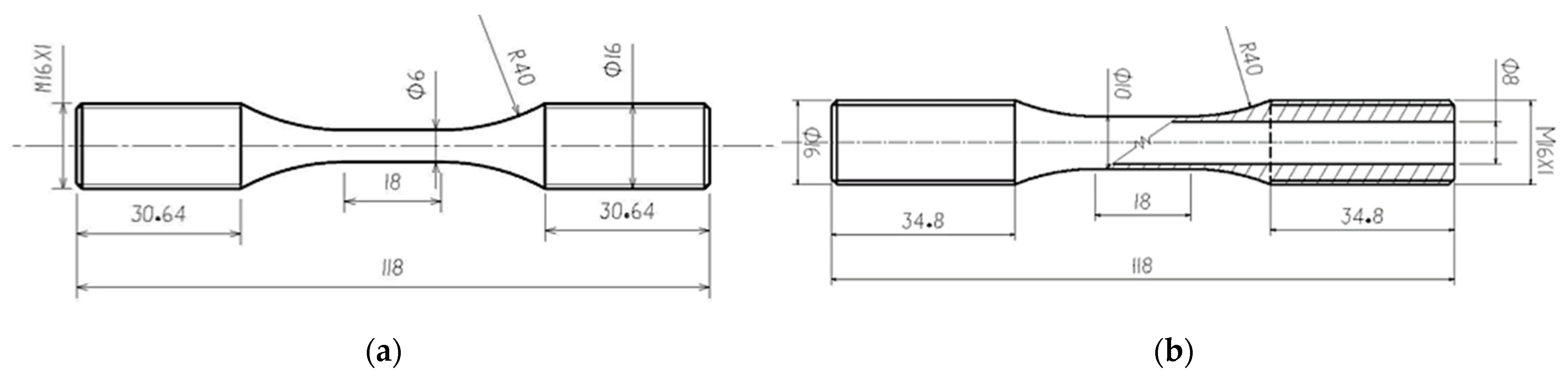
2. Materials and Methods
3. Results and Discussions
3.1. Static Mechanical Properties
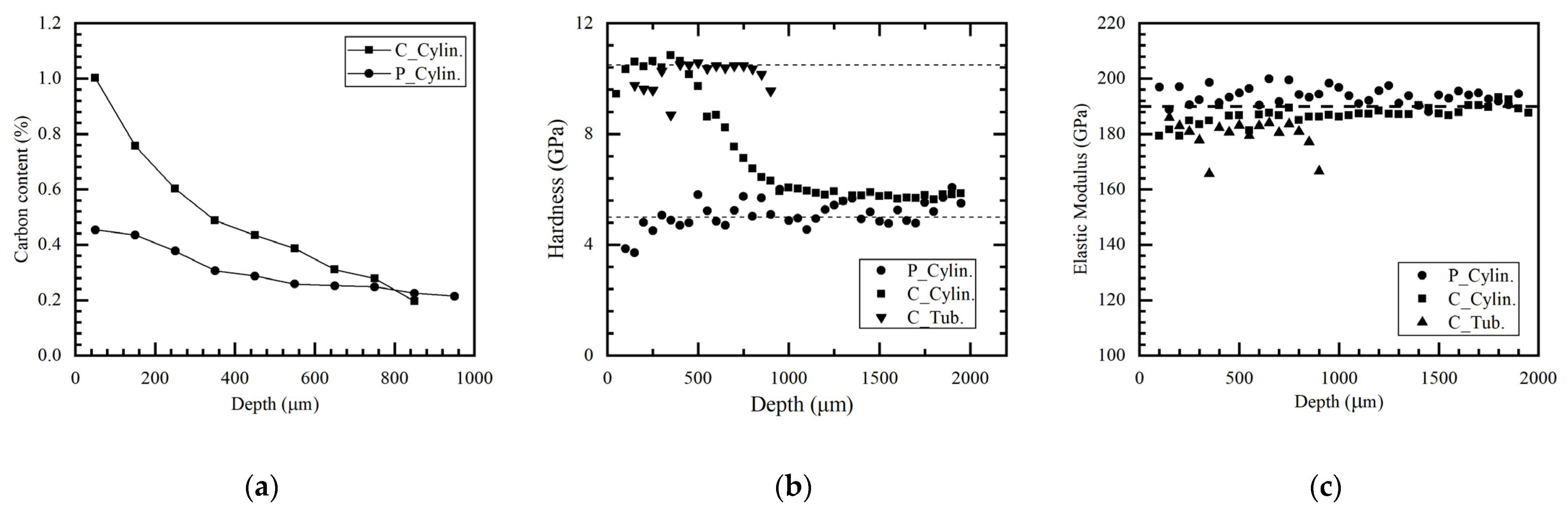
3.1.1. Distributions of Hardness and Elastic Modulus
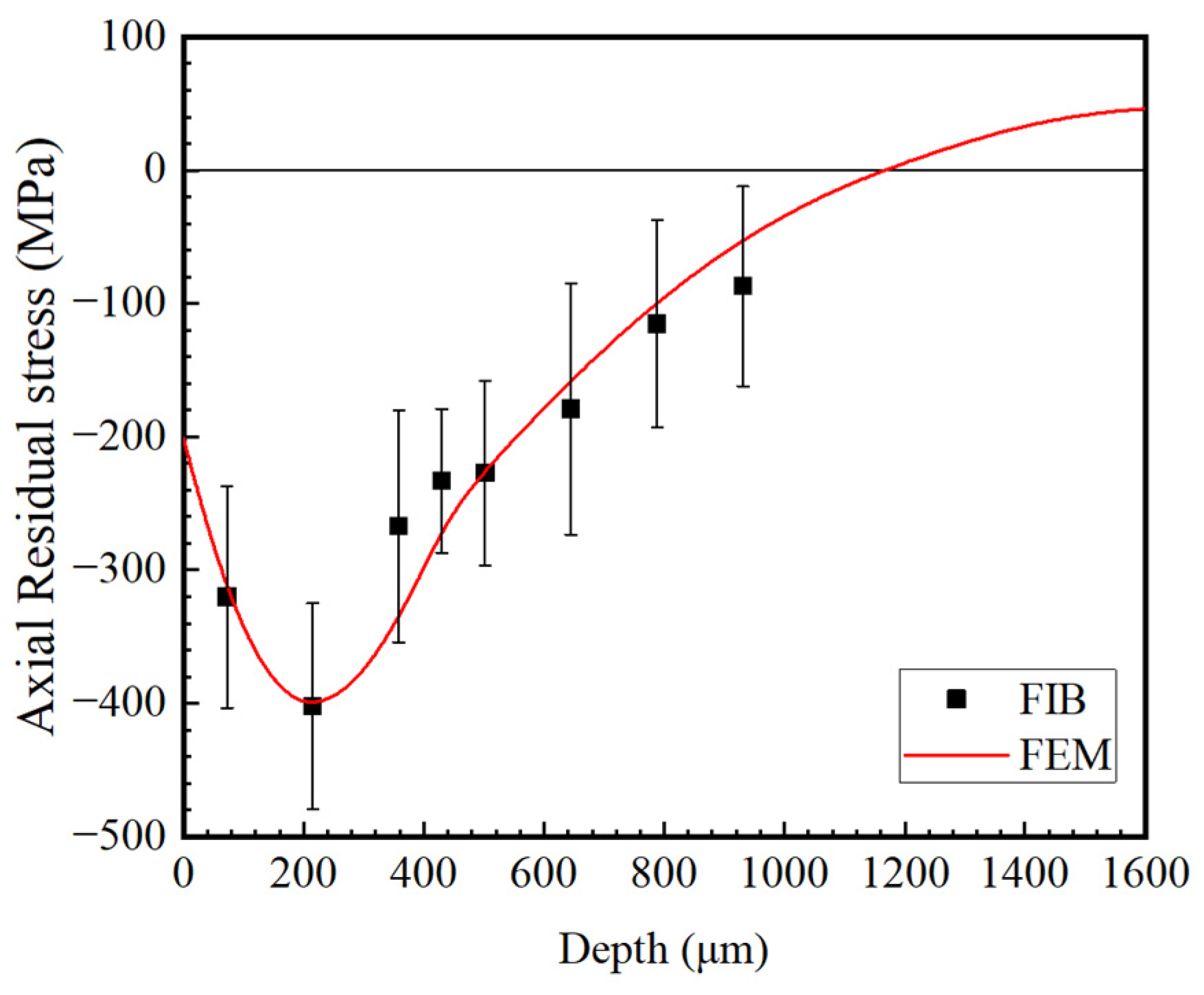
3.1.2. Distribution of Residual Stress
3.1.3. Stress–Strain Curves
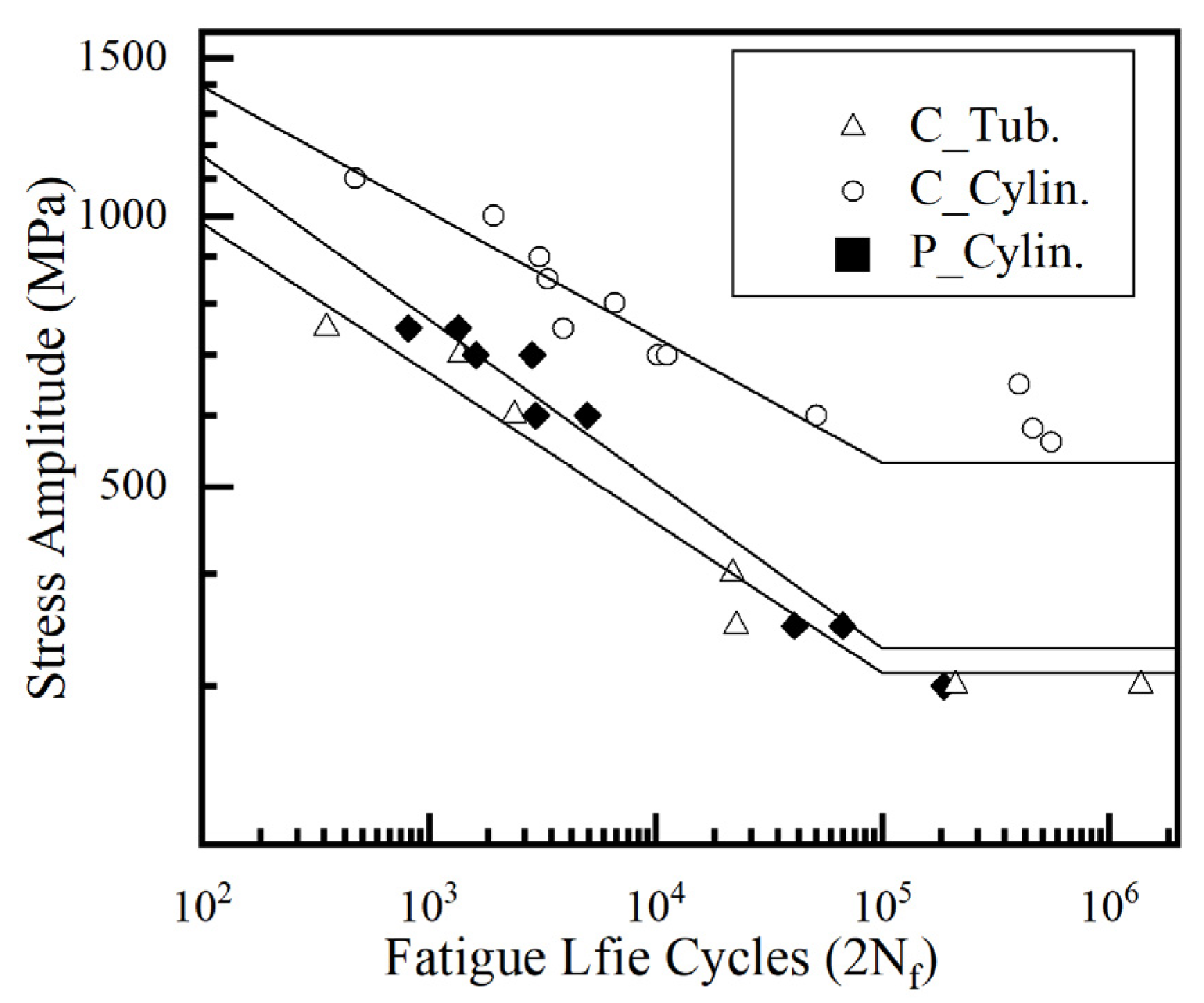
3.2. Fatigue Tests and Properties
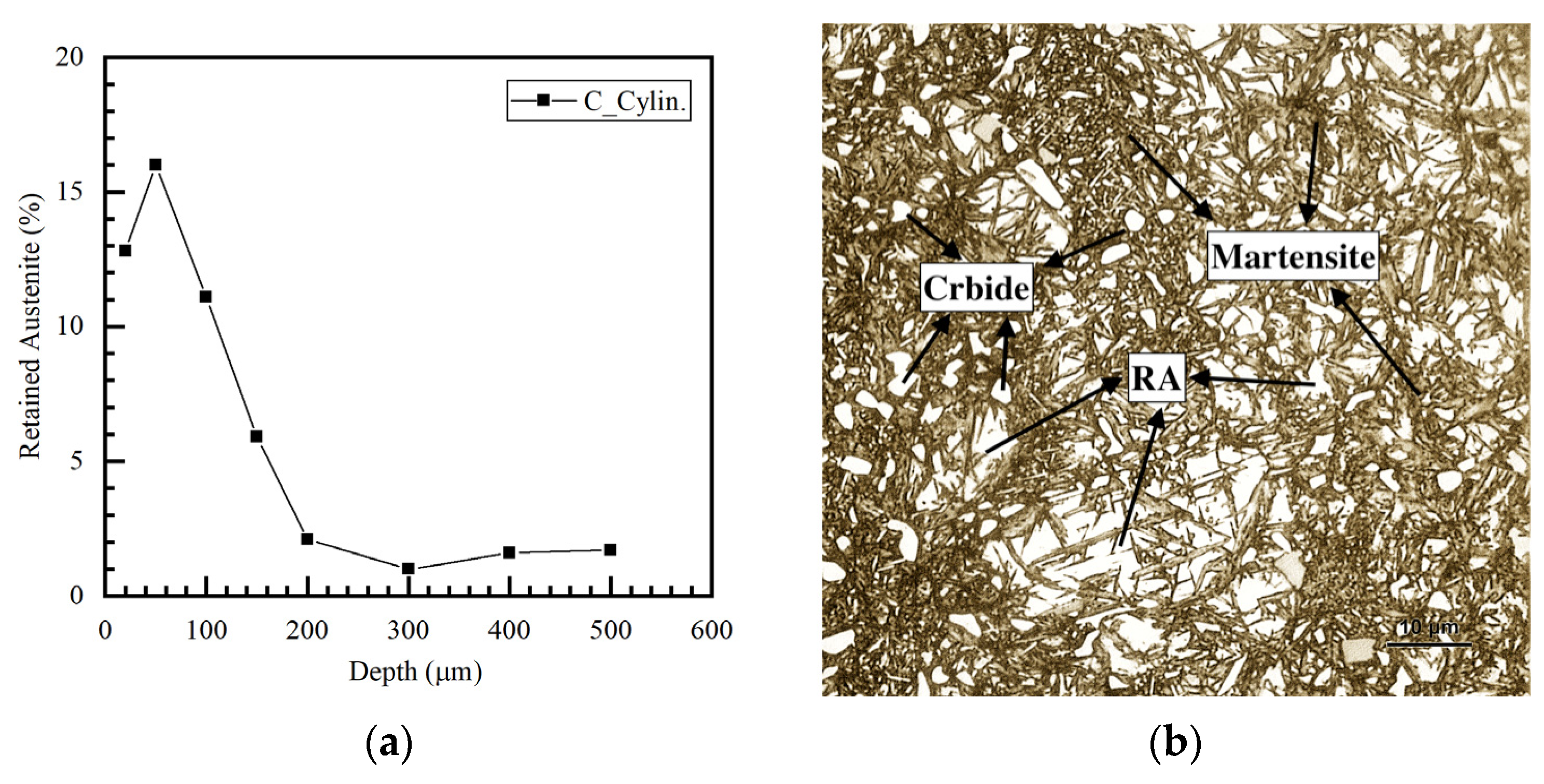
3.3. Damage Mechanism
4. Conclusions
- Although the case-carburized solid specimen can be considered a combination of the carburized case and the pseudo-carburized steel, the overall mechanical behavior of the case-carburized material is much closer to that of the completely carburized materials. This means that the mechanical behavior of the carburized case dominates that of the case-carburized parts. In the low-cycle fatigue (LCF) domain, however, the fatigue performance of the case-carburized material is significantly better than that of the two types of homogeneous materials. Furthermore, the fatigue performance of the completely carburized material is slightly worse than that of the pseudo-carburized material.
- SEM fractographs were obtained from the fracture surfaces of three types of specimens. Compared with the uniform material specimens, under the stress-controlled LCF test, the fatigue nucleation in the case-carburized specimen might not initiate from the surface of the specimen but in the transition zone, and the microcracks are always more prone to propagate to the softer core material.
- The carbon content in the 18Cr2Ni4WA low-carbon steel specimens does not improve their low-cycle fatigue properties. However, the graded performance and the compressive residual stress induced by the carburization process could be the primary factors in enhancing the fatigue life of case-carburized components. For ultra-high-power gear transmission systems in the GTF engine, the evaluation of low-cycle fatigue for gears should mainly consider the influences of the carburized case on the carburized gears.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Woods, J.L.; Daniewicz, S.R.; Nellums, R. Increasing the bending fatigue strength of carburized spur gear teeth by presetting. Int. J. Fatigue 1999, 21, 549–556. [Google Scholar] [CrossRef]
- Min, G.; Guoming, C. The Heat Treatment Technique in Gear Manufacturing of China. Heat Treat. Met. 2005, 30, 30–37. [Google Scholar]
- Stickels, C.A. Carburizing, Friction, Lubrication, and Wear Technology, ASM Handbook; ASM International: Metals Park, OH, USA, 1992; Volume 18, p. 1778. [Google Scholar]
- Bonglae, J.; Shahriar, S.; Yongbo, S.; Ali, F. Cyclic deformation and fatigue behavior of carburized automotive gear steel and predictions including multiaxial stress states. Int. J. Fatigue 2017, 100, 454–465. [Google Scholar]
- Kanchanomai, C.; Limtrakarn, W. Effect of Residual Stress on Fatigue Failure of Carburized Low- Carbon Steel. J. Mater. Eng. Perform. 2008, 17, 879–887. [Google Scholar] [CrossRef]
- Guoming, C. Review on Carburizing and Hardening Technology of Gears in China. Heat Treat Met. 2008, 33, 25–33. [Google Scholar]
- Tokaji, K.; Kohyama, K.; Akita, M. Fatigue behaviour and fracture mechanism of a 316 stainless steel hardened by carburizing. Int. J. Fatigue 2004, 26, 543–551. [Google Scholar] [CrossRef]
- Jeddi, D.; Lieurade, H.P. Effect of retained austenite on high cycle fatigue behavior of carburized 14NiCr11 steel. Procedia Eng. 2010, 2, 1927–1936. [Google Scholar] [CrossRef]
- Farfán, S.; Rubio-González, C.; Cervantes-Hernández, T.; Mesmacque, G. High cycle fatigue, low cycle fatigue and failure modes of a carburized steel. Int. J. Fatigue 2004, 26, 673–678. [Google Scholar] [CrossRef]
- Yongmin, Y.; Yazheng, L.; Leyu, Z.; Sheng, X.; Guochun, W. Carburizing law and microstructure of 23CrNi3Mo drill steel. Mater. Sci. Technol. 2013, 21, 102–108. [Google Scholar]
- Zhiyong, H.; Danièle, W.; Qingyuan, W.; Claude, B. Effect of carburizing treatment on the “fish eye” crack growth for a low alloyed chromium steel in very high cycle fatigue. Mater. Sci. Eng.-A 2013, 559, 790–797. [Google Scholar]
- Dengo, C.; Meneghetti, G.; Dabala, M. Experimental analysis of bending fatigue strength of plain and notched case-hardened gear steels. Int. J. Fatigue 2015, 80, 145–161. [Google Scholar] [CrossRef]
- Stickels, C.A. HeatTreating, ASM Handbook; ASM International: Metals Park, OH, USA, 1991; Volume 4, p. 2136. [Google Scholar]
- Nathan, A.B.; Nagaraj, K.A.; Ghatu, S.; Michael, A.K. Determination of constitutive response of plastically graded materials. Int. J. Plast. 2011, 27, 728–738. [Google Scholar]
- Choi, I.S.; Dao, M.; Suresh, S. Mechanics of indentation of plastically graded materials-I: Analysis. J. Mech. Phys. Solids 2008, 56, 157–171. [Google Scholar] [CrossRef]
- Choi, I.S.; Detor, A.J.; Schwaiger, R.; Dao, M.; Schuh, C.A.; Suresh, S. Mechanics of indentation of plastically graded materials—II: Experiments on nanocrystalline alloys with grain size gradients. J. Mech. Phys. Solids 2008, 56, 172–183. [Google Scholar] [CrossRef]
- Narasimhan, R. Analysis of indentation of pressure sensitive plastic solids using the expanding cavity model. Mech. Mater. 2004, 36, 633–645. [Google Scholar] [CrossRef]
- Loganathan, T.; Purbolaksono, J.; Inayat-Hussain, J.; Wahab, N. Effects of carburization on expected fatigue life of alloys steel shafts. Mater. Des. 2011, 32, 3544–3547. [Google Scholar]
- Nathan, A.; Ghatu, S.; Nagaraj, K.; Michael, A. A new reverse analysis to determine the constitutive response of plastically graded case hardened bearing steels. Int. J. Solids Struct. 2011, 48, 584–591. [Google Scholar]
- Junjie, Y.; Keji, P. Elastoplastic Behavior of Case-Carburized 18Cr2Ni4WA Steel by Indenter Testing. J. Aerosp. Eng. 2019, 32, 04019045. [Google Scholar]
- Dao, M.; Chollacoop, N.; Van Vliet, K.J.; Venkatesh, T.A.; Suresh, S. Computational modeling of the forward and reverse problems in instrumented sharp indentation. Acta Mater. 2001, 49, 3899–3918. [Google Scholar] [CrossRef]
- Asi, O.; Can, A.C.; Pineault, J.; Belassel, M. The relationship between case depth and bending fatigue strength of gas carburized SAE 8620 steel. Surf. Coat. Technol. 2007, 201, 5979–5987. [Google Scholar] [CrossRef]
- Zhinan, Y.; Yulong, J.; Fucheng, Z.; Ming, Z.; Nawaz, B.; Chunlei, Z. Microstructural evolution and performance change of a carburized nanostructured bainitic bearing steel during rolling contact fatigue process. Mater. Sci. Eng.-A 2018, 725, 98–107. [Google Scholar]
- Kwofie, S. An exponential stress function for predicting fatigue strength and life due to mean stresses. Int. J. Fatigue 2001, 23, 829–836. [Google Scholar] [CrossRef]
- Patricio, E.C.; Nima, S.; Steven, R.D.; Robert, D.M. Fatigue behavior of Ti-6Al-4V ELI including mean stress effects. Int. J. Fatigue 2017, 99, 87–100. [Google Scholar]




| Type - | E GPa | MPa | Fracture Stress MPa | Fracture Strain % |
|---|---|---|---|---|
| C.Tub. | 197.0 | 1102.0 | 1262.0 | 0.93 |
| C.Cylin. | 197.0 | 1059.0 | 1313.0 | 1.13 |
| P.Cylin. | 197.0 | 674.0 | 973.0 | 5.03 |
| Type - | A MPa | n - | MPa | - |
|---|---|---|---|---|
| C.Tub. | 2113.8 | −0.1666 | 310.7 | 0.9149 |
| C.Cylin. | 2649.5 | −0.1396 | 531.2 | 0.8967 |
| P.Cylin. | 2715.3 | −0.1829 | 330.4 | 0.9524 |
| Type - | MPa | MPa | - | - |
|---|---|---|---|---|
| Based on C.Tub. | 492.9 | 1262.0 | 1.3980 | 0.8501 |
| Based on P.Cylin. | 449.5 | 973.0 | 0.9996 | 0.8006 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, J.; Yang, J. Mechanical Behavior and Low-Cycle Fatigue Performance of a Carburized Steel for GTF Engines. Processes 2023, 11, 1275. https://doi.org/10.3390/pr11041275
Cao J, Yang J. Mechanical Behavior and Low-Cycle Fatigue Performance of a Carburized Steel for GTF Engines. Processes. 2023; 11(4):1275. https://doi.org/10.3390/pr11041275
Chicago/Turabian StyleCao, Juan, and Junjie Yang. 2023. "Mechanical Behavior and Low-Cycle Fatigue Performance of a Carburized Steel for GTF Engines" Processes 11, no. 4: 1275. https://doi.org/10.3390/pr11041275
APA StyleCao, J., & Yang, J. (2023). Mechanical Behavior and Low-Cycle Fatigue Performance of a Carburized Steel for GTF Engines. Processes, 11(4), 1275. https://doi.org/10.3390/pr11041275







