Low-Carbon Optimal Scheduling Model for Peak Shaving Resources in Multi-Energy Power Systems Considering Large-Scale Access for Electric Vehicles
Abstract
:1. Introduction
- (1)
- The charging and discharging characteristics of electric vehicles are analyzed, and the total investment cost of electric vehicles, the performance degradation cost, maintenance cost, and battery energy storage efficiency cost model of the battery charging and discharging cycle are established. Considering the conversion of electrothermal energy storage and electric hydrogen energy storage and their participation in power grid regulation characteristics, the total investment cost, maintenance cost, and operation cost models of electrothermal energy storage and electric hydrogen energy storage are established.
- (2)
- The carbon emission characteristics of coal-fired units and the carbon emission cost model are studied. The relationship between the actual carbon emissions and the carbon emission quota of the multi-energy power system is analyzed, and a carbon emission cost model of the multi-energy power system is established.
- (3)
- Considering the nonlinear relationship between multi-energy power system peaking unit commitment and carbon emissions, peaking economy, energy supply reliability, energy supply economy, and safety and stability, a multi-objective optimal scheduling model of a multi-energy power system considering large-scale access of electric vehicles is established. A multi-objective optimization model of a multi-energy power system based on a non-dominated sorting genetic algorithm (NSGA-II) is proposed.
2. Electric Vehicle and Its Comprehensive Cost Model
2.1. Electric Vehicle Model
2.2. Comprehensive Cost Model of Electric Vehicle
2.2.1. Calculation of Total Investment Cost of Electric Vehicle
2.2.2. Performance Degradation Cost Calculation of Battery Charge–Discharge Cycle of Electric Vehicle
2.2.3. Maintenance Cost Calculation of Electric Vehicle
2.2.4. Cost Calculation of Battery Energy Storage Efficiency of Electric Vehicle
3. Comprehensive Cost Model of Multi-Energy Storage System
3.1. Comprehensive Cost Model of Electric Heating Energy Storage System
3.1.1. Calculation of Total Investment Cost of Electric Heating Storage System
3.1.2. Maintenance Cost Calculation of Electric Heating Energy Storage System
3.1.3. Cost Calculation of Electric Heating Energy Storage System
3.1.4. Cost Calculation of Heat Purchase for Electric Heating Energy Storage System
3.2. Comprehensive Cost Model of Electric Hydrogen Energy Storage System
3.2.1. Calculation of the Total Investment Cost of the Electric Hydrogen Energy Storage System
3.2.2. Maintenance Cost Calculation of Electric Hydrogen Energy Storage System
3.2.3. Cost Calculation of Electro-Hydrogen Energy Storage Efficiency of Electric Hydrogen Energy Storage System
4. Carbon Emission Cost Model of Multi-Energy Power System
4.1. Carbon Emission Model of Coal-Fired Energy Supply
4.2. Carbon Emission Cost Model of Coal-Fired Energy Supply
4.3. Carbon Transaction Cost of Multi-Energy Power System
5. Multi-Objective Optimal Scheduling Model for Peak Regulation of Multi-Energy Power System
5.1. Optimization Objective
5.2. Constraint Condition
5.2.1. Multi-Energy Power Balance Constraints
5.2.2. Constraints on the Scope of Flexible Resource Regulation
5.2.3. Constraints on the Characteristics of Flexible Resource Regulation Response
5.2.4. Reserve Constraint of Forecasting Deviation in Peak Regulating Demand
5.2.5. Electric Vehicle Charging and Discharging Constraints
5.3. Solving Algorithm

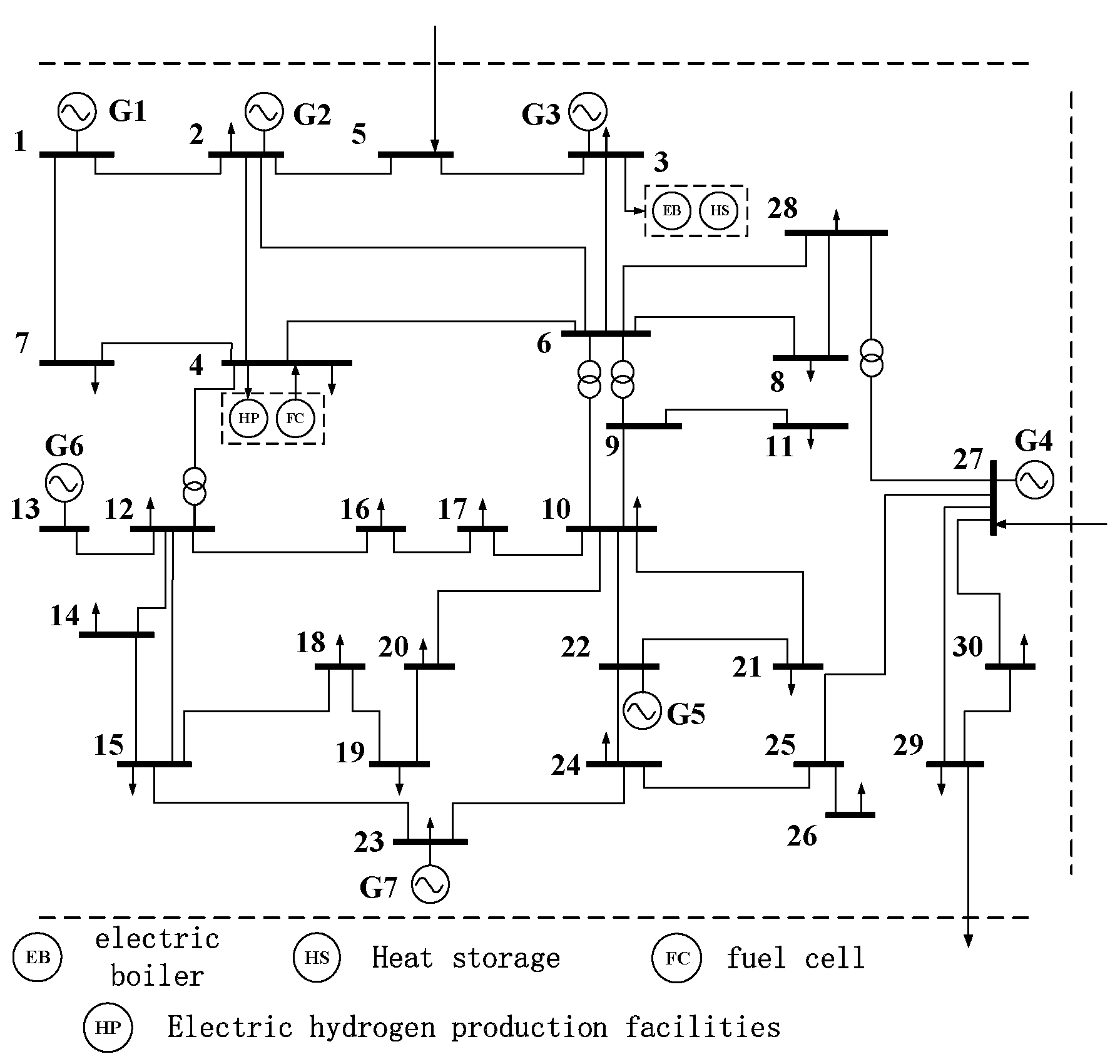
6. Simulation
| Power Type | Power Capacity (MW) |
|---|---|
| Wind power | 200 MW |
| Photovoltaic | 160 MW |
| Thermal power | 120 MW |
| Energy Storage Type | Charging Efficiency | Energy Release Efficiency | Energy Storage Capacity (MW) |
|---|---|---|---|
| Electric heating energy storage system | 80% | 80% | 60 |
| electric vehicle | 85% | 85% | 120 |
| Electric hydrogen Energy Storage System | 50% | 50% | 70 |

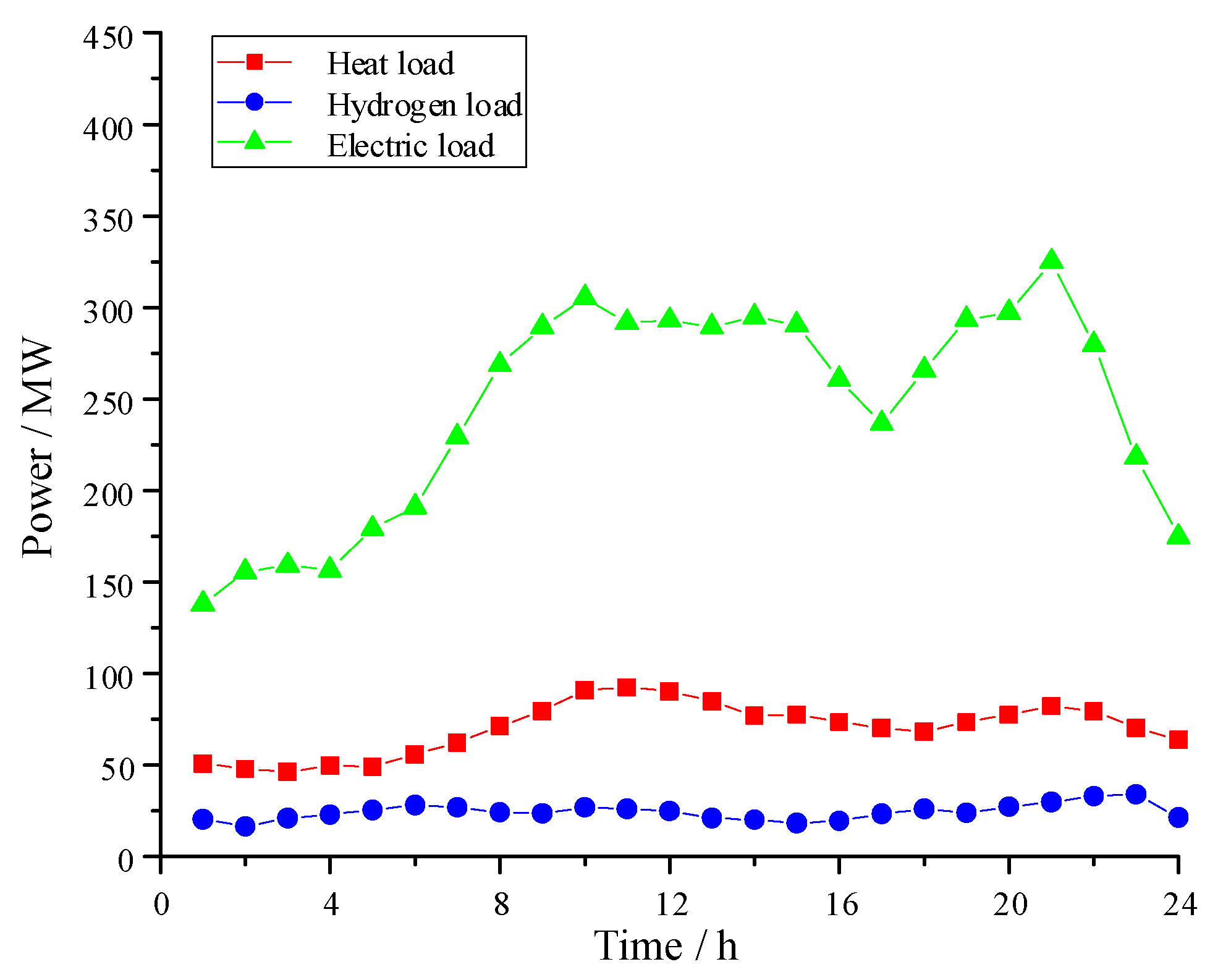
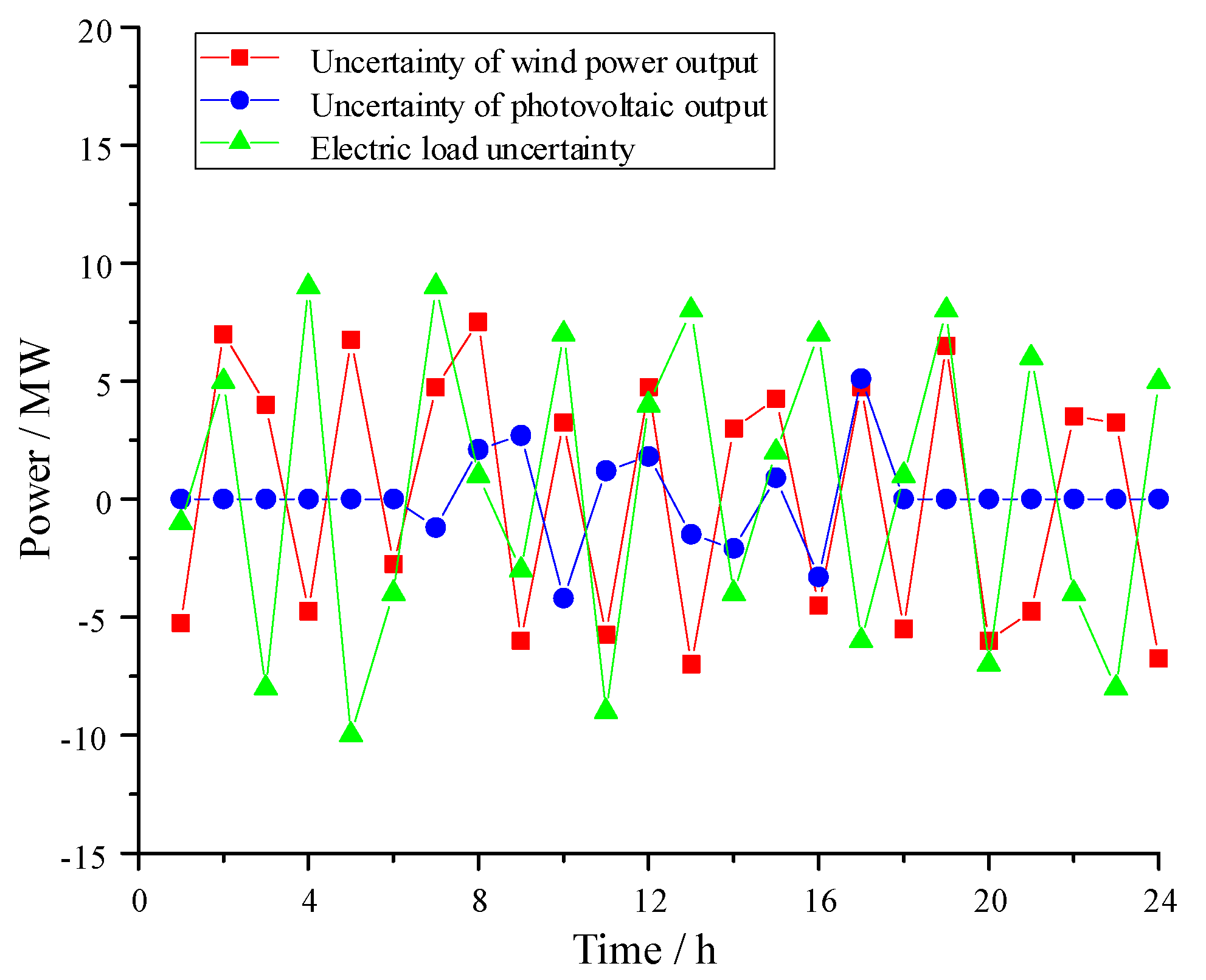
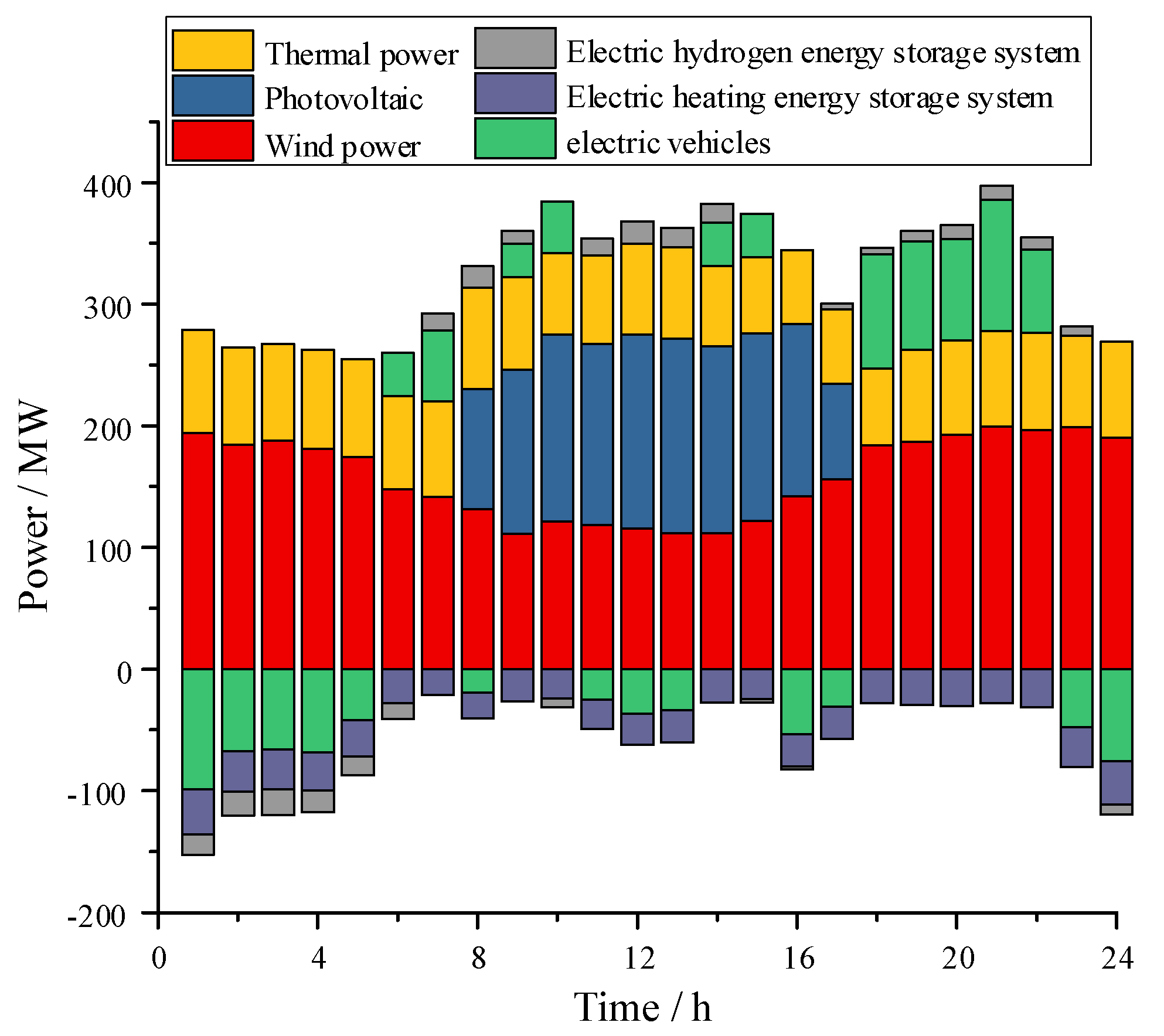

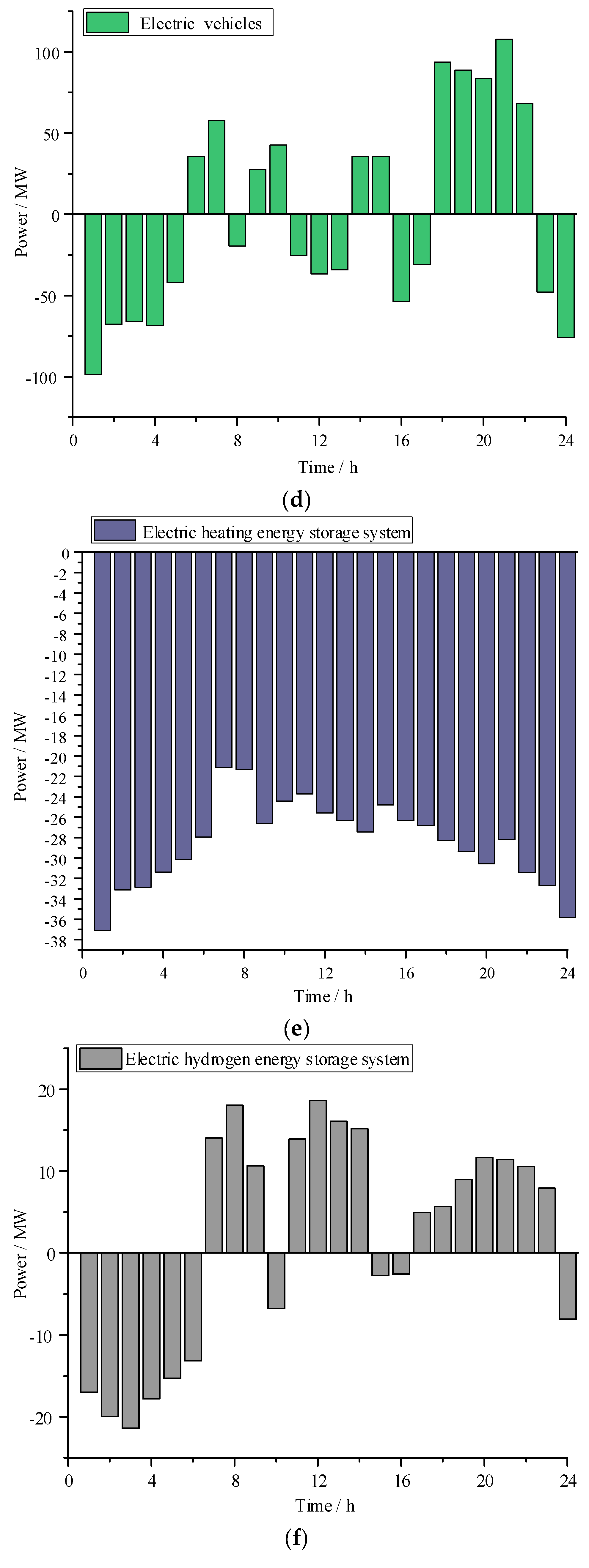

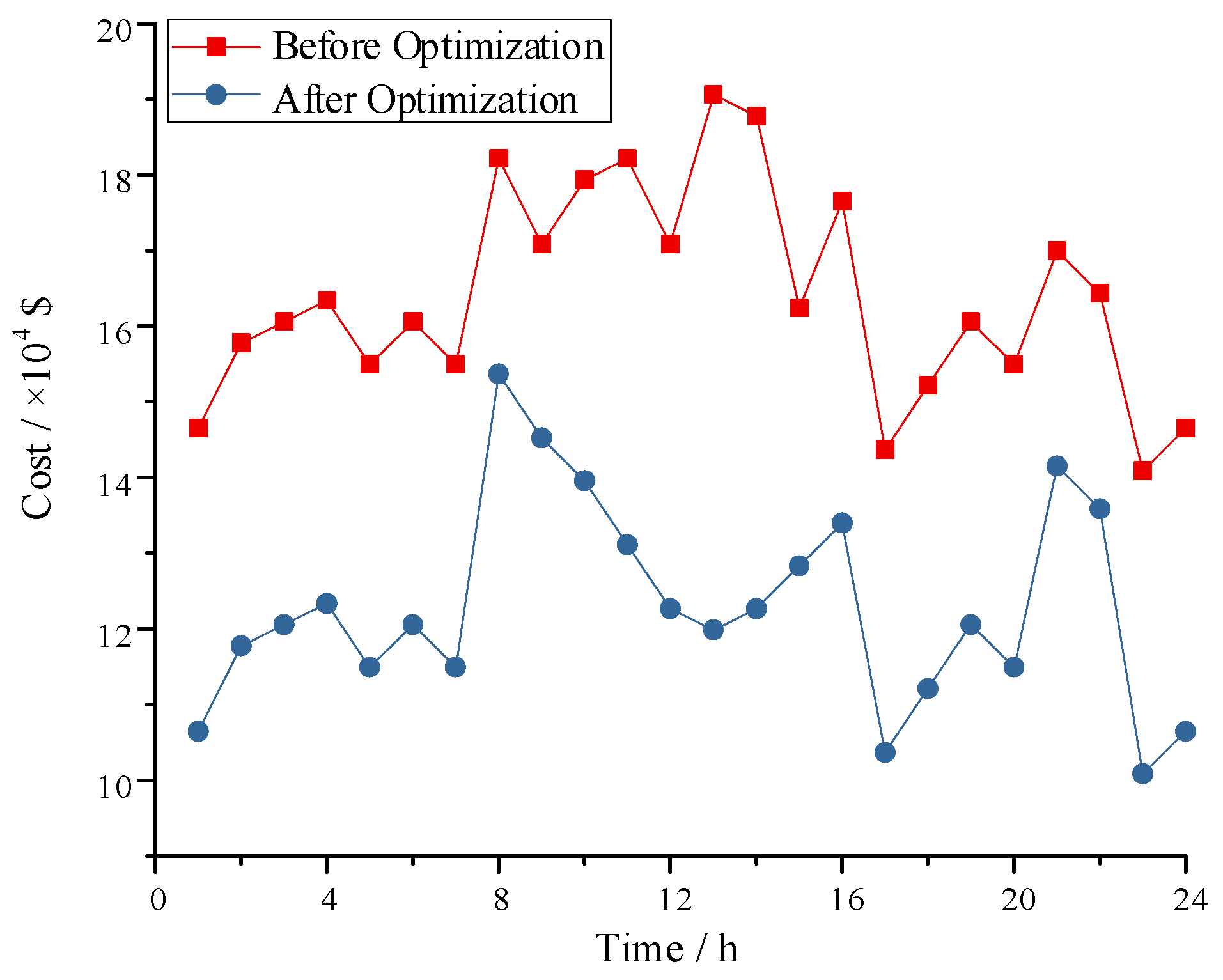
7. Conclusions
- (1)
- From the aspects of investment construction, operation maintenance, and operation efficiency of the electric heating energy storage system, the electric vehicle, and the electric hydrogen energy storage system, a comprehensive cost calculation method of the multi-energy power system energy storage is proposed, and an accurate analysis of the operation peak adjustment cost of the multi-energy storage participating in the peak adjustment system is realized.
- (2)
- The optimal scheduling method of peak regulation resources for the multi-energy power system is proposed, which not only considers the economy of peak regulation of the multi-energy power system but also considers the demand of carbon emission reduction in the system, thus achieving reductions in the carbon emission cost of the system.
- (3)
- The optimal scheduling of peak regulating resources can also help to improve the level and capacity of the energy storage system and new energy units in a multi-energy power system to participate in peak regulating, improving the level of new energy consumption in the system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclatures
| , | the lower limit and upper limit of the total charging and discharging power of the electric vehicle during the t period |
| the driving and stopping probability of electric vehicles during the t period | |
| EV | the total number of electric vehicles |
| the discharge power of a single electric vehicle | |
| the charging power of a single electric vehicle | |
| , | the discharging and charging efficiency of an electric vehicle |
| the total investment cost of electric vehicle | |
| the charging and discharging power of the electric vehicle | |
| the storage capacity of electric vehicle | |
| , , , , | the fitting coefficient of the total investment cost of the electric vehicle |
| the capacity attenuation function of chemical battery in the electric vehicle | |
| the battery type constant in the electric vehicle, which is used to describe the corresponding attenuation rate of batteries with different electrolyte types and ion types | |
| battery activation energy in electric vehicle | |
| the battery temperature in the electric vehicle | |
| the gas constant | |
| the power law relation index | |
| the number of charge and discharge cycles of the battery in the electric vehicle | |
| the difference between the charging and discharging power of the electric vehicle and the rated power | |
| the actual charging and discharging power of batteries in the electric vehicle | |
| the rated charging and discharging power of the battery in the electric vehicle | |
| the influence coefficient of single charge and discharge power of electric vehicle on battery capacity attenuation | |
| the battery performance state of the electric vehicle | |
| the nominal capacity of the electric vehicle | |
| the performance degradation cost corresponding to a single charge–discharge cycle of the electric vehicle | |
| , | the purchase cost coefficient of battery itself |
| the maintenance cost of electric vehicle | |
| the proportion of maintenance cost of electric vehicle. | |
| the energy loss rate of electric vehicle | |
| , | the input energy and output energy of the electric vehicle. |
| the battery energy storage efficiency cost of the electric vehicle | |
| the electricity price of the grid when the electric vehicle is storing electric energy | |
| the energy storage power of the electric vehicle | |
| the operation time of the electric vehicle under the energy storage state. | |
| the grid non-wind abandoning price when the electric vehicle carries out electric energy storage. | |
| the total investment cost of the electric heating energy storage system; | |
| , , , , , , , | the cost of equipment resistance heater, the cost of system heat storage body, the cost of gas-water heat exchange equipment, the cost of equipment insulation layer, the cost of high-voltage control cabinet, the cost of other auxiliary equipment, the cost of land occupation and the construction cost in the total investment cost of the electric heating energy storage system. |
| the electric heating power | |
| , , | the corresponding cost coefficient |
| heat storage capacity | |
| , , | the corresponding cost coefficients |
| output power of the electric heating energy storage system | |
| , , | the corresponding cost coefficients |
| external area of the electric heating energy storage system equipment | |
| the cost of thermal insulation material per unit area of the system equipment; | |
| the volume of the system heat storage body; | |
| the heat storage density of the system heat storage body; | |
| the density of the system heat storage body; | |
| the margin coefficient of the system heat storage body | |
| , | the height and width of the system heat storage body respectively; |
| , | the corresponding cost coefficient of |
| , , | represent the corresponding cost coefficients of |
| , , | the corresponding cost coefficients of |
| , , | the corresponding cost coefficients of |
| , , , , | the fitting coefficient of the total investment cost. |
| the maintenance cost of the electric heating energy storage system | |
| the proportion of maintenance cost. | |
| where represents the purchasing cost of wind power abandonment of the electric heating energy storage system; | |
| the wind abandonment price of the power grid; | |
| the corresponding electric power of the electric heating storage system; | |
| the purchasing cost of wind power abandonment of the electric heating energy storage system; | |
| the wind discard price of the power grid. | |
| the heat purchase cost of thermal peak regulation resources purchased by the electric heating energy storage system | |
| the unit price of heat for other heat sources or heating plants | |
| the heating support power provided by other heat sources or heating plants for the electric heating energy storage systems. | |
| the total investment cost of the electric hydrogen energy storage system; | |
| the input power of electro-hydrogen production in the electric hydrogen energy storage system; | |
| the output power of hydrogen fuel cell of the electro-hydrogen energy storage system; | |
| the energy storage capacity of the electric hydrogen energy storage system. | |
| the maintenance cost of the electric hydrogen energy storage system; | |
| the proportion of maintenance cost of the electric hydrogen energy storage system. | |
| the energy loss ratio of the electric hydrogen energy storage system; | |
| , | the energy input and output of the electric hydrogen energy storage system. |
| the efficiency cost of the electric hydrogen energy storage system; | |
| the power grid wind abandon price during electrolytic hydrogen production; | |
| the electrolytic hydrogen production power of the electric hydrogen energy storage system | |
| the non-wind curtailment price of the grid. | |
| the carbon dioxide emission in the process of burning coal for energy supply; | |
| the carbon emission factor of coal consumed in the process of coal-fired energy supply; | |
| the total coal consumption for coal-fired power supply process; | |
| the average low calorific value of coal consumed in the process of coal-fired energy supply | |
| the carbon content per unit calorific value of coal consumed in the process of coal-fired energy supply | |
| the carbon oxidation rate of coal consumed in coal-fired energy supply process | |
| the correction coefficient of coal quality difference in the process of coal-fired power supply. | |
| the carbon emission cost of the coal-fired power supply; | |
| , , , , | the carbon emission parameter of the coal-fired boiler; |
| equivalent output power of the coal-fired boiler; | |
| the carbon emission corresponding to fuel combustion per unit weight | |
| the fuel consumption of the coal-fired boiler under the operation mode of oil injection depth adjustment; | |
| the maximum equivalent output power of the coal-fired boiler under the conventional regulation operation mode; | |
| the minimum equivalent output power of the coal-fired boiler under the operation mode of no oil injection depth adjustment; | |
| the minimum equivalent output power of the coal-fired boiler under the operation mode of adjusting the oil injection depth. | |
| the carbon emission quota of multi-energy power system; | |
| the carbon emission quota per unit electricity quantity of the multi-energy power system; | |
| the equivalent electric load power actually consumed by network node | |
| the multi-energy power system at time | |
| the carbon transaction cost of the multi-energy power system; | |
| the actual total carbon emissions of the multi-energy power systems | |
| the carbon price of the multi-energy power system at time ; | |
| the output of coal-fired boiler of the multi-energy power system at time ; | |
| the carbon dioxide emission coefficient of coal consumed by coal-fired boilers in the multi-energy power systems. | |
| the peak adjustment cost of traditional synchronous power supply; | |
| the price of primary energy consumed by traditional synchronous power sources such as hydroelectric, thermal or nuclear power units; | |
| , , | the primary energy consumption coefficient of traditional synchronous power supply, the primary energy consumption coefficient under rated working conditions and the primary energy consumption coefficient below the output reduction limit; |
| the peak regulating power demand of multi-energy power system in a time scale; | |
| , | the upper and lower limits for normal adjustment of traditional synchronous power sources such as hydroelectric, thermal or nuclear power units; |
| the output reduction limit of traditional synchronous power sources such as hydroelectric, thermal or nuclear power units. | |
| the peak adjustment cost of energy storage in the multi-energy power system; | |
| , , | the investment cost of the multi-energy storage system construction, basic operation and maintenance cost, and the corresponding electricity price within the time scale; |
| , , | the depreciation coefficient of investment cost, basic operation and maintenance cost and power purchase cost of multi-energy storage system; |
| , , | life attenuation coefficient of multi-energy storage system; is the peak regulating power demand of multi-energy power system in a time scale . |
| the peak adjustment cost of energy storage in the multi-energy power system; | |
| the basic operation cost composed of the investment depreciation and operation and maintenance cost of the new energy power supply participating in peak regulation during the grid-connected operation; | |
| the peak adjustment cost coefficient of new energy power supply participating in peak adjustment under the corresponding basic operation cost; | |
| the corresponding electricity price within the time scale ; | |
| the cost coefficient of electricity price when new energy power supplies participate in peak regulation; | |
| the peak regulating power demand of the multi-energy power system in time scale . | |
| the forecast deviation cost of peak regulating demand for the multi-energy power system; | |
| the power prediction deviation of peak regulating demand considered when optimizing the combination of peak regulating units in a multi-energy power system; | |
| the unit cost corresponding to the purchase of standby capacity of peak regulation for multi-energy power system; | |
| the backup cost coefficient of multi-energy power system purchase of peak regulation; | |
| the corresponding electricity price in the time scale ; | |
| the power cost coefficient of the standby peak-regulating unit caused by more or less power generation in time scale . |
References
- Zhou, X.; Zhao, Q.; Zhang, Y.; Sun, L. Integrated energy production unit: An innovative concept and design for energy transition toward low-carbon development. CSEE J. Power Energy Syst. 2021, 7, 1133–1139. [Google Scholar]
- Gutierrez-Martinez, V.; Moreno-Bautista, C.; Lozano-Garcia, J.; Pizano-Martinez, A.; Zamora-Cardenas, E.A.; Gomez-Martinez, M.A. A Heuristic Home Electric Energy Management System Considering Renewable Energy Availability. Energies 2019, 12, 671. [Google Scholar] [CrossRef]
- Niknam, T.; Azizipanah-Abarghooee, R.; Roosta, A.; Amiri, B. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch. Energy 2018, 42, 530–545. [Google Scholar] [CrossRef]
- Wang, R.; Sun, Q.; Hu, W.; Li, Y.; Ma, D.; Wang, P. SoC-Based Droop Coefficients Stability Region Analysis of the Battery for Stand-Alone Supply Systems With Constant Power Loads. IEEE Trans. Power Electron. 2021, 36, 7866–7879. [Google Scholar] [CrossRef]
- Xu, D.; Zhong, F.; Bai, Z.; Wu, Z.; Yang, X.; Gao, M. Real-time multi-energy demand response for high-renewable buildings. Energy Build. 2023, 281, 112764. [Google Scholar] [CrossRef]
- Sun, P.; Teng, Y.; Chen, Z. Robust coordinated optimization for multi-energy systems based on multiple thermal inertia numerical simulation and uncertainty analysis. Appl. Energy 2021, 296, 116982. [Google Scholar] [CrossRef]
- Cui, M.; Zhang, J.; Wu, H.; Hodge, B.-M. Wind-friendly flexible ramping product design in multi-timescale power system operations. IEEE Trans. Sustain. Energy 2017, 8, 1064–1075. [Google Scholar] [CrossRef]
- Teng, Y.; Sun, P.; Leng, O.; Chen, Z.; Zhou, G. Optimal Operation Strategy for Combined Heat and Power System Based on Solid Electric Thermal Storage Boiler and Thermal Inertia. IEEE Access 2019, 7, 180761–180770. [Google Scholar] [CrossRef]
- Nandakumar, N.; Annaswamy, A.M. Impact of increased renewables on natural gas markets in eastern united states. J. Mod. Power Syst. Clean Energy 2017, 5, 424–438. [Google Scholar] [CrossRef]
- Nosair, H.; Bouffard, F. Flexibility envelopes for power system operational planning. IEEE Trans. Sustain. Energy 2015, 6, 800–809. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, T.; Litvinov, E. A unified framework for defining and measuring flexibility in power system. IEEE Trans. Power Syst. 2015, 31, 339–347. [Google Scholar] [CrossRef]
- Sun, P.; Yun, T.; Chen, Z. Multi-objective robust optimization of multi-energy microgrid with waste treatment. Renew. Energy 2021, 178, 1198–1210. [Google Scholar] [CrossRef]
- Li, Y.; Gao, D.W.; Gao, W.; Zhang, H.; Zhou, J. Double-Mode Energy Management for Multi-Energy System via Distributed Dynamic Event-Triggered Newton-Raphson Algorithm. IEEE Trans. Smart Grid 2020, 11, 5339–5356. [Google Scholar] [CrossRef]
- Zhao, J.; Zheng, T.; Litvinov, E. Variable resource dispatch through Do-Not-Exceed limit. IEEE Trans. Power Syst. 2015, 30, 820–828. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Liang, X.; Huang, B. Event-triggered based distributed cooperative energy management for multienergy systems. IEEE Trans. Ind. Inf. 2019, 15, 2008–2022. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Dazhong, M.; Xuguang, H. Line Impedance Cooperative Stability Region Identification Method for Grid-Tied Inverters Under Weak Grids. IEEE Trans. Smart Grid 2020, 11, 2856–2866. [Google Scholar] [CrossRef]
- Rui, W.; Qiuye, S.; Pinjia, Z.; Yonghao, G.; Dehao, Q.; Peng, W. Reduced-Order Transfer Function Model of the Droop-Controlled Inverter via Jordan Continued-Fraction Expansion. IEEE Trans. Energy Convers. 2020, 35, 1585–1595. [Google Scholar] [CrossRef]
- Huang, W.J.; Zhang, N.; Yang, J.W.; Wang, Y.; Kang, C. Optimal Configuration Planning of Multi-Energy Systems Considering Distributed Renewable Energy. IEEE Trans. Smart Grid 2019, 10, 1452–1464. [Google Scholar] [CrossRef]
- Fumo, N.; Mago, P.J.; Chamra, L.M. Emission operational strategy for combined cooling, heating, and power systems. Appl. Energy 2019, 86, 2344–2350. [Google Scholar] [CrossRef]
- Zheng, J.; Zhou, Z.; Zhao, J.; Wang, J. Effects of the operation regulation modes of district heating system on an integrated heat and power dispatch system for wind power integration. Appl. Energy 2018, 230, 1126–1139. [Google Scholar] [CrossRef]
- Cheng, X.; Lee, W.-J.; Sahni, M.; Cheng, Y.; Lee, L.K. Dynamic Equivalent Model Development to Improve the Operation Efficiency of Wind Farm. IEEE Trans. Ind. Appl. 2016, 52, 2759–2767. [Google Scholar] [CrossRef]
- Teng, Y.; Sun, P.; Hui, Q.; Li, Y.; Chen, Z. A model of electro-thermal hybrid energy storage system for autonomous control capability enhancement of multi-energy microgrid. CSEE J. Power Energy Syst. 2019, 5, 489–497. [Google Scholar]
- Li, J.F.; Xing, Y.; Huang, X.J. The Planning Method of the Multi-Energy Cloud Management Platform with Key Technologies and P2P Trade of Prosumers. Processes 2022, 10, 2272. [Google Scholar] [CrossRef]
- Wang, R.; Ma, D.; Li, M.-J.; Sun, Q.; Zhang, H.; Wang, P. Accurate Current Sharing and Voltage Regulation in Hybrid Wind/Solar Systems: An Adaptive Dynamic Programming Approach. IEEE Trans. Consum. Electron. 2022, 68, 261–272. [Google Scholar] [CrossRef]
- Sun, Z.; Shen, Y.; Chen, Z.; Teng, Y.; Qian, X. Interval Prediction Method for Wind Speed Based on ARQEA Optimized by Beta Distribution and SWLSTM. Front. Energy Res. 2022, 10, 927260. [Google Scholar] [CrossRef]
- Jin, H.; Teng, Y.; Zhang, T.; Wang, Z.; Chen, Z. A deep neural network coordination model for electric heating and cooling loads based on IoT data. CSEE J. Power Energy Syst. 2020, 6, 22–30. [Google Scholar]
- Teng, Y.; Hui, Q.; Chen, Z. Availability estimation of wind power forecasting and optimization of day-ahead unit commitment. J. Mod. Power Syst. Cle. 2019, 7, 1675–1683. [Google Scholar] [CrossRef]
- Zheng, T.; Dai, Z.M.; Yao, J.H. Economic Dispatch of Multi-Energy System Considering Load Replaceability. Processes 2019, 7, 570. [Google Scholar] [CrossRef]
- Wang, R.; Liu, H.; Li, M.-J.; Sun, Q.; Li, X.; Wang, P. Fast Charging Control Method for Electric Vehicle-to-Vehicle Energy Interaction Devices. IEEE Trans. Transp. Electrif. 2022. Early Access. [Google Scholar] [CrossRef]
- Li, Y.; Gao, D.W.; Gao, W.; Zhang, H.; Zhou, J. A Distributed Double-Newton Descent Algorithm for Cooperative Energy Management of Multiple Energy Bodies in Energy Internet. IEEE Trans. Ind. Inf. 2021, 17, 5993–6003. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, S.; Luo, W.; Wu, L. Intrusion-Detector-Dependent Distributed Economic Model Predictive Control for Load Frequency Regulation with PEVs Under Cyber Attacks. Circuits and Systems I: Regular Papers. IEEE Trans. 2021, 68, 3857–3868. [Google Scholar]
- Hu, Z.; Liu, S.; Wu, L. Credibility-based distributed frequency estimation for plug-in electric vehicles participating in load frequency control. Int. J. Electr. Power Energy Syst. 2021, 130, 106997. [Google Scholar] [CrossRef]
- Cheng, S.; Teng, Y.; Zuo, H.; Chen, Z. Power Balance Partition Control Based on Topology Characteristics of Multi-Source Energy Storage Nodes. Front. Energy Res. 2022, 10, 547. [Google Scholar] [CrossRef]
- Tan, Z.; Guo, H.; Lin, H.; Tan, Q.; Yang, S.; Gejirifu, D.; Ju, L.; Song, X. Robust Scheduling Optimization Model for Multi-Energy Interdependent System Based on Energy Storage Technology and Ground-Source Heat Pump. Processes 2019, 7, 27. [Google Scholar] [CrossRef]
- Ramos-Teodoro, J.; Gil, J.D.; Roca, L.; Rodríguez, F.; Berenguel, M. Optimal Water Management in Agro-Industrial Districts: An Energy Hub’s Case Study in the Southeast of Spain. Processes 2021, 9, 333. [Google Scholar] [CrossRef]
| Before Optimization | After Optimization | |
|---|---|---|
| Carbon emission cost of multi energy power systems | 13.13 | 6.12 |
| Peak shaving cost of traditional synchronous power supply | 243.8288 | 140.4215 |
| Peak shaving cost of energy storage | 72.837 | 101.136 |
| Peak shaving cost of new energy sources | 39.356 | 49.907 |
| Bias cost of peak shaving demand prediction in multi energy power systems | 212.9002 | 131.012 |
| total cost | 582.052 | 428.5965 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dai, K.; Zhang, K.; Li, J.; Liu, L.; Chen, Z.; Sun, P. Low-Carbon Optimal Scheduling Model for Peak Shaving Resources in Multi-Energy Power Systems Considering Large-Scale Access for Electric Vehicles. Processes 2023, 11, 1532. https://doi.org/10.3390/pr11051532
Dai K, Zhang K, Li J, Liu L, Chen Z, Sun P. Low-Carbon Optimal Scheduling Model for Peak Shaving Resources in Multi-Energy Power Systems Considering Large-Scale Access for Electric Vehicles. Processes. 2023; 11(5):1532. https://doi.org/10.3390/pr11051532
Chicago/Turabian StyleDai, Kang, Kun Zhang, Jicheng Li, Liang Liu, Zhe Chen, and Peng Sun. 2023. "Low-Carbon Optimal Scheduling Model for Peak Shaving Resources in Multi-Energy Power Systems Considering Large-Scale Access for Electric Vehicles" Processes 11, no. 5: 1532. https://doi.org/10.3390/pr11051532
APA StyleDai, K., Zhang, K., Li, J., Liu, L., Chen, Z., & Sun, P. (2023). Low-Carbon Optimal Scheduling Model for Peak Shaving Resources in Multi-Energy Power Systems Considering Large-Scale Access for Electric Vehicles. Processes, 11(5), 1532. https://doi.org/10.3390/pr11051532








