Research on Two-Way Contra-Rotating Axial-Flow Pump–Turbine with Various Blade Angles in Pump Mode
Abstract
1. Introduction
2. Research Model
2.1. Pump Parameters
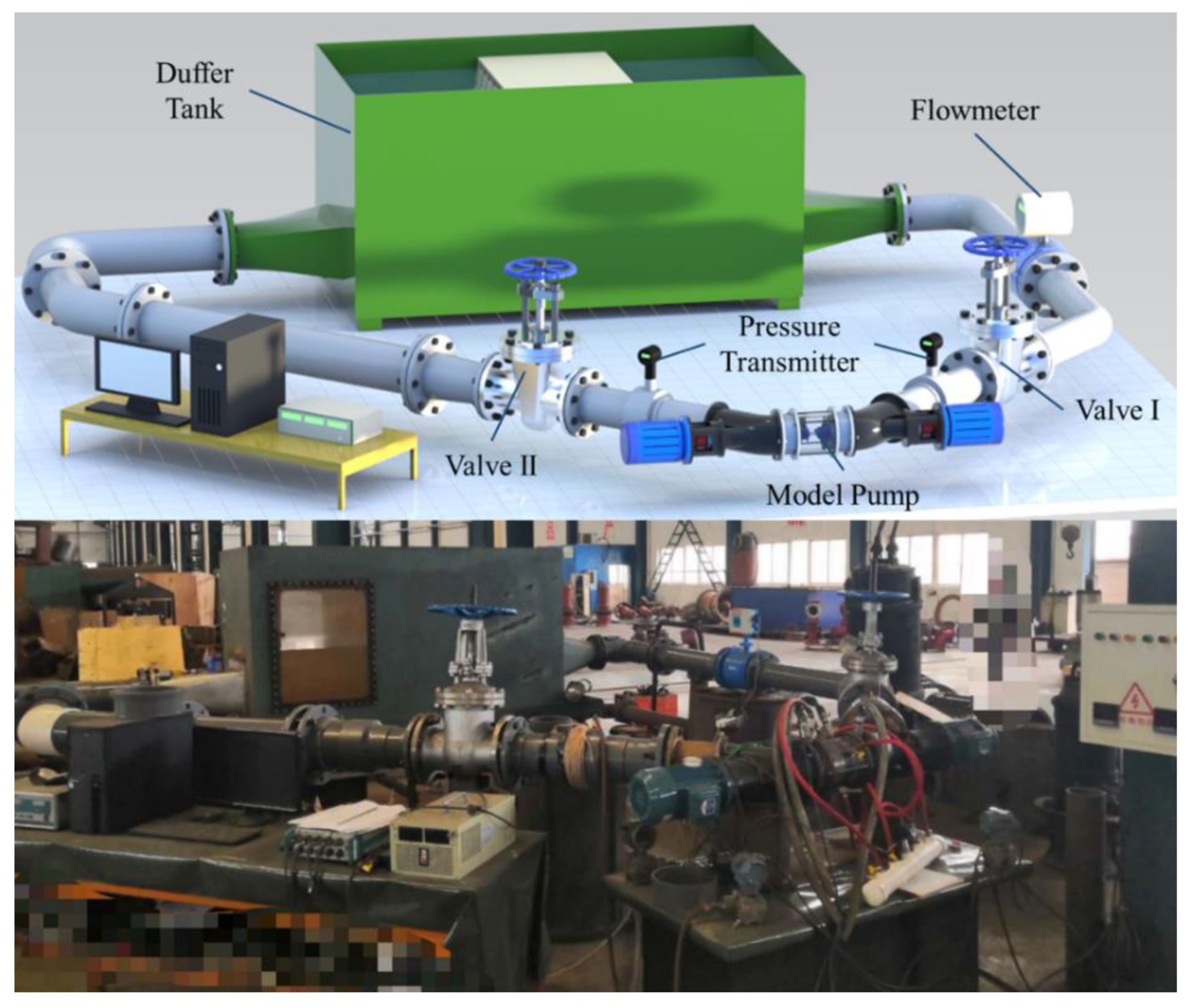
2.2. Experimental Methods
2.3. Numeral Calculation Methods
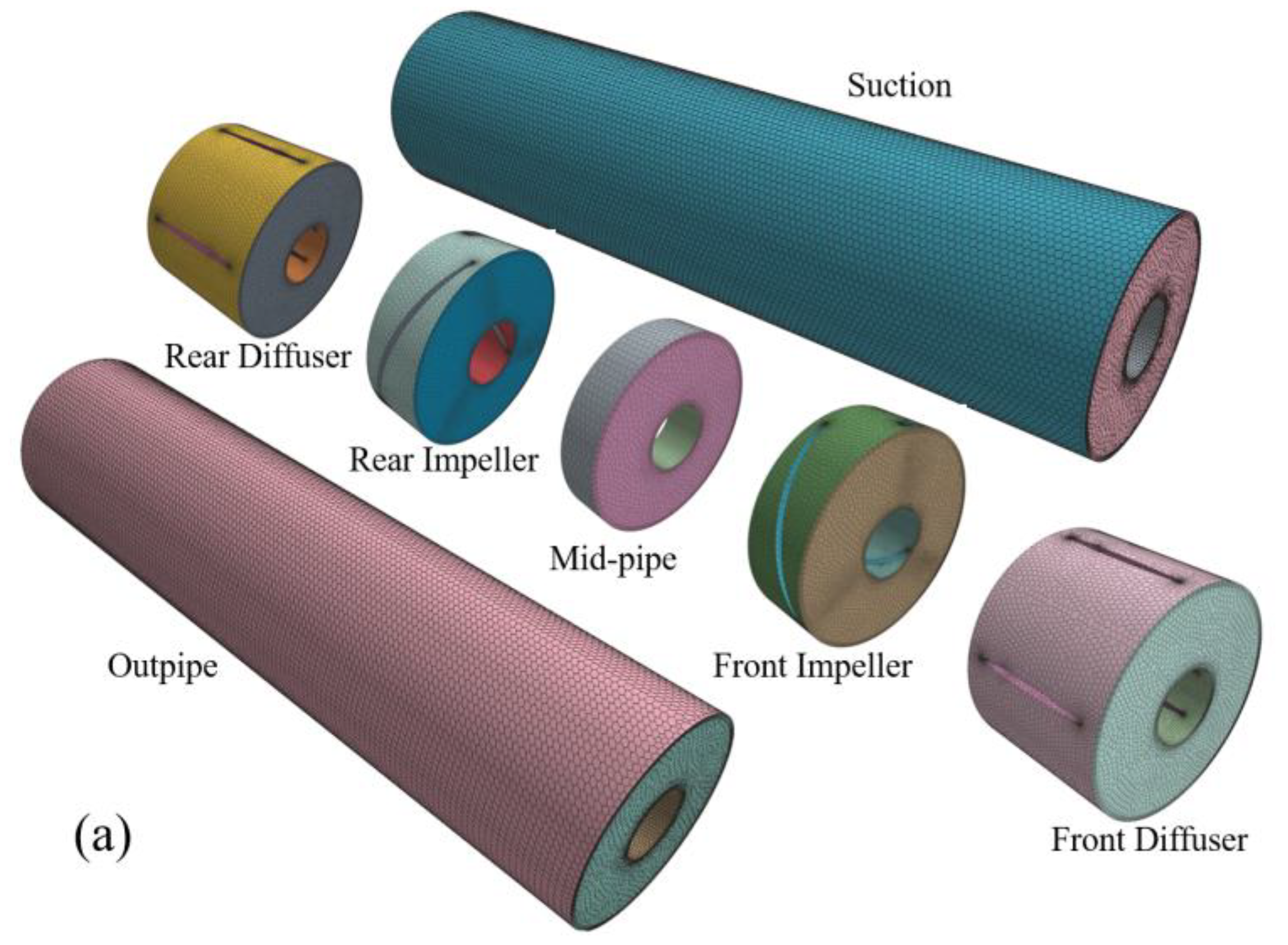
2.3.1. Calculation Model
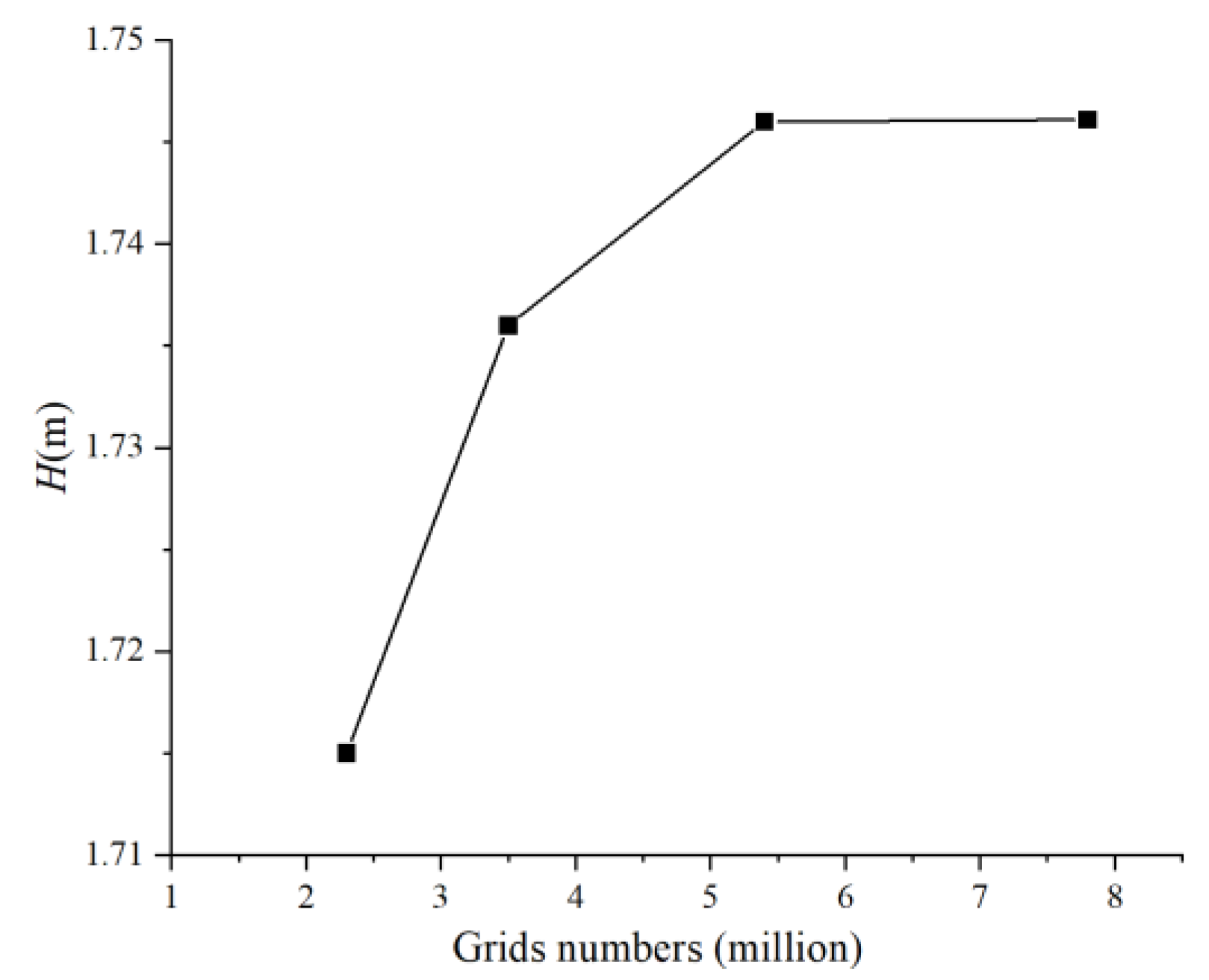
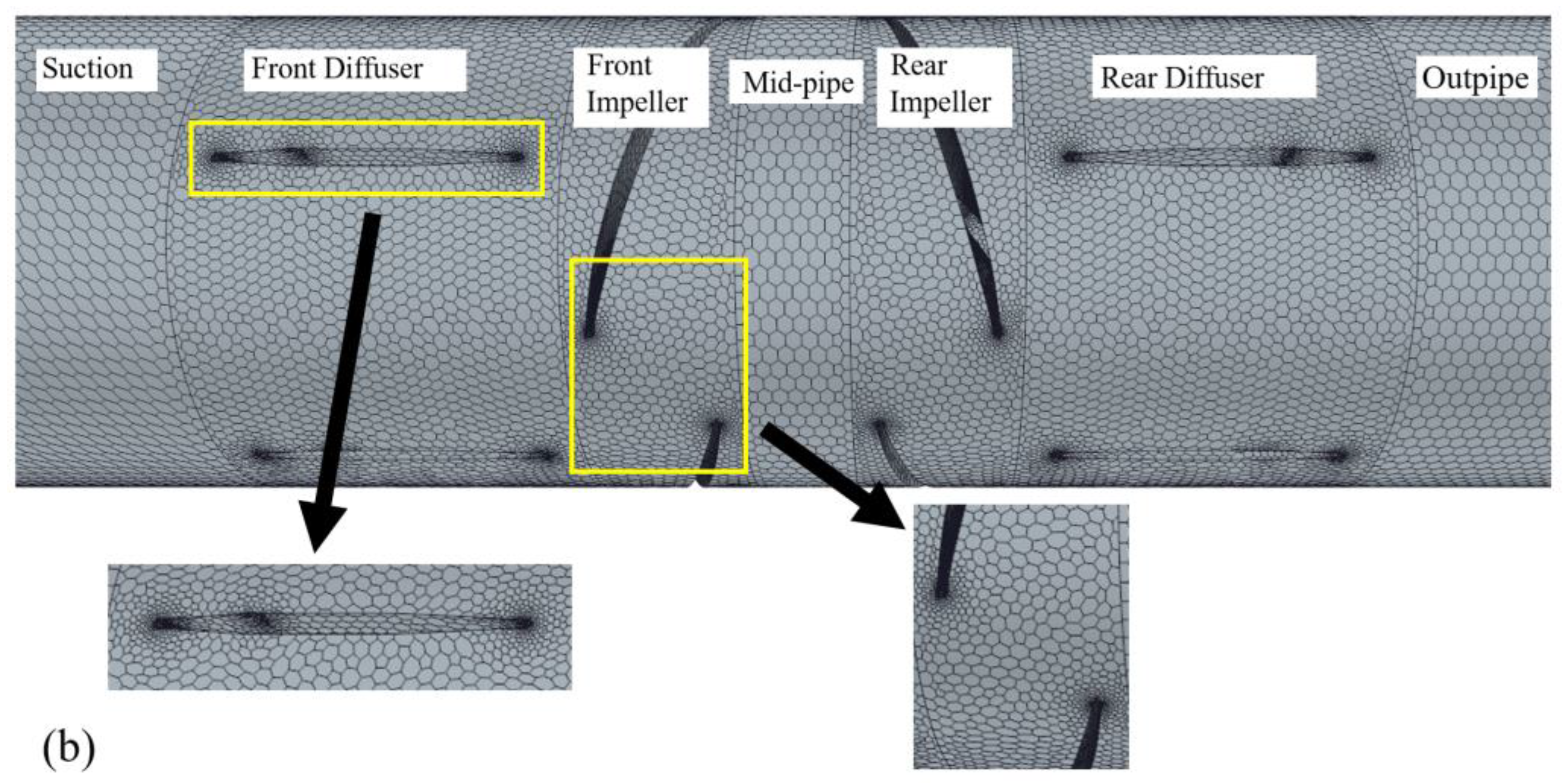
2.3.2. Meshing
2.3.3. Calculation Settings
2.3.4. Calculation Method
3. Internal Flow Field Analysis
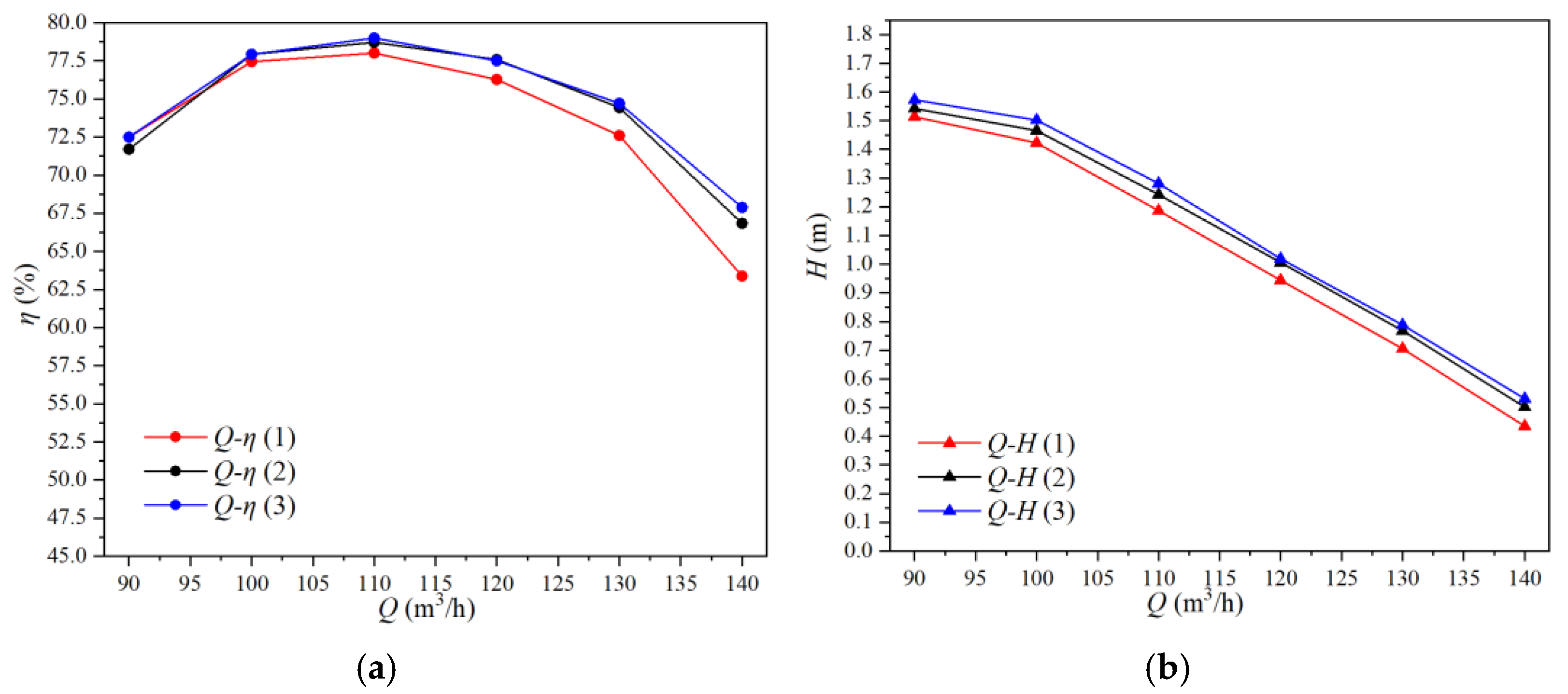
3.1. Performance Test in Pump Mode
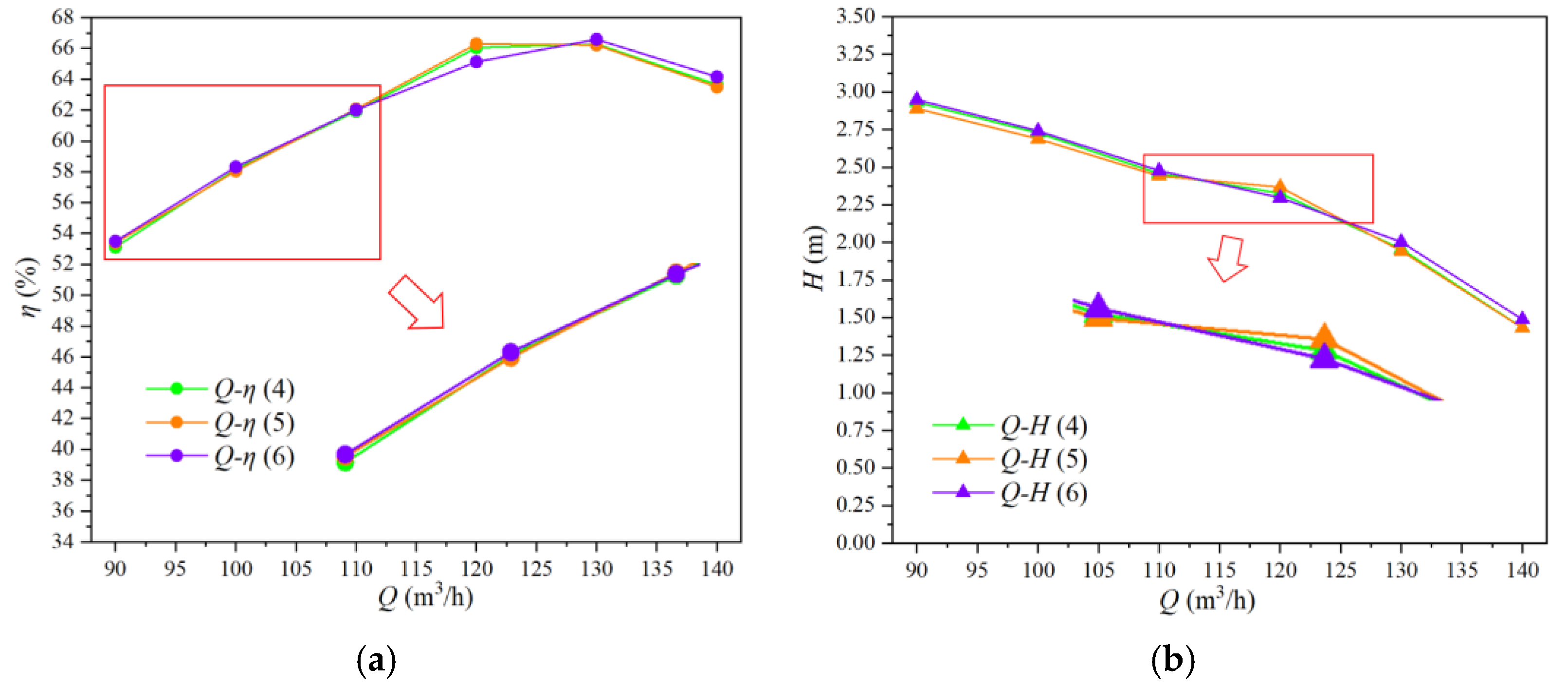
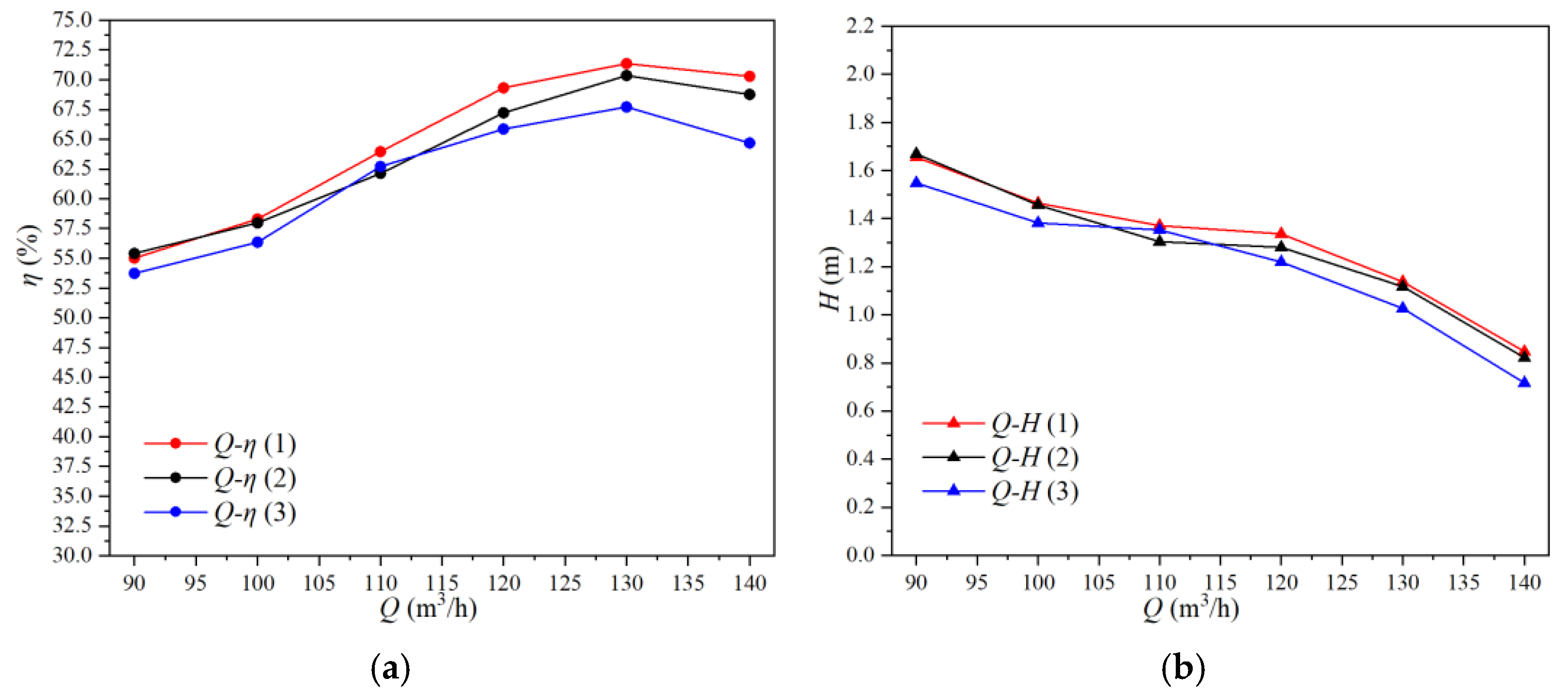
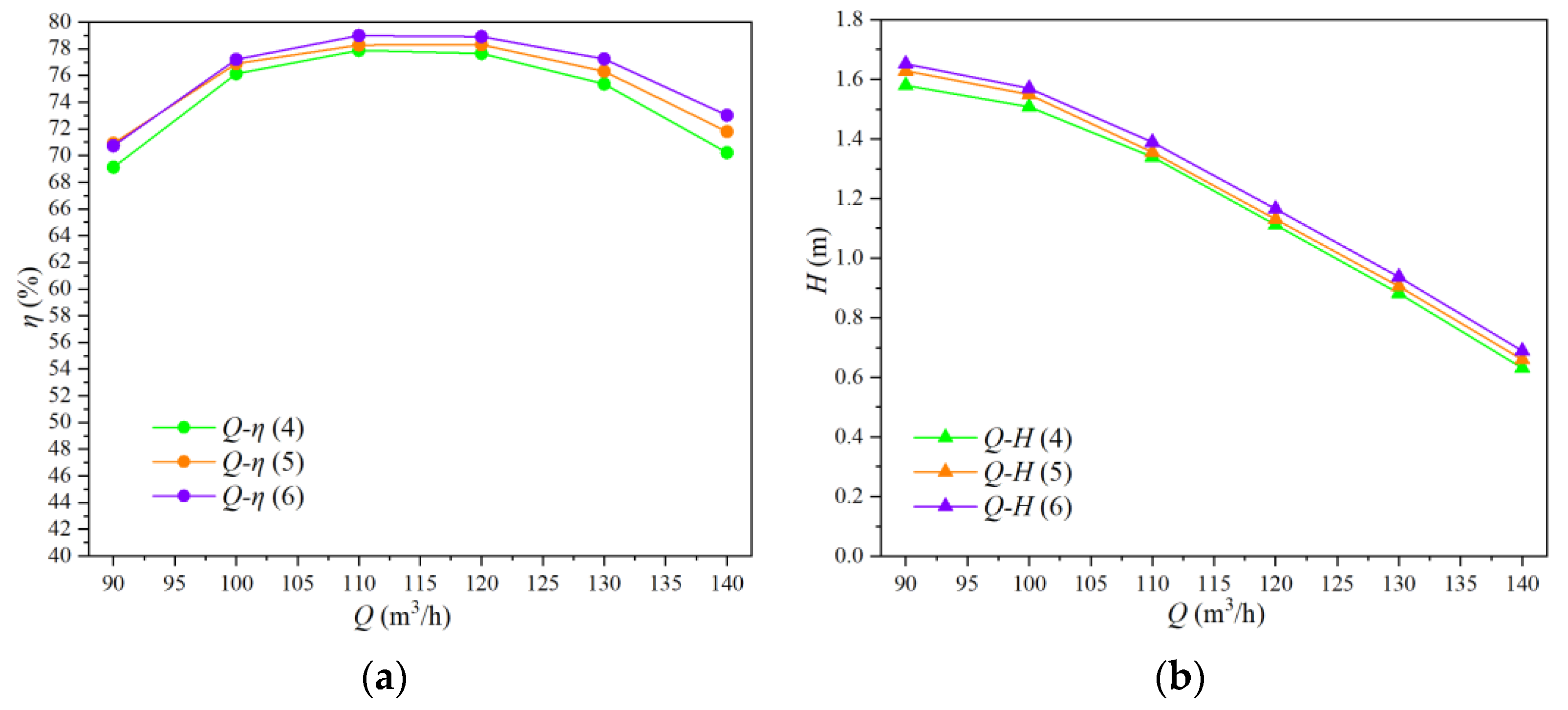
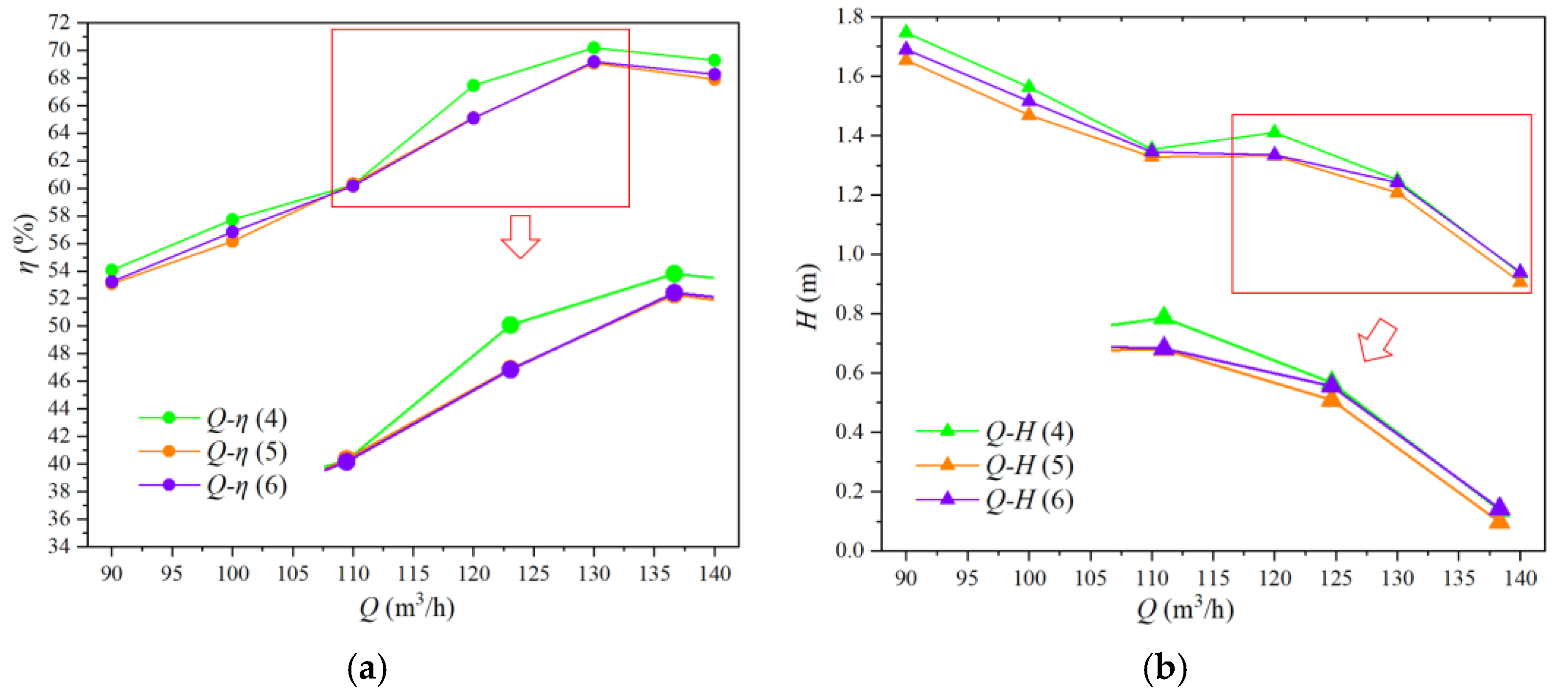
3.2. Performance Analysis on Different Blade Angles
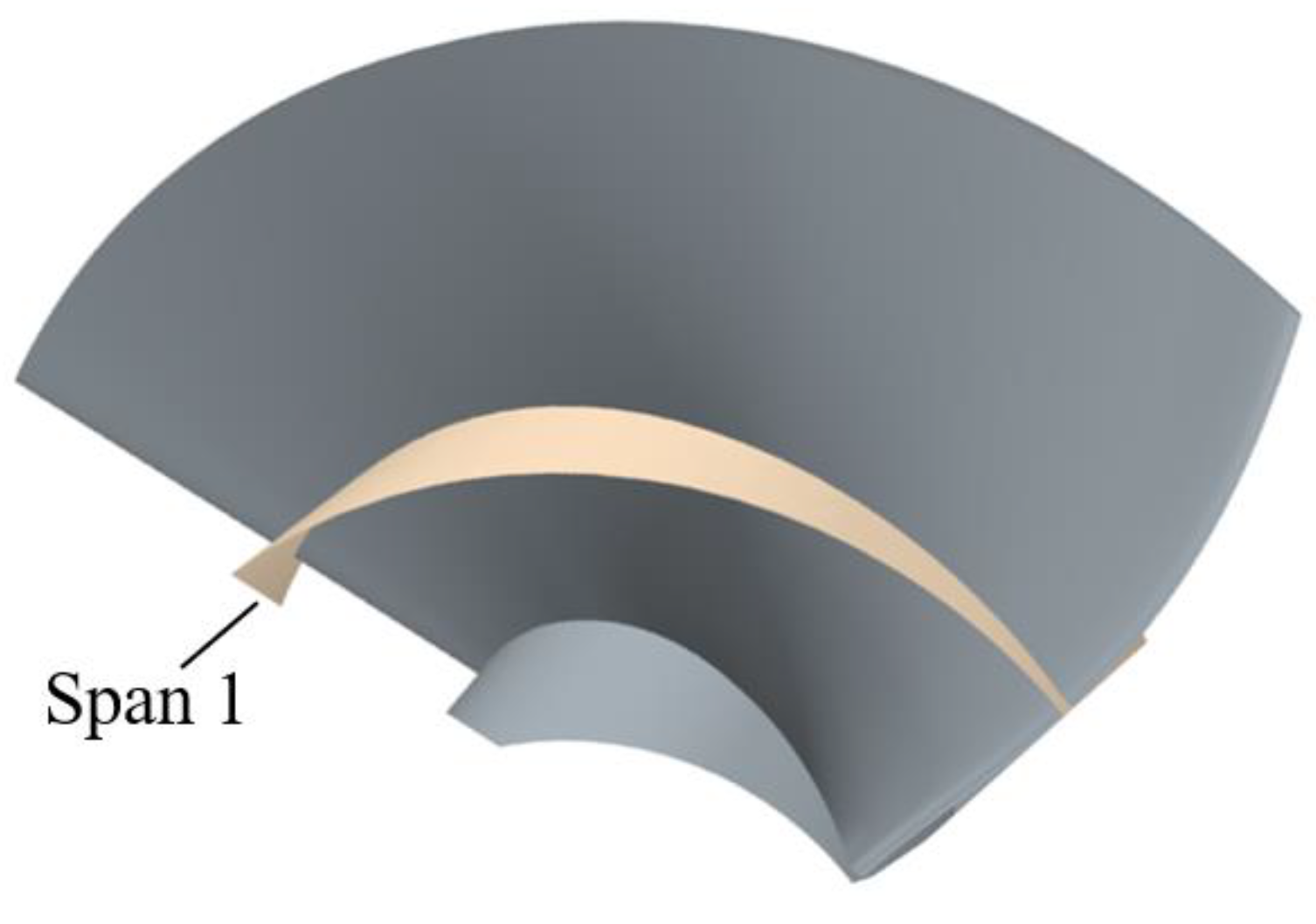
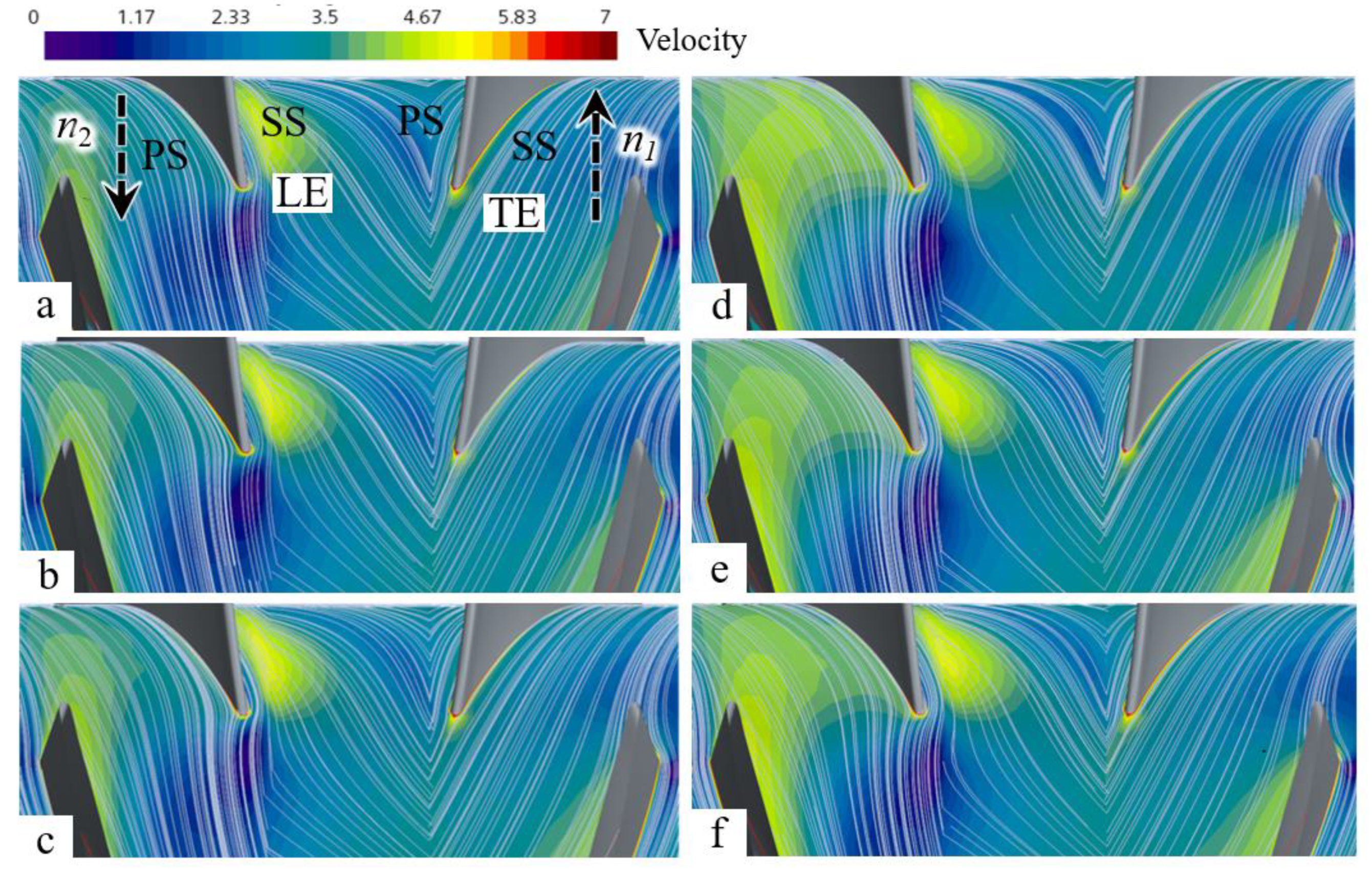
3.3. Streamline Analysis
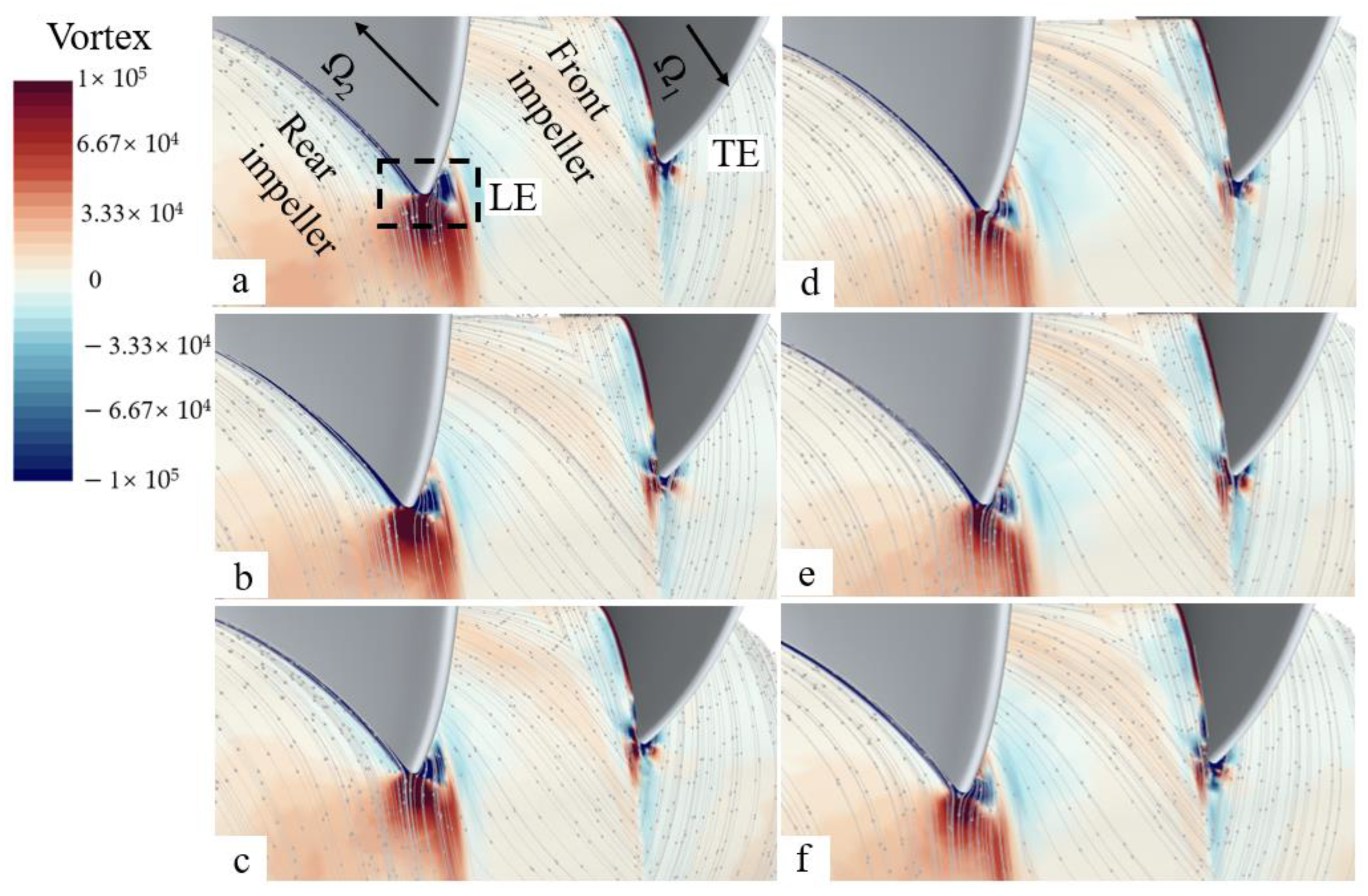
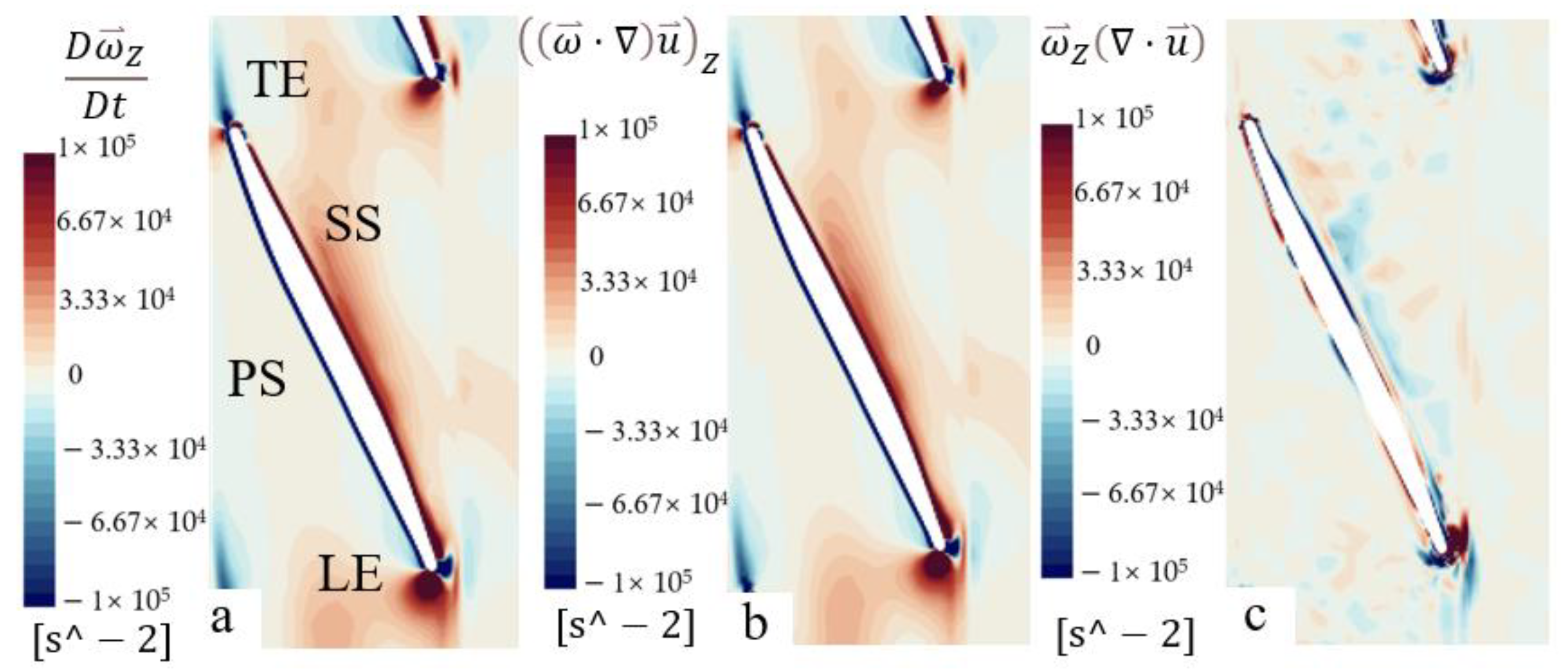
3.4. Vorticity Analysis
4. Conclusions
- (1)
- When the inlet angle remains unchanged and the outlet angle decreases (the inlet angle of the rear impeller decreases), it reduces the inlet flow rate and loss of the rear impeller, affecting the performance of the rear impeller and causing changes in the performance of the two-way pump–turbines.
- (2)
- Compared to each term of the vorticity equation on different spans of the two-stage impeller, the vorticity in this area is mainly dominated by the vortex stretching term, which means that significant vorticity in LE of the rear impeller is generated by LE impact water of the rear impeller.
- (3)
- Different blade angles will have a certain impact on the internal flow situation of the two-way pump–turbine. The variation in different inlet blade angles is not significant for the vorticity variations in the two-stage impeller.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sangiuliano, S.J. Community energy and emissions planning for tidal current turbines: A case study of the municipalities of the Southern Gulf Islands Region, British Columbia. Renew. Sustain. Energy Rev. 2017, 76, 1–8. [Google Scholar] [CrossRef]
- Li, Y.; Lence, B.J.; Calisal, S.M. An integrated model for estimating energy cost of a tidal current turbine farm. Energy Convers. Manag. 2011, 52, 1677–1687. [Google Scholar] [CrossRef]
- Qian, P.; Feng, B.; Liu, H.; Tian, X.; Si, Y.; Zhang, D. Review on configuration and control methods of tidal current turbines. Renew. Sustain. Energy Rev. 2019, 108, 125–139. [Google Scholar] [CrossRef]
- Charlier, R.H. A “sleeper” awakes: Tidal current power. Renew. Sustain. Energy Rev. 2003, 7, 515–529. [Google Scholar] [CrossRef]
- Cao, L.L.; Watanabe, S.; Imanishi, T.; Momosaki, S.; Furukawa, A. On high efficiency operation of contra-rotating axial flow pump with rotational speed control toward effective energy saving. IOP Conf. Ser. Mater. Sci. Eng. 2012, 15, 042027. [Google Scholar] [CrossRef]
- Cao, L.; Che, B.; Hu, L.; Wu, D.Z. Design method of water jet pump towards high cavitation performances. IOP Conf. Ser. Mater. Sci. Eng. 2016, 129, 012067. [Google Scholar] [CrossRef]
- Clarke, J.; Connor, G.; Grant, A.; Johnstone, C.; Ordonez-Sanchez, S. Analysis of a single point tensioned mooring system for station keeping of a contra-rotating marine current turbine. IET Renew. Power Gener. 2010, 4, 473–487. [Google Scholar] [CrossRef]
- Muis, A.; Sutikno, P.; Suwono, A.; Hartono, F. Comparative study on performance of very low head axial hydraulic turbine using a single rotor and a contra-rotating rotor. Appl. Mech. Mater. 2015, 758, 165–172. [Google Scholar] [CrossRef]
- Shigemitsu, T.; Takeshima, Y.; Ogawa, Y.; Fukutomi, J. Internal flow of contra-rotating small hydroturbine at off- design flow rates. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 102008. [Google Scholar] [CrossRef]
- Huang, R.; Ji, B.; Luo, X.; Zhai, Z.; Zhou, J. Numerical investigation of cavitation-vortex interaction in a mixed-flow waterjet pump. J. Mech. Sci. Technol. 2015, 29, 3707–3716. [Google Scholar] [CrossRef]
- Guo, Q.; Huang, X.; Qiu, B. Numerical investigation of the blade tip leakage vortex cavitation in a waterjet pump. Ocean Eng. 2019, 187, 106170. [Google Scholar] [CrossRef]
- Kan, K.; Zhang, Q.; Xu, Z.; Zheng, Y.; Gao, Q.; Shen, L. Energy loss mechanism due to tip leakage flow of axial flow pump as turbine under various operating conditions. Energy 2022, 255, 124532. [Google Scholar] [CrossRef]
- Sanders, A.J.; Papalia, J.; Fleeter, S. Multi-blade row interactions in a transonic axial compressor: Part I—Stator particle image velocimetry (PIV) investigation. J. Turbomach. 2002, 124, 10–18. [Google Scholar] [CrossRef]
- Shigemitsu, T.; Furukawa, A.; Watanabe, S.; Okuma, K.; Fukutomi, J. Internal flow measurement with ldv at design point of contra-rotating axial flow pump. J. Fluid Sci. Technol. 2009, 4, 723–734. [Google Scholar] [CrossRef]
- Momosaki, S.; Usami, S.; Watanabe, S.; Furukawa, A. Numerical simulation of internal flow in a contrarotating axial flow pump. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012046. [Google Scholar] [CrossRef]
- Zhang, D.; Katayama, Y.; Watanabe, S.; Tsuda, S.-I.; Furukawa, A. Numerical study on loss mechanism in rear rotor of contra-rotating axial flow pump. Int. J. Fluid Mach. Syst. 2020, 13, 241–252. [Google Scholar] [CrossRef]
- Furukawa, A.; Shigemitsu, T.; Watanabe, S. Performance test and flow measurement of contrarotating axial flow pump. J. Therm. Sci. 2007, 16, 7–13. [Google Scholar] [CrossRef]
- Cao, L.; Watanabe, S.; Momosaki, S.; Imanishi, T.; Furukawa, A. Low speed design of rear rotor in contra-rotating axial flow pump. Int. J. Fluid Mach. Syst. 2013, 6, 105–112. [Google Scholar] [CrossRef]
- Cao, L.; Watanabe, S.; Imanishi, T.; Yoshimura, H.; Furukawa, A. Experimental analysis of flow structure in contra-rotating axial flow pump designed with different rotational speed concept. J. Therm. Sci. 2013, 22, 345–351. [Google Scholar] [CrossRef]
- An, C.; Chen, Y.; Zhu, R.; Wang, X.; Yang, Y.; Shi, J. Internal Flow Phenomena of Two-Way Contral Rotating Axial Flow Pump-Turbine in Pump Mode under Variable Speed. J. Appl. Fluid Mech. 2023, 16, 285–297. [Google Scholar] [CrossRef]
- Shih, T.-H.; Liou, W.W.; Shabbir, A.; Yang, Z.; Zhu, J. A New k-Epsilon Eddy Viscosity Model for High Reynolds Number Turbulent Flows: Model Development and Validation; NASA Technical Memorandum; NASA: Washington, DC, USA, 1994.
- Yu, Z. Numerical and Physical Investigation of Tip Leakage Vortex Cavitating Flows; Beijing Institute of Technology: Beijing, China, 2016. [Google Scholar]
- Li, X.; Chen, B.; Luo, X.; Zhu, Z. Effects of flow pattern on hydraulic performance and energy conversion characterisation in a centrifugal pump. Renew. Energy 2020, 151, 475–487. [Google Scholar]
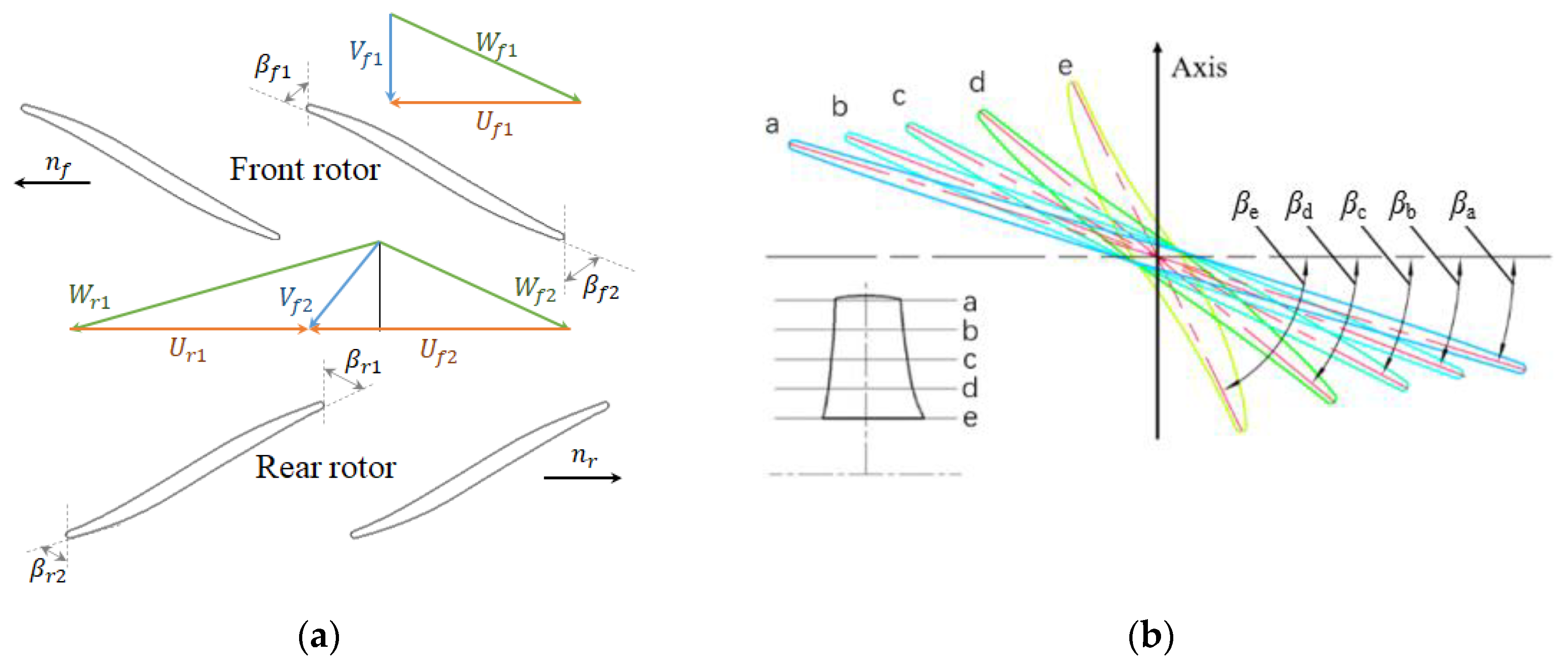





| Number | 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|---|
| Inlet blade angles | β1a | 15.5° | 11° | 10.5° | 10° | ||
| β1b | 18.5° | 14° | 12° | 12.5° | |||
| β1c | 22.5° | 16.5° | 14° | 15° | |||
| β1d | 28° | 21° | 18° | 19.5° | |||
| β1e | 37° | 30° | 26° | 28° | |||
| Outlet blade angles | β2a | 12° | 12° | 12.5° | 12.5° | ||
| β2b | 14.5° | 13.8° | 14.5° | 14.5° | |||
| β2c | 19° | 17.2° | 18° | 18.5° | |||
| β2d | 27.5° | 23.5° | 26.5° | 28.5° | |||
| β2e | 50° | 43.5° | 53.5° | 62.5° | |||
| Project | Type | Accuracy | |
|---|---|---|---|
| 1 | Pressure transmitter | WT3000 | 0.2% |
| 2 | Electromagnetic flowmeter | KEFC | ±0.5% |
| 3 | Photoelectric tachometer | DT2243C | ±0.05% |
| 4 | Three-phase multifunction energy meter | BK8E | ±0.5% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; An, C.; Zhang, R.; Fu, Q.; Zhu, R. Research on Two-Way Contra-Rotating Axial-Flow Pump–Turbine with Various Blade Angles in Pump Mode. Processes 2023, 11, 1552. https://doi.org/10.3390/pr11051552
Chen Y, An C, Zhang R, Fu Q, Zhu R. Research on Two-Way Contra-Rotating Axial-Flow Pump–Turbine with Various Blade Angles in Pump Mode. Processes. 2023; 11(5):1552. https://doi.org/10.3390/pr11051552
Chicago/Turabian StyleChen, Yiming, Ce An, Rongyong Zhang, Qiang Fu, and Rongsheng Zhu. 2023. "Research on Two-Way Contra-Rotating Axial-Flow Pump–Turbine with Various Blade Angles in Pump Mode" Processes 11, no. 5: 1552. https://doi.org/10.3390/pr11051552
APA StyleChen, Y., An, C., Zhang, R., Fu, Q., & Zhu, R. (2023). Research on Two-Way Contra-Rotating Axial-Flow Pump–Turbine with Various Blade Angles in Pump Mode. Processes, 11(5), 1552. https://doi.org/10.3390/pr11051552






