Study on the Internal Flow Characteristics of Long and Short Blade Runners of a 1000 MW Francis Turbine under Different Opening Conditions
Abstract
1. Introduction
2. Research Object
2.1. Francis Turbine Model and Parameters
2.2. Balance Equations and Turbulence Model
2.3. Grid Independence Validation and CFD Setup
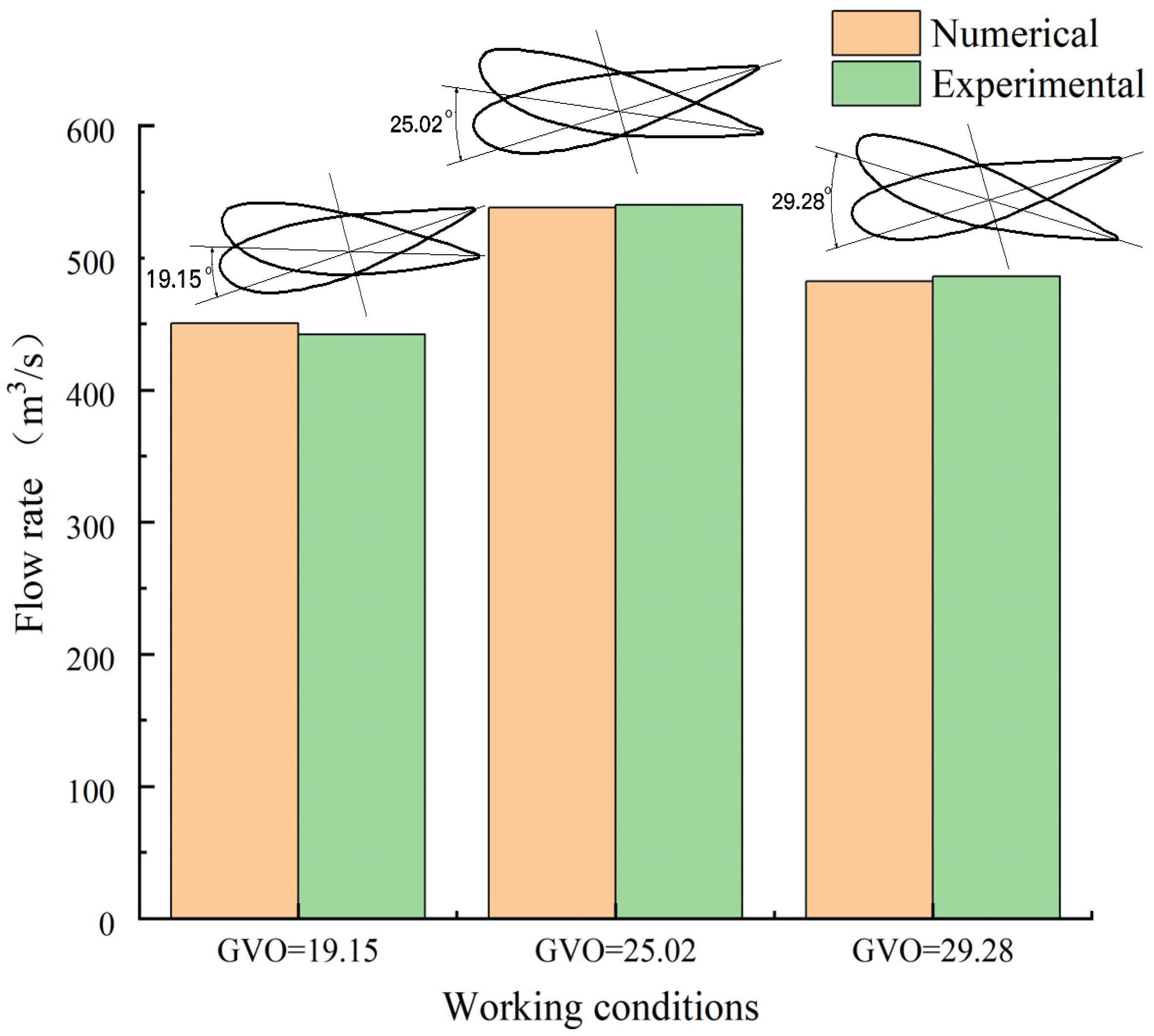
2.4. Condition Selection and Experimental Verification
3. Results and Analysis
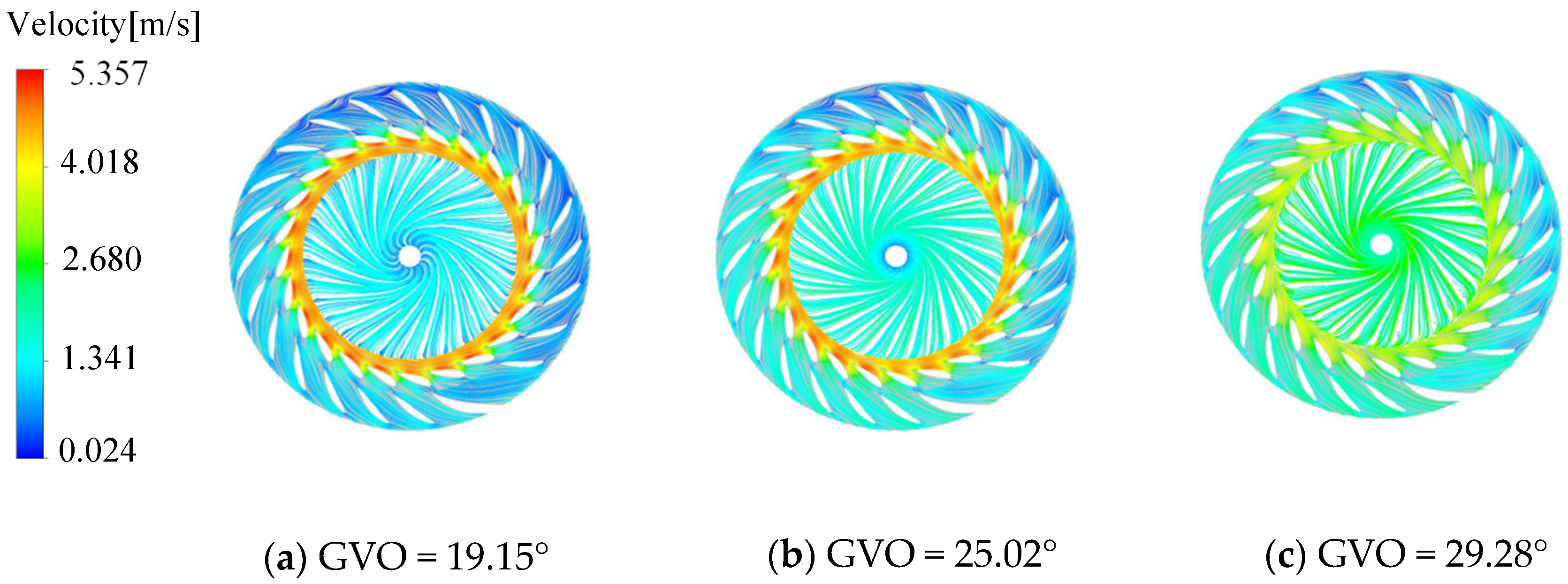
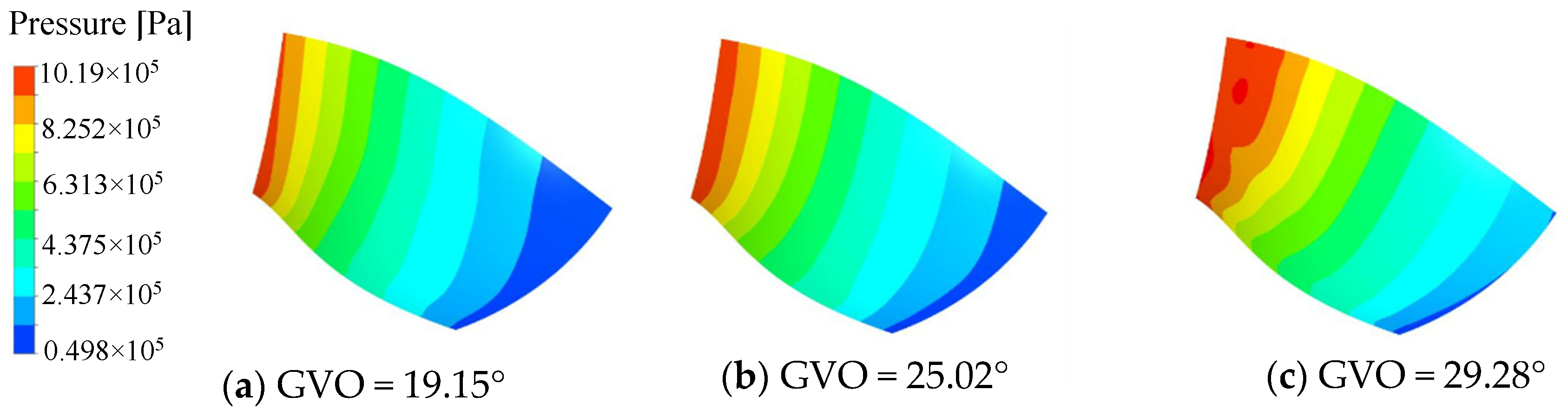
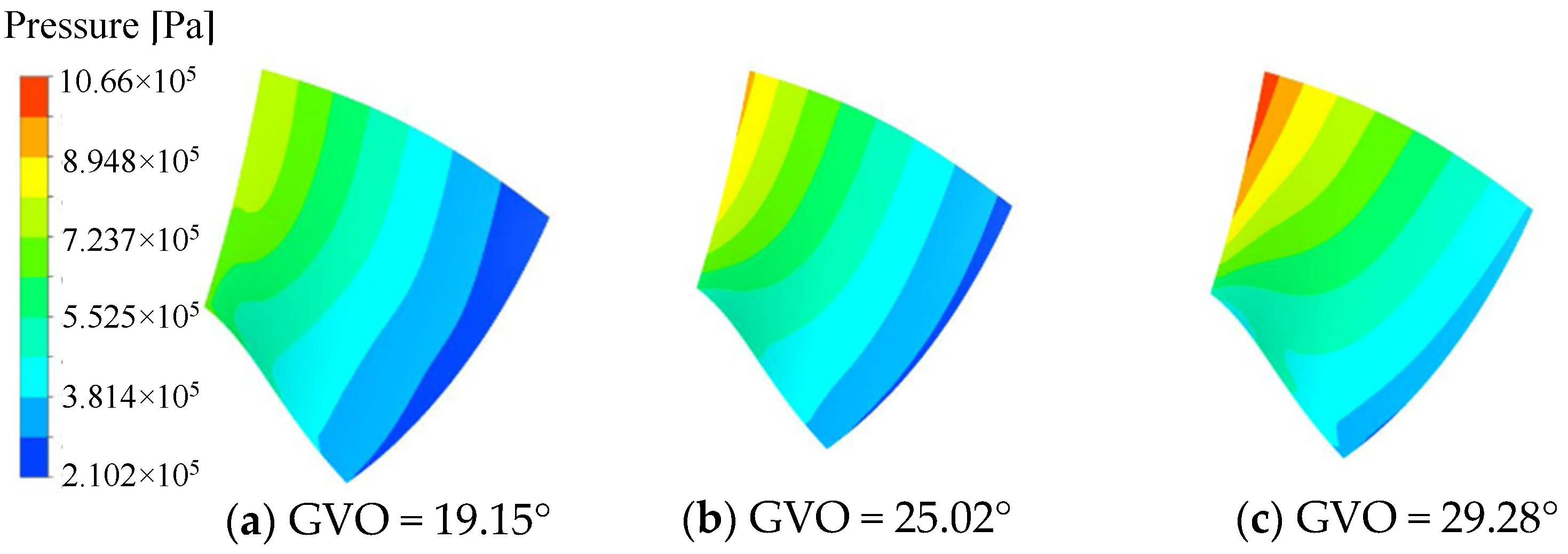
3.1. Internal Flow Analysis of the Runner at Different Opening Conditions
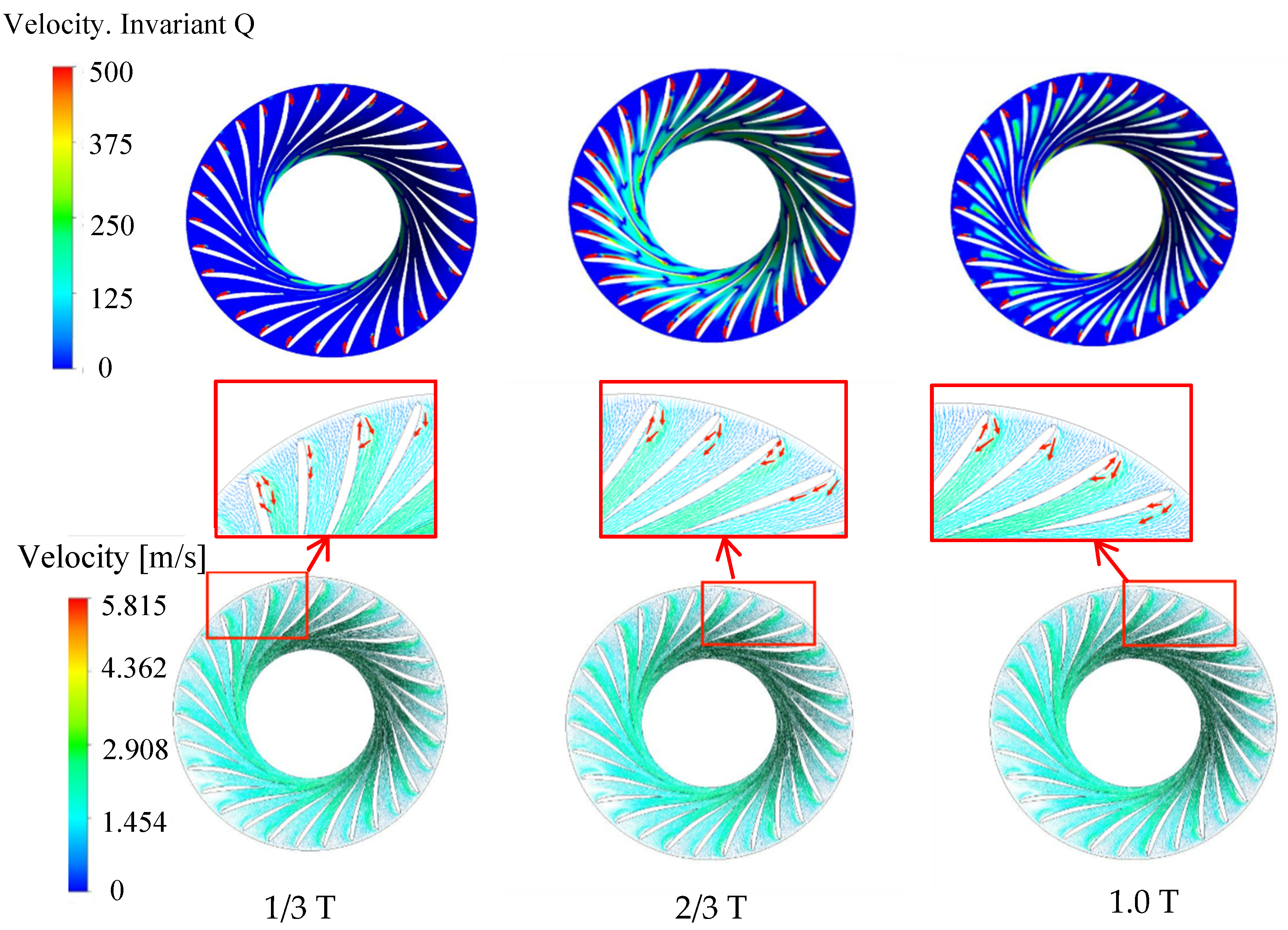
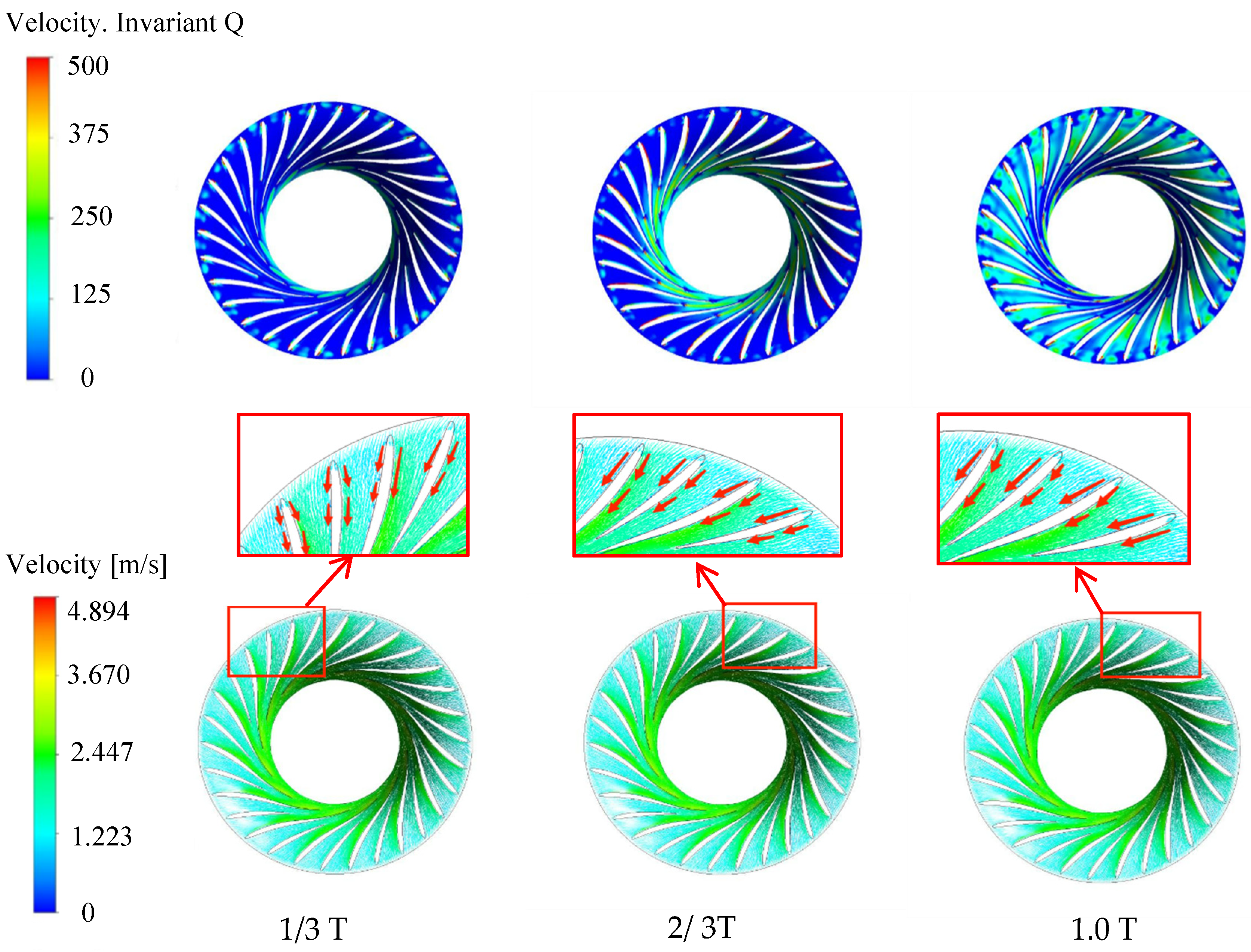
3.2. Vortex and Velocity Distribution in Runner at Different Opening Conditions
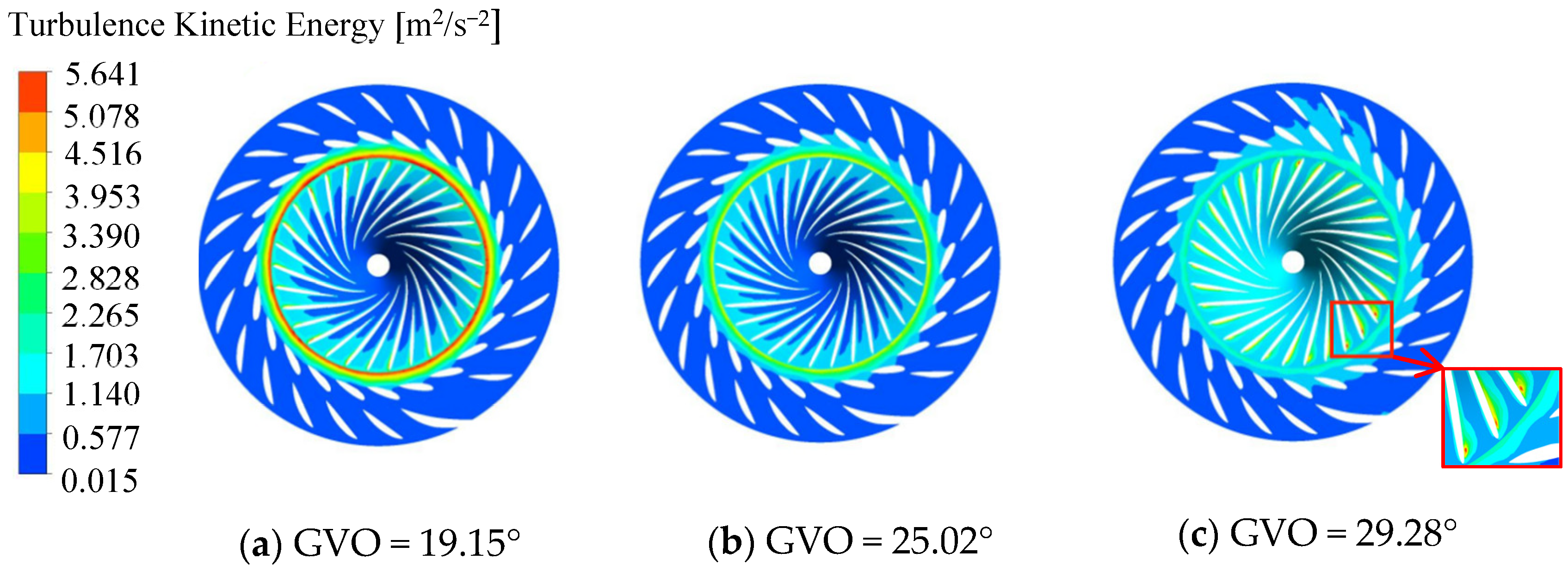
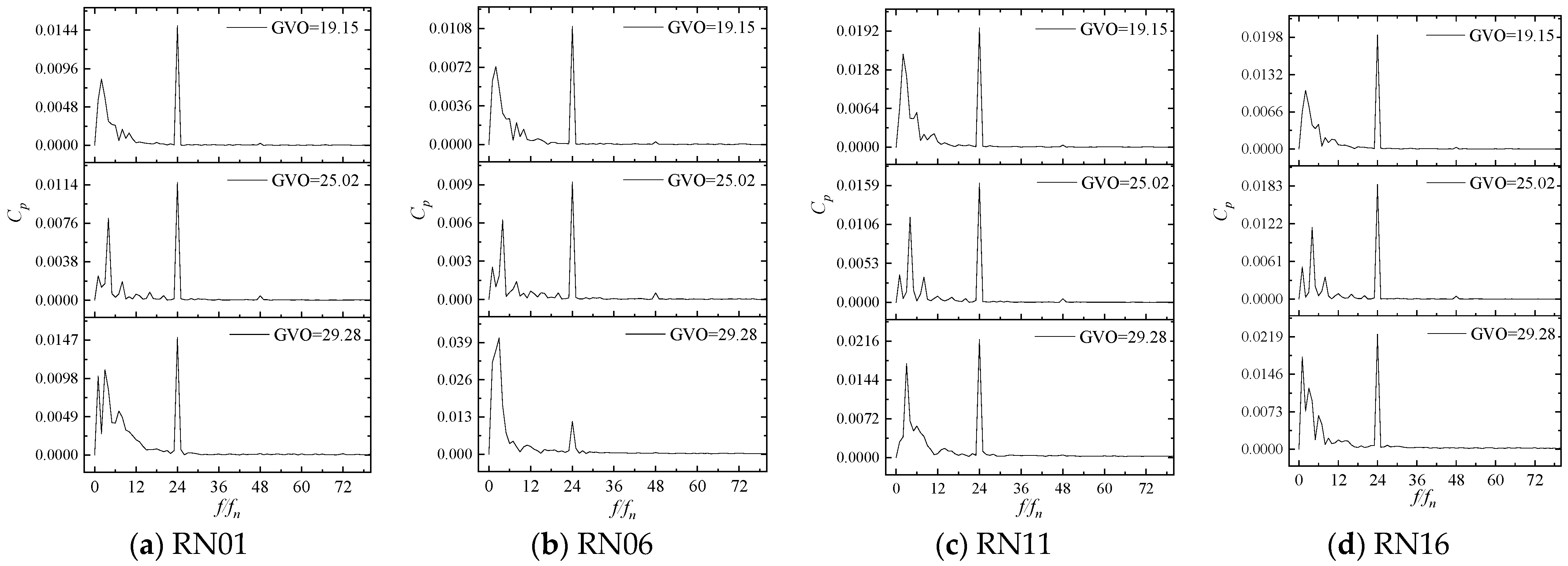
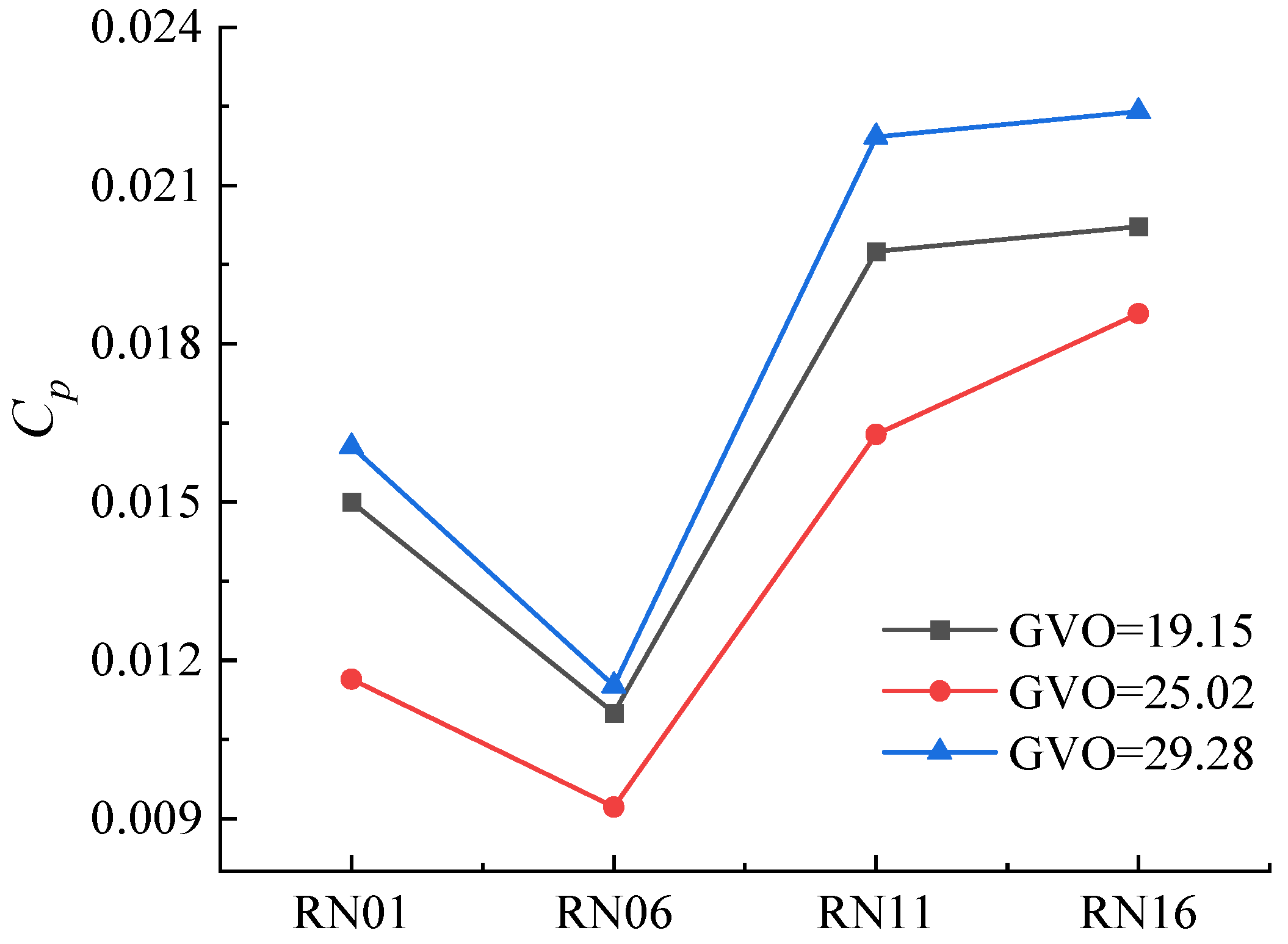
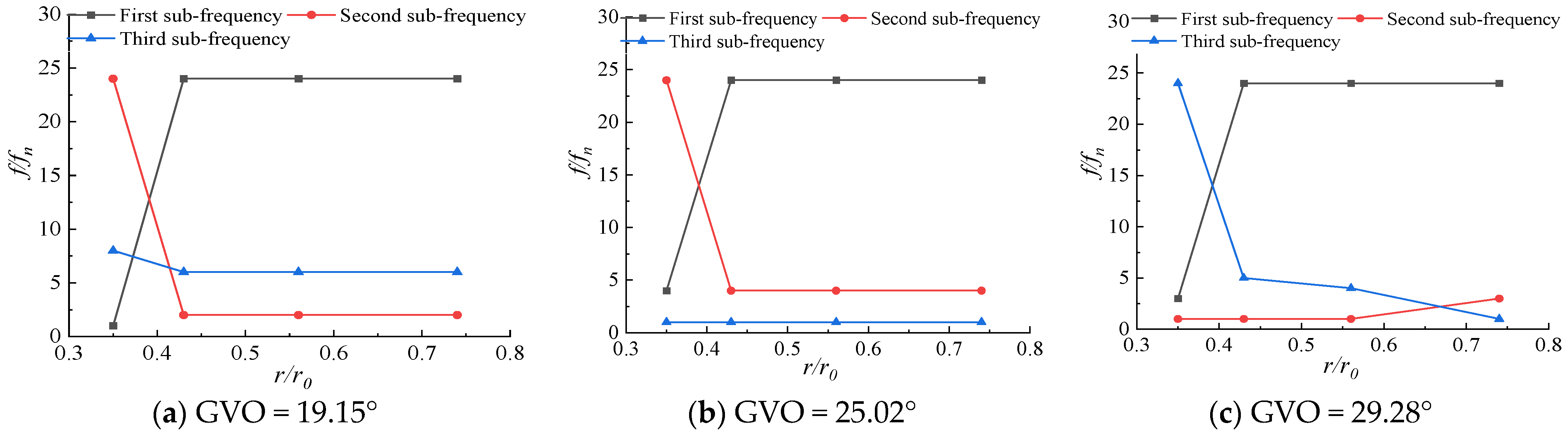
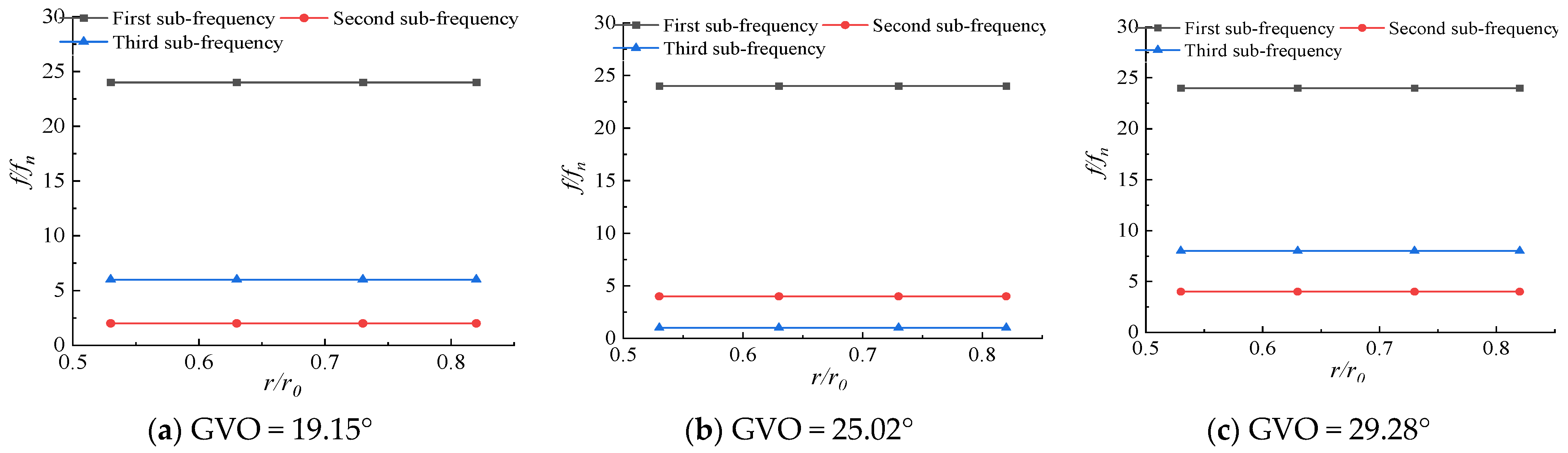
3.3. Pressure Pulsation in Runner at Different Opening Conditions
4. Conclusions
- The internal streamline of the long and short blade runner is uniform, and there is no obvious unstable flow, such as backflow and vortex. It can be seen that the long and short blades can change the inflow of the runner inlet and reduce the hydraulic loss. The dynamic and static interference between the guide vane and the runner induces the local high-speed flow mainly concentrated in the vaneless area. As the opening decreases, the dynamic and static interference at the vaneless area gradually becomes significant. The pressure on the pressure surface of the blade is significantly higher than that on the suction surface, and the pressure distribution gradient is more uniform, showing a gradual decrease from the runner inlet to the outlet.
- Under the condition of GVO = 19.15°, the vortex in the runner mainly appears near the suction surface and gradually evolves from the runner inlet to the outlet. Under the condition of GVO = 25.02°, there are few vortex areas, and the small vorticity vortex area evolves from the blade near the outlet to the blade passage area. Under the condition of GVO = 29.28°, due to the large impact between the incoming flow and the blade pressure surface, a large vorticity vortex area appears near the blade pressure surface, and the vortex evolves from the runner outlet area to the inlet.
- The first sub-frequency of pressure pulsation in the runner is basically 24fn, which corresponds to the frequency of dynamic and static interference. The amplitude of first sub-frequency at the GVO = 29.28° condition is the largest, and the dynamic and static interference is the most obvious. The pressure pulsation amplitude from the runner inlet to the outlet gradually decreases along the flow direction. As the distance from the runner inlet increases, the unstable flow gradually performs a leading role in the pressure pulsation.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, Q.X.; Song, G.Y.; Wu, S.Y. Technology innovation and quality control of manufacturing of the first million-unit long and short blade runner of Baihetan Hydropower Station. In Proceedings of the 2019 Annual Conference of the Chinese Hydraulic Engineering Society, Nanjing, China, 10–12 May 2019; China Water Resources and Hydropower Press: Beijing, China, 2019; Volume 1, pp. 533–537. [Google Scholar]
- Wang, H.M.; Qing, D.Q.; Wei, X.Z.; Zhao, Y.; Chen, Y.L. Research and development and progress of hydraulic engineering of long and short blade runners of Harbin electric Francis pump. Hydropower Pumped Storage 2016, 2, 38–43. [Google Scholar]
- Wang, Z.N.; Sun, L.G.; Guo, P.C. Analysis and suppression of blade passage vortex formation in Francis turbine. J. Hydroelectr. Power 2020, 39, 113–120. [Google Scholar]
- Gentner, C.; Stachle, M.; Sallaberger, M. Unsteady numerical analysis of pressure pulsations in the spiral casing and runner of a pump turbine. In Proceedings of the 21st IAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 9–12 September 2002. [Google Scholar]
- Jacquet, C.; Fortes-Patella, R.; Balarac, L.; Houdeline, J.B. CFD Investigation of Complex Phenomena in s-Shape Region of Reversible Pump-Turbine. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Grenoble, France, 4–8 July 2016; Volume 49. [Google Scholar]
- Zhang, W.; Chen, Z.; Zhu, B.; Zhang, F. Pressure fluctuation and flow instability in S-shaped region of a reversible pump-turbine. Renew. Energy 2020, 154, 826–840. [Google Scholar] [CrossRef]
- Braun, O.; Kueny, J.; Avellan, F. Numerical analysis of flow phenomena related to unstable energy—Discharge characteristic of a pump-turbine in pump mode. In Proceedings of the Fluids Engineering Division Summer Meeting, Houston, TX, USA, 19–23 June 2005; pp. 1075–1080. [Google Scholar]
- Lowys, P.Y.; Paquet, F.; Couston, M. Onboard measurements of pressure and strain pulsation in a model of low head Francis turbine-part 2: Measurements and preliminary analysis results. In Proceedings of the 21st IAHR Symposium on Hydraulic Machinery and Systems, Lausanne, Switzerland, 9–12 September 2002; pp. 873–880. [Google Scholar]
- Gohil, P.P.; Saini, R.P. CFD: Numerical analysis and performance prediction in Francis turbine. In Proceedings of the 2014 1st International Conference on Non Conventional Energy (ICONCE 2014), Kalyani, India, 16–17 January 2014. [Google Scholar]
- Kurosawa, S.; Lim, S.; Enomoto, Y. Virtual model test for a Francis turbine. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Canberra, Australia, 27–29 January 2010; Volume 12. [Google Scholar]
- Yang, J.; Peng, C.; Li, C.; Liu, X.; Liu, J.; Wang, Z. Design and verification of Francis turbine working in sand laden hydro-power plant. Renew. Energy 2023, 207, 40–46. [Google Scholar] [CrossRef]
- Tang, Q.; Yu, A.; Wang, Y.; Tang, Y.; Wang, Y. Numerical analysis of vorticity transport and energy dissipation of inner-blade vortex in Francis turbine. Renew. Energy 2023, 203, 634–648. [Google Scholar] [CrossRef]
- Murugesan, C.; Rudramoorthy, R. Numerical and experimental study of single stage and multistage centrifugal mixed flow submersible borewell pumps. Int. J. Fluid Mach. Syst. 2016, 9, 107–118. [Google Scholar] [CrossRef]
- Booth, C.P.; Leggoe, J.W.; Aman, Z.M. The Use of Computational Fluid Dynamics to Predict the Turbulent Dissipation Rate and Droplet Size in a Stirred Autoclave. Chem. Eng. Sci. 2019, 196, 433–443. [Google Scholar] [CrossRef]
- Khawar, R.; Ho, H.S. Influence of lateral flow contraction on bed shear stress estimation by using measured turbulent kinetic energy. Exp. Therm. Fluid Sci. 2022, 139, 110742. [Google Scholar]
- Li, P.; Jin, F.; Tao, R.; Zhang, F.; Xiao, R. Unsteady Simulation of the Internal Flow in a Tubular Pump Considering Tip-Leakage Flow. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Dhulikhel, Kavre, Nepal, 22–23 November 2021; Volume 1037. [Google Scholar]
- He, Q.L.; Huang, X.X.; Bi, H.L.; Yang, M.Q.; Yang, H.X.; Wang, Z.W. Draft Tube Vortex Rope Analysis of a Pump-turbine Unit under Different Operating Conditions. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Trondheim, Norway, 26 June–1 July 2022; Volume 1079. [Google Scholar]
- Skripkin, S.G.; Tsoy, M.A.; Kuibin, P.A.; Shtork, S.I. Aperiodic pressure pulsation under non optimal hydraulic turbine regimes at low swirl number. J. Phys. Conf. Ser. 2017, 899, 022016. [Google Scholar] [CrossRef]
- Miao, S.H.; Zhang, H.B.; Zhang, J.W.; Wang, X.H.; Shi, F.X. Unsteady flow characteristics of energy conversion in impeller of centrifugal pump as turbine. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2022, 236, 1502–1511. [Google Scholar] [CrossRef]
- Qian, C.; Yang, L.H.; Qi, Z.P.; Yang, C.X. Analysis of the axial force distribution characteristics of multistage pumps and its correlation with hydraulic property. Adv. Mech. Eng. 2022, 14, 16878132221130565. [Google Scholar]
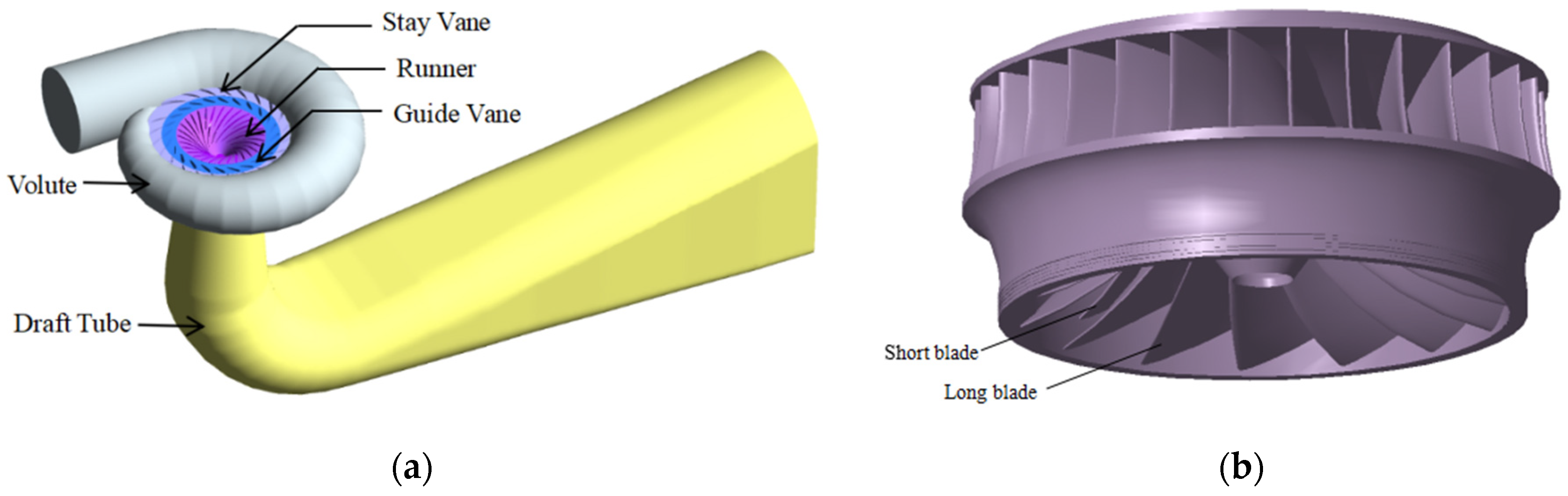







| Parameters | Value |
|---|---|
| Maximum head Hd, m | 243.1 |
| Rated head Hd, m | 202 |
| Rated rotational speed nd, r/min | 107.1 |
| Rated flow rate Qd, m3/s | 538.8 |
| Rated output Pd, MW | 1015 |
| Stay vane blade number, Z1 | 23 |
| Guide vane blade number, Z2 | 24 |
| Runner blade number, Z3 | 15 + 15 |
| Runner inlet diameter D1, mm | 8710 |
| Runner outlet diameter D2, mm | 7340 |
| Runner inlet width b1, mm | 1570 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Lu, Y.; Liu, K.; Zhang, Z.; Li, H.; Huang, X.; Zhao, W.; Wang, Z. Study on the Internal Flow Characteristics of Long and Short Blade Runners of a 1000 MW Francis Turbine under Different Opening Conditions. Processes 2023, 11, 1796. https://doi.org/10.3390/pr11061796
Chen H, Lu Y, Liu K, Zhang Z, Li H, Huang X, Zhao W, Wang Z. Study on the Internal Flow Characteristics of Long and Short Blade Runners of a 1000 MW Francis Turbine under Different Opening Conditions. Processes. 2023; 11(6):1796. https://doi.org/10.3390/pr11061796
Chicago/Turabian StyleChen, Hao, Yonggang Lu, Kui Liu, Zequan Zhang, Honghui Li, Xingxing Huang, Weiqiang Zhao, and Zhengwei Wang. 2023. "Study on the Internal Flow Characteristics of Long and Short Blade Runners of a 1000 MW Francis Turbine under Different Opening Conditions" Processes 11, no. 6: 1796. https://doi.org/10.3390/pr11061796
APA StyleChen, H., Lu, Y., Liu, K., Zhang, Z., Li, H., Huang, X., Zhao, W., & Wang, Z. (2023). Study on the Internal Flow Characteristics of Long and Short Blade Runners of a 1000 MW Francis Turbine under Different Opening Conditions. Processes, 11(6), 1796. https://doi.org/10.3390/pr11061796










