Performance Evaluation of Ingenious Crow Search Optimization Algorithm for Protein Structure Prediction

Abstract

Protein structure prediction is one of the important aspects while dealing with critical diseases. An early prediction of protein folding helps in clinical diagnosis. In recent years, applications of metaheuristic algorithms have been substantially increased due to the fact that this problem is computationally complex and time-consuming. Metaheuristics are proven to be an adequate tool for dealing with complex problems with higher computational efficiency than conventional tools. The work presented in this paper is the development and testing of the Ingenious Crow Search Algorithm (ICSA). First, the algorithm is tested on standard mathematical functions with known properties. Then, the application of newly developed ICSA is explored on protein structure prediction. The efficacy of this algorithm is tested on a bench of artificial proteins and real proteins of medium length. The comparative analysis of the optimization performance is carried out with some of the leading variants of the crow search algorithm (CSA). The statistical comparison of the results shows the supremacy of the ICSA for almost all protein sequences.

1. Introduction

Proteins are one of the essential macromolecules of human organisms. Due to their complicated structure and importance in bioinformatics, protein structure prediction attracts diverse researchers. Proteins are combinations of different types of chains of amino acids and can fold into various states. These folding structures are known as 3D structures of protein and play different important roles, including as catalysts in various reactions, as structural units, in the reporting of signals and as transport channels in living organisms. Understanding the 3D structure is also helpful in treating various diseases, such as Alzheimer’s disease and cystic fibrosis.

The basic methods of detecting protein structure are X-ray crystallography and NMR spectroscopy. However, these methods require an excessive amount of money and time and, hence, are less adopted. The prediction of protein structure via the relation between the linear sequence of amino acids and the protein’s 3D structure was conducted in [1,2]. In later years, the prediction of protein structure based on the fact that the most stable folding of protein is one which has minimum free energy [2,3,4,5]. In mathematical terms, the free energy reflects different types of bonding between protein molecules, such as hydrophilic, solvent, hydrogen and entropic effects. As this function is nonconvex, protein structure prediction can be considered a global optimization problem. This prediction method is performed in two stages: firstly, a physical form of protein is assumed, and secondly, the energy function is calculated through any optimization algorithm. The HP model [3] and AB-off lattice model [4] are two physical models widely used for the first stage. Recently, protein structure prediction has been converted into an optimization problem from a bioinformatics problem and has been solved using various nature-inspired algorithms [5,6,7,8].

An algorithm selection process based on fitness landscape is presented in [5]. The artificial bee colony (ABC) algorithm and its different improved versions have been applied to this protein folding structure problem [6,7,8] and prove that metaheuristic approaches are good alternative ways of solving this np-hard optimization problem. Different variants of the DE algorithm were applied to PSP in [9,10,11]. Along with this, the list of successful metaheuristic algorithms applied to PSP also includes the improved harmony search [12], gradient gravitational search algorithm [13], particle search algorithm [14], ant colony algorithm [15], genetic tabu search [16], an adaptive differential evolution algorithm [17], chaotic grasshopper algorithm [18] and many more. This literature review indicates the importance of the protein structure problem and also promotes the fact that other newly developed algorithms can be applied to discover some new results. Recently, algorithms inspired by nature and animal behavior have revolutionized the world with their problem-solving capabilities [5,6,7,8]. The crow search algorithm is one of them and has been successfully applied to many problems, such as the frequency modulation synthesis problem, model order reduction and other design problems [19]. Furthermore, some recent applications and facts reported in references [20,21,22,23,24] motivated the authors to conduct detailed investigations of the development of new bridging in existing CSA. Some interesting approaches regarding the integration of neural networks and real-life problems, such as bidding strategy planning and response prediction, have been demonstrated very prominently in references [25,26,27]. Similarly, a deep-learning-based approach was employed for protein structure prediction in reference [28]. Likewise, the gradient-based gravitational search algorithm has been employed for conformational searches of the basic building blocks of proteins [29]. In reference [30], the identification of essential proteins using chemical reaction optimization and machine learning has been performed. Inspired by these possibilities, we propose an ingenious crow search algorithm (ICSA) to solve the aforementioned protein folding problem. This work is an extension of the work reported previously by the authors as we change the cosine function with the exponential function. The following are the main contributions of this manuscript:

• The protein folding problem has been discussed, and the problem is formulated by keeping the AB-off lattice model in consideration.
• An application of the newly proposed ICSA has been explored on a predefined bench of mathematical functions and proteins, and evaluation of the algorithm has been conducted.
• A meaningful comparison between the performance of various crow search variants and crow search itself has been conducted on the basis of statistical attribute analysis, box plot analysis and execution time analysis.

The remaining part of the paper is organized into several sections: Section 2 presents the problem formulation of protein structure prediction with energy minimization. Section 3 depicts the development steps of the ICSA and the basic details of the implemented algorithm. Section 4 presents the results of the simulation on the conventional benchmark functions and protein benches. Section 5 concludes the research work in this paper with suggestions for the future direction of research work.

2. Problem Formulation

In this paper, we have used the AB-off lattice model, which is a generalized form of the HP model. According to this model, particles are connected to each other with chemical bonds of unit length and then fold into a 3D structure. The model which possesses the lowest energy is the most stable among all possible structures. This energy is formed by two types of interactions: one is intermolecular (between protein and other solvent molecules) and the other is intramolecular (between any two protein molecules). In this way, the AB-off lattice model considers atomic interactions in calculating energy function, which are left over in the HP model. Instead of 20 different types of amino acids, this model only considers two residues named A (hydrophobic) and B (hydrophilic). Any protein sequence of length r consists of total (r − 2) bend angles ${\varphi }_2, {\varphi }_3,\dots ,{\varphi }_{r-1}.$ A bend angle is an angle between any two amino acids, whose direction can be random, i.e., clockwise as well as anticlockwise. The energy and other terms of the protein structure problem can be mathematically given by the following equations:

$$E={\displaystyle \sum _{i=2}^{r-1}\frac{\left(1-\cos {\varphi }_i\right)}{4}}+4{\displaystyle \sum _{i=1}^{r-2}{\displaystyle \sum _{j=i+2}^r\left[d_{ij}^{-12}-I\left({\tau }_i,{\tau }_j\right)d_{ij}^{-6}\right]}}$$

(1)

$$d_{ij}=\sqrt{{\left[1+{\displaystyle \sum _{k=i+1}^{j-1}\cos \left({\displaystyle \sum _{l=i+1}^k{\varphi }_l}\right)}\right]}^2+{\left[{\displaystyle \sum _{k=i+1}^{j-1}\sin \left({\displaystyle \sum _{l=i+1}^k{\varphi }_l}\right)}\right]}^2}$$

(2)

$$I\left({\tau }_i,{\tau }_j\right)=\frac{1}{8}\left[1+{\tau }_i+{\tau }_j+5{\tau }_i{\tau }_j\right]$$

(3)

where E is the energy function to be minimized, and $d_{ij}$ is the corresponding distance between residue i and j. $I\left({\tau }_i,{\tau }_j\right)$ is the value representing the bonding between residues, such as for the AA bond $I\left({\tau }_i,{\tau }_j\right)=1$, for the BB bond $I\left({\tau }_i,{\tau }_j\right)=0.5$ and for the AB or BA bonds $I\left({\tau }_i,{\tau }_j\right)=-0.5$.

3. Ingenious Crow Search Algorithm

The crow is considered as a genius bird among other species. The study in [20] shows that its brain size is bigger in comparison to other birds of its size. A crow shows its superior behavior in hiding and stealing its food, mimicking voices and in the mirror test. Crows live in a flock and present a natural example of the optimization process in searching for food, hiding it from others and following each other to know the location of food. Askarzadeh proposed the crow search algorithm (CSA) inspired by these characteristics, which became very popular due to its simple structure and a smaller number of parameters. Many researchers presented improved variants of CSA and applied them to solve real engineering problems [19,22,24]. Authors proposed chaotic variants of CSA to solve the feature selection problem in [21]. A modified version of CSA has been applied in [22] to solve the economic load dispatch problem. In [23], the authors employ improved crow search algorithm (ImCSA) for energy problems. The best selection of conductors in a radial distribution network has been addressed in [24]. In [19], the authors present an intelligent CSA inculcating two modifications in CSA, namely opposition-based learning and the cosine position updation rule. The proposed variant has also been verified in some real engineering problems, such as model order reduction and structural design problems. Furthermore, an exponential function-based mechanism is introduced in this version to make it the exponential function-based ingenious crow search algorithm (ICSA):

• The first is opposition-based learning, which is used in the initialization phase, when the crows generate their positions. Out of the total crows, half of the crows generate their position randomly, and the remaining half generate it according to the following definition.

Definition 1:

Let $z=\left(z_1,z_2,\dots ,z_r\right)$ is a point in a space of R dimensions where $z_i$ is a real number for $i\in \left\{1,2,\dots ,r\right\}$ and $i\in \left[a,b\right]$ then opposite points set of z is given as $\overline{z}=\left({\overline{z}}_1,{\overline{z}}_2,\dots ,{\overline{z}}_r\right)$ or we can also write

$${\overline{z}}_i=\left[a_i+b_i-z_i\right]$$

(4)

2.

The second modification is an acceleration factor based on exponential function, which acts as a bridging mechanism between the exploration and exploitation stages of the optimization process. In comparison with a linear function, a cosine function provides better results as it has a high gradient in the exploration stage, which means that it explores a bigger area which helps in finding the solution. Later on, when the gradient is low, the area shrunk during the second half and led to the avoidance of local minima trapping. This acceleration factor can be given mathematically as

$$AF=1-\exp (t/T)$$

(5)

Let us consider the total number of crows in a flock as N, and the location of hidden food is given by $H_i^j$, which is considered as the best position of crow i, for $i=\left\{1,\dots ,N\right\}$. $U_i^j$ is the ith crow position at jth iteration. Initially, half of the population of crows generates their position randomly and the other half by Equation (4). Suppose a crow i follows crow y at iteration j, then two cases are possible: either crow y knows that crow i is following it and it tries to fool it by changing its position swiftly or crow y does not know that it is being followed. These two cases inculcated with the abovementioned modifications can be represented mathematically as

$$U_i^{j+1}=\{\begin{array}{c}{U}_i^j+\left(AF\right)R_i{L}_i\left(H_i^j-U_i^j\right) if R_i\ge A{P}^{i,j}\\ a random number otherwise\end{array}$$

(6)

where $L_i=$ flight length of ith crow, $R_i=$ a random number such that $R_i=\left[0,1\right]$, and $A{P}^{i,j}=$ awareness probability of the crow, which helps to create a balance between the exploitation and exploration stages.

In every iteration, the crow updates the location of its food by the following equation:

$$H_i^{j+1}=\{\begin{array}{c}{U}_i^{j+1} ,\hspace{1em}\hspace{1em}\hspace{1em}fn\left(U_i^{j+1}\right) is better than fn\left(H_i^j\right)\\ \hspace{1em}\hspace{1em}{H}_i^j\hspace{1em}\hspace{1em}\hspace{1em}otherwise\end{array}$$

(7)

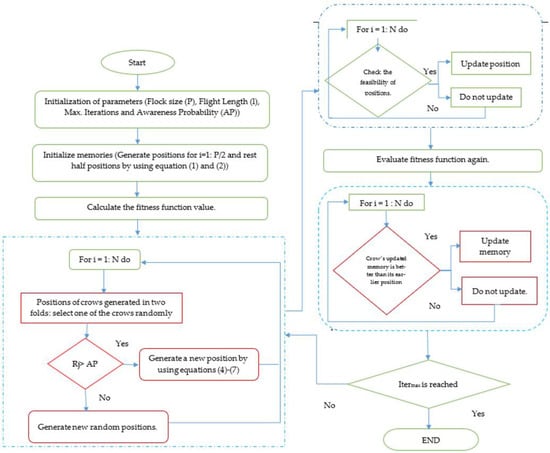
For the easy understanding of readers, a flow chart of the ICSA [19] is given in Figure 1.

Figure 1. Flow chart of the ingenious crow search algorithm.

Furthermore, the implementation details of the ICSA have been depicted in the following algorithm.

• For implementing any real-life optimization problem, the designer requires the identification of variable composition. In this structure prediction problem, we have to calculate the dimension of the variables as per the sequence length. Hence, the dimension of the solution string is calculated as per size of the sequence.
• As it is a known fact that the folding can be conducted between [−180,180], the upper and lower bounds of the variables have been assigned as per these boundary conditions. From this, it can be observed that the initialization of the number of crows along with their research directions can be finalized with the help of sequence size and range of bend angles.
• For further implementation of the algorithm, the energy function has been evaluated with every iteration of the ICSA, and the values of memory as well fitness function are stacked in an array. Then, the optimal values are retained, and further processing in order to improve the solution quality has been started with the help of the position update equation.

Furthermore, as per the stopping criterion of the ICSA, this process is stopped, and optimal values of energy function and corresponding angle values are stored.

4. Simulation and Results

For proving the efficacy of the proposed ICSA, a detailed investigation has been conducted in this section. First, the performance is evaluated for some standard functions, and then, the performance is evaluated for some artificial protein benches for the determination of the optimal structure.

4.1. Evaluation of ICSA on Conventional Benchmark Functions

Table 1 shows the diverse characteristics of various functions, along with dimensions and bounds. From this table, it is observed that the functions used in this experimentation have two characteristics, i.e., unimodal (with one minima) and multimodal (with multiple minima, including global and local), and possess complex landscapes. For the evaluation of the exploration and exploitation virtues, both of these landscape evaluations are required.

Table 1. Definition of standard benchmark functions.

Function	Dim	Range	Min. Value
$F_1(x)={\displaystyle \sum _{i=1}^n}{x}_i^2$	30	[−100,100]	0
$F_2(x)={\displaystyle \sum _{i=1}^n}\left|x_i\right|+{\displaystyle \prod _{i=1}^n}\left|x_i\right|$	30	[−10,10]	0
$F_3(x)={\displaystyle \sum _{i=1}^n}({\displaystyle \sum _{j-1}^i}{x}_j{)}^2$	30	[−100,100]	0
$F_4(x)={\mathit{max}}_i\{\left|x_i\right|,1\le i\le n\}$	30	[−100,100]	0
$F_5(x)={\displaystyle \sum _{i=1}^{n-1}}[100(x_{i+1}-x_i^2{)}^2+(x_i-1{)}^2]$	30	[−30,30]	0
$F_6(x)={\displaystyle \sum _{i=1}^{n-1}}(x_i+0.5{)}^2$	30	[−100,100]	0
$F_7(x)={\displaystyle \sum _{i=1}^{n-1}}i{x}_i^4+random\left[\mathrm{0,1}\right]$	30	[−1.28,1.28]	0
$F_8(x)={\displaystyle \sum _{i=1}^n}-x_i\mathit{sin}(\sqrt{\left|x_i\right|})$	30	[−500,500]	−418.9829 × 5
$F_9(x)={\displaystyle \sum _{i=1}^n}[x_i^2-10\mathit{cos}(2\pi x_i+10)]$	30	[−5.12,5.12]	0
$\begin{array}{cc}\hfill F_{10}(x)=-20\mathit{exp}(& -0.2\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{x}_i^2})\hfill \\ & -\mathit{exp}(\frac{1}{n}{\displaystyle \sum _{i=1}^n}\mathit{cos}(2\pi x_i))+20\hfill \\ & +e\hfill \end{array}$	30	[−32,32]	0
$F_{11}(x)=\frac{1}{4000}{\displaystyle \sum _{i=1}^n}{x}_i^2-{\displaystyle \prod _{i=1}^n}\mathit{cos}(\frac{x_i}{\sqrt{i}})+1$	30	[−600,600]	0
$$\begin{gathered} F_{12}(x)=\frac{\pi }{n}\left\{10\mathit{sin}(\pi y_i)+{\sum }_{i=1}^{n-1}(y_i-1{)}^2[1+ \\ 10{\mathit{sin}}^2(\pi y_{i+1})+(y_n-1{)}^2]\right\}+ \\ {\sum }_{i=1}^{n}u\left(x_i,\mathrm{10,100,4}\right)y_i=1+\frac{x_{i+1}}{4} \end{gathered}$$ $u\left({\mathrm{x}}_i,\mathrm{a},\mathrm{k},\mathrm{m}\right)=\left\{\begin{array}{cc}k{\left({\mathrm{x}}_i-\mathrm{a}\right)}^m& x>a\\ 0& -a<x_i<a\\ k{\left(-x_i-a\right)}^m& x_i-a\end{array}\right\}$	30	[−50,50]	0

As we know, metaheuristics are based on the generation of random numbers in between the bounds for given variables, and they explore the search space in a very effective manner; hence, the results obtained from these algorithms always differ from run to run. Hence, for reporting the results of these algorithms, statistical attribute depiction is acutely required. Hence, in this experimentation, our aim is to run various improved versions of the crow search algorithm along with the proposed one and conduct the evaluation of the optimization properties on the basis of statistical attribute depiction. The following attributes are chosen for depiction of the optimization results.

• Mean of the fitness values obtained from 20 independent runs.
• Maximum fitness values obtained from 20 independent runs (Worst value as minimization is performed).
• Minimum fitness values obtained from 20 independent runs (Best value as minimization is performed).
• Standard Deviation of the fitness values obtained from 20 independent runs.

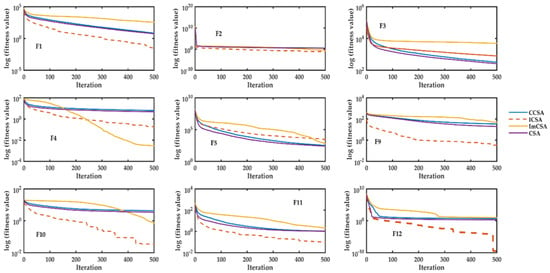
Some of the crow search variants have been taken in the analysis, in this experimentation all optimization algorithms are run for minimization purpose. For the optimization environment, search agent no. (30), maximum iteration (500) and total no. of independent runs (20) are kept constant for all the algorithms. Figure 2 shows the convergence property analysis of these algorithms. It can be observed from these plots that with the exponential modification, the convergence of the ICSA is higher as compared to the parent algorithm and other prominent variants of the CSA.

Figure 2. Convergence characteristics of conventional benchmark functions.

The results of the statistics attribute analysis have been showcased in Table 2. The following points are observed from this analysis.

Table 2. Statistical attribute analysis on conventional benchmark functions.

Function	Parameter	CCSA [21]	ICSA	ImCSA [23]	CSA	Function	Parameter	CCSA [21]	ICSA	ImCSA [23]	CSA
F1	Mean	6.862046	0.031499	371.7069	5.606232	F7	Mean	0.058742	0.058667	0.00209	0.031414
	Max	13.02088	0.603666	2978.315	12.38207		Max	0.098207	0.109524	0.006988	0.074844
	Min	2.310426	1.68E−08	2.01E−06	1.688793		Min	0.023507	0.021947	7.16E−05	0.003457
	SD	3.340716	0.134802	806.7395	2.928814		SD	0.020186	0.025329	0.001671	0.017421
F2	Mean	3.170929	0.068385	0.286378	2.62875	F8	Mean	−6709.28	−3805.25	−4814.16	−6657.98
	Max	4.810244	0.575082	3.658114	3.987891		Max	−5012.01	−3140.88	−2626.53	−5498.49
	Min	1.405213	4.61E−05	0.00042	1.515934		Min	−8371.41	−4417.09	−9016.28	−7919.51
	SD	0.910725	0.173323	0.844995	0.740529		SD	907.5612	453.158	2107.081	650.6592
F3	Mean	323.0571	797.5047	5011.694	260.3749	F9	Mean	33.98402	0.340106	48.68747	19.87135
	Max	531.1665	1733.91	10026.44	541.7801		Max	54.01139	4.837234	158.7266	40.31614
	Min	196.5237	256.5388	649.7462	77.18435		Min	19.8377	8.43E−09	0.000102	0.500648
	SD	99.44027	408.3196	2623.501	122.8966		SD	10.06463	1.113659	48.36721	9.957675
F4	Mean	6.308253	0.188467	0.002976	4.844995	F10	Mean	4.300276	0.033443	0.720454	3.476109
	Max	8.140264	1.737154	0.018445	7.114288		Max	7.323363	0.621233	9.006787	4.978548
	Min	3.981577	7.91E−05	8.24E−05	1.400564		Min	2.893833	2.89E−05	0.002134	1.547676
	SD	1.160448	0.482095	0.004275	1.564157		SD	1.218795	0.138743	2.051522	0.861077
F5	Mean	324.046	2903.36	642.9959	247.6814	F11	Mean	1.076878	0.097822	2.082308	1.032996
	Max	555.5641	12040.52	5802.284	638.3758		Max	1.138195	0.52547	8.259849	1.08654
	Min	188.2174	271.7245	28.7011	28.65027		Min	1.024521	0.007396	1.68E−06	0.938069
	SD	89.8575	3460.403	1538.028	127.9758		SD	0.033668	0.14415	2.304979	0.045092
F6	Mean	8.512082	0.180113	242.2761	5.755481	F12	Mean	4.95529	3.21E−10	10.17759	2.026635
	Max	18.40242	1.703808	1797.644	13.4591		Max	10.47527	1.97E−09	19.87467	4.821795
	Min	3.876712	2.59E−08	2.48E−06	1.820985		Min	1.112488	4.59E−11	5.52E−06	0.161102
	SD	3.538109	0.412308	465.7808	2.824979		SD	2.547375	4.63E−10	5.21975	1.325975

• From this table, it has been observed that for unimodal functions (F1–F7), the ICSA is performs well and the proposed exponential function-based mechanism helps the algorithm in convergence. Unimodal functions are those functions that possess only one minimum in a given search space. Hence, it can be concluded that the proposed exponential-driven mechanism helps the algorithm to find the minima very efficiently and helps the algorithm in convergence.
• In addition, in a few of multimodal functions, such as F8 to F12, the performance is not compromised. Hence, it can be observed that the exploration and exploitation virtues of the ICSA have been enhanced with the inculcation of opposition-based learning and the proposed exponential-driven function. The results of standard deviation and their optimal values for the ICSA have been showcased in boldface and depict the superior quality of the optimization by the proposed ICSA. The proposed mechanisms help the ICSA to avoid local minima stagnation and provide a big leap in the position updation phase (due to exponential function).

4.2. Application of ICSA to Protein Structure Prediction

In this section, simulation and the results of the ICSA are discussed in relation to the protein bench, showcased in the previous subsection. In reference, it has already been shown by the authors in the previous subsection that the ICSA outperforms the original CSA and some of the leading variants of CSA on standard benchmark functions. Furthermore, to test the efficacy of the algorithm, benches of protein are considered here. The characteristics of these protein benches are shown in Table 3.

Table 3. Evaluation bench for PSP problem.

S. No.	Name	Length	Sequence
1	Asm1	4	ABAB
2	Asm2	4	AAAA
3	As1	5	AAAAB
4	As2	5	AAAAA
5	Am1	13	ABBABBABABBAB
6	Am2	17	ABABBAABBBAAABABA
7	Rs1 (1BXP)	13	ABBBBBBABBBAB

A. Statistical Attribute Analysis (SAA)

As we know that metaheuristics instill some degree of uncertainty in producing the results of the optimization process, it is an established practice to report the results in terms of mean values, maximum values, minimum values and standard deviation values of independent runs. To adhere to the same practice, these statistical attributes are exhibited in Table 4.

• The results depicted in Table 3 are calculated by taking 20 independent runs into consideration. To make the competition fair, the maximum no. of function evaluations has been kept constant for all participating algorithms. The following points can be observed from these results:
• The bench of protein is divided into three major parts, namely very small, small and medium length. Along with this, a real sequence has also been considered. From the observation table, we can conclude that the algorithms gave almost the same values of free energy for Asm1 and Asm2 when compared; however, the values of standard deviation of the results are optimal for the ICSA. These results are depicted in boldface.
• Inspecting the values of mean As1 and As2, it can be clearly observed that these values are optimal for the ICSA. Along with this fact, in As2, standard deviation is also optimal. These results are considered as affirmative, and it can be concluded that the ICSA works well for these proteins.

Table 4. Statistical attribute analysis.

PS	SA	CSA	CCSA	ImCSA	ICSA
Asm1	Mean	−0.64938	−0.64876	−0.64935	−0.64938
	Minimum	−0.64938	−0.64934	−0.64938	−0.64938
	Maximum	−0.64938	−0.64628	−0.64885	−0.64938
	Standard Deviation	1.99E−16	0.000693	0.000117	1.92E−16
Asm2	Mean	−1.67633	−1.67219	−1.67178	−1.67633
	Minimum	−1.67633	−1.67597	−1.67633	−1.67633
	Maximum	−1.67633	−1.66024	−1.58531	−1.67633
	Standard Deviation	4.86E−16	0.004327	0.020352	4.61E−16
As1	Mean	−1.57712	−1.51277	−1.54829	−1.57822
	Minimum	−1.58944	−1.57024	−1.58944	−1.58944
	Maximum	−1.4772	−1.46993	−1.32764	−1.4772
	Standard Deviation	0.034475	0.028738	0.071696	0.034547
As2	Mean	−2.76032	−2.71044	−2.78057	−2.80884
	Minimum	−2.84828	−2.83731	−2.84828	−2.84828
	Maximum	−2.46639	−2.59715	−2.45111	−2.46639
	Standard Deviation	0.112435	0.063695	0.093985	0.090723
Am1	Mean	−0.76309	0.284905	−0.6902	−1.11339
	Minimum	−2.1577	−0.14584	−1.56744	−1.69817
	Maximum	−0.01221	0.589463	−0.01221	−0.40284
	Standard Deviation	0.664084	0.250181	0.504168	0.522875
Am2	Mean	−2.987	0.90737	−2.58315	−3.23951
	Minimum	−4.61511	0.030558	−4.52953	−4.99724
	Maximum	−1.19216	1.910105	−0.79697	−1.15554
	Standard Deviation	1.107474	0.482412	1.029253	1.064372
Rs1	Mean	−0.6866	0.204919	−0.7064	−0.94874
	Minimum	−1.62337	−0.0458	−1.45093	−1.68243
	Maximum	−0.09148	0.432196	−0.09148	−0.09148
	Standard Deviation	0.480141	0.145814	0.475126	0.577632

On further inspection, for the medium-size and real protein sequence, we have observed that the mean values are optimal in case of the ICSA, and the algorithm shows promising results. Hence, it can be concluded that acceleration factor-driven bridging and opposition-based learning substantially enhance the performance of the algorithm.

B. Iterative Time Analysis (ITA)

It is a known fact that the execution time of the algorithm is quite important while dealing with complex engineering problems. Unlike classical problems, protein structure prediction is a complex problem, and the execution time for the identification of protein structure is an essential requirement to judge the performance of the algorithm. Taking this fact into consideration, the execution times for independent runs have been calculated, and mean values for the algorithms are depicted in Table 5.

Table 5. Iterative Time Analysis.

PS	CSA	CCSA	ImCSA	ICSA
Asm1	0.001632	0.002855	0.008275	0.001577
Asm2	0.001651	0.002378	0.008295	0.001604
As1	0.00268	0.00323	0.009296	0.0026
As2	0.00274	0.003219	0.009372	0.002648
Am1	0.040414	0.040534	0.047735	0.040257
Am2	0.086517	0.087693	0.093003	0.086233
Rs1	0.040848	0.041592	0.047092	0.040451

By inspecting the values of mean execution time, it can be easily concluded that the ICSA gives fast and optimal results. The execution time for different protein sequences is optimal for the ICSA and depicted in boldface in Table 5.

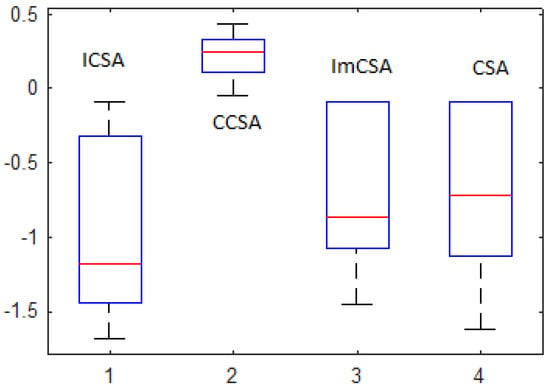
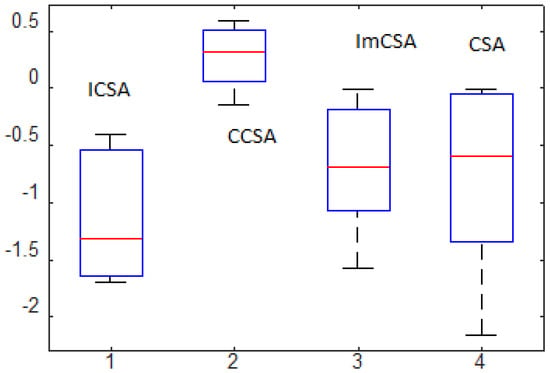
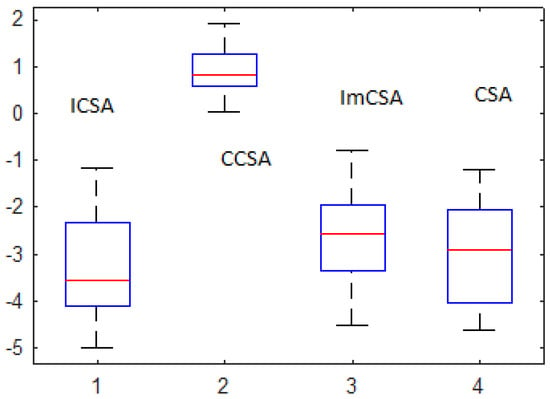
C. Box Plot Analysis (BPA)

To compare the optimization performance of the competitors, BPA is also conducted. Diagrams are plotted for the Am1, Am2 and Rs1 sequences. These are depicted in Figure 3, Figure 4 and Figure 5. From these, one can observe that the mean values are optimal and the interquartile range of the ICSA is satisfactory as compared to other participating algorithms. From this analysis, the supremacy of the proposed variant over the CSA and other variants is confirmed.

Figure 3. BPA for Rs1.

Figure 4. BPA for Am1.

Figure 5. BPA for Am2.

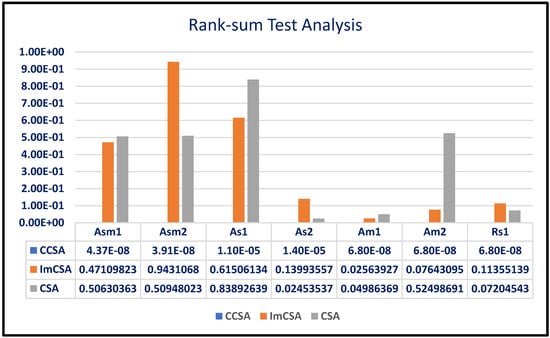
D. Rank-sum Test Analysis

Figure 6 shows rank-sum test analysis results in terms of p-values to compare the ICSA with competitors. The Wilcoxon rank-sum test is conducted to find the statistical significance of the algorithm as compared to other as metaheuristics instill uncertainty in producing results.

Figure 6. Rank-sum Test Analysis.

From the figure, it can be seen that the CCSA is totally different from the ICSA as the p-values associated with this comparison are less than 0.05 for all the sequences. It is also worth mentioning here that a significance difference exists between the CSA for some of the sequences. However, in the case of the ImCSA, the performance of ICSA is comparable with ImCSA.

E. Extended Experiments on Real Protein Sequences

To extend the analysis of the proposed algorithm, we tested the algorithm for prediction of the structure of the following real proteins. The details of these proteins are shown in Table 6; these are taken from [31], and more details are available at Protein Data Bank (PDB, http://www.rcsb.org/pdb/home/home.do, the access date 15 April 2023) [32].

Table 6. Bench of real proteins.

S.No.	Nomenclature of Protein [31] (Length of Sequence)	Sequence Considered
RP-1.	2ZNF (18)	ABABBAABBABAABBABA
RP-2.	1CB3 (13)	BABBBAABBAAAB
RP-3.	1BX1 (16)	ABAABBAAAAABBABB
RP-4.	1EDP (17)	ABABBAABBBAABBABA
RP-5.	1EDN (21)	ABABBAABBBAABBABABAAB
RP-6.	1SP7 (24)	AAAAAAAABAAABAABBAAAABBB
RP-7.	2H3S (25)	AABBAABBBBBABBBABAABBBBBB
RP-8.	1FYG (25)	ABAAABAABBAABBAABABABBABA
RP-9.	1T2Y (25)	ABAAABAABBABAABAABABBAABB
RP-10.	2KPA (26)	ABABABBBAAAABBBBABABBBBBBA
RP-11.	1ARE (29)	BBBAABAABBABABBBAABBBBBBBBBBB
RP-12.	1K48 (29)	BAAAAAABBAAAABABBAAABABBAAABB

For evaluating the performance of the ICSA, statistical attributes (SA), such as mean, maximum, minimum and standard deviation, of the fitness function over 29 independent runs are reported in Table 7. The optimal values of the fitness function mean have been shown in boldface in the table. It is observed that the fitness values of the proposed ICSA are optimal for many proteins. Since the mean value of the optimization run is an important parameter to depict the algorithm performance, this has been chosen to showcase the efficacy of the ICSA. It is worth mentioning here that while dealing with long-length protein sequences, the algorithm showed sluggish behavior and took more time for convergence. Hence, a convergence improvement scheme may be employed in the future.

Table 7. Evaluation of ICSA on real protein bench.

Sequence	SA	CSA	CCSA	ImCSA	ICSA	Sequence	SA	CSA	CCSA	ImCSA	ICSA
RP-1	Mean	−2.3791931	−0.7886972	−1.7198855	−2.4001344	RP-7	Mean	−1.3065694	−0.3117043	−0.5407107	−1.4724554
	Max	0.0267368	0.2064326	−0.6176313	0.0267386		Max	0.0064462	0.4984838	0.0063101	0.0063656
	Min	−5.0663166	−2.6839571	−3.4270418	−4.3176683		Min	−3.5274819	−1.7353797	−2.0208762	−2.8963254
	SD	1.3375592	0.855751	0.7766258	1.2731138		SD	1.3601746	0.7018831	0.6578956	1.0617478
RP-2	Mean	−0.9197507	−0.1272179	−0.5434708	−1.1124384	RP-8	Mean	−3.6225088	−2.2060117	−2.5448055	−3.6272946
	Max	0.1393805	0.235523	0.1393802	0.1393803		Max	−0.5703019	−1.1118433	−1.554185	−1.1893901
	Min	−3.1515092	−1.7230257	−2.9664274	−3.027823		Min	−5.730837	−3.6879032	−3.6678783	−5.5395026
	SD	1.2288456	0.457233	0.938032	1.1736009		SD	1.1702585	0.8962653	0.6790631	1.5134546
RP-3	Mean	−4.061345	−2.0771745	−2.6960923	−4.073643	RP-9	Mean	−3.9554999	−1.5579017	−1.9065653	−3.9567796
	Max	−1.3752103	−0.9003451	−1.010259	−2.391513		Max	0.0042479	0.5740143	0.0039736	0.0040509
	Min	−6.2571965	−3.4880659	−6.3372388	−5.9779379		Min	−6.7932439	−3.7696626	−5.0893686	−6.1911524
	SD	1.3004085	0.7643066	1.2378757	0.881331		SD	1.5168258	1.3738249	1.0519291	1.6046706
RP-4	Mean	−1.6090671	−0.3213995	−1.0254915	−1.277614	RP-10	Mean	−3.2471186	−1.0720838	−2.4729678	−2.8468528
	Max	−0.4528852	0.3969437	−0.159538	0.1053464		Max	−0.8728514	−0.0972439	−1.070647	−0.3651848
	Min	−3.1296681	−1.408081	−1.9635722	−3.2492808		Min	−5.1931067	−2.1187554	−4.9041739	−5.848072
	SD	0.9139286	0.5580195	0.5432835	1.0252792		SD	1.1630649	0.6546535	1.0042202	1.2853246
RP-5	Mean	−1.5179187	−0.472523	−1.4763197	−1.6676075	RP-11	Mean	−1.7560662	−0.3524027	−1.3875453	−1.3565324
	Max	0.0745548	0.4167209	0.0745165	0.0745474		Max	−0.1602364	0.2812715	−0.1905263	−0.1585026
	Min	−3.9066747	−3.0887209	−4.3472688	−4.7164015		Min	−3.3050487	−1.662606	−2.931173	−3.3910932
	SD	1.2562795	0.9778551	0.9856835	1.4249971		SD	1.0160831	0.6426634	0.7622098	1.2438222
RP-6	Mean	−8.9429712	−4.9479063	−6.4622347	−9.0543114	RP-12	Mean	−5.8367209	−2.8724377	−3.7033946	−4.8984339
	Max	−5.9611104	−1.285182	−3.7284173	−5.4037268		Max	−2.5869554	−0.4310465	−0.2096519	−0.2091465
	Min	−11.30546	−9.0011959	−10.247179	−13.325058		Min	−8.8135235	−4.9994968	−6.6499219	−7.9420245
	SD	1.4720603	1.7702774	1.688918	1.8708891		SD	2.0337375	1.4132917	1.878015	1.765799

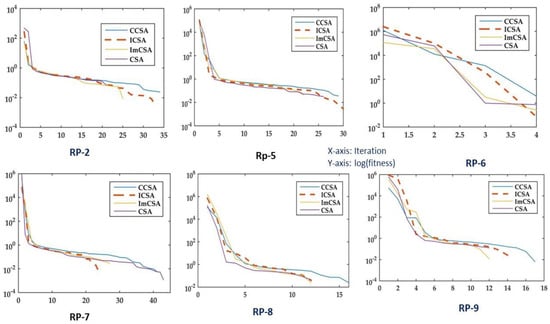
From Table 7, it has been observed that the proposed ICSA exhibits a better response in terms of mean values of SA. Hence, to verify this, convergence curves of RP-2, RP-5, RP-6, RP-7, RP-8 and RP-9 are plotted in Figure 7. From the figure, it has been observed that the ICSA exhibits a slightly better convergence property as compared with other variants of the CSA and the CSA itself. From this point of view, the proposed modification appears more meaningful for the PSP problem.

Figure 7. Convergence property analysis.

5. Conclusions

The ingenious crow search algorithm (ICSA) is proposed with a new bridging exponential operator for carrying out the protein structure prediction problem. Opposition theory has been implemented in the initialization phase, along with the exponential-driven position update mechanism. The ICSA has been tested on some of the standard benchmark functions and applied to the protein structure prediction problem. The following are the major conclusions of this work:

• Before experimenting on the complex protein sequence, the ICSA has been tested over some of the conventional benchmark functions. These functions are known functions, i.e., the minima and search range are priorly known. The comparative analysis with some of the published versions of the CSA shows that the algorithm is substantially improved with the application of a new exponential-driven factor and opposition-based learning. A detailed investigation in terms of statistical analysis of the fitness has been carried out to exhibit the efficacy of the proposed ICSA.
• A bench of various protein sequences is considered for testing the efficacy of the ICSA and some of the leading versions of the crow search algorithm and its variants. The bench consists of real and artificial sequences of protein.
• An extended analysis of the algorithm has been conducted with the help of a real protein bench. The bench consists of a real protein sequence of medium length. The algorithm is evaluated with other opponents on the basis of convergence and SA.
• Optimization performance has been compared with the help of various analyses, such as SAA, ETA and statistical significance evaluation with the help of the rank-sum test. We observed that the ICSA provides the optimal solution in less computation time, and in some cases, a degree of uniqueness exists in the obtained results.
• Convergence curves for different conventional functions have been plotted to showcase the optimization efficacy of the ICSA.

For future experimentation, a local search algorithm for enhancing the accuracy of the prediction will be proposed and tested on artificial as well as real protein sequences. In addition, rigorous analysis of some long-length sequences will be executed in the future by the authors.