Research on the Mesoscopic Characteristics of Kelvin–Helmholtz Instability in Polymer Fluids with Dissipative Particle Dynamics
Abstract
:1. Introduction
2. Problem Setup
3. DPD Method and Polymer Model
3.1. The DPD Method
3.2. The Polymer Model
3.3. Integration Algorithms
4. Simulation Results and Discussion
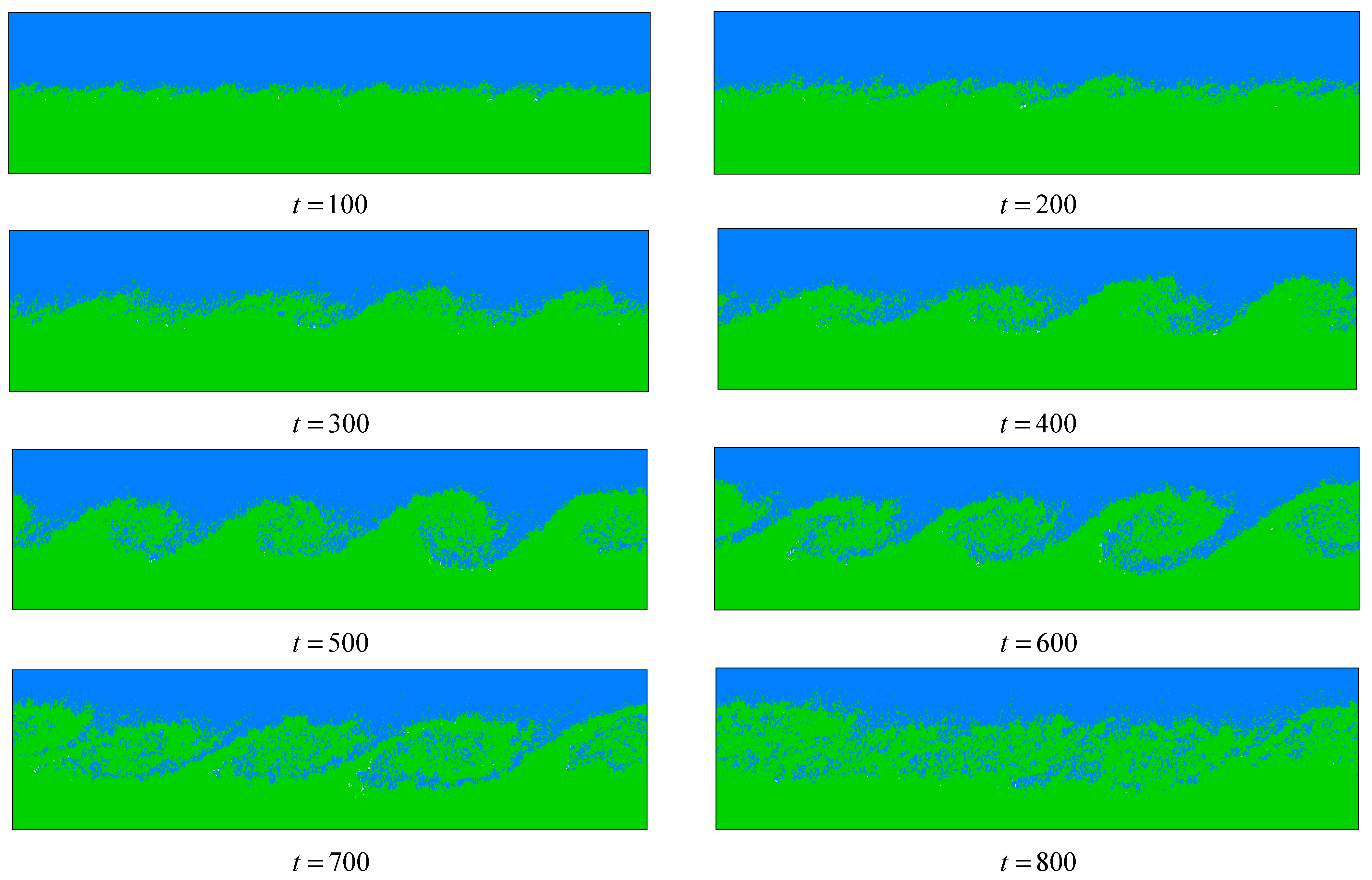
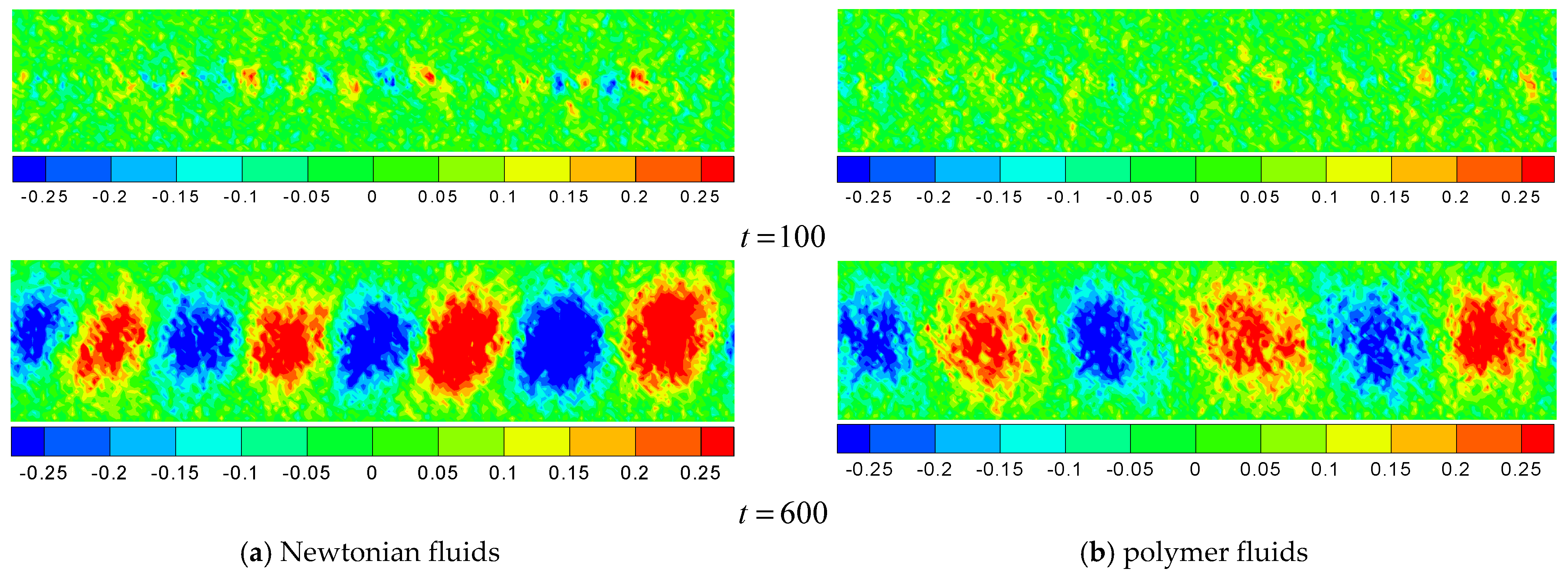
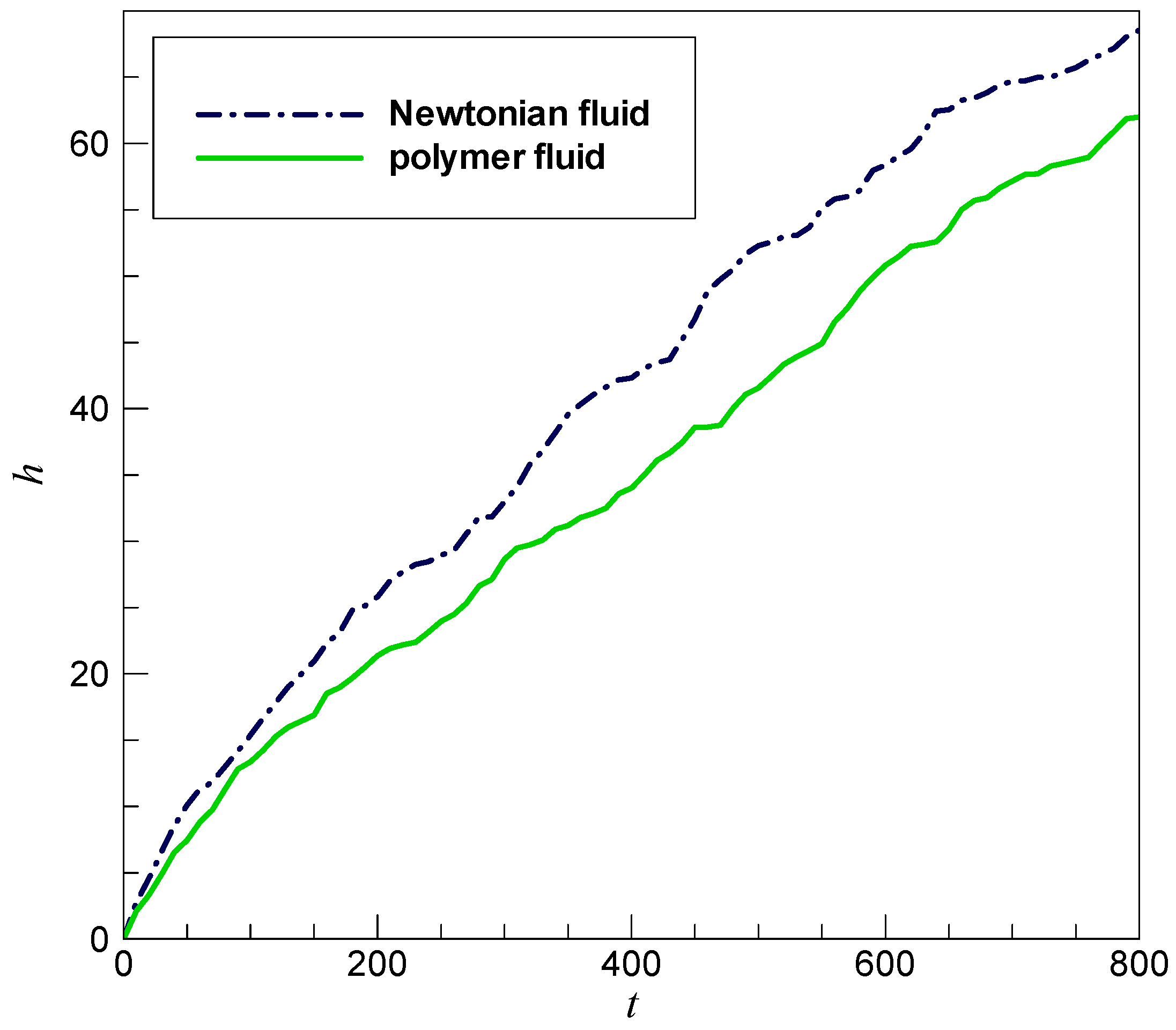
4.1. KH Instability in Newtonian Fluids
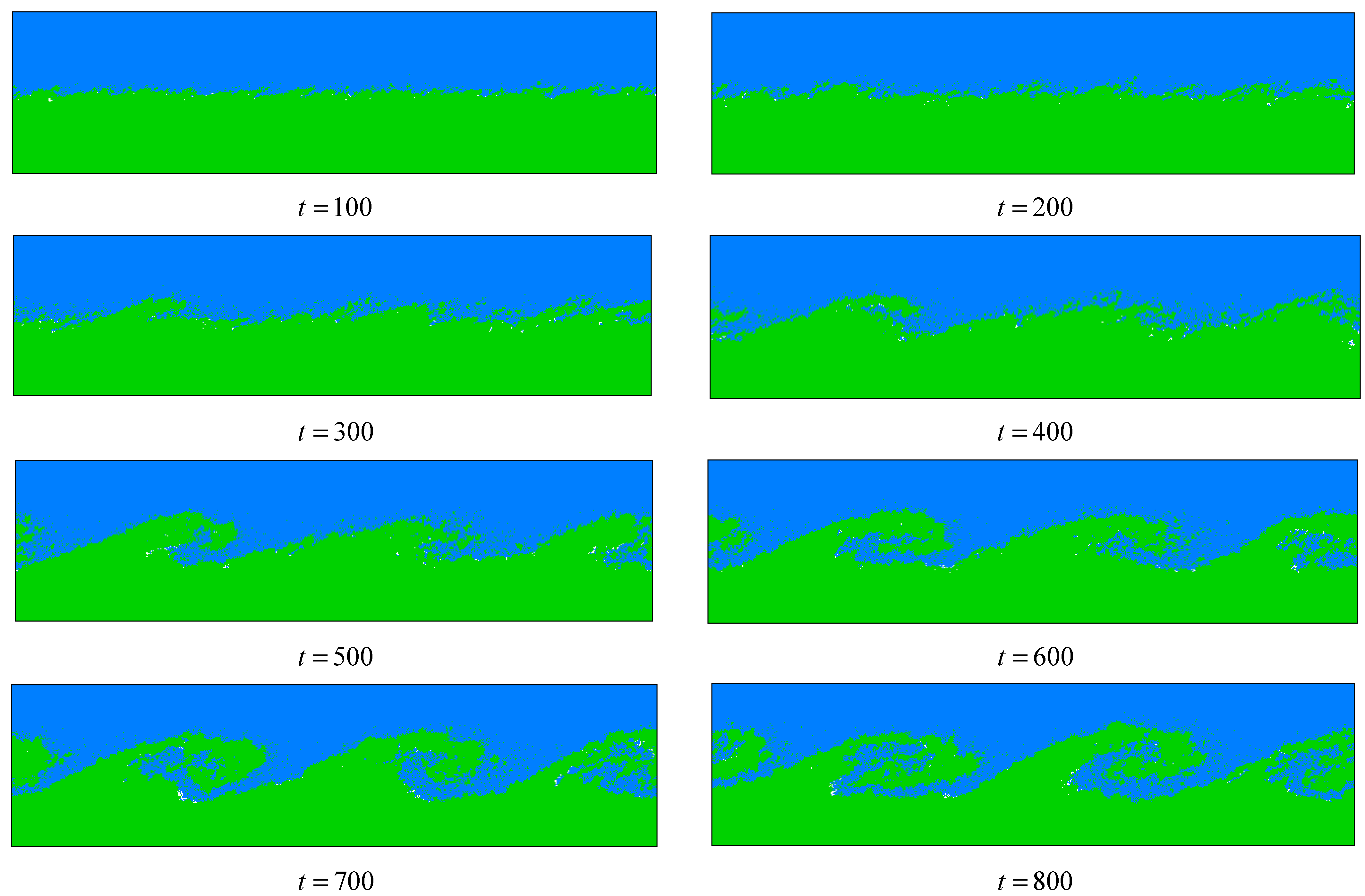
4.2. KH Instability in Polymer Fluids
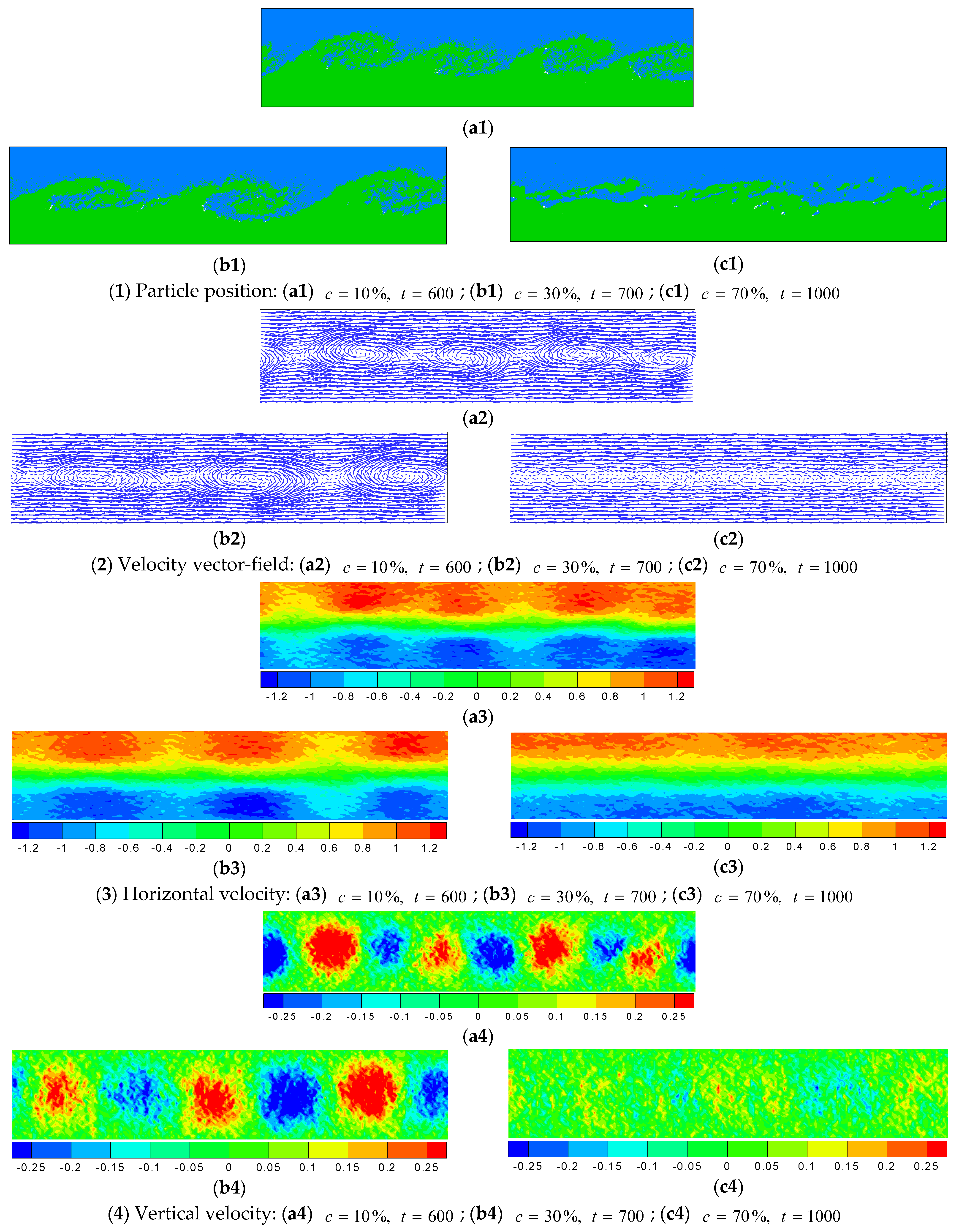
4.3. Effect of Polymer Concentration
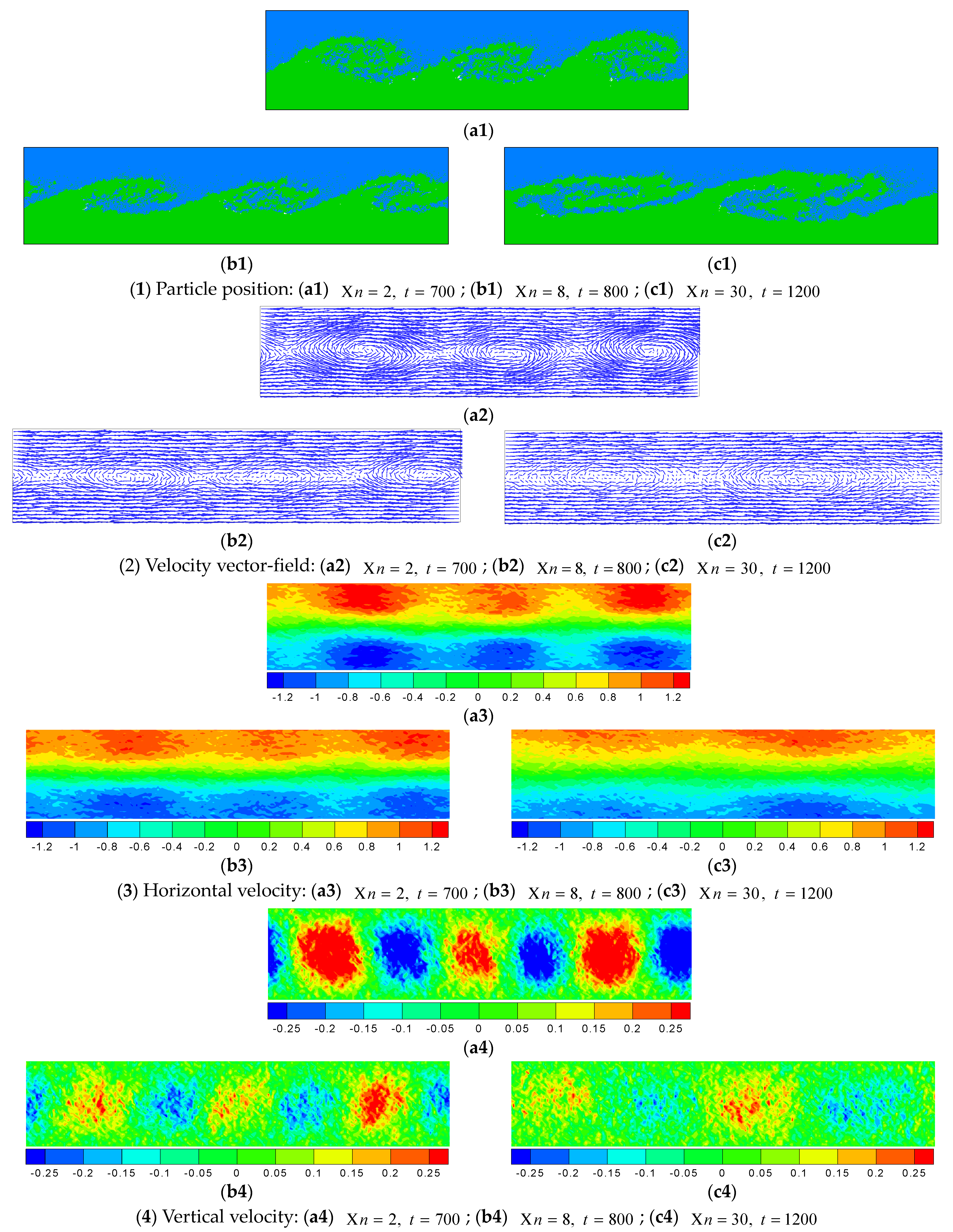
4.4. Effect of Chain Length
4.5. Effect of Polymer Extensibility
5. Summary and Conclusions
- (1)
- The DPD algorithm is validated by simulating the KH instability that occurs in the shear flow of Newtonian fluids, and the mesoscopic results of the present simulation for Newtonian fluids are qualitatively consistent with previous experimental and numerical results.
- (2)
- The characteristics of the KH instability that occurs in the flow of polymer fluids are explored with the validated DPD code. It is shown that, in contrast with their Newtonian counterparts, the waves and vortexes forming in the shear flow of polymer fluids grow more slowly, and these vortexes are flattened. In particular, the roll-up interface is conspicuously elongated and does not break up due to the reason that the polymer chains make the liquid micelles join together. Thus, the polymer hinders the mixing of fluids and suppresses the generation of turbulence. It is also observed that there is almost no small vortex appearing in the development process of the KH instability due to the inhibition of the polymer.
- (3)
- The effects of the polymer concentration on the KH instability are researched. The results show that with the polymer concentration increasing, the inhibitory effect becomes more conspicuous, the mixing of two polymer fluids reduces, and the transition from laminar to turbulence is even more restrained.
- (4)
- The effects of the chain length and extensibility of the polymer on the KH instability are also investigated. For the case of a long chain or high extensibility, the effect of the polymer on the flow structure is more profound. When the chain length gets longer, even the concentration remains constant, the formation of the waves and vortexes is delayed to a later simulation time, and the vortexes become longer and more flattened. This kind of situation also occurs when the polymer extensibility increases. The most striking effect of the high extensibility is the complete suppression of all vortex structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| coefficient of conservative force | |
| coefficient of entanglement force | |
| concentration | |
| resultant force | |
| conservative force | |
| dissipative force | |
| random force | |
| spring force | |
| entanglement force | |
| height of computational domain | |
| coefficient of spring force | |
| Boltzmann temperature | |
| side length of the unit cell | |
| length of the computational domain | |
| particle mass | |
| particle displacement | |
| bond length | |
| cutoff radius | |
| time step | |
| time | |
| boundary shear velocity | |
| particle velocity | |
| chain length | |
| Flory–Huggins parameter | |
| coefficient of dissipative force | |
| empirical coefficient | |
| coefficient of random force | |
| computational domain |
References
- Fu, Y.; Qin, H. The physics of spontaneous parity-time symmetry breaking in the Kelvin–Helmholtz instability. New J. Phys. 2020, 22, 083040. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Zhang, G.; Lin, C.; Lai, H.; Liu, Z. Nonequilibrium and morphological characterizations of Kelvin–Helmholtz instability in compressible flows. Front. Phys. 2019, 14, 43602. [Google Scholar] [CrossRef] [Green Version]
- Fu, Q.; Deng, X.; Yang, L. Kelvin–Helmholtz instability of confined Oldroyd-B liquid film with heat and mass transfer. J. Non-Newton. Fluid Mech. 2019, 267, 28–34. [Google Scholar] [CrossRef]
- Awasthi, M.K. Kelvin–Helmholtz instability of viscoelastic liquid-viscous gas interface with heat and mass transfer. Int. J. Therm. Sci. 2021, 161, 106710. [Google Scholar] [CrossRef]
- Farajzadeh, R.; Bayareh, M. Numerical study of Kelvin–Helmholtz instability of Newtonian and non-Newtonian fluids. AUT J. Mech. Eng. 2022, 6, 249–260. [Google Scholar]
- Kanarska, Y.; Shchepetkin, A.; McWilliams, J.C. Algorithm for non-hydrostatic dynamics in the Regional Oceanic Modeling System. Ocean Model. 2007, 18, 143–174. [Google Scholar] [CrossRef]
- Lesieur, M. Turbulence in Fluids; Kluwer Academic: Dordrecht, The Netherlands, 1997. [Google Scholar]
- IJzerman, W.L.; van Groesen, E. Low-dimensional model for vortex merging in the two-dimensional temporal mixing layer. Eur. J. Mech.-B/Fluids 2001, 20, 821–840. [Google Scholar] [CrossRef]
- Marmottant, P.; Villermaux, E. On Spray Formation. J. Fluid Mech. 2004, 498, 73–111. [Google Scholar] [CrossRef] [Green Version]
- Kim, H.J.; Karthikeyan, S.; Rigney, D. A simulation study of the mixing, atomic flow and velocity profiles of crystalline materials during sliding. Wear 2009, 267, 1130–1136. [Google Scholar] [CrossRef]
- Fullmer, W.D.; Ransom, V.H.; de Bertodano, M.A.L. Linear and nonlinear analysis of an unstable, but well-posed, one-dimensional two-fluid model for two-phase flow based on the inviscid Kelvin–Helmholtz instability. Nucl. Eng. Des. 2014, 268, 173–184. [Google Scholar] [CrossRef]
- Thorpe, S.A. Experiments on instability and turbulence in a stratified shear flow. J. Fluid Mech. 1973, 61, 731–751. [Google Scholar] [CrossRef]
- Tauber, W.; Unverdi, S.O.; Tryggvason, G. The nonlinear behavior of a sheared immiscible fluid interface. Phys. Fluids 2002, 14, 2871–2885. [Google Scholar] [CrossRef] [Green Version]
- Rikanati, A.; Alon, U.; Shvarts, D. Vortex-merger statistical-mechanics model for the late time self-similar evolution of the Kelvin–Helmholtz instability. Phys. Fluids 2003, 15, 3776–3785. [Google Scholar] [CrossRef]
- Sohn, S.I.; Yoon, D.; Hwang, W. Long-time simulations of the Kelvin–Helmholtz instability using an adaptive vortex method. Phys. Rev. E 2010, 82, 046711. [Google Scholar] [CrossRef]
- Shadloo, M.S.; Yildiz, M. Numerical modeling of Kelvin–Helmholtz instability using smoothed particle hydrodynamics. Int. J. Numer. Methods Engng. 2011, 87, 988–1006. [Google Scholar] [CrossRef]
- Braeunig, J.P.; Chauveheid, D.; Ghidaglia, J.M. A totally Eulerian finite volume solver for multi-material fluid flows III: The low Mach number case. Eur. J. Mech.-B/Fluids 2013, 42, 10–19. [Google Scholar] [CrossRef]
- Rahmani, M.; Lawrence, G.A.; Seymour, B.R. The effect of Reynolds number on mixing in Kelvin–Helmholtz billows. J. Fluid Mech. 2014, 759, 612–641. [Google Scholar] [CrossRef]
- Wingstedt, E.M.M.; Fossum, H.E.; Reif, B.P.; Werne, J. Anisotropy and shear-layer edge dynamics of statistically unsteady, stratified turbulence. Phys. Fluids 2015, 27, 065106. [Google Scholar] [CrossRef] [Green Version]
- Ducoin, A.; Loiseau, J.-C.; Robinet, J.-C. Numerical investigation of the interaction between laminar to turbulent transition and the wake of an airfoil. Eur. J. Mech.-B/Fluids 2016, 57, 231–248. [Google Scholar] [CrossRef] [Green Version]
- Szubert, D.; Asproulias, I.; Grossi, F.; Duvigneau, R.; Hoarau, Y.; Braza, M. Numerical study of the turbulent transonic interaction and transition location effect involving optimisation around a supercritical aerofoil. Eur. J. Mech.-B/Fluids 2016, 55, 380–393. [Google Scholar] [CrossRef]
- Cadot, O.; Kumar, S. Experimental characterization of viscoelastic effects on two- and three-dimensional shear instabilities. J. Fluid Mech. 2000, 416, 151–172. [Google Scholar] [CrossRef]
- Azaiez, J.; Homsy, G. Linear stability of free shear flow of viscoelastic liquids. J. Fluid Mech. 1994, 268, 37–69. [Google Scholar] [CrossRef] [Green Version]
- Azaiez, J.; Homsy, G. Numerical simulation of non-newtonian free shear flows at high Reynolds numbers. J. Non-Newton. Fluid Mech. 1994, 52, 333–374. [Google Scholar] [CrossRef]
- Kumar, S.; Homsy, G.M. Direct numerical simulation of hydrodynamic instabilities in two- and three-dimensional viscoelastic free shear layers. J. Non-Newton. Fluid Mech. 1999, 83, 249–276. [Google Scholar] [CrossRef]
- Yu, Z.; Phan-Thien, N. Three-dimensional roll-up of a viscoelastic mixing layer. J. Fluid Mech. 2004, 500, 29–53. [Google Scholar] [CrossRef]
- Richter, D.; Iaccarino, G.; Shaqfeh, E.S.G. Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate Reynolds numbers. J. Fluid Mech. 2010, 651, 415–442. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, S.K.; Dharodi, V.S.; Das, A.; Patel, B.G.; Kaw, P. Evolution of sheared flow structure in Visco-Elastic fluids. AIP Conf. Proc. 2014, 1582, 55–65. [Google Scholar]
- Zhang, R.; He, X.; Doolen, G.; Chen, S. Surface tension effects on two-dimensional two-phase Kelvin–Helmholtz instabilities. Adv. Water Resour. 2001, 24, 461–478. [Google Scholar] [CrossRef]
- Gan, Y.; Xu, A.; Zhang, G.; Li, Y. Lattice Boltzmann study on Kelvin–Helmholtz instability: Roles of velocity and density gradients. Phys. Rev. E 2011, 83, 056704. [Google Scholar] [CrossRef] [Green Version]
- Redapangu, P.R.; Sahu, K.C.; Vanka, S.P. A study of pressure-driven displacement flow of two immiscible liquids using a multiphase lattice Boltzmann approach. Phys. Fluids 2012, 24, 102110. [Google Scholar] [CrossRef] [Green Version]
- Fakhari, A.; Lee, T. Multiple-relaxation-time lattice Boltzmann method for immiscible fluids at high Reynolds numbers. Phys. Rev. E 2013, 87, 023304. [Google Scholar] [CrossRef]
- Glosli, J.N.; Richards, D.F.; Caspersen, K.J.; Rudd, R.E.; Gunnels, J.A.; Streitz, F.H. Extending stability beyond CPU millennium: A micron-scale atomistic simulation of Kelvin–Helmholtz instability. In Proceedings of the 2007 ACM/IEEE Conference on Supercomputing, New York, NY, USA, 10–16 November 2007. [Google Scholar]
- Ashwin, J.; Ganesh, R. Kelvin Helmholtz instability in strongly coupled Yukawa liquids. Phys. Rev. Lett. 2010, 104, 215003. [Google Scholar]
- Zhang, L.; Ouyang, J.; Zhang, X.H. The coupling of element-free Galerkin method and molecular dynamics for the incompressible flow problems. Microfluid. Nanofluid. 2011, 10, 809–820. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating microscopic hydrodynamic phenomena with dissipative particle dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Español, P.; Warren, P. Statistical mechanics of dissipative particle dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Marsh, C. Theoretical Aspect of Dissipative Particle Dynamics. Ph.D. Thesis, University of Oxford, Oxford, UK, 1998. [Google Scholar]
- Satoh, A.; Chantrell, R.W. Application of the dissipative particle dynamics method to magnetic colloidal dispersions. Mol. Phys. 2006, 104, 3287–3302. [Google Scholar] [CrossRef]
- Tiwari, A.; Abraham, J. Dissipative-particle-dynamics model for two-phase flows. Phys. Rev. E 2006, 74, 056701. [Google Scholar] [CrossRef]
- Liu, M.B.; Meakin, P.; Huang, H. Dissipative particle dynamics simulation of multiphase fluid flow in microchannels and microchannel networks. Phys. Fluids 2007, 19, 033302. [Google Scholar] [CrossRef]
- Duong-Hong, D.; Wang, J.S.; Liu, G.R.; Chen, Y.Z.; Han, J.Y.; Hadjiconstantinou, N.G. Dissipative particle dynamics simulations of electroosmotic flow in nano-fluidic devices. Microfluid. Nanofluid. 2008, 4, 219–225. [Google Scholar] [CrossRef]
- Tiwari, A.; Abraham, J. Dissipative particle dynamics simulations of liquid nanojet breakup. Microfluid. Nanofluid. 2008, 4, 227–235. [Google Scholar] [CrossRef]
- Li, Z.; Hu, G.H.; Wang, Z.L.; Ma, Y.B.; Zhou, Z.W. Three dimensional flow structures in a moving droplet on substrate: A dissipative particle dynamics study. Phys. Fluids 2013, 25, 072103. [Google Scholar] [CrossRef]
- Liu, H.; Jiang, S.; Chen, Z.; Liu, M.; Chang, J.; Wang, Y.; Tong, Z. Mesoscale study of particle sedimentation with inertia effect using dissipative particle dynamics. Microfluid. Nanofluid. 2015, 18, 1309–1315. [Google Scholar] [CrossRef]
- Tosenberger, A.; Salnikov, V.; Bessonov, N.; Babushkina, E.; Volpert, V. Particle Dynamics Methods of Blood Flow Simulations. Math. Model. Nat. Phenom. 2011, 6, 320–332. [Google Scholar] [CrossRef]
- Pan, W.; Tartakovsky, A.M. Dissipative particle dynamics model for colloid transport in porous media. Adv. Water Resour. 2013, 58, 41–48. [Google Scholar] [CrossRef]
- Liang, X.; Wu, J.; Yang, X.; Tu, Z.; Wang, Y. Investigation of oil-in-water emulsion stability with relevant interfacial characteristics simulated by dissipative particle dynamics. Colloids Surf. A Physicochem. Eng. Asp. 2018, 546, 107–114. [Google Scholar] [CrossRef]
- Gharibvand, A.J.; Norouzi, M.; Shahmardan, M.M. Dissipative particle dynamics simulation of magnetorheological fluids in shear flow. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 103. [Google Scholar] [CrossRef]
- Nardai, M.M.; Zifferer, G. Simulation of dilute solutions of linear and star-branched polymers by dissipative particle dynamics. J. Chem. Phys. 2009, 131, 124903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fan, X.; Phan-Thien, N.; Yong, N.T.; Wu, X.; Xu, D. Microchannel flow of a macromolecular suspension. Phys. Fluids 2003, 15, 11–21. [Google Scholar] [CrossRef]
- Fan, X.; Phan-Thien, N.; Chen, S.; Wu, X.; Ng, T.Y. Simulating flow of DNA suspension using dissipative particle dynamics. Phys. Fluids 2006, 18, 063102. [Google Scholar] [CrossRef]
- Zhu, Y.L.; Liu, H.; Lu, Z.Y. A highly coarse-grained model to simulate entangled polymer melts. J. Chem. Phys. 2012, 136, 144903. [Google Scholar] [CrossRef]
- Karatrantos, A.; Clarke, N.; Composto, R.J.; Winey, K.I. Topological entanglement length in polymer melts and nanocomposites by a DPD polymer model. Soft Matter 2013, 9, 3877–3884. [Google Scholar] [CrossRef]
- Li, Y.; Qian, H.J.; Lu, Z.Y.; Shi, A.C. Note: Effects of polydispersity on the phase behavior of AB diblock and BAB triblock copolymer melts: A dissipative particle dynamics simulation study. J. Chem. Phys. 2013, 139, 096101. [Google Scholar] [CrossRef] [PubMed]
- Posel, Z.; Rousseau, B.; Lísal, M. Scaling behaviour of different polymer models in dissipative particle dynamics of unentangled melts. Mol. Simul. 2014, 40, 1274–1289. [Google Scholar] [CrossRef]
- Moeendarbary, E.; Ng, T.Y.; Zangeneh, M. Dissipative particle dynamics: Introduction, methodology and complex fluid applications—A review. Int. J. Appl. Mech. 2009, 1, 737–763. [Google Scholar] [CrossRef]
- Liu, M.B.; Liu, G.R.; Zhou, L.W.; Chang, J.Z. Dissipative particle dynamics (DPD): An overview and recent developments. Arch. Comput. Methods Eng. 2015, 22, 529–556. [Google Scholar] [CrossRef] [Green Version]
- Dzwinel, W.; Alda, W.; Yuen, D.A. Cross-Scale Numerical Simulations Using Discrete Particle Models. Mol. Simul. 1999, 22, 397–418. [Google Scholar] [CrossRef]
- Dzwinel, W.; Yuen, D.A. Mixing driven by Rayleigh–Taylor instability in the mesoscale modeled with dissipative particle dynamics. Int. J. Mod. Phys. C 2001, 12, 91–118. [Google Scholar] [CrossRef]
- Tiwari, A.; Abraham, J. A two-component two-phase dissipative particle dynamics model. Int. J. Numer. Methods Fluids 2009, 59, 519–533. [Google Scholar] [CrossRef]
- Li, Y.G.; Geng, X.G.; Wang, H.P.; Zhuang, X.; Ouyang, J. Simulating the frontal instability of lock-exchange density currents with dissipative particle dynamics. Mod. Phys. Lett. B 2016, 30, 1650200. [Google Scholar] [CrossRef]
- Li, Y.G.; Geng, X.G.; Zhuang, X.; Wang, L.H.; Ouyang, J. Simulating the Rayleigh-Taylor instability in polymer fluids with dissipative particle dynamics. Eur. Phys. J. Plus 2016, 131, 103. [Google Scholar] [CrossRef]
- Li, Y.; Zhai, J.; Xu, D.; Chen, G. The study of Plateau–Rayleigh instability with DPD. Eur. Phys. J. Plus 2021, 136, 648. [Google Scholar] [CrossRef]
- Kong, Y.; Manke, C.W.; Madden, W.G.; Schlijper, A.G. Simulation of a confined polymer in solution using the dissipative particle dynamics method. Int. J. Thermophys. 1994, 15, 1093–1099. [Google Scholar] [CrossRef]
- Chen, S.; Phan-Thien, N.; Fan, X.J.; Khoo, B.C. Dissipative particle dynamics simulation of polymer drops in a periodic shear flow. J. Non-Newton. Fluid Mech. 2004, 118, 65–81. [Google Scholar] [CrossRef]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef] [Green Version]
- AlSunaidi, A.; den Otter, W.K.; Clarke, J.H.R. Liquid-crystalline ordering in rod-coil diblock copolymers studied by mesoscale simulations. Philos. Trans. R. Soc. Lond. A 2004, 362, 1773–1781. [Google Scholar] [CrossRef]
- Li, Y.G.; Geng, X.G.; Ouyang, J.; Zang, D.Y.; Zhuang, X. A hybrid multiscale dissipative particle dynamics method coupling particle and continuum for complex fluid. Microfluid. Nanofluid. 2015, 19, 941–952. [Google Scholar] [CrossRef]
- Goujon, F.; Malfreyt, P.; Tildesley, D.J. Mesoscopic simulation of entanglements using dissipative particle dynamics: Application to polymer brushes. J. Chem. Phys. 2008, 129, 034902. [Google Scholar] [CrossRef] [Green Version]
- Sirk, T.W.; Slizoberg, Y.R.; Brennan, J.K.; Lisal, M.; Andzelm, J.W. An enhanced entangled polymer model for dissipative particle dynamics. J. Chem. Phys. 2012, 136, 134903. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Xue, Y.; Qian, H.; Lu, Z.; Sun, C. A practical method to avoid bond crossing in two-dimensional dissipative particle dynamics simulations. J. Chem. Phys. 2008, 129, 024902. [Google Scholar] [CrossRef]
- Lee, H.G.; Kim, J. Two-dimensional Kelvin–Helmholtz instabilities of multi-component fluids. Eur. J. Mech.-B/Fluids 2015, 49, 77–88. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, G.; Li, Y.; Wang, H.; Li, S. Research on the Mesoscopic Characteristics of Kelvin–Helmholtz Instability in Polymer Fluids with Dissipative Particle Dynamics. Processes 2023, 11, 1755. https://doi.org/10.3390/pr11061755
Wu G, Li Y, Wang H, Li S. Research on the Mesoscopic Characteristics of Kelvin–Helmholtz Instability in Polymer Fluids with Dissipative Particle Dynamics. Processes. 2023; 11(6):1755. https://doi.org/10.3390/pr11061755
Chicago/Turabian StyleWu, Guorong, Yanggui Li, Heping Wang, and Shengshan Li. 2023. "Research on the Mesoscopic Characteristics of Kelvin–Helmholtz Instability in Polymer Fluids with Dissipative Particle Dynamics" Processes 11, no. 6: 1755. https://doi.org/10.3390/pr11061755
APA StyleWu, G., Li, Y., Wang, H., & Li, S. (2023). Research on the Mesoscopic Characteristics of Kelvin–Helmholtz Instability in Polymer Fluids with Dissipative Particle Dynamics. Processes, 11(6), 1755. https://doi.org/10.3390/pr11061755







