A Novel Energy-Intensity Model Based on Time Scale for Quasi-Continuous Production in Iron and Steel Industry

Abstract

Energy intensity is an important assessment indicator of energy consumption. Unfortunately, the traditional energy intensity model (TEIM) has obvious limitations when applied to quasi- continuous production process, especially for small time scales (STS). Therefore, a novel energy intensity model (NEIM) has been established in this study. The NEIM includes three main stages. Firstly, the statistical period and time scale have been determined. Secondly, the concept of workpiece valid weight has been proposed for a given time scale. Then the specific calculation method has also been established. Thirdly, a NEIM has been suggested according to the definition of energy intensity. The application results for a reheating furnace show that the NEIM’s effectiveness has been verified via comparison with the TEIM for large time scale (LTS) and critical time scale (CTS), whereas the NEIM still has validity at STS. Additionally, calculation results for the NEIM reflect more trend information at LTS and CTS; whereas, more dynamic information has been reflected at STS. The aim of this research was to expand the NEIM application for different time scales. Meanwhile, NEIM can also be applied to various energy-consuming facilities.

1. Introduction

With the rapid development of industry, human civilization has made continuous progress. However, this has been accompanied by a sharp increase in energy consumption [1,2] and serious environmental damage [3,4]. Mankind is facing an unprecedented energy crisis [5,6] and environmental pressures [7]. Iron and steel production, for instance, have experienced extensive and rapid development (especially in China) characterized by the continuous and large-scale growth of steel production. Meanwhile, energy consumption has also increased sharply. Therefore, the demand for energy conservation and carbon reduction in the iron and steel industry is still urgent, especially under the current “carbon peak” and “carbon neutrality” pressures [8].

Lean energy operation is a common energy-saving measure adopted by iron and steel enterprises [9]. Generally, lean energy operation is mainly to maximize energy efficiency which can be represented by Equation (1).

$$\eta =\frac{Q_1+Q_2}{Q}$$

(1)

In which,

$\eta$: Energy efficiency in the statistical period;

$Q_1$: the amount of energy fully used for product processing in the statistical period, tce (ton coal equivalent);

$Q_2$: the amount of energy recovered, tce;

$Q$: the total amount of energy supplied, tce.

In general, if certain amounts of product are processed, $Q_1$ is a constant. Therefore, the improvement of energy efficiency can be achieved in the following two methods: reducing $Q$ or increasing $Q_2$.

In summary, these two methods can be achieved via production-equipment optimization and process-flow-structure optimization.

Production equipment is the most basic component in iron and steel enterprises, such as sinter machines, coke ovens, blast furnaces, convertor furnaces, reheating furnaces, etc. The energy efficiencies of production equipment directly determine the amount of energy consumption. Generally, production-equipment optimization mainly includes: waste heat and energy recovery (such as from Sinter vertical coolers [10], top gas pressure recovery turbine generator sets of the blast furnaces [11], coke dry-quenching systems [12], waste heat of blast-furnace slag [13], regenerative reheating furnaces [14]) and energy-efficiency improvements (such as pulverized-coal injection technologies in blast furnaces [15], oxy-fuel combustion technology [16], regenerative combustion technology [17], waste heat utilization technology [18,19], etc.).

Iron and steel enterprises are typical process industries. Various types of production equipment are combined through specific process structures to complete the product-processing tasks. In other words, whether the process structure and operation modes are reasonable will also have a significant impact on the quantity of energy consumption. Qi Zhang et al. [20] have put forward a full length material-energy nexus-flow combined model, which has proven that the process-flow-structure optimization is beneficial to reduce energy consumption and CO₂ emission. Biao Lu et al. [21] have also proposed an energy-intensity optimization model for a production system in iron and steel.

Therefore, lean energy operation has been to continuously improve the energy efficiency through production-equipment optimization and process-flow-structure optimization. Unfortunately, the $Q_1$ value of Equation (1) is very difficult to derive. Therefore, energy efficiency ($\eta$ in Equation (1)) can not be easily calculated. Generally, there is an inverse correlation between energy efficiency and energy intensity, that is, the higher the energy efficiency, the lower the energy intensity, and vice versa. Consequently, energy intensity is a monetary indicator of energy efficiency [22]. By contrast, energy intensity can be derived easily.

In general, energy intensity is the energy consumption per unit output value in a specific statistical period [23], such as the consumption per ton of steel [24] and energy consumption per ton of product in various production processes [25] in the iron and steel industry, specific energy consumption and baseline energy consumption of cement [26], etc. Moreover, the concept of energy intensity has found applications in comparison, analysis, and assessment of energy efficiency in various industries or countries [27,28,29,30,31].

Obviously, the various application scenarios of energy intensity have a common feature in previous studies: LTS. In other words, energy intensity is limited to large statistical periods, such as year, quarter, month, or week. Therefore, traditional energy intensity is an average value over this large statistical period.

The obvious question becomes: could energy intensity be applied to an STS? Unfortunately, the problem is seldom discussed in any scenarios.

For example, the calculation of energy intensity at STS is very difficult for large-area research objects, such as some local districts [32,33,34], countries [35,36], or enterprises [37,38,39,40]; whereas, energy-intensity variation can assess its dynamic-fluctuation characteristic for quasi-continuous-production at STS. Furthermore, whether the energy-supply strategy is reasonable can also be evaluated.

There are seldom problems with the TEIM application for quasi-continuous production at LTS. Unfortunately, there would be huge irrationalities with energy intensity calculations at STS. In general, the yield of quasi-continuous production is greater than zero at LTS (as shown in Figure 1a, there is a change in the number of workpieces at the ${∆\mathrm{t}}_{\mathrm{i},1}$ time interval, which is an LTS mode). Then, the energy intensity, which has been calculated through TEIM, can be acceptable at this time scale. However, the yield of quasi-continuous production is poor at some STSs, or even zero (as shown in Figure 1b, there is no change in the number of workpieces at ${∆\mathrm{t}}_{\mathrm{i},2}$, which is an STS mode). At this time, the quasi-continuous production energy intensity is meaningless through TEIM at this STS; whereas, the production process is still consuming energy. Therefore, there is a huge contradiction between the energy intensity calculation result via the TEIM and the actual energy consumption.

Therefore, quasi-continuous-production energy intensity will face the embarrassment of being unable to be calculated for some STSs. Fortunately, data-driven technologies have been successfully applied in the energy network [41]. Consequently, NEIM, which can calculate energy intensity at any time scale (especially for STS) for quasi-continuous production, has been established based on data analysis in this paper. The dynamic characteristics of energy intensity have also been deeply analyzed based on this model. Furthermore, this NEIM has wider applicability at different time scales for quasi-continuous production, and can also be applied to various energy consuming facilities.

2. Methodology

2.1. The Determination of Statistical Period and Time Scale

2.1.1. The Determination of Statistical Period

It is assumed that the statistical period is $\left[T_1,T_2\right]$.

2.1.2. The Determination of Time Scale

The statistical period can be divided into different time scales, such as several minutes, hours, days, months, years, etc. These time scales can be denoted as $∆T$ ($∆T$ belongs to several minutes, hours, days, months, years, etc., and $∆T\le T_2-T_1$). Therefore, statistical period ($\left[T_1,T_2\right]$) can be divided into several time periods at $∆T$ time intervals.

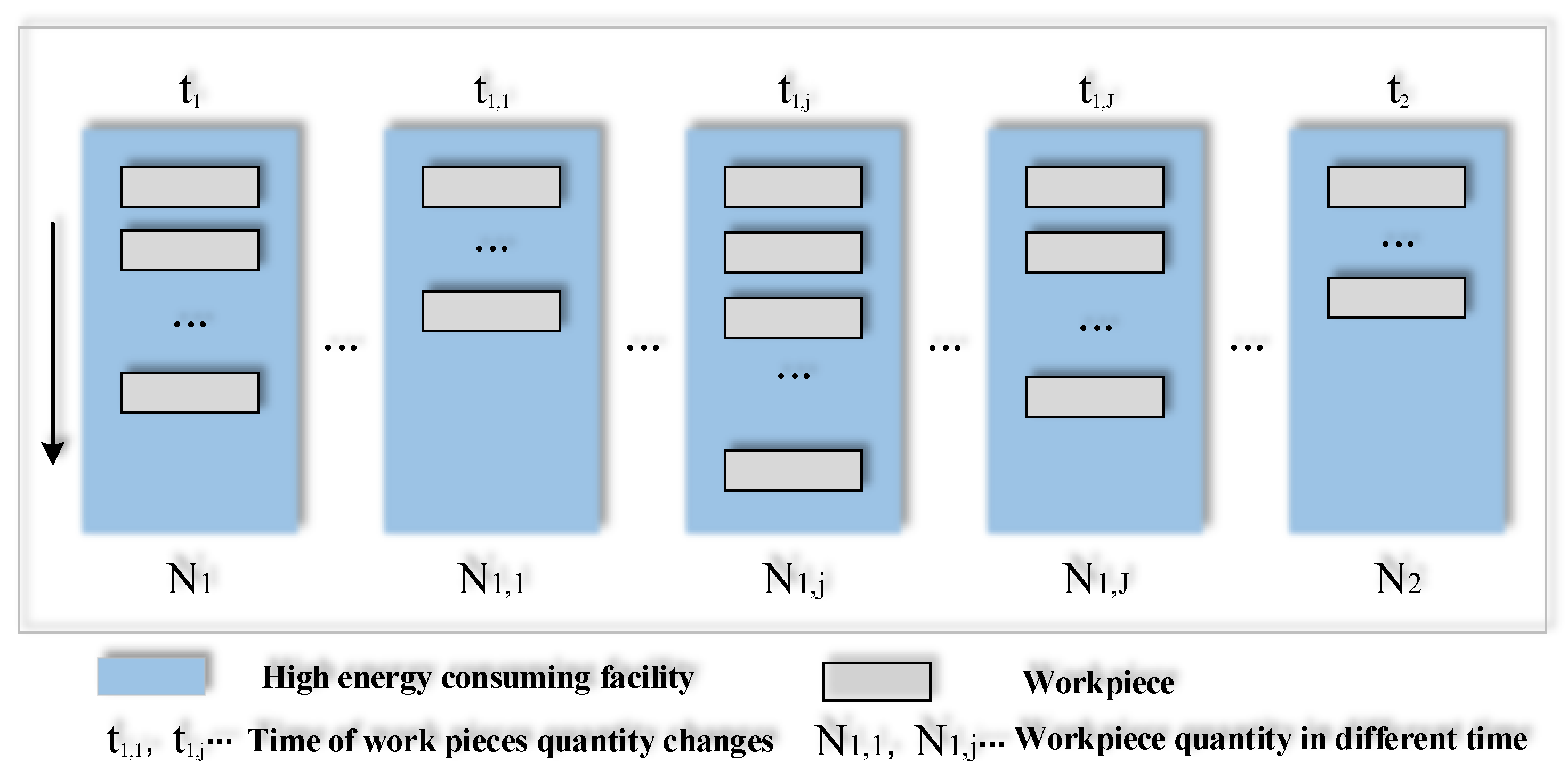
2.2. NEIM Establishment in Some Time Scale

Hypothetical conditions are shown as follows:

(1)

Statistical period ($\left[T_1,T_2\right]$);

(2)

Time scale ($\left[t_1,t_2\right]$), in which time interval $∆t=t_2-t_1$;

(3)

Time scale ($\left[t_1,t_2\right]$) $\le$ Statistical period ($\left[T_1,T_2\right]$).

Therefore, the energy-intensity model is shown as Equation (2) at the $\left[t_1,t_2\right]$ time scale.

$$e_{[t_1,t_2]}=\frac{E_{[t_1,t_2]}}{W_{[t_1,t_2]}}$$

(2)

In which,

$e_{[t_1,t_2]}$: energy intensity calculated by new model in time scale ($\left[t_1,t_2\right]$), GJ/t;

$E_{[t_1,t_2]}$: energy consumption in $\left[t_1,t_2\right]$ time scale, GJ;

$W_{[t_1,t_2]}$: the valid weight of workpiece in $\left[t_1,t_2\right]$ time scale, t.

As shown in Equation (2), $E_{[t_1,t_2]}$ and $W_{[t_1,t_2]}$ are the core in the energy-intensity calculation process.

2.3. $E_{[t_1,t_2]}$ Calculation at the $\left[t_1,t_2\right]$ Time Scale

Energy consumption cumulative value in time t₁ and t₂ can be calculated, as shown in Equation (3):

$$E_{[t_1,t_2]}=E_{t_2}-E_{t_1}$$

(3)

In which,

$E_{t_1}$, $E_{t_2}$: energy consumption cumulative value in time $t_1$ and $t_2$, GJ;

2.4. $W_{[t_1,t_2]}$ Calculation in $\left[t_1,t_2\right]$ Time Scale

There are four cases of workpiece-quantity change over the $\left[t_1,t_2\right]$ time scale, as shown in Figure 2.

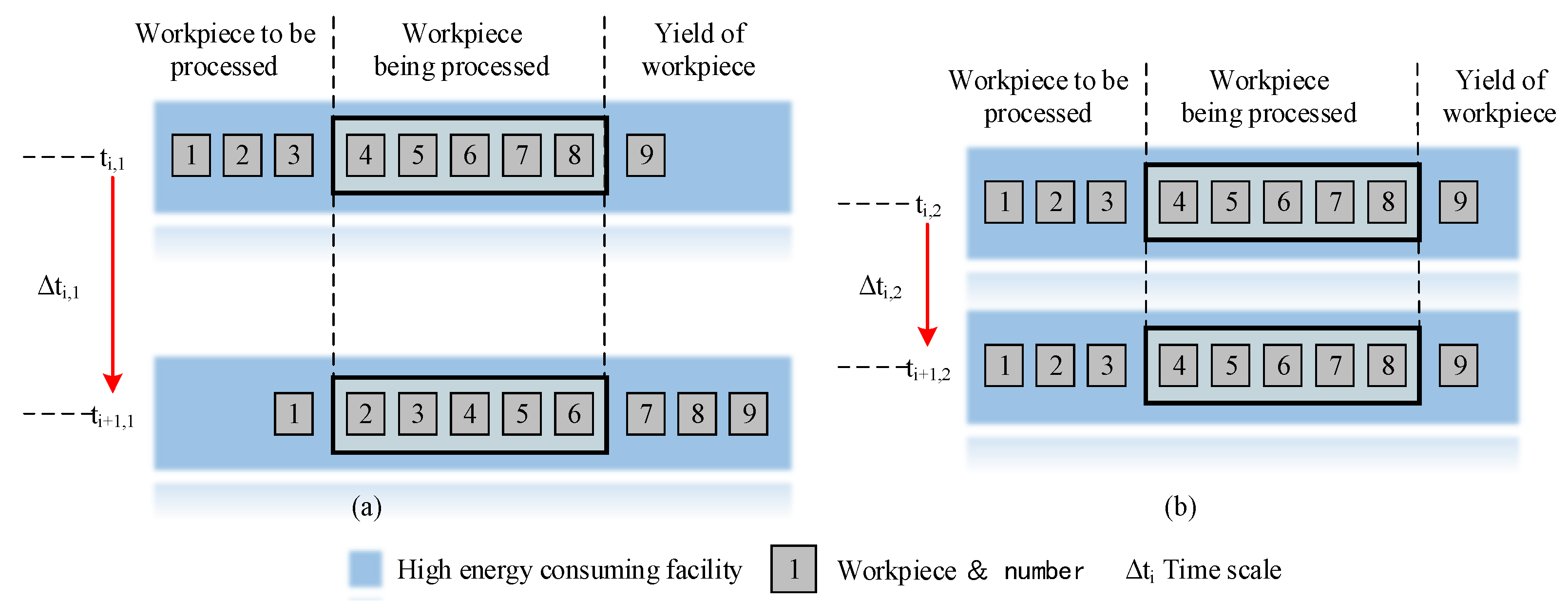
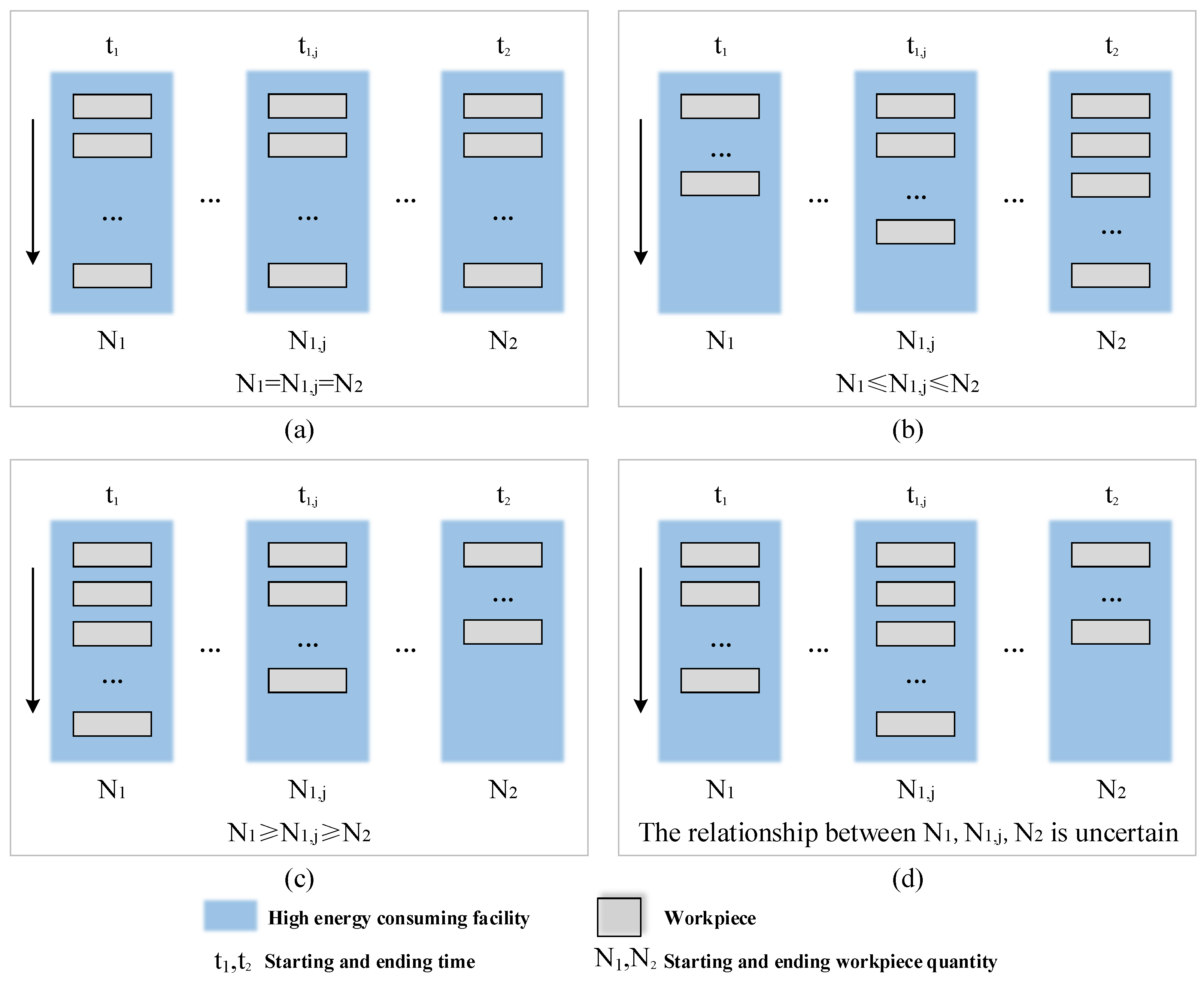
2.4.1. No Change in the Number of Workpieces

There is no change in the number of workpieces, as shown in Figure 2a. The $i\mathrm{t}\mathrm{h}$ workpiece weight can be denoted as $W_i(i=1\cdots N)$. Meanwhile, the total processing time of this workpiece is denoted as $T_i$. It is vital that the $i\mathrm{t}\mathrm{h}$ workpiece-processing time accounts for a part of the total processing time ($T_i$). Therefore, the workpiece weight should be weighted at the $\left[t_1,t_2\right]$ time scale. The weighting process is as Equation (4):

$$W_i^{\prime }=\frac{t_2-t_1}{T_i}·W_i$$

(4)

${\omega }_i=\frac{t_2-t_1}{T_i}$, consequently:

$$W_i^{\prime }={\omega }_i·W_i$$

Similarly, the weighting process of other workpiece weights should also be handled in this way. Therefore, the total valid weight should be represented as Equation (5).

$$W_{[t_1,t_2]}=\sum _{i=1}^N{W}_i^{\prime }$$

(5)

2.4.2. Change in the Number of Workpieces

In general, there are three scenarios in which the number of workpieces change.

Scenario 1 (as shown in Figure 2b): The number of workpieces increases gradually. Generally, this scenario often occurs at the beginning of production. Initially, energy intensity is relatively high. With the increasing number of workpieces, energy intensity will be smaller and smaller. Energy intensity eventually stabilizes. This is the process of increasing production.

Scenario 2 (as shown in Figure 2c): The number of workpieces decreases gradually. In general, this scenario often occurs at the end of production. Initially, energy intensity is relatively low. With the decreasing number of workpieces, energy intensity will be higher and higher. This is the process of reducing production.

Scenario 3 (as shown in Figure 2d): The number of workpieces increases or decreases according to the production plan. Usually, this scenario occurs in normal production. This is the process of production fluctuation.

In any case, time and quantity of workpiece changes should be recorded in quasi-continuous production (as shown in Figure 3). Then, a series of {time, workpiece quantity} sequence pairs is formulated in the $\left[t_1,t_2\right]$ time scale. The sequence-pair change process is shown as follows in Figure 3.

$$\left\{\begin{array}{c}\left(t_1,N_1\right)\to \left(t_{\mathrm{1,1}},N_{\mathrm{1,1}}\right)\to \cdots \left(t_{1,j},N_{1,j}\right)\to \left(t_{1,j+1},N_{1,j+1}\right)\cdots \\ \to \left(t_{1,J},N_{1,J}\right)\to \left(t_2,N_2\right)\end{array}\right\}$$

In which,

$\left(t_{1,j},N_{1,j}\right)\to \left(t_{1,j+1},N_{1,j+1}\right)$: workpiece quantity is $N_{1,j}$ from time $t_{1,j}$ to time $t_{1,j+1}$. Then, workpiece quantity becomes $N_{1,j+1}$ from time $t_{1,j+1}$. $\left(t_1,N_1\right)\to \left(t_{\mathrm{1,1}},N_{\mathrm{1,1}}\right)$ and $\left(t_{1,J},N_{1,J}\right)\to \left(t_2,N_2\right)$ respectively indicates that workpiece quantity is $N_1$ and $N_{1,J}$($N_{1,J}=N_2$) in $\left[t_1,t_{\mathrm{1,1}}\right]$ and $\left[t_{1,J},t_2\right]$ time periods. Therefore, the calculation methods of total valid weight of all workpieces are slightly different in three time periods $\left[t_1,t_{\mathrm{1,1}}\right]$, $\left[t_{1,j},t_{1,j+1}\right]$, $\left[t_{1,J},t_2\right]$.

Figure 3. Change process of workpiece-quantity $[t_1,t_2]$ time scales.

Figure 3. Change process of workpiece-quantity $[t_1,t_2]$ time scales.

Total valid weight of all workpieces in the $\left[t_1,t_{\mathrm{1,1}}\right]$ time period as shown in Equation (6).

$$W_{[t_1,t_{\mathrm{1,1}}]}=\sum _{i=1}^{N_1}\frac{t_{\mathrm{1,1}}-t_1}{{Ty}_i}·W_i$$

(6)

In which,

$W_{[t_1,t_{\mathrm{1,1}}]}$: total valid weight of all workpieces in the $\left[t_1,t_{\mathrm{1,1}}\right]$ time period, ton;

$N_1$: the workpiece quantity in the $\left[t_1,t_{\mathrm{1,1}}\right]$ time period;

${Ty}_i$: the actual processing time interval of the $i\mathrm{t}\mathrm{h}$ workpiece, min;

$W_i$: the actual weight of the $i\mathrm{t}\mathrm{h}$ workpiece, ton.

Total valid weight of all workpieces in the $\left[t_{1,j},t_{1,j+1}\right]$ time period as shown in Equation (7).

$$W_{[t_{1,j},t_{1,j+1}]}=\sum _{i=1}^{N_{1,j}}\frac{t_{1,j+1}-t_{1,j}}{{Ty}_i}·W_i$$

(7)

In which,

$W_{[t_{1,j},t_{1,j+1}]}$: total valid weight of all workpieces in $\left[t_{1,j},t_{1,j+1}\right]$ time period, ton;

$N_{1,j}$: the workpiece quantity in the $\left[t_{1,j},t_{1,j+1}\right]$ time period;

Total valid weight of all workpieces in the $\left[t_{1,J},t_2\right]$ time period as shown in Equation (8).

$$W_{[t_{1,J},t_2]}=\sum _{i=1}^{N_{1,J}}\frac{t_2·t_{1,J}}{{Ty}_i}·W_i$$

(8)

In which,

$W_{[t_{1,J},t_2]}$: total valid weight of all workpieces in $\left[t_{1,J},t_2\right]$ time period, ton;

$N_{1,J}$: the workpiece quantity in $\left[t_{1,J},t_2\right]$ time period;

Consequently, total valid weight of all workpieces for the $\left[t_1,t_2\right]$ time scale should be calculated as shown in Equation (9).

$$W_{[t_1,t_2]}=W_{[t_1,t_{\mathrm{1,1}}]}+\sum _{j=1}^{J-1}{W}_{[t_{1,j},t_{1,j+1}]}+W_{\left[t_{1,J},t_2\right]}$$

(9)

In which,

$W_{[t_1,t_2]}$: total valid weight of all workpieces in $[t_1,t_2]$ time scale, ton.

3. Case Study

The energy consumption of reheating furnaces accounts for 15–20% of the total energy consumption and 70% of the energy consumption of the rolling process [42]. Therefore, the energy intensity of reheating furnaces should be actively concerned. Meanwhile, reheating furnaces are typical quasi-continuous production process.

In actual production data of a reheating furnace, for instance, the validity of this NEIM has been further confirmed. Then, the dynamic-change regularity of energy intensity has also been analyzed for different time scales. The production-data statistical period of this reheating furnace is [1 March 2020 00:00:00, 20 June 2020 23:59:59] (${\mathrm{T}}_1$ = 1 March 2020 00:00:00,${\mathrm{T}}_2$ = 20 June 2020 23:59:59).

3.1. The Division of Different Time Scales

The division of different time scales is shown in

Table 1. The division of different time scales.

No.	$\mathbf{Time}\mathbf{Scale}\mathbf{(}\mathbf{∆}\mathit{T}\mathbf{)}$	No.	$\mathbf{Time}\mathbf{Scale}\mathbf{(}\mathbf{∆}\mathit{T}\mathbf{)}$
1	5 min	7	8 h
2	10 min	8	1 day
3	30 min	9	7 days
4	1 h	10	14 days
5	2 h	11	28 days
6	4 h

.

3.2. The Energy-Intensity Calculation Results in Different Time Scales

The energy-intensity-calculation results for different time scales are shown in

Table 2. Energy -intensity calculation results in different time scales.

No.	Time Scale	Average Value (GJ/t)		Standard Deviation		Variation Coefficient
		Novelty	Tradition	Novelty	Tradition	Novelty	Tradition
1	28 Days	1.52	1.52	0.186	0.093	0.123	0.061
2	14 Days	1.56	1.57	0.288	0.254	0.185	0.162
3	7 Days	1.57	1.57	0.405	0.315	0.257	0.201
4	1 Days	1.49	1.58	0.275	0.774	0.185	0.491
5	8 h	1.58	1.83	0.444	1.579	0.280	0.864
6	4 h	1.60	2.11	0.658	2.245	0.412	1.065
7	2 h	1.72	2.28	0.798	2.532	0.464	1.111
8	1 h	1.76	2.48	0.867	2.777	0.492	1.122
9	30 min	1.82	2.66	0.956	3.016	0.524	1.133
10	10 min	1.96	3.05	1.135	3.489	0.578	1.145

. In order to compare with TEIM, the calculation results of this NEIM and TEIM are all listed in Table 2.

3.3. The Validity of this NEIM

Variation coefficient is a very valid parameter, which can compare the dispersion degree of two groups of data based on eliminating the influence of scale and dimension. Firstly, the dispersion degree will be smaller if the variation coefficient is smaller. Secondly, if the variation coefficients of two groups of data are similar, it indicates that they have the same dispersion degree. In this paper, the variation coefficient has been selected to compare the calculation results of TEIM and NEIM at different time scales (as shown in Figure 4).

As shown in Figure 4, three regions have been divided (LTS region, CTS region, STS region).

3.3.1. Computational-Performance Analysis of Two Energy-Intensity Models at Different Time Scales

(1)

LTS region

The variation coefficients of two energy-intensity models are both small and have little difference in the LTS region (time scales: 28 days and 14 days). This shows that the dispersion degrees of two energy-intensity-calculation results also have little difference. In other words, the performance of two energy-intensity models is similar in the LTS region. Furthermore, the variation coefficient of TEIM is slightly smaller than that of NEIM. Consequently, the performance of TEIM is slightly better than NEIM.

(2)

CTS region

The variation coefficient of two energy-intensity models is characterized as follows in the CTS region:

The variation coefficient of two energy-intensity models increases gradually with the decrease of time scale, but it is still similar. On the one hand, the performance of two energy-intensity models has begun to deteriorate with the decrease of time scale. On the other hand, their performance is still similar.

The variation coefficient of the traditional intensity model is gradually larger than that of NEIM with the decrease of time scale. It shows that the deterioration degree of TEIM gradually becomes greater than that of NEIM.

Generally, although the performance of NEIM is not much different from that of TEIM, the performance of TEIM has been gradually worse than that of NEIM in CTS region.

(3)

STS region

The variation coefficient of two energy-intensity models is characterized as follows in the STS region:

The variation coefficient of two energy-intensity models has increased significantly with the decrease of time scale.

At any STS, the variation coefficient of traditional energy intensity is much greater than that of NEIM.

Therefore, TEIM has become ineffective in the STS region. That is, the performance of NEIM is obviously better than that of TEIM in the STS region.

3.3.2. NEIM Validity Analysis at Different Time Scales

TEIM is essentially oriented to production results. In actual production, TEIM is generally applied to the energy-intensity calculation (total energy consumption/production output in statistical time period) at daily, weekly, monthly, or annual time scales. The common opinion is that TEIM is valid at LTS. If NEIM is consistent with TEIM at LTS, it is considered that NEIM is also effective.

(1)

NEIM validity analysis in the LTS and CTS regions

As shown in Table 2, regardless of energy-intensity average value or energy-intensity variation coefficient, there is little difference between NEIM and TEIM in the LTS and CTS regions. Because of the validity of TEIM in the LTS region and CTS region, NEIM is as valid as TEIM in the LTS and CTS regions. It should also be noted that the calculated results of NEIM and TEIM have begun to shift in the CTS region.

(2)

NEIM validity analysis in the STS region

There is a great possibility of production output fluctuation in the STS region. There is no production output at a certain STS. At this time, the calculation result of TEIM is infinite at this STS. Furthermore, the possibility of violent energy-intensity fluctuation increases with the decrease of time scale for TEIM. As shown in Table 2, energy-intensity variation coefficient increases with the decrease of time scale. Therefore, TEIM has gradually failed with the reduction of time scale. Fortunately, the increasing range of energy intensity average value and energy-intensity variation coefficient is very limited in the STS region. Consequently, NEIM is still valid in the STS region.

3.3.3. Summary

Generally, NEIM has wider applicability than TEIM. The main reason is that TEIM is oriented to production results, whereas NEIM is oriented to production process. Therefore, TEIM will lose the effective workpiece-production output information in production process at a certain time scale. Furthermore, the calculation error of the traditional energy- intensity model arises, especially in the STS region.

4. Discussion

As shown in Figure 5, the whole statistical time period has been divided into four areas according to a ‘28 days’ time scale, namely area I, area II, area III, area IV. Accordingly, each area shows only one energy-intensity average value over the ‘28 days’ time scale. Each area shows two energy intensity average values at the ‘14 days’ time scale. Each area shows four energy intensity average values over the ‘7 days’ time scale. Each area shows 28 energy intensity average values at the ‘1 day’ time scale.

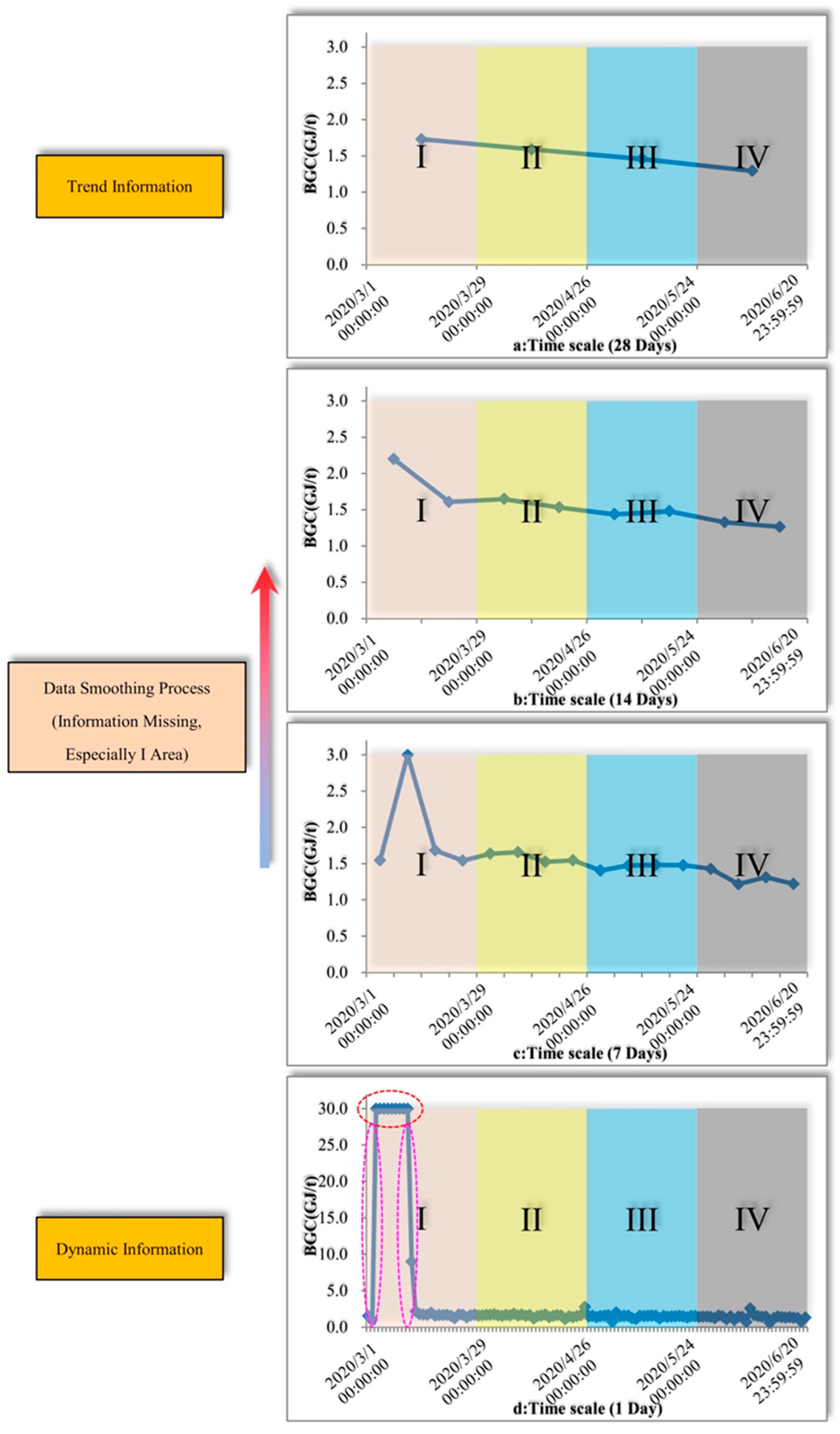
4.1. Time Scale and Information Expression

Time scale and information expression can be achieved through Figure 5.

Essentially, the calculation result of energy intensity at LTS is the coarsening process of the calculation result of energy intensity at STS, that is, the smoothing process. It mainly embodies the following two characteristics of the smoothing process.

4.1.1. Production Status Information Loss

As shown in Figure 5d (‘1 day’ time scale), the red circular frame in area I is the energy-intensity characteristic of the reheating furnace when it is shut down. Strictly, the production output at the time of shutdown is 0, and energy intensity is infinite. For convenience, it has been replaced by 30, and the same below. Unfortunately, the production status information has been completely lost at ‘7 days’, ’14 days’, ’28 days’ time scales.

4.1.2. Other Dynamic Information Loss

Because the factors restricting the production process (equipment status, upstream and downstream production status, gas supply, etc.) have great uncertainty at STS, the calculation results of energy intensity are more volatile. With the continuous increase of time scale, the uncertainly of these influencing factors will decrease, and the volatility of energy intensity will also decrease. Therefore, in the smoothing process from STS to LTS, the characteristic information of energy-intensity dynamic operation is continuously lost.

Generally, more dynamic information of energy intensity has been reflected at STS, whereas energy intensity reflects more trend information at LTS.

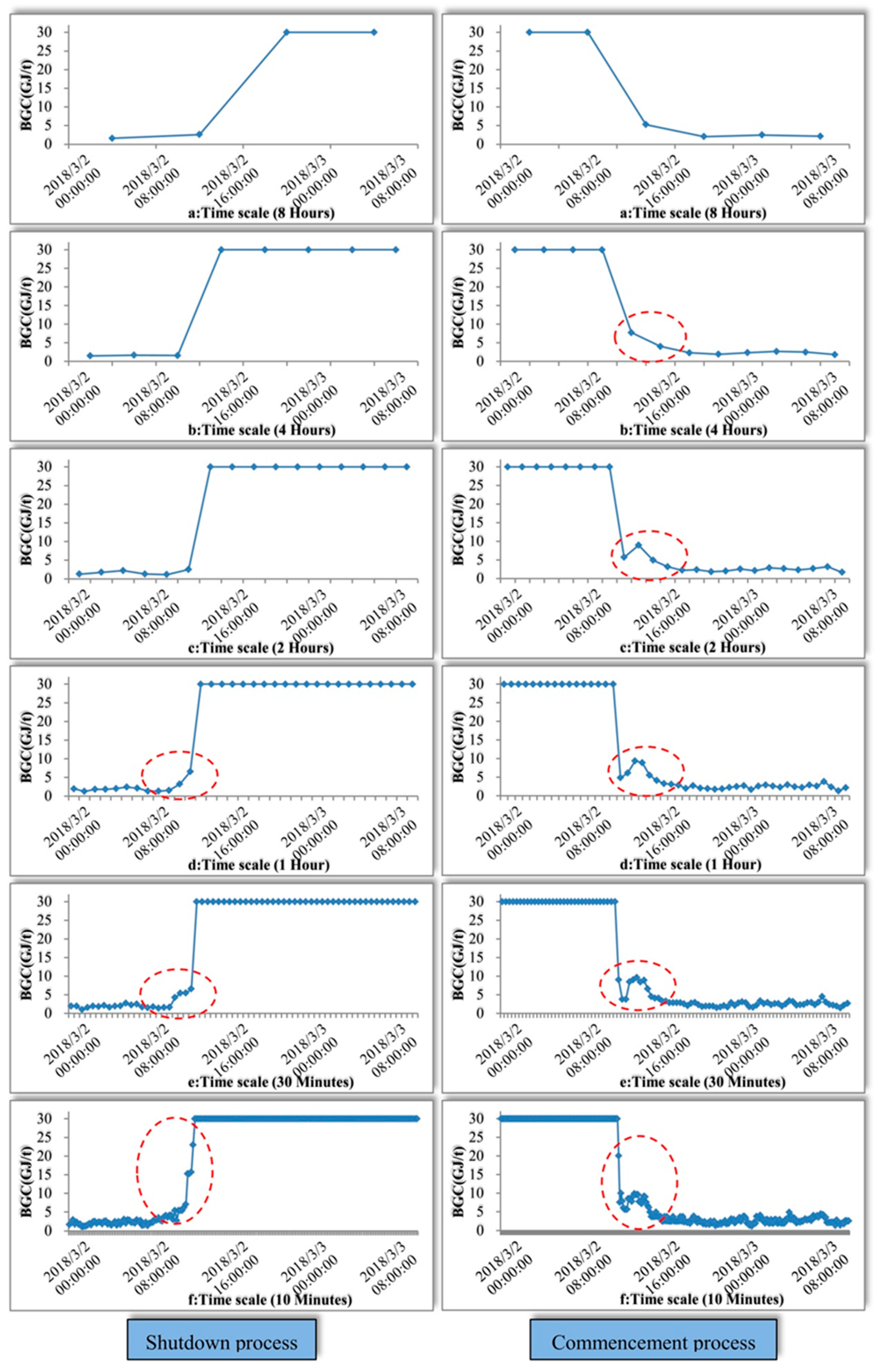
4.2. Energy Intensity Transient Dynamic Characteristics at STS

We further analyzed area I in Figure 5d, that is, the two fuchsia parts. There is a transition process from normal production to shutdown (shutdown process) and from shutdown to normal production (commencement process). However, at an LTS (such as the ‘1 day’ time scale), the performance of the transition process is not obvious. In order to be more familiar with this transition process, it should be carried out at a smaller scale. Therefore, the shutdown process and commencement processes of case-reheating furnaces are all shown at different STSs (‘8 h’, ‘4 h’, ‘2 h’, ‘1 h’, ’30 min’, and ’10 min’ time scales), as shown in Figure 6.

4.2.1. Shutdown Process

During the shutdown process, the energy intensity of a reheating furnace is a process of gradually increasing to infinity (30 GJ/t). With the gradual decrease of time scale, an increasing trend in shutdown process becomes more and more obvious, especially for less than ‘1 h’ time scales, as shown in the red block diagram of Figure 5 during the shutdown process.

4.2.2. Commencement Process

In commencement processes, the energy intensity of a reheating furnace is a process of gradual reduction. Energy-intensity levels can be gradually stabilized only after the whole production process is stable, especially for less than ‘4 h’ time scales, as shown in the red block diagram of Figure 6 during the commencement process.

5. Conclusions

In this paper, a NEIM, which is oriented to quasi-continuous production, has been established. The NEIM includes three main stages: the determination of statistical period and time scale; the definition of work-piece valid weight; and the establishment of NEIM. The case study indicates that NEIM has a wider range of application scenarios compared to TEIM. The specific conclusions are as follows:

(1)

On the basis of characteristics of quasi-continuous production, NEIM has been established. Through the comparative analysis of the validity with TEIM, NEIM has wider applicability at different time scales. In particular, TEIM has failed at STS, whereas NEIM is still valid.

(2)

The application of NEIM for reheating furnaces at different time scales (10 min, 30 min, 1 h, 2 h, 4 h, 8 h, 1 day, 7 days, 14 days, 28 days) shows that energy-intensity calculation results reflect more trend information at LTS, whereas production status information has been completely lost in some LTSs (7 days, 14 days, 28 days). Meanwhile, the energy-intensity calculation results can express clearer representation of production-status information in some STSs, especially for 10 min STS or 30 min STS during shutdown and commencement process.

(3)

According to the physical demand, TEIM and NEIM can be selected. Significantly, these two models have different data requirements. On the one hand, TEIM only requires production data and energy consumption data during statistical periods. On the other hand, energy intensity can be calculated by combing specific manufacturing-technology and production-process data. Therefore, NEIM requires better data requirements than TEIM.

(4)

NEIM can be applied not only to quasi-continuous production such as reheating furnaces, but also to other similar production processes. Furthermore, through energy-intensity calculation at different time scales, energy-supply-strategy rationality can be further evaluated and discussed for different energy consuming facilities.