Impacts of Inlet Circumferential Distortions on the Aerodynamic Performance of a Transonic Axial Compressor
Abstract
:1. Introduction
2. Numerical Method
2.1. Distortion Model
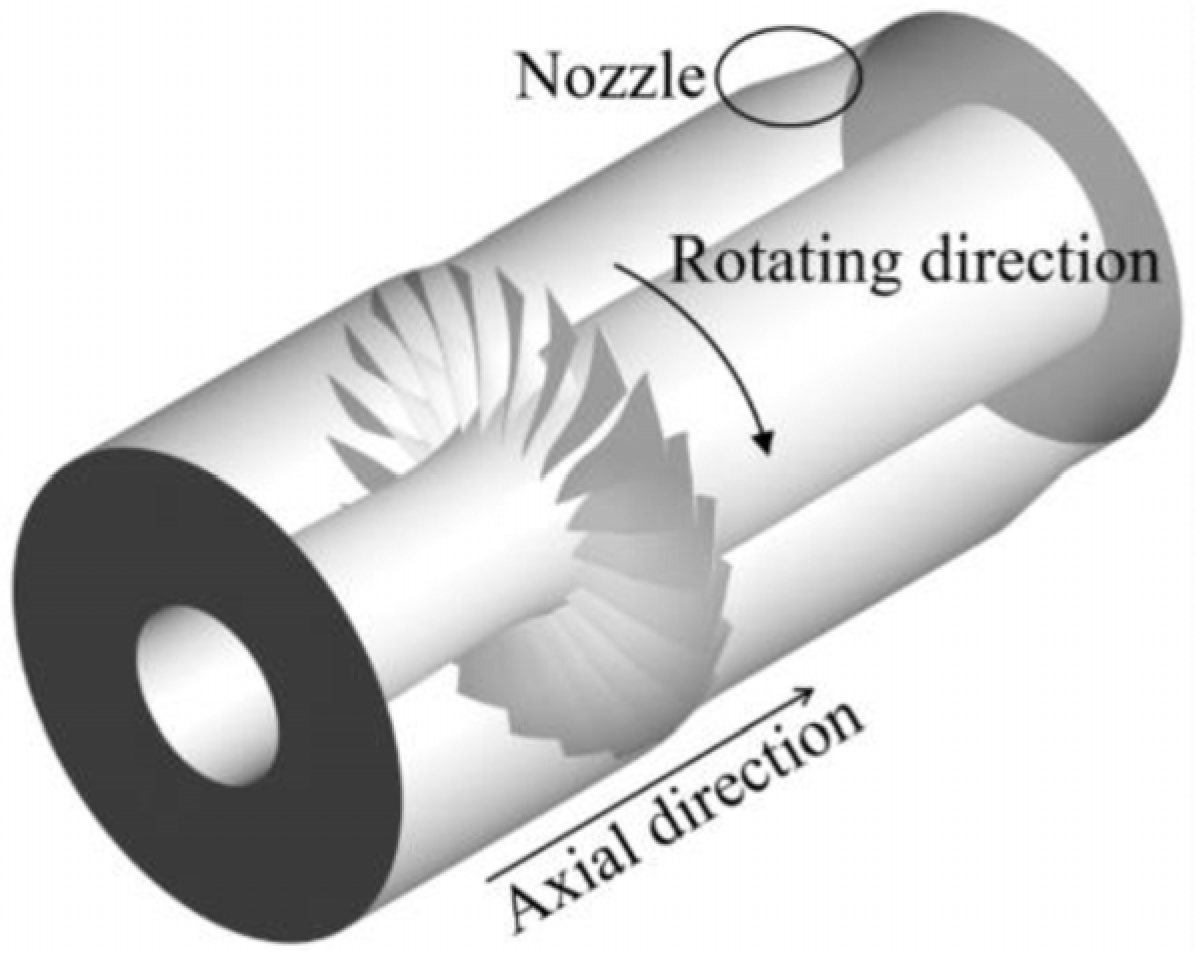
2.2. Compressor Model
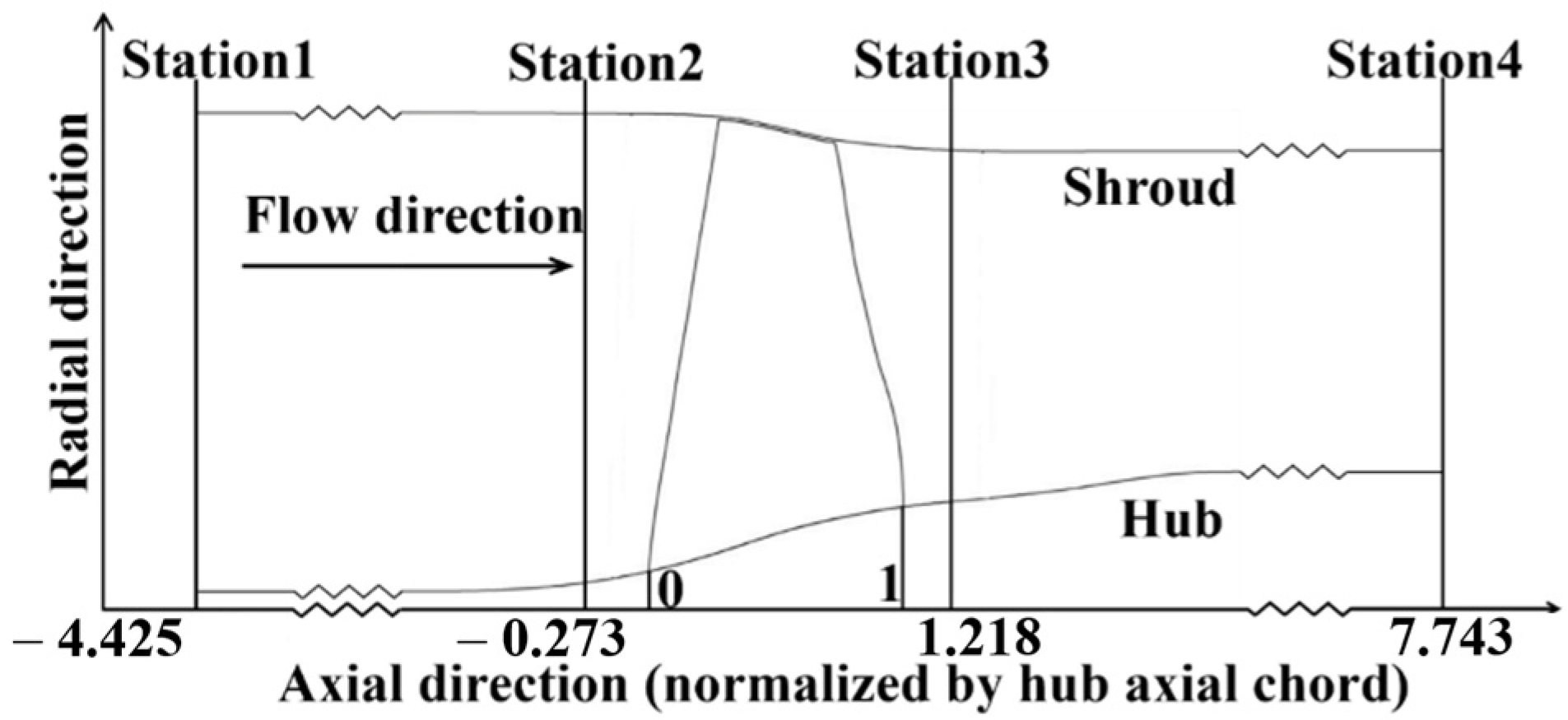
2.3. Computational Scheme
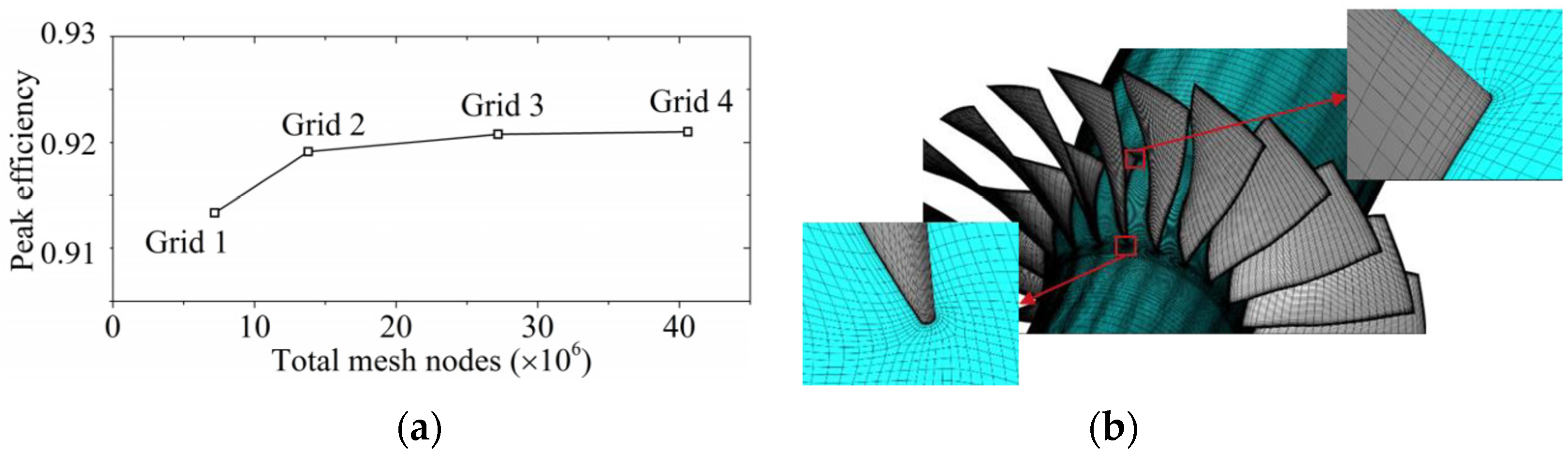
2.4. Grid Strategy
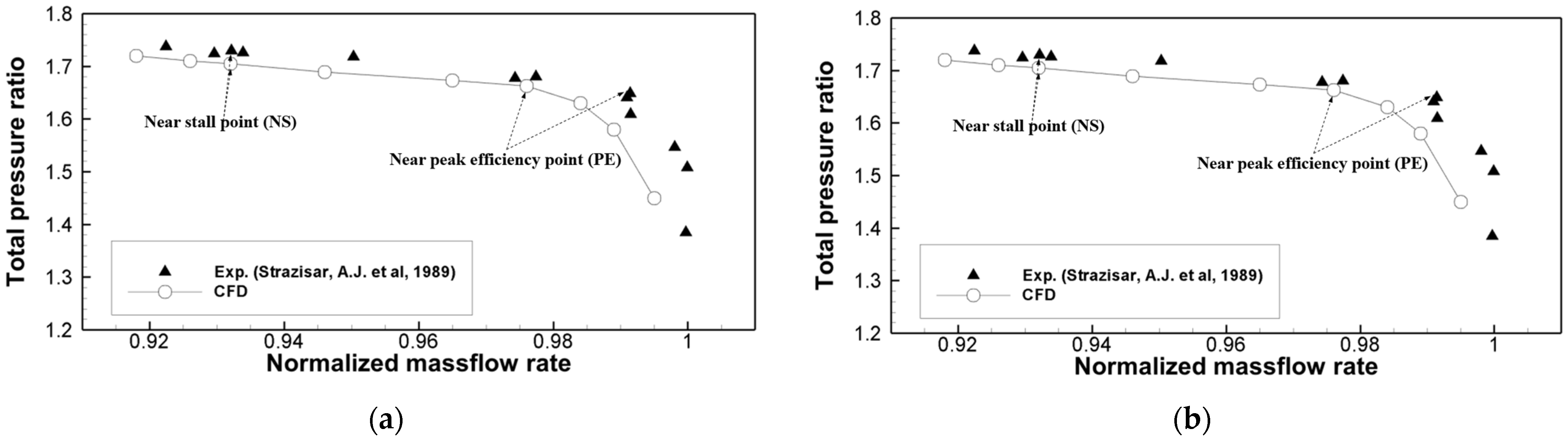
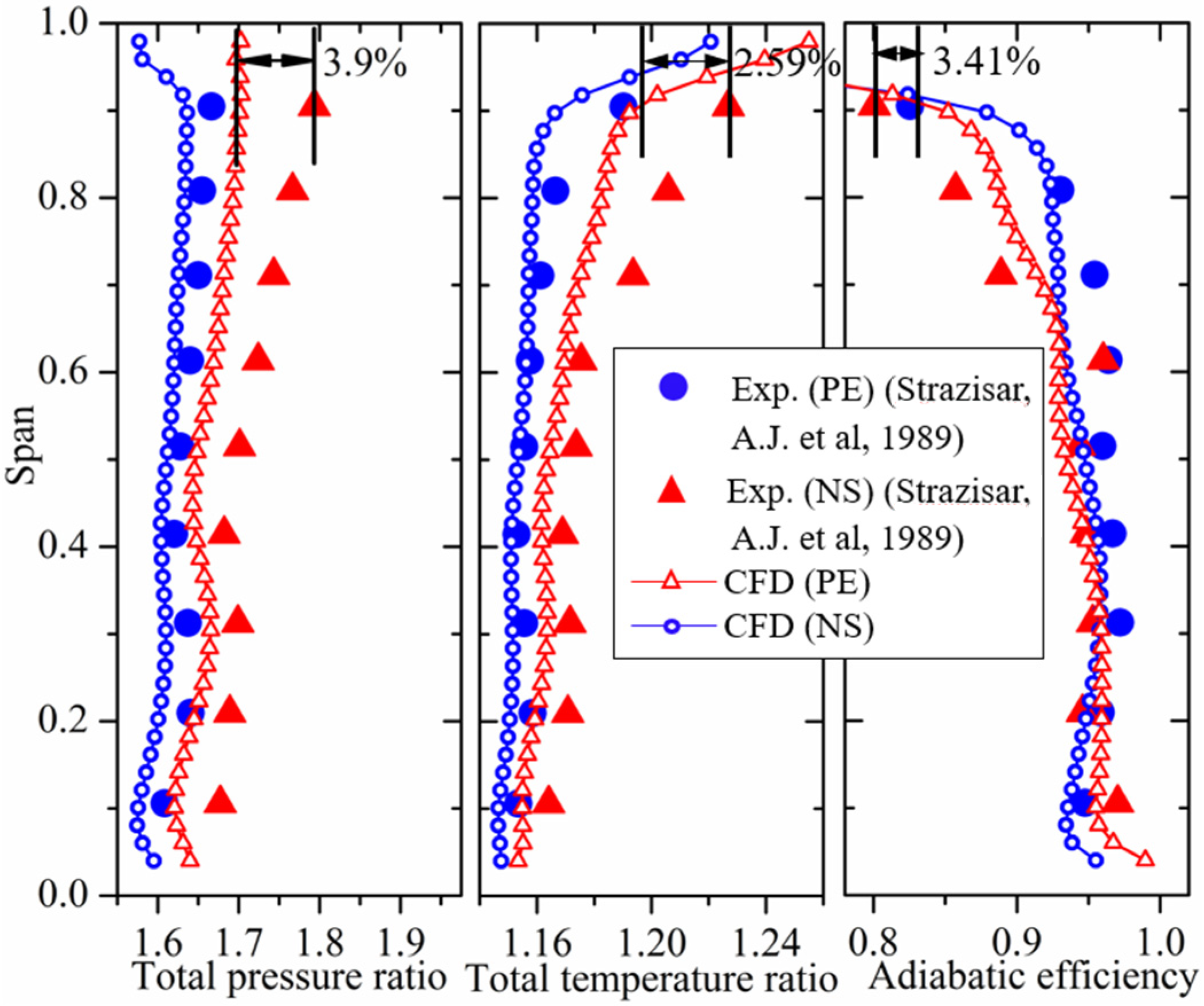
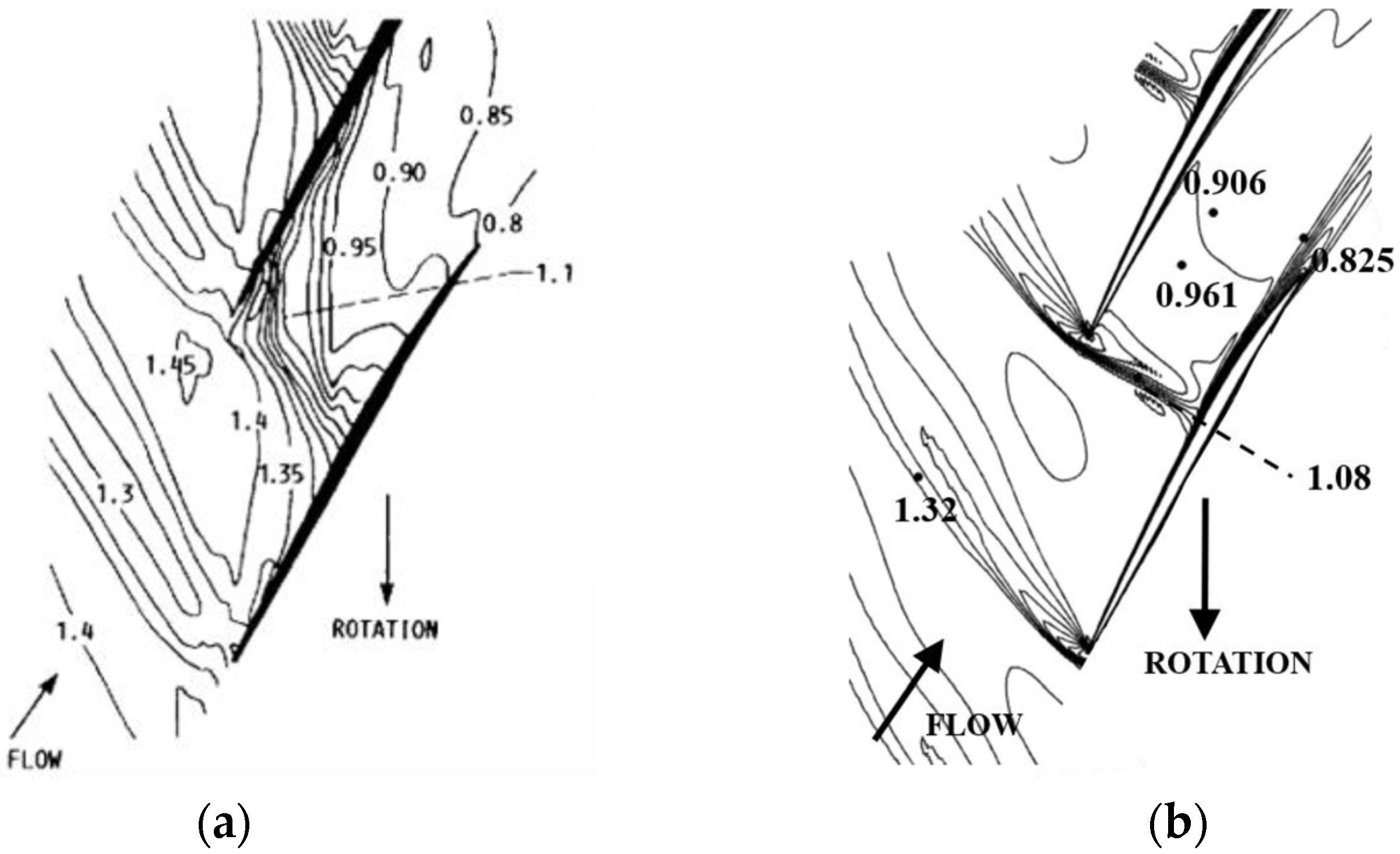
2.5. Validation
3. Results and Discussion
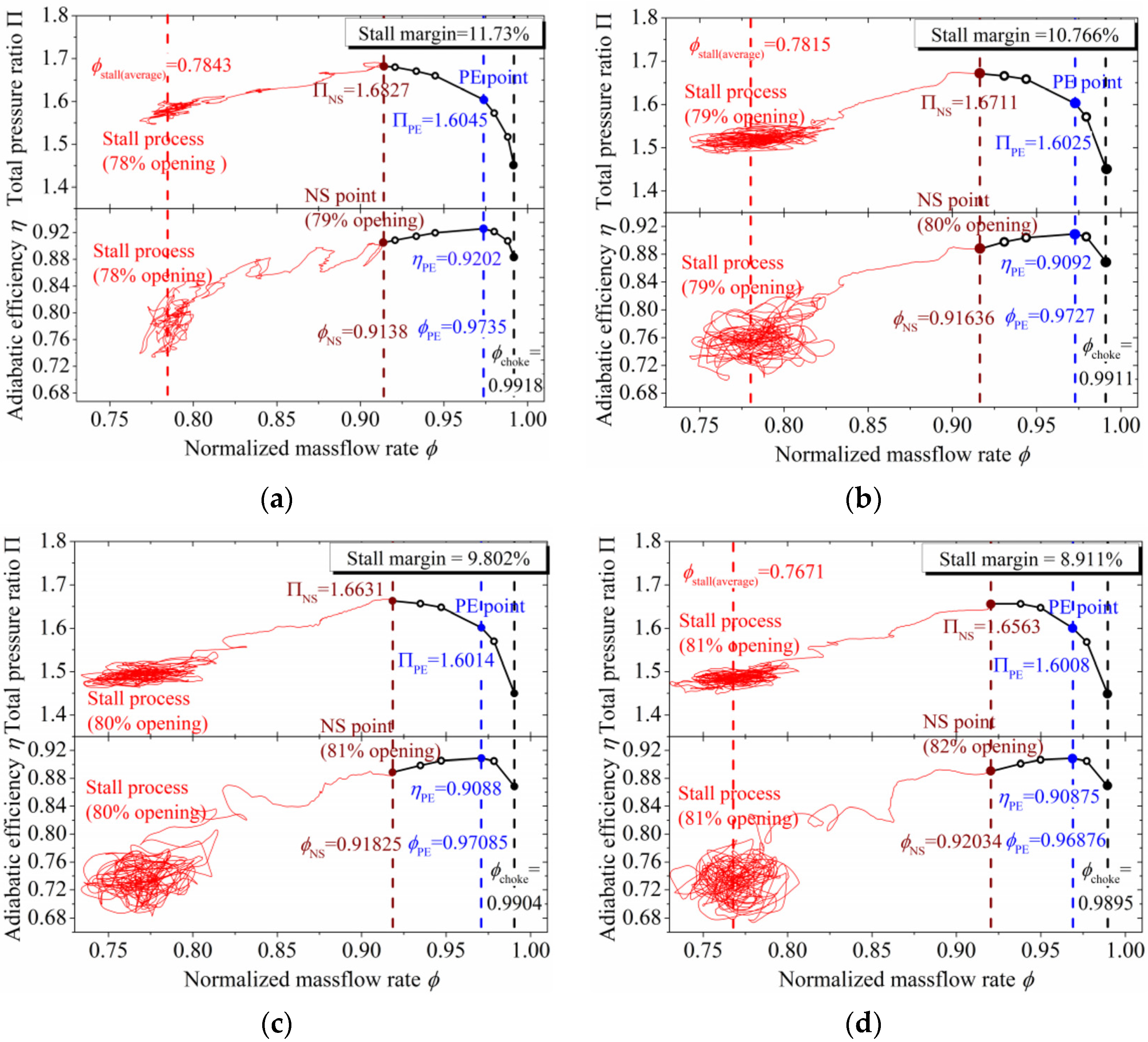
3.1. Overall Performance
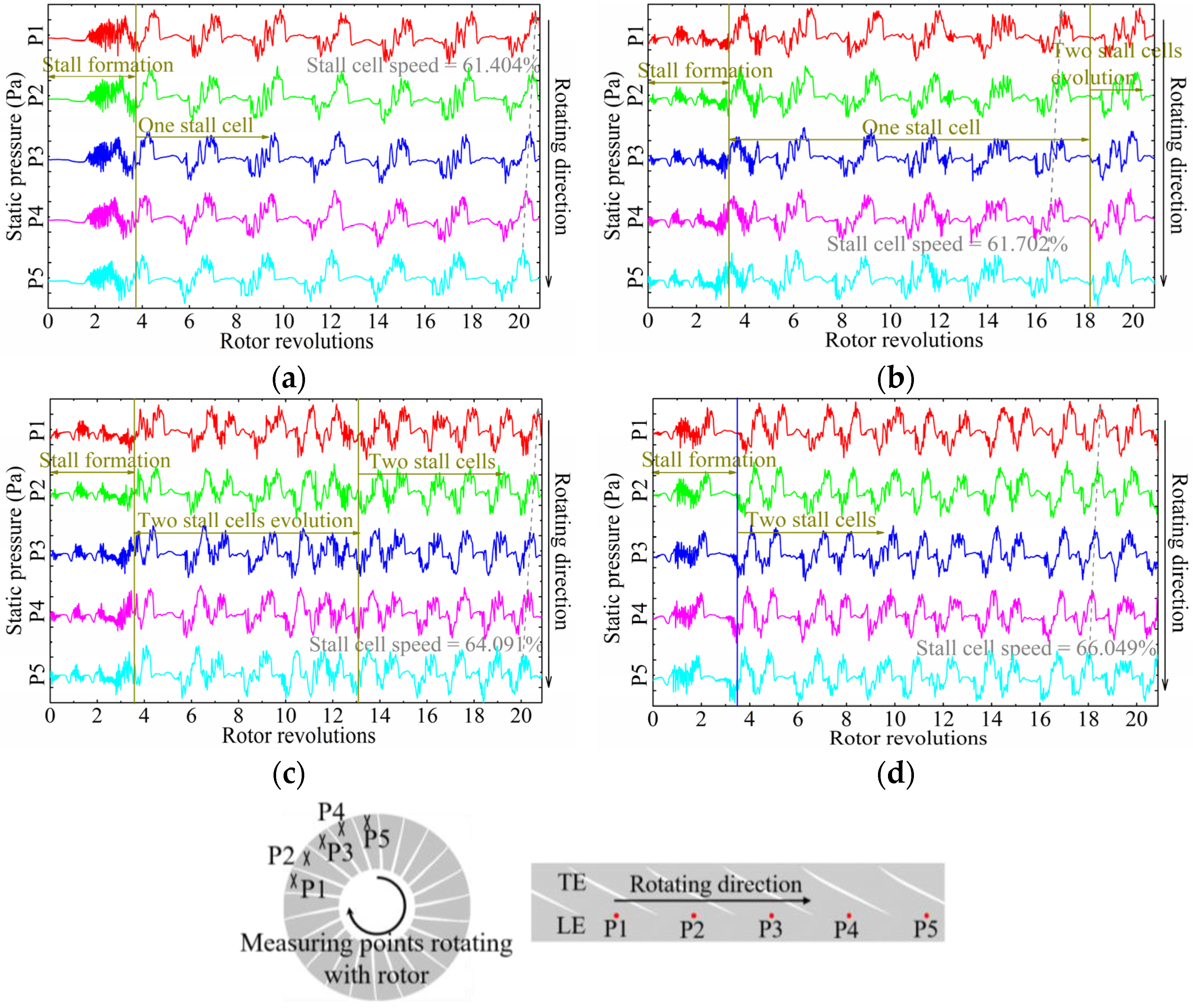
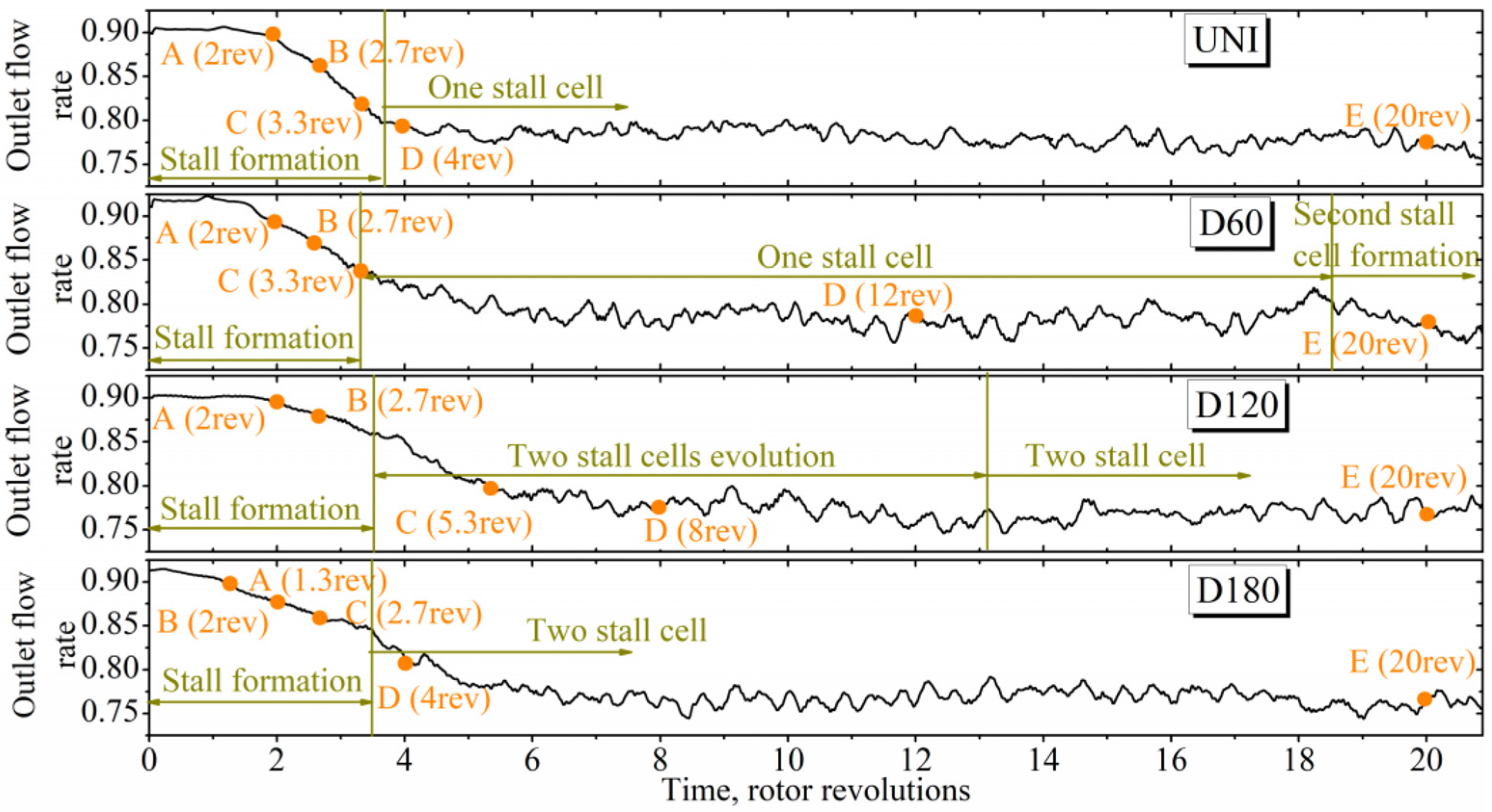
3.2. Impacts on Stall Process
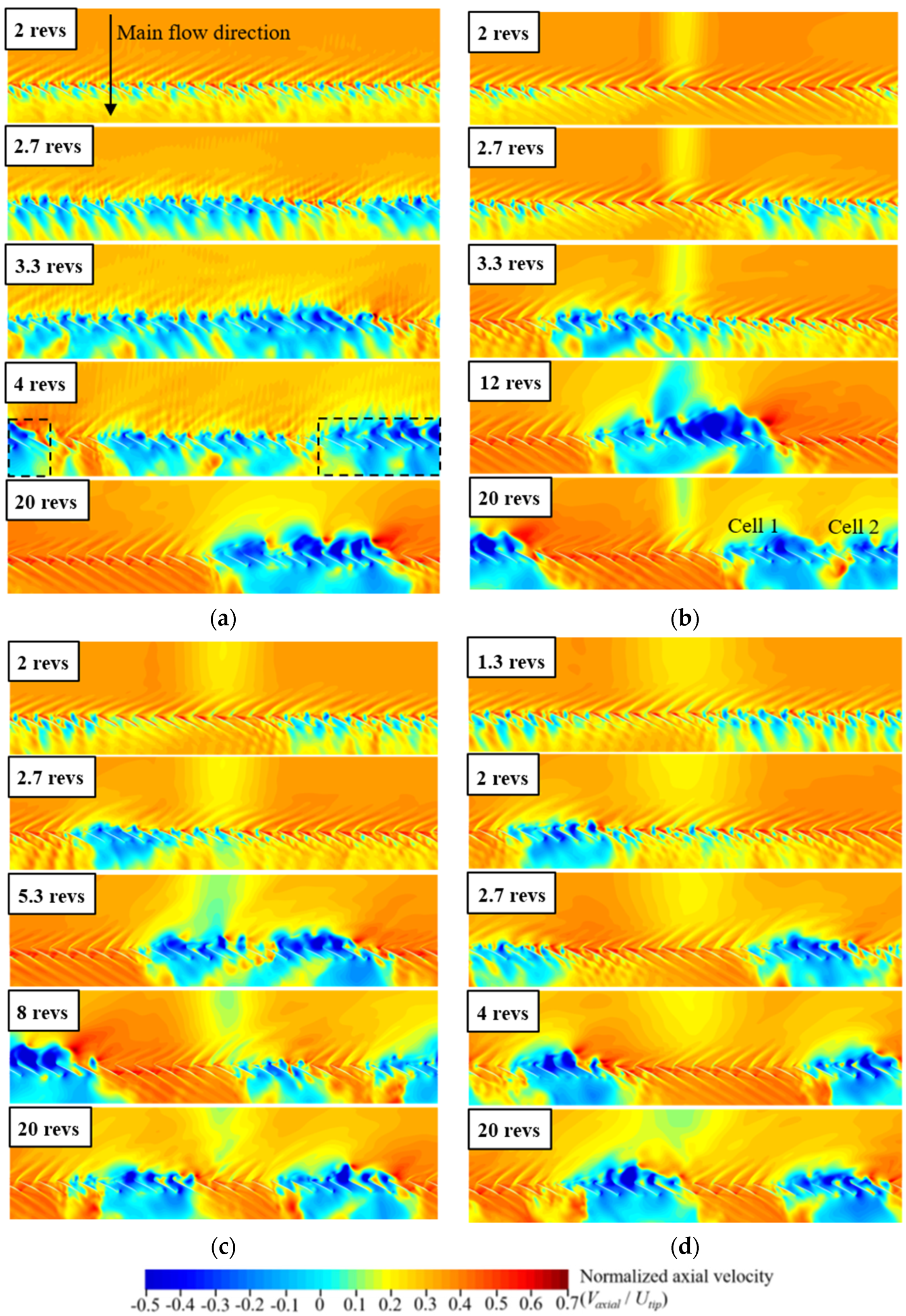
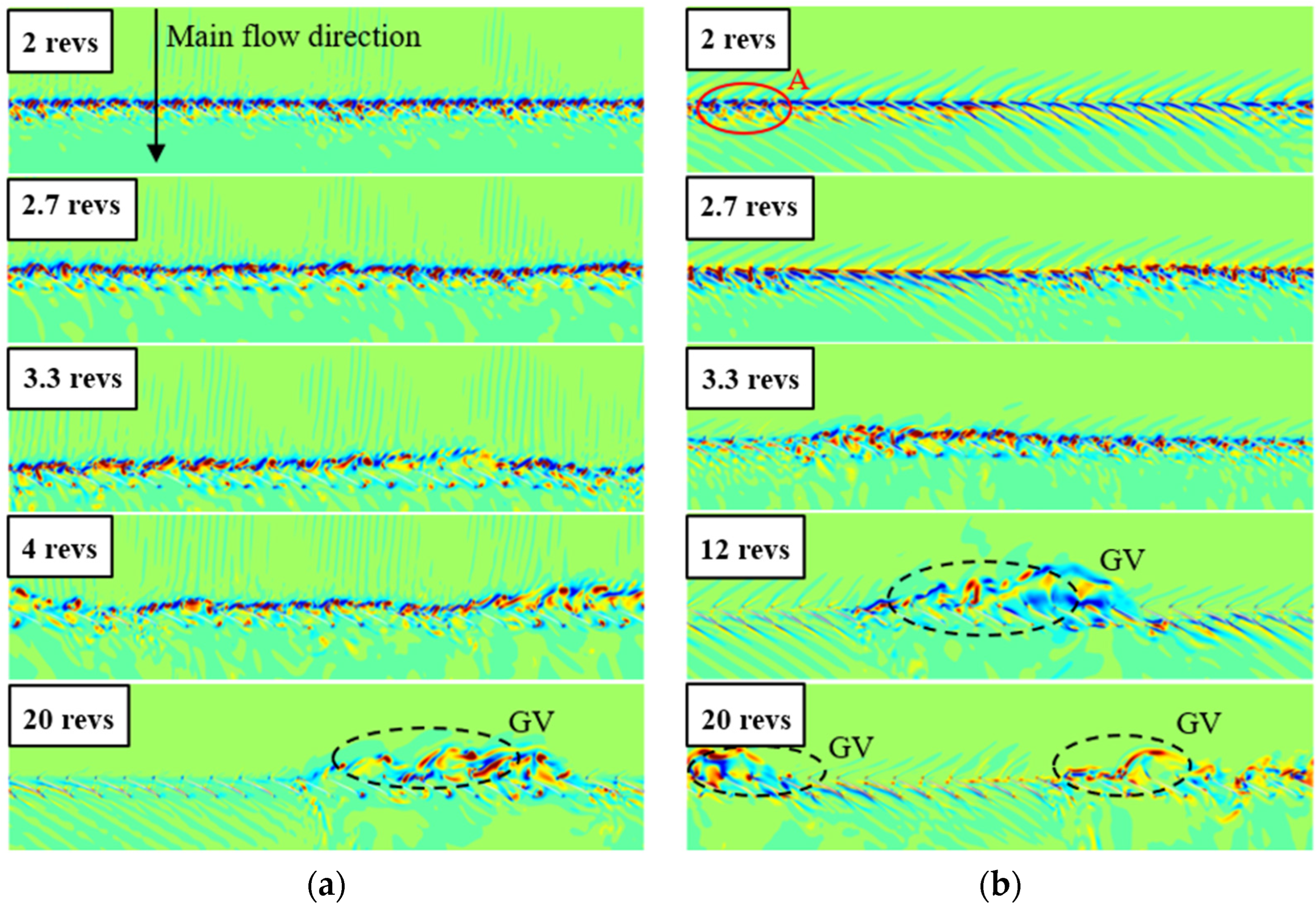
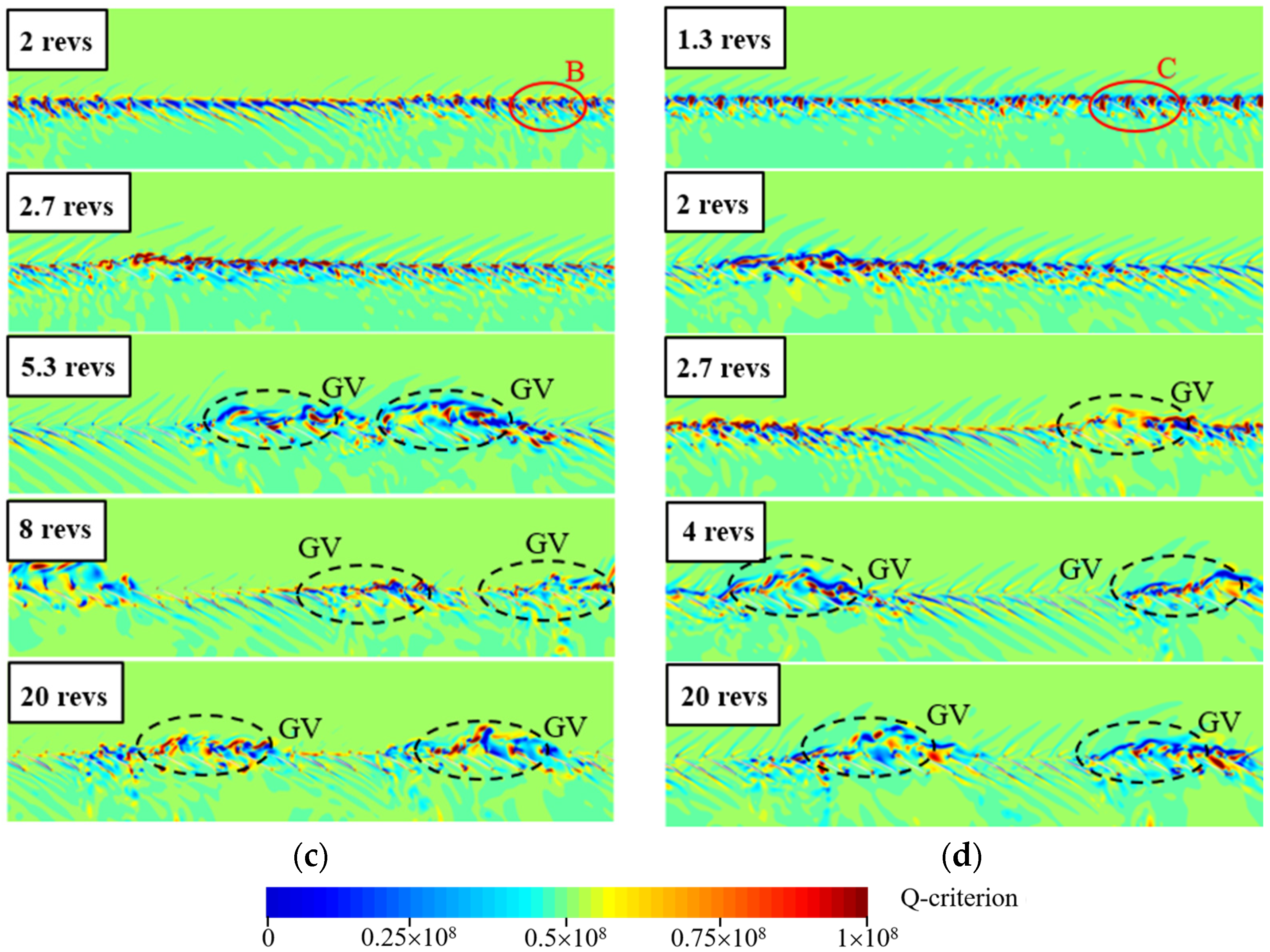
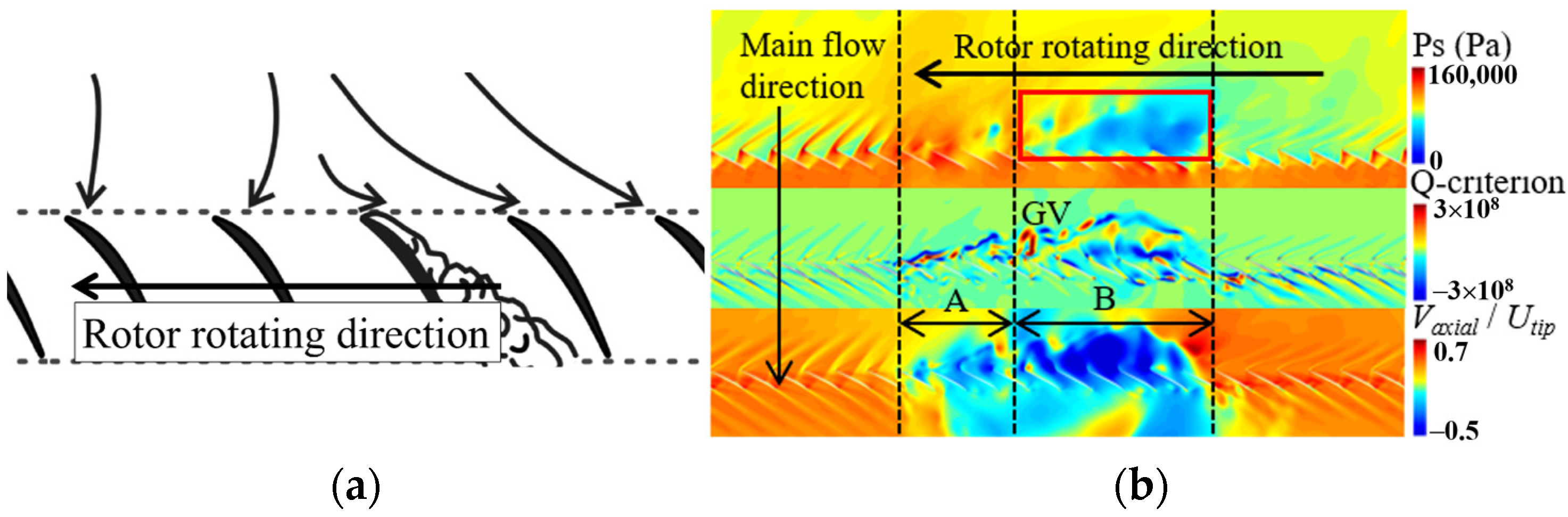
3.3. Formation Process of the Initial Stall Cell
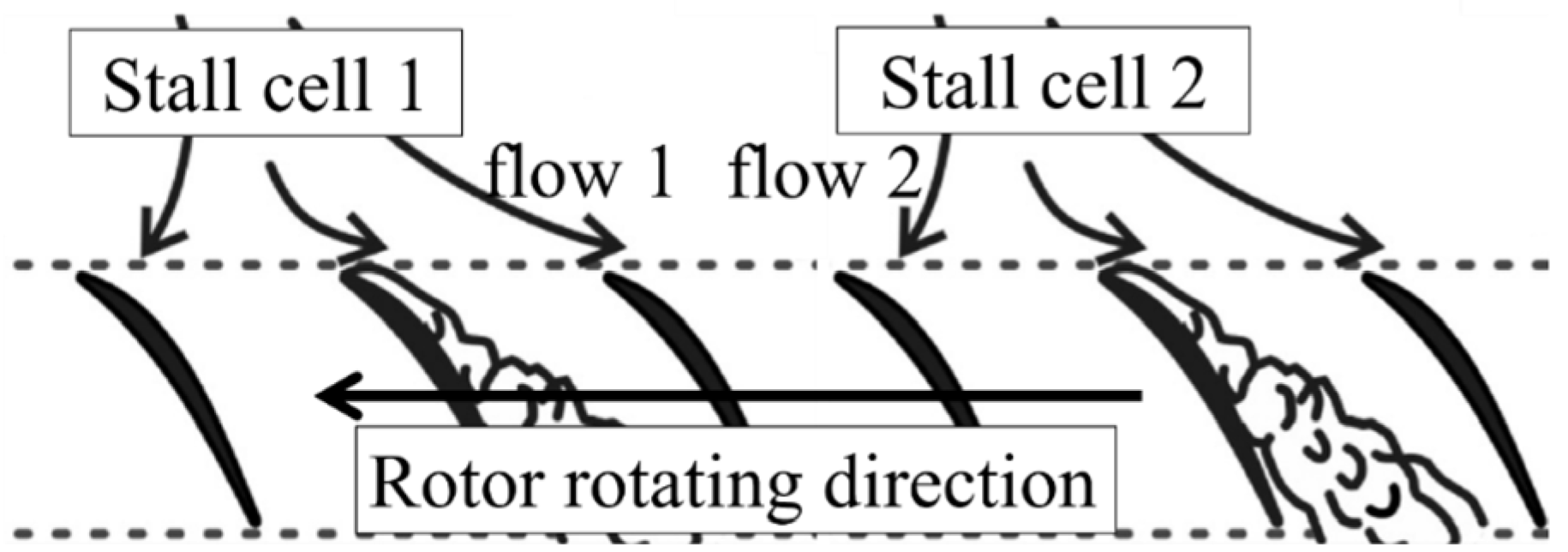
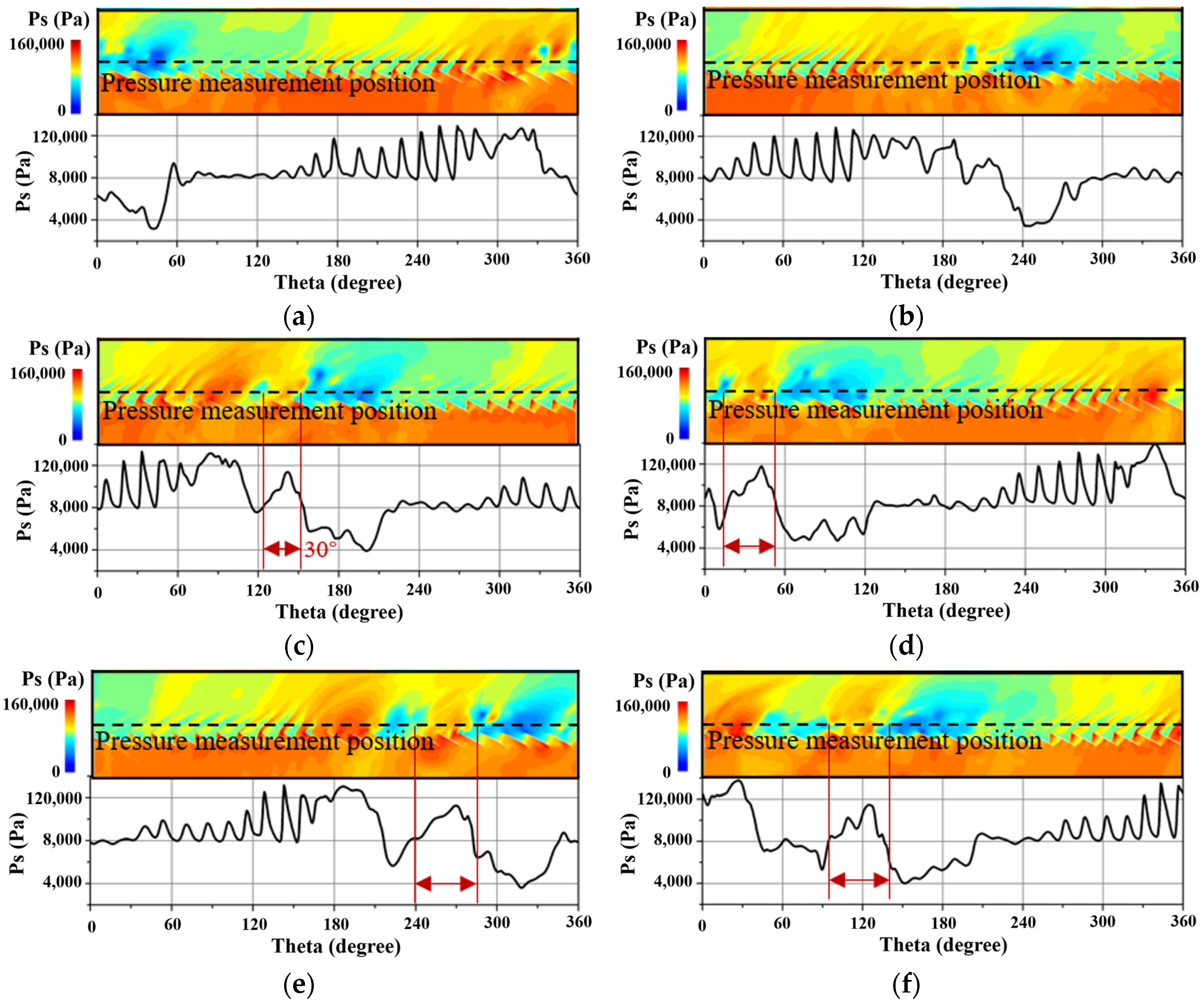
3.4. Propagation of the Stall Cells
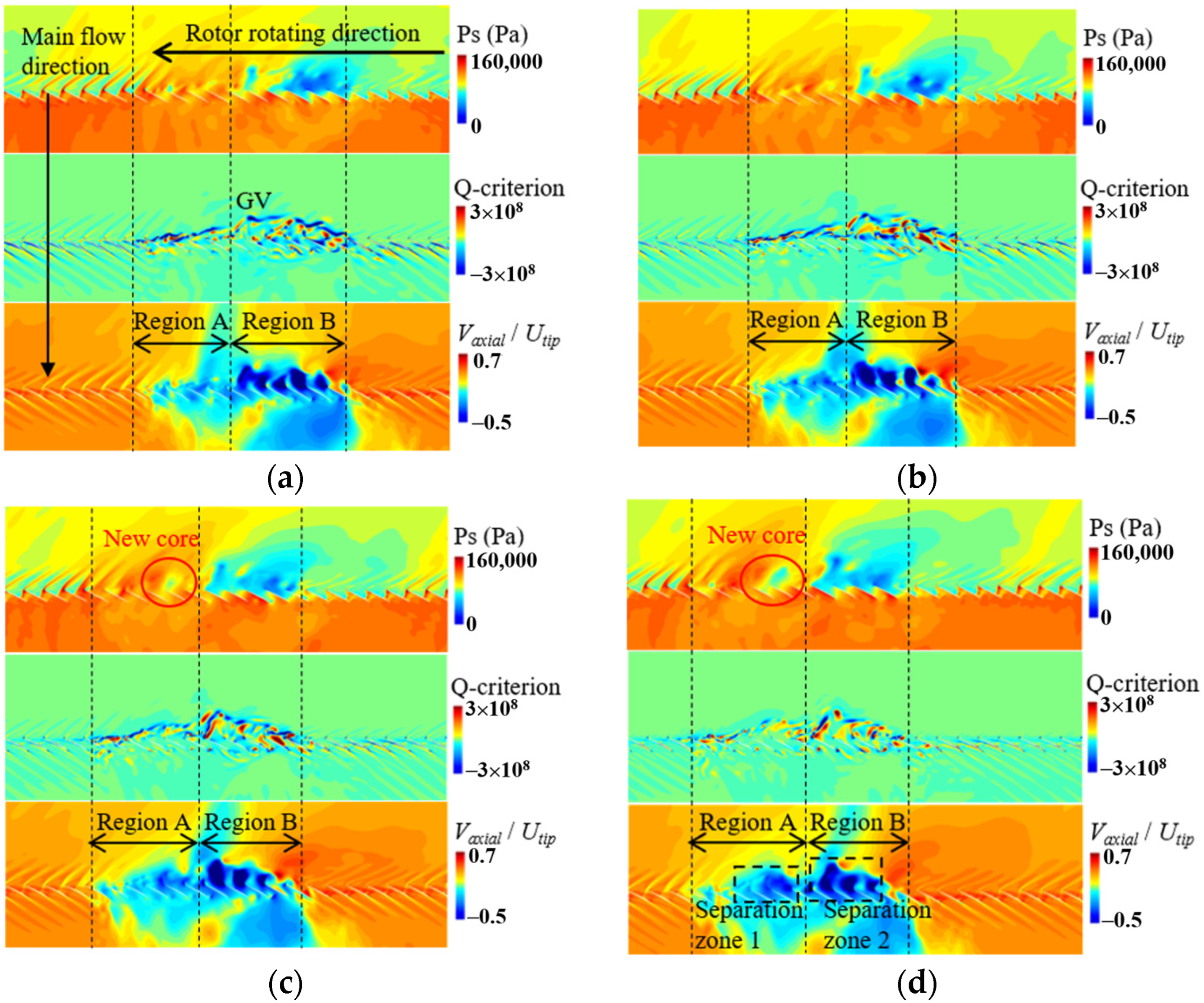
3.5. Formation Process of the Second Stall Cell
3.6. Rotating Distortion
4. Conclusions
- ▪
- It was due to the distorted inflow that the decreasing of the choke flow, the efficiency, and the total pressure ratio were observed. Moreover, the performance deteriorated further when the influence range of distortion increased. Furthermore, compared with the uniform inflow, the stall margins in D60_10, D120_10, and D180_10 cases decreased by 0.964%, 1.928%, and 2.819%, respectively.
- ▪
- Based on the analysis during the stall process, it was found that only one stall cell was produced with uniform inflow within 21 revs. Meanwhile, GV could also be found in the flow field, which is believed to be one of the most important characteristics of a stall cell.
- ▪
- Under the distorted inlet conditions, a new vortex core was produced. When the vorticity of the core was strong enough, a secondary stall cell was formed around the core. The new stall cell could be produced earlier and faster with the increasing of the distorted region. Because of the repulsive interaction between two stall cells, the circumferential distance between the cells became larger and larger until their relative position remained stable.
- ▪
- The stall margin was clearly influenced by the rotating distortion. It was noted that the margin decreased sharply when the distortion rotating speed was positive and as much as 0.75.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| m | mass flow rate (kg/s) |
| mPE | mass flow rate under peak efficiency condition (kg/s) |
| mNS | mass flow rate under near stall condition (kg/s) |
| Ps | static pressure (N/m2) |
| r | radius (m) |
| rhub | hub radius (m) |
| rshroud | shroud radius (m) |
| UTip | blade tip rotating speed (m/s) |
| Vaxial | axial velocity (m/s) |
| γ | distortion strength coefficient |
| θ | pitch wise position (rad) |
| λ | spanwise position |
| Π | total pressure ratio |
| ρ | density (kg/m3) |
| ρref | reference density (kg/m3) |
| φ | relative phase angle (rad) |
| ω1 | angular speed of distortion (rad/s) |
References
- Reid, C. The Response of Axial Flow Compressors to Intake Flow Distortion. In Proceedings of the ASME Turbo Expo (ASME Paper 69-GT-29), Cleveland, OH, USA, 9–13 March 1969. [Google Scholar]
- Stenning, A.H. Inlet Distortion Effects in Axial Compressors. J. Fluids Eng. 1980, 102, 7–13. [Google Scholar] [CrossRef]
- Hynes, T.P.; Greitzer, E.M. A Method for Assessing Effects of Circumferential Flow Distortion on Compressor Stability. J. Turbomach. 1987, 109, 371–379. [Google Scholar] [CrossRef]
- Morton, W.K.; Lazalier, G.R.; Rose, C.D.; Lauer, R.F. On-Line Distortion Analysis System for Inlet-Engine Testing. In Proceedings of the ASME Turbo Expo (ASME Paper 91-GT-166), Orlando, FL, USA, 3–6 June 1991. [Google Scholar]
- Fortin, J.; Moffatt, W.C. Inlet Flow Distortion Effects on Rotating Stall. In Proceedings of the ASME Turbo Expo (ASME Paper 90-GT-215), Brussels, Belgium, 11–14 June 1990; Volume 79047, p. V001T01A068. [Google Scholar]
- Spakovszky, Z.S.; Weigl, H.J.; Paduano, J.D.; van Schalkwyk, C.M.; Suder, K.L.; Bright, M.M. Rotating Stall Control in a High-Speed Stage With Inlet Distortion: Part I—Radial Distortion. J. Turbomach. 1999, 121, 510–516. [Google Scholar] [CrossRef]
- Spakovszky, Z.S.; van Schalkwyk, C.M.; Weigl, H.J.; Paduano, J.D.; Suder, K.L.; Bright, M.M. Rotating Stall Control in a High-Speed Stage With Inlet Distortion: Part II—Circumferential Distortion. J. Turbomach. 1999, 121, 517–524. [Google Scholar] [CrossRef]
- Longley, J.P.; Shin, H.W.; Plumley, R.E.; Silkowski, P.D.; Day, I.J.; Greitzer, E.M.; Tan, C.S.; Wisler, D.C. Effects of Rotating Inlet Distortion on Multistage Compressor Stability. J. Turbomach. 1996, 118, 181–188. [Google Scholar] [CrossRef]
- Hah, C.; Rabe, D.C.; Sullivan, T.J.; Wadia, A.R. Effects of Inlet Distortion on the Flow Field in a Transonic Compressor Rotor. In Proceedings of the ASME Turbo Expo (ASME Paper 96-GT-547), Birmingham, UK, 10–13 June 1996. [Google Scholar]
- Yao, J.; Gorrell, S.E.; Wadia, A.R. High-Fidelity Numerical Analysis of Per-Rev-Type Inlet Distortion Transfer in Multistage Fans—Part I: Simulations With Selected Blade Rows. J. Turbomach. 2010, 132, 041014. [Google Scholar] [CrossRef]
- Yao, J.; Gorrell, S.E.; Wadia, A.R. High-Fidelity Numerical Analysis of Per-Rev-Type Inlet Distortion Transfer in Multistage Fans—Part II: Entire Component Simulation and Investigation. J. Turbomach. 2010, 132, 041015. [Google Scholar] [CrossRef]
- Zhao, B.; Sun, H.; Wang, L.; Song, M. Impact of Inlet Distortion on Turbocharger Compressor Stage Performance. Appl. Therm. Eng. 2017, 124, 393–402. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, F.; Chen, J.; Nie, C. Effects of Rotating Inlet Distortion on Flow Stability of an Axial Compressor. In Proceedings of the AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit (AIAA Paper 2007-5062), Cincinnati, OH, USA, 8–11 July 2007. [Google Scholar]
- Page, J.H.; Hield, P.; Tucker, P.G. Effect of Inlet Distortion Features on Transonic Fan Rotor Stall. J. Turbomach. 2018, 140, 071008. [Google Scholar] [CrossRef]
- Fuqun, C.; Wenlan, L.; Zongyuan, W.; Mengzi, C. An Experimental Investigation of Response of a Turbojet Engine to Inlet Distortion. In Proceedings of the ASME Turbo Expo (ASME Paper 85-IGT-12), Beijing, China, 1–7 September 1985. [Google Scholar]
- Li, H.D.; He, L. Single-Passage Analysis of Unsteady Flows Around Vibrating Blades of a Transonic Fan Under Inlet Distortion. J. Turbomach. 2002, 124, 285–292. [Google Scholar] [CrossRef]
- Zhu, G.; Liu, X.; Yang, B.; Song, M. A Study of Influences of Inlet Total Pressure Distortions on Clearance Flow in an Axial Compressor. J. Eng. Gas Turbines Power 2021, 143, 101010. [Google Scholar] [CrossRef]
- Strazisar, A.J.; Wood, J.R.; Hathaway, M.D.; Suder, K.L. Laser Anemometer Measurements in a Transonic Axial-flow Fan Rotor; NASA: Chicago, IL, USA, 1989. [Google Scholar]
- Menter, F.R. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Yang, B.; Gu, C. The Effects of Radially Distorted Incident Flow on Performance of Axial-Flow Fans With Forward-Skewed Blades. ASME J. Turbomach. 2013, 135, 011039. [Google Scholar] [CrossRef]
- Zhang, W.; Stapelfeldt, S.; Vahdati, M. Influence of the Inlet Distortion on Fan Stall Margin at Different Rotational Speeds. Aerosp. Sci. Technol. 2020, 98, 105668. [Google Scholar] [CrossRef]
- Zhang, W.; Vahdati, M. A Parametric Study of the Effects of Inlet Distortion on Fan Aerodynamic Stability. J. Turbomach. 2018, 141, 011011. [Google Scholar] [CrossRef]
- Zhu, G.; Yang, B. Optimization of Slots-Groove Coupled Casing Treatment for an Axial Transonic Compressor. J. Turbomach. 2020, 142, 081003. [Google Scholar] [CrossRef]
- Emmons, H.; Pearson, C.; Grant, H. Compressor Surge and Stall Propagation. Trans. Am. Soc. Mech. Eng. 1955, 77, 455–467. [Google Scholar] [CrossRef]
- Zhang, J.X. The Unseady Mechanism and the Role of Tip Clearance Flow in Distortion Induced Instability in an Axial Compressor. Doctral Thesis, Graduated School of the Chinese Academy of Sciences, Beijing, China, 2007. (In Chinese). [Google Scholar]

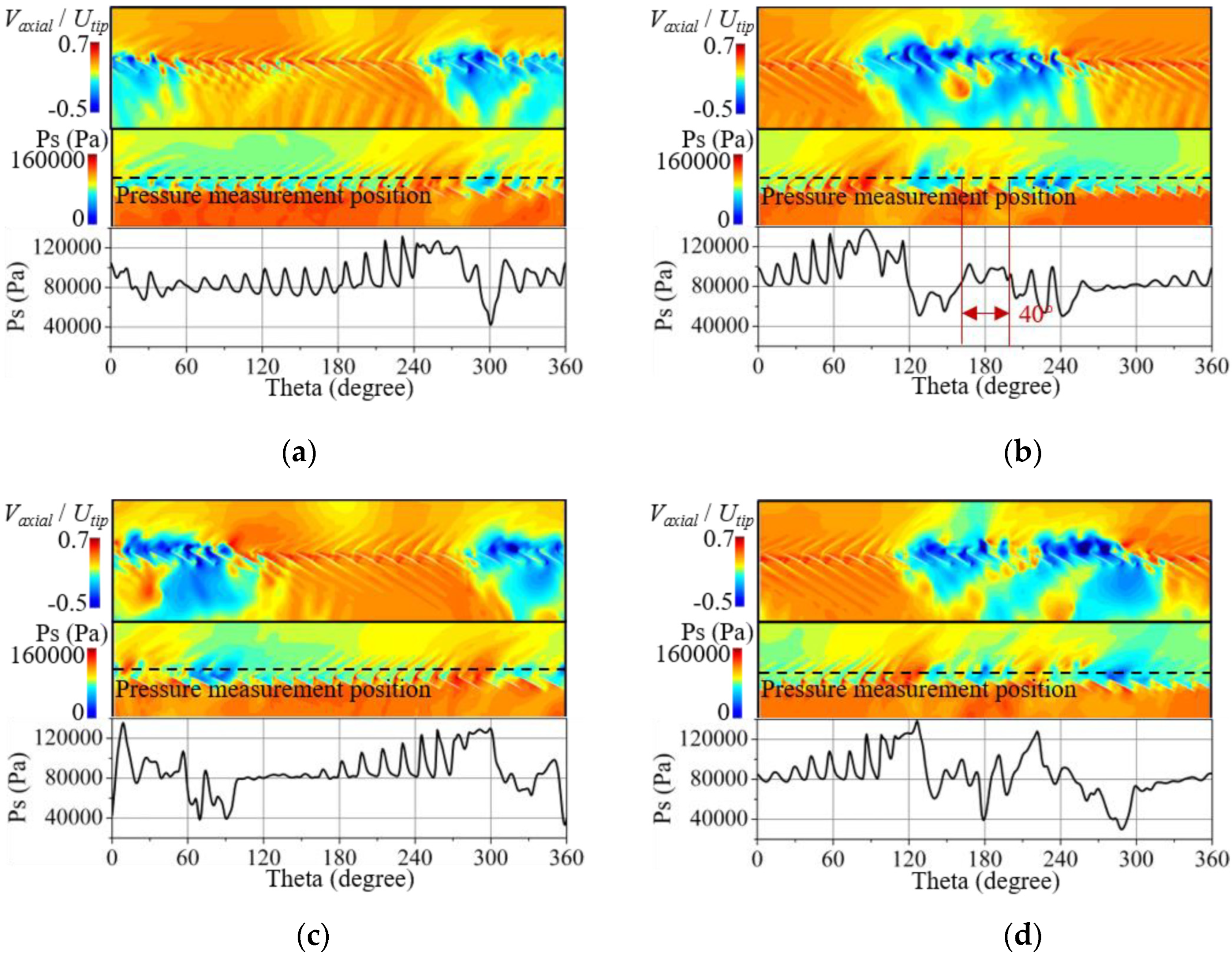
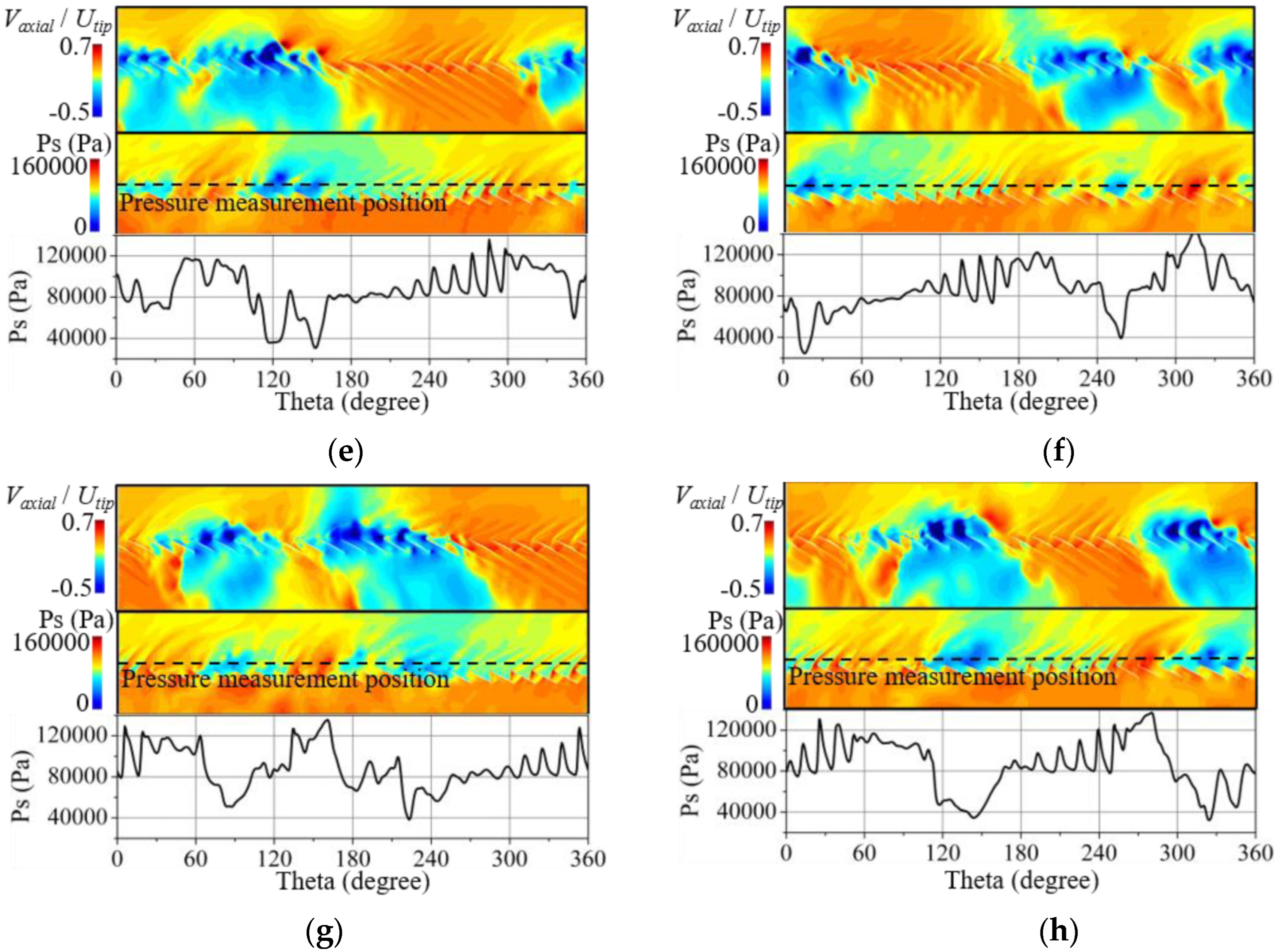
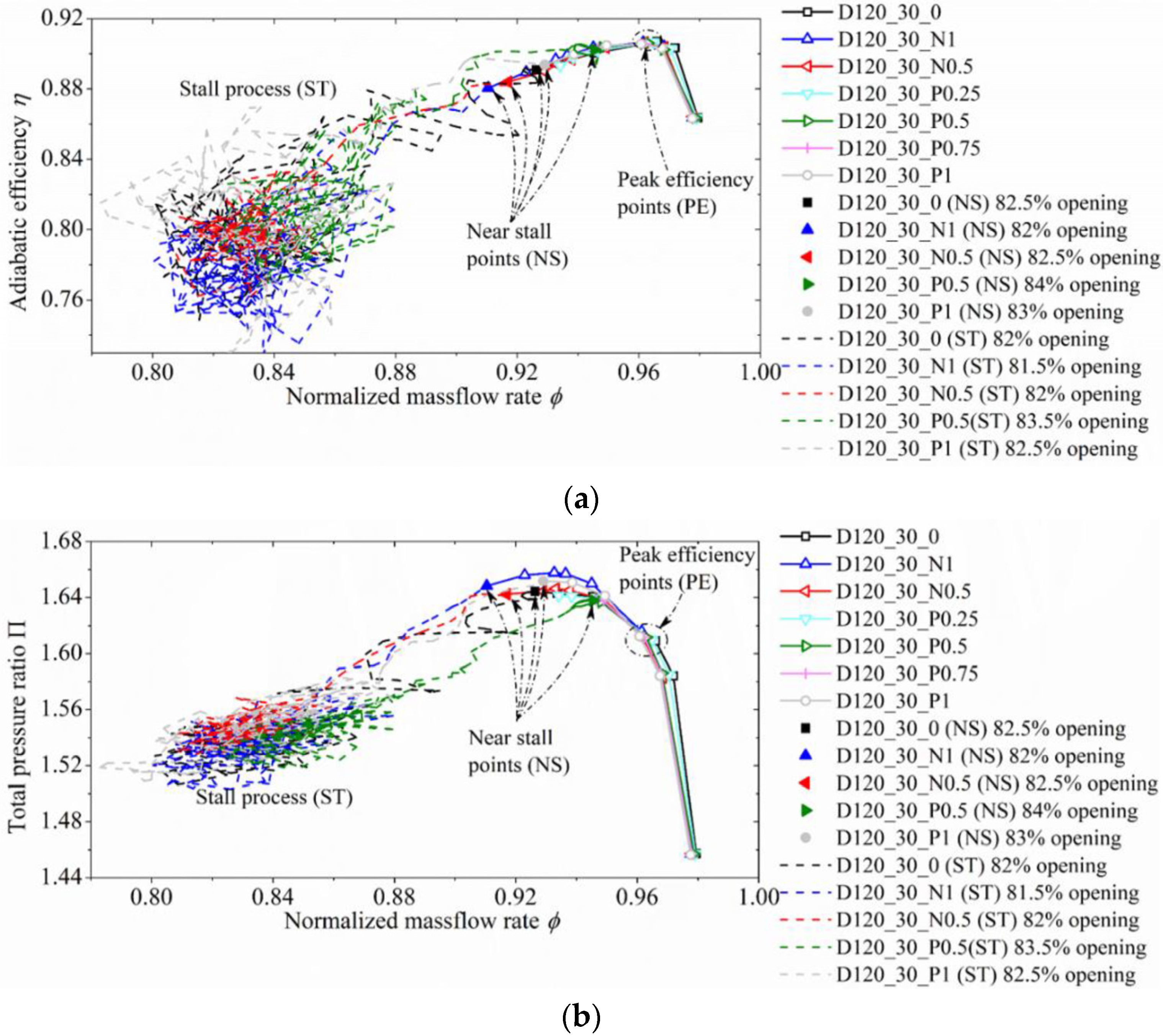
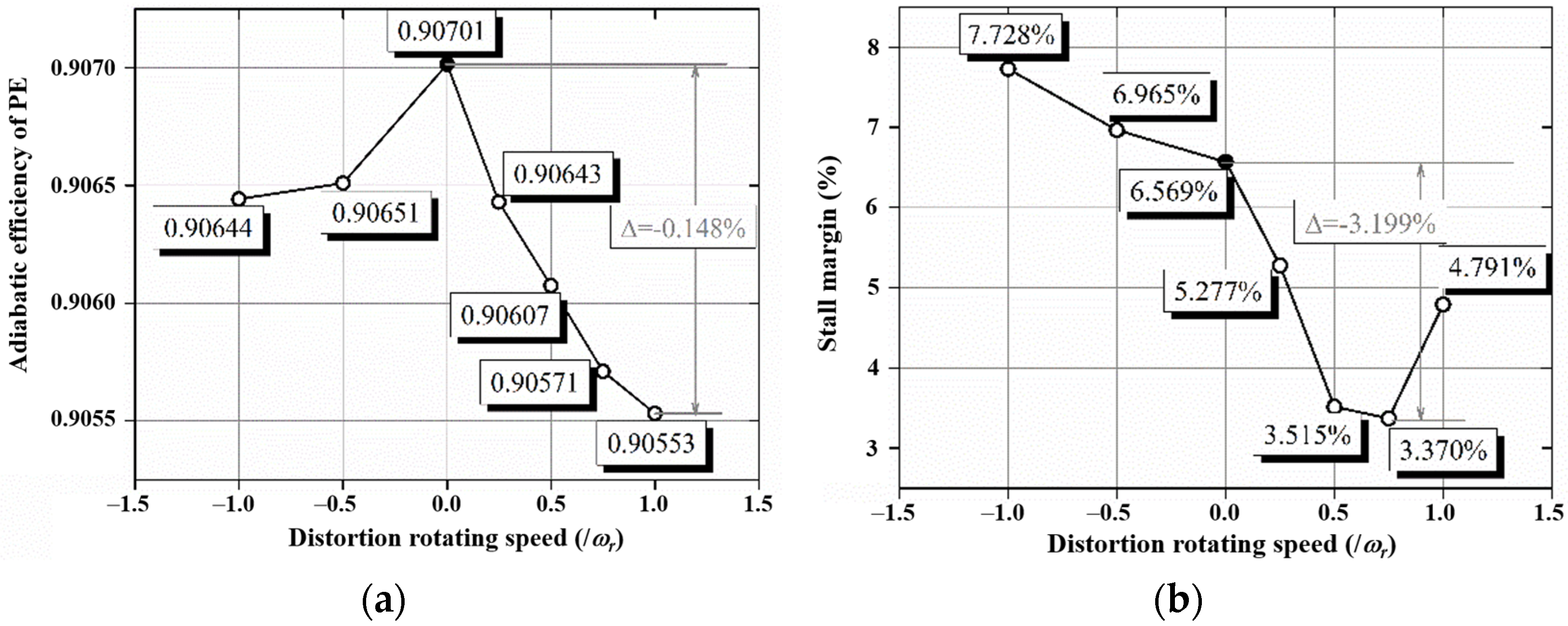
| Test Cases | Distortion Speed (RPM) | Strength γ | Circumferential Range Angle (degree) | Radial Position λ1/λ2 |
|---|---|---|---|---|
| UNI | \ | \ | \ | \ |
| D60_10 | 0 | 0.1 | 60 | 0.7/1 |
| D120_10 | 0 | 0.1 | 120 | 0.7/1 |
| D180_10 | 0 | 0.1 | 180 | 0.7/1 |
| Test Cases | Distortion Speed (ωDIS/ωr) | Strength γ | Circumferential Range Angle (Degree) | Radial Position λ1/λ2 |
|---|---|---|---|---|
| D120_30_0 | 0 | 0.3 | 120 | 0.7/1 |
| D120_30_N1 | −1 | 0.3 | 120 | 0.7/1 |
| D120_30_N0.5 | −0.5 | 0.3 | 120 | 0.7/1 |
| D120_30_P0.25 | 0.25 | 0.3 | 120 | 0.7/1 |
| D120_30_P0.5 | 0.5 | 0.3 | 120 | 0.7/1 |
| D120_30_P0.75 | 0.75 | 0.3 | 120 | 0.7/1 |
| D120_30_P1 | 1 | 0.3 | 120 | 0.7/1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, B.; Zhu, G. Impacts of Inlet Circumferential Distortions on the Aerodynamic Performance of a Transonic Axial Compressor. Processes 2023, 11, 2175. https://doi.org/10.3390/pr11072175
Yang B, Zhu G. Impacts of Inlet Circumferential Distortions on the Aerodynamic Performance of a Transonic Axial Compressor. Processes. 2023; 11(7):2175. https://doi.org/10.3390/pr11072175
Chicago/Turabian StyleYang, Bo, and Guoming Zhu. 2023. "Impacts of Inlet Circumferential Distortions on the Aerodynamic Performance of a Transonic Axial Compressor" Processes 11, no. 7: 2175. https://doi.org/10.3390/pr11072175
APA StyleYang, B., & Zhu, G. (2023). Impacts of Inlet Circumferential Distortions on the Aerodynamic Performance of a Transonic Axial Compressor. Processes, 11(7), 2175. https://doi.org/10.3390/pr11072175





