Experimental Studies of Methane Adsorption on Activated Carbon and 3D Graphene Materials
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Characterization
2.3. Gas Adsorption Measurements
3. Results and Discussion
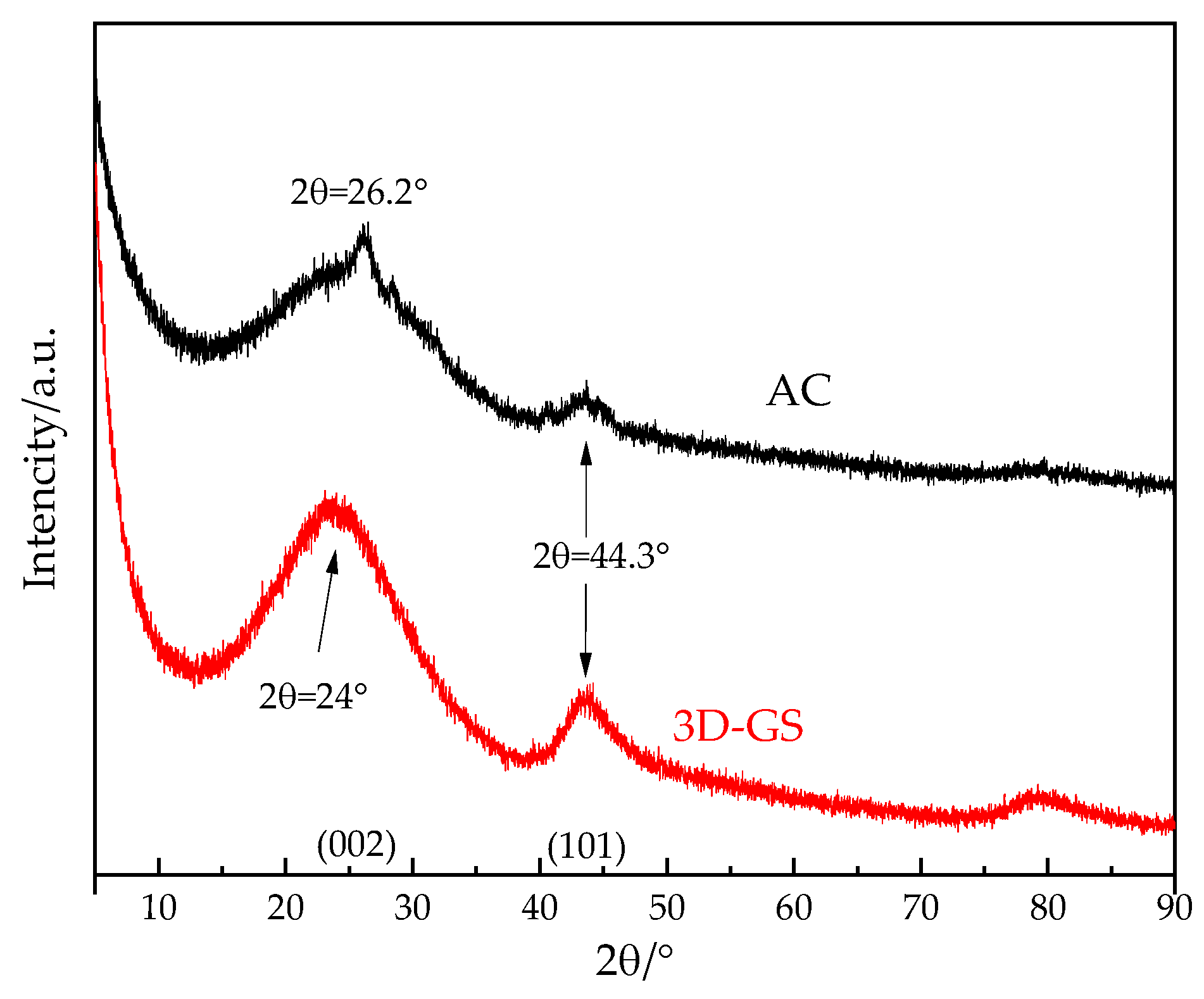
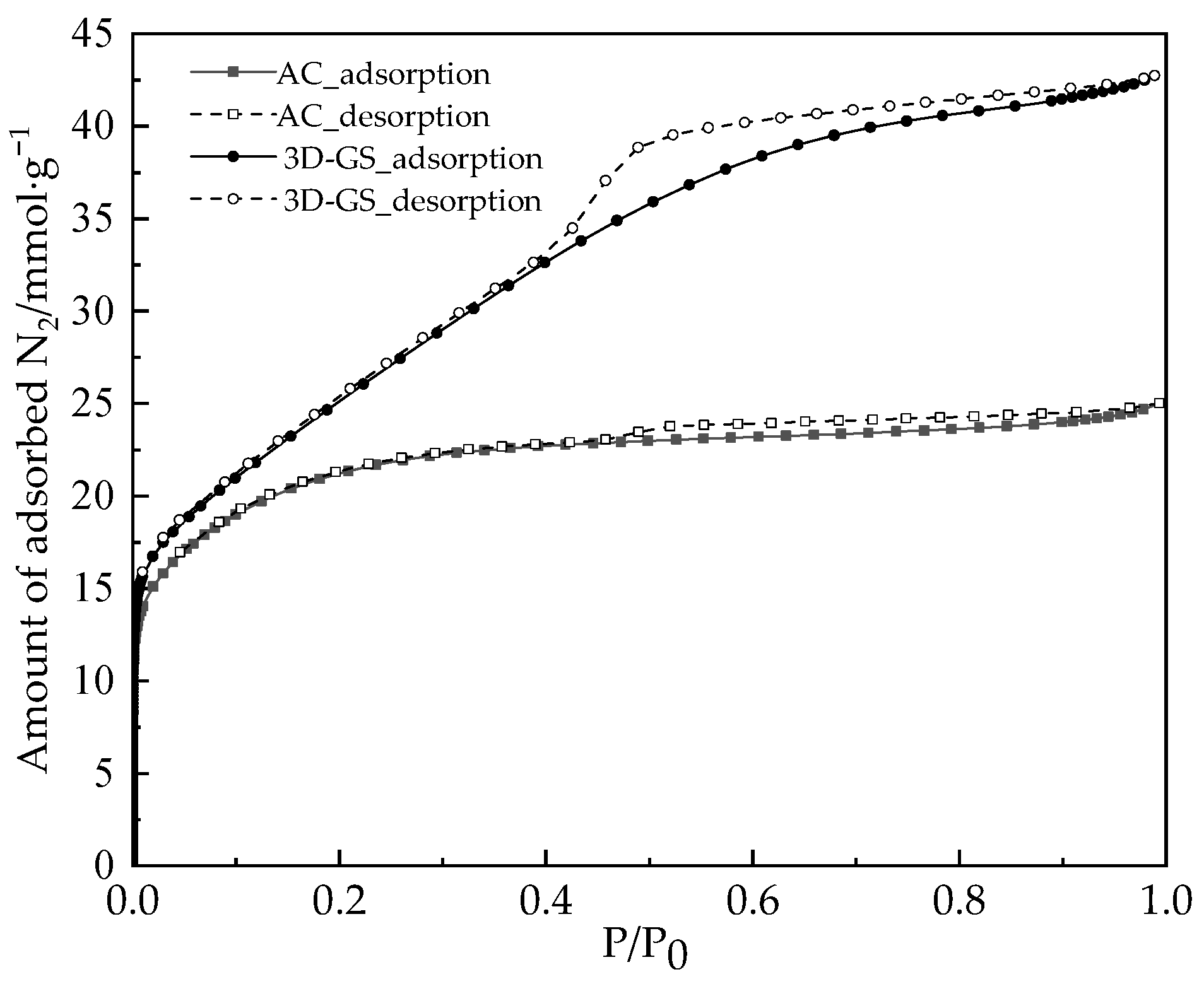
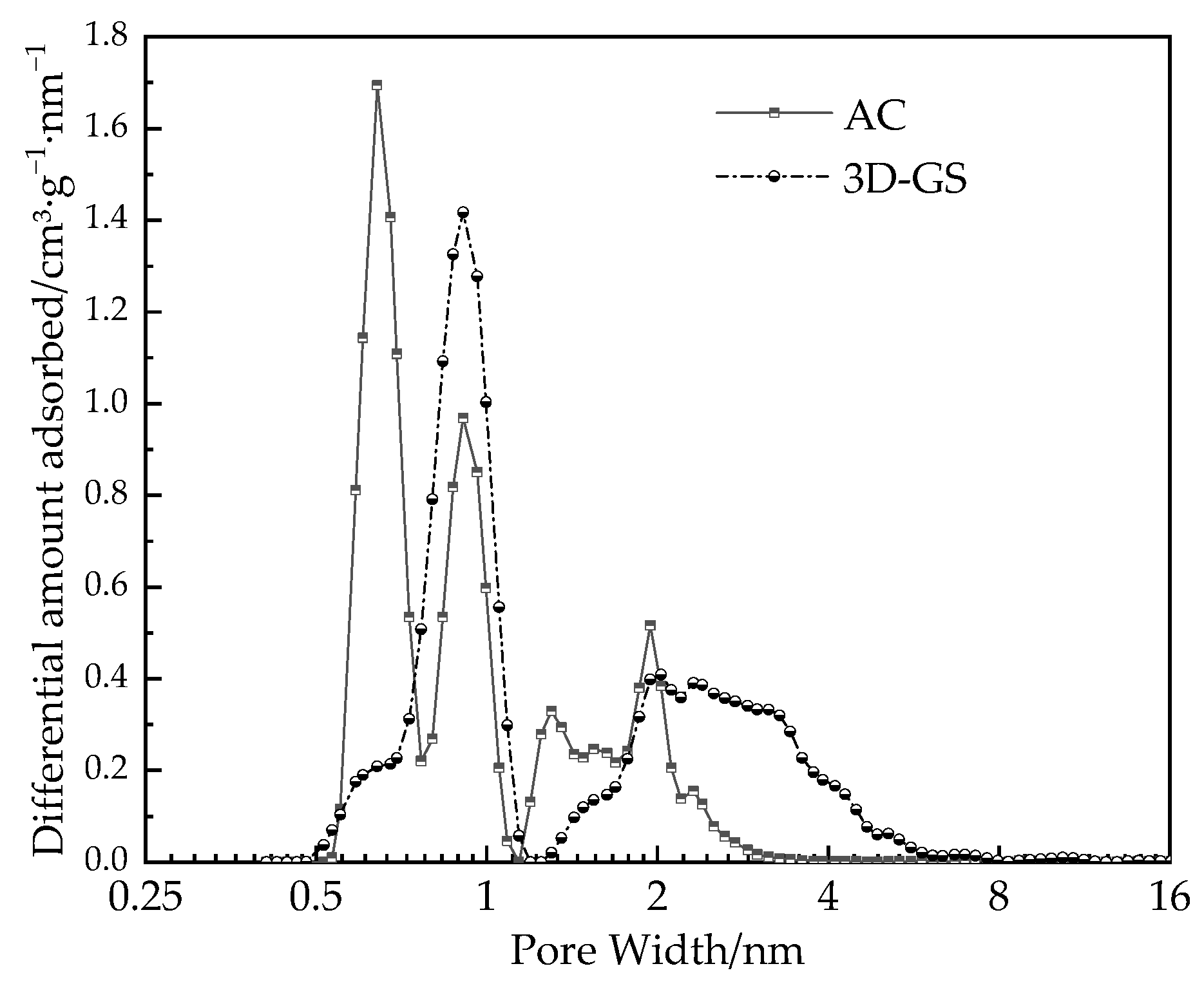
3.1. Pore Structures
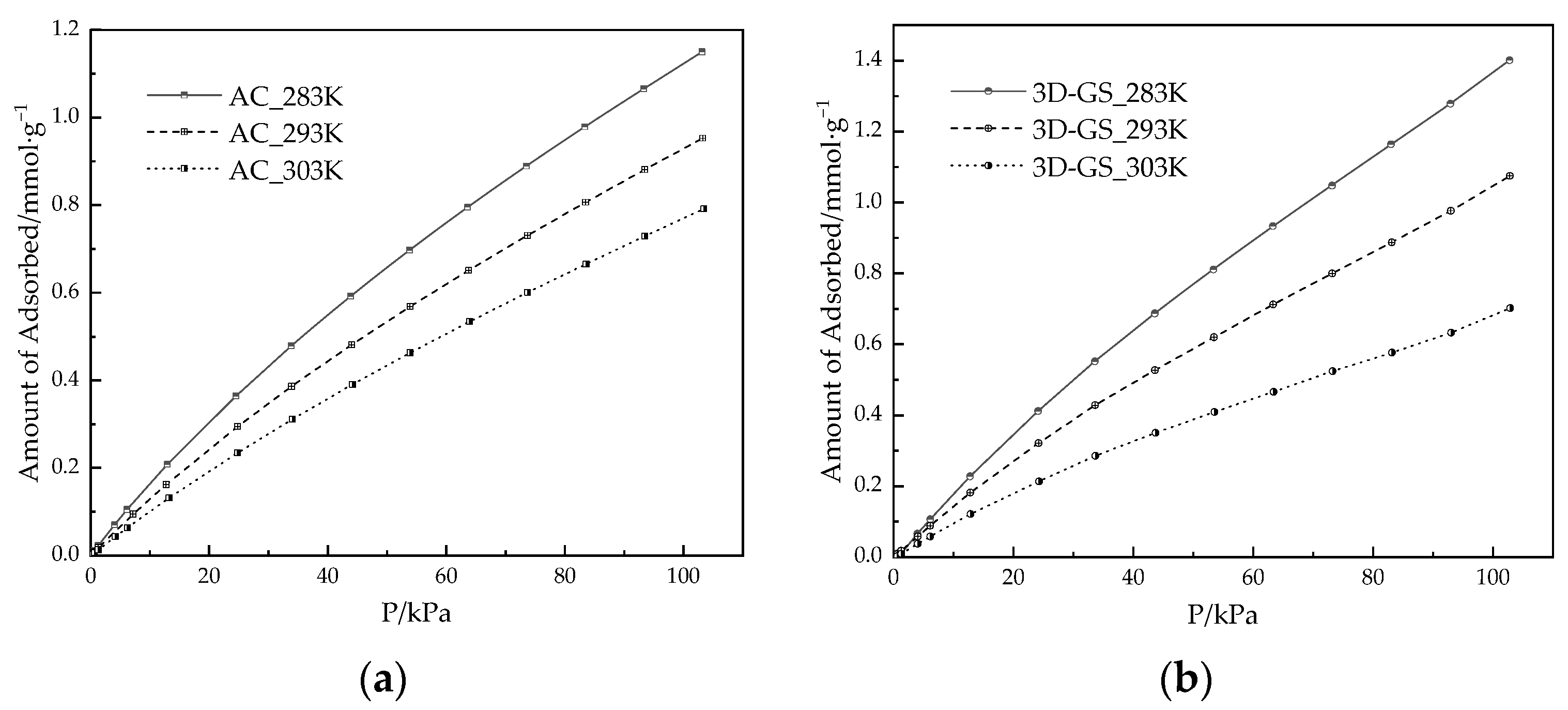
3.2. Adsorption Equilibrium at Low Surface Coverage Region
3.2.1. Adsorption Equilibrium
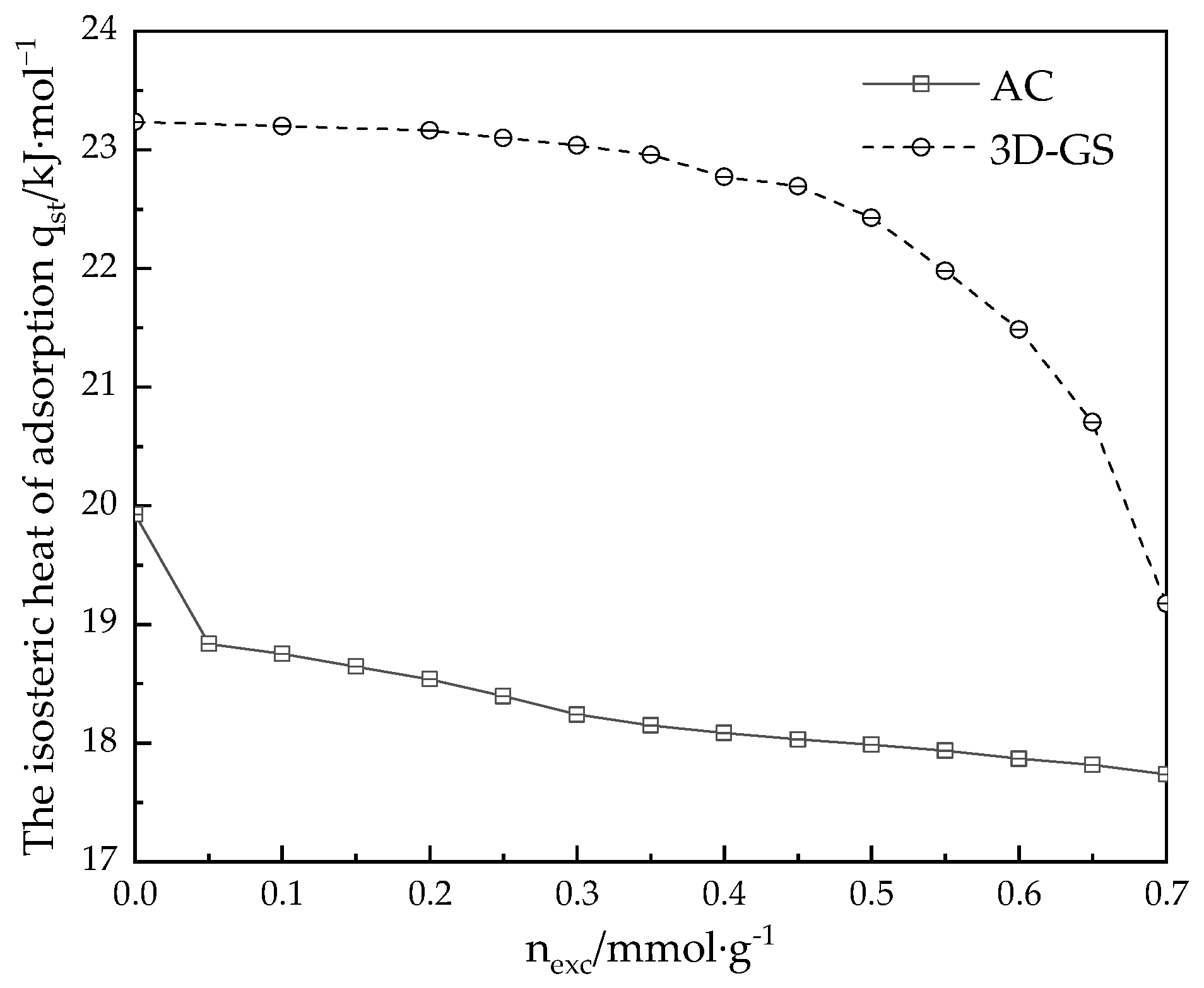
3.2.2. Isosteric Heat of Adsorption
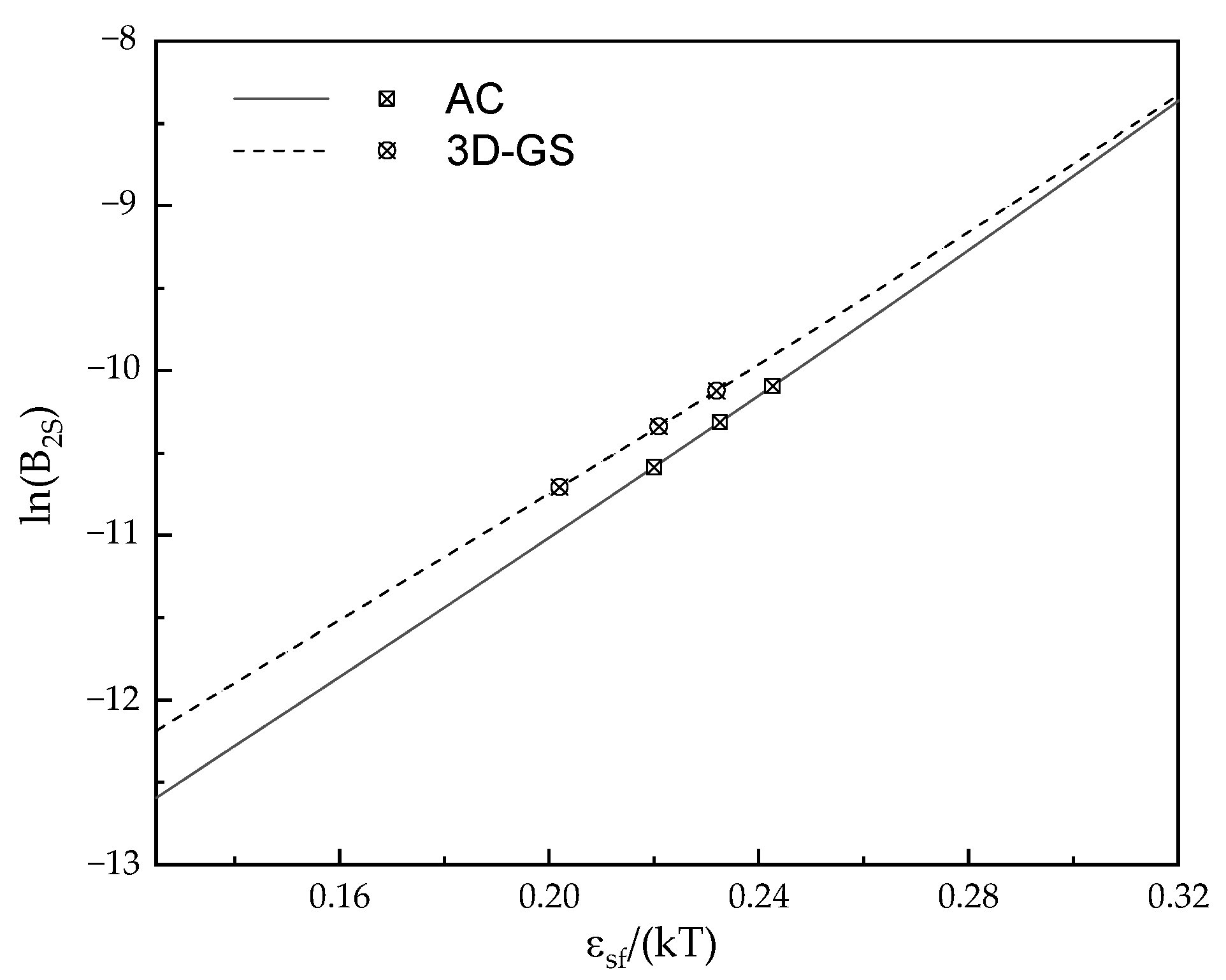
3.2.3. Thermodynamic Framework for Potential Well between Methane-Adsorbent
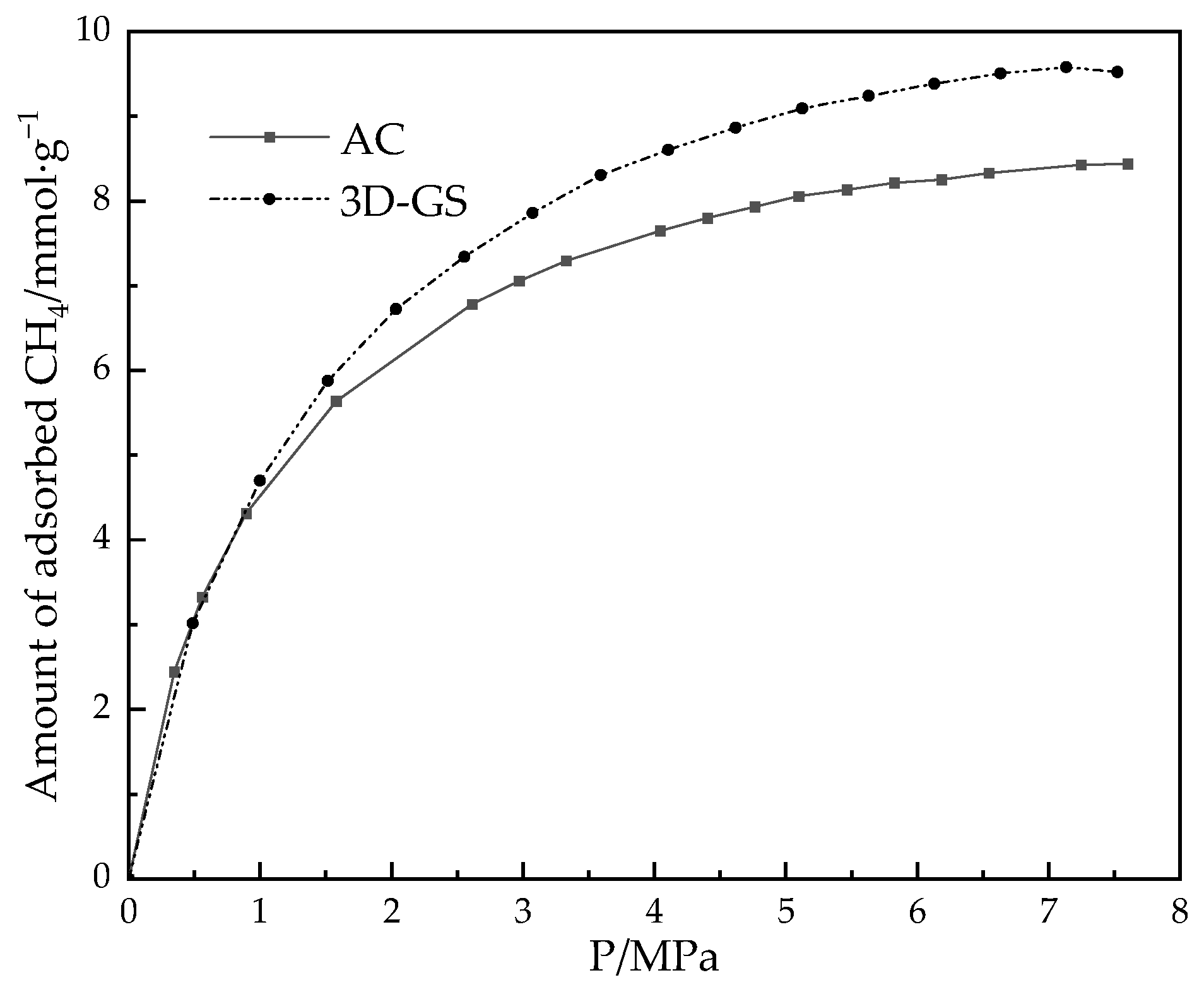
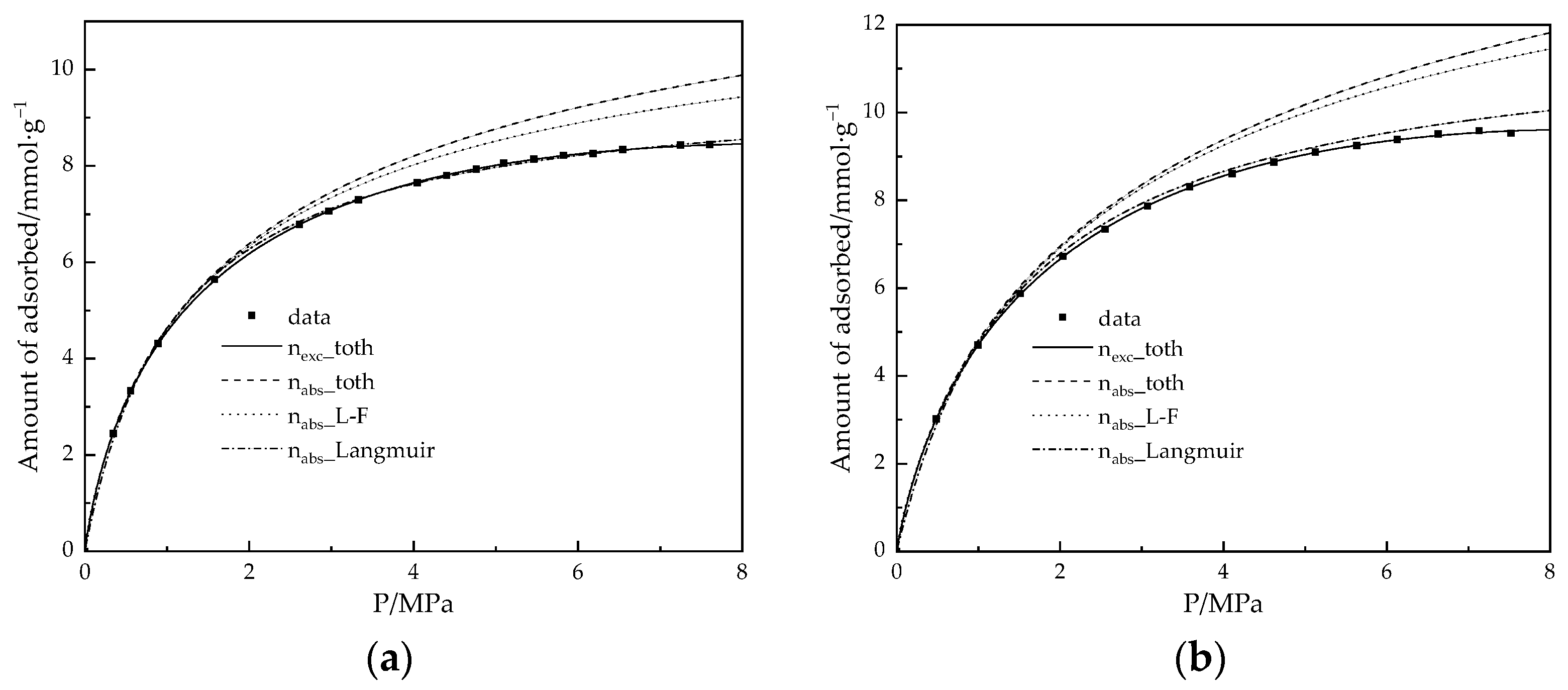
3.3. Adsorption Equilibrium at High Pressure
4. Conclusions
- (1)
- The 3D-GS is a more promising storage medium for ANG than AC in terms of the specific surface area and pore volume. The limit isosteric heat of methane adsorption on the AC and 3D-GS is about 19.93 kJ/mol and 23.23 kJ/mol, respectively. The methane storage capacities of both carbon-based materials AC and 3D-GS are, respectively, 7.86 mmol·g−1 and 8.9 mmol·g−1 at 298 K and 35 bar. Meanwhile, the SBET of 3D-GS is around 2045 m2·g−1, which is larger than that of AC (1629 m2·g−1). It can therefore be concluded that under high pressure, the SBET is still the main factor determining the adsorption amount.
- (2)
- The potential well between methane molecules and the AC is larger than that in the 3D-GS. Considering the heterogeneous surface of carbon-based materials, the framework to determine the potential well between adsorbate–adsorbent is built by PSD determined by 2D-NLDFT. Using Boltzmann distribution approximation for the fluid density on the heterogeneous surface, the adsorption potential well between methane molecules and the AC and 3D-GS was shown to be, respectively, about 68.14 K and 64.73 K. Both values are close to that of using the Lorentz–Berthelot combining rules (64.4 K); this indicates that 2D-NLDFT is accurate in characterizing the PSD of carbon-based materials. Meanwhile, the potential well between methane and carbon-based materials decreases as the temperature increases. This indicates that the capacity of methane uptake is enhanced at lower temperatures.
- (3)
- The Toth equation is the most suitable model for predicting methane adsorption on carbon-based materials than that of the Langmuir and L-F equation. After determining the values of the parameters by nonlinearly fitting on the experimental data covering the pressure range from 0 to 8 MPa at 298 K, the Toth equation can predict the experimental data of hydrogen adsorption on the carbon-based materials AC and 3D-GS with mean relative deviations of less than 0.25% and can determine that the density of the adsorbed phase is less than 26.5 mol/L of the liquid methane. This indicates that methane molecules gather in a state similar to compressed gas. The results also verify the rationality of the Toth equation.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| the second Virial constants (m3·g−1) | |
| parameter for Langmuir, L-F and Toth equations (mmol g−1 MPa−1) | |
| the distance of interlayer determined by Bragg’s law (nm) | |
| the bulk gas fugacity (MPa) | |
| the pore width for 10-4-3 potential (nm) | |
| Henry’s law constant (mmol·g−1·kPa−1) | |
| Number of states, 1,2,3… | |
| Boltzmann constant (J·K−1) | |
| N | sum |
| the amount of adsorption (mmol·g−1) | |
| pressure (MPa) | |
| adsorption heat (kJ·mol−1) | |
| Constant for gas | |
| temperature (K) | |
| external potential (J) | |
| pore width (nm) | |
| the distance from carbon atom at surface (nm) | |
| Greek Symbols | |
| the association strength (nm) | |
| energy well depth for L-J fluid and solid (J) | |
| the weighted packing fraction profile | |
| degree (°) | |
| density (nm−3) | |
| size well depth for L-J fluid and solid (nm) | |
| Subscripts and superscripts | |
| 0 | saturation |
| a | adsorbed phase |
| abs | absolute |
| bulk | bulk density of fluid |
| exc | excess |
| ff | fluid–fluid |
| ss, sf | solid–solid, solid–fluid |
| Abbreviations | |
| 2D-NLDFT | 2D non-local density functional theory |
| EDS | energy dispersive spectrum |
| PSD | pore size distribution |
| SEM | scanning electron microscopy |
| XRD | X-ray diffraction |
References
- Park, J.E.; Lee, G.B.; Hwang, S.Y.; Kim, J.H.; Hong, B.U.; Kim, H.; Kim, S. The Effects of Methane Storage Capacity Using Upgraded Activated Carbon by KOH. Appl. Sci. 2018, 8, 1596. [Google Scholar] [CrossRef]
- Shkolin, A.V.; Strizhenov, E.M.; Chugaev, S.S.; Men’shchikov, I.E.; Gaidamavichute, V.V.; Grinchenko, A.E.; Zherdev, A.A. Natural Gas Storage Filled with Peat-Derived Carbon Adsorbent: Influence of Nonisothermal Effects and Ethane Impurities on the Storage Cycle. Nanomaterials 2022, 12, 4066. [Google Scholar] [CrossRef]
- Men’shchikov, I.E.; Shkolin, A.V.; Strizhenov, E.M.; Khozina, E.V.; Chugaev, S.S.; Shiryaev, A.A.; Fomkin, A.A.; Zherdev, A.A. Thermodynamic Behaviors of Adsorbed Methane Storage Systems Based on Nanoporous Carbon Adsorbents Prepared from Coconut Shells. Nanomaterials 2020, 10, 2243. [Google Scholar] [CrossRef]
- Memetova, A.; Tyagi, I.; Karri, R.R.; Kumar, V.; Tyagi, K.; Suhas; Memetov, N.; Zelenin, A.; Pasko, T.; Gerasimova, A.; et al. Porous carbon-based material as a sustainable alternative for the storage of natural gas (methane) and biogas (biomethane): A review. Chem. Eng. J. 2022, 446, 137373. [Google Scholar] [CrossRef]
- Ruiz Zardoya, A.; Oregui Bengoetxea, I.; Lopez Martinez, A.; Loroño Lucena, I.; Orosa, J.A. Methodological Design Optimization of a Marine LNG Internal Combustion Gas Engine to Burn Alternative Fuels. J. Mar. Sci. Eng. 2023, 11, 1194. [Google Scholar] [CrossRef]
- Sapag, K.; Vallone, A.; Blanco, A.G.; Solar, C. Adsorption of methane in porous materials as the basis for the storage of natural gas. In Natural Gas; Intech Open: London, UK, 2010; Chapter 10; pp. 205–244. ISBN 978-953-307-112-1. [Google Scholar]
- Braslaw, J.; Nasea, J.J.; Golovoy, A. Low pressure methane storage system for vehicles preliminary concept evaluation. In Proceedings of the 4th International Conference on Alternative Energy Sources, Miami Beach, FL, USA, 14–16 December 1981; Veziroglu, T.N., Ed.; Ann Arbor Science Publishers: Ann Arbor, MI, USA, 1982. [Google Scholar]
- Lin, Y.Y.; Nassau, C.J. The MOVE projects and importance of engineering design. In Proceedings of the 10th International Conference on Applied Mechanisms and Machine Science, China (CCAMMS), Sanya, China, 29 November–1 December 2013. [Google Scholar]
- Rodríguez-Reinoso, F.; Silvestre-Albero, J. Methane Storage on Nanoporous Carbons, Nanoporous Materials for Gas Storage; Springer: Berlin/Heidelberg, Germany, 2019; pp. 209–226. [Google Scholar]
- Ursueguía, D.; Díaz, E.; Ordóñez, S. Metal-Organic Frameworks (MOFs) as methane adsorbents: From storage to diluted coal mining streams concentration. Sci. Total Environ. 2021, 790, 148211. [Google Scholar] [CrossRef]
- Li, B.; Wen, H.M.; Zhou, W.; Xu, J.Q.; Chen, B. Porous Metal-Organic Frameworks: Promising Materials for Methane Storage. Chem 2016, 1, 557–580. [Google Scholar] [CrossRef]
- Mahmoud, E.; Ali, L.; El Sayah, A.; Alkhatib, S.A.; Abdulsalam, H.; Juma, M.; Al-Muhtaseb, A.H. Implementing Metal-Organic Frameworks for Natural Gas Storage. Crystals 2019, 9, 406. [Google Scholar] [CrossRef]
- Mirzaei, S.; Ahmadpour, A.; Shao, Z.; Arami-Niya, A. Rational design of carbon-based materials for purification and storage of energy carrier gases of methane and hydrogen. J. Energy Storage 2022, 56, 105967. [Google Scholar] [CrossRef]
- Zhu, Z.W.; Zheng, Q.R.; Wang, Z.H.; Tang, Z.; Chen, W. Hydrogen adsorption on graphene sheets and nonporous graphitized thermal carbon black at low surface coverage. Int. J. Hydrog. Energy 2017, 42, 18465–18472. [Google Scholar] [CrossRef]
- Zhu, Z.W.; Zheng, Q.R. Methane adsorption on the graphene sheets, activated carbon and carbon black. Appl. Therm. Eng. 2016, 108, 605–613. [Google Scholar] [CrossRef]
- Ertas, A.; Boyce, C.T.R.; Gulbulak, U. Experimental Measurement of Bulk Thermal Conductivity of Activated Carbon with Adsorbed Natural Gas for ANG Energy Storage Tank Design Application. Energies 2020, 13, 682. [Google Scholar] [CrossRef]
- Peng, X.; Ji, H. Control mechanism of small organic molecules on methane adsorption capacity of coal. Fuel 2023, 331, 125904. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Z.; Zhang, M.; Yang, H. Experimental Study on Fractal Characteristics of Adsorption Pore Structure of Coal. Processes 2023, 11, 78. [Google Scholar] [CrossRef]
- Yick, T.; Gangoli, V.S.; Orbaek White, A. Comparing Ultralong Carbon Nanotube Growth from Methane over Mono- and Bi-Metallic Iron Chloride Catalysts. Nanomaterials 2023, 13, 2172. [Google Scholar] [CrossRef]
- Li, T.Y.; Wang, Y.S.; Zhang, M.Y.; Liu, B.-Y.; Zheng, Z.; Hao, G.-P.; Lu, A.-H. Carbon nanofibers with gas selective layer containing rich and accessible ultramicropores for methane/nitrogen separation. Chem. Eng. J. 2023, 462, 142118. [Google Scholar] [CrossRef]
- Li, S.; Yan, R.; Cai, M.; Jiang, W.; Zhang, M.; Li, X. Enhanced antibiotic degradation performance of Cd0.5Zn0.5S/Bi2MoO6 S-scheme photocatalyst by carbon dot modification. J. Mater. Sci. Technol. 2023, 164, 59–67. [Google Scholar] [CrossRef]
- Liu, R.; Hou, L.; Yue, G.; Li, H.; Zhang, J.; Liu, J.; Miao, B.; Wang, N.; Bai, J.; Cui, Z.; et al. Progress of Fabrication and Applications of Electrospun Hierarchically Porous Nanofibers. Adv. Fiber Mater. 2022, 4, 604–630. [Google Scholar] [CrossRef]
- Li, S.; Cai, M.; Wang, C.; Liu, Y. Ta3N5/CdS Core-Shell S-scheme Heterojunction Nanofibers for Efficient Photocatalytic Removal of Antibiotic Tetracycline and Cr(VI): Performance and Mechanism Insights. Adv. Fiber Mater. 2023, 5, 994–1007. [Google Scholar] [CrossRef]
- Engel, L.J.; Turko, J.W. Gaseous Hydrocarbon Fuel Storage System and Power Plant for Vehicles and Associated Refueling Apparatus. U.S. Patent 4,522,159, 13 April 1983. [Google Scholar]
- Sevilla, M.; Mokaya, R. Energy storage applications of activated carbons: Supercapacitors and hydrogen storage. Energy Environ. Sci. 2014, 7, 1250. [Google Scholar] [CrossRef]
- Hu, Z.; Srinivasan, M.P.; Ni, Y. Novel activation process for preparing highly microporous and mesoporous activated carbons. Carbon 2001, 39, 877–886. [Google Scholar] [CrossRef]
- ARPA-E. List of MOVE Projects Funded ARPA-E MOVE. 2012. Available online: http://arpa-e.energy.gov/?q=arpa-e-programs/move (accessed on 20 June 2023).
- Lozano-Castelló, D.; Cazorla-Amorós, D.; Linares-Solano, A.; Quinn, D.F. Influence of pore size distribution on methane storage at relatively low pressure: Preparation of activated carbon with optimum pore size. Carbon 2002, 40, 989–1002. [Google Scholar] [CrossRef]
- Altwala, A.; Mokaya, R. Modulating the porosity of activated carbons via pre-mixed precursors for simultaneously enhanced gravimetric and volumetric methane uptake. J. Mater. Chem. A 2022, 10, 13744–13757. [Google Scholar] [CrossRef]
- Gadipelli, S.; Guo, Z.X. Graphene-based materials: Synthesis and gas sorption, storage and separation. Prog. Mater. Sci. 2015, 69, 1–60. [Google Scholar] [CrossRef]
- Baykasoglu, C.; Mert, H.; Deniz, C.U. Grand canonical Monte Carlo simulations of methane adsorption in fullerene pillared graphene nanocomposites. J. Mol. Graph. Model. 2021, 106, 107909. [Google Scholar] [CrossRef]
- Roy, S.; Ghosh, B.D.; Goh, K.L.; Ahn, H.J.; Chang, Y.W. Super expanded freestanding 3D graphene foam as a versatile platform for CO2 capture and hydrogenation. Chem. Eng. J. 2023, 466, 143326. [Google Scholar] [CrossRef]
- Umar, E.; Ikram, M.; Haider, J.; Nabgan, W.; Imran, M.; Nazir, G. 3D graphene-based material: Overview, perspective, advancement, energy storage, biomedical engineering and environmental applications a bibliometric analysis. J. Environ. Chem. Eng. 2023, 11, 110339. [Google Scholar] [CrossRef]
- Wibawa, P.J.; Nur, M.; Asy’ari, M.; Nur, H. SEM, XRD and FTIR analyses of both ultrasonic and heat generated activated carbon black microstructures. Heliyon 2020, 6, 03546. [Google Scholar] [CrossRef]
- Karakehya, N. Effects of one-step and two-step KOH activation method on the properties and supercapacitor performance of highly porous activated carbons prepared from Lycopodium clavatum spores. Diam. Relat. Mater. 2023, 135, 109873. [Google Scholar] [CrossRef]
- Lazzarini, A.; Piovano, A.; Pellegrini, R.; Agostini, G.; Rudic, S.; Lamberti, C.; Groppo, E. Graphitization of Activated Carbons: A Molecular-level Investigation by INS, DRIFT, XRD and Raman Techniques. Phys. Procedia 2016, 85, 20–26. [Google Scholar] [CrossRef]
- Basheer, A.O.; Odeh, A.A.; Al-Douri, Y. Structural analysis and characterization of date palm fiber-based low-cost carbon nanotubes and nanostructured powder activated carbon. Heliyon 2023, 9, 18811. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhang, M. Water Vapor Adsorption on Desiccant Materials for Rotary Desiccant Air Conditioning Systems. Processes 2023, 11, 2166. [Google Scholar] [CrossRef]
- Zhu, Z.W.; Zheng, Q.R. Investigation of cryo-adsorption hydrogen storage capacity of rapidly synthesized MOF-5 by mechanochemical method. Int. J. Hydrog. Energy 2023, 48, 5166. [Google Scholar] [CrossRef]
- Donohue, M.D.; Aranovich, G.L. Classification of Gibbs adsorption isotherms. Adv. Colloid Interface Sci. 1998, 76, 137. [Google Scholar] [CrossRef]
- Landers, J.; Gor, G.Y.; Neimark, A.V. Density functional theory methods for characterization of porous materials. Colloids Surf. A Physicochem. Eng. Asp. 2013, 437, 3–32. [Google Scholar] [CrossRef]
- Ustinov, E.A.; Do, D.D.; Fenelonov, V.B. Pore size distribution analysis of activated Carbopacks: Application of density functional theory using nongraphitized Carbopack black as a reference system. Carbon 2006, 44, 653–663. [Google Scholar] [CrossRef]
- Neimark, A.V.; Lin, Y.; Ravikovitch, P.I. Quenched solid density functional theory and pore size analysis of micro-mesoporous carbons. Carbon 2009, 47, 1617–1628. [Google Scholar] [CrossRef]
- Lucena, S.M.P.; Oliveira, J.C.A.; Gonçalves, D.V.; Silvino, P.F.G.; Dantas, S.; Neimark, A.V. Pore size analysis of carbons with heterogeneous kernels from reactive molecular dynamics model and quenched solid density functional theory. Carbon 2021, 183, 672–684. [Google Scholar] [CrossRef]
- Miyasaka, K.; Neimark, A.V.; Terasaki, O. Density Functional Theory of in Situ Synchrotron Powder X-ray Diffraction on Mesoporous Crystals: Argon Adsorption on MCM-41. J. Phys. Chem. C 2009, 113, 791–794. [Google Scholar] [CrossRef]
- Jagiello, J.; Olivier, J.P. 2D-NLDFT adsorption models for carbon slit-shaped pores with surface energetical heterogeneity and geometrical corrugation. Carbon 2013, 55, 70–80. [Google Scholar] [CrossRef]
- Jagiello, J.; Jaroniec, M. 2D-NLDFT adsorption models for porous oxides with corrugated cylindrical pores. J. Colloid Interface Sci. 2018, 532, 588–597. [Google Scholar] [CrossRef]
- Jagiello, J.; Kenvin, J. Consistency of carbon nanopore characteristics derived from adsorption of simple gases and 2D-NLDFT models. Advantages of using adsorption isotherms of oxygen (O2) at 77K. J. Colloid Interface Sci. 2019, 542, 151–158. [Google Scholar] [CrossRef]
- Linstrom, P.J.; Mallard, W.G. (Eds.) NIST Chemistry WebBook; NIST Standard Reference Database Number 69; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2022; p. 20899.
- Do, D.D.; Do, H.D.; Tran, K.N. Analysis of Adsorption of Gases and Vapors on Nonporous Graphitized Thermal Carbon Black. Langmuir 2003, 19, 5656. [Google Scholar] [CrossRef]
- Han, B.; Chakraborty, A.; Saha, B.B. Isosteric Heats and Entropy of Adsorption in Henry’s Law Region for Carbon and MOFs Structures for Energy Conversion Applications. Int. J. Heat Mass Transf. 2022, 182, 122000. [Google Scholar] [CrossRef]
- Daniel, D.W.; Gelb, L.D. Extension of the Steele 10-4-3 potential for adsorption calculations in cylindrical, spherical, and other pore geometries. J. Chem. Phys. 2011, 135, 84703. [Google Scholar]
- Clark, A. The Theory of Adsorption and Catalysis; Academic Press: New York, NY, USA, 1970. [Google Scholar]
- Bénard, P.; Chahine, R. Determination of the Adsorption Isotherms of Hydrogen on Activated Carbons above the Critical Temperature of the Adsorbate over Wide Temperature and Pressure Ranges. Langmuir 2001, 17, 1950–1955. [Google Scholar] [CrossRef]
- Duh, D.M.; Henderson, D.; Rowley, R.L. Some effects of deviations from the Lorentz-Berthelot combining rules for mixtures of Lennard-Jones fluids. Mol. Phys. 1997, 91, 1143–1147. [Google Scholar]
- Zheng, Q.R.; Ji, X.W.; Gao, S.; Wang, X.H. Adsorption equilibrium of hydrogen on graphene sheets and activated carbon. Cryogenics 2014, 61, 143–148. [Google Scholar] [CrossRef]
- Brunauer, S.; Emmett, P.H.; Teller, E. Adsorption of gases in multimolecular layers. J. Am. Chem. Soc. 1938, 60, 309–319. [Google Scholar] [CrossRef]
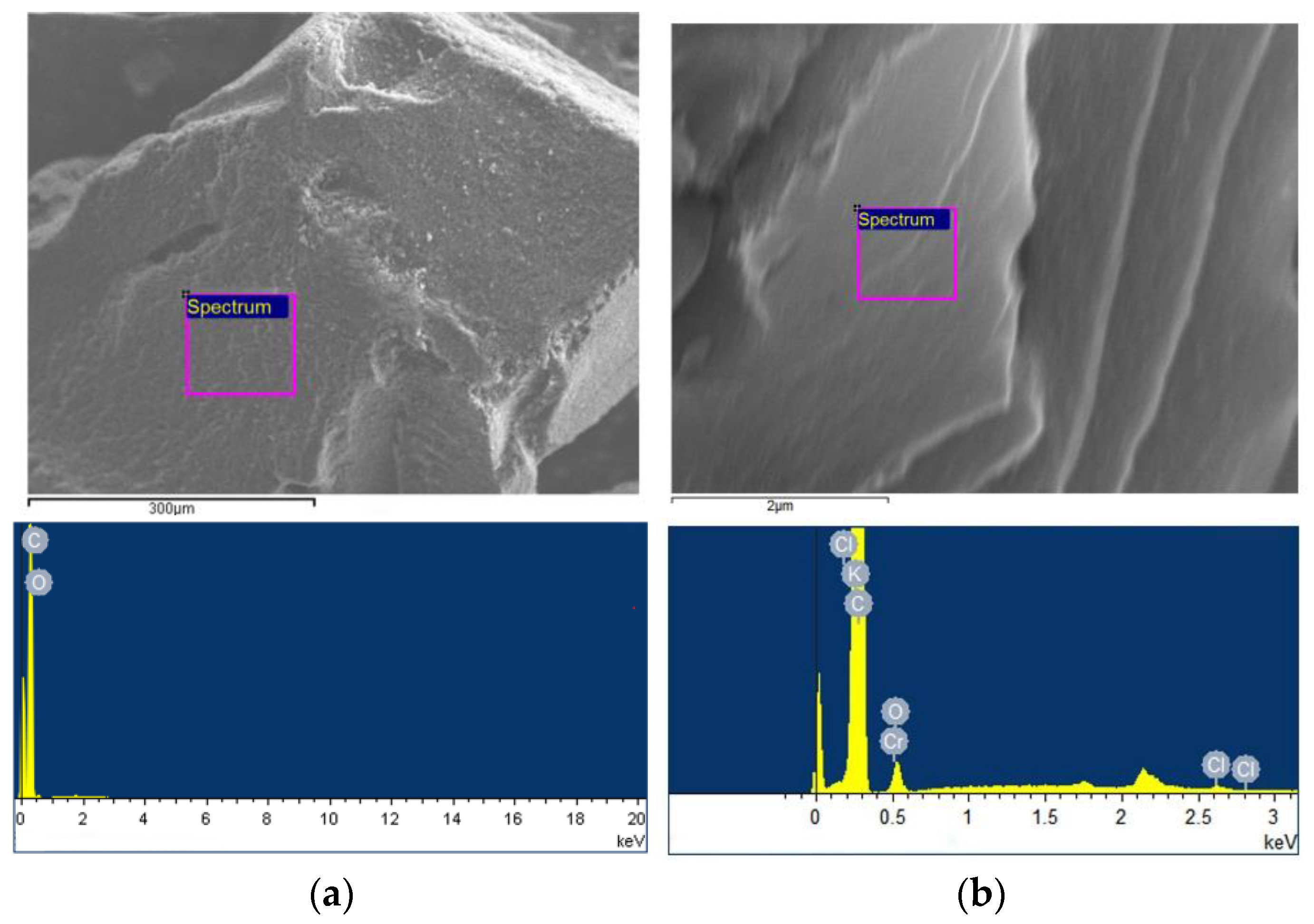

| AC | 3D-GS | ||
|---|---|---|---|
| Element | Atom Concentration/% | Element | Atom Concentration/% |
| C | 95.91 | C | 67.00 |
| O | 4.09 | O | 32.24 |
| -- | -- | Cl | 0.31 |
| -- | -- | K | 0.15 |
| -- | -- | Cr | 0.30 |
| Total | 100 | Total | 100 |
| Simple | 3D-GS | AC |
|---|---|---|
| BET specific surface area SBET | 2045 | 1637 |
| Micropore volume | 0.544 | 0.65 |
| Mesopore volume | 0.838 | 0.142 |
| T/K | ||||
|---|---|---|---|---|
| AC | 3D-GS | AC | 3D-GS | |
| 283 | 0.01758 | 0.01706 | 41.3633 | 40.1398 |
| 293 | 0.01362 | 0.01327 | 33.1783 | 32.3257 |
| 303 | 0.01004 | 0.00887 | 25.2921 | 22.3448 |
| T/K | ||
|---|---|---|
| AC | 3D-GS | |
| 283 | 68.67 | 65.64 |
| 293 | 68.14 | 64.73 |
| 303 | 66.66 | 62.11 |
| Parameters | Langmuir Equation | L-F Equation | Toth Equation | |||
|---|---|---|---|---|---|---|
| AC | 3D-GS | AC | 3D-GS | AC | 3D-GS | |
| /mmol g−1 | 9.9161 | 12.292 | 12.758 | 17.875 | 16.498 | 24.1 |
| /mmol g−1 MPa−1 | 0.8907 | 0.6365 | 0.5086 | 0.2918 | 0.8682 | 0.5227 |
| -- | -- | 0.8191 | 0.8052 | 0.5832 | 0.554 | |
| /mol·L−1 | 45,230 | 113.86 | 36.252 | 22.8248 | 25.31 | 19.513 |
| δ/% | 0.8191 | 0.7835 | 0.1648 | 0.2657 | 0.1622 | 0.2342 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Zhang, M. Experimental Studies of Methane Adsorption on Activated Carbon and 3D Graphene Materials. Processes 2023, 11, 2487. https://doi.org/10.3390/pr11082487
Zhu Z, Zhang M. Experimental Studies of Methane Adsorption on Activated Carbon and 3D Graphene Materials. Processes. 2023; 11(8):2487. https://doi.org/10.3390/pr11082487
Chicago/Turabian StyleZhu, Ziwen, and Muyuan Zhang. 2023. "Experimental Studies of Methane Adsorption on Activated Carbon and 3D Graphene Materials" Processes 11, no. 8: 2487. https://doi.org/10.3390/pr11082487
APA StyleZhu, Z., & Zhang, M. (2023). Experimental Studies of Methane Adsorption on Activated Carbon and 3D Graphene Materials. Processes, 11(8), 2487. https://doi.org/10.3390/pr11082487





