Stability Analysis: Two-Area Power System with Wind Power Integration
Abstract
:1. Introduction
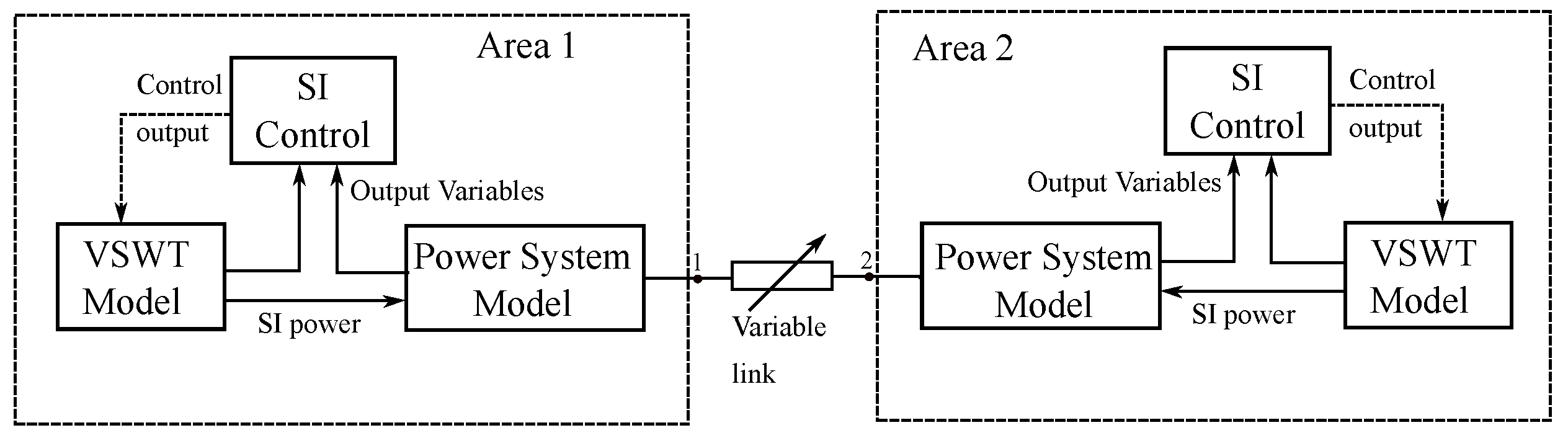
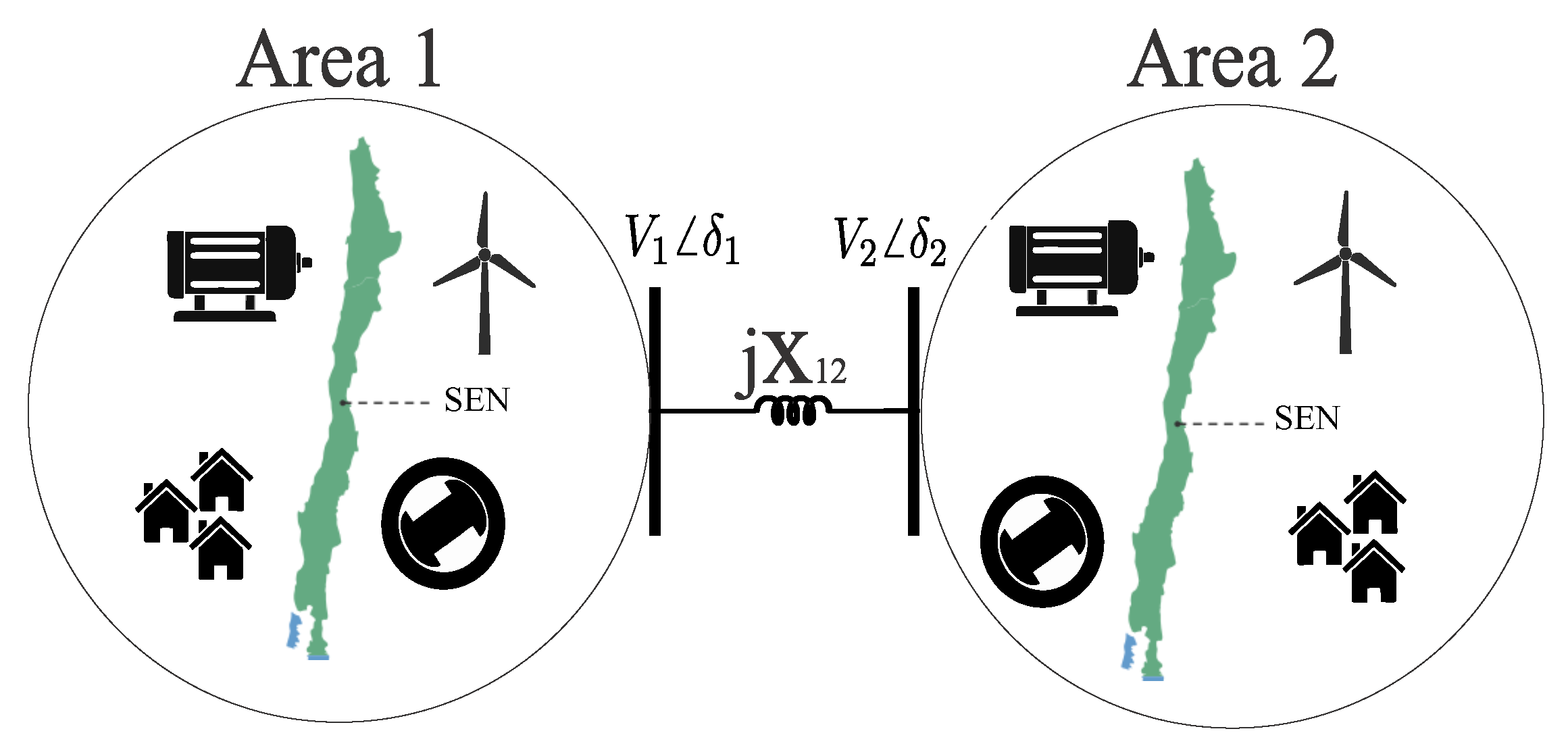
2. Problem Formulation
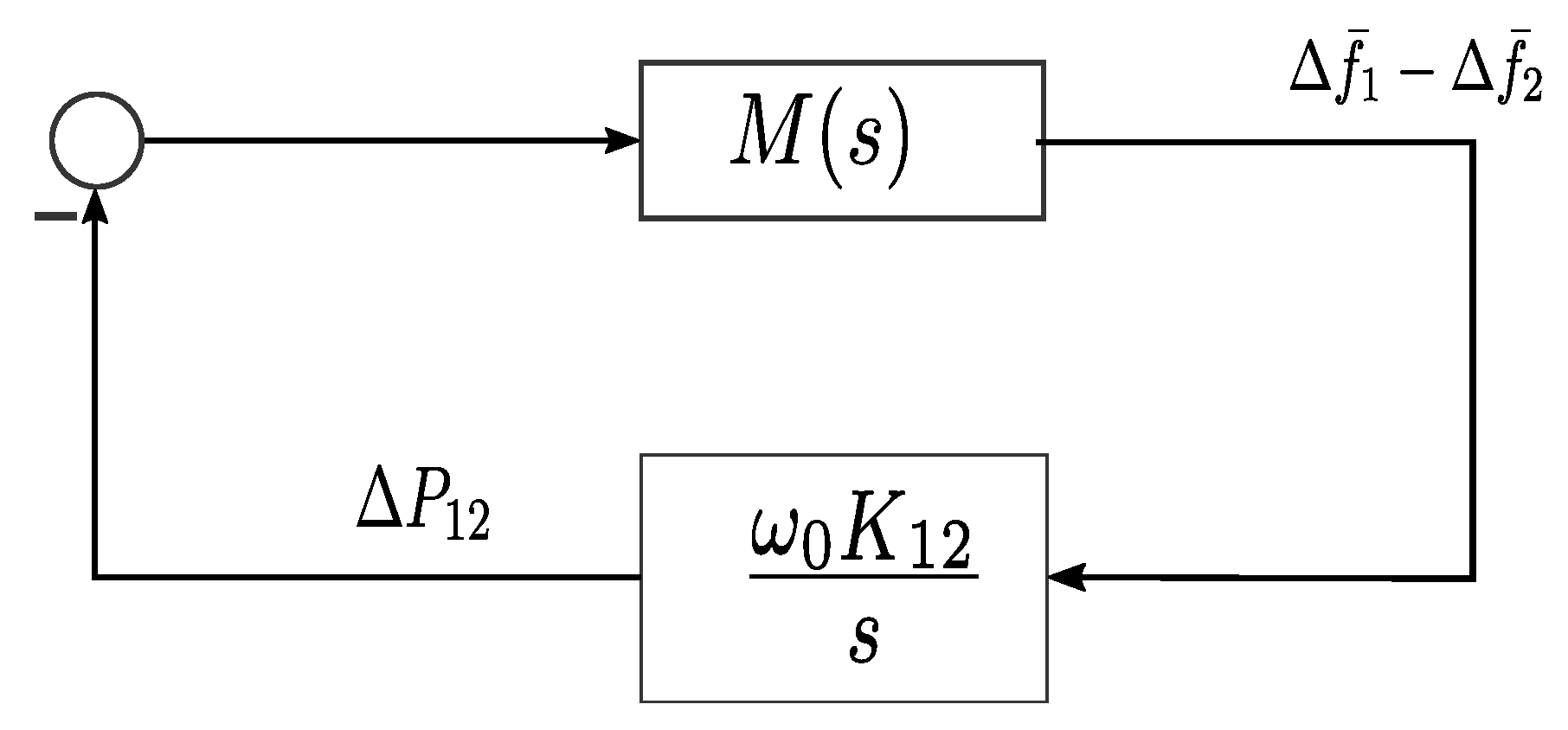
2.1. Power System Frequency Dynamic Model
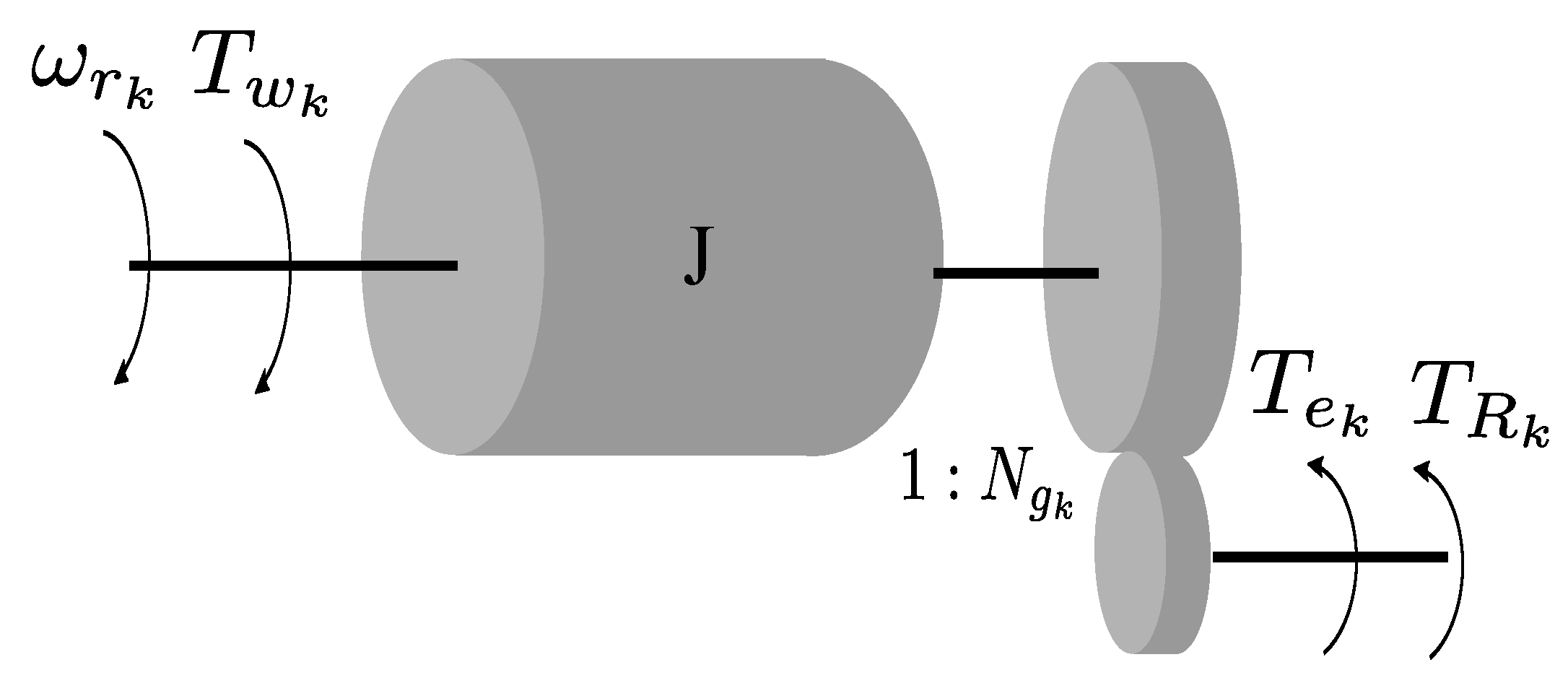
2.2. Wind Power Plant and SI Control
- VSWT angular speed (rad/s),
- J VSWT combined moment of inertia (MNm),
- VSWT mechanical torque (MNm),
- torque reference from MPPT control (MNm),
- torque reference from the SI control (MNm),
- gearbox speed ratio (-),
- proportional and integral gains of MPPT control,
- wind speed (m/s),
- air density (kg/),
- rotor-swept radius (m)
- A VSWT rotor-swept area (),
- VSWT power coefficient,
- VSWT tip speed ratio,
- VSWT pitch angle (),
2.3. Optimal Area SI Controller
2.4. Validation of Wind Power Dynamics Linearization
3. Study Case
3.1. State Feedback Gains
3.2. Quadratic Performance Index Matrices
4. Results
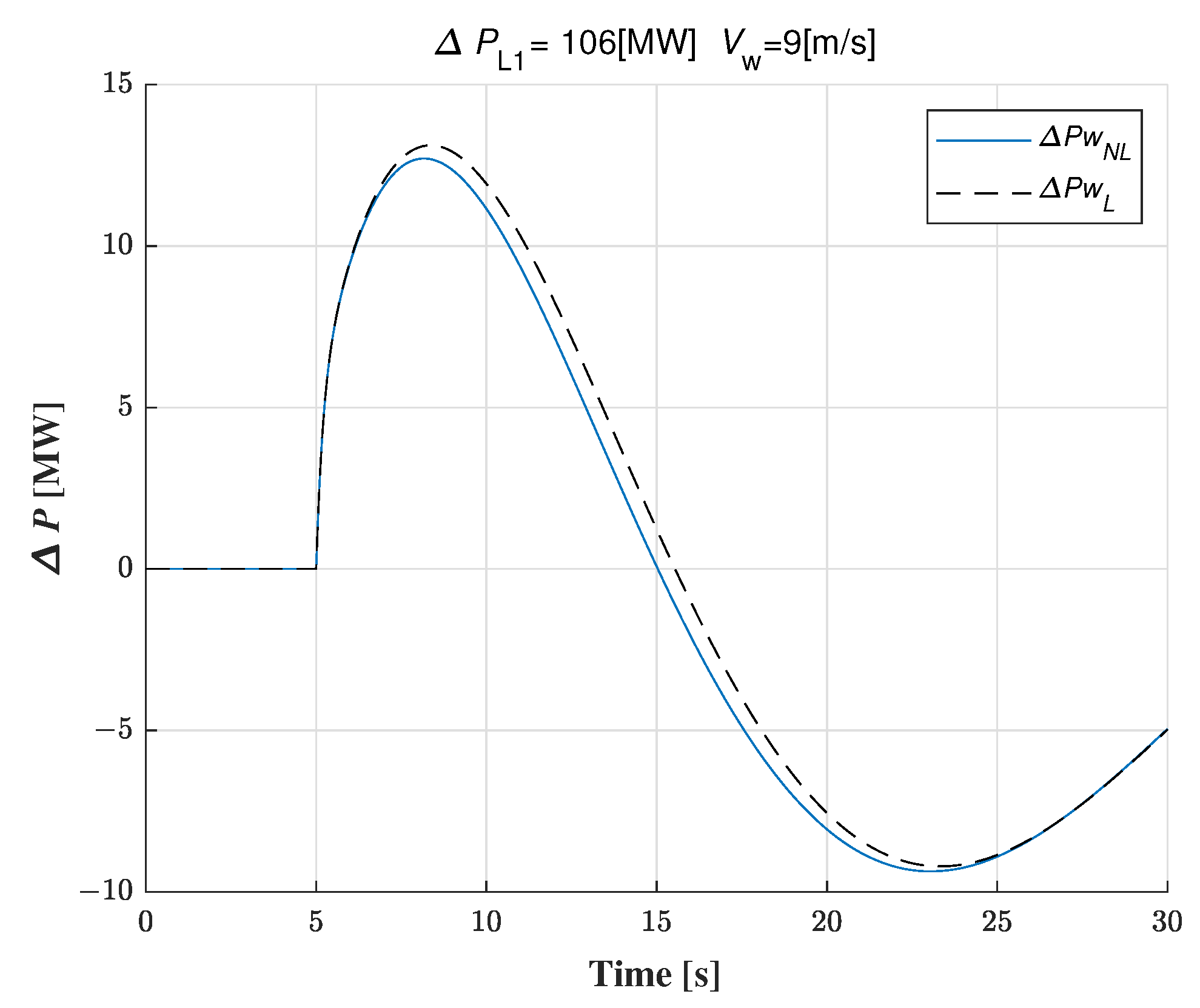
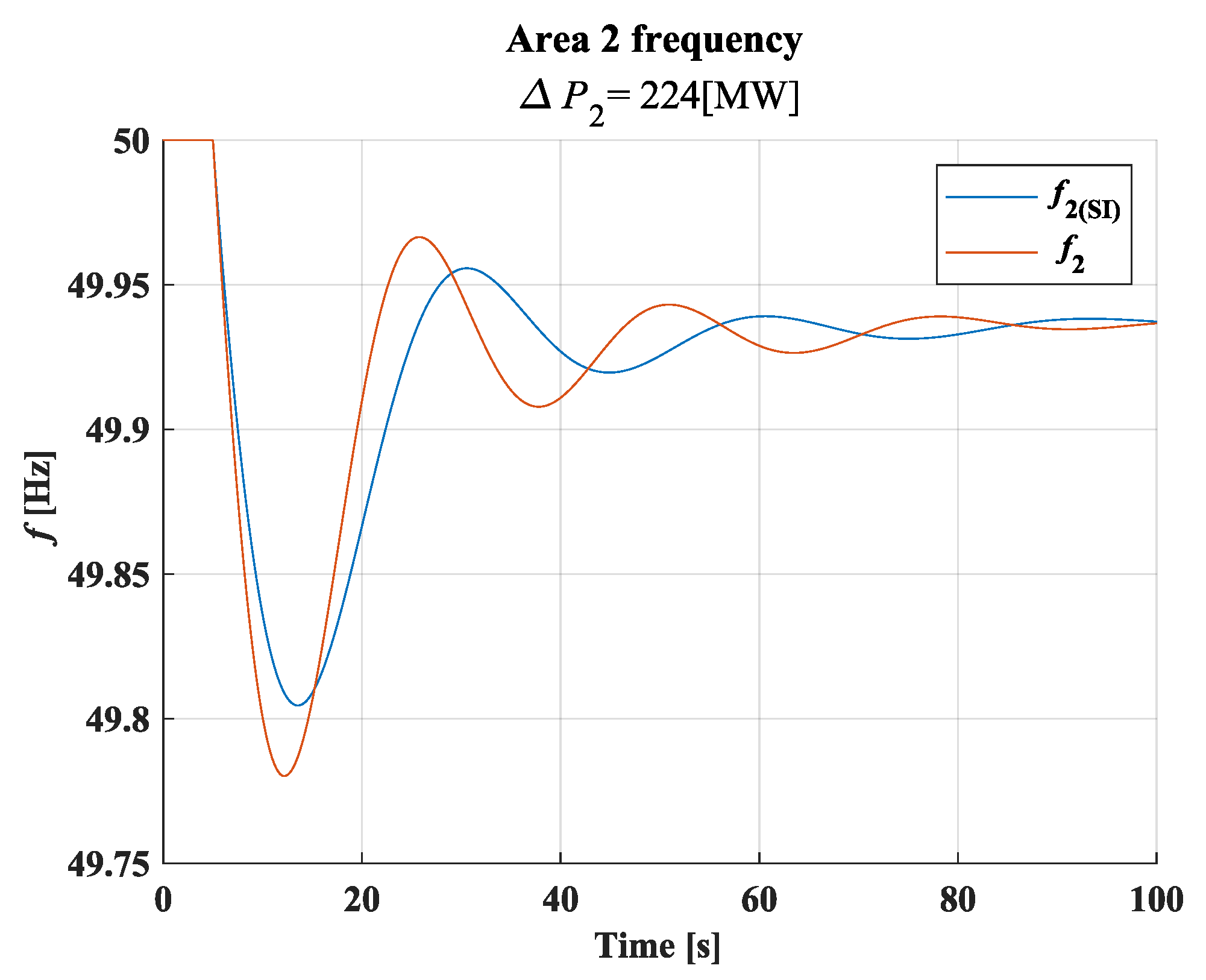
4.1. Frequency Response
4.2. Performance Indicators
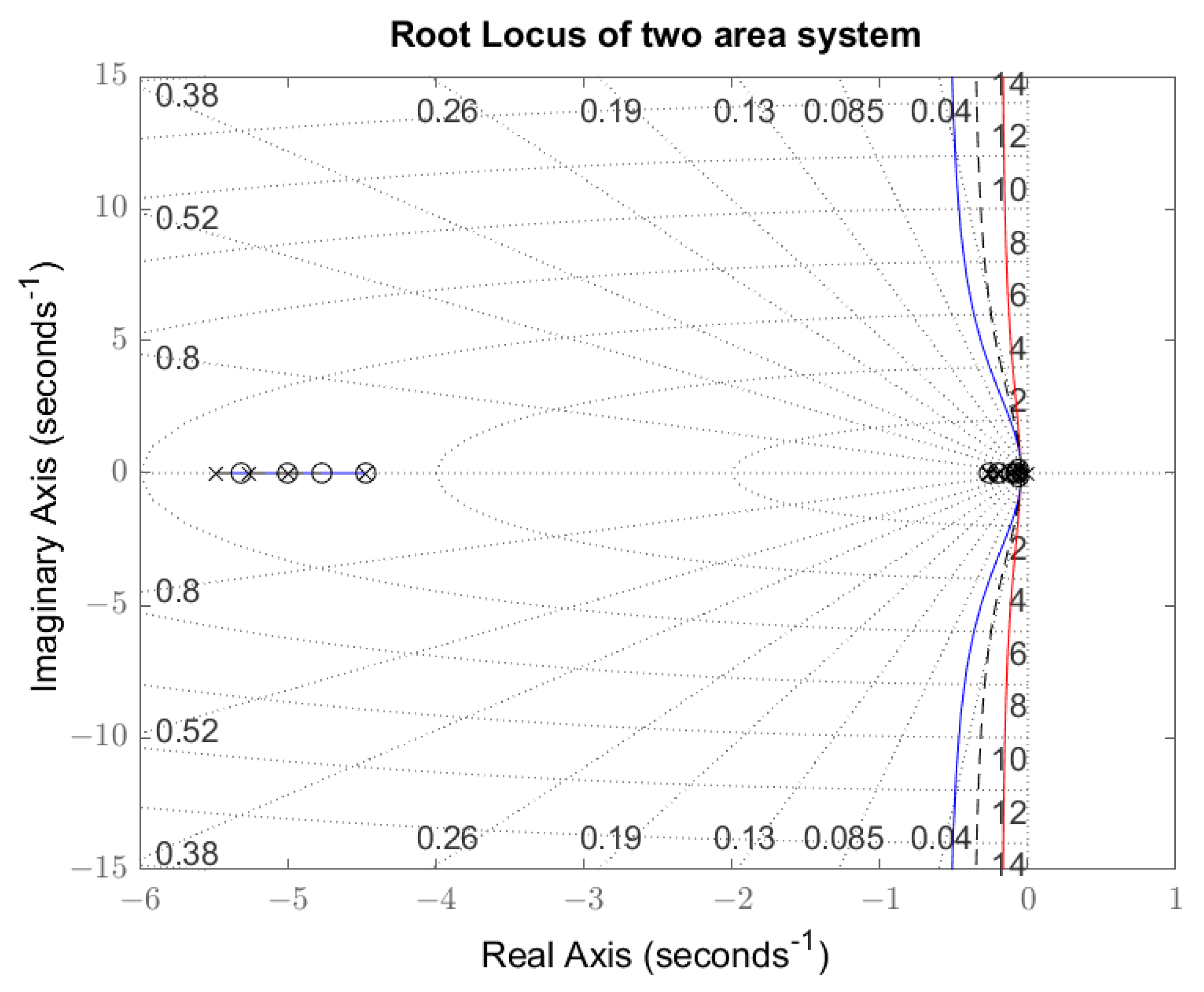
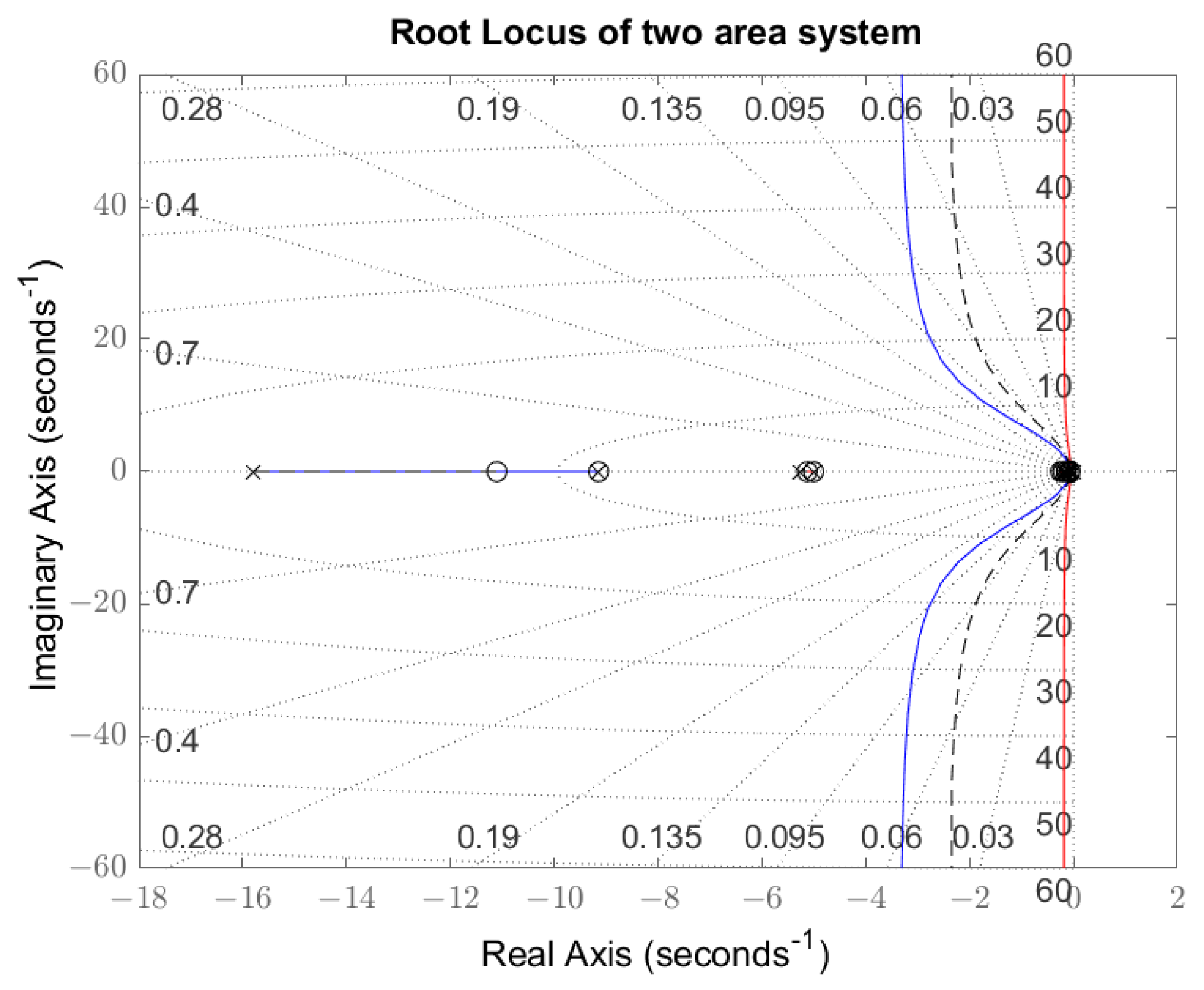
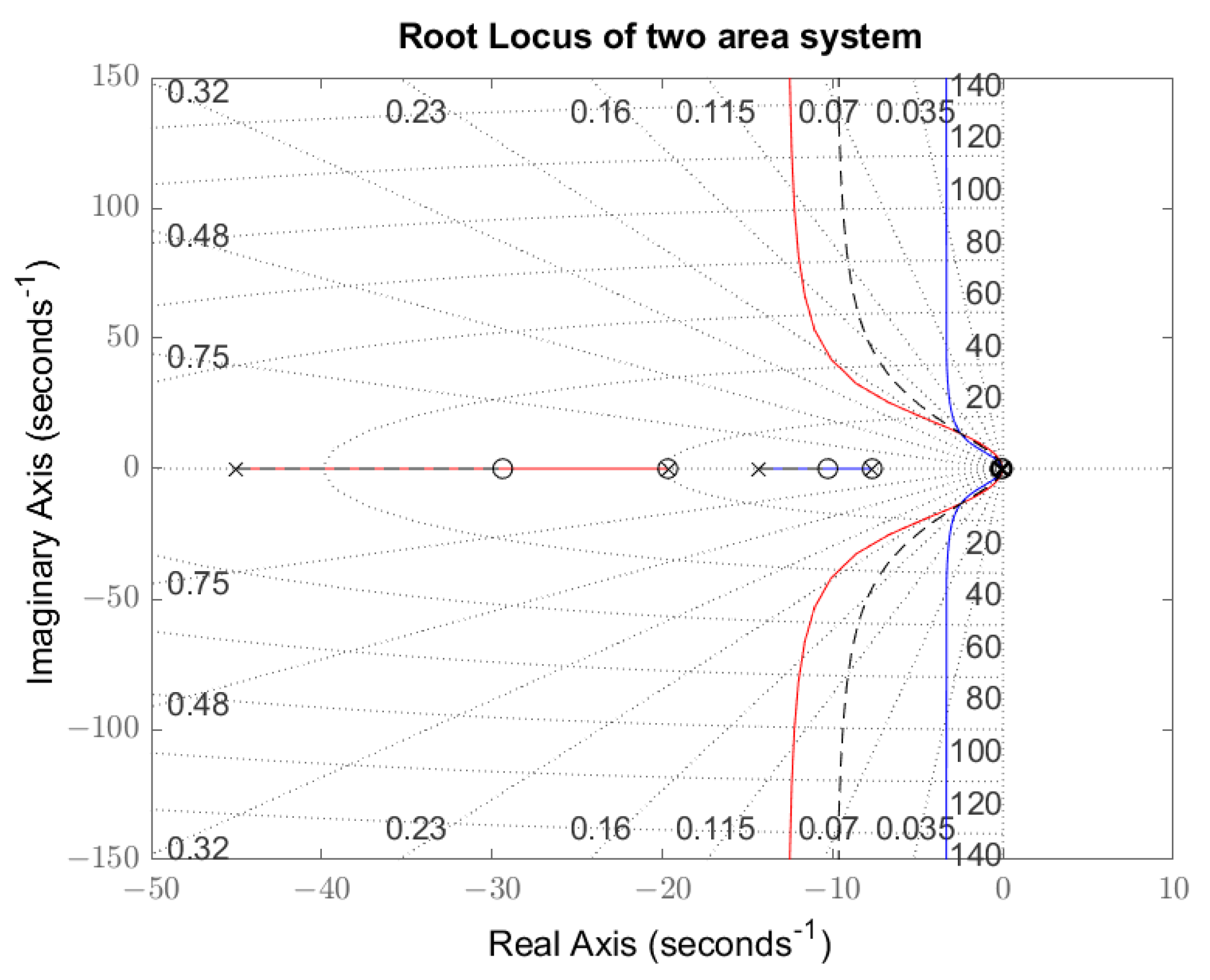
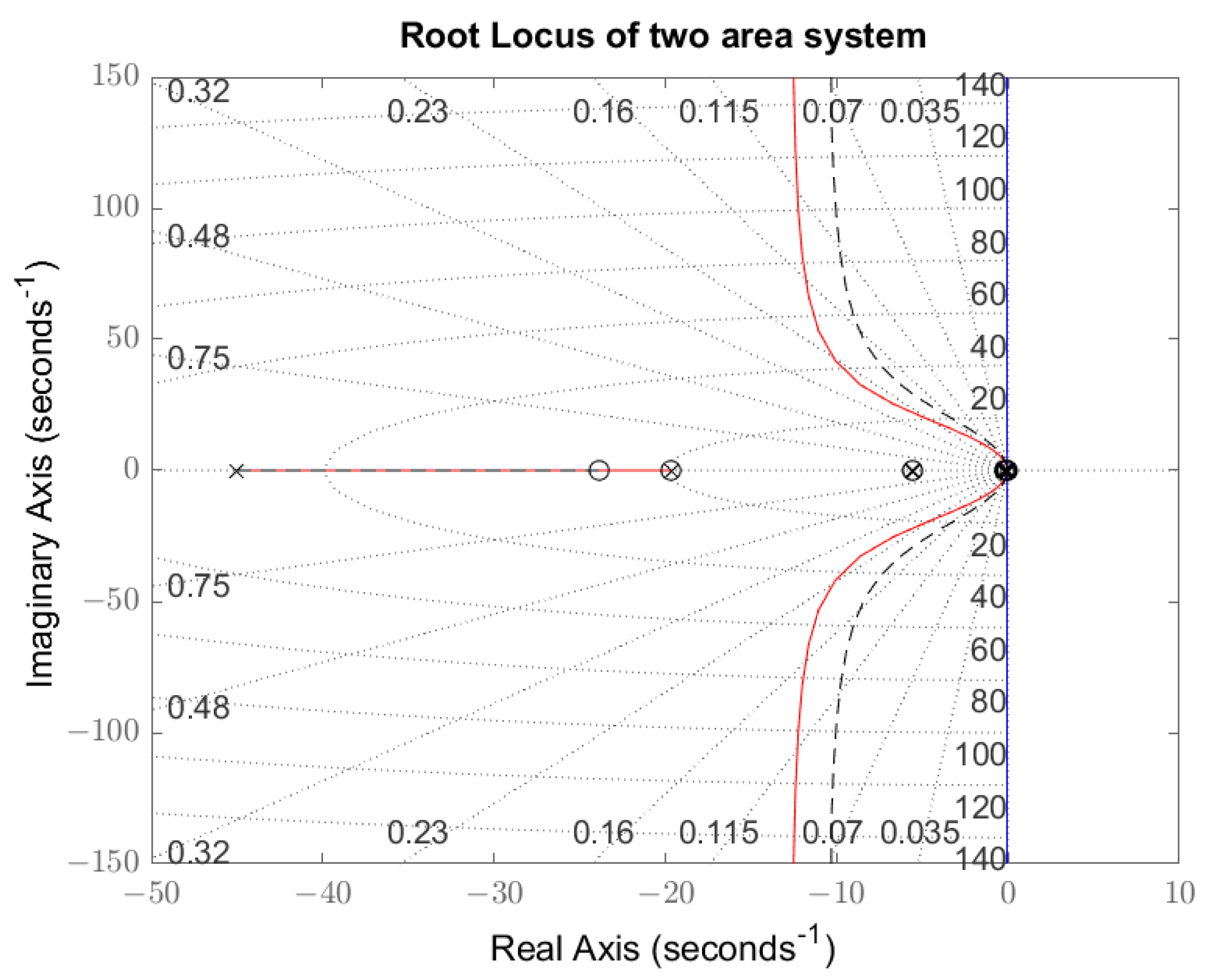
4.3. Root Locus
- case 1 in red, where both areas are equal, each one having an inertia varying between 822.4 and 4652.8 [MWs/Hz] and global transfer function ;
- case 2 in blue, where both areas are equal, each one having an inertia varying between 1862.2 and 4040.0 [MWs/Hz] and global transfer function ; and
- case 3 in dashed-black, where area-1 and area-2 are different, with values of total inertia between and and transfer function .
5. Discussion
5.1. Analysis of Results
5.1.1. Frequency Response
5.1.2. Root-Locus
5.2. Advantages and Limitations of the Proposed Method
5.3. Conclusions and Recommendations
5.4. Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
- The following abbreviations are used in this manuscript:
| AGC | Automatic generation control, |
| BESS | Battery energy storage system, |
| DMPC | Decentralized model predictive control, |
| FPC | Fast primary control, |
| I | Integral control, |
| LFC | Load frequency control, |
| LMI | Linear matrix inequality, |
| MPPT | Maximum power point tracking, |
| PEIT | Power electronics interfaced technologies, |
| PFC | Primary frequency control, |
| PI | Proportional–integral control, |
| PID | Proportional–integral–derivative control, |
| PMU | Phasor measurement unit, |
| RES | Renewable energy sources, |
| RoCoF | Rate of change of frequency, |
| SFC | Secondary frequency control, |
| SI | Synthetic inertia, |
| SISO | Single input single output, |
| TFC | Tertiary frequency control, |
| TSO | Transmission system operator, |
| VSWT | Variable speed wind turbine. |
| Nomenclature | |
| A | VSWT rotor-swept area (); |
| Close loop power system state space matrix; | |
| Global power system state space matrix; | |
| Area 1, area-2 power system state matrices; | |
| Coupling matrix between area 1 and link; | |
| Coupling matrix between area 2 and link; | |
| State space matrices of wind power turbines; | |
| Perturbation and input matrices of area-1; | |
| Perturbation and input matrices of area-2; | |
| Global power system input matrix; | |
| Global power system perturbation matrix; | |
| C | Global power system output matrix; |
| VSWT power coefficient; | |
| Nominal frequency [Hz]; | |
| Frequency variation [Hz]; | |
| Transfer function between and ; | |
| Overall governor transfer function; | |
| Transfer function between and ; | |
| Transfer function between output and impulse input; | |
| H | represents inertia [MWs/Hz]; |
| J | VSWT combined moment of inertia (MNm); |
| Performance index; | |
| K | State space feedback gain; |
| Kinetic energy [MWs]; | |
| Governor droop [MW/Hz]; | |
| Synchronizing torque between area-1 and area-2; | |
| Proportional and integral gains of MPPT control; | |
| Gearbox speed ratio (-); | |
| Global area transfer function; | |
| P | Solution of Riccati equation; |
| Power interchange between areas [MW]; | |
| , | Power imbalance, area-1 and area-2 [MW]; |
| Overall mechanic power variation of an area [MW]; | |
| , | Wind power, area-1 and area-2 [MW]; |
| Q | Performance index constant matrices; |
| R | Performance index constant matrices; |
| Rotor-swept radius (m); | |
| Torque reference from MPPT control (MNm); | |
| Torque reference from the SI control (MNm); | |
| VSWT mechanical torque (MNm); | |
| Module of area 1 voltage [kV]; | |
| Module of area 2 voltage [kV]; | |
| Wind speed (m/s); | |
| Link equivalent reactance []; | |
| State space variable of wind power turbines; | |
| Global power system state space vector; | |
| VSWT pitch angle (); | |
| Angular difference between voltages of area-1 and area-2; | |
| VSWT tip speed ratio; | |
| Air density (kg/); | |
| Impulse function; | |
| VSWT angular speed (rad/s). |
Appendix A
Numerical Values
- J 11.776 (MNm),
- 133 (-),
- , [MNm s]
- [MNm]
- 9 (m/s),
- 1.1945 (kg/),
- R 63.278 (),
- 0.5 (-),
- 9.9 (-)5,
- 0 ().
References
- Agathokleous, C.; Ehnberg, J. A quantitative study on the requirement for additional inertia in the european power system until 2050 and the potential role of wind power. Energies 2020, 13, 2309. [Google Scholar] [CrossRef]
- Ulbig, A.; Borsche, T.S.; Andersson, G. Impact of Low Rotational Inertia on Power System Stability and Operation; IFAC: Prague, Czech Republic, 2014; Volume 19, pp. 7290–7297. [Google Scholar] [CrossRef]
- Kundur, P.; Paserba, J.; Ajjarapu, V.; Andersson, G.; Bose, A.; Canizares, C.; Hatziargyriou, N.; Hill, D.; Stankovic, A.; Taylor, C.; et al. Definition and classification of power system stability. IEEE Trans. Power Syst. 2004, 19, 1387–1401. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Yang, G.; Nielsen, A.H.; Jensen, P.H. Combination of synchronous condenser and synthetic inertia for frequency stability enhancement in low-inertia systems. IEEE Trans. Sustain. Energy 2019, 10, 997–1005. [Google Scholar] [CrossRef]
- Li, Q.; Ren, B.; Tang, W.; Wang, D.; Wang, C.; Lv, Z. Analyzing the inertia of power grid systems comprising diverse conventional and renewable energy sources. Energy Rep. 2022, 8, 15095–15105. [Google Scholar] [CrossRef]
- Rapizza, M.R.; Canevese, S.M. Fast frequency regulation and synthetic inertia in a power system with high penetration of renewable energy sources: Optimal design of the required quantities. Sustain. Energy Grids Netw. 2020, 24, 100407. [Google Scholar] [CrossRef]
- Fang, J.; Tang, Y.; Li, H.; Blaabjerg, F. The Role of Power Electronics in Future Low Inertia Power Systems. In Proceedings of the 2018 IEEE International Power Electronics and Application Conference and Exposition (PEAC), Shenzhen, China, 4–7 November 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Ratnam, K.S.; Palanisamy, K.; Yang, G. Future low-inertia power systems: Requirements, issues, and solutions—A review. Renew. Sustain. Energy Rev. 2020, 124, 109773. [Google Scholar] [CrossRef]
- Dreidy, M.; Mokhlis, H.; Mekhilef, S. Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 2017, 69, 144–155. [Google Scholar] [CrossRef]
- Bonfiglio, A.; Invernizzi, M.; Labella, A.; Procopio, R. Design and Implementation of a Variable Synthetic Inertia Controller for Wind Turbine Generators. IEEE Trans. Power Syst. 2019, 34, 754–764. [Google Scholar] [CrossRef]
- Riquelme, E.; Fuentes, C.; Chavez, H. A review of limitations of wind synthetic inertia methods. In Proceedings of the 2020 IEEE PES Transmission and Distribution Conference and Exhibition—Latin America, T and D LA, Montevideo, Uruguay, 28 September–2 October 2020. [Google Scholar] [CrossRef]
- Pelletier, M.; Phethean, M.; Nutt, S. Grid code requirements for artificial inertia control systems in the New Zealand power system. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–7. [Google Scholar]
- Brisebois, J.; Aubut, N. Wind farm inertia emulation to fulfill Hydro-Québec’s specific need. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–29 July 2011; pp. 1–7. [Google Scholar] [CrossRef]
- Massaro, F.; Musca, R.; Vasile, A.; Zizzo, G. A simulation study for assessing the impact of energy storage systems for Fast Reserve with additional synthetic inertia control on the Continental Europe synchronous area. Sustain. Energy Technol. Assessm. 2022, 53, 102763. [Google Scholar] [CrossRef]
- Grebe, E.; Kabouris, J.; López Barba, S.; Sattinger, W.; Winter, W. Low frequency oscillations in the interconnected system of Continental Europe. In Proceedings of the IEEE PES General Meeting, Minneapolis, MN, USA, 25–29 July 2010; pp. 1–7. [Google Scholar] [CrossRef]
- Mohamed, T.H.; Bevrani, H.; Hassan, A.A.; Hiyama, T. Decentralized model predictive based load frequency control in an interconnected power system. Energy Convers. Manag. 2011, 52, 1208–1214. [Google Scholar] [CrossRef]
- Ojaghi, P.; Rahmani, M. LMI-Based Robust Predictive Load Frequency Control for Power Systems with Communication Delays. IEEE Trans. Power Syst. 2017, 32, 4091–4100. [Google Scholar] [CrossRef]
- Tabassum, F.; Rana, M.S. Robust Control of Frequency for Multi-Area Power System. In Proceedings of the 2020 IEEE Region 10 Symposium (TENSYMP), Dhaka, Bangladesh, 5–7 June 2020; pp. 86–89. [Google Scholar] [CrossRef]
- Raj, T.D.; Kumar, C.; Kotsampopoulos, P.; Fayek, H.H. Load Frequency Control in Two-Area Multi-Source Power System Using Bald Eagle-Sparrow Search Optimization Tuned PID Controller. Energies 2023, 16, 2014. [Google Scholar] [CrossRef]
- Kumar Maurya, A.; Khan, H.; Ahuja, H. Stability Control of Two-Area of Power System Using Integrator, Proportional Integral and Proportional Integral Derivative Controllers. In Proceedings of the 2023 International Conference on Artificial Intelligence and Smart Communication (AISC), Greater Noida, India, 27–29 January 2023; pp. 273–278. [Google Scholar] [CrossRef]
- Ma, M.; Zhang, C.; Shao, L.; Sun, Y. Primary frequency regulation for multi-area interconnected power system with wind turbines based on DMPC. In Proceedings of the Chinese Control Conference, CCC. IEEE Computer Society, Chengdu, China, 27–29 July 2016; Volume 2016, pp. 4384–4389. [Google Scholar] [CrossRef]
- Riquelme, E.; Chavez, H.; Barbosa, K.A. RoCoF-Minimizing H Norm Control Strategy for Multi-Wind Turbine Synthetic Inertia. IEEE Access 2022, 10, 18268–18278. [Google Scholar] [CrossRef]
- Yedrzejewski, N.; Giusto, A. Potential impact of wind-based Synthetic Inertia on the Frequency Response of the Argentine-Uruguayan Interconnected Power Systems. In Proceedings of the 2022 IEEE PES Innovative Smart Grid Technologies—Asia (ISGT Asia), Auckland, New Zealand, 21–24 November 2023; pp. 505–509. [Google Scholar] [CrossRef]
- Roy, N.K.; Islam, S.; Podder, A.K.; Roy, T.K.; Muyeen, S.M. Virtual Inertia Support in Power Systems for High Penetration of Renewables—Overview of Categorization, Comparison, and Evaluation of Control Techniques. IEEE Access 2022, 10, 129190–129216. [Google Scholar] [CrossRef]
- Adu, J.A.; Tossani, F.; Pontecorvo, T.; Ilea, V.; Vicario, A.; Conte, F.; D’Agostino, F. Coordinated Inertial Response Provision by Wind Turbine Generators: Effect on Power System Small-Signal Stability of the Sicilian Network. In Proceedings of the 2022 IEEE International Conference on Environment and Electrical Engineering and 2022 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Prague, Czech Republic, 28 June–1 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Kundur, P.; Balu, N.J.; Lauby, M.G. Power System Stability and Control; The EPRI Power System Engineering Series; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Anderson, P.M.; Mirheydar, M. A low-order system frequency response model. IEEE Trans. Power Syst. 1990, 5, 720–729. [Google Scholar] [CrossRef]
- Chávez, H.; Hezamsadeh, M.R.; Carlsson, F. A simplified model for predicting primary control inadequacy for nonresponsive wind power. IEEE Trans. Sustain. Energy 2016, 7, 271–278. [Google Scholar] [CrossRef]
- Liu, Y.z.; Zhao, D.w.; Zhang, L.; Zhu, L.z.; Chen, N. Simulation study on transient characteristics of DFIG wind turbine systems based on dynamic modeling. In Proceedings of the 2014 China International Conference on Electricity Distribution (CICED), Shenzhen, China, 23–26 September 2014; pp. 1408–1413. [Google Scholar] [CrossRef]
- Duan, G.R.; Yu, H.H. LMIs in Control Systems: Analysis, Design and Applications, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Tan, W. Tuning of PID load frequency controller for power systems. Energy Convers. Manag. 2009, 50, 1465–1472. [Google Scholar] [CrossRef]






| No. | Load | H | |||||
|---|---|---|---|---|---|---|---|
| [MW] | [MW] | [GWs] | [] | [] | [s] | [s] | |
| 1 | 128.0 | 7154.2 | 70.1 | 2088.0 | 2804.0 | 12.0 | 0.96 |
| 2 | 152.0 | 6963.1 | 65.5 | 1617.5 | 2620.0 | 18.8 | 3.19 |
| 3 | 190.0 | 7132.1 | 85.6 | 2286.9 | 3426.4 | 11.8 | 0.69 |
| 4 | 320.0 | 8693.1 | 104.3 | 1461.6 | 4172.0 | 17.4 | 1.24 |
| 5 | 480.0 | 7507.6 | 116.3 | 1866.6 | 4652.8 | 14.7 | 1.83 |
| 6 | 320.0 | 7619.9 | 85.1 | 1202.0 | 3402.0 | 4.5 | 0.04 |
| 7 | 120.0 | 6774.3 | 67.2 | 949.0 | 2689.6 | 94.9 | 6.52 |
| 8 | 194.0 | 6070.7 | 46.6 | 1420.0 | 1862.4 | 14.6 | 2.80 |
| 9 | 374.0 | 6836.4 | 57.4 | 843.9 | 2296.4 | 13.3 | 2.97 |
| 10 | 70.0 | 6179.4 | 20.6 | 691.6 | 822.4 | 32.7 | 6.28 |
| 11 | 140.0 | 7627.3 | 65.5 | 1949.1 | 2619.6 | 26.4 | 4.30 |
| 12 | 146.0 | 7627.3 | 62.9 | 1939.0 | 2516.8 | 25.1 | 4.68 |
| 13 | 132.0 | 7260.7 | 53.4 | 2002.1 | 2136.0 | 20.2 | 3.25 |
| 14 | 153.0 | 7242.6 | 93.0 | 2960.4 | 3720.8 | 26.9 | 5.36 |
| 15 | 224.0 | 7613.3 | 101.0 | 1735.7 | 4040.0 | 9.5 | 1.13 |
| 16 | 195.0 | 8697.8 | 59.9 | 1484.5 | 2395.2 | 14.7 | 2.67 |
| 17 | 160.0 | 7350.4 | 77.3 | 1507.4 | 3090.8 | 4.5 | 0.59 |
| 18 | 170.0 | 7239.0 | 84.6 | 1403.5 | 3385.2 | 18.6 | 3.84 |
| 19 | 106.0 | 5255.9 | 55.4 | 1168.5 | 2217.6 | 8.5 | 1.59 |
| 20 | 260.0 | 6862.1 | 39.8 | 1600.4 | 1590.4 | 15.4 | 3.83 |
| 21 | 190.0 | 4542.8 | 64.6 | 18.7 | 2583.2 | 87.4 | 4.88 |
| 22 | 116.0 | 8252.4 | 48.3 | 1921.0 | 1932.4 | 21.2 | 4.81 |
| Figure | ||
|---|---|---|
| Figure 9 and Figure 10 | [0.0987 −0.0008 0.3677 −0.4309] | [−0.1044 −0.0006 0.3312 −0.5065] |
| Figure 11 and Figure 12 | [−0.1977 −0.0070 0.7150 −0.3407] |
| Indicator | No Control | SI Control | % |
|---|---|---|---|
| RoCoF [Hz/s] | −0.0554 | −0.0551 | −0.5183 |
| Nadir [Hz] | 49.780 | 49.804 | +0.050 |
| Indicator | No Control | SI Control | % |
|---|---|---|---|
| RoCoF [Hz/s] | −0.1202 | −0.1164 | −3.1400 |
| Nadir [Hz] | 49.680 | 49.740 | +0.128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barrueto Guzmán, A.; Chávez Oróstica, H.; Barbosa, K.A. Stability Analysis: Two-Area Power System with Wind Power Integration. Processes 2023, 11, 2488. https://doi.org/10.3390/pr11082488
Barrueto Guzmán A, Chávez Oróstica H, Barbosa KA. Stability Analysis: Two-Area Power System with Wind Power Integration. Processes. 2023; 11(8):2488. https://doi.org/10.3390/pr11082488
Chicago/Turabian StyleBarrueto Guzmán, Aldo, Héctor Chávez Oróstica, and Karina A. Barbosa. 2023. "Stability Analysis: Two-Area Power System with Wind Power Integration" Processes 11, no. 8: 2488. https://doi.org/10.3390/pr11082488
APA StyleBarrueto Guzmán, A., Chávez Oróstica, H., & Barbosa, K. A. (2023). Stability Analysis: Two-Area Power System with Wind Power Integration. Processes, 11(8), 2488. https://doi.org/10.3390/pr11082488







