Molecular Modeling of Supercritical Processes and the Lattice—Gas Model
Abstract
:1. Introduction
2. Molecular Level
2.1. Ideal Systems
2.2. Non-Ideal Systems and the Lattice-Gas Model
3. Thermodynamics and Kinetics
- The second law of thermodynamics and connection between models of equilibrium and kinetics;
- A self-consistence of equilibrium and kinetics in ideal systems;
- A self-consistence of equilibrium and kinetics in non-ideal systems;
- The equations of a state for non-ideal systems and their connection with kinetic models;
- Why it is impossible to use factors of activity for the AC in kinetic models;
- Thermodynamic parameters of the critical area and the requirement of technologies.
3.1. The Second Law of Thermodynamics and Connection between Models of Equilibrium and Kinetics
3.2. Self-Consistence of Equilibrium and Kinetics in Ideal Systems
3.3. Self-Consistence of Equilibrium and Kinetics in Non-Ideal Systems
3.4. The Equations of a State for Non-Ideal Systems and Their Connection with Kinetic Models
3.5. Why It Is Impossible to Use Factors of Activity for AC in Kinetic Models
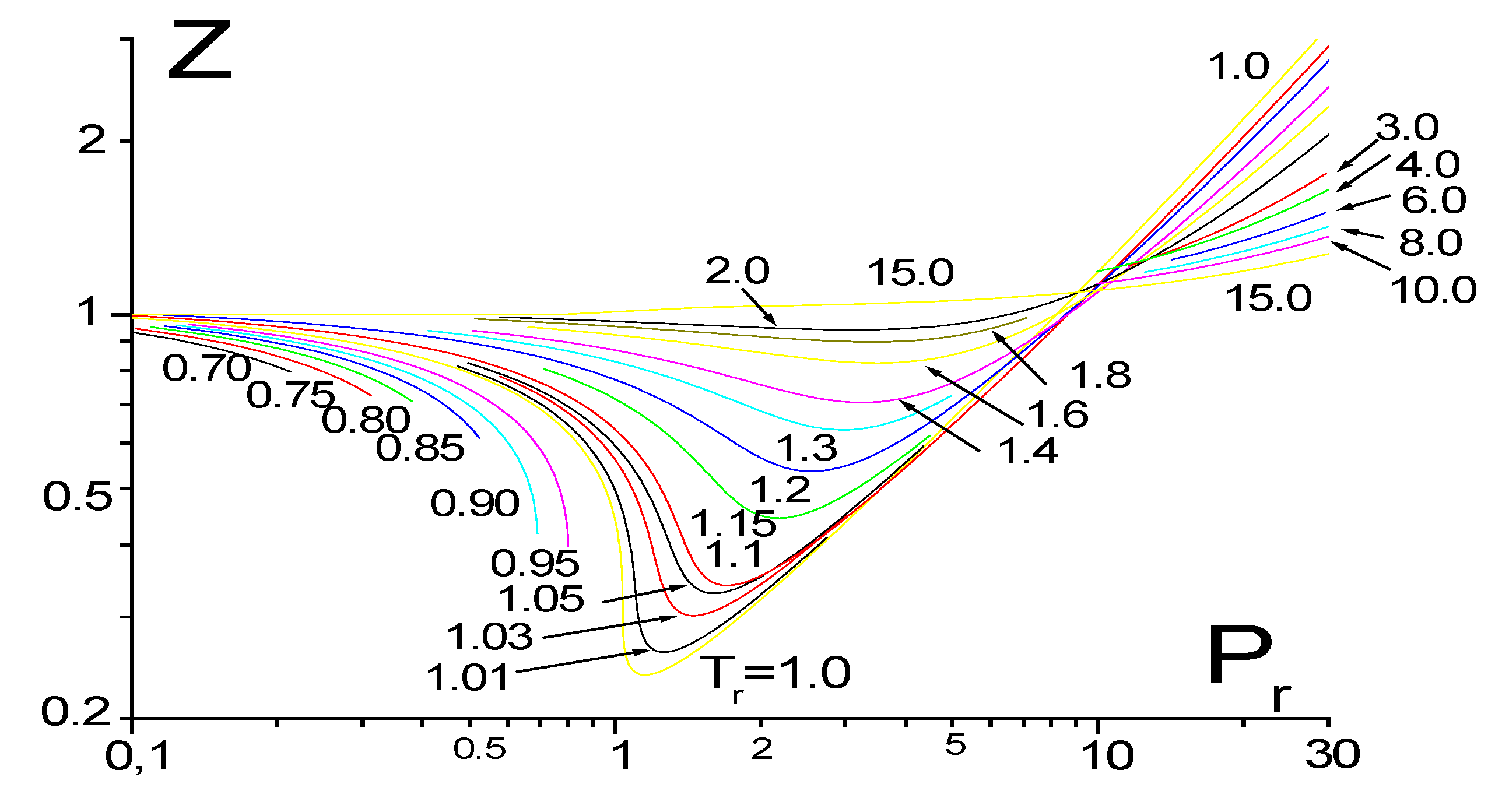
3.6. Thermodynamic Parameters of the Critical Area and the Requirement of Technologies
4. Model of the Effective Pair Potential
4.1. Internal Motions of Particles
4.2. Vapor–Liquid Systems
5. Influence of SCFs on Equilibrium and Kinetic Characteristics
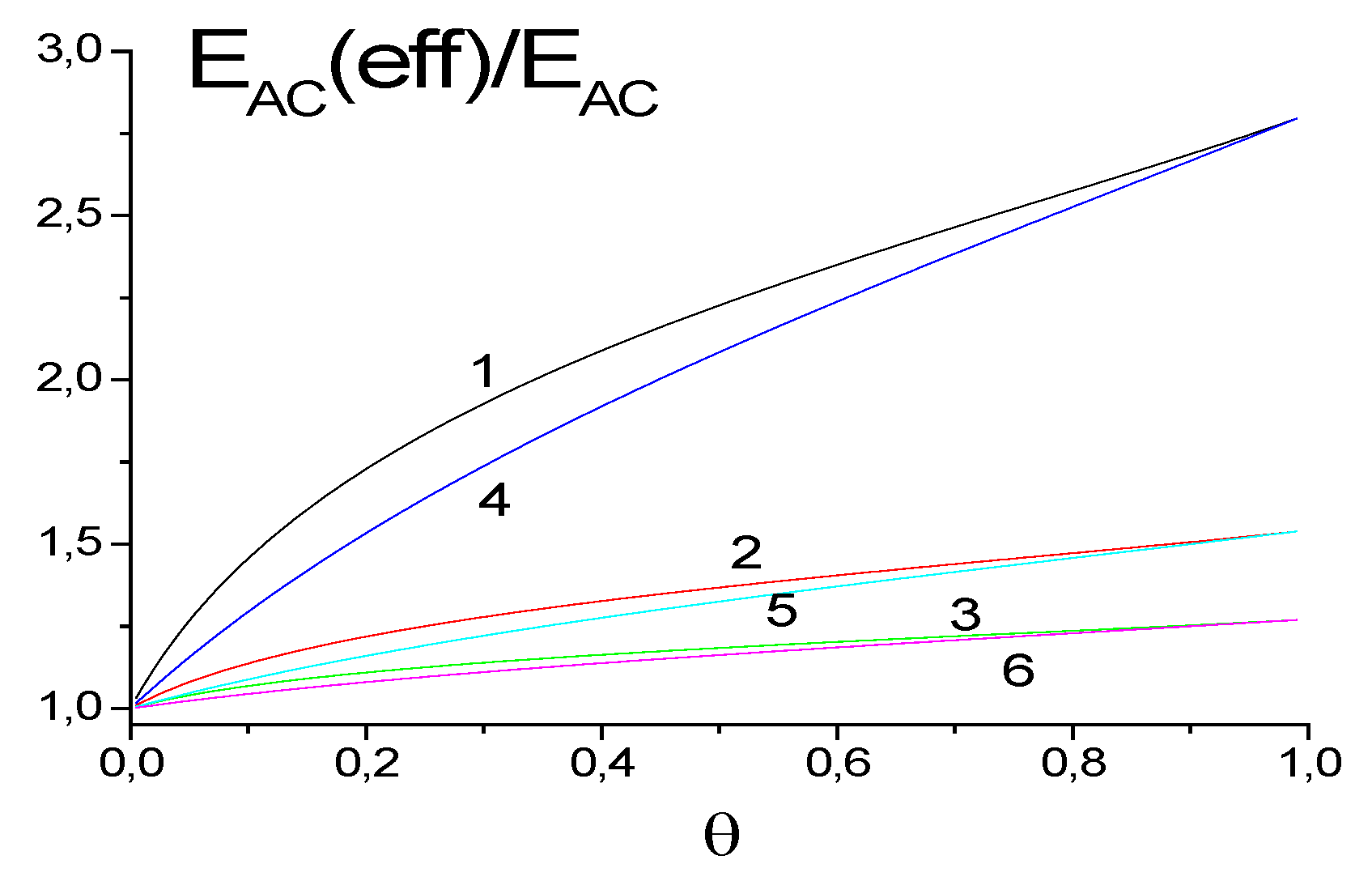
5.1. Effect of SCFs on the Characteristics of Adsorption Processes
5.2. Effect of an SCF on the Concentration Dependence of the Rate of a Reaction
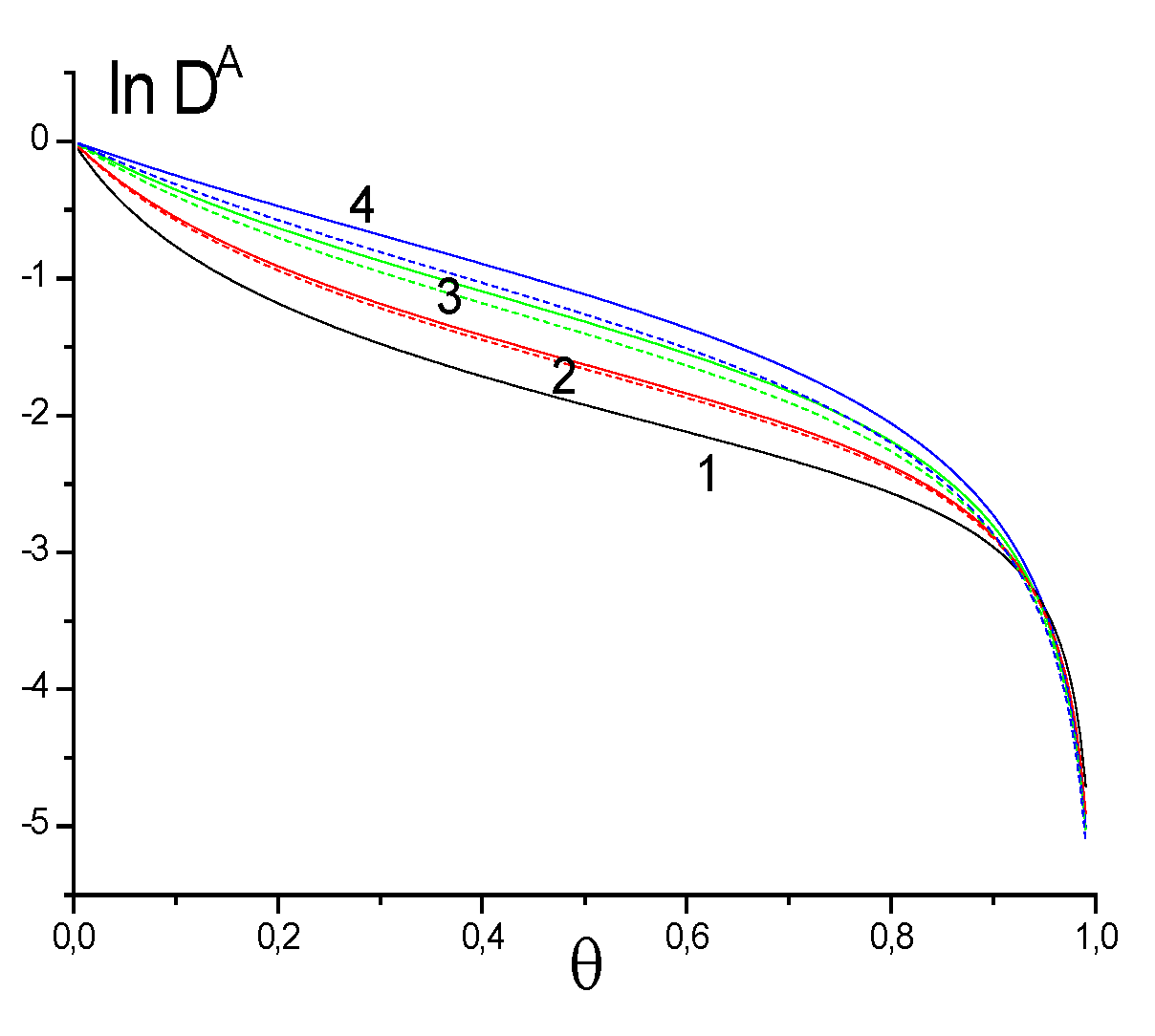
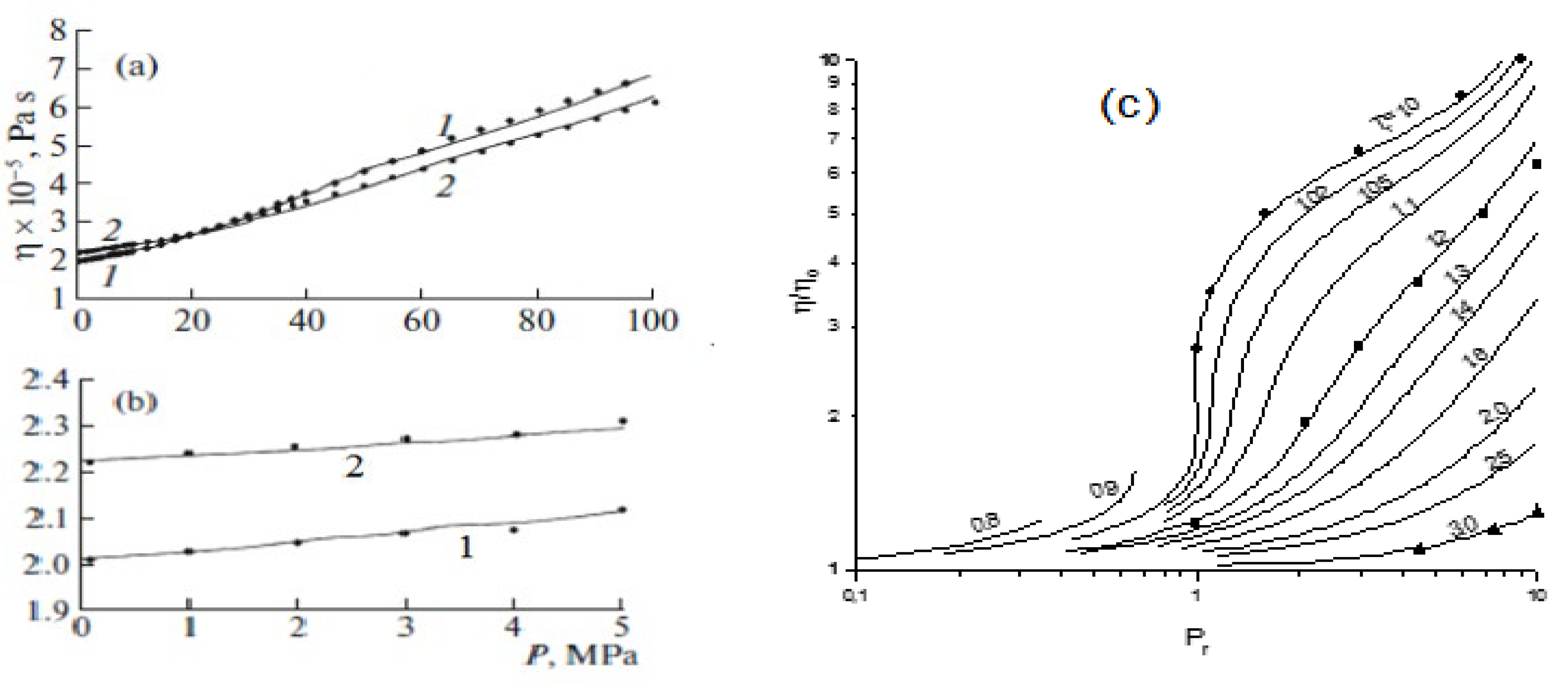
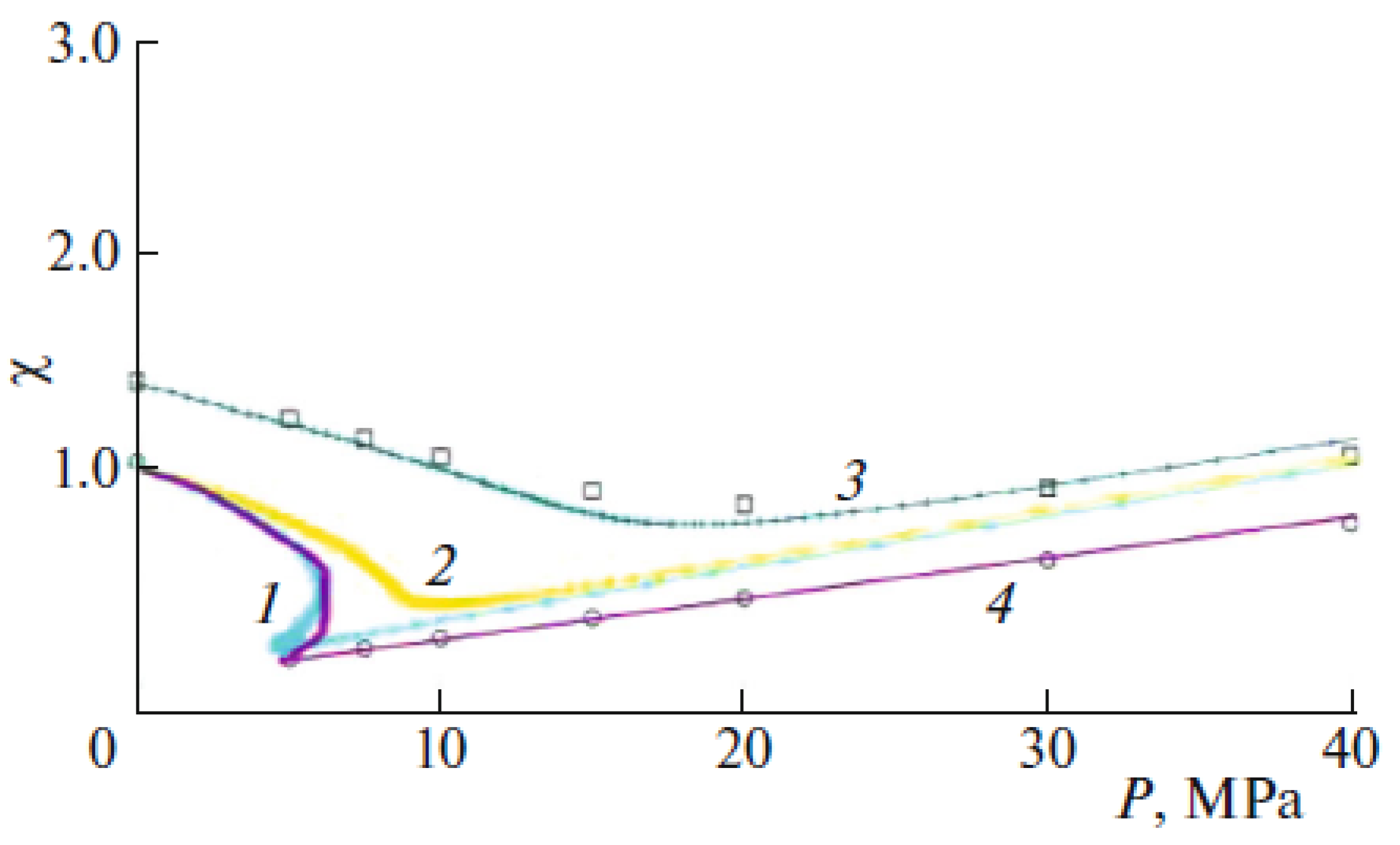
5.3. Effect of an SCF on the Concentration Dependence of the Dissipative Coefficients
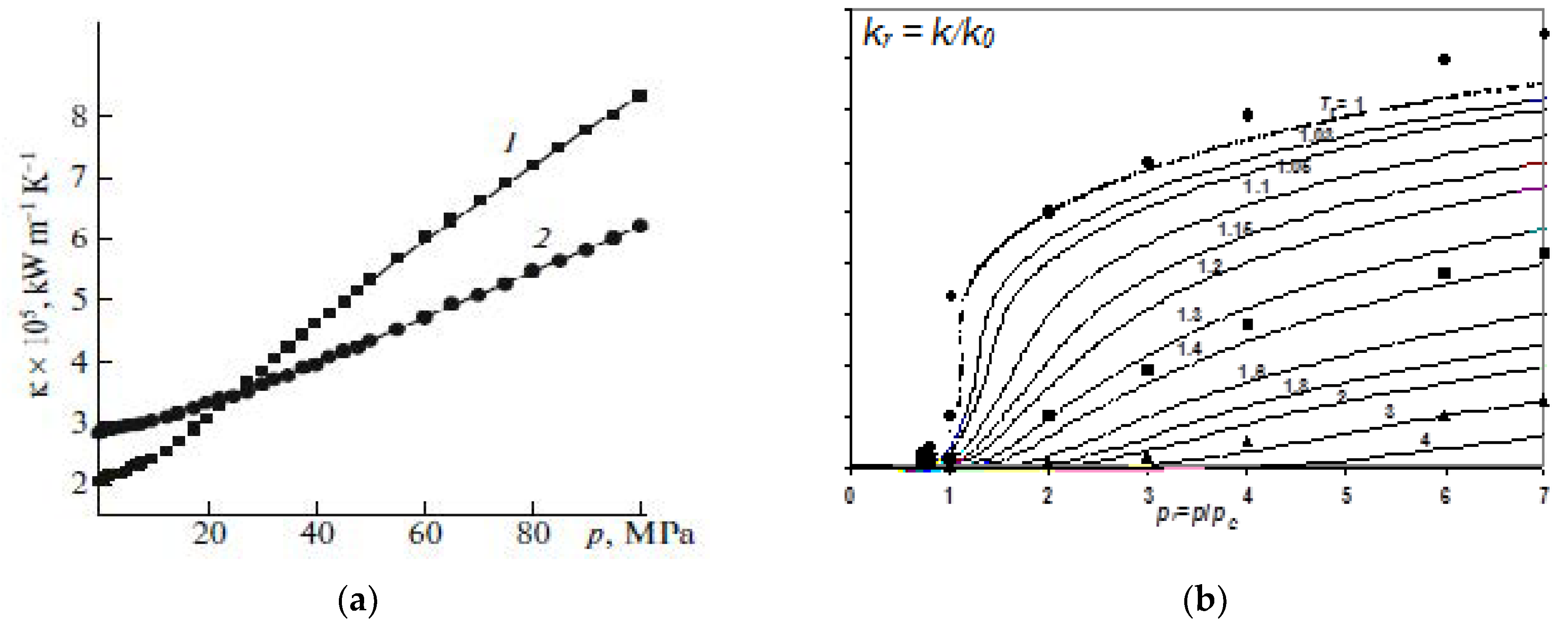
6. LGM and Dissipative Coefficients
7. Extension of the Models
7.1. Nonspherical Potential Functions
7.2. Water Molecules
7.3. Kinetic Equations
8. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| ai0 | pre-exponential factor of the Henry constant for molecules of type i |
| dtr | triple interaction parameter associated with its energy ε3 |
| Di* | partial self-diffusion coefficient for molecules of type i |
| Eij | reaction’s energy of activation between i and j reagents |
| EA(ef) | effective activation energy of desorption |
| kB | Boltzmann constant |
| kij | rate constant of elementary reaction i + j → products |
| kij0 | rate constant pre-exponential factor for elementary reaction i + j → products |
| k1 and k2 | reaction rate constants in the forward and backward directions |
| K | equilibrium constant of the stage |
| M | number of sites in the system |
| ni | concentration of i-type molecules |
| Qi | energy of i-particle bonding with the surface |
| Q | amount of heat |
| Qs | statistical sum of the system |
| P | pressure |
| Pi | partial pressure of i-type molecules |
| P({γfi},τ) | probability of finding the system at the time τ in a state {γfi}. For the sake of brevity, this state is denoted as {I} ≡ {γfi} |
| s | number of occupation states of any cell or site |
| S | entropy |
| Sm | molecular property in flow |
| T | temperature |
| tfhij = θfhij/θfi | function of the conventional probability of j particles being near i particles (fh represents the numbers of sites containing these particles) |
| U | internal energy |
| Uij | rate of an elementary stage of a bimolecular reaction i + j → products |
| Ufi(α) | rate of the elementary single-site stage i ↔ b with number α in the site f |
| Ufgij(α) | rate of the elementary two- site stage i + jα ↔ b + dα with number α in two sites fg |
| V | volume of the system |
| u | contribution from the vibrational motion of molecules to energy parameters |
| Wα({I} → {II}) | probability of the elementary process α which resulted at time τ in the transfer of the system from the initial state {I} to the final state {II} |
| xi = θi/θ | mole fraction of component i among all molecules of the mixture. |
| z | nearest neighbors of any site or cell |
| zfg* | the number of possible hops to nearest-neighbor sites g for the fth cell along the direction in which the label moves |
| Z | compressibility factor |
| α | number of stages in the total process |
| αi | activity coefficient of i-type reagents |
| αij* | denotes the activity coefficients of ACs |
| αij = εij*/εij, for simplicity αij = α | is used for both reagents |
| γfi | variable determined the occupation state of site with number f (1 ≤ f ≤ M) by particle of type i (1 ≤ i ≤ s) |
| εij | parameter of this interaction between ij pairs of neighboring particles |
| εij* | interaction parameter for reaction AC using i-type particles and neighboring j-type particles |
| η | shear viscosity coefficient |
| κ | heat capacity coefficient |
| κD | mean square displacement of particles in a solid in the harmonic approximation |
| λ | average cell size |
| non-ideality function for the two-site stage | |
| non-ideality function for a one-site stage | |
| μi | chemical potential of component i |
| μi0 | chemical potential of the standard state for component i |
| ρ | mean free path of a particle |
| θi | concentration of particles type i in the (surface or bulk)) system |
| θ = ∑I = 1s−1θi | complete occupancy of a lattice system by all i components of the system, 1 ≤ i ≤ s − 1 |
| θfhij | probability of two particles i and j being on nearest neighboring sites f and h (for homogeneous system θij, is the pair particle distribution function) |
| νi | stoichiometric coefficient |
Appendix A. Kinetics Equation in the LGM
References
- Savage, P.E.; Gopalan, S.; Mizan, T.I.; Martino, C.J.; Brock, E.E. Reactions at supercritical conditions: Applications and fundamentals. AIChE J. 1995, 41, 1723–1778. [Google Scholar] [CrossRef]
- Galkin, A.A.; Lunin, V.V. Subcritical and supercritical water: A universal medium for chemical reactions. Russ. Chem. Rev. 2005, 74, 21–35. [Google Scholar] [CrossRef]
- Zalepugin, D.Y.; Tilkunova, N.A.; Chernyshova, I.V.; Polyakov, V.S. Development of Technologies based on Supercritical Fluids. Sverhkriticheskie Flyuidy Teor. Prakt. 2006, 1, 27–51. [Google Scholar]
- Bogdan, V.I.; Koklin, A.E.; Kazansky, V.B. Regeneration of Deactivated Palladium Catalysts of Selec-tive Acetylene Hydrogenation be the Supercritical CO2. Sverhkriticheskie Flyuidy Teor. Prakt. 2006, 1, 5–12. [Google Scholar]
- Knez, Ž.; Markočič, E.; Leitgeb, M.; Primožič, M.; Hrnčič, M.K.; Škerget, M. Industrial applications of supercritical fluids: A review. Energy 2014, 77, 235–243. [Google Scholar] [CrossRef]
- Gandhi, K.; Arora, S.; Kumar, A. Industrial applications of supercritical fluid extraction: A review. Int. J. Chem. Stud. 2017, 5, 336–340. [Google Scholar]
- Mukhopadhyay, M. Natural Extracts Using Supercritical Carbon Dioxide; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar] [CrossRef]
- Gopaliya, P.; Kamble, P.R.; Kamble, R.; Chauhan, C.S. A Review Article on Supercritical Fluid Chroma-tography. Int. J. Pharma Res. Rev. 2014, 3, 59–66. [Google Scholar]
- Martinez, A.C.; Meireles, M.A.A. Application of Supercritical Fluids in the Conservation of Bioactive Compounds: A Review. Food Public Health 2020, 10, 26–34. [Google Scholar]
- Bhardwaj, L.; Sharma, P.K.; Visht, S.; Garg, V.K.; Kumar, N. A review on methodology and application of supercritical fluid technology in pharmaceutical industry. Pharm. Sin. 2010, 1, 183–194. [Google Scholar]
- Sapkale, G.N.; Patil, S.M.; Surwase, U.S.; Bhatbhage, P.K. Supercritical Fluid Extraction. Int. J. Chem. Sci. 2010, 8, 729–743. [Google Scholar]
- Gumerov, F.M.; Gabitov, F.R.; Gazizov, R.A.; Bilalov, T.R.; Yarullin, R.S. Future Trends of Sub- and Supercritical Fluids Appli-cation in Biodiezel Fuel Production. Sverhkriticheskie Flyuidy Teor. Prakt. 2006, 1, 66–76. [Google Scholar]
- Gumerov, F.M.; Sabirzyanov, A.N.; Gumerova, G.I. Sub- and Supercritical Fluids in Processes of Polymer Processing; Fan: Kazan, Russia, 2007. [Google Scholar]
- Myasoedov, B.F.; Kulyako, Y.M.; Shadrin, A.Y.; Samsonov, M.D. Supercritical Fluid Extraction of Radionuclides. Sverhkriticheskie Flyuidy Teor. Prakt. 2007, 2, 5–24. [Google Scholar]
- Ahmad, T.; Masoodi, F.A.; Rather, S.A.; Wani, S.M.; Gull, A. Supercritical Fluid Extraction: A Review. J. Biol. Chem. Chron. 2019, 5, 114–122. [Google Scholar] [CrossRef]
- Parhi, R.; Suresh, P. Supercritical Fluid Technology: A Review. J. Adv. Pharm. Sci. Technol. 2013, 1, 13–36. [Google Scholar] [CrossRef]
- Zhou, J.; Gullón, B.; Wang, M.; Gullón, P.; Lorenzo, J.M.; Barba, F.J. The Application of Supercritical Fluids Technology to Recover Healthy Valuable Compounds from Marine and Agricultural Food Processing By-Products: A Review. Processes 2021, 9, 357. [Google Scholar] [CrossRef]
- Aymonier, C.; Loppinet-Serani, A.; Reverón, H.; Garrabos, Y.; Cansell, F. Review of supercritical fluids in inorganic materials science. J. Supercrit. Fluids 2006, 38, 242–251. [Google Scholar] [CrossRef]
- Manjare, S.D.; Dhingra, K. Supercritical fluids in separation and purification: A review. Mater. Sci. Energy Technol. 2019, 2, 463–484. [Google Scholar] [CrossRef]
- De Groot, S.R.; Mazur, P. Nonequilibrium Thermodynamics; North-Holland: Amsterdam, The Netherlands, 1962. [Google Scholar]
- Haase, R. Thermodynamik der Irreversible Processe; Dr. Dierrich Steinkopff Verlag: Darmstadt, Germany, 1963. [Google Scholar]
- Prigogine, I.; Kondepudi, D. Modern Thermodynamics: From Heat Engines to Dissipative Structures; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Hirschfelder, J.O.; Curtiss, C.F.; Bird, R.B. Molecular Theory of Gases and Liquids; Wiley: New York, NY, USA, 1954. [Google Scholar]
- Balescu, R. Equilibrium and Nonequilibrium Statistical Mechanics; Wiley-Interscience Publication Jonh Wiley and Sons: Hoboken, NJ, USA, 1975. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; Fluid Mechanics; Pergamon: New York, NY, USA, 1987; Volume 6. [Google Scholar]
- Bird, R.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Collins, R. Fluid Flow through Porous Materials; Wiley: New York, NY, USA, 1964. [Google Scholar]
- Sheydegger, A.E. The Physics of Flow through Porous Media, 3rd ed.; University of Toronto Press: Toronto, ON, Canada, 1974. [Google Scholar]
- Nigmatulin, R.I. Fundamentals of Mechanics of Heterogeneous Media; Nauka: Moscow, Russia, 1973. [Google Scholar]
- Nicholaevsky, V.N. Mechanics of Porous and Fractured Media; Nedra: Moscow, Russia, 1984. [Google Scholar]
- Glasstone, S.; Laidler, K.J.; Eyring, H. The Theory of Rate Processes: The Kinetics of Chemical Reactions, Viscosity, Diffusion, and Electrochemical Phenomena; Van Nostrand: New York, NY, USA, 1941. [Google Scholar]
- Entelis, S.G.; Tiger, R.P. Reaction Kinetics in the Liquid Phase; Khimiya: Moscow, Russia, 1973. [Google Scholar]
- Moelwyn-Hughes, E.A. The Chemical Statics and Kinetics of Solutions; Academic Press: London, UK; New York, NY, USA, 1971. [Google Scholar]
- Benson, S.W. The Foundations of Chemical Kinetics; McGrow–Hill: New York, NY, USA, 1960. [Google Scholar]
- Kiperman, S.L. Foundations of Chemical Kinetics in Heterogeneous Catalysis; Khimiya: Moscow, Russia, 1979. [Google Scholar]
- Volmer, M.; Flood, H. Tröpfchenbildung in Dämpfen. Z. Phys. Chem. 1934, 170A, 273–285. [Google Scholar] [CrossRef]
- Volmer, M.; Vollmer, M. Kinetics of New Phase Formation; Plenum: New York, NY, USA, 1983. [Google Scholar]
- Fuchs, N.A. Mechanic of Aerosols; Khimiya: Moscow, Russia, 1959. [Google Scholar]
- Erkey, C.; Türk, M. Modeling of particle formation in supercritical fluids (SCF). Supercrit. Fluid Sci. Technol. 2021, 8, 239–259. [Google Scholar] [CrossRef]
- Helfgen, B.; Türk, M.; Schaber, K. Hydrodynamic and aerosol modelling of the rapid expansion of supercritical solutions (RESS-process). J. Supercrit. Fluids 2003, 26, 225–242. [Google Scholar] [CrossRef]
- Fletcher, K. Methods in Computational Fluid Dynamics; Wiley: New York, NY, USA, 1991; Volumes 1 and 2. [Google Scholar]
- Hoffman, K.A.; Steve, T.C. Computation Fluid Dynamics; Engineering Education System: Wichite, KS, USA, 2000; Volumes 1–3. [Google Scholar]
- Strang, G.; Fix, G. Theory of Finite Element Method; Wiley: New York, NY, USA, 1977. [Google Scholar]
- Zinkevych, O.; Morgan, K. Finite Elements and Approximation; Wiley: New York, NY, USA, 1986. [Google Scholar]
- Tovbin, Y.K. (Ed.) Method of Molecular Dynamics in Physical Chemistry; Nauka: Moscow, Russia, 1996. [Google Scholar]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids; Claredon Press: Oxford, UK, 2002. [Google Scholar]
- Haile, J.M. Molecular Dynamics Simulation: ElementaryMethods; Wiley: New York, NY, USA, 1992. [Google Scholar]
- Coccotti, G.; Hoover, W.G. (Eds.) Molecular Dynamics Simulation of Statistical Mechanics Systems; North-Holland: Amsterdam, The Netherlands, 1986; 610p. [Google Scholar]
- Evans, D.J.; Morriss, G.P. Statistical Mechanics of Nonequilibrium Liquids, 2nd ed.; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Binder, K. (Ed.) Monte Carlo Methods in Statistical Physics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 1979. [Google Scholar]
- Nicolson, D.; Parsonage, N.G. Computer Simulation and The Statistical Mechanics of Adsorption; Academic Press: New York, NY, USA, 1982. [Google Scholar]
- Allen, M.P. Introduction to Monte Carlo simulations. In Observation, Prediction and Simulation of Phase Transitions in Complex Fluids; Baus, M., Rull, L.F., Ryckaert, J.-P., Eds.; Kluwer Academic Publishers: Boston, MA, USA, 1995; p. 339. [Google Scholar]
- Jorgensen, W.L. Monte Carlo simulations for liquids. In Encyclopedia of Computational Chemistry; Schleyer, P.V.R., Ed.; Wiley: New York, NY, USA, 1998; p. 1754. [Google Scholar]
- Jorgensen, W.L.; Tirado-Rives, J. Monte Carlo vs. Molecular Dynamics for Conformational Sampling. J. Phys. Chem. 1996, 100, 14508–14513. [Google Scholar] [CrossRef]
- Binder, K.; Landau, D.P. Capillary condensation in the lattice gas model: A Monte Carlo study. J. Chem. Phys. 1992, 96, 1444–1454. [Google Scholar] [CrossRef]
- Lemak, A.S.; Balabaev, N.K. A Comparison Between Collisional Dynamics and Brownian Dynamics. Mol. Simul. 1995, 15, 223–231. [Google Scholar] [CrossRef]
- Lemak, A.S.; Balabaev, N.K. Molecular dynamics simulation of a polymer chain in solution by collisional dynamics method. J. Comput. Chem. 1996, 17, 1685–1695. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics; Oxford University Press: Oxford, UK, 1976. [Google Scholar]
- Lebowitz, J.K.; Montroll, E.W. (Eds.) Nonequilibrium Phenomena I. The Boltzman Equation. Studies in Statistical Mechanics; North-Holland Publishing Company: Amsterdam, The Netherlands; New York, NY, USA; Oxford, UK, 1983. [Google Scholar]
- Gardiner, C.W. Handbook of Stochastic Methods (for Physics, Chemistry and Natural Science), 2nd ed.; Haken, H., Ed.; Springer Series in Synergetics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA; Tokyo, Japan, 1985; Volume 13. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Mohamad, A.A. Lattice Boltzmann Method: Fundamentals and Engineering. Applications with Computer Codes; Springer: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Timm, K.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E. The Lattice Boltzmann Method: Principles and Practice; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Hill, T.L. Statistical Mechanics. Principles and Selected Applications; McGraw–Hill: New York, NY, USA, 1956. [Google Scholar]
- Huang, K. Statistical Mechanics; Wiley: New York, NY, USA, 1963. [Google Scholar]
- Tovbin, Y.K. Theory of Physicochemical Processes at the Gas–Solid Interface; CRC: Boca Raton, FL, USA, 1991. [Google Scholar]
- Tovbin, Y.K. Molecular Approach to Micro-dynamics: Transfer of Molecules in Narrow Pores. Russ. J. Phys. Chem. A 2002, 76, 64–70. [Google Scholar]
- Tovbin, Y.K. Molecular Theory of Adsorption in Porous Solids; CRC: Boca Raton, FL, USA, 2017. [Google Scholar]
- Wolfram, S. Cellular Automata. Los Alamos Sci. 1983, 9, 2. [Google Scholar]
- Toffoli, T.; Margolus, N. Cellular Automata Machines; The MIT Press: Cambridge, MA, USA, 1987. [Google Scholar]
- Wolfram, S. A New Kind of Science; Wolfram Media: Champaign, IL, USA, 2002. [Google Scholar]
- Kier, L.B.; Seybold, P.G.; Cheng, C.-K. Cellular Automata Modeling of Chemical Systems; Springer: Dordrecht, The Netherlands, 2005; 175p. [Google Scholar]
- Wolf-Gladrow, D.A. Lattice-Gas Cellular Automata and Lattice Boltzmann Models: An Introduction; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Goto, M.; Roy, B.C.; Kodama, A.; Hirose, T. Modeling Supercritical Fluid Extraction Process Involving Solute-Solid Interaction. J. Chem. Eng. Jpn. 1998, 31, 171–177. [Google Scholar] [CrossRef]
- Oliveira, E.L.G.; Silvestre, A.J.D.; Silva, C.M. Review of kinetic models for supercritical fluid extraction. Chem. Eng. Res. Des. 2011, 89, 1104–1117. [Google Scholar] [CrossRef]
- Al-Jabari, M. Kinetic models of supercritical fluid extraction. J. Sep. Sci. 2002, 25, 477–489. [Google Scholar] [CrossRef]
- Sovová, H. Rate of the vegetable oil extraction with supercritical CO2—I. Modelling of extraction curves. Chem. Eng. Sci. 1994, 49, 409–414. [Google Scholar] [CrossRef]
- Sovová, H. Mathematical model for supercritical fluid extraction of natural products and extraction curve evaluation. J. Supercrit. Fluids 2005, 33, 35–52. [Google Scholar] [CrossRef]
- Sovová, H. Steps of supercritical fluid extraction of natural products and their characteristic times. J. Supercrit. Fluids 2012, 66, 73–79. [Google Scholar] [CrossRef]
- Rai, A.; Punase, K.D.; Mohanty, B.; Bhargava, R. Evaluation of models for supercritical fluid extraction. Int. J. Heat Mass Transf. 2014, 72, 274–287. [Google Scholar] [CrossRef]
- Promraksa, A.; Siripatana, C.; Rakmak, N.; Chusri, N. Modeling of Supercritical CO2 Extraction of Palm Oil and Tocopherols Based on Volumetric Axial Dispersion. J. Supercrit. Fluids 2020, 166, 105021. [Google Scholar] [CrossRef]
- Roodpeyma, M.; Street, C.; Guigard, S.E.; Stiver, W.H. A hydrodynamic model of a continuous supercritical fluid extraction system for the treatment of oil contaminated solids. Sep. Sci. Technol. 2017, 53, 44–60. [Google Scholar] [CrossRef]
- Garcia, E.C.C.; Rabi, J.A. Lattice-Boltzmann Simulation of Supercritical Fluid Extraction of Essential Oil from Gorse: Influence of Process Parameters on Yields. In Proceedings of the 14th WSEAS International Conference on Mathematics and Computers in Biology and Chemistry, Baltimore, MD, USA, 17–19 September 2013; pp. 62–67, ISBN 978-960-474-333-9. [Google Scholar]
- Duba, K.S.; Fiori, L. Supercritical fluid extraction of vegetable oils: Different approach to modeling the mass transfer kinetics. Chem. Eng. Trans. 2015, 43, 1051–1056. [Google Scholar] [CrossRef]
- Markom, M.; Hassim, N.; Hasan, M.; Daud, W.R.W. Modeling of supercritical fluid extraction by enhancement factor of cosolvent mixtures. Sep. Sci. Technol. 2020, 56, 1290–1302. [Google Scholar] [CrossRef]
- Gadkari, P.V.; Balaraman, M. Mass transfer and kinetic modelling of supercritical CO2 extraction of fresh tea leaves (Camellia sinensis L.). Braz. J. Chem. Eng. 2017, 34, 799–810. [Google Scholar] [CrossRef]
- Dimić, I.; Pezo, L.; Rakić, D.; Teslić, N.; Zeković, Z.; Pavlić, B. Supercritical Fluid Extraction Kinetics of Cherry Seed Oil: Kinetics Modeling and ANN Optimization. Foods 2021, 10, 1513. [Google Scholar] [CrossRef]
- Cabeza, A.; Sobrón, F.; García-Serna, J.; Cocero, M. Simulation of the supercritical CO2 extraction from natural matrices in packed bed columns: User-friendly simulator tool using Excel. J. Supercrit. Fluids 2016, 116, 198–208. [Google Scholar] [CrossRef]
- Amani, M.; Ardestani, N.S.; Honarvar, B. Experimental Optimization and Modeling of Supercritical Fluid Extraction of Oil from Pinus gerardiana. Chem. Eng. Technol. 2021, 44, 578–588. [Google Scholar] [CrossRef]
- Bushnaq, H.; Krishnamoorthy, R.; Abu-Zahra, M.; Hasan, S.W.; Taher, H.; Alomar, S.Y.; Ahmad, N.; Banat, F. Supercritical Tech-nology-Based Date Sugar Powder Production: Process Modeling and Simula-tion. Processes 2022, 10, 257. [Google Scholar] [CrossRef]
- Wilhelmsen, Ø.; Aasen, A.; Skaugen, G.; Aursand, P.; Austegard, A.; Aursand, E.; Gjennestad, M.A.; Lund, H.; Linga, G.; Hammer, M. Thermodynamic Modeling with Equations of State: Present Challenges with Established Methods. Ind. Eng. Chem. Res. 2017, 56, 3503–3515. [Google Scholar] [CrossRef]
- Salmani, H.J.; Karkhanechi, H.; Moradi, M.R.; Matsuyama, H. Thermodynamic modeling of binary mixtures of ethylenediamine with water, methanol, ethanol, and 2-propanol by association theory. RSC Adv. 2022, 12, 32415–32428. [Google Scholar] [CrossRef]
- Congedo, P.M.; Rodio, M.G.; Tryoen, J.; Abgrall, R. Reliable and Robust Thermodynamic Model for Liquid-Vapor Mixture; [Re-search Report] RR-8439, INRIA. hal-00922816; HAL: Lyon, France, 2013. [Google Scholar]
- Alanazi, A.; Bawazeer, S.; Ali, M.; Keshavarz, A.; Hoteit, H. Thermodynamic modeling of hydrogen–water systems with gas impurity at various conditions using cubic and PC-SAFT equations of state. Energy Convers. Manag. X 2022, 15, 100257. [Google Scholar] [CrossRef]
- Matos, I.Q.; Varandas, J.S.; Santos, J.P. Thermodynamic Modeling of Azeotropic Mixtures with [EMIM][TfO] with Cubic-Plus-Association and Cubic EOSs. Braz. J. Chem. Eng. 2018, 35, 363–372. [Google Scholar] [CrossRef]
- Yeoh, H.S.; Chong, G.H.; Azahan, N.M.; Rahman, R.A.; Choong, T.S.Y. Solubility Measurement Method and Mathematical Modeling in Supercritical Fluids. Eng. J. 2013, 17, 67–78. [Google Scholar] [CrossRef]
- Peng, D.Y.; Robinson, D.B. A New Two-Constant Equation of State. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Mukhopadhyay, M.; Rao, G.V.R. Thermodynamic modeling for supercritical fluid process design. Ind. Eng. Chem. Res. 1993, 32, 922–930. [Google Scholar] [CrossRef]
- Bilalov, T.R.; Zavjalova, N.B.; Gumerov, F.M. Phase Diagram of the Supercritical Carbon Dioxide–Ethylcarbitol System. Sverhkriticheskie Flyuidy Teor. Prakt. 2019, 14, 27–33. [Google Scholar] [CrossRef]
- Bilalov, T.R.; Gumerov, F.M.; Khairutdinov, V.F.; Khabriev, I.S.; Gabitov, F.R.; Zaripov, Z.I.; Ga-niev, A.A.; Mazanov, C.V. Phase Equilibrium of the Binary System Propylene Glycol—Propane/Butane. Sverhkriticheskie Flyuidy Teor. Prakt. 2020, 15, 79–86. [Google Scholar] [CrossRef]
- Zakharov, A.A.; Bilalov, T.R.; Gumerov, F.M. Solubility of Ammonium Palmitate in Supercritical Carbon Dioxide. Sverhkriticheskie Flyuidy Teor. Prakt. 2015, 12, 60–70. [Google Scholar] [CrossRef]
- Gumerov, F.M.; Gabitov, F.R.; Gazizov, R.A.; Bilalov, T.R.; Yakushev, I.A. Determination of Phase Equilibria Parameters in Binary Systems Containing Components of Biodiezel Fuel and Supercritical Carbon Dioxde. Sverhkriticheskie Flyuidy Teor. Prakt. 2006, 1, 89–100. [Google Scholar]
- Bazaev, A.R.; Karabekova, B.K.; Abdurashidova, A.A. p, ρ, T, and x dependences for supercritical water-aliphatic alcohol mixtures. Sverhkriticheskie Flyuidy Teor. Prakt. 2013, 8, 11–38. [Google Scholar] [CrossRef]
- Durakovic, G.; Skaugen, G. Analysis of Thermodynamic Models for Simulation and Optimisation of Organic Rankine Cycles. Energies 2019, 12, 3307. [Google Scholar] [CrossRef]
- Bruno, T.J.; Ely, J.F. (Eds.) Supercritical Fluid Technology: Reviews in Modem Theory and Applications; CRC Press Taylor & Francis Group: Boca Raton, FL, USA, 1991. [Google Scholar]
- Tovbin, Y. Lattice-gas model in kinetic theory of gas-solid interface processes. Prog. Surf. Sci. 1990, 34, 1–235. [Google Scholar] [CrossRef]
- Temkin, M.I. Kinetics of ammonia synthesis at high pressures. Zhurnal Fiz. Khimii 1950, 24, 1312–1323. [Google Scholar]
- Marcus, R.A. Chemical and Electrochemical Electron-Transfer Theory. Annu. Rev. Phys. Chem. 1964, 15, 155–196. [Google Scholar] [CrossRef]
- Dogonadze, R.R.; Kuznetsov, A.M. Kinetics of heterogeneous chemical reactions in solutions. Itogi Nauki Tekh. Ser. Kinet. Katal. 1978, 5. [Google Scholar]
- Kuznetsov, A.M.; Ulstrup, J. Electron Transfer in Chemistry and Biology; John Wiley & Sons, Ltd.: Chichester, UK, 1999; 350p. [Google Scholar]
- Clausius, R. Mechanical Theory of Heat; John van Voorst: London, UK, 1867. [Google Scholar]
- Tovbin, Y.K. Second Law of Thermodynamics, Gibbs’ Thermodynamics, and Relaxation Times of Thermodynamic Parameters. Russ. J. Phys. Chem. A 2021, 95, 637–658. [Google Scholar] [CrossRef]
- Gibbs, J.W. On the Equilibrium of Heterogeneous Substances. Trans. Conn. Acad. Arts Sci. 1878, 16, 441–458. [Google Scholar] [CrossRef]
- Gibbs, J.W. The Collected Works of J. W. Gibbs, in 2 Volumes; Longmans Green: New York, NY, USA, 1928; Volume 1. [Google Scholar]
- Tovbin, Y.K. Small Systems and Fundamentals of Thermodynamics; CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar]
- Fisher, M.E. The Nature of Critical Points; Lectures in Theoretical Physics; University of Colorado Press: Boulder, CO, USA, 1965; Volume VII. [Google Scholar]
- Novikov, I.I. Equation of States of Gas and Liquids; Nauka: Moscow, Russia, 1965. [Google Scholar]
- Walas, S.M. Phase Equilibria in Chemical Engineering; The C.W. Nofsinger Company Butterworth Publisher: Boston, MA, USA; London, UK; Wellington, New Zealand; Durban, South Africa; Toronto, ON, Canada, 1985. [Google Scholar]
- Guggenheim, E.A. Mixtures; Clarendon: Oxford, UK, 1952. [Google Scholar]
- Barker, J.A. Cooperative Orientation Effects in Solutions. J. Chem. Phys. 1952, 20, 1526–1532. [Google Scholar] [CrossRef]
- Prigogine, I.P. The Molecular Theory of Solutions; Interscience: Amsterdam, The Netherlands; New York, NY, USA, 1957. [Google Scholar]
- Smirnova, N.A. The Molecular Theory of Solutions; Khimiya: Leningrad, Russia, 1987. [Google Scholar]
- Tovbin, Y.K.; Titov, S.V. Role of local environment relaxation in calculating the reaction rates for nonideal reaction systems. Sverhkriticheskie Flyuidy Teor. Prakt. B 2011, 6, 35–48. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Theory of adsorption—Desorption kinetics on flat heterogeneous surfaces. In Equiliblia and Dynamics of Gas Adsorption on Heterogeneous Solid Surfaces; Rudzinski, W., Steele, W.A., Zgrablich, G., Eds.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 201–284. [Google Scholar]
- Lifshits, I.M. To the theory of real solutions. Zh. Eksp. Teor. Fiz. 1939, 9, 481–499. [Google Scholar]
- Krichevskii, I.R. Phase Equilibria at High Pressures; Goskhimizdat: Moscow, Russia, 1963. [Google Scholar]
- Borovskii, I.B.; Gurov, K.P.; Marchukova, Y.E.; Ugaste, Y.E. Interdiffusion Processes in Alloys; Gurov, K.P., Ed.; Nauka: Moscow, Russia, 1973. [Google Scholar]
- Gurov, K.P.; Kartashkin, B.A.; Ugaste, Y.E. Mutual Diffusion in Multicomponent Metal Alloys; Nauka: Moscow, Russia, 1981. [Google Scholar]
- Lazarev, A.V.; Tatarenko, P.A.; Tatarenko, K.A. Gas-Dynamic Model of the Expansion of a Pulse Jet of Supercritical Carbon Dioxide: The Strategy of the Experiment. Sverhkriticheskie Flyuidy Teor. Prakt. 2017, 12, 3–13. [Google Scholar] [CrossRef]
- Nikolaev, P.N. The singular points and phase diagram of the supercritical region of a substance. Mosc. Univ. Phys. Bull. 2014, 69, 146–151. [Google Scholar] [CrossRef]
- Semenchenko, V.K. Selected Chapters in Theoretical Physics; EDUCATION: Moscow, Russia, 1966. [Google Scholar]
- Nishikawa, K.; Kusano, K.; Arai, A.A.; Morita, T. Density fluctuation of a van der Waals fluid in supercritical state. J. Chem. Phys. 2003, 118, 1341–1346. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Molecular Aspects of Lattice Models of Liquid and Adsorption Systems. Russ. J. Phys. Chem. A 1995, 69, 105–113. [Google Scholar]
- Tovbin, Y.K. Modern State of the Lattice- Theory of Adsorption. Russ. J. Phys. Chem. A 1998, 72, 675–683. [Google Scholar]
- Bogolyubov, N.N. Problems of Dynamic Theory in Statistical Physics; Gostekhizdat: Moscow, Russia, 1946. [Google Scholar]
- Fisher, I.Z. Statistical Theory of Liquids; Chicago University: Chicago, IL, USA, 1964. [Google Scholar]
- Croxton, C.A. Liquid State Physics–A Statistical Mechanical Introduction; Cambridge University Press: Cambridge, UK, 1974. [Google Scholar]
- Martynov, G.A. Classical Static Physics; Fluid Theory; Intellekt: Dolgoprudnyi, Russia, 2011. [Google Scholar]
- Tovbin, Y.K.; Senyavin, M.M.; Zhidkova, L.K. Modified cell theory of fluids. Russ. J. Phys. Chem. A 1999, 73, 245–253. [Google Scholar]
- Ono, S.; Kondo, S. Molecular Theory of Surface Tension in Liquids, Handbuch der Physik; Springer: Berlin/Heidelberg, Germany, 1960. [Google Scholar]
- Zagrebnov, V.A.; Fedyanin, B.K. Spin-phonon interaction in the ising model. Theor. Math. Phys. 1972, 10, 84–93. [Google Scholar] [CrossRef]
- Plakida, N.M. The method of two-time Green’s functions in the theory of anharmonic crystals. In Statistical Physics and Quantum Field Theory; Nauka: Moscow, Russia, 1973; pp. 205–240. [Google Scholar]
- Batalin, O.Y.; Tovbin, Y.K.; Fedyanin, V.K. Equilibrium properties of a liquid in a modified lattice model. Zhurnal Fiz. Khimii 1979, 53, 3020–3023. [Google Scholar]
- Fedyanin, V.K. Thermodynamics of a Lattice System of Particles of Different Sizes with Contact Are-as of Different Types. In Theoretical Methods for Describing the Properties of Solutions; Interschool Collection of Scientific Works: Ivanovo, Russia, 1987; pp. 40–44. [Google Scholar]
- Tovbin, Y.K. Allowing for Intermolecular Vibrations in the Thermodynamic Functions of a Liquid Inert Gas. Russ. J. Phys. Chem. A 2019, 93, 603–613. [Google Scholar] [CrossRef]
- Barker, J.A. Lattice Theories of the Liquid State; Pergamon Press: Oxford, UK, 1963. [Google Scholar]
- Shakhparonov, M.I. Introduction to the Molecular Theory of Solutions; GITTL: Moscow, Russia, 1956. [Google Scholar]
- Morachevskii, A.G.; Smirnova, N.A.; Piotrovskaya, E.M.; Kuranov, G.L.; Balashova, I.M.; Pukinskiy, I.B.; Alekseeva, M.V.; Viktoriv, A.I. Thermodynamics of Liquid-Vapour Equilibrium; Morachevskii, A.G., Ed.; Khimiya: Leningrad, Russia, 1989. [Google Scholar]
- Kaplan, I.G. Introduction to the Theory of Molecular Interactions; Nauka: Moscow, Russia, 1982; 312p. [Google Scholar]
- Kiselev, A.V.; Poshkus, D.P.; Yashin, Y.I. Molecular Basis of Adsorption Chromatography; Khimiya: Moscow, Russia, 1986; 269p. [Google Scholar]
- Egorov, B.V.; Komarov, V.N.; Markachev, Y.E.; Tovbin, Y.K. Concentration dependence of viscosity under conditions of its clustering. Russ. J. Phys. Chem. A 2000, 74, 778–783. [Google Scholar]
- Tovbin, Y.K.; Komarov, V.N. Calculation of Compressibility and Viscosity of Non-ideal Gases with if Framework of the Lattice Model. Russ. J. Phys. Chem. A 2001, 75, 490–495. [Google Scholar]
- Komarov, V.N.; Tovbin, Y.K. Self-Consistent Calculation of the Compressibility and Viscosity of Dense Gases in the Lattice-Gas Model. High Temp. 2003, 41, 181–188. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Many-Particle Interactions in Equilibrium Theories of Adsorption and Absorption. Zhurnal Fiz. Khimii 1987, 61, 2711–2716. [Google Scholar]
- Tovbin, Y.K.; Komarov, V.N. Calculation of the compressibility coefficient of a mixture of dense gases. Russ. J. Phys. Chem. A 2005, 79, 1807–1813. [Google Scholar]
- Reid, R.C.; Sherwood, T.K. The Properties of Gases and Liquids. (The Restimation and Correlation); MeGrav-Hill Boch Company: New York, NY, USA; San Francisco, CA, USA; Toronto, ON, Canada; London, UK; Sydney, Austria, 1966. [Google Scholar]
- Sengers, J.M.H.L.; Klein, M.; Gallagher, J. Pressure—Volume Temperature Relationships of Gases—Virial Coefficients, 3rd ed.; American Institute of Physics Handbook; American Institute of Physics: New York, NY, USA, 1972; 2364p. [Google Scholar]
- Rabinovich, V.A.; Vasserman, A.A.; Nedostup, V.I.; Veksler, L.S. Thermophysical Properties of Neon, Argon, Krypton, and Xenon; Standartgiz: Moscow, Russia, 1976. [Google Scholar]
- Crain, E.W.; Santag, R.E. The P-V-T Behavior of nitrogen, argon and their mixtures. Adv. Cryog. Eng. 1966, 11, 379. [Google Scholar]
- Komarov, V.N.; Rabinovich, A.B.; Tovbin, Y.K. Calculation of concentration dependences of the transport characteristics of binary mixtures of dense gases. High Temp. 2007, 45, 463–472. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Lattice gas model in the molecular-statistical theory of equilibrium systems. Russ. J. Phys. Chem. A 2005, 79, 1903–1920. [Google Scholar]
- Tovbin, Y.K. Calculation of Adsorption Characteristics in the “Quasi-Point” Approximation Based on the Lattice Gas Model. Russ. J. Phys. Chem. A 1998, 72, 2053–2058. [Google Scholar]
- Tovbin, Y.K.; Rabinovich, A.B.; Votyakov, E.V. Calibration functions in approximate methods for calculating the equilibrium of adsorption characteristics. Russ. Chem. Bull. 2002, 51, 1667–1674. [Google Scholar] [CrossRef]
- Tovbin, Y.K.; Rabinovich, A.B. Phase Diagrams of Adsorption Systems and Calibration Functions in the Lattice-Gas Model. Langmuir 2004, 20, 6041–6051. [Google Scholar] [CrossRef]
- Patashinskii, A.Z.; Pokrovskii, V.L. Fluctuation Theory of Phase Transitions; Nauka: Moscow, Russia, 1975. [Google Scholar]
- Stanley, H.E. Introduction to Phase Transitions and Critical Phenomena; Clarendon: Oxford, UK, 1971. [Google Scholar]
- Ma, S.-K. Modern Theory of Critical Phenomena; W.A.Benjamin, Inc.: London, UK, 1976. [Google Scholar]
- Tsiklis, D.S. Dense Gases; Khimiya: Moscow, Russia, 1977. [Google Scholar]
- Kruse, A.; Dinjus, E. Hot compressed water as reaction medium and reactant: Properties and synthesis reactions. J. Supercrit. Fluids 2007, 39, 362–380. [Google Scholar] [CrossRef]
- Rabinovich, A.B.; Tovbin, Y.K. Supercritical fluid effect on the rates of elementary bimolecular reactions. Kinet. Catal. 2011, 52, 471–479. [Google Scholar] [CrossRef]
- Cooper, A.I. Polymer synthesis and processing using supercritical carbon dioxide. J. Mater. Chem. 2000, 10, 207–234. [Google Scholar] [CrossRef]
- McHugh, M.A.; Krukonis, V.J. Supercritical Fluid Extraction: Principles and Practice; Butter-Worth Publishers: Stoneham, MA, USA, 1994. [Google Scholar]
- Rabinovich, A.B.; Tovbin, Y.K. Effect of a supercritical fluid on the characteristics of sorption processes. Russ. Chem. Bull. 2010, 59, 1–6. [Google Scholar] [CrossRef]
- Franck, E.U. Physicochemical Properties of Supercritical Solvents (Invited Lecture). Berichte Bunsengesellschaft Physikalische Chemie 1984, 88, 820–825. [Google Scholar] [CrossRef]
- Lemenovskii, D.A.; Yurin, S.A.; Timofeev, V.V.; Popov, V.K.; Bagratashvili, V.N.; Gorbaty, Y.E.; Brusova, G.P.; Lunin, V.V. Reactions of Ozone with Organic Substrates in Supercritical Carbon Dioxide. Sverhkriticheskie Flyuidy Teor. Prakt. 2007, 2, 30–42. [Google Scholar]
- Tovbin, Y.K. Molecular grounds of the calculation of equilibrium and transport characteristics of inert gases and liquids in complex narrow-pore systems. Russ. Chem. Bull. 2003, 52, 869–881. [Google Scholar] [CrossRef]
- Anisimov, M.A.; Rabinovich, V.A.; Sychev, V.V. Thermodynamics of Critical State; Energoatomizdat: Moscow, Russia, 1990. [Google Scholar]
- Chapman, S.; Cowling, T. The Mathematical Theory of Nonequilibrium Gases; Cambridge University Press: Cambridge, UK, 1953. [Google Scholar]
- DiMarzio, E.A. Statistics of Orientation Effects in Linear Polymer Molecules. J. Chem. Phys. 1961, 35, 658–669. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Liquid Crystals; Cambridge University: Cambridge, UK, 1977. [Google Scholar]
- Bazarov, I.P.; Gevorkyan, E.V. Statistical Theory of Solid and Liquid Crystals; Moscow State University: Moscow, Russia, 1983. [Google Scholar]
- Tovbin, Y.K. Refinement of taking into account molecule sizes in the lattice gas model. Russ. J. Phys. Chem. A 2012, 86, 705–708. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Possibilities of the Molecular Modeling of Kinetic Processes under Supercritical Conditions. Russ. J. Phys. Chem. A 2021, 95, 429–444. [Google Scholar] [CrossRef]
- Vukalovich, M.P.; Altunin, V.V. Thermophysical Properties of Carbon Dioxide; Atomizdat: Moscow, Russia, 1965. [Google Scholar]
- Titov, S.V.; Tovbin, Y.K. Lattice model of a polar liquid. Russ. Chem. Bull. 2011, 60, 11–19. [Google Scholar] [CrossRef]
- Titov, S.V.; Tovbin, Y.K. A molecular model of water based on the lattice gas model. Russ. J. Phys. Chem. A 2011, 85, 194–201. [Google Scholar] [CrossRef]
- Bell, G.M. Statistical mechanics of water: Lattice model with directed bonding. J. Phys. C Solid State Phys. 1972, 5, 889–905. [Google Scholar] [CrossRef]
- Bell, G.M.; Salt, D.W. Three-dimensional lattice model for water/ice system. J. Chem. Soc. Faraday Trans. 1976, 72, 76–86. [Google Scholar] [CrossRef]
- Franks, F. (Ed.) Water: A Comprehensive Treatise; Plenum: New York, NY, USA; London, UK, 1972; Volume 1. [Google Scholar]
- Eisenberg, D.; Kautsman, V. Structure and Properties of Water; Gidrometeoizdat: Leningrad, Russia, 1975. [Google Scholar]
- Tovbin, Y.K.; Titov, S.V. Role of local environment relaxation in calculating the rates of elementary processes in vapor-liquid systems. Russ. J. Phys. Chem. A 2013, 87, 185–190. [Google Scholar] [CrossRef]
- Frenkel, Y.I. Kinetic Theory of Liquids; Oxford University: London, UK, 1946. [Google Scholar]
- Angell, C.A. Water: A Comprehensive Treatise; Franks, F., Ed.; Plenum: New York, NY, USA, 1978; Volume 7, p. 23. [Google Scholar]
- Malenkov, G.; Tytik, D.; Zheligovskaya, E. Structural and dynamic heterogeneity of computer simulated water: Ordinary, supercooled, stretched and compressed. J. Mol. Liq. 2003, 106, 179–198. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Kinetic equations for processes of local rearrangement of molecular systems. Russ. J. Phys. Chem. B 2011, 5, 256–270. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Taking environment into account in the theory of liquid-phase reaction rates with electron transfer in the discrete solvent model. Russ. J. Phys. Chem. A 2011, 85, 238–244. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Kinetic equation for the processes of local reorganization of molecular systems with charged species. Russ. J. Phys. Chem. B 2012, 6, 716–729. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Local equations of state in nonequilibrium heterogeneous physicochemical systems. Russ. J. Phys. Chem. A 2017, 91, 403–424. [Google Scholar] [CrossRef]
- Gaydamaka, S.N.; Timofeev, V.V.; Guryev, Y.V.; Lemenovskiy, D.A.; Brusova, G.P.; Parenago, O.O.; Bagratashvili, V.N.; Lunin, V.V. Processing of coked Pt-Re/γ-Al2O3 catalysts with high-concentration ozone dissolved in supercritical carbon dioxide. Sverhkriticheskie Flyuidy Teor. Prakt. 2010, 5, 76–91. [Google Scholar] [CrossRef]
- Adamson, A. The Physical Chemistry of Surfaces; Wiley: New York, NY, USA, 1976. [Google Scholar]
- Barker, J.A.; Henderson, D. What is “liquid”? Understanding the states of matter. Rev. Mod. Phys. 1976, 48, 587–671. [Google Scholar] [CrossRef]
- Tovbin, Y.K. The problem of a self-consistent description of the equilibrium distribution of particles in three states of aggregation. Russ. J. Phys. Chem. A 2006, 80, 1554–1566. [Google Scholar] [CrossRef]
- Tovbin, Y.K. A Theory of Liquid-Phase Reaction Rates Including Coulomb Terms in the Lattice Gas Model. Russ. J. Phys. Chem. A 1996, 70, 1655–1660. [Google Scholar]
- Prigogine, I.; Defay, R. Chemical Thermodynamics; Longmans Green and Co.: London, UK, 1954. [Google Scholar]
- Glauber, R.J. Time-Dependent Statistics of the Ising Model. J. Math. Phys. 1963, 4, 294–307. [Google Scholar] [CrossRef]
- Tovbin, Y.K. Kinetics and equilibrium in ordered systems. Dokl. AN SSSR 1984, 277, 917–921. [Google Scholar]
- Tovbin, Y.K. Concentration Dependence of the Transfer Coefficients of Molecules in Mesopores in the Capillary-Condensation Region. Russ. J. Phys. Chem. A 1998, 72, 1298–1303. [Google Scholar]
- Reif, F. Statistical Physics. Berkeley Physics Course; Mcgraw–Hill Book Company: New York, NY, USA, 1965; Volume 5. [Google Scholar]






Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tovbin, Y.K. Molecular Modeling of Supercritical Processes and the Lattice—Gas Model. Processes 2023, 11, 2541. https://doi.org/10.3390/pr11092541
Tovbin YK. Molecular Modeling of Supercritical Processes and the Lattice—Gas Model. Processes. 2023; 11(9):2541. https://doi.org/10.3390/pr11092541
Chicago/Turabian StyleTovbin, Yuri Konstantinovich. 2023. "Molecular Modeling of Supercritical Processes and the Lattice—Gas Model" Processes 11, no. 9: 2541. https://doi.org/10.3390/pr11092541
APA StyleTovbin, Y. K. (2023). Molecular Modeling of Supercritical Processes and the Lattice—Gas Model. Processes, 11(9), 2541. https://doi.org/10.3390/pr11092541