Pneumatic Noise Study of Multi-Stage Sleeve Control Valve
Abstract
:1. Introduction
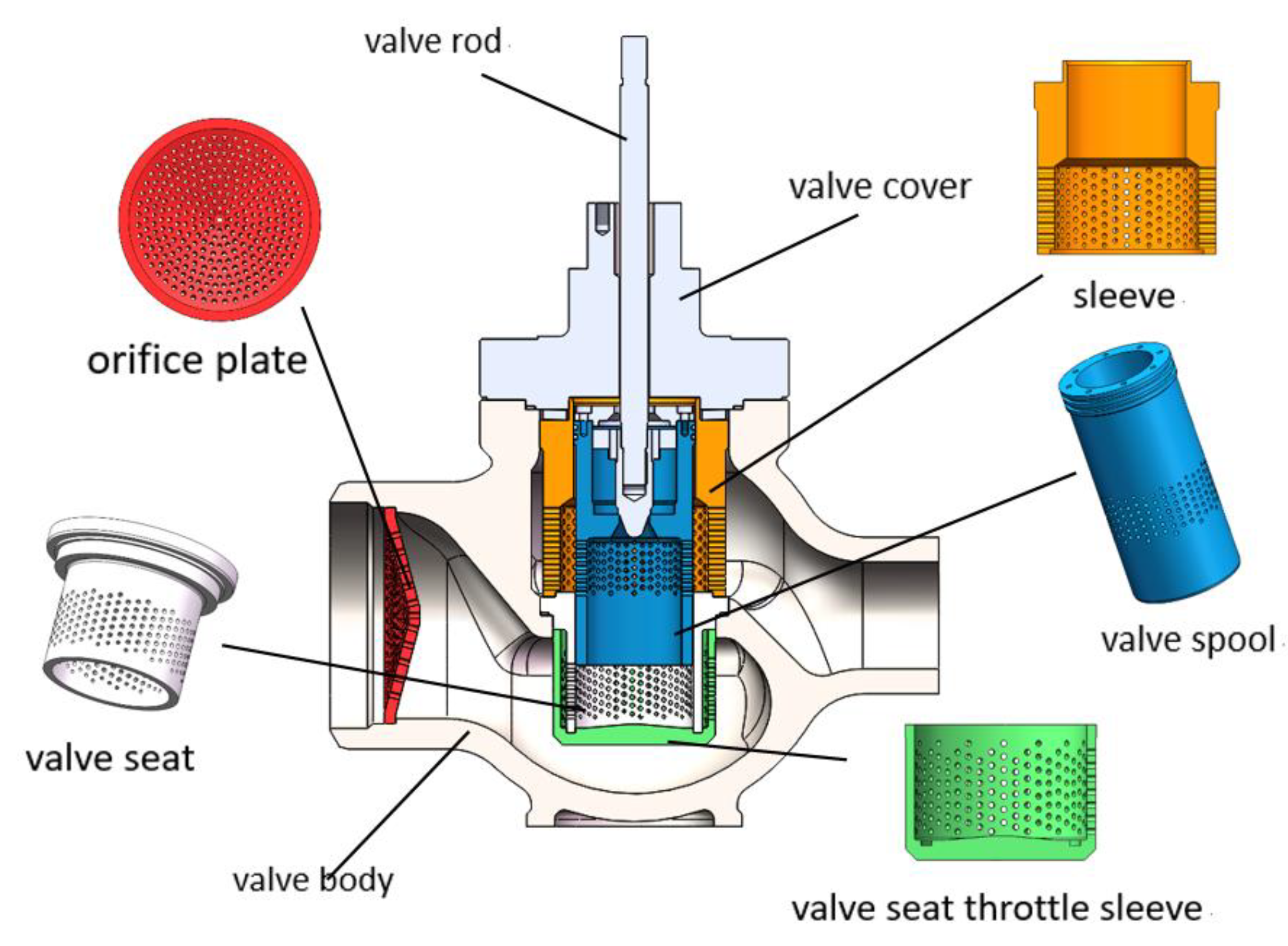
2. Valve Structure and Working Principle
3. Flow Field Calculation
3.1. Geometric Model and Meshing
3.2. Calculation Method
3.3. Calculation Results and Analysis
4. Sound Field Calculation
4.1. The FW-H Acoustic Fitting Theory
4.2. Calculation Method
4.3. Calculation Results and Analysis
4.4. Numerical Simulation Method Validation
5. Conclusions
- Analysis of the steam medium within the control valve under operating conditions revealed important aspects such as the Mach number, turbulence, and static pressure distribution. It was observed that the disturbance caused by high-speed flow in the valve components increased the intensity of turbulence energy. Consequently, the high turbulence energy led to steam pressure pulsations, which served as a primary source of noise.
- The study revealed a symmetrical distribution of sound pressure levels along the tube and valve system of the control valve. Furthermore, it was observed that pneumatic noise exhibited directional characteristics, with significantly higher noise levels detected upstream and downstream of the valve compared to other regions.
- Among the many monitoring points selected, the noise of monitoring point 8 was 157.86 dB (A) in theoretical calculation and 161.95 dB (A) in numerical analysis, and the difference between the two results was 4.09 dB (A). At monitoring point 6, the difference was 1.16 dB (A). The error of the monitoring points was less than 5%, which verifies the effectiveness of the numerical simulation method.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, P.W.; Wang, Y.K. Practical Technology of Control Valves; Machinery Industry Press: Beijing, China, 2017. [Google Scholar]
- Qian, J.Y.; Wu, J.Y.; Jin, Z.J. Research progress on vibration characteristics of regulation valve. J. Vib. Shock 2020, 39, 1–13+21. [Google Scholar]
- Chen, F.; Wang, F.; Wei, L.; Qian, J.; Jin, Z. Research progress of noise in pressure reducing valve. J. Drain. Irrig. Mach. Eng. 2019, 37, 49–57. [Google Scholar]
- Wang, J.D.; Tang, H. Prediction of Flow Noise in a Controlling-valve Using CFD Method. Noise Vib. Control. 2014, 34, 106–109. [Google Scholar]
- Zeng, L.F.; Liu, G.W.; Mao, J.R.; Wang, S.S.; Yuan, Q.; Yuan, H.; Wang, K.G.; Zhang, J.J.; Xu, Y.T. Flow-induced vibration and noise in control valve. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 3368–3377. [Google Scholar] [CrossRef]
- Liu, C.W.; Li, Y.X.; Wang, W.C.; Xie, Z.Z. Analysis on the mechanism of aero-acoustic noise generated by gas flow through valves of natural gas pipelines. J. Vib. Shock 2014, 33, 152–157. [Google Scholar]
- Wu, Y.; Huang, C.; Chen, C.J.; Wang, Z.H.; Liu, J.W.; Li, S.X. Noise Characteristics Analysis for Steam Turbine Bypass Valve Based on Fluid-Structure-Acoustic Interaction Using BEM Method. Chem. Eng. Mach. 2023, 50, 354–360. [Google Scholar]
- Liao, J.; Hao, J.S.; Liu, B.X.; Yang, H.H.; Wang, W.B. Study on Generation and Control Mechanism of Aerodynamic Noise of Eccentric Rotary Valves. Noise Vib. Control 2022, 42, 285–292. [Google Scholar]
- Nord, M. Reducing the Noise from Control Valves. Chem. Eng. 2022, 129, 34–36. [Google Scholar]
- Sun, Y.; Wu, J.; Xu, J.; Bai, X. Flow Characteristics Study of High-Parameter Multi-Stage Sleeve Control Valve. Processes 2022, 10, 1504. [Google Scholar] [CrossRef]
- Chen, M.R. Research on Aerodynamic Noise Characteristics and Noise Reduction Technology of Steam Temperature Pressure Regulating Valve; Zhejiang University: Zhejiang, China, 2022. [Google Scholar]
- Hou, C.W. Study on Aerodynamic Noise and Fluid-Induced Vibration of Orifice-Type Sleeve Control Valve; Zhejiang University: Zhejiang, China, 2022. [Google Scholar]
- Fan, L.H.; Cai, G.H. Exploration on Aerodynamic Noise Characteristics for Control Valve of Steam Turbine. Appl. Mech. Mater. 2012, 2029, 395–400. [Google Scholar] [CrossRef]
- Shi, H.Q.; Zhou, X.; Zhou, A.M.; Zhang, B.H.; Li, S.X. Numerical simulation of fluid-solid coupling noise in marine three-way control valve. J. Appl. Acoust. 2023, 5, 1–12. [Google Scholar]
- Sun, C.Z.; Yu, X.H.; Zong, X.; Lai, C.Z. Prediction of Noise Induced by Turbulent Flow in a Control Valve. J. Eng. Thermophys. 2017, 38, 1866–1871. [Google Scholar]
- Xu, F.; He, E.M. Simulation of Flow-Induced Noise Generation on Orifice Plates in an Aircraft Climate Control System. J. Northwestern Polytech. Univ. 2017, 35, 608–614. [Google Scholar]
- Li, S.J.; Han, C.F.; Yu, F.; Liu, G.M. A Vibration-to-sound conversion method for prediction of valves aerodynamic noise. Acta Acust. 2018, 43, 239–245. [Google Scholar]
- Fenini, L.; Quaroni, L.N.; Malavasi, S. Estimation of aerodynamic noise of diaphragms through IEC 60534-8-3 and CFD. Meas. Control 2021, 54, 189–195. [Google Scholar] [CrossRef]
- Li, S.X.; Zhang, X.; Wang, Y.; Hu, J.; Hao, J.S.; Wang, R.Y. Research on aerodynamic noise prediction of multistage sleeve regulating valve. Autom. Instrum. 2013, 32–33. [Google Scholar]
- Wei, L.; Zhu, G.; Qian, J.; Fei, Y.; Jin, Z. Numerical Simulation of Flow-Induced Noise in High Pressure Reducing Valve. PLoS ONE 2015, 10, e0129050. [Google Scholar] [CrossRef] [PubMed]
- IEC 60534-2-3; Industrial-Process Control Valves-Part 2-3: Flow capacity-Test procedures. International Electrotechnical Commission (IEC): Geneva, Switzerland, 2015.
- Curle, N. The influence of solid boundaries on aerodynamic sound. Proc. R. Soc. Lond. A 1955, 231, 505–514. [Google Scholar]
- Ffowcs Williams, J.E.; Hawkings, D.L. Sound Generation by Turbulence and Surfaces in Arbitrary Motion. Philosophical Transactions of the Royal Society of London. Ser. A Math. Phys. Sci. 1969, 264, 321–342. [Google Scholar]
- GB/T 17213.15-2017; Industrial-Process Control Valves—Part 8-3: Noise Considerations—Control Valve Aerodynamic Noise Prediction Method. Shanghai Industrial Automation Instrumentation Research Institute: Shanghai, China, 2017.











| Maximum Size/mm | Number of Grids × 106 | Mass Flow/(kg·s−1) |
|---|---|---|
| 1.5 | 3.24 | 20.56 |
| 1.8 | 2.85 | 20.66 |
| 2.0 | 2.70 | 20.68 |
| 2.5 | 2.43 | 21.02 |
| 3.0 | 1.98 | 21.65 |
| 3.8 | 0.99 | 24.40 |
| Medium | Vapor |
|---|---|
| Inlet pressure | 6.86 Mpa |
| Inlet temperature | 284.9 °C |
| Outlet pressure | 1 Mpa |
| Viscosity | 1.89 × 10−5 kg/(m·s−1) |
| Density | 35.7 kg/m3 |
| Valve walls | Adiabatic no-slip boundary |
| Residual Setting | Start of Calculation | After 10,000 Steps |
|---|---|---|
| Courant number | 1 | 5 |
| Turbulent Kinetic Energy | 0.2 | 0.8 |
| Turbulent Dissipation Rate | 0.2 | 0.8 |
| Turbulent Viscosity | 0.2 | 1 |
| Solid | 0.2 | 1 |
| Type Fluid | Vapor |
|---|---|
| Mass flow rate | m = 20 kg/s |
| Valve inlet absolute pressure | P1 = 6.86 MPa |
| Valve outlet absolute pressure | P2 = 1 MPa |
| Inlet density | ρ1 = 35.7 kg/m3 |
| Inlet absolute temperature | T1 = 558.05 K (284.9 °C) |
| Specific heat ratio | γ = 1.885 |
| Molecular mass | M = 19.8 kg/kmol |
| Required Cv | Cv = 101 |
| Valve size | DN125 |
| Valve outlet diameter | D = 0.241 m |
| Internal pipe diameter | D1 = 0.241 m |
| Differential pressure ratio | x = 0.985 |
| Absolute Vena contracta pressure at subsonic flow conditions | Pvc = −1,482,098 pa |
| Vena contracta differential pressure ratio at critical flow conditions | xvcc = 0.542 |
| Differential pressure ratio at critical flow conditions | Xc = 0.438 |
| Recovery correction factor | α = 0.817 |
| Differential pressure ratio at breakpoint | XB = 0.683 |
| Differential pressure ratio where region of constant acoustical efficiency begins | XCE = 0.944 |
| Regime definition | XCE < X, Regime V. |
| Hydraulic diameter of a single flow passage | dH = 0.575 |
| Diameter of a circular orifice | do = 3.582 |
| Valve style modifier | Fd = 0.16 |
| Jet diameter | Dj = 0.007 |
| Strouhal number of free jet at peak frequency | Stp = 0.2 |
| Correction factor of sound effect coefficient | Aη = −3.8 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, J.; Shi, Y.; Meng, X.; Zhang, B.; Li, D. Pneumatic Noise Study of Multi-Stage Sleeve Control Valve. Processes 2023, 11, 2544. https://doi.org/10.3390/pr11092544
Jia J, Shi Y, Meng X, Zhang B, Li D. Pneumatic Noise Study of Multi-Stage Sleeve Control Valve. Processes. 2023; 11(9):2544. https://doi.org/10.3390/pr11092544
Chicago/Turabian StyleJia, Jianbo, Yan Shi, Xianyu Meng, Bo Zhang, and Dameng Li. 2023. "Pneumatic Noise Study of Multi-Stage Sleeve Control Valve" Processes 11, no. 9: 2544. https://doi.org/10.3390/pr11092544






