Spatial Structure Characteristics of Underground Reservoir Water Storage Space in Coal Mines Considering Shape Characteristics of Crushed Rock
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Shape Indicators of Crushed Rock
2.3. Test Design
2.4. Test Procedures
3. Results
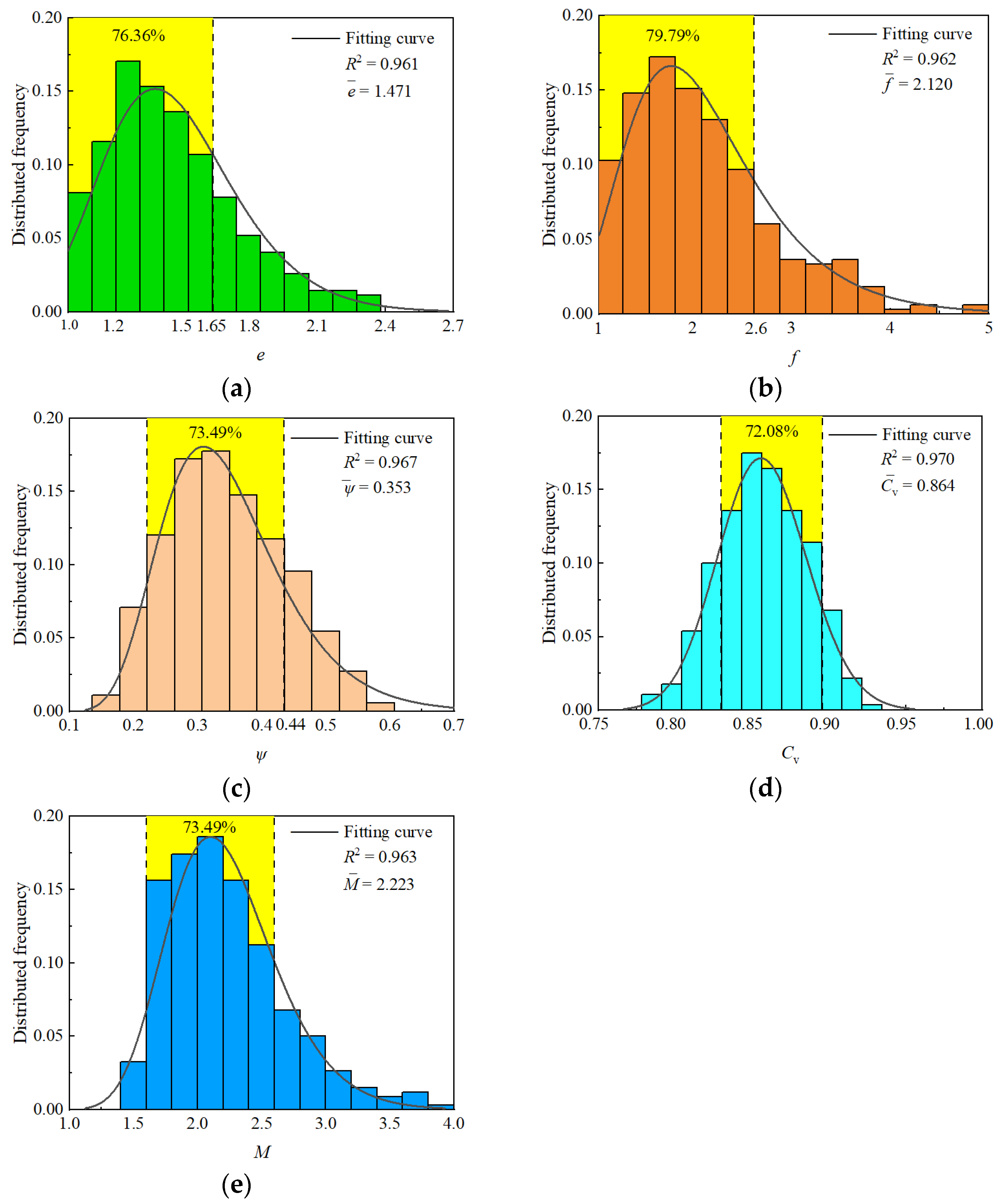
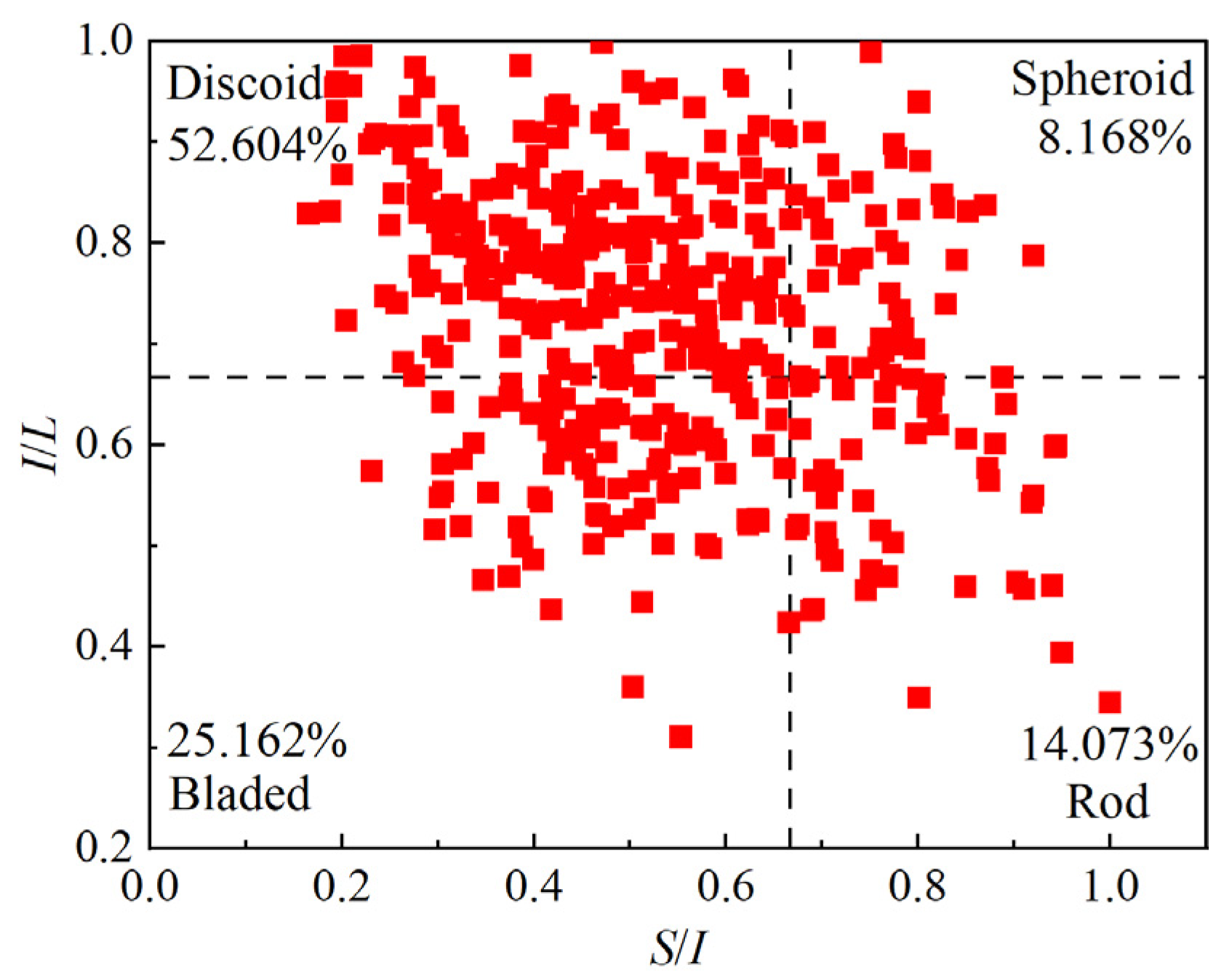
3.1. Statistical Analysis of the Shape Characteristics of Crushed Rock
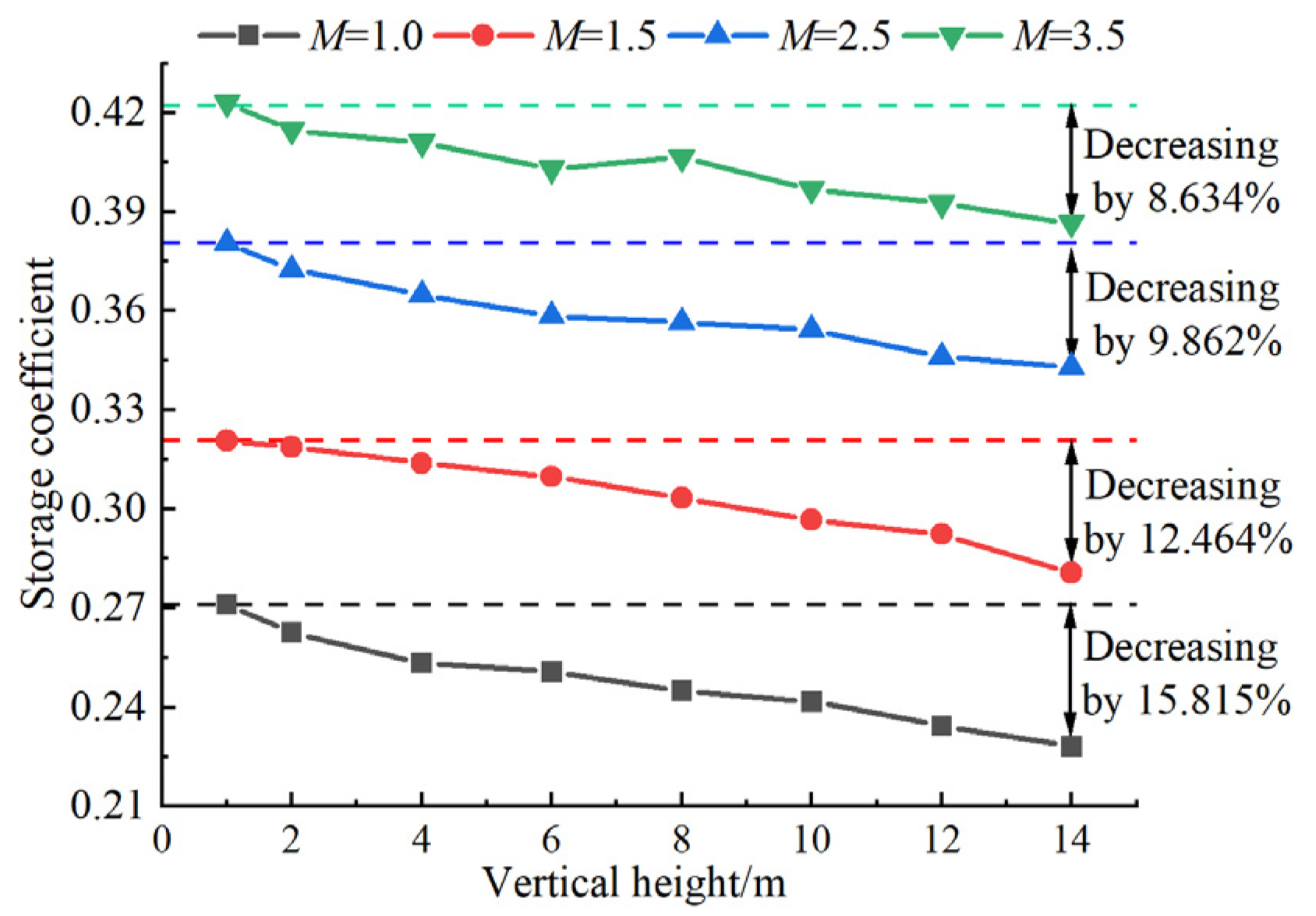
3.2. Variation Law of Storage Coefficient
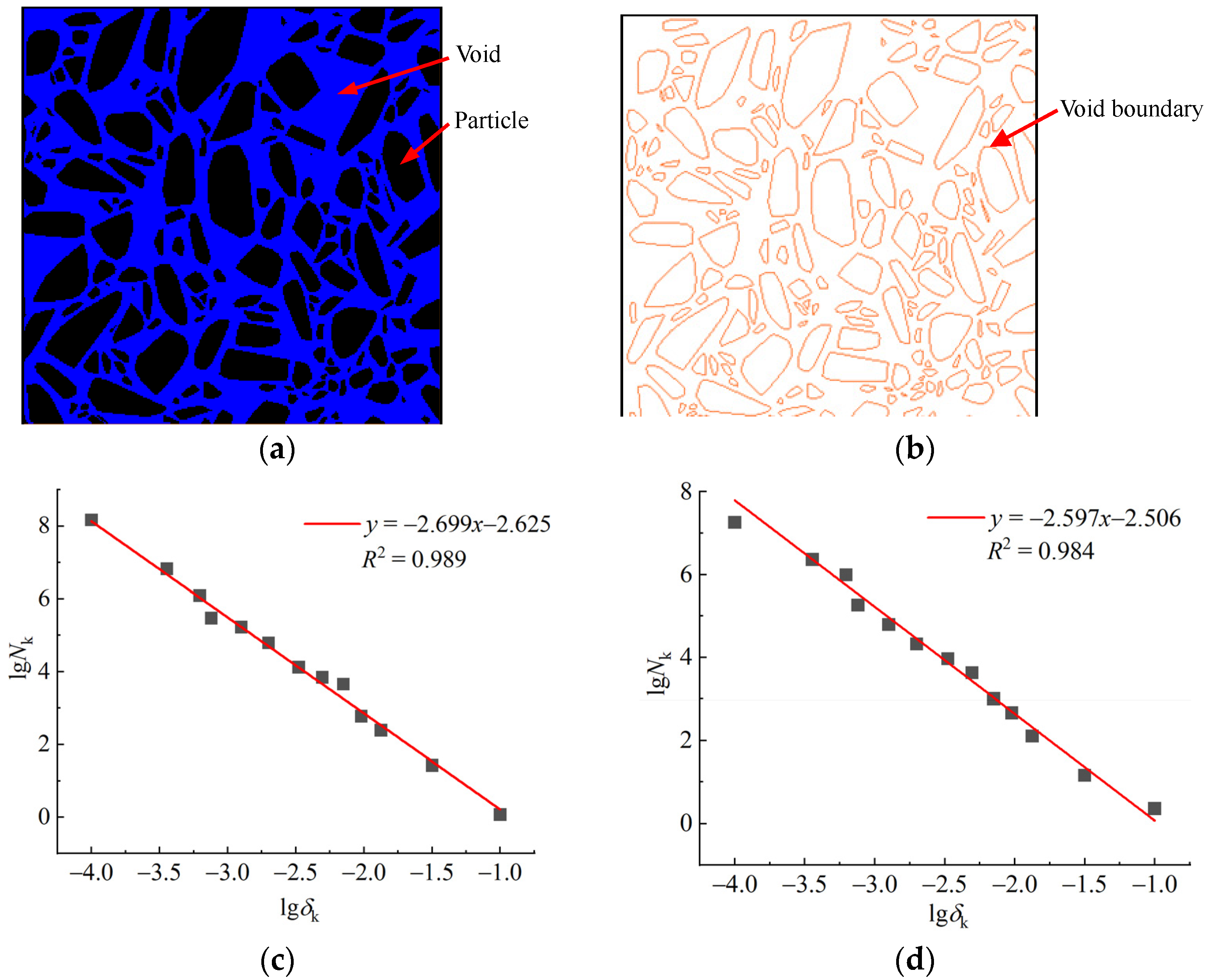
3.3. Variation Law of Fractal Dimension of Water Storage Space
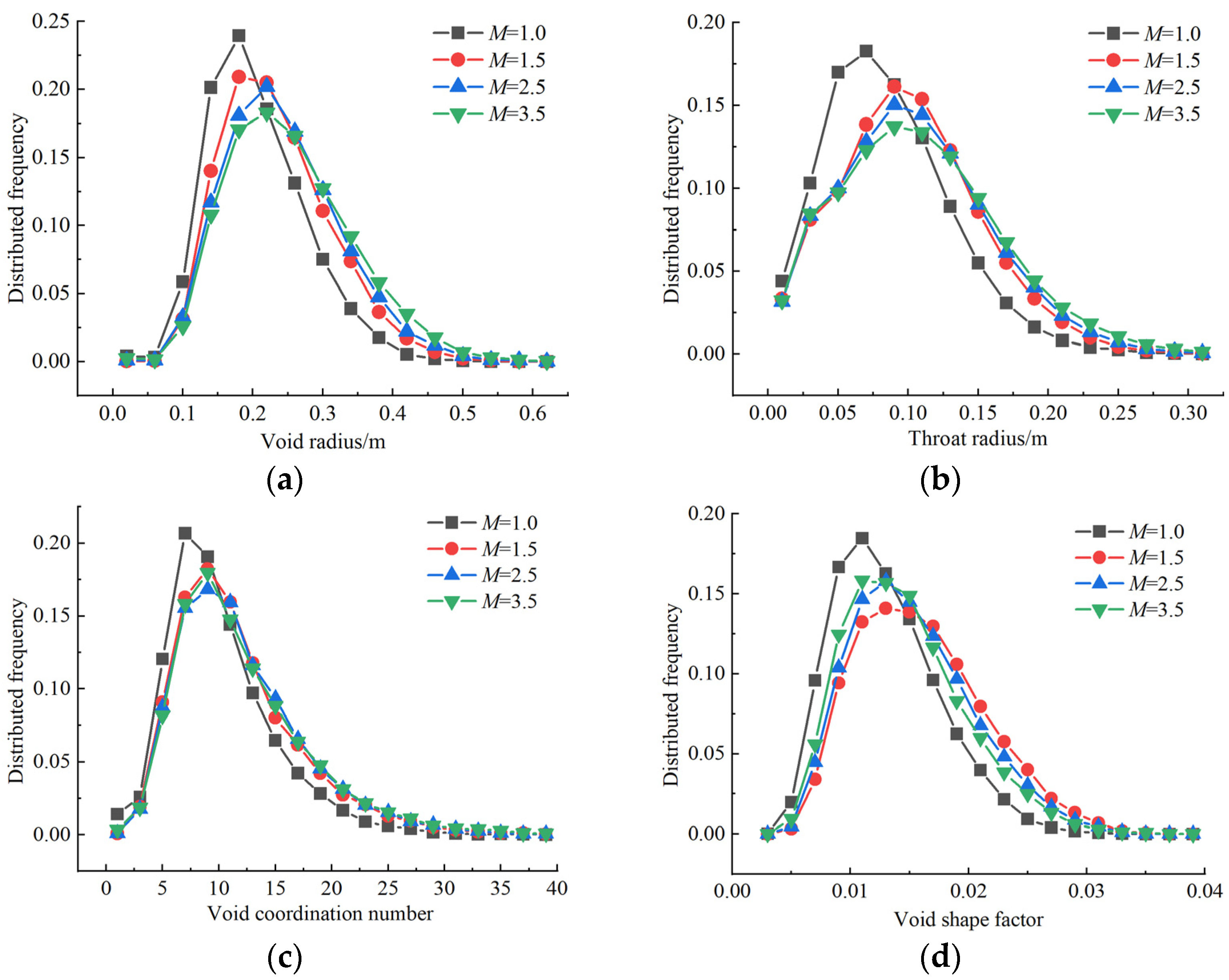
3.4. Variation Law of Void Network Structure
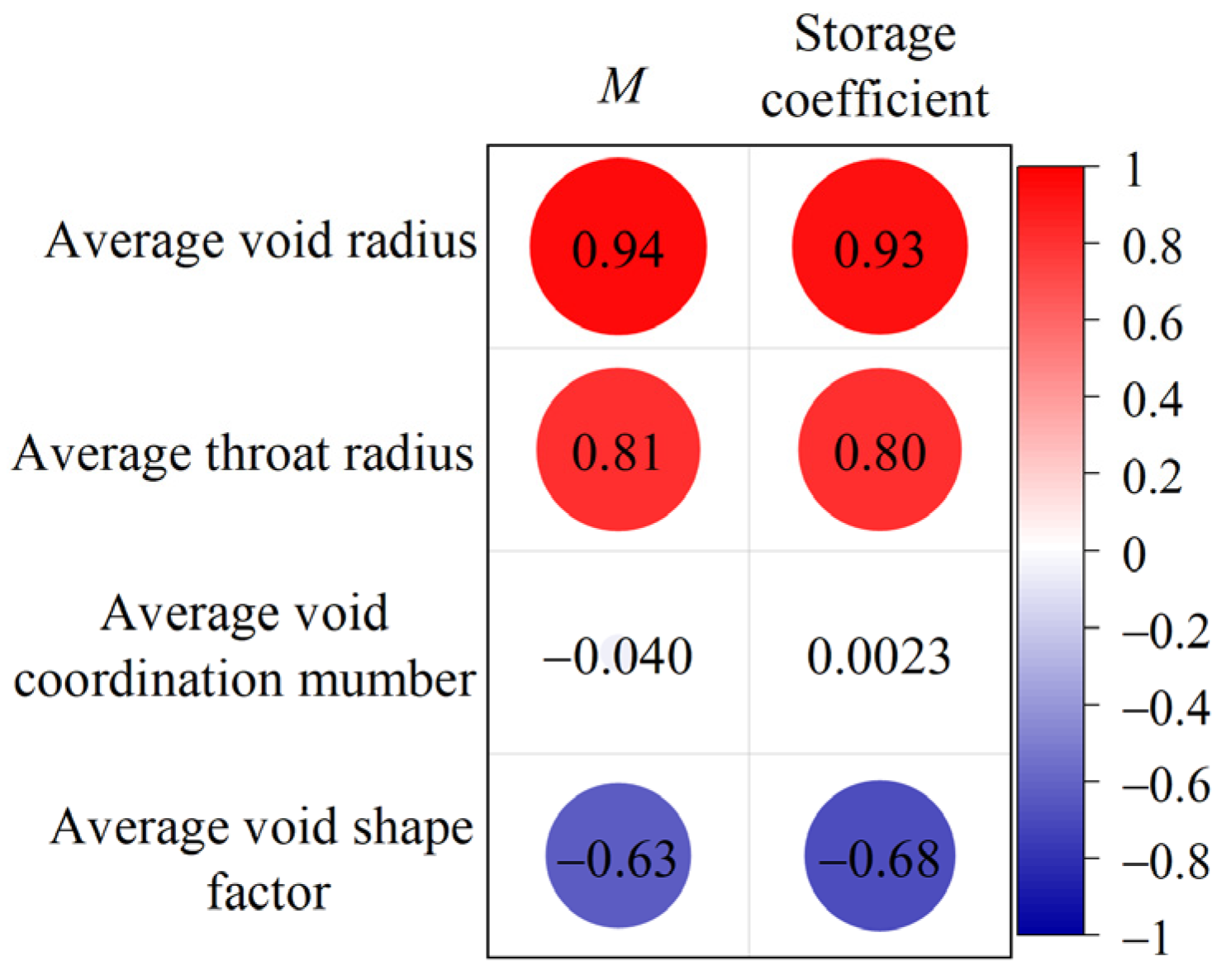
4. Discussion
5. Conclusions
- (1)
- Crushed rock exhibits a lognormal distribution in its shape characteristic parameters at different scales, with a predominant discoid shape, which accounts for more than 50%. The shape coefficient M can be utilized as a comprehensive indicator to characterize the shape characteristics of crushed rock.
- (2)
- Within the range of the values studied, the average storage coefficient and average contact force of the packing system of crushed rock both increase exponentially as the shape coefficient M increases, and the increase is 50.1% and 11.7% from M = 1 to 3.5, respectively. The storage coefficient decreases as the spatial height of the packing model increases. Additionally, the decrease is smaller when the shape coefficient M is smaller.
- (3)
- Within the range of the values studied, the spatial structure of water storage space exhibits self-similarity, the void fractal dimensions are all distributed in the range of 2.659 to 2.711, and the void boundary fractal dimensions are all distributed in the range of 2.489 to 2.645. The void fractal dimension is influenced by both the void ratio and the complexity of the void structure, while the void boundary fractal dimension is more effective in representing the spatial complexity of water storage space. The complexity of the water storage space structure and the inhomogeneity of void distribution both increased gradually with the increase in the shape coefficient M.
- (4)
- When comparing the non-spherical particle system with the spherical particle system, it is observed that the spherical particle system has smaller water storage space, lower connectivity among voids, and more irregular void space. In the non-spherical particle system, the water storage space becomes larger as the shape of crushed rock becomes more irregular, resulting in more irregular void space. However, there is no significant effect on void connectivity. The shape of crushed rock has a significant impact on the overall structure characteristics of water storage space. It influences the local void radius, throat radius, and void shape factor of the packing system.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gu, D.Z. Theory framework and technological system of coal mine underground reservoir. J. China Coal Soc. 2015, 40, 239–246. [Google Scholar]
- Reisi, M.; Mostofinejad, D.; Ramezanianpour, A. Computer simulation-based method to predict packing density of aggregates mixture. Adv. Powder Technol. 2018, 29, 386–398. [Google Scholar] [CrossRef]
- Zhao, L.; Zhang, S.; Huang, D.; Wang, X.; Zhang, Y. 3D shape quantification and random packing simulation of rock aggregates using photogrammetry-based reconstruction and discrete element method. Constr. Build Mater. 2020, 262, 119986. [Google Scholar] [CrossRef]
- Xiang, P.; Sun, L.H.; Ji, H.G.; Gao, Y.; Liu, Y.J. Dynamic distribution characteristics and determination method of caving zone in large mining height working face. J. Min. Saf. Eng. 2017, 34, 861–867. [Google Scholar]
- Song, Y.J.; Cheng, G.Q.; Guo, W.J. Study of distribution of overlying strata fissures and its porosity characteristics. Rock Soil Mech. 2011, 32, 533–536. [Google Scholar]
- Wang, B.F.; Liang, B.; Jiang, L.G.; Li, G.; Li, C.Y. Fractal calculation and application of water storage in void of crushed rock mass. Chin. J. Rock Mech. Eng. 2015, 34, 1444–1451. [Google Scholar]
- Ju, J.F.; Xu, J.L.; Zhu, W.B. Storage capacity of underground reservoir in the Chinese western water-short coalfield. J. China Coal Soc. 2017, 42, 381–387. [Google Scholar]
- Fang, J.; Song, H.Q.; Xu, J.J.; Yang, L.Z.; Li, Z.Y. Storage coefficient calculation model of coal mine underground reservoir considering effect of effective stress. J. China Coal Soc. 2001, 46, 451–468. [Google Scholar]
- Szlazak, J. The determination of a coefficient of longwall gob permeability. Arch. Min. Sci. 2019, 44, 3750–3759. [Google Scholar]
- Zhang, J.W.; Wang, H.L.; Chen, S.J.; Li, Y.L. Compressive deformation characteristics of large-size crushed rock. J. China Coal Soc. 2018, 43, 1000–1007. [Google Scholar]
- Chen, X.X.; Su, C.D.; Tang, X.; Gu, W.B. Experimental study of effect of water-saturated state on compaction property of crushed stone from coal seam roof. Chin. J. Rock Mech. Eng. 2014, 33, 3318–3326. [Google Scholar]
- Deng, K.Z.; Zhou, M.; Tan, Z.X. Study on laws of rock mass breaking induced by mining. J. China Univ. Min. Technol. 1998, 27, 261–264. [Google Scholar]
- Ma, Z.G.; Lan, T.; Pan, Y.G.; Ma, J.G.; Zhu, F.H. Experimental study on porous change law of saturated broken mudstone during creep. Chin. J. Rock Mech. Eng. 2009, 28, 447–454. [Google Scholar]
- Ma, Z.G.; Miao, X.X.; Chen, Z.Q.; Li, Y.S. Experimental study on permeability of broken coal. Rock Soil Mech. 2009, 30, 985–988+996. [Google Scholar]
- Su, C.D.; Gu, M.; Tang, X.; Gu, W.B. Experimental study of compaction characteristics of crushed stones from coal seam roof. Chin. J. Rock Mech. Eng. 2012, 31, 18–26. [Google Scholar]
- Li, J.M.; Huang, Y.L.; Pu, H.; Gao, H.; Li, Y.; Ouyang, S.; Guo, Y. Influence of block shape on macroscopic deformation response and meso-fabric evolution of crushed gangue under the triaxial compression. Powder Technol. 2021, 384, 112–124. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, Y.X.; Tu, S.H.; Zhang, T. Numerical simulation of compaction and re-breaking characteristics of coal and rock samples in goaf. Chin. J. Geotech. Eng. 2020, 42, 696–704. [Google Scholar]
- Pang, Y.H.; Li, Q.S.; Cao, G.M.; Zhou, B.J. Analysis and calculation method of underground reservoir water storage space composition. J. China Coal Soc. 2019, 44, 557–566. [Google Scholar]
- Landauer, J.; Kuhn, M.; Nasato, D.S.; Foerst, P.; Briesen, H. Particle shape matters—Using 3D printed particles to investigate fundamental particle and packing properties. Powder Technol. 2021, 361, 711–718. [Google Scholar] [CrossRef]
- Seidler, G.T.; Martinez, G.; Seeley, L.H.; Kim, K.H.; Behne, E.A.; Zaranek, S.; Chapman, B.D.; Heald, S.M.; Brewe, D.L. Granule-by-granule reconstruction of a sandpile from X-ray microtomography data. Phys. Rev. E 2000, 62, 8175–8181. [Google Scholar] [CrossRef]
- Cao, Y.X.; Chakrabortty, B.; Barker, G.C.; Mehta, A.; Wang, Y.J. Bridges in three-dimensional granular packings: Experiments and simulations. EPL 2013, 102, 24004. [Google Scholar] [CrossRef][Green Version]
- Lin, M.C.; Zhou, W.; Liu, J.Y.; Ma, G.; Cao, X.X. A topological view on microscopic structural evolution for granular material under loading and unloading path. Comput. Geotech. 2022, 141, 104530. [Google Scholar] [CrossRef]
- Karpenko, M.; Stosiak, M.; Deptuła, A.; Urbanowicz, K.; Nugaras, J.; Krolczyk, G.; Zak, K. Performance evaluation of extruded polystyrene foam for aerospace engineering applications using frequency analyses. Int. J. Adv. Manuf. Technol. 2023, 126, 5515–5526. [Google Scholar] [CrossRef]
- Shepherd, R.F.; Conrad, J.C.; Sabuwala, T.; Gioia, G.G.; Lewis, J.A. Structural evolution of cuboidal granular media. Soft Matter 2012, 8, 4795–4801. [Google Scholar] [CrossRef]
- Zhang, L.H.; Deng, M.; Zhang, S.H.; Huang, D.L.; Qiao, N.; Gong, J. Effects of particle shape on triaxial compression behaviours of realistic ballast particles based on M-A-V-L particle shape evaluation system. Granul. Matter 2023, 25, 4. [Google Scholar]
- Mo, P.Q. Internal rolling method for particle shape evaluation and reconstruction. PLoS ONE 2020, 15, e0242162. [Google Scholar] [CrossRef]
- Pan, J.H.; Zhang, J.M.; Wang, R. Influence of small particle surface asperities on macro and micro mechanical behavior of granular material. Int. J. Numer. Anal. Met. 2022, 46, 961–978. [Google Scholar] [CrossRef]
- Suhr, B.; Six, K. Simple particle shapes for DEM simulations of railway ballast: Influence of shape descriptors on packing behaviour. Granul. Matter 2020, 22, 112–124. [Google Scholar] [CrossRef]
- Xie, Y.H.; Yang, Z.X.; Barreto, D.; Jiang, M.D. The influence of particle geometry and the intermediate stress ratio on the shear behavior of granular materials. Granul. Matter 2017, 19, 35. [Google Scholar] [CrossRef]
- Nie, J.Y.; Zhao, J.; Cui, Y.F.; Li, D.Q. Correlation between grain shape and critical state characteristics of uniformly graded sands: A 3D DEM study. Acta Geotech. 2022, 17, 2783–2798. [Google Scholar] [CrossRef]
- Zheng, J.; Hryciw, R.D. A corner preserving algorithm for realistic DEM soil particle generation. Granul. Matter 2016, 18, 84. [Google Scholar] [CrossRef]
- Sun, H.; Gao, Y.T.; Elmo, D.; Jin, A.B.; Wu, S.C.; Leonardo, D. A study of gravity flow based on the upside-down drop shape theory and considering rock shape and breakage. Rock Mech. Rock Eng. 2019, 52, 881–893. [Google Scholar] [CrossRef]
- Sun, H.; Zhu, D.F.; Jin, A.B.; Wu, S.C.; Yin, Z.S. Flow characteristics of caved ore and rock based on inhomogeneous particle size distribution. Chin. J. Nonferrous Met. 2022, 32, 2433–2445. [Google Scholar]
- Naderi, S.; Zhang, M. An integrated framework for modelling virtual 3D irregulate particulate mesostructured. Powder Technol. 2019, 355, 808–819. [Google Scholar] [CrossRef]
- Sun, H.; Jin, A.B.; Elmo, D.; Wu, S.C.; Gao, Y.T. A numerical based approach to calculate ore dilution rates using rolling resistance model and upside-down drop shape theory. Rock Mech. Rock Eng. 2020, 53, 4639–4652. [Google Scholar] [CrossRef]
- Zhou, B.; Ku, Q.; Wang, H.B.; Wang, J.F. Particle classification and intra-particle void structure of carbonate sands. Eng. Geol. 2020, 279, 105889. [Google Scholar] [CrossRef]
- Cho, G.C.; Dodds, J.; Santamarina, J.C. Particle shape effects on packing density, stiffness, and strength: Natural and crushed sands. J. Geotech. Geoenviron. 2006, 133, 591–602. [Google Scholar] [CrossRef]
- Se, Y.F.; Bhattachary, S.; Lee, S.J.; Lee, C.H.; Shin, M. A new interpretation of three-dimensional particle geometry: M-A-V-L. Transp. Geotech. 2020, 23, 100328. [Google Scholar]
- Jebli, I.; Belouadha, F.Z.; Kabbaj, M.I.; Tilioua, A. Prediction of solar energy guided by pearson correlation using machine learning. Energy 2021, 224, 120109. [Google Scholar] [CrossRef]
- Li, X.B.; Wei, W.; Wang, L. Fractal dimension of digital 3D rock models with different void structures. Energies 2022, 15, 7461. [Google Scholar] [CrossRef]
- Li, X.B.; Luo, M.; Liu, J.P. Fractal characteristics based on different statistical objects of process-based digital rock models. J. Pet. Sci. Eng. 2019, 179, 19–430. [Google Scholar] [CrossRef]
- Li, X.B.; Wei, W.; Wang, L. A new method for evaluating the pore structure complexity of digital rocks based on the relative value of fractal dimension. Mar. Pet. Geol. 2022, 141, 105694. [Google Scholar] [CrossRef]
- Zhang, W.B.; Hu, X.L.; Tannant, D.D.; Zhou, B. Quantifying the influence of grain morphology on sand hydraulic conductivity: A detailed pore-scale study. Comput. Geotech. 2021, 135, 104147. [Google Scholar] [CrossRef]
- Silin, D.; Patzek, T. Void space morphology analysis using maximal inscribed spheres. Phys. A 2006, 371, 336–360. [Google Scholar] [CrossRef]
- Wang, H.M. Study on Fractal Characteristics and Network Model of Porous Media Pore Structure. Master’s Thesis, Dalian University of Technology, Dalian, China, 2013. [Google Scholar]
- Fei, W.B.; Guillermo, A.N. Impact of three-dimensional sphericity and roundness on coordination number. J. Geotech. Geoenviron. 2020, 146, 06020025. [Google Scholar] [CrossRef]
- Nadimi, S.; Fonseca, J. A micro finite-element model for soil behaviour. Geotechnique 2017, 68, 290–302. [Google Scholar] [CrossRef]
- Zhou, Y.X.; Ma, G.; Mei, J.Z.; Zhao, J.D.; Zhou, W. Microscopic origin of shape-dependent shear strength of granular materials: A granular dynamics perspective. Acta Geotech. 2021, 17, 2697–2710. [Google Scholar] [CrossRef]
- Kandasami, R.K.; Murthy, T.G. Manifestation of particle morphology on the mechanical behaviour of granular ensembles. Granul. Matter 2017, 19, 21. [Google Scholar] [CrossRef]






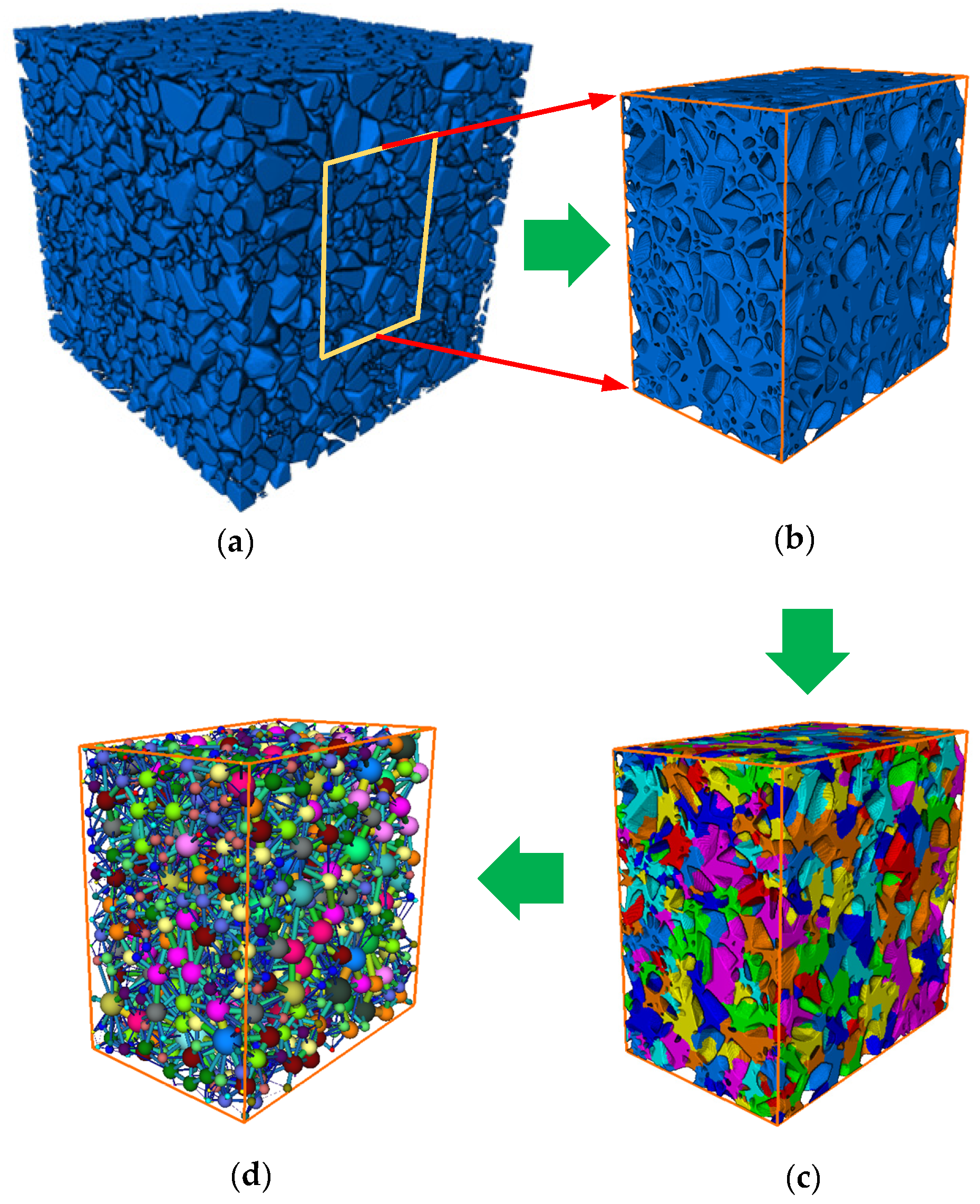
| Shape Description Scale | Shape Indicators | Formulas | Value Ranges | Descriptive Features |
|---|---|---|---|---|
| The first scale | Long-to-medium axis ratio e | ≥1 | It represents the needle-like degree of the particle, and the larger the value, the more elongated the particle. | |
| Medium-to-short axis ratio f | ≥1 | It represents the flaky degree of the particle, and the larger the value, the more flaky the particle. | ||
| Sphericity ψ | 0~1 | It represents the proximity of the particle to the sphere, and the closer the value is to 1, the closer the particle shape is to the sphere. | ||
| The second scale | Convexity Cv | 0~1 | It represents the angular characteristics of the particle, and the smaller the value, the more angular the particle. | |
| Shape coefficient M | ≥1 | The value is 1 for spheres and greater than 1 for non-spherical particles, and the larger the value, the more irregular the particle. |
| Parameters of 52,304 Fully-Mechanized Mining Face of Daliuta Coal Mine | Numerical Model Parameters | ||
|---|---|---|---|
| Height of caving zone | 15 m | Characterization unit model of crushed rock | 15 m |
| Overlying stress | 3.0–6.5 MPa | Overlying stress | 5 MPa |
| Wall | Rigid Block | |||||
|---|---|---|---|---|---|---|
| Normal Stiffness/ (N·m−1) | Shear Stiffness/ (N·m−1) | Friction Coefficient | Normal Stiffness/ (N·m−1) | Shear Stiffness/ (N·m−1) | Density/ (kg·m−3) | Friction Coefficient |
| 1 × 109 | 1 × 109 | 0.50 | 5 × 108 | 5 × 108 | 2300 | 0.55 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qin, X.; Cao, Z.; Wei, L.; Li, P.; Sun, H. Spatial Structure Characteristics of Underground Reservoir Water Storage Space in Coal Mines Considering Shape Characteristics of Crushed Rock. Processes 2023, 11, 2611. https://doi.org/10.3390/pr11092611
Qin X, Cao Z, Wei L, Li P, Sun H. Spatial Structure Characteristics of Underground Reservoir Water Storage Space in Coal Mines Considering Shape Characteristics of Crushed Rock. Processes. 2023; 11(9):2611. https://doi.org/10.3390/pr11092611
Chicago/Turabian StyleQin, Xuan, Zhiguo Cao, Lichang Wei, Peng Li, and Hao Sun. 2023. "Spatial Structure Characteristics of Underground Reservoir Water Storage Space in Coal Mines Considering Shape Characteristics of Crushed Rock" Processes 11, no. 9: 2611. https://doi.org/10.3390/pr11092611
APA StyleQin, X., Cao, Z., Wei, L., Li, P., & Sun, H. (2023). Spatial Structure Characteristics of Underground Reservoir Water Storage Space in Coal Mines Considering Shape Characteristics of Crushed Rock. Processes, 11(9), 2611. https://doi.org/10.3390/pr11092611









