Exploring Bayesian Optimization for Photocatalytic Reduction of CO2
Abstract
:1. Introduction
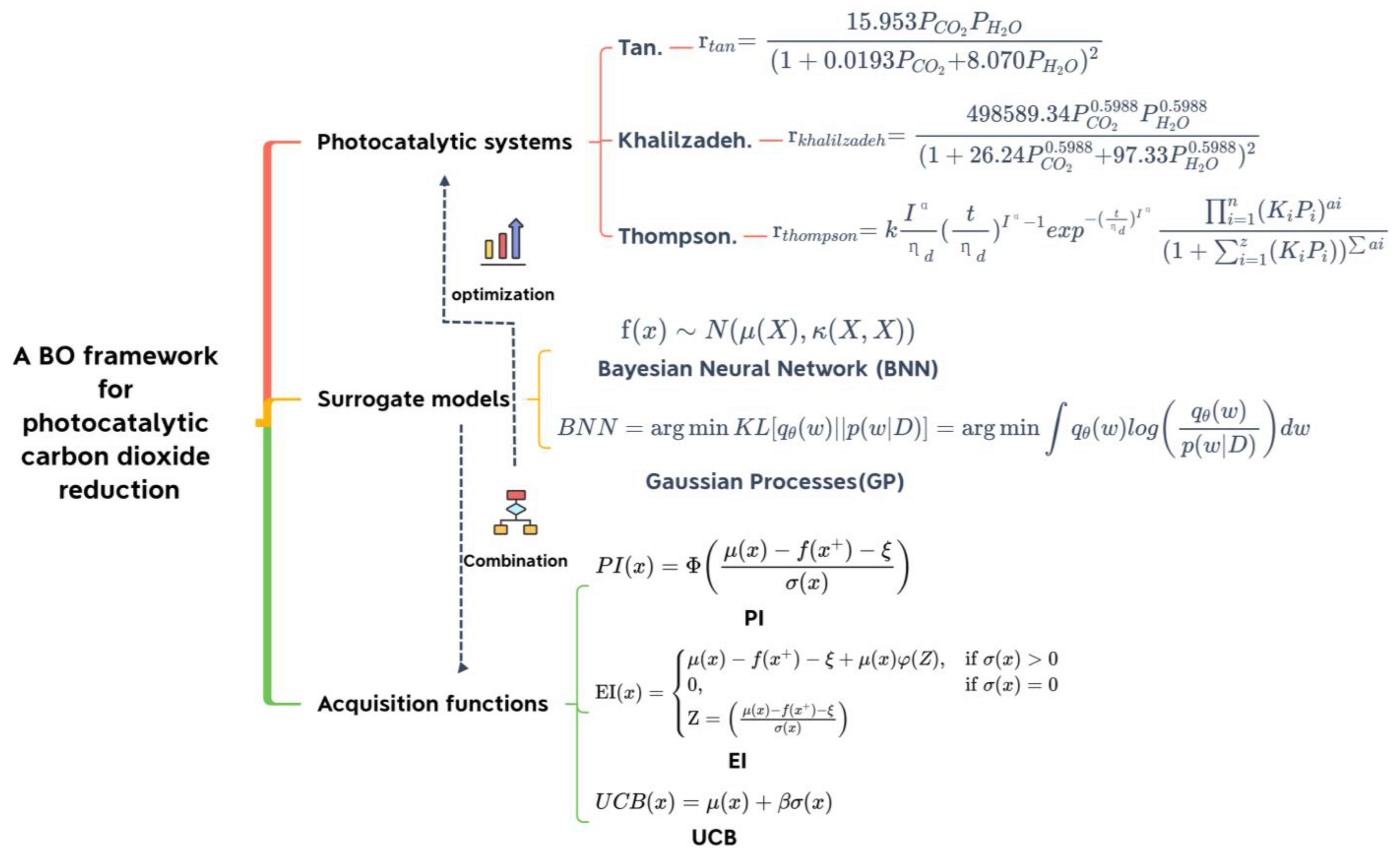
2. Methods and Models
2.1. Optimization Methods
2.1.1. Bayesian Optimization
2.1.2. Surrogate Model
2.1.3. Acquisition Function
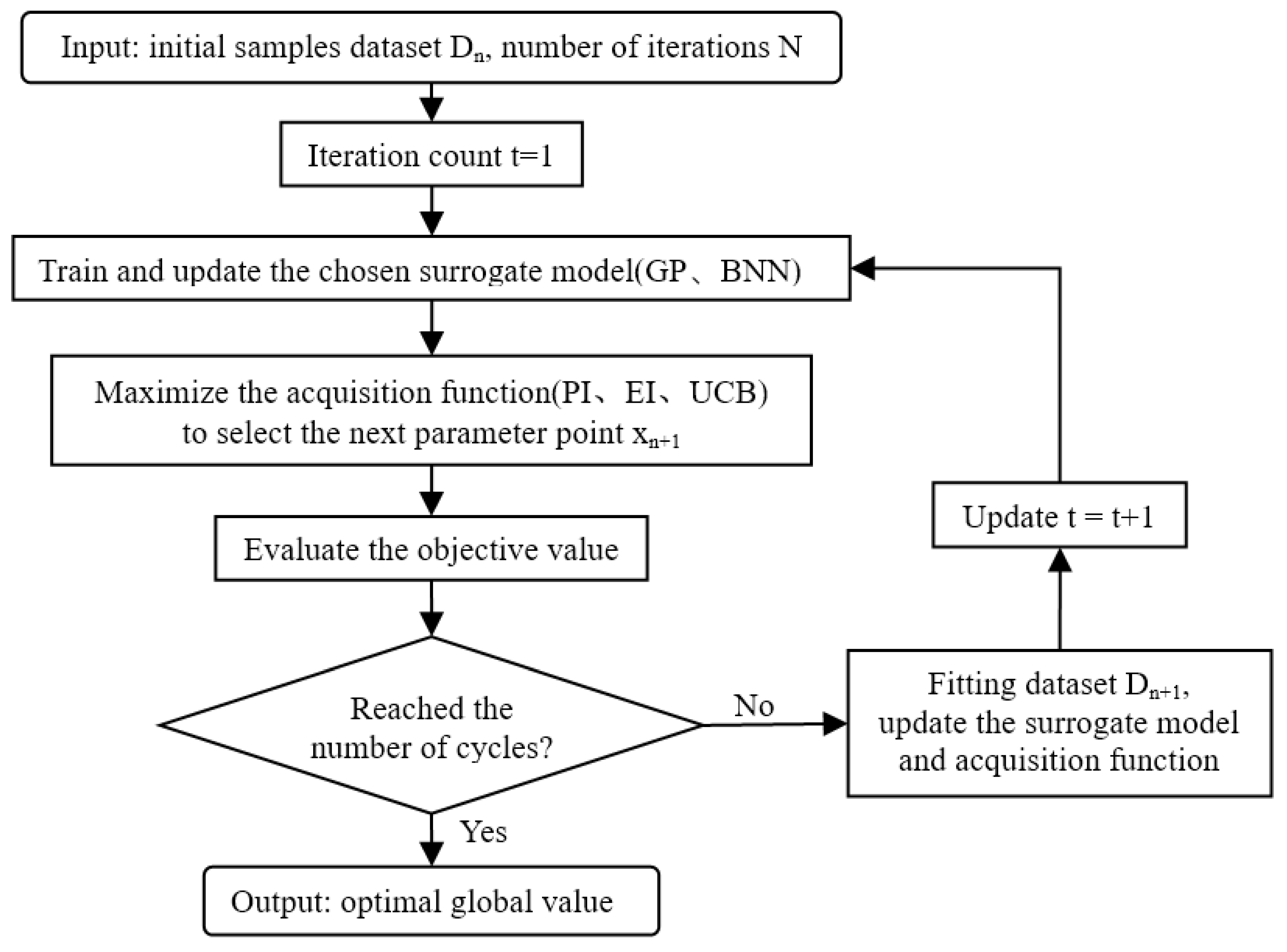
2.1.4. Algorithm
- (1)
- Begin with t = 1;
- (2)
- Pre-sample, build initial samples [38], train and update the chosen surrogate model , ;
- (3)
- For i = 1, 2,..., measure the CO2 photocatalytic properties represented by known parameter values [39] (partial pressure and/or deactivation time h) ;
- (4)
- Maximize the acquisition function to determine the next evaluated process parameter value : ;
- (5)
- Evaluate the objective function value ;
- (6)
- Fitting data: , update the probability surrogate model;
- (7)
- Update t = t + 1;
- (8)
- BO actively iterates increases from t times to N times in the feedback loop until it finds the optimal global value (see Equation (7)).
2.1.5. Design of Experiments (DOE)
2.1.6. Langmuir–Hinshelwood (L-H) Mechanism
2.2. Kinetic Models
2.2.1. L-H-Based Kinetic Model
2.2.2. A Probabilistic L-H-Based Dynamic Kinetic Model
2.3. CO2 Photoreduction Kinetic Model
2.3.1. Tan
2.3.2. Khalilzadeh
2.3.3. Thompson
3. Results
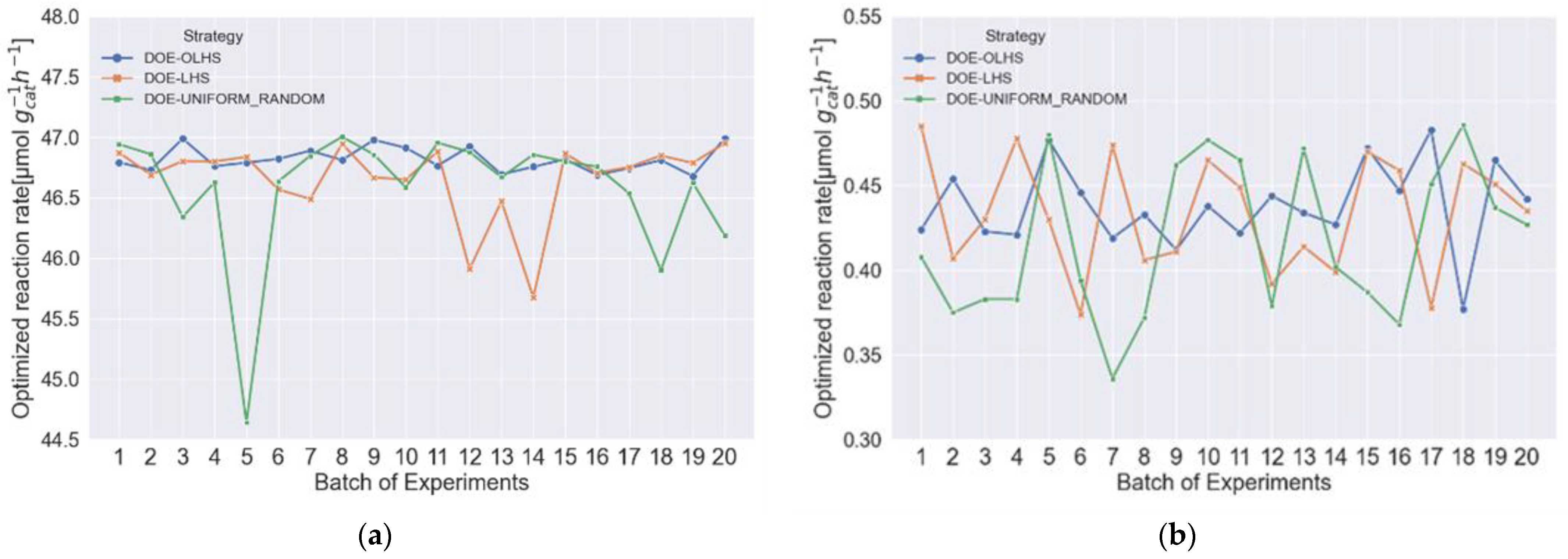
3.1. Comparing Different Traditional DOE Methods in Two-Dimensional Space
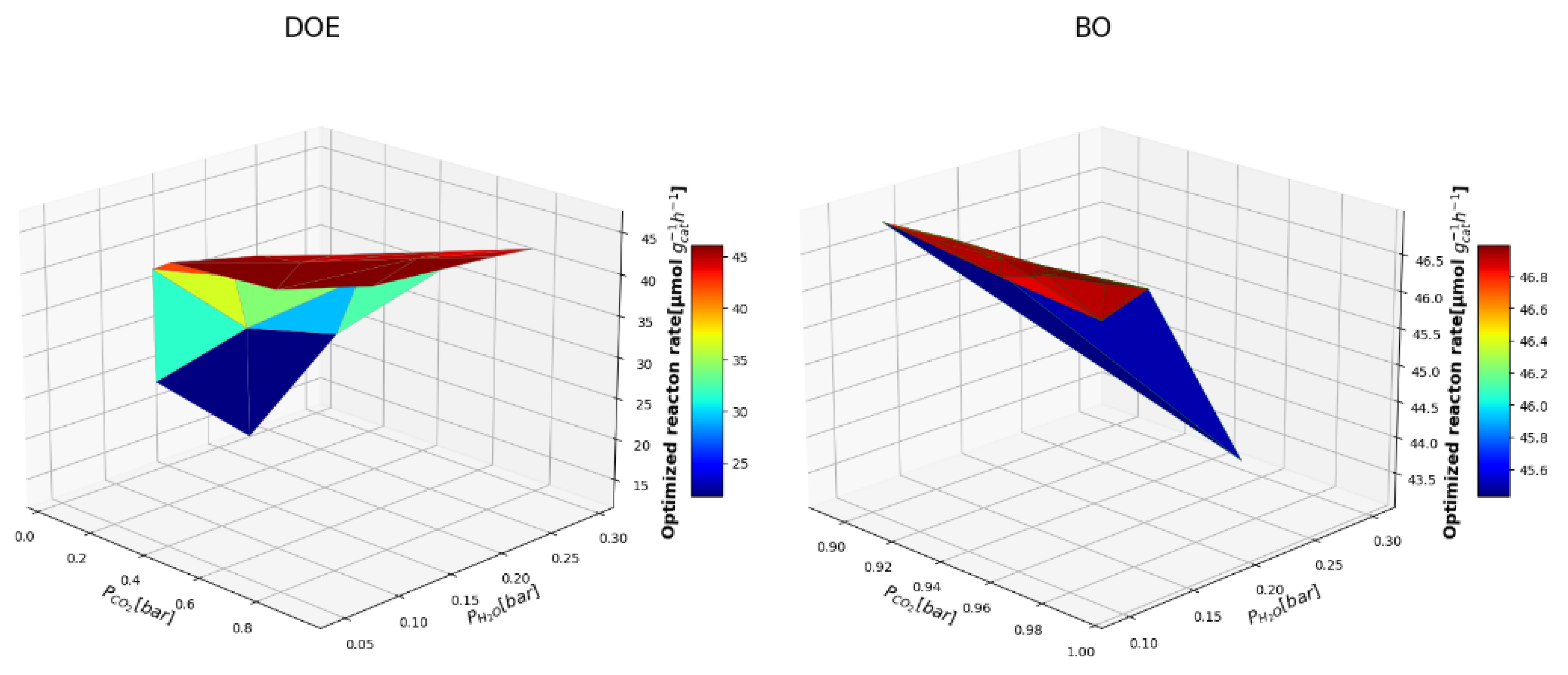
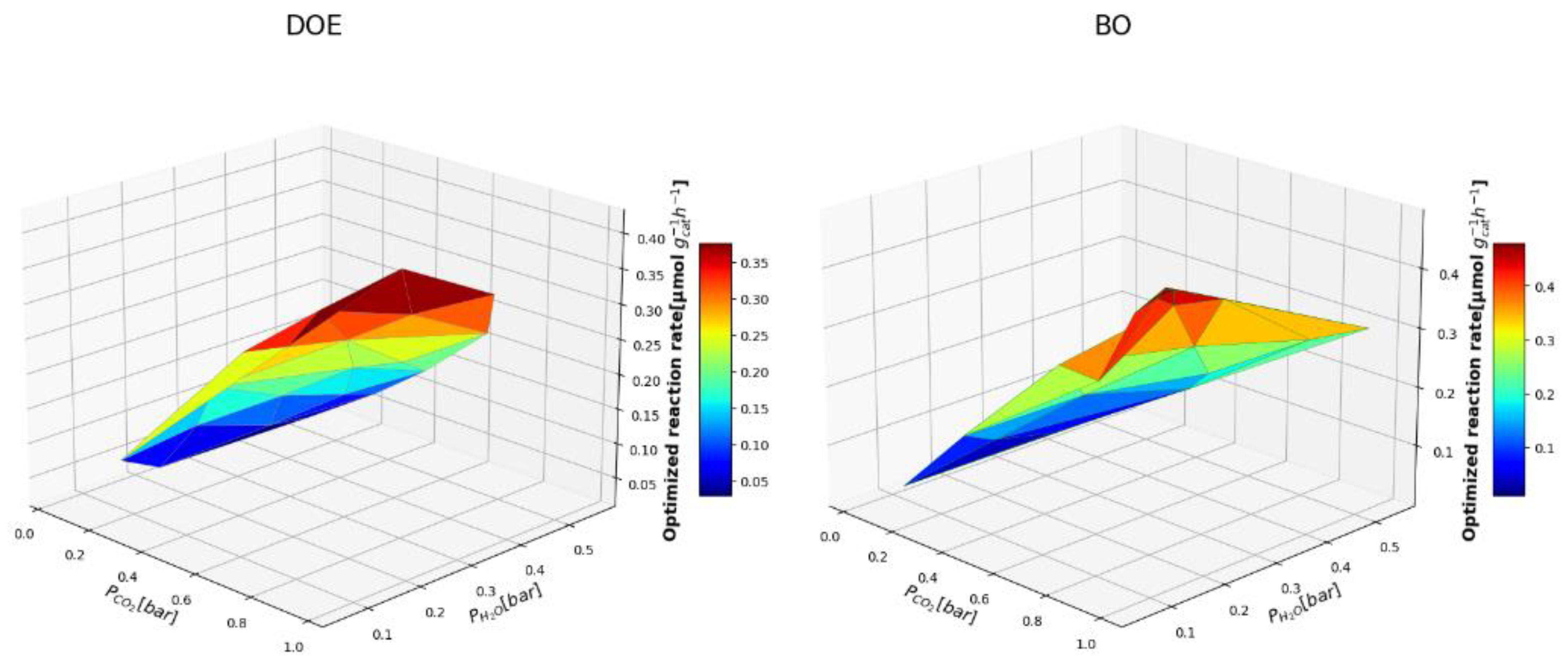
3.2. Comparing BO and DOE-OLHS
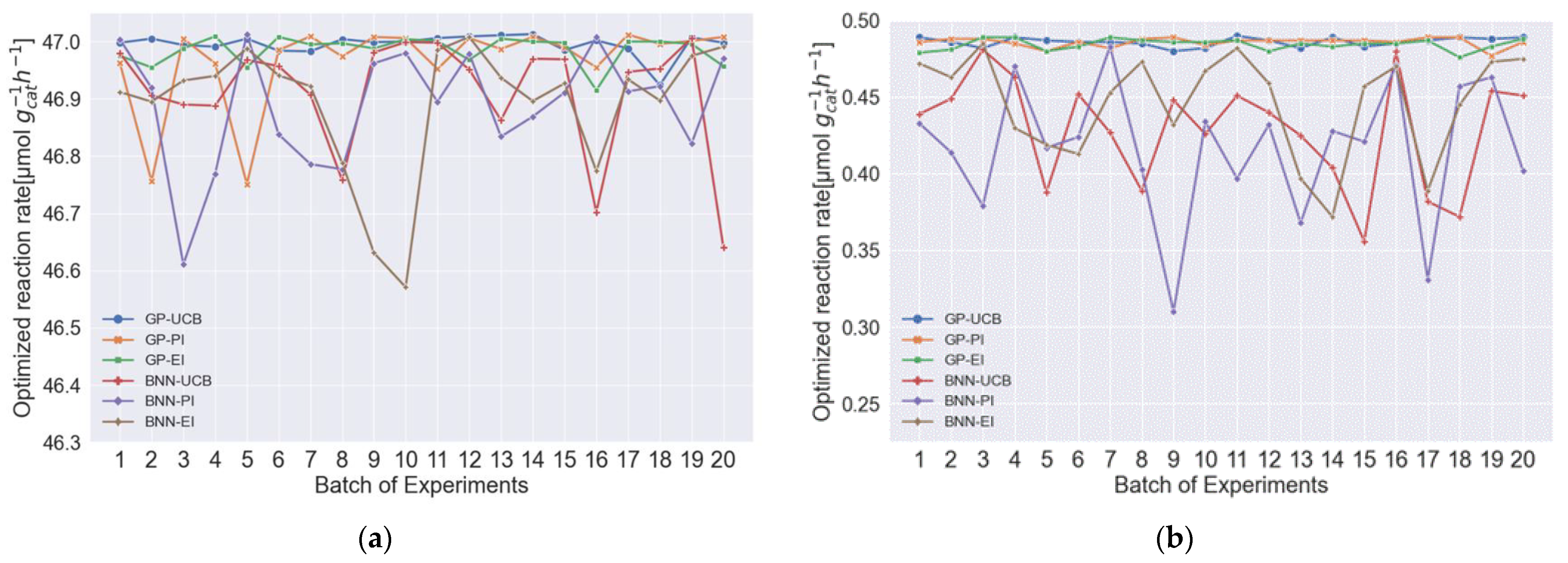
3.3. Investigating the Effects of Different Combinations of Surrogate Models and Acquisition Functions
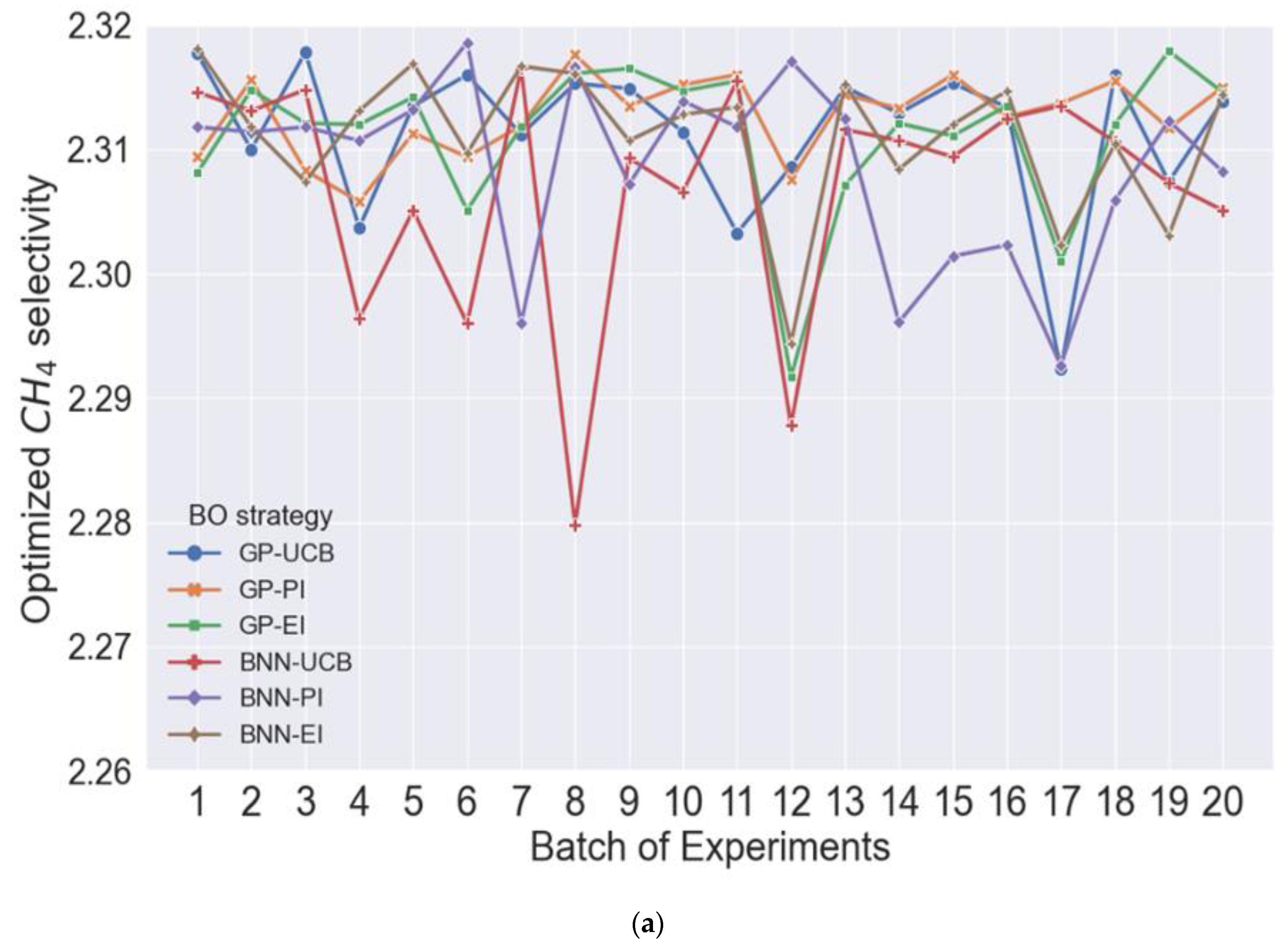
3.4. Optimization of Product Selectivity including Catalyst Deactivation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tahir, M.; Amin, N.S. Indium-doped TiO2 nanoparticles for photocatalytic CO2 reduction with H2O vapors to CH4. Appl. Catal. B Environ. 2015, 162, 98–109. [Google Scholar] [CrossRef]
- Tan, L.-L.; Ong, W.-J.; Chai, S.-P.; Mohamed, A.R. Photocatalytic reduction of CO2 with H2O over graphene oxide-supported oxygen-rich TiO2 hybrid photocatalyst under visible light irradiation: Process and kinetic studies. Chem. Eng. J. 2017, 308, 248–255. [Google Scholar] [CrossRef]
- Khalilzadeh, A.; Shariati, A. Fe-N-TiO2/CPO-Cu-27 nanocomposite for superior CO2 photoreduction performance under visible light irradiation. Solar Energy 2019, 186, 166–174. [Google Scholar] [CrossRef]
- Sips, R. On the Structure of a Catalyst Surface. J. Chem. Phys. 1948, 16, 490–495. [Google Scholar] [CrossRef]
- Thompson, W.A.; Sanchez Fernandez, E.; Maroto-Valer, M.M. Probability Langmuir-Hinshelwood based CO2 photoreduction kinetic models. Chem. Eng. J. 2020, 384, 123356. [Google Scholar] [CrossRef]
- Bu, X.; Xie, G.; Peng, Y.; Chen, Y. Kinetic modeling and optimization of flotation process in a cyclonic microbubble flotation column using composite central design methodology. Int. J. Miner. Process. 2016, 157, 175–183. [Google Scholar] [CrossRef]
- Danesh, S.M.S.; Faghihian, H.; Shariati, S. Sulfonic Acid Functionalized SBA-3 Silica Mesoporous Magnetite Nanocomposite for Safranin O Dye Removal. Silicon 2018, 11, 1817–1827. [Google Scholar] [CrossRef]
- Jin, H.; Zhu, J.; Hu, J.; Li, Y.; Zhang, Y.; Huang, X.; Ding, K.; Chen, W. Structural and electronic properties of tungsten trioxides: From cluster to solid surface. Theor. Chem. Acc. 2011, 130, 103–114. [Google Scholar] [CrossRef]
- Purkait, P.K.; Majumder, S.; Roy, S.; Maitra, S.; Chandra Das, G.; Chaudhuri, M.G. Enhanced heterogeneous photocatalytic degradation of florasulam in aqueous media using green synthesized TiO2 nanoparticle under UV light irradiation. Inorg. Chem. Commun. 2023, 155, 111017. [Google Scholar] [CrossRef]
- Lais, A.; Gondal, M.A.; Dastageer, M.A.; Al-Adel, F.F. Experimental parameters affecting the photocatalytic reduction performance of CO2 to methanol: A review. Int. J. Energy Res. 2018, 42, 2031–2049. [Google Scholar] [CrossRef]
- Murray, P.M.; Bellany, F.; Benhamou, L.; Bucar, D.K.; Tabor, A.B.; Sheppard, T.D. The application of design of experiments (DoE) reaction optimisation and solvent selection in the development of new synthetic chemistry. Org. Biomol. Chem. 2016, 14, 2373–2384. [Google Scholar] [CrossRef] [PubMed]
- Niedz, R.P.; Evens, T.J. Design of experiments (DOE)—History, concepts, and relevance to in vitro culture. Vitr. Cell. Dev. Biol. Plant 2016, 52, 547–562. [Google Scholar] [CrossRef]
- Lee, B.C.Y.; Mahtab, M.S.; Neo, T.H.; Farooqi, I.H.; Khursheed, A. A comprehensive review of Design of experiment (DOE) for water and wastewater treatment application—Key concepts, methodology and contextualized application. J. Water Process Eng. 2022, 47, 102673. [Google Scholar] [CrossRef]
- Anika, N.A.; Tanzeem, N.; Gupta, H.S. Design of Experiment (DoE): Implementation in Determining Optimum Design Parameters of Portable Workstation. Engineering 2020, 12, 25–32. [Google Scholar] [CrossRef]
- Bowden, G.D.; Pichler, B.J.; Maurer, A. A Design of Experiments (DoE) Approach Accelerates the Optimization of Copper-Mediated (18)F-Fluorination Reactions of Arylstannanes. Sci. Rep. 2019, 9, 11370. [Google Scholar] [CrossRef] [PubMed]
- Lucks, S.; Brunner, H. In Situ Generated Palladium on Aluminum Phosphate as Catalytic System for the Preparation of β,β-Diarylated Olefins by Matsuda–Heck Reaction. Org. Process Res. Dev. 2017, 21, 1835–1842. [Google Scholar] [CrossRef]
- Caron, S.; Thomson, N.M. Pharmaceutical Process Chemistry: Evolution of a Contemporary Data-Rich Laboratory Environment. J. Org. Chem. 2015, 80, 2943–2958. [Google Scholar] [CrossRef]
- Emmerich, M.T.M.; Giannakoglou, K.C.; Naujoks, B. Single- and multiobjective evolutionary optimization assisted by Gaussian random field metamodels. IEEE Trans. Evol. Comput. 2006, 10, 421–439. [Google Scholar] [CrossRef]
- Shuai, D. Hyper parameter optimization of CNN based on improved Bayesian Optimization algorithm. Appl. Res. Comput. 2018, 36, 1984–1987. [Google Scholar] [CrossRef]
- Rasmussen, C.E. Gaussian Processes in Machine Learning. In Advanced Lectures on Machine Learning, Proceedings of the ML Summer Schools 2003, Canberra, Australia, 2–14 February 2003, Tübingen, Germany, 4–16 August 2003; Revised Lectures; Bousquet, O., von Luxburg, U., Rätsch, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2004; pp. 63–71. [Google Scholar] [CrossRef]
- Kusner, M.J.; Paige, B.; Hernández-Lobato, J.M. Grammar Variational Autoencoder. Mach. Learn. 2017, 2017, 1945–1954. [Google Scholar] [CrossRef]
- Cui, J.; Yang, B. Survey on Bayesian optimization methodology and applications. J. Softw. 2018, 29, 3068–3090. (In Chinese) [Google Scholar] [CrossRef]
- Häse, F.; Roch, L.M.; Kreisbeck, C.; Aspuru-Guzik, A. Phoenics: A Bayesian Optimizer for Chemistry. ACS Cent. Sci. 2018, 4, 1134–1145. [Google Scholar] [CrossRef]
- Seifrid, M.; Pollice, R.; Aguilar-Granda, A.; Morgan Chan, Z.; Hotta, K.; Ser, C.T.; Vestfrid, J.; Wu, T.C.; Aspuru-Guzik, A. Autonomous Chemical Experiments: Challenges and Perspectives on Establishing a Self-Driving Lab. ACC Chem. Res. 2022, 55, 2454–2466. [Google Scholar] [CrossRef] [PubMed]
- Shields, B.J.; Stevens, J.; Li, J.; Parasram, M.; Damani, F.; Alvarado, J.I.M.; Janey, J.M.; Adams, R.P.; Doyle, A.G. Bayesian reaction optimization as a tool for chemical synthesis. Nature 2021, 590, 89–96. [Google Scholar] [CrossRef] [PubMed]
- Christensen, M.; Yunker, L.P.E.; Adedeji, F.; Häse, F.; Roch, L.M.; Gensch, T.; dos Passos Gomes, G.; Zepel, T.; Sigman, M.S.; Aspuru-Guzik, A.; et al. Data-science driven autonomous process optimization. Commun. Chem. 2021, 4, 112. [Google Scholar] [CrossRef]
- Deshwal, A.; Simon, C.M.; Doppa, J.R. Bayesian optimization of nanoporous materials. Mol. Syst. Des. Eng. 2021, 6, 1066–1086. [Google Scholar] [CrossRef]
- Taw, E.; Neaton, J.B. Accelerated Discovery of CH4 Uptake Capacity Metal–Organic Frameworks Using Bayesian Optimization. Adv. Theory Simul. 2022, 5, 515. [Google Scholar] [CrossRef]
- Xie, Y.; Zhang, C.; Deng, H.; Zheng, B.; Su, J.W.; Shutt, K.; Lin, J. Accelerate Synthesis of Metal-Organic Frameworks by a Robotic Platform and Bayesian Optimization. ACS Appl. Mater. Interfaces 2021, 13, 53485–53491. [Google Scholar] [CrossRef]
- Pang, Y.; Zang, X.; Li, H.; Liu, J.; Chang, Q.; Zhang, S.; Wang, C.; Wang, Z. Solid-phase microextraction of organophosphorous pesticides from food samples with a nitrogen-doped porous carbon derived from g-C3N4 templated MOF as the fiber coating. J. Hazard. Mater. 2020, 384, 121430. [Google Scholar] [CrossRef]
- Hao, W.; Dit-Yan, Y. A Survey on Bayesian Deep Learning. ACM Comp. Surv. 2020, 53, 1–37. [Google Scholar] [CrossRef]
- Lei, B.; Kirk, T.Q.; Bhattacharya, A.; Pati, D.; Qian, X.; Arroyave, R.; Mallick, B.K. Bayesian optimization with adaptive surrogate models for automated experimental design. npj Comput. Mater. 2021, 7, 194. [Google Scholar] [CrossRef]
- Ronquist, F.; Teslenko, M.; van der Mark, P.; Ayres, D.L.; Darling, A.; Hohna, S.; Larget, B.; Liu, L.; Suchard, M.A.; Huelsenbeck, J.P. MrBayes 3.2: Efficient Bayesian Phylogenetic Inference and Model Choice Across a Large Model Space. Syst. Biol. 2012, 61, 539–542. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Blaschko, M.B. Additive Tree-Structured Conditional Parameter Spaces in Bayesian Optimization: A Novel Covariance Function and a Fast Implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 3024–3036. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Z.; Judith, B.; Hedvig, K.; Stephan, M. Advances in Variational Inference. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2008–2026. [Google Scholar] [CrossRef]
- Hutter, F.; Hoos, H.H.; Leyton-Brown, K. Sequential Model-Based Optimization for General Algorithm Configuration. In Lecture Notes in Computer Science; Coello, C.A.C., Ed.; Learning and Intelligent Optimization, LION 2011; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6683. [Google Scholar] [CrossRef]
- Coley, C.W.; Eyke, N.S.; Jensen, K.F. Autonomous Discovery in the Chemical Sciences Part I: Progress. Angew. Chem. Int. Ed. Engl. 2020, 59, 22858–22893. [Google Scholar] [CrossRef] [PubMed]
- Lookman, T.; Balachandran, P.V.; Xue, D.; Yuan, R. Active learning in materials science with emphasis on adaptive sampling using uncertainties for targeted design. npj Comput. Mater. 2019, 5, 21. [Google Scholar] [CrossRef]
- Coley, C.W. Defining and Exploring Chemical Spaces. Trends Chem. 2021, 3, 133–145. [Google Scholar] [CrossRef]
- Jin, R.; Chen, W.; Sudjianto, A. An efficient algorithm for constructing optimal design of computer experiments. J. Stat. Plan. Inference 2005, 134, 268–287. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Wang, X.; Zhang, Z.; Zhao, J.; Yan, J.; Du, Y.; Zhang, H.; Ma, D. Complete CO Oxidation by O2 and H2O over Pt–CeO2−δ/MgO Following Langmuir–Hinshelwood and Mars–van Krevelen Mechanisms, Respectively. ACS Catal. 2021, 11, 11820–11830. [Google Scholar] [CrossRef]
- Matsubara, Y. Standard Electrode Potentials for the Reduction of CO2 to CO in Acetonitrile–Water Mixtures Determined Using a Generalized Method for Proton-Coupled Electron-Transfer Reactions. ACS Energy Lett. 2017, 2, 1886–1891. [Google Scholar] [CrossRef]
- Kumar, K.V.; Porkodi, K.; Rocha, F. Langmuir–Hinshelwood kinetics—A theoretical study. Catal. Commun. 2008, 9, 82–84. [Google Scholar] [CrossRef]
- Pholdee, N.; Bureerat, S. An efficient optimum Latin hypercube sampling technique based on sequencing optimisation using simulated annealing. Int. J. Syst. Sci. 2013, 46, 1780–1789. [Google Scholar] [CrossRef]
- Ayyub, B.M.; Lai, K.-L. Selective Sampling in Simulation-Based Reliability Assessment. Int. J. Press. Vessel. Pip. 1991, 46, 229–249. [Google Scholar] [CrossRef]
- Corona, P.; Franceschi, S.; Pisani, C.; Portoghesi, L.; Mattioli, W.; Fattorini, L. Inference on diversity from forest inventories: A review. Biodivers. Conserv. 2015, 26, 3037–3049. [Google Scholar] [CrossRef]
- Lee, J.-H.; Ko, Y.-D.; Yun, I.-G.; Han, K.-H. Comparison of Latin Hypercube Sampling and Simple Random Sampling Applied to Neural Network Modeling of HfO2 Thin Film Fabrication. Trans. Electr. Electron. Mater. 2006, 7, 210–214. [Google Scholar] [CrossRef]
- Belkin, M. Fit without fear: Remarkable mathematical phenomena of deep learning through the prism of interpolation. Mach. Learn. 2021, 30, 203–248. [Google Scholar] [CrossRef]
- Semenova, E.; Williams, D.P.; Afzal, A.M.; Lazic, S.E. A Bayesian neural network for toxicity prediction. Comput. Toxicol. 2020, 16, 100133. [Google Scholar] [CrossRef]
- Dawson, J.M.; Davis, T.A.; Gomez, E.L.; Schock, J. A self-supervised, physics-aware, Bayesian neural network architecture for modelling galaxy emission-line kinematics. Mon. Not. R. Astron. Soc. 2021, 503, 574–585. [Google Scholar] [CrossRef]
- Kingma, D.P.; Welling, M. Auto-Encoding Variational Bayes. arXiv 2013, arXiv:1312.6114. [Google Scholar]
- Häse, F.; Aldeghi, M.; Hickman, R.J.; Roch, L.M.; Aspuru-Guzik, A. Gryffin: An algorithm for Bayesian optimization of categorical variables informed by expert knowledge. Appl. Phys. Rev. 2021, 8, 48164. [Google Scholar] [CrossRef]
- Abdullah, H.; Khan, M.M.R.; Yaakob, Z.; Ismail, N.A. A kinetic model for the photocatalytic reduction of CO2 to methanol pathways. IOP Conf. Ser. Mater. Sci. Eng. 2019, 702, 012026. [Google Scholar] [CrossRef]
- Luong, G.K.T.; Ku, Y. Enhanced photocatalytic reduction of Cr(VI) in aqueous solution by UV/TiO2 process in the presence of Fe(III): Performance, kinetic, and mechanisms. Chem. Eng. Process. Process Intensif. 2022, 181, 109135. [Google Scholar] [CrossRef]
- Liu, T.; Yu, X.; Yin, H. Study of Top-down and Bottom-up Approaches by Using Design of Experiment (DoE) to Produce Meloxicam Nanocrystal Capsules. AAPS PharmSciTech 2020, 21, 79. [Google Scholar] [CrossRef] [PubMed]
- Vardhan, H.; Mittal, P.; Adena, S.K.; Mishra, B. Long-circulating polyhydroxybutyrate-co-hydroxyvalerate nanoparticles for tumor targeted docetaxel delivery: Formulation, optimization and in vitro characterization. Eur. J. Pharm. Sci. 2017, 99, 85–94. [Google Scholar] [CrossRef] [PubMed]
- Alkanad, K.; Hezam, A.; Al-Zaqri, N.; Bajiri, M.A.; Alnaggar, G.; Drmosh, Q.A.; Almukhlifi, H.A.; Neratur Krishnappagowda, L. One-Step Hydrothermal Synthesis of Anatase TiO2 Nanotubes for Efficient Photocatalytic CO2 Reduction. ACS Omega 2022, 7, 38686–38699. [Google Scholar] [CrossRef]
- Deng, H.; Zhu, X.; Chen, Z.; Zhao, k.; Cheng, G. Oxygen vacancy engineering of TiO2-x nanostructures for photocatalytic CO2 reduction. Carbon Lett. 2022, 32, 1671–1680. [Google Scholar] [CrossRef]


| Kinetic Model Name | Catalyst | Catalyst Shape | Reaction Time (h) | Photoreactor | Type of Light Source |
|---|---|---|---|---|---|
| Tan [2] | 5GO-OTiO2 | Yellowish solid powder, binary nanocomposites, hybrid heterostructures | 8 | Continuous gas flow reactor | Xenon arc lamp |
| Khalilzadeh [3] | 0.12%Fe-0.5%N/ TiO2 | Nanoparticles, crystal structure | 1 | Pyrex vessel and quartz tube | 70W mercury lamp |
| Thompson [5] | P25 TiO2 | Coating method, pure and cracks, similar coverage | 5 | Photo differential photoreactor | OmniCure S2000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Yang, X.; Zhang, C.; Zhang, Z.; Su, A.; She, Y.-B. Exploring Bayesian Optimization for Photocatalytic Reduction of CO2. Processes 2023, 11, 2614. https://doi.org/10.3390/pr11092614
Zhang Y, Yang X, Zhang C, Zhang Z, Su A, She Y-B. Exploring Bayesian Optimization for Photocatalytic Reduction of CO2. Processes. 2023; 11(9):2614. https://doi.org/10.3390/pr11092614
Chicago/Turabian StyleZhang, Yutao, Xilin Yang, Chengwei Zhang, Zhihui Zhang, An Su, and Yuan-Bin She. 2023. "Exploring Bayesian Optimization for Photocatalytic Reduction of CO2" Processes 11, no. 9: 2614. https://doi.org/10.3390/pr11092614
APA StyleZhang, Y., Yang, X., Zhang, C., Zhang, Z., Su, A., & She, Y.-B. (2023). Exploring Bayesian Optimization for Photocatalytic Reduction of CO2. Processes, 11(9), 2614. https://doi.org/10.3390/pr11092614







