Molecular Dynamics Calculation of the Coordination Behavior of Yb (III) in Sodium Carbonate Solution
Abstract
:1. Introduction
2. Methods and Materials
2.1. Raw Materials
2.2. Research Methods
2.2.1. Dissolution Experiments
2.2.2. MD and DFT Calculations
2.2.3. UV Test
3. Results and Discussion
3.1. Yb (III) Dissolution Law
3.2. Molecular Dynamic Calculations
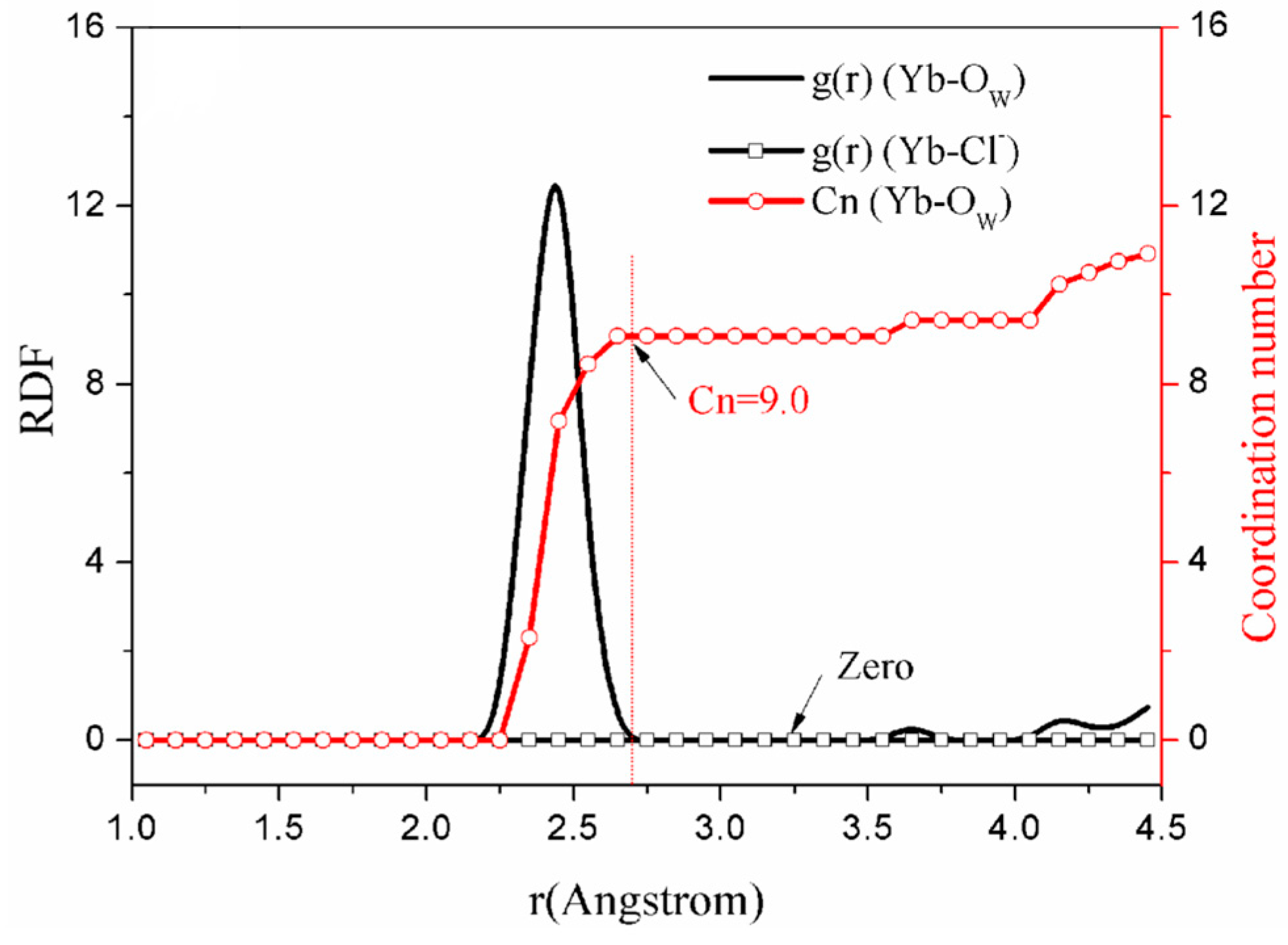
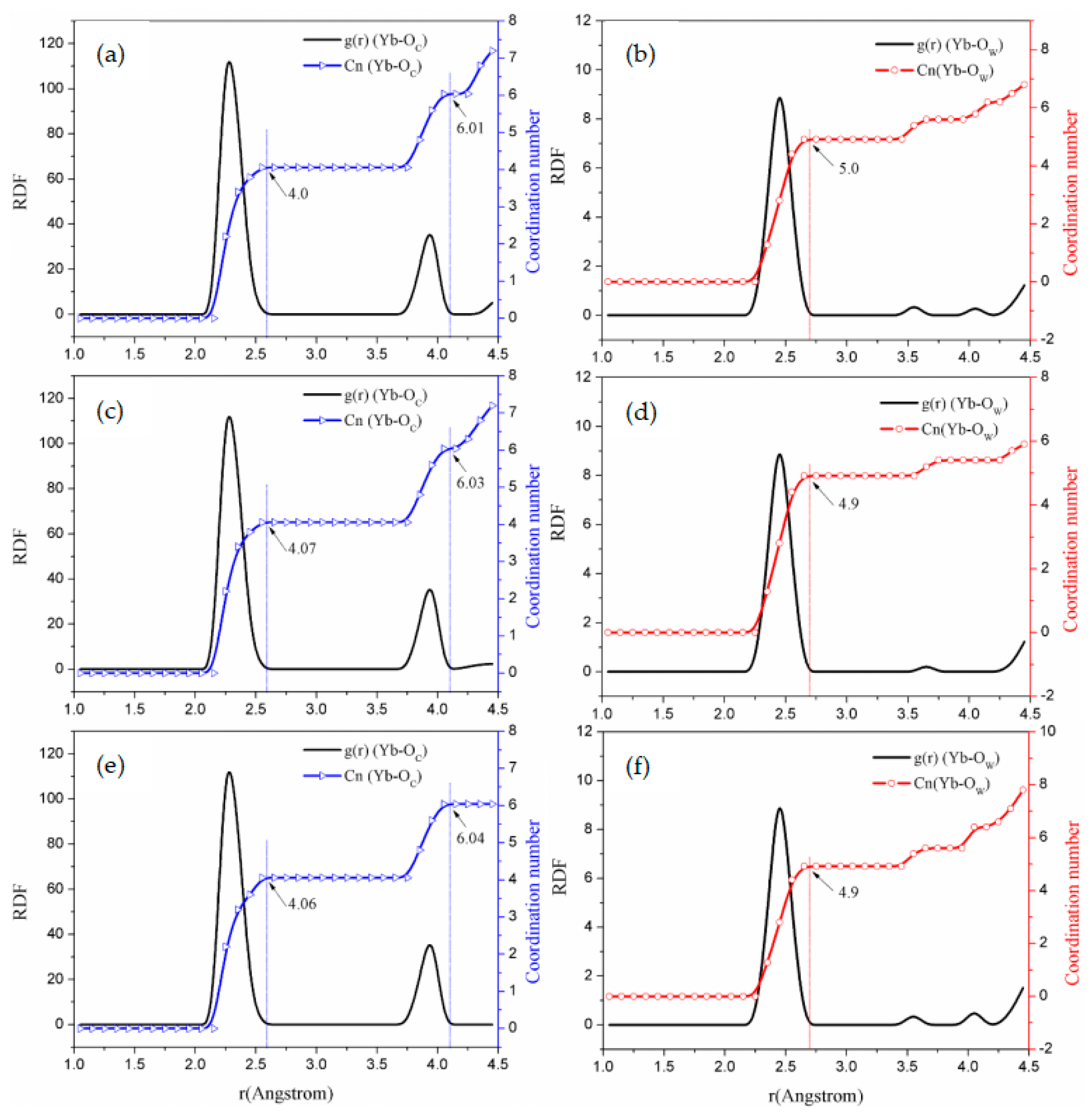
3.2.1. Radial Distribution Function and Coordination Behavior
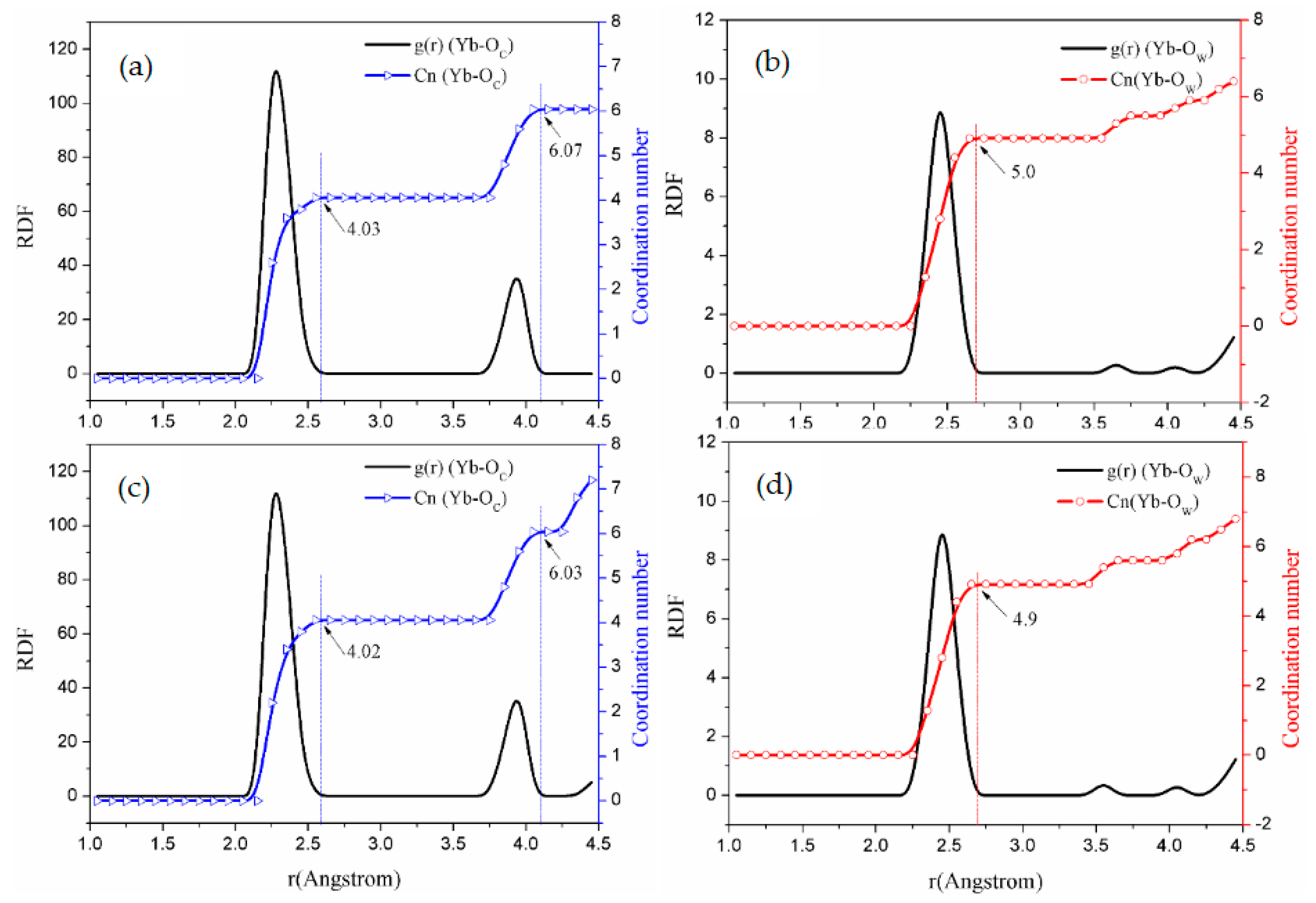
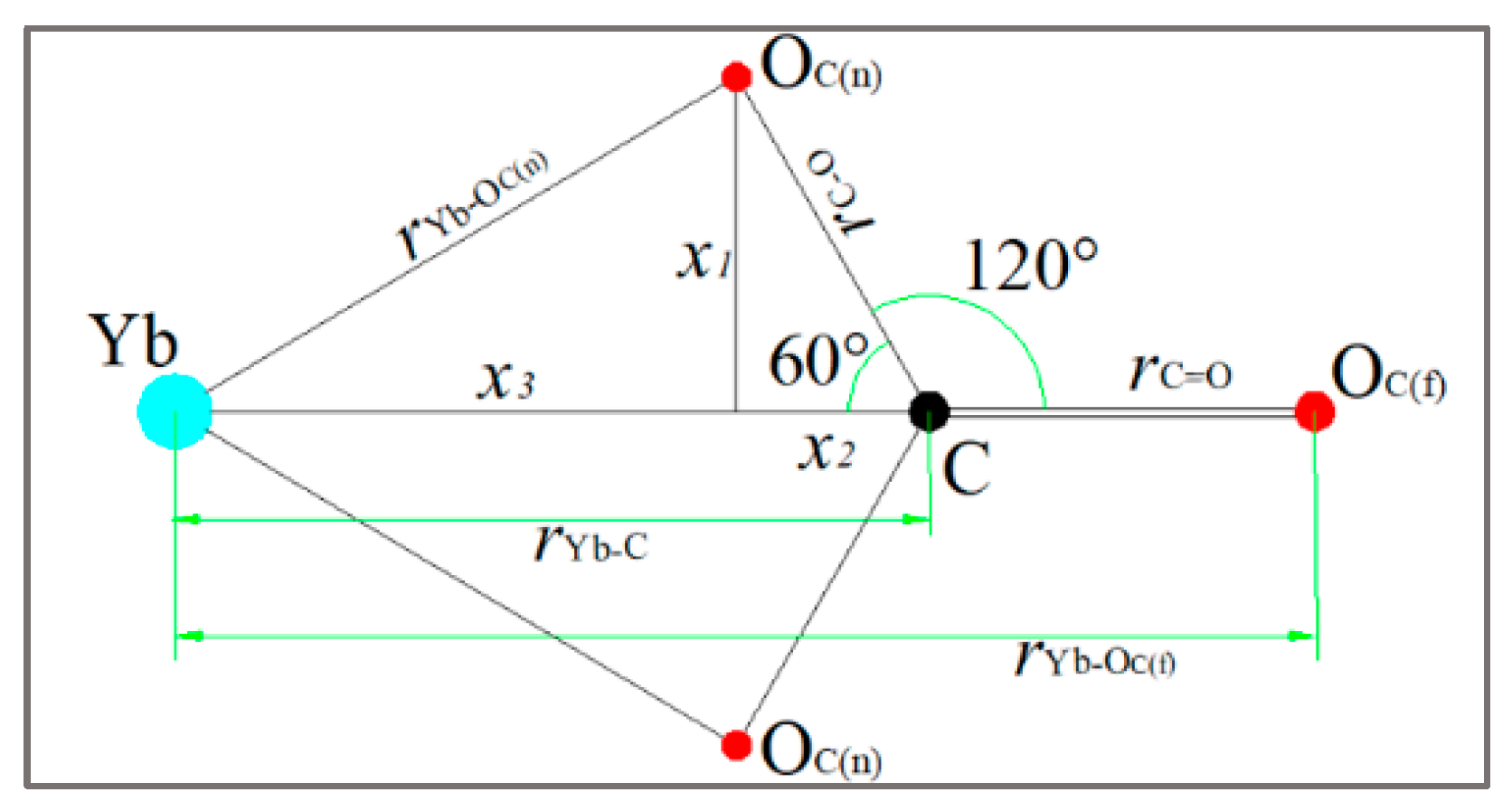
3.2.2. Coordinating Behavior
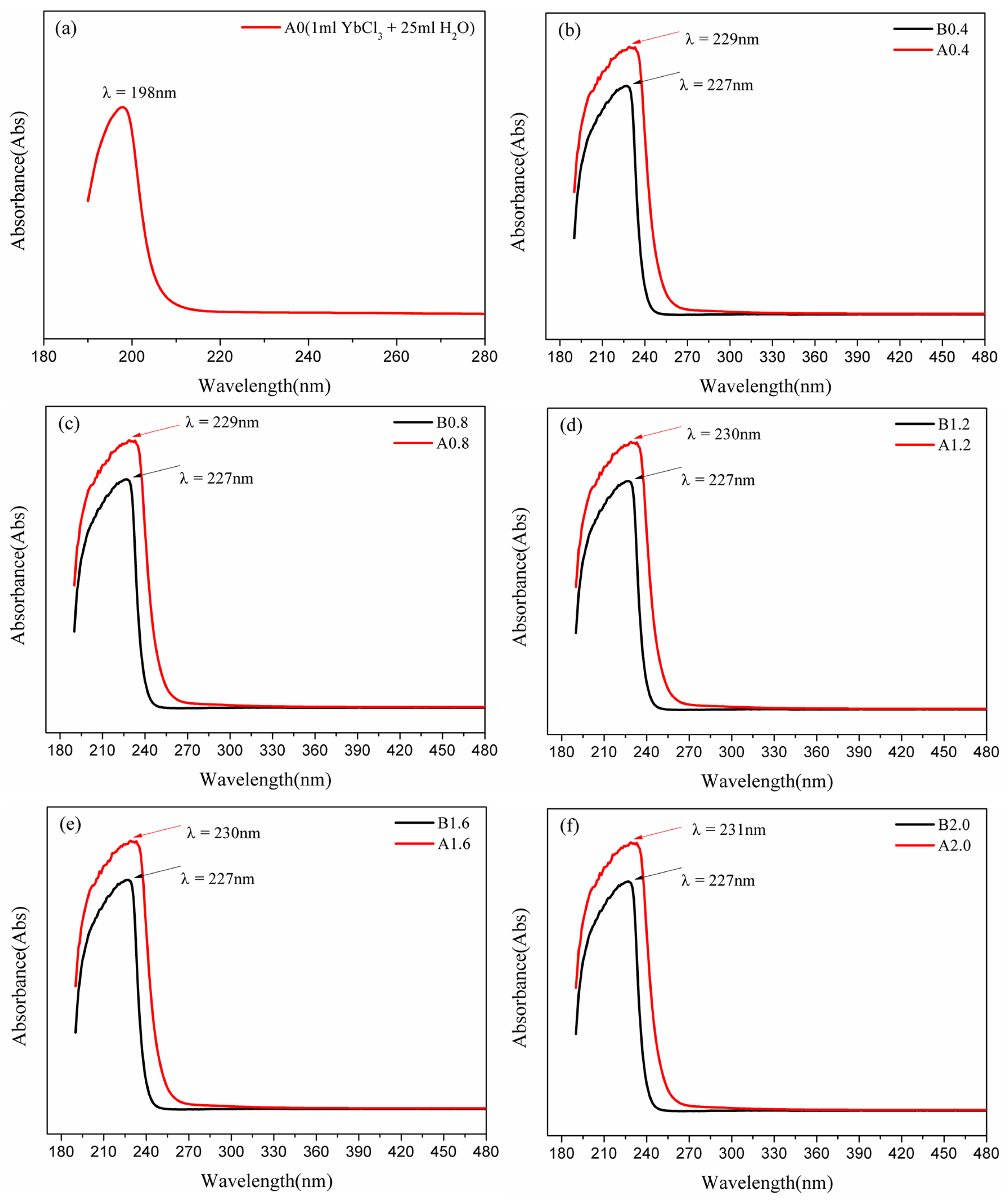
3.3. UV-Vis Spectrum
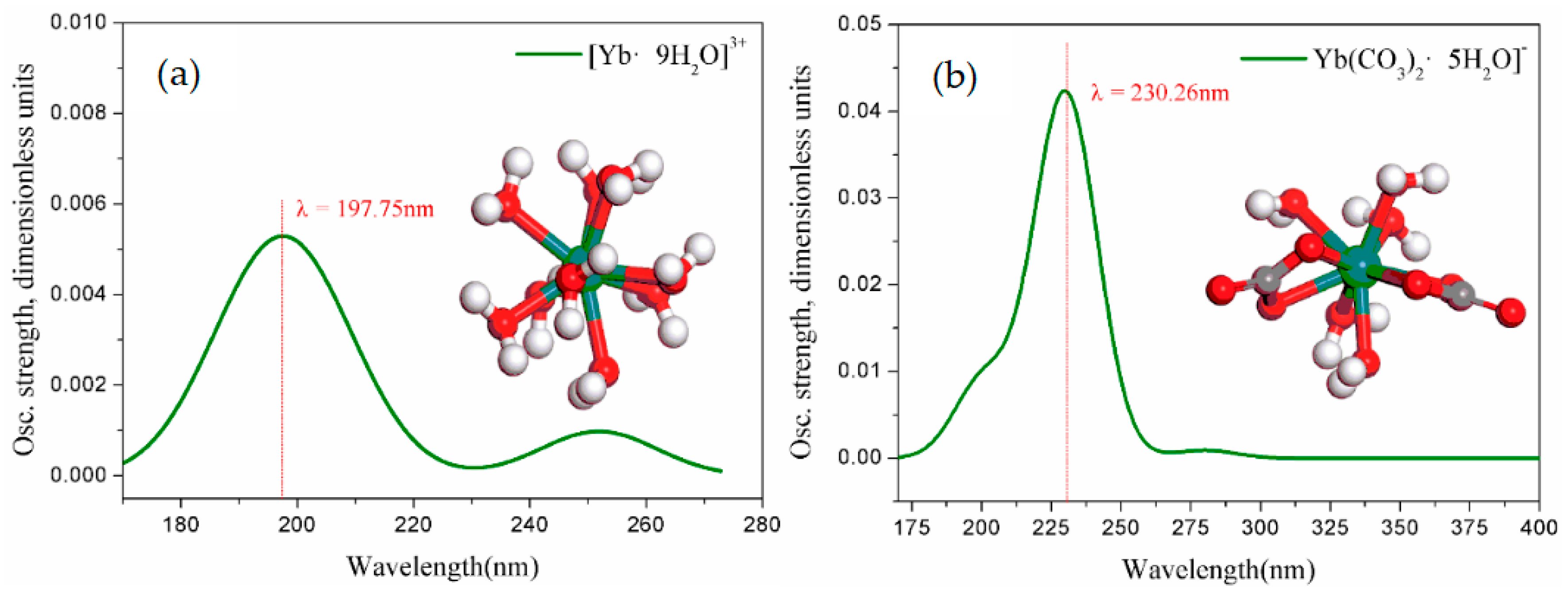
3.4. Structure and UV Spectrum of DFT Calculations
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Takagi, K.; Hirayama, Y.; Okada, S.; Yamaguchi, W.; Ozaki, K. Novel powder processing technologies for production of rare-earth permanent magnets. Sci. Technol. Adv. Mater. 2021, 22, 150–159. [Google Scholar] [CrossRef]
- Prokofev, P.A.; Kolchugina, N.B.; Skotnicova, K.; Burkhanov, G.S.; Kursa, M.; Zheleznyi, M.V.; Dormidontov, N.A.; Cegan, T.; Bakulina, A.S.; Koshkidko, Y.S.; et al. Blending Powder Process for Recycling Sintered Nd-Fe-B Magnets. Materials 2020, 13, 3049. [Google Scholar] [CrossRef]
- Nelson, J.J.M.; Schelter, E.J. Sustainable Inorganic Chemistry: Metal Separations for Recycling. Inorg. Chem. 2019, 58, 979–990. [Google Scholar] [CrossRef]
- Lixandru, A.; Venkatesan, P.; Jönsson, C.; Poenaru, I.; Hall, B.; Yang, Y.; Walton, A.; Güth, K.; Gauß, R.; Gutflfleisch, O. Identifification and recovery of rare-earth permanent magnets from waste electrical and electronic equipment. Waste Manag. 2017, 68, 482–489. [Google Scholar] [CrossRef]
- Kuz’Min, M.D.; Skokov, K.; Jian, H.; Radulov, I.; Gutflfleisch, O. Towards high-performance permanent magnets without rare earths. J. Phys. Condens. Matter 2014, 26, 64205. [Google Scholar] [CrossRef]
- Xiong, Y.; Kuang, W.; Zhao, J.; Liu, H.Z. Ionic liquid-based synergistic extraction of rare earths nitrates without diluent: Typical ion-association mechanism. Sep. Purif. Technol. 2017, 179, 349–356. [Google Scholar] [CrossRef]
- Jha, M.K.; Kumari, A.; Panda, R.; Kumar, J.R.; Yoo, K.; Lee, J.Y. Review on hydrometallurgical recovery of rare earth metals. Hydrometallurgy 2016, 165, 2–26. [Google Scholar] [CrossRef]
- Vogit, M.; Rodriguez-Blanco, J.D.; Vallina, B.; Benning, L.G.; Oelkers, E.H. An experimental study of hydroxyl bastnasite solubility in aqueous solutions at 25 °C. Chem. Geol. 2016, 430, 70–77. [Google Scholar] [CrossRef]
- Safarbali, R.; Yaftian, M.R.; Zamani, A. Solvent extraction-separation of La(III), Eu(III) and Er(III) ions from aqueous chloride medium using carbamoyl-carboxylic acid extractants. J. Rare Earths 2016, 1, 91–98. [Google Scholar] [CrossRef]
- Shen, X.L.; Xing, M.M.; Tian, Y.; Fu, Y.; Peng, Y.; Luo, X.X. Upconversion photoluminescence properties of SrY2O4: Er3+, Yb3+ under 1550 and 980 nm excitation. J. Rare Earths 2016, 34, 458–463. [Google Scholar] [CrossRef]
- Xiao, Y.F.; Long, Z.; Huang, X.W.; Feng, Z.Y.; Cui, D.L.; Wang, L.S. Study on non-saponification extraction process for rare earth separation. J. Rare Earths 2013, 31, 512–516. [Google Scholar] [CrossRef]
- Reiller, P.E.; Vercouter, T.; Duro, L.; Ekberg, C. Thermodynamic data provided through the Funmig project: Analyses and prospective. Appl. Geochem. 2012, 27, 414–426. [Google Scholar] [CrossRef]
- Jeanvoine, Y.; Miró, P.; Martelli, F.; Cramer, C.J.; Spezia, R. Electronic Structure and Bonding of Lanthanoid(III) Carbonates. Phys. Chem. Chem. Phys. 2012, 14, 14822–14831. [Google Scholar] [CrossRef]
- Thakur, P.; Xiong, Y.L.; Borkowski, M. An improved thermodynamic model for the complexation of trivalent actinides and lanthanide with oxalic acid valid to high ionic strength. Chem. Geol. 2015, 413, 7–17. [Google Scholar] [CrossRef]
- Philippini, V.; Vercouter, T.; Aupiais, J.; Topin, S.; Ambard, C.; Chaussé, A.; Vitorge, P. Evidence of different stoichiometries for the limiting carbonate complexes across the lanthanide(III) series: A capillary electrophoresis-mass spectrometry study. Electrophoresis 2008, 29, 2041–2050. [Google Scholar] [CrossRef]
- Philippini, V.; Vercouter, T.; Vitorge, P. Evidence of different stoichiometries for the limiting carbonate complexes across the lanthanide(III) series. J. Solut. Chem. 2010, 39, 747–769. [Google Scholar] [CrossRef]
- Migliorati, V.; Serva, A.; Sessa, F.; Lapi, A.; D’Angelo, P. Influence of Counterions on the hydration Structure of Lanthanide Ions in Dilute Aqueous Solutions. J. Phys. Chem. B 2018, 122, 2779–2791. [Google Scholar] [CrossRef]
- Vercouter, T.; Vitorge, P.; Trigoulet, N.; Giffaut, E.; Moulin, C. and the limiting carbonate complexes of other M3+f-elements in aqueous solutions: A solubility and TRLFS study. New J. Chem. 2005, 29, 544–553. [Google Scholar]
- Tang, J.; Johannesson, K.H. Rare earth elements adsorption onto carrizo sand: Influence of strong solution complexation. Chem. Geol. 2010, 279, 120–133. [Google Scholar] [CrossRef]
- Martelli, F.; Jeanvoine, Y.; Vercouter, T.; Beuchat, C.; Vuilleumier, R.; Spezia, R. Hydration properties of lanthanoid(III) carbonate complexes in liquid water determined by polarizable molecular dynamics simulations. Phys. Chem. Chem. Phys. 2014, 16, 3693–3705. [Google Scholar] [CrossRef]
- D’Angelo, P.; Spezia, R. Hydration of Lanthanoids(III) and Actinoids(III): An Experimental/Theoretical Saga. Chem. Eur. J. 2012, 18, 11162–11178. [Google Scholar] [CrossRef] [PubMed]
- Migliorati, V.; Serva, A.; Terenzio, F.M.; D’Angelo, P. Development of Lennard-Jones and Buckingham Potentials for Lanthanoid Ions in Water. Inorg. Chem. 2017, 56, 6214–6224. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.L.; Niu, F.; Liu, D.H.; Yang, S.M.; Yang, Y.M.; Tong, Z.F. Molecular Dynamics Simulations of Y(III) Coordination and Hydration Properties. RSC Adv. 2019, 9, 32085–32096. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Zhang, X.; Li, K.; Wang, L.; Niu, F.; Liu, D.; Meng, Y. Maintenance of the Metastable State and Induced Precipitation of Dissolved Neodymium (III) in an Na2CO3 Solution. Minerals 2021, 11, 952. [Google Scholar] [CrossRef]
- Tong, Z.F.; Xie, Y.B.; Zhang, Y.H. Molecular dynamics simulation on the interaction between polymer inhibitors and β-dicalcium silicate surface. J. Mol. Liq. 2018, 259, 65–75. [Google Scholar] [CrossRef]
- Cheng, Y.M.; Yang, Z.W.; Liao, J.Y.; Qiu, J.B.; Song, Z.G.; Yang, Y. Color tunable up conversion emission in CeO2: Yb, Er three-dimensional ordered microporous materials. J. Rare Earths 2015, 33, 599–603. [Google Scholar] [CrossRef]
- Yang, Y.M.; Zhang, X.L.; Li, L.; Wei, T.M.; Li, K.Z. Metastable Dissolution Regularity of Nd3+ in Na2CO3 Solution and Mechanism. ACS Omega 2019, 4, 9160–9168. [Google Scholar] [CrossRef]
- Cetin, A.; Ilk Capar, M.; Zakharov, A.V. Miscibility and diffusivity of water in organic acids: Molecular dynamics simulations. J. Mol. Liq. 2019, 294, 111630. [Google Scholar] [CrossRef]
- Saxena, A.; Sept, D. Multisite Ion Models That Improve Coordination and Free Energy Calculations in Models Dynamics Simulations. J. Chem. Theory Comput. 2013, 9, 3538–3542. [Google Scholar] [CrossRef]
- Chopra, M.; Choudhury, N. Adsorption of uranyl ions from its aqueous solution by functionalized carbon nanotubes: A molecular dynamics simulation study. J. Mol. Liq. 2019, 294, 111569. [Google Scholar] [CrossRef]
- Tomono, H.; Nada, H.; Zhu, F.; Sakamoto, T.; Nishimura, T.; Kato, T. Effects of Magnesium Ions and Water Molecules on the Structure of Amorphous Calcium Carbonate: A Molecular Dynamics Study. J. Phys. Chem. B 2013, 117, 14849–14856. [Google Scholar] [CrossRef] [PubMed]
- Wan, H.; Yi, P.; Qu, J.; Bu, X.; Yang, W.; Li, H. Adsorption Behaviors of Straight-Chain Alkanes on a Molybdenite [001]/[100] Surface: A Molecular Dynamics Study. Minerals 2021, 11, 489. [Google Scholar] [CrossRef]
- Ma, Y.M.; Gao, Y.; Yang, Y.; Li, W.Y.; Shi, P.; Wang, S.; Tang, W.W. Thermodynamic analysis and molecular dynamic simulation of the solubility of vortioxetine hydrobromide in three binary solvent mixtures. J. Mol. Liq. 2018, 272, 676–688. [Google Scholar] [CrossRef]
- Soumya, S.; Sheemol, V.N.; Amba, P.; Mohamed, A.P.; Ananthakumar, S. Sn and Ag Doped ZnO Quantum Dots with PMMA by in Situ Polymerization for UV/IR Protective, Photochromic Multifunctional Hybrid Coatings. Sol. Energy Mater. Sol. Cells 2018, 174, 554–565. [Google Scholar] [CrossRef]
- Zhang, H.Y.; Jiang, Y.; Yan, H.; Yin, C.; Tan, T.W.; Spoel, D.V. Free energy calculations of ionic hydration consistent with the experimental hydration free energy of the proton. J. Phys. Chem. Lett. 2017, 8, 2705–2715. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, C.; Niu, F.; Gao, S.; Dong, J. Molecular Dynamics Study on the Leaching of Zinc-Bearing Dust Sludge by Choline Chloride-Malonic Acid. Minerals 2021, 11, 1080. [Google Scholar] [CrossRef]
- Zhao, S.L.; Ma, Y.M.; Tang, W.W. Thermodynamic analysis and molecular dynamic simulation of solid-liquid phase equilibrium of griseofulvin in three binary solvent systems. J. Mol. Liq. 2019, 274, 111600. [Google Scholar] [CrossRef]
- Zhou, M.; Jiang, T.; Yang, S.T.; Xue, X.X. Sintering behaviors and consolidation mechanism of high-chromiun vanadium and titanium magnetite fines. Int. J. Miner. Metall. Mater. 2015, 22, 917–925. [Google Scholar] [CrossRef]
- Hu, G.Q.; Sun, Y.Q.; Xie, Y.X.; Wu, S.S.; Zhang, X.J.; Zhuang, J.L.; Hu, C.F.; Lei, B.F.; Liu, Y.L. Synthesis of Silicon Quantum Dots with Highly Efficient Full-Band UV Absorption and Their Applications in Antiyellowing and Resistance of Photodegradation. ACS Appl. Mater. Inter. 2019, 11, 6634–6643. [Google Scholar] [CrossRef]
- Hess, S.C.; Permatasari, F.A.; Fukazawa, H.; Schneider, E.M.; Balgis, R.; Ogi, T.; Okuyama, K.; Stark, W.J. Direct Synthesis of Carbon Quantum Dots in Aqueous Polymer Solution: One-Pot Reaction and Preparation of Transparent UV-Blocking Films. J. Mater. Chem. A 2017, 5, 5187–5194. [Google Scholar] [CrossRef]
- Johannesson, K.H.; Lyons, W.B. The rare earth element geochemistry of Mono Lake water and the important of carbonate complexing. Limnol. Oceanogr. 1994, 39, 1141–1154. [Google Scholar] [CrossRef]
- Serna-Carrizales, J.C.; Zárate-Guzmán, A.I.; Aguilar-Aguilar, A.; Forgionny, A.; Bailón-García, E.; Flórez, E.; Gómez-Durán, C.F.A.; Ocampo-Pérez, R. Optimization of Binary Adsorption of Metronidazole and Sulfamethoxazole in Aqueous Solution supported with DFT Calculations. Processes 2023, 11, 1009. [Google Scholar] [CrossRef]
- Yan, Y.N.; Xu, Y.; Hunang, X.W.; Feng, Z.Y.; Hou, Y.K.; Li, K.; Wang, L.S.; Hu, Y. Process optimization of neodymium chloride solutions precipitated by magnesium bicarbonate. J. Rare Earths 2019, 37, 437–442. [Google Scholar] [CrossRef]
- Lai, F.G.; Gao, G.H.; Huang, L.; Xiao, Y.F.; Yang, R.; Li, K.Z. Compound leaching of rare earth from the ion-adsorption type rare earth ore with magnesium sulfate and ascorbic acid. Hydrometallurgy 2018, 179, 25–35. [Google Scholar]
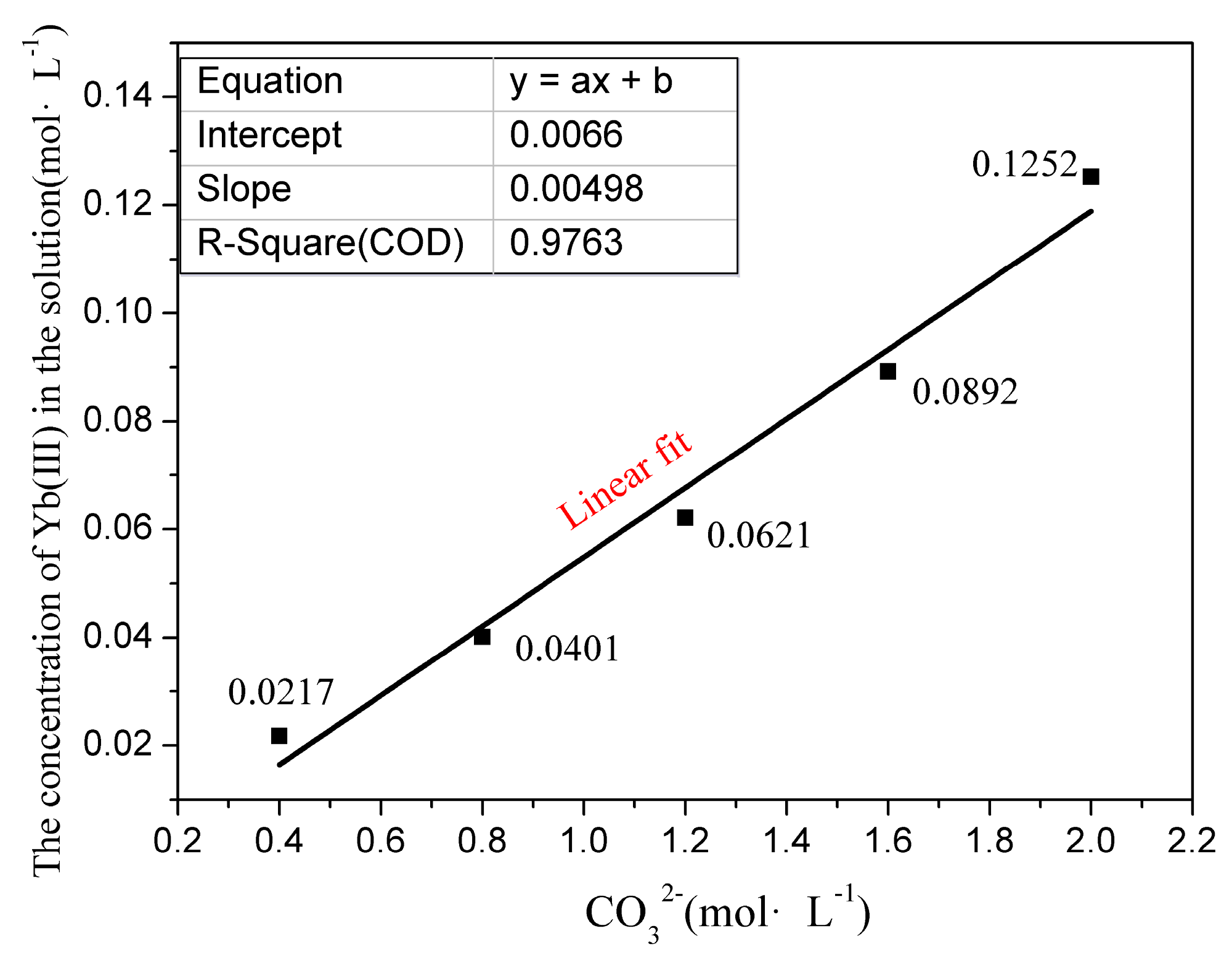
| Concentration of H+ (mol·L−1) | Specific Gravity (g·mL−1) | RE Impurities/REO (mg·L−1) | ||||||
|---|---|---|---|---|---|---|---|---|
| <0.10 | 1.0575 | |||||||
| <10 | <10 | <10 | <10 | <10 | <10 | <10 | ||
| <10 | <10 | <10 | <10 | <10 | <10 | <10 | ||
| Systems | Solutions | Terms | Number of Solution Particles | ||||
|---|---|---|---|---|---|---|---|
| a | - solution ρ: 1.012 g·, pH: 4.4 | Components | |||||
| Number | 5 | 15 | / | / | 4444 | ||
| Weight (%) | 0.5 | 0.7 | / | / | 98.8 | ||
| b | - solution 0.4 mol·L−1 ρ: 1.08 g·, pH: 12.35 | Components | |||||
| Number | 1 | 3 | 24 | 48 | 4388 | ||
| Weight (%) | 0.1 | 0.1 | 1.8 | 1.3 | 96.7 | ||
| c | - solution 0.8 mol·L−1 ρ: 1.098 g·, pH: 12.37 | Components | |||||
| Number | 2 | 6 | 48 | 96 | 4312 | ||
| Weight (%) | 0.2 | 0.3 | 3.5 | 2.7 | 93.3 | ||
| d | - solution 1.2 mol·L−1 ρ: 1.118 g·, pH: 12.40 | Components | |||||
| Number | 3 | 9 | 72 | 144 | 4236 | ||
| Weight (%) | 0.3 | 0.4 | 5.2 | 4.0 | 90.1 | ||
| e | - solution 1.6 mol·L−1 ρ: 1.138 g·, pH: 12.41 | Components | |||||
| Number | 4 | 12 | 96 | 192 | 4160 | ||
| Weight (%) | 0.4 | 0.5 | 6.8 | 5.2 | 87.1 | ||
| f | - solution 2.0 mol·L−1 ρ: 1.158 g·, pH: 12.41 | Components | |||||
| Number | 5 | 15 | 120 | 240 | 4084 | ||
| Weight (%) | 0.5 | 0.6 | 8.4 | 6.4 | 84.1 | ||
| Systems | (Å) | CnYb-O (r < 2.6 Å) | (Å) | CnYb-O (r < 4.0 Å) | (Å) | (1st Peak Valley) | |||
|---|---|---|---|---|---|---|---|---|---|
| a | / | / | / | / | / | / | / | 2.42 | 9.0 |
| b | 2.32 | 4.03 | 3.95 | 6.07 | 4.00 | 2.10 | 1.90 | 2.45 | 5.0 |
| c | 2.32 | 4.02 | 3.95 | 6.03 | 4.00 | 2.00 | 2.00 | 2.45 | 5.0 |
| d | 2.32 | 4.0 | 3.95 | 6.01 | 4.00 | 2.00 | 2.00 | 2.45 | 5.1 |
| e | 2.32 | 4.07 | 3.95 | 6.03 | 4.10 | 2.00 | 2.05 | 2.45 | 5.0 |
| f | 2.32 | 4.06 | 3.95 | 6.04 | 4.10 | 2.00 | 2.05 | 2.45 | 5.0 |
| Ions | Composition | (Å) | (Å) |
|---|---|---|---|
| a | / | 2.40 | |
| b | 2.32 | 2.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lan, Q.; Yang, Y.; Xie, Z.; Guo, H.; Liu, D.; Zhang, X. Molecular Dynamics Calculation of the Coordination Behavior of Yb (III) in Sodium Carbonate Solution. Processes 2023, 11, 2624. https://doi.org/10.3390/pr11092624
Lan Q, Yang Y, Xie Z, Guo H, Liu D, Zhang X. Molecular Dynamics Calculation of the Coordination Behavior of Yb (III) in Sodium Carbonate Solution. Processes. 2023; 11(9):2624. https://doi.org/10.3390/pr11092624
Chicago/Turabian StyleLan, Qiaofa, Youming Yang, Ziyu Xie, Haoran Guo, Donghui Liu, and Xiaolin Zhang. 2023. "Molecular Dynamics Calculation of the Coordination Behavior of Yb (III) in Sodium Carbonate Solution" Processes 11, no. 9: 2624. https://doi.org/10.3390/pr11092624
APA StyleLan, Q., Yang, Y., Xie, Z., Guo, H., Liu, D., & Zhang, X. (2023). Molecular Dynamics Calculation of the Coordination Behavior of Yb (III) in Sodium Carbonate Solution. Processes, 11(9), 2624. https://doi.org/10.3390/pr11092624








