Abstract
Paraxanthine (PX), a major metabolite of caffeine, a protective agent against Alzheimer’s and Parkinson’s disease, and a promising drug for the treatment of post-COVID 2019 anosmia and ageusia, has been studied in the solid state and protein–ligand complex. Partial disorder in PX, caused by the methyl group at the N(7) position, has been modelled and discussed. The relationship between the unusual structural disorder and the propensity to form a specific system of non-covalent bonds was analyzed. Three 1H-14N NMR-NQR (nuclear magnetic resonance–nuclear quadrupole resonance) experimental techniques were used, namely multiple frequency sweeps, Larmor frequency scanning, and the two-frequency irradiation, followed by solid-state computational modelling (density functional theory, supplemented by quantum theory of atoms in molecules, 3D Hirshfeld surfaces, and reduced density gradient), and molecular docking approaches. New quantitative methods for estimating changes in the global pattern of interactions under the influence of rotation of the methyl group in N(7) based on the Pompeiu–Hausdorff and Bhattacharayya metrics and the Wasserstein distance have been proposed and applied. A spectrum consisting of 12 lines, indicating the presence of 4 chemically inequivalent nitrogen sites in the PX molecule, was recorded, and the lines’ assignment to particular sites was made. The influence of the methyl rotation on the eigenvalues and eigenvectors of the electric field gradient tensor, NQR parameters, and resonance line positions was modelled in the solid (GGA/RPBE, m-GGA/RSCAN) and cluster (Minnesota M062X hybrid). Three factors have been found to determine structural disorder in PX: larger crystal voids near the methyl at N(7) than at N(1) (opening the path for the disorder), hyperconjugation strongly affecting the density distribution in the five-membered ring, and the involvement of the methyl group at N(7) in many non-covalent bonds that intercept (capture) subsequent jumping protons. The Pompeiu–Hausdorff and Bhattacharayya metrics and the Wasserstein distance confirmed the changes in the distribution and strength of non-covalent interactions throughout the molecule as a result of methyl rotation. This effect is clearly visible regardless of the type of metric, and its order of magnitude is consistent with the modulation effect of the NQR spectra (experimental and calculated). Through molecular docking, it was discovered that the PX moiety in protein–ligand complexes adopt the same methyl group conformation at N(7) as in the solid state. It was found that the cooperation–competition between the C-H⋯O hydrogen bonds and C-H⋯H-C dispersion interactions is the crucial factor that impedes methyl rotation and induces structural disorder, as well as being an important factor in the formation of the protein–ligand complexes.
1. Introduction
Methylxanthines are natural purine alkaloids found in beverages, dietary components, supplements, and pharmacologic agents (drugs and para-pharmaceuticals) that have important clinical applications [,]. One of them, paraxanthine (PX; 1,7-dimethylxanthine; 1,7-dimethyl-3H-purine-2,6-dione), Figure 1, is the major metabolite of caffeine (CF; 1,3,7-trimethylxanthine), namely 1,3,7-trimethyl-1H-purine-2,6-(3H,7H)-dione) [,].
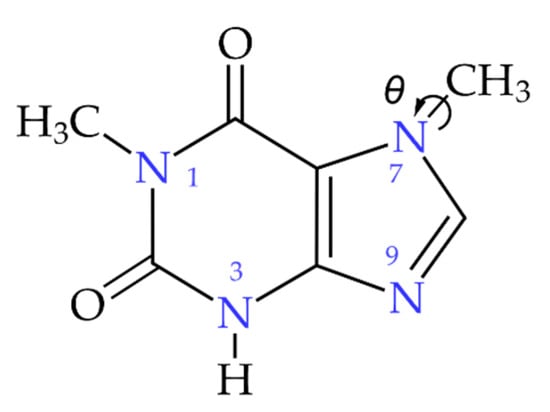
Figure 1.
Structural formula of paraxanthine (1,7-dimethylxanthine; 1,7-dimethyl-3H-purine-2,6-dione); the θ angle describes the disorder of the methyl group at the N(7) position of the heterocyclic ring: eclipsed (θ ≅ 0°; ABC) or staggered (θ ≅ 60°; DEF).
It is solely the result of demethylation of caffeine at position 3 by the catalytic action of cytochrome P450 subtypes 1A2 (90%) and 1A1, 2E1, 3A4, and 2D6 (10%) in liver parenchymal cells (hepatocytes) [,,,]. PX exists as a xenobiotic metabolite in all living organisms, from bacteria [] to mammals [], but no known plant or food contains PX because it is not accumulated (due to very slow N1-methylation of 7-methylxanthine) [].
It is believed that the contribution of PX to the pharmacological action attributed to CF is significant. Molecular mechanism of PX action is determined by its potent but nonselective antagonism to adenosine A1, A2A, and A2B receptors, which are involved in such processes as regulation of myocardial, oxygen consumption, and coronary blood flow, as well as in neurotransmitters, such as dopamine and glutamate, and in inflammation and immune responses []. Thus, it affects fundamental human processes, such as sleep, arousal, cognition, learning, and memory, and can stimulate the central nervous system, as well as the muscular, respiratory and circularity systems [,,,,,,,]. PX treatment may affect short-term memory, reasoning, response time to cognitive challenges, and help to sustain attention []. PX, unlike CF, is a potent dopaminergic and protects against neurodegeneration and loss of synaptic function []. PX, rather than CF, has recently been reported to reduce the risk of developing Alzheimer’s and Parkinson’s diseases [,,,]. It was approved by the FDA for the treatment of most reversible obstructive airway diseases (e.g., chronic bronchitis, emphysema, and asthma), but later relegated from the treatment of chronic obstructive pulmonary disease (COPD) due to an imbalance between benefits and side effects []. Unapproved by the FDA indications include sleep apnea and infant apnea cardiogenic pulmonary [], obesity reduction, and treatment of chronic fibrogenic or even carcinogenic liver disorders []. PX also attracts some interest in agriculture due to its significant allelopathic potential [,]. Recently, during the coronavirus pandemic, PX, which may act as an antagonist of adenosine receptors that modulate taste (A2B) and odor (A1, A2A), has gained interest as a promising drug in the treatment of anosmia (smell blindness) and ageusia (taste blindness), the most common post-COVID 2019 complications [,]. Given that anosmia is associated with an increased risk of depression, PX also seems to offer hope for its treatment [,].
Although PX has a very broad spectrum of activity and application area, only limited physicochemical data are available on this compound. It is much less studied than other methylxanthines [] and has not even been classified by the International Agency for Research on Cancer (IARC) []. Limiting factors are the lack of natural sources of PX, its fast metabolism, and the high cost of samples. Recently, we explained the role of hydrogen bonding and π⋯π stacking in the context of the disorder and solubility of CF polymorphs [] and its two minor metabolites, TB and TP []. Although PX, unlike CF, TB, and TP, is poorly soluble in water (only 1.0 for PX versus 2160, 330, and 7.36 mg/mL at 25 °C for CF, TB, and TP, respectively []), the anhydrous PX crystal was obtained and its structure has been resolved by X-ray diffraction with a final R-factor of 3.81% at 150 K and RT []. In contrast to CF, PX easily crystallizes in the anhydrous form, which was attributed exclusively to the formation of lateral hydrogen bonds []. CF exhibits typical disorder that arises in the cases when there are different, almost thermodynamically equivalent, variants of the molecule arrangement. Subtle changes in crystallization conditions or phase transitions cause CF molecules to rearrange from symmetrically disordered to totally ordered. However, disordered regions still may be present in the crystal, but do not diffract X-rays due to the effect of structural heterogeneity or dynamic motions. In the PX structure, only one methyl group (the one at N(7)) is disordered, and only at 293 K (at 100 K no disorder is detected); hence, the structural disorder is unique and refers to the multiple conformations of the substituents in the crystal lattice.
This paper attempts to explain the nature of this unusual structural disorder in relation to the propensity to form specific non-covalent bonds. Cooperation–competition of specific non-covalent long-range (electrostatic, inductive, dispersive, and attractive) and short-range (exchange and repulsion) interactions is crucial for the stabilization of solid phase structures. The interplay of various canonical interactions (hydrogen bonds, hydrophobic interactions) and a variety of non-canonical interactions (C–H⋯π, O–H⋯π, N–H⋯π, π⋯π stacking) play an important role in protein stability. So far, the intermolecular hydrogen bonds N–H⋯O have been considered in PX []. However, the presence of two kinds of strong acceptors (N, O) and the disorder associated with two methyl groups donating protons suggests that mainly electrostatic C–H⋯O and C–H⋯N hydrogen bonds (intra- or intermolecular) or homopolar C–H⋯H–C dihydrogen bonds governed by dispersion, may also occur and be of importance. Both intramolecular hydrogen bonds and dispersion interactions deliver the energetic contributions, the importance of which has been increasingly noticed in different compounds [,,,,]. The key question is what types of non-covalent bonds are actually formed in a disordered crystal structure of PX, how strong they are, and to what extent their individual binding capabilities facilitate or hinder order/disorder in the solid state or formation of the protein–ligand complex.
We applied a unique technique, 1H–14N NMR-NQR double resonance spectroscopy, which is highly sensitive to the changes in the local environment and more sensitive than NMR, IR, or powder X-ray diffraction (PXRD) []. Although NQR spectra, which are sensitive to all interactions modifying the electron density in the nearest vicinity of the nitrogen site, give some clues about the bonds involving nitrogen or their nature, they cannot provide a complete description of intermolecular interactions in the crystal lattice. However, in combination with the solid-state computational methods (Bader’s quantum theory of atoms in molecules [], QTAIM; Johnson’s reduced density gradient, RDS [], and Spackman’s Hirshfeld surfaces [,]), it has been discovered to be a valuable tool for this purpose [,,,]. A combination of the above techniques allows determination of a good quality structure, and, thus, a high-quality wavefunction, which is crucial to discover the role of non-covalent bonds in the disorder of methyl groups. New quantitative methods for estimating changes in the global pattern of interactions under the influence of rotation of the methyl group in N(7) based on the Pompeiu–Hausdorff and Bhattacharayya metrics and the Wasserstein distance have been proposed and applied. This approach is beneficial for evaluating the sources of partial crystal disorder. The specific binding mode, critical to biological activity, can be strengthened or disrupted by the disorder, affecting certain physicochemical properties, such as polymorphism, solubility, and stability. Structurally disordered regions play an important role in protein–protein and protein–ligand interactions, facilitating their mutual matching. It has been shown that a comprehensive study of the interaction pattern in disordered structures can be a predictor of the capability of individual conformers to bind to the target.
In view of the above, we hope that our research will be beneficial in the areas related to drug development.
2. Materials and Methods
2.1. Material
All material was purchased from Sigma-Aldrich, Poznań, Poland, PL, unless otherwise stated. The quality control of raw material was performed by FT IR. The purity of the powdered sample was confirmed to be above 98%, higher than the ACS grade. The PX sample was not subjected to prior recrystallization or any additional purification. The powdered sample was degassed and sealed in a glass ampoule.
2.2. Methods
Experimental Nuclear Quadrupole Resonance (NQR)
Measurements were performed at room temperature (295 K). We used two different techniques, namely multiple frequency sweeps and Larmor frequency scanning, to determine the lowest 14N NQR frequencies ν0 at all nitrogen positions in the molecule and to locate the 14N NQR frequencies ν+ and ν−. The two-frequency irradiation technique was finally used to increase the resolution of determination of the NQR frequencies ν+ and ν− to about ±5 kHz. A complete description of the basics of these techniques can be found in our previous papers.
2.3. Computational Density Functional Theory
2.3.1. Spectra Simulation—Cluster Technique
The quantum chemical calculations required for the QTAIM analysis were carried out within the density functional theory (DFT) approach rooted in the Kohn–Sham [] theorem, generalized by Levy []. This approach is an attractive compromise, providing useful accuracy and favorable algorithmic complexity. The Minnesota M062X hybrid meta, a high-nonlocality exchange–correlation functional with a double amount of nonlocal exchange (2X) [], and an all electron split-valence basis set 6-311 + G(d,p), were used for the single molecule and cluster calculations. M062X, which has a 54% HF exchange, gives high values for the systems with non-covalent forces, which is one of the fundamental disadvantages of classical DFT approaches. X-ray crystallography at the usual resolution often fails to directly access the positions of light atoms; thus, the proton positions were corrected (optimized). A complete description of the basics of the cluster technique can be found in our previous papers [,,]. The calculations were performed using a Gaussian 16 rev. C01 [].
2.3.2. Spectra Simulation—Solid-State Technique
Different generalized gradient approximations (GGA) functionals, which depend on both ρ and dρ/dr, were used. They provide an increase in accuracy, but often with an additional computational cost. The GGA functionals, namely RPBE (revised Perdew, Burke, and Ernzerhof) [], PBE (Perdew, Burke, and Ernzerhof) [], WC (Wu and Cohen) [], PBEsol (Perdew et al.) [], PW91 (Perdew et al.) [], were probed. The addition of the Tkatchenko–Scheffler [] (DFT-TS) correction for dispersion to some GGA functionals was found to be useful. Additionally, the usefulness of the modern semi-local density functional, which satisfies all known constraints that an exact density functional must meet, namely m-GGA rSCAN (Sun, Ruzsinsky, and Perdew [,], revised by Bartok and Yates) [] was checked. The gauge including projector-augmented waves (GI)PAW exploiting the full translational symmetry of a crystal and on-the-fly generation ultrasoft (OTFG) potentials were used.
The principal components of a second-rank symmetric electric field gradient (EFG) tensor, (i = x, y and z; V(r)—external electrostatic potential, satisfying the relationship ), were obtained after diagonalization of the following tensor, calculated at the selected level of theory:
where ρ(r) is the electron density, ri is the projection of the vector onto the x, y, and z axes, and δij is Dirac’s delta function. The EFG tensor consists of six independent components in the principal axis system. It is fully described by the three principal components and three eigenvectors, which describe the orientation of the principal axes with respect to an arbitrary frame. The tensor is traceless; therefore, only two eigenvalues are mutually independent. For this reason, two parameters are sufficient to describe the EFG tensor, namely the quadrupole coupling constant e2qQ/h and the asymmetry parameter η. The 14N NQR frequencies, which are observable, are related to these parameters as follows:
The 14N NQR resonance frequencies can be derived from these parameters using the following set of equations:
which are useful in the case of theoretical calculations. The nuclear quadrupole moment of 14N equal to 2.044 fm2 [] was assumed.
The components of the electric field gradient (EFG) tensor are highly sensitive to the structure quality, including the positions of hydrogen atoms []. Therefore, the PX structure was partially and fully optimized. Full optimization was performed upon the assumption of a fixed unit cell.
2.4. Analysis of the Topology of Interactions—Quantum Theory of Atoms in Molecules
Theoretical analysis of the topology of intermolecular interactions was performed within Bader’s quantum theory of atoms in molecules (QTAIM) []. The DFT wavefunction calculated using the Minnesota M062X hybrid functional and an all electron 6-311 + G(d,p) basis set was used. The differentiation of the nucleus, bond-, ring-, and cage-critical points, denoted as NAP (nuclear critical point; local maximum of the electron density with all curvatures negative), BCP (bond-critical point; saddle point local maximum of the electron density with two curvatures negative), RCP ring-critical point; saddle point local minimum of the electron density with two curvatures positive), and CCP (cage-critical point; local minimum of the electron density with all curvatures positive) was based on analysis of the stationary points. The so-called topological descriptors, including the electron density at BCP, ρ(rBCP), three eigenvalues of the principal components of Hessian matrix, namely λ1, λ2, and λ3, electron density at the bond critical point, BCP, ρBCP(r), its Laplacian, ΔρBCP(r), the potential electron energy density, VBCP(r), the kinetic electron energy density, GBCP(r), and the total electron energy density, HBCP(r), were calculated at each BCPs. The λ2 and Δρ descriptors provide information about the nature of the interactions. Four other descriptors (λ3, VBCP(r), GBCP(r), and HBCP(r)) allow a bond strength estimation. In general, the hydrogen bond energy can be estimated using the well-known formulas derived using partitioning of the electron density scheme [] proposed by Espinosa−Molins−Lecomte [], as follows:
and by Matta [], as follows:
and by Emamian (for neutral complexes) [], as follows:
and by Afonin [], as follows:
and by Nikolaienko [], as follows:
However, these formulas must be treated attentively because the results can be over-or under-interpreted in the case of intramolecular hydrogen bonds.
The reduced electron density gradient (RDG) is derived from QTAIM parameters and defined as follows:
where ∇ρ(r) is the electron density gradient and ρ(r) is electron density; Equation (12) helps to detect interactions that were uncertain or not revealed by QTAIM []. The plot of RDG(r) versus the electron density multiplied by the sign of the λ2 Hessian eigenvalue, sign(λ2)ρ(r), reveals characteristic spikes in the low-gradient and low-density regions as long as the non-covalent contacts are present in the crystalline structure. The spikes not reaching RDG(r) indicate interactions missed by QTAIM due to failure to detect critical points. The nature of non-covalent interactions can be inferred from the sign of λ2. Depending on its value, they are classified as attractive (stabilizing; λ2 < 0) or repulsive (destabilizing; λ2 > 0). A spike in the low-gradient, low-density region at λ2 < 0 suggests a stabilizing interactions, such as a hydrogen bonding; a smaller spike accompanied with only slightly negative λ2 indicates a weakly stabilizing interaction and a spike associated with λ2 > 0 indicates the absence of non-covalent interactions. The results of the RDG analysis were visualized using VMD [].
2.5. Exploration of Intermolecular Interaction Patterns—3D Hirshfeld Surface Analysis
Exploration of intermolecular interaction patterns and packing capacities in the solid was performed within the 3D Hirshfeld surfaces (3D HS) approach []. 3D HS is defined as the outer contour of a space, in which a molecule occupies in a crystalline environment. This surface was constructed using the so-called molecular weight function (a quotient of the promolecule and procrystal electron density). Three types of descriptors were evaluated, namely dnorm, shape index, and curvedness of the surface []. Intermolecular interactions were visualized on the dnorm surface mapped to the 3D HS in a red–white–blue scheme (red was used for short contacts, white for contacts of about van der Waals radii, and blue for the remaining ones). The flatness of the 3D HS was described using the shape index and curvedness of the surface mapped over the 3D HS being described. The decomposition of the 3D HS into a 2D ‘molecular fingerprint’ (2D FP) map [] was carried out. The 2D FP (plot of the distances of each surface point to the nearby interior and exterior atoms di versus de) summarizes the distribution of interactions of the molecule with its environment. The enrichment ratio, EXY, a descriptor which is defined as the ratio of the proportion of the actual contacts in a crystal and the theoretical proportion of random contacts [] was calculated based on 2D FP. It describes each atom’s propensity to form or avoid contact.
2.6. Comparison of the Differences in Interactions Patterns Due to the Methyl Group Rotation—Mathematical Metrics
A comparison of the differences/similarity between of the intermolecular interactions pattern due to the methyl group rotation was performed using a few metrics defined as follows:
- Pompeiu–Hausdorff metrics [], which measures how far two subsets of a metric space are from each other, as in the following Equation (13):where d can be calculated as the Manhattan distance, as follows:or as the Euclidian distance, as follows:
- The Bhattacharayya coefficient [], which is a distance between two probability distributions, as follows:
- The Wasserstein distance (Kantorovich–Rubinstein metric) [], which is a function defined between probability distributions on a given metric space, as follows:where sup represents the supremum, inf represents the infimum, pi, qi are interactions in each structure, and dist are permutations of all pi, qi , and sum runs overall.
We previously successfully used the Manhattan and Euclidian metrics and Bhattacharayya distance to compare interaction patterns across polymorphic forms [].
2.7. Exploration of Binding—Molecular Docking
Molecular docking (MD) is a widely used technique in screening of novel therapeutic agents. This technique requires both the knowledge of the ligand structure and a reliable 3D X-ray crystal structure of protein. The MGLTools software (ver 1.5.7) was used to convert the files with these structures to the .pdbqt format. MD was performed using AutoDock [] and AutoDock Vina98Vina []. Two techniques were used to dock a template docking and docking with defined searched space around the active site. The score function being a linear combination of different terms (steric, van der Waals, hydrogen bonding, electrostatic, torsion and sp2-sp2) was used. Based on the scoring function’s estimation of the protein–ligand binding energy, the optimum pose was chosen. The approach for docking the ligands in the protein pocket was identical to that described earlier []. Exploration of protein–ligand hydrophobic interactions was performed using LigPlot+ [,].
3. Results and Discussion
3.1. 1H-14N NQDR Spectrum
As the first technique for the location of 14N NQR frequencies, we used multiple frequency sweeps [] and Larmor frequency scanning []. The proton polarization period was set to 30 s and the relaxation period was set to 0.5 s. We used linear frequency sweeps with the frequency limits of 1.6 MHz and 3.5 MHz. The duration of a single sweep was set to 10 ms. The average amplitude of the rf magnetic field during the sweep was approximately equal to 2 mT. The proton Larmor frequency scan was performed in steps of 10 kHz. At each value of the proton Larmor frequency, we took four measurements and made an average of the four proton NMR signals. The measurements were performed at room temperature (295 K).
Using this technique, we observed a broad dip in the frequency range between 220 kHz and 270 kHz and two narrower dips centered at 530 kHz and 730 kHz. The dips are shown in Figure 2 as the low-frequency part of the 14N NQR spectrum of PX. Since there are four nitrogen positions in a PX molecule, the broad dip represents an overlap of two dips.
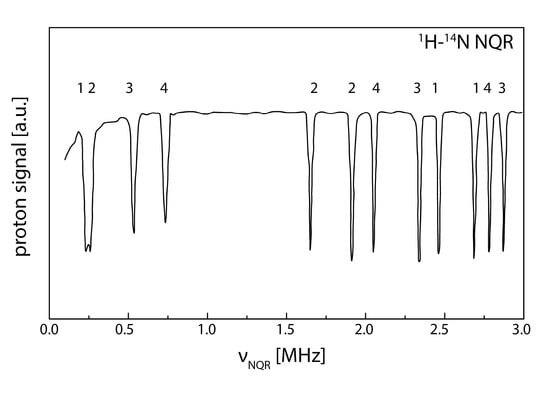
Figure 2.
The experimentally determined 14N NQR spectrum in paraxanthine (indexes 1,2,3,4 for individual nitrogen atoms see Table 1).
In the next step, we located the higher 14N NQR frequencies ν+ and ν− by varying the frequency limits of the sweeps. First, we set the proton Larmor frequency to 220 kHz and, by varying the upper frequency limit, we observed a step in the proton NMR signal at a frequency of 2.690 MHz. By varying the lower frequency limit, we observed a step at a frequency of 2.460 MHz, so the three 14N NQR frequencies corresponding to this nitrogen position, which we label as N(1), are approximately equal to 2.690 MHz, 2.460 MHz, and 230 kHz, respectively. Then, we fixed the proton Larmor frequency at 270 kHz and repeated the measurement. We observed the steps in the proton NMR signal at the frequencies 1.910 MHz and 1.650 MHz, so the three 14N NQR frequencies from this nitrogen position, which we label as N(2), are approximately equal to 1.910 MHz, 1.650 MHz, and 260 kHz. At the third nitrogen position, N(3), the 14N NQR frequencies were located at 2.870 MHz, 2.340 MHz, and 530 kHz, whereas at the fourth nitrogen position, N(4), they were located at 2.780 MHz, 2.050 MHz, and 730 kHz.
In order to increase the resolution to about ±5 kHz, we used the two-frequency irradiation technique as the final step []. The two rf magnetic fields were applied as a series of repetitive pulses with a pulse length of 1 ms. The amplitudes of the two rf magnetic fields were set to 0.2 mT. The experimentally determined 14N NQR spectrum is shown in Figure 2, and the frequencies e2qQ/h and η, calculated using Equation (3), are listed in Table 1.

Table 1.
14N NQR frequencies, quadrupole coupling constants e2qQ/h, and the asymmetry parameters η in paraxanthine at T = 295 K.
Figure 2 is in fact a merge of five double resonance spectra, with the spectrum below 800 kHz obtained by multiple frequency sweeps and proton Larmor frequency scanning, and the other four spectra obtained by the two-frequency irradiation technique. The low-frequency dips are broader than the high-frequency ones, which is a result of the idiosyncrasy of the techniques used. The width of the low-frequency dip is mainly determined by the proton NMR linewidth, whereas the width of the high-frequency dip is determined by magnetic field broadening of the 14N NQR line and by the inhomogeneity of the low magnetic field.
The spectrum of PX, as in Figure 2, similarly to that of TP [], is “clean”, i.e., the lines are not anomalously broadened, with a similar full width at half maximum (FWHM), which suggests no evidence of structural disorder. The lack of multiplicity suggests the presence of equivalent molecules per unit cell, which is in good agreement with the X-ray data []. The electronic environment of all four nitrogen nuclei in the PX molecule is different, so they are chemically inequivalent. All four nitrogen sites have distinctly different e2Qq/h and η values, although two of them, N(1) and N(7), are equally substituted with an electron donating and hyperconjugative methyl group, whose σ-bond is delocalized toward the adjacent π orbital, but N(1) and N(7) belong to different heterocyclic rings, six- and five-membered, respectively. The five-membered ring is more strained, which affects the values of the components of the EFG tensor and the orientation of its principal axes. In addition, the methyl group at N(1) is located between two oxygen atom species, whose lone pairs are adjacent to the π system. The oxygen atom exerts an electron-withdrawing (inductive) effect, but its lone pairs cause an electron-donating effect (resonance effect), which is the opposite and much stronger. Thus, N(1) should be electron-rich compared to N(7), and its η should be smaller. Other clues to help assign the resonance lines come directly from a comparison of NQR parameters with those previously obtained for TB or TP [,]. Based on these data, it seems that the two sets of resonance lines yielding the lowest η should be assigned to the sites N(1) and N(7), while the other two should be assigned to the remaining N(3) and N(9) ones, but it is by no means certain. Several overlapping factors, in addition to simple substituent effects, such as the poorly differentiated environment of quadrupolar sites (especially methyl ones), their high sensitivity to proton positions, and the disorder of protons in the methyl group at N(7), make it difficult to reliably assign the signals to nitrogen sites in PX. The quantitative analysis of NQR parameters in solid systems may be further complicated by influences from the surroundings, including various non-covalent bonds, which disturb the bonding situation of the nitrogen atoms.
As a result, an unambiguous assignment of nitrogen signals based solely on the NQR spectra is not possible. The simulation of the 14N NQR spectra of the other heterocyclic compounds has revealed that NQR parameters were extremely sensitive, even to the influence of distant nitrogen atoms [,]. Therefore, we performed quantum chemistry calculations in two variants (cluster and solid-state). They make it possible to take into account the effects of substituents, hybridization, and intermolecular interactions, including those that are distant, when modeling NQR spectra. Both strategies require a consistent, high-quality crystalline structure as the input. The Cambridge Structural Database (CSD) contains only two PX crystalline structures. While the low-temperature structure of PX (CCDC FIDSAN []) is fully ordered, in the RT structure (CCDC FIDSAN1 []) the methyl group substituted at N(7) equally occupied two orientations. These orientations, named ABC and DEF, differ by an angle of 60° (which corresponds to the torsion angle 120°), Figure 1. Rotational disorder, per se, is not surprising, since the disorder was observed in CF [,], and the classic Arrhenius-type rotation of methyl groups is expected near RT.
Therefore, various models have been proposed to study and describe the structural disorder that can affect the assignment of lines in the resonance spectrum. In the first model, a low-temperature ordered structure (with X-ray protons, with optimized protons, and a fully optimized structure with a fixed unit cell) was used as the input for the calculations. Since in the classical, Arrhenius type of methyl group rotation, the classical jumps of methyl groups at low temperatures are considered to be frozen, this model with a good approximation describes a completely ordered system and can be treated as the so-called reference point (corresponding to a rigid structure). Then, a simple model of disorder (the so-called direct disorder), assuming a disordered PX structure at RT, with proton occupation determined directly from X-ray data, was analyzed. This structure was probed in three variants (with X-ray protons, with protons optimized, and a fully optimized structure with a fixed unit cell). Finally, the averaging model, that assumes the average of the two substructures RT ABC and RT DEF retracted from disordered structure at RT and differing only in the conformation of the methyl group at N(7), was proposed. The calculations were performed for this model in three variants (with X-ray protons, with protons optimized, and a fully optimized structure with a fixed unit cell). The results are listed in Table 2, Tables S1 and S2, and visualized in Figure 3 and Figure S1.

Table 2.
The 14N NQR parameters for paraxanthine calculated theoretically at the GGA/RPBE level with TS DFT-D correction.
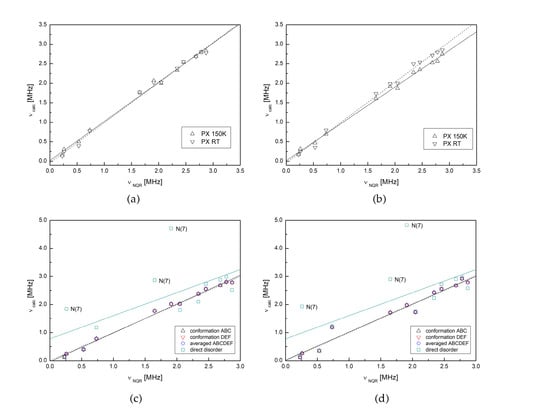
Figure 3.
The correlation between the experimental and calculated at the GGA level NQR frequencies for paraxanthine. (a) GGA/RPBE—ordered structure; (b) m-GGA/rSCAN—ordered structure; proton positions optimized at the same level of theory; (c) GGA/RPBE—disordered structure; (d) m-GGA/rSCAN—disordered structure.
The assumption of the low-temperature (150 K) PX structure and the crystallographic proton positions resulted in a significant overestimation of η for >N(3)H and unreliable set of the resonance lines, which suggests that its proton is involved in a strong hydrogen bond and shifted towards the acceptor (=O). This unsatisfactory result was found to be independent of the choice of the functional or basis set. Full optimization of the geometry, with a fixed unit cell allowed us to obtain NQR parameters that were quite well correlated with the experimental ones (high Pearson’s coefficient and small standard deviation) and underestimated by only about 4%. Unfortunately, such a procedure requires costly and time-consuming calculations, regardless of the level of theory. Moreover, the conformation of the methyl groups after optimization is far from the original one.
Calculations performed at the theoretical level of GGA/RBPE, assuming a low-temperature structure and proton positions optimized at the same level, allow reasonable NQR parameters to be obtained at a relatively low computational cost. The Pearson correlation coefficient is high, the dispersion is low and the NQR frequencies obtained from these parameters are reproduced very well. The modern m-GGA/RSCAN functional, which is much more computationally demanding, produces results similarly well correlated with experimental data, but the NQR parameters are reproduced with slightly lower accuracy. The use of the other GGA functionals (e.g., BLYP, WC, PBSOL, PW91, M11L, M06) gave the same signal assignments, although their use results in a set of frequencies less consistent with the experimental ones (the discrepancy concerns mainly nitrogen >N(3)H and, to a lesser extent, -N(9)=).
An attempt to model disorder defined directly i.e., by assigning it to particular protons based on the X-ray data (RT direct disorder), failed. The electron densities at both nitrogen atoms, N(7) and, to a much lesser extent, N(1), are poorly reproduced using this model and have led to the unreliable EFG tensor components and resonance frequencies, as in Table 2 and Figure S1c,d. It is, therefore, obvious that the wavefunction obtained by this method cannot be used for further analysis of the non-covalent interactions.
On the contrary, the model that averages two structures RT ABC and RT DEF (named as RT ABCDEF averaged) is quite reliable, as seen in Table 2 and Figure S1a,b. Both structures, RT ABC and RT DEF, differ in the conformation of the methyl group at N(7), as in Figure 1, in which only in the RT DEF structure is close to the low-temperature one. The underestimation of e2Qq/h and overestimation of η only for the >N(3)H site suggests its participation in the strong hydrogen bond N–H⋯O and, consequently, the shift in the proton from nitrogen towards the acceptor (=O). In the PX structure, the N–H⋯O bonds do not occur singly, but in pairs i.e., two N(3)H⋯O(2) hydrogen bond link two PX molecules into a dimer. At higher temperatures, the probability that the concerted proton jumps in such a double bond increase. These jumps average the electron density at the nitrogen site >N(3)H and the EFG tensor, which results in the lower-than-expected values of e2Qq/h and η.
The cluster calculations confirmed the assignment of the signals obtained based on the solid-state calculations, but also provided a high-quality wavefunction for further QTAIM analysis. The cluster technique, which takes into account all intermolecular interactions only in the immediate vicinity of the molecule and modern hybrid M062X functional with all-electron basis set 6-311 + G(d,p), yielded NQR parameters that are very well correlated with the experimental data, as in Table 3 and Figures S2 and S3.

Table 3.
The 14N NQR parameters for paraxanthine, calculated theoretically at M062X level, assuming clusters of 15 molecules.
The results obtained at the M062X level, assuming the RT ABCDEF averaged model, are very close to those obtained using the solid-state technique at the GGA/RPBE level (calculations for the direct model with weighted proton positions are not feasible using the cluster technique). The bouncing of points off the linear regression νM062X(νNQR) at low temperature, as in Figure S2, suggests that for =N(9)–, the eQqh−1 should be higher but the asymmetry parameter should be lower. This effect may result from the averaging of the EFG tensor components caused by the rotation of the methyl group at N(7), proton transfer in the N(9) hydrogen bond, or other actors modulating non-covalent bonds.
The rotation of methyl group is not free, and different factors including steric and electronic effects modify the barrier and bring contributions to the structural disorder. Moreover, methyl group surroundings, especially nearby groups, respond to or cooperate with the methyl rotation and modify the barrier. The simulation of the rotation of the methyl group at N(7) permits testing of the influence of these factors. The estimated barrier for the rotation along the threefold axis, as in Figure 4, is 53.95 kJ/mol per cluster, i.e., about 3.60 kJ/mol per single molecule.
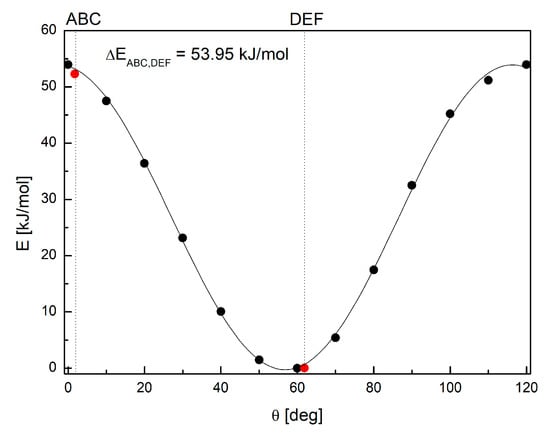
Figure 4.
The changes in the total energy of the cluster upon the rotation of the methyl group at N(7) in paraxanthine; red points indicate experimental configurations, and solid line E = 26.975cos(3θ) (correlation coefficient r2 = 0.99885, curve fit standard deviation s = 4.383). The red points indicate experimental conformations (RT ABC and RT DEF).
The shape of the E(θ) curve is typical of threefold rotational potential. Thus, if an excitation takes place, the staggered conformer would be favored over the eclipsed. The barrier for the methyl group rotation is higher than RT at 296 K (2.479 kJ/mol) and 77 K (0.640 kJ/mol); thus, at room temperature it should exhibit quantum tunnelling enabled by the function overlap. In this temperature range, however, it is more likely that the rotation of the methyl group will be hindered.
Crystal voids in RT ABC (overall volume 14.50 Å3, area 192.86 Å2,) are much smaller than those in RT DEF (overall volume 26.93 Å3, area 208.16 Å2); their asphericity is higher (0.237 versus 0.192) but their globularity is lower (0.138 versus 0.192). The shape of the crystal voids around the methyl group at N(7) reveals more space around it than around N(1) and opens a path for structural disorder at N(7). It supports the predominance of the θ = 60° conformation, which, in the absence of activation, is more stable. Simulation proves that the rotation of the methyl group at N(7) modulates the EFG tensor, and, consequently, the NQR parameters and resonance frequencies, Figure 5.
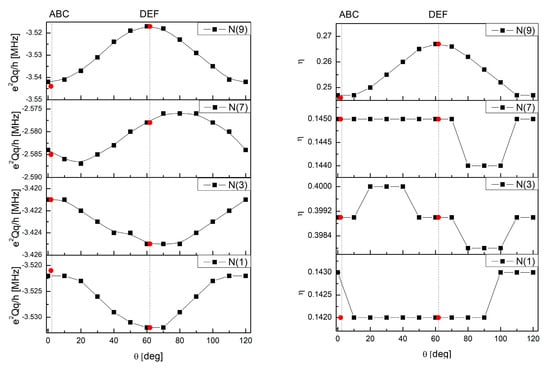
Figure 5.
The changes of the NQR parameters of all four nitrogen sites upon the rotation of the methyl group at N(7) in paraxanthine: e2Qq/h(θ) (left) and η(θ) (right). The red points indicate experimental conformations (RT ABC and RT DEF).
Unexpectedly, it affects the eigenvalues and, to a lesser extent, eigenvectors of EFG tensors, at all nitrogens, not only N(7). For nitrogen atoms in six-membered and five-membered rings, two different trends in the e2Qq/h(θ) relationship are evident, as in Figure 5.
As the angle increases, the e2Qq/h value for the N(1) and N(3) sites decreases, but for N(7) and N(9), it increases. In addition, e2Qq/h(θ) of N(9) shows the greatest variability. The e2Qq/h(θ) variation can be relatively easily explained by the pure hyperconjugation, which causes the delocalization of the σ electrons of the C-H bond of the methyl group to the π orbital of the sp2-hybridized nitrogen atom (due to the rotation of the methyl group around the N-C bond, all three C-H bonds of the methyl group are involved in this hyperconjugation). Although e2Qq/h is modulated for all nitrogen sites, the asymmetry parameter changes significantly only for nitrogens N(7) and N(9), which is surprising. This suggests a strong susceptibility of N(9) to electron delocalization associated with hyperconjugation and the influence of additional factors elsewhere. The shape of the e2Qq/h(θ) and η(θ) curves for N(9), similar to E(θ), confirms this conclusion. The orientation of the X, Y, and Z axes of the EFG tensor is different for –N(1)CH3, >N(3)H, and –N(7)CH3 than it is for =N(9)–, as in Figure 6.
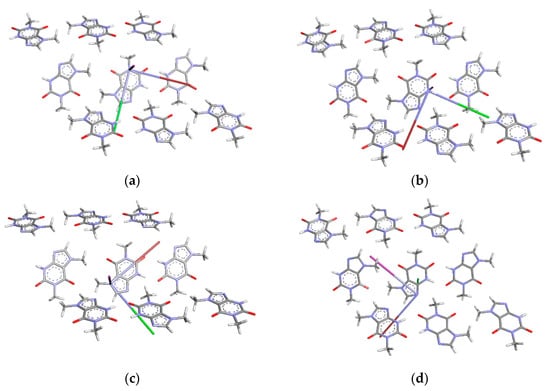
Figure 6.
The orientation of the X, Y, and Z axes of the EFG tensor at (a) –N(1)CH3, (b) >N(3)H, (c) –N(7)CH3, and (d) =N(9)– (the Z-axis depicted in magenta, the Y-axis in maroon, and the X-axis in green). The Z-axis is perpendicular to the plane of the central molecule in (a–c) and lies in the plane of the central molecule in (d) (the clusters were cut from the RT DEF structure with optimized proton positions).
While in the case of the former orientation, the ZZ-axis is perpendicular to the plane of the molecule, in the case of the latter one it lies in its plane. The XX and YY axes of the EFG tensor for –N(1)CH3 and –N(7)CH3 are oriented differently (rotated by an angle of about 30° around the ZZ-axis) and its YY-axis points outside the ring for the former orientation and inside for the latter one. It seems that the rotation of the methyl group should disturb the axes of the EFG tensor at N(9) because its ZZ-axis lies in the plane of the molecule and is directed to the inside of the ring. However, the plot of eQqxx/h, eQqyy/h versus eQqzz/h, as in Figure S4, reveals a completely different nature of the EFG tensor at N(7) compared to that of the other nitrogen sites. This effect is visible both in experimental results and modelling, regardless of the calculation method.
Analysis of the orientation of the main EFG tensor axes upon methyl rotation reveals how they are really affected by the reorientation. The reorientation angles of the EFG tensor axes are small; their values do not exceed 2.4°, as in Figure 7.
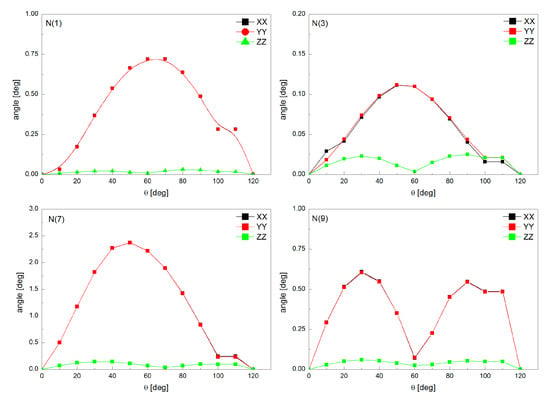
Figure 7.
The changes in the orientation of the EFG tensor axes at individual sites upon the rotation of the methyl group at N(7).
The largest axes deviations occur for nitrogen N(7) and concern the XX and YY axes, while the smallest ones occur for N(3). The differences between the orientations of all three EFG axes for the RT ABC and RT DEF conformations are negligible for N(9). Analysis of the resonant frequencies allows assessment of the impact of rotation on the NQR spectrum. The largest frequency shifts are predicted for N(9), but their magnitude is small (5%) and within the FWHM of the resonance line, as in Figure S5. The lack of differences between the individual FWHMs of the experimental NQR resonance lines indicates that the effect of the rotation at each site should be similar or that the shape of the resonance lines does not reveal the presence of rotation. However, the rotation of the methyl group modulates values of the EFG tensor and the positions of the axes, which results in the shifts in all the spectral lines, especially for N(9). This is clearly visible from the calculation results.
There is one more factor to consider, namely the role of the non-covalent bonds in the methyl rotation in the crystal structure. Analysis of these interactions should shed more light on the very different nature of N(7) and N(9) and should be useful in describing the nature of the disorder of the N(7) methyl group.
3.2. Intermolecular Interactions Pattern in Crystal
The strongest non-covalent interactions in crystals are usually hydrogen bonds. According to the Etter [] rule, the molecule tends to form as many hydrogen bonds as possible. PX can theoretically realize up to twenty-one different types of intermolecular hydrogen bonds (via three donor hydrogen atoms of each methyl group and one hydrogen atom of >N(3)H, and three acceptor atoms N(9) and two O). However, two methyl groups actually limit the ability of nitrogen atoms to participate in strong hydrogen bonds, and, thus, only one strong hydrogen bond (through the >N(3)H group as donor and any of the three acceptor atoms) seem feasible. The essential question is what types of bonds are formed in the crystal structure and what their strengths are. It should help clarify which of them involve nitrogen atoms and to what extent their specific bonding abilities facilitate methyl group disorder.
A combined analysis of 3D Hirshfeld surfaces (3D HS) and 2D molecular fingerprints (2D FP) derived from 3D HS, provided insight into the ten types of the homo- and hetero-nuclear intermolecular interactions in PX crystals, as in Table 4 and Figure 8.

Table 4.
Percentage contributions to the 3D Hirshfeld surface area calculated for each pair of species.
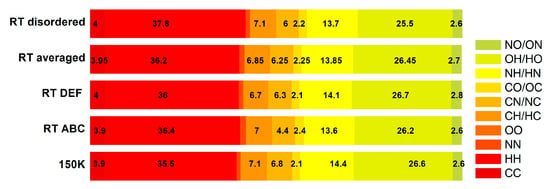
Figure 8.
Percentage contributions to the 3D Hirshfeld surface area from various intermolecular contacts.
Approximately 83% of all interactions of the complex surface consist of four contact types, namely H⋯H, N⋯H/H⋯N, O⋯H/H⋯O, and C⋯H/H⋯C, all of which involve protons. The distribution of these contacts is much more influenced by temperature (6.92%) than by disorder (0.54%). As the temperature increases, the percentage contributions in PX shift from H⋯C/C⋯H, O⋯H/H⋯O, and N⋯H/H⋯N to H⋯H. In general, for all heavy atoms, differences are within error (0.1%), but those for protons are only slightly higher (0.5%). Thus, the effect of temperature and disorder is weakly manifested (the surface percentage only changes by 0.407% for RT DEF, 0.284% for RT ABC, and 0.296% for the RT disordered structure, respectively).
As much as approximately 60% of the PX molecular surface is generated by H atoms, while the other elements (C, N, and O) contribute to much smaller, but almost equivalent percentages, from about 12 to 16%, as in Table 5. The values of the enrichment ratio of the intermolecular contacts, EXY, which reveal privileged (EXY > 1) and disfavored (EXY < 1) contacts between each of the two atomic species, X and Y, are collected in Table 5 and shown in Figure 9. They increase with temperature by only 0.218%, which mainly reflects the reorientation of the -CH3 group.

Table 5.
Enrichment ratios (EXY) characterizing the various contacts in PX.
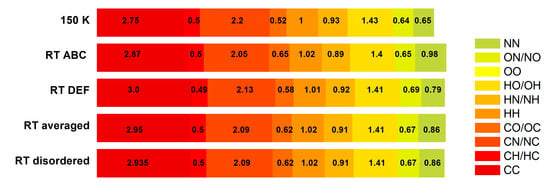
Figure 9.
The enrichment ratios from the various contacts.
The five C and four N atoms in the two heterocyclic rings are exposed to the molecular surface because they each have three (C) and two or three (N) bonds (trigonal planar sp2 hybridization) and their p orbitals participate in π bonds above and below the ring. The C⋯C contacts in PX are significantly enriched (ECN ≈ 2.75); therefore, C species seem the preferred interaction partners for C, but are less privileged compared to O (ECO ≈ 1.27) or N (ECN ≈ 1.34). These three types of contacts have enrichment ratios much higher than unity, suggesting their high contribution to π⋯π stacking. The decrease in temperature (i.e., change from RT DEF to LT) reduces the ECC enrichment factor by only 0.19%, which, while maintaining the ECO and ECN values, suggests a weakening of π⋯π stacking between carbon atoms. However, the contribution of C atoms to the surface is small (11%), and the percentage of C⋯C to the 3D Hirshfeld surface area is only 4%, so the role of C⋯C is overestimated. C⋯H contacts are not favored, their enrichment ratio is low, and ECH ≈ 0.50, because H atoms participate in the formation of hydrogen bonds. The H⋯H contacts appear with an enrichment ratio equal to unity (EHH ≈ 1.0), despite their strong competition with O and N hydrogen acceptors (H⋯O, EOH ≈ 1.22 and H⋯N, ENH ≈ 1.18). They are not impoverished due to the presence of high hydrogen content. The O⋯H/H⋯O contacts exhibit high enrichment values (EOH ≈ 1.22), because they are favored in crystal packing. Two oxygen atoms form intermolecular bonds of the type N–H⋯O (–NH from –NH) and C–H⋯O. For the same reason, the O⋯O contacts are impoverished (EOO ≈ 0.57). The contacts N⋯H/H⋯N show enrichment values higher than unity (ENH ≈ 1.18). Thus, the existence of the C–H⋯N hydrogen bond is raised, and the N⋯N contacts are impoverished (ENN ≈ 0.70). Overall, the favored interaction partners for N, whose contribution to the 3D HS molecular surface is of about 14.1%, are only C and H species, while N and O are disfavored.
The percentage contributions to local 3D HS were calculated for a single species, and four nitrogen atoms, two oxygen atoms, two carbons of methyl groups, and two methyl groups are listed in Table 6.

Table 6.
Percentage contributions to the local 3D Hirshfeld surface area calculated for a single species.
Temperature has little effect on these percentages. The difference between the percentage contributions to the local 3D Hirshfeld surface area from nitrogen atoms does not exceed 1.404%. At both oxygen sites, these percentages at LT and RT differ by only 0.917%, while at the carbons from methyl groups at N(1) and N(7) they differ by 0.678%. Surprisingly, the difference in the percentage contributions to the local 3D Hirshfeld surface calculated for N(9) and N(3) is insignificant, even though N(3) is covalently bound to H, while N(9) only accepts a proton and forms a N–H⋯O hydrogen bond. This confirms that the N–H⋯O hydrogen bond is strong and thermally stable. The contributions of the methyl groups substituted at N(1) and N(7) differ by 2.067% and temperature influence them in 2.358%. Thus, the main changes in the interactions pattern are rather minor, involving the methyl groups and reflecting their disorder.
A little more information about the types of interactions and their location is provided by 3D HS results, which, with the normalized contact distance dnorm, shape index, and curvedness mapped over this surface, are shown in Figure 10.
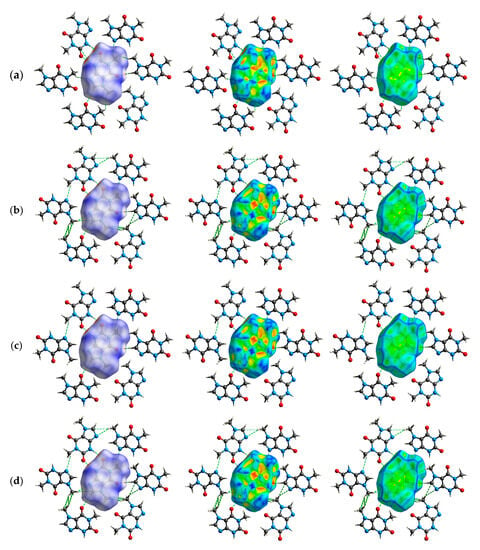
Figure 10.
The crystal structure of paraxanthine with dnorm (left), shape index (centre), and curvedness (right) over total 3D Hirshfeld surface for (a) LT 150K, (b) RT ABC, (c) RT DEF, and (d) RT disordered structure.
The 3D HS surfaces are sufficient to identify most of the forces stabilizing the crystal structure. However, the shape index and curvedness maps are much more useful for identifying the presence of π–π stacking or intramolecular interactions. The red/blue triangular patches in the shape index and the flat patches in the curvature are essentially the only reliable methods of identifying the presence of these interactions, which are very faint on 3D HS normal surfaces.
Intermolecular hydrogen bonds are indicated in the 3D HS surface by intense red to white areas, as in Figure 10. The relevant parameters, namely dnorm, shape index, and curvedness, which describe these hydrogen bonds, are listed in Table 7.

Table 7.
The parameters dnorm, shape index, and curvedness characterizing the intermolecular hydrogen bonds in paraxanthine.
Intense red areas in the 3D HS located near =O(2) and H (from –N(3)H) represent the lowest value of dnorm = −0.6156 a.u. (−0.6012 a.u. for RT ABC; −0.5994 a.u. for RT DEF), which confirms the presence of a pair of strong N(3)–H⋯O(2) hydrogen bonds forming a dimer. These bonds are short RO⋯N = 2.809 Å (2.820 Å for RT ABC and RT DEF) and only slightly nonlinear <NHO = 171.1° (167° for RT ABC and RT DEF). The brighter red area near –O(6)= and H from –C(8)H moiety represents the dnorm value of −0.1792 a.u. (−0.1258 a.u. for RT ABC; −0.120 a.u. for RT DEF). It indicates the presence of a weak C(8)–H⋯O(6) hydrogen bond, that is long, RC⋯O = 3.439 Å (3.511 Å for RT ABC and RT DEF), and highly nonlinear, <CHO = 175.53° (176.35° for RT ABC and RT DEF). The light pink area near –O(2)= and H (from –N(1)CH3 moiety) represents the value of dnorm 0.1752 a.u. (0.3293 a.u. for RT ABC and 0.2277 a.u. for RT DEF) and indicates the presence of a weak C–H⋯O(2) hydrogen bond, that is long, RC⋯O = 3.406 Å (3.504 Å for RT ABC and RT DEF), and highly nonlinear <CHO = 119.56° (122.37° for RT ABC and RT DEF).
The almost white area near –N(9)= and H (from –N(1)CH3) moiety represents the value of dnorm 0.019 a.u. (0.052 a.u. for RT ABC; 0.098 a.u. for RT DEF). It indicates the presence of a weak C–H⋯N(9)) hydrogen bond, which is long RC⋯N = 3.390 Å (3.357 Å for RT ABC and RT DEF) and highly nonlinear <CHO = 138.26° (127.3° for RT ABC and RT DEF). The light pink areas near O(6) and H (from –N(7)CH3) represent the value of dnorm −0.0753 a.u. (−0.0569 a.u. for RT ABC; −0.0612 a.u. for RT DEF). They imply the presence of a pair of weak C–H⋯O(6) hydrogen bonds (C–H from –N(7)CH3), which are long RC⋯O = 3.0916 Å (3.116 Å RT for ABC and RT DEF) and very highly nonlinear <CHO = 90.03° (91.38° for RT ABC and RT DEF).
The white areas in 3D HS describe the dispersive contacts C–H⋯H–C mainly between the protons from neighboring N(7)CH3 groups. Their two pairs (RHH = 2.300 Å and RCC = 3.543 Å at LT, and RHH = 2.324 Å and RCC = 3.572 Å RT DEF) form a dimer. The remaining proton of N(7)CH3 participates in dispersive contact C–H⋯H–C (RHH = 2.135 Å and RCC = 3.572 Å) with a proton from N(1)CH3. There are fewer dispersive contacts in the RT ABC structure—only one proton of N(7)CH3 participates in the H⋯H of only 1.655 Å. The H⋯H contacts in each case are shorter than twice the van der Waals radius of hydrogen (2.40 Å), which suggests that dispersion forces involve both H⋯H and C⋯H. For some compounds, dispersion forces involving C⋯H may be even stronger than those involving H⋯H, but such an arrangement in PX is precluded by the EXY enrichment ratios, as in Table 5.
Intramolecular interactions are also present but difficult to find. They can only be detected on the local 3D HS surface with the curvature mapped on this surface generated for the acceptor (O(6)). In RT ABC, both methyl groups at N(1) and N(7) seem to be involved in the intramolecular hydrogen bonds CH⋯O, while in RT DEF only methyl substituted at N(7) seems to participate in such a bond.
Multiple interatomic contacts contribute to the interlayered π⋯π stacking, such as N(7)⋯N(3) of 3.415 Å (3.463 Å for RT ABC and RT DEF); C(8)⋯N(1) of 3.361 Å (3.396 Å for RT ABC and RT DEF); C(6)⋯N(9) of 3.352 Å (3.399 Å for RT ABC and RT DEF); C(4)⋯C(5) of 3.378 Å (3.420 Å for RT ABC and RT DEF) and C(2)⋯N(7) of 3.441 Å (3.439 Å for RT ABC and RT DEF), with the distance between layers of 3.351 Å. The displacement of the molecules relative to each other in adjacent layers weakens the π⋯π stacking. Therefore, there are only two types of interatomic contacts that contribute to the π⋯π stacking: N(1)⋯C(6) of 3.419 Å (3.497 Å RT ABC) and N(7)⋯C (C from N(1)CH3) of 3.440 Å (3.481 Å RT ABC) with an interlayer distance of 3.436 Å. All these π⋯π stacking interactions are visible only for the shape index mapped over 3D HS surface as characteristic mixed red/blue triangular patches.
In order to verify the presence of interactions, mainly directional, the characteristic features of the 2D fingerprint (2D FP), obtained from the 3D HS, were further analyzed, as in Figure 11.
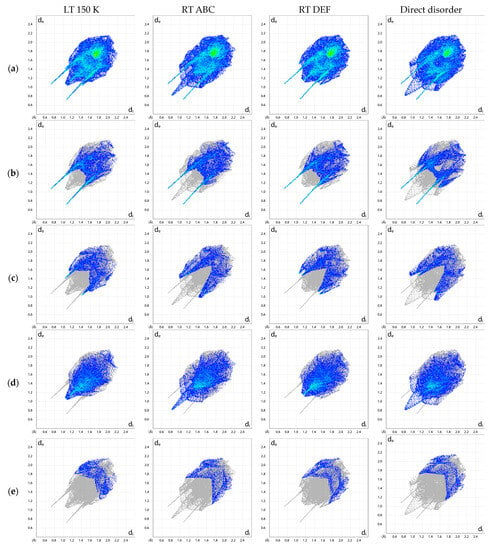
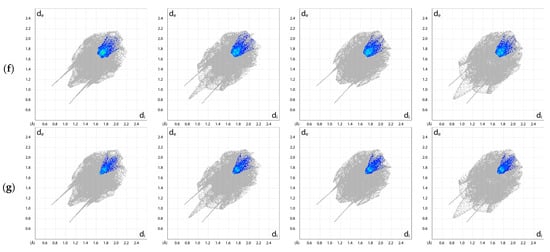
Figure 11.
2D molecular fingerprinting of the interaction patterns in different paraxanthine structures (protons optimized). (a) All, (b) O⋯H/H⋯O, (c) N⋯H/H⋯N, (d) H⋯H, (e) C⋯H/H⋯C, (f) N⋯C/C⋯N, and (g) C⋯C.
In general, the 2D FP results for LT and RT DEF are in 98.9% similar, while those for RT ABC and the disordered structure differ by as much as 27.7%, mainly in the central part of the fingerprint and along the axis of symmetry i.e., de ≅ di. In the 2D FP plot in Figure 11b, the O⋯H/H⋯O contacts describing intramolecular C–H⋯O and intermolecular N–H⋯O hydrogen bonds are represented by symmetric spikes (‘‘wings’’), which are very sharp and long at de + di ~1.8 Å (de + di ~1.75 Å for the RT ABC and DEF). These interactions cover an area of 26.6% (26.2% for the RT ABC, 26.7% for RF DEF, 26.45% for the RT averaged, and only 25.5% for the disordered structures) of the total 3D HS. The N⋯H/H⋯N contacts are represented by the most external symmetric spikes consisting of two components, which are wide at de + di ~2.7 Å and sharp at de + di ~2.4 Å (de + di ~2.0 Å for the optimised geometry), as in Figure 11c. These interactions cover a smaller area of 14.4% (13.6% for the RT ABC, 14.1% for RF DEF, 13.85% for the RT averaged, and 13.7% for the disordered structures) of the total 3D HS. The individual 2D FPs differ significantly in a wide spike in the central region that describes the dispersion interactions: a single H⋯H at de + di ~1.6 A in RT ABC and disordered structure and a pair of H⋯H at de + di ~2.3 Å in RT DEF and LT, as in Figure 11d. This indicates significantly stronger H⋯H interactions in RT ABC compared to LT and RT DEF.
The C⋯H/H⋯C contacts are represented in 2D FP by the widest spikes at de + di ~3.00 Å, as in Figure 11e. They cover 7.1% (7% for the RT ABC, 6.7% for RF DEF, 6.85% for the RT averaged, and 7.1% for the disordered structures) of the total 3D HS. These contacts are significantly weaker than those involving C–H⋯H–C.
The C⋯O/O⋯C contacts bring a very small contribution of 2.1% (2.4% for the RT ABC, 2.1% for RF DEF, 2.25% for the RT averaged, and 2.2% for the disordered structures) and are represented by wide wings de + di ~3.40 Å (3.10 Å for the optimized geometry) located in the middle area of the entire fingerprint. The O⋯N/N⋯O contacts bring a small contribution of 2.6 (2.6% for the RT ABC, 2.8% for RF DEF, 2.7% for the RT averaged, and 2.6% for the disordered structures). The high contribution is brought by weak H⋯H interactions, which cover 35.5% (36.4% for the RT ABC, 36% for RF DEF, 36.2% for the RT averaged, and 37.8% for the disordered structures) of the total 3D HS. In the 2D FP, they are reflected by the cloud of scattered points and wide joined spikes at de + di ~2.0 Å. The contribution brought by C⋯N/N⋯C and N⋯N contacts, which covers 6.8% (6.2% for the RT ABC, 6.3% for RF DEF, 6.25% for the RT averaged, and 6% for the disordered structures) and 1.1% (1.6% for the RT ABC, 1.2% for RF DEF, 1.4% for the RT averaged, and 1.2% for the disordered structures), as in Figure 11f, mainly describes the interlayer π⋯π stacking interactions. The contribution brought by C⋯C contacts covers 3.9% (4.0% for the remaining structures), as in Figure 11g. Carbon, being less electronegative than nitrogen, has a lower capability to stabilize valence electron density. Hence, it exhibits greater reactivity and plays a key role in π-stacking.
Local 2D molecular fingerprints of –N(1)CH3, >N(3)H, –N(7)CH3, and –N(9)=, generated on 3D HS for individual nitrogen atoms, as in Figure S6, vary from one nitrogen site to another, both in shape and percentage. While the upper narrow wing attributed to the NC covalent bond is common and featureless, the lower one matters, because it shows a considerable variation in the number and type of non-covalent interactions.
The local 2D FPs suggests that N(1) and N(7) participate only in covalent NC bonds. The >N(3)H also participates in such bonds but additionally to a covalent NH bond, which is a donor for strong hydrogen bond N–H⋯O. Nitrogen –N(9)=, apart from NC, participates in the intermolecular C–H⋯N hydrogen bond. These two nitrogen atoms, N(3) and N(9), are crucial to the bonding pattern in the PX structure. A deeper insight into local FPs reveals a small, easily overlooked wing that indicates the involvement of N(7) in the C–H⋯N bonding between adjacent molecules. It supports the π-π stacking, which can, therefore, be stronger than average.
The local 2D FP for the oxygen atom O(2) reveals two sharp wings, with the upper one attributed to the OC covalent bond at de + di = 1.3 Å and the bottom one attributed to two hydrogen bonds: N–H⋯O at de + di = 1.85 Å and C–H⋯O at de + di = 2.7 Å. The analysis of the local 2D FP for the oxygen atom O(6) reveals a sharp upper wing attributed to the OC covalent bond at de + di = 1.3 Å and a bottom wider wing attributed to hydrogen bonds (weaker intermolecular C–H⋯O at de + di = 2.5 Å and stronger intramolecular C–H⋯O at de + di = 2.2 Å). The wing describing the intramolecular hydrogen bond C–H⋯O differs significantly from those describing the intermolecular hydrogen bonds. It is specific, and very wide and scattered. The analysis of local, atomic, 2D molecular fingerprints helps to find the very weak intramolecular hydrogen bonds C–H⋯O, which meet the Gilli criterion [].
The examination of changes in global 2P FP caused by the rotation of the methyl group in N(7) reveals changes in the distribution and strength of non-covalent interactions in the entire molecule. They can be quantified using the Pompeiu–Hausdorff and Bhattacharayya metrics and the Wasserstein distance, as in Figure 12.
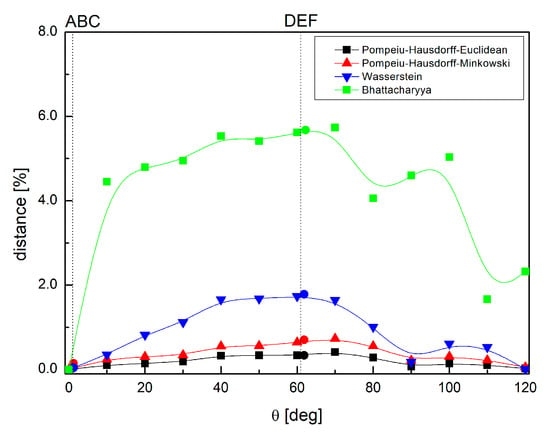
Figure 12.
The changes in the molecular 2D FP upon the rotation of the methyl group at N(7) in paraxanthine. The solid circle points indicate experimental conformations (RT ABC and RT DEF).
The Pompeiu–Hausdorff distance between 2D FP upon methyl rotation does not exceed 0.5% (the global minimum and maximum, at θ = 0° and θ = 60°, respectively). The Wasserstein distance, which allows identification of the dissimilarity between the 2D FP distributions, does not exceed 2% (the global minimum and maximum, at θ = 0° and θ = 60°, respectively). Both methods describe, quite well, the differences in the distribution of interactions, which occupy mainly the central region of the fingerprint (di = de axis). The Bhattacharayya distance, which allows identification of differences in the strength of the interactions, does not exceed 6% (the global minimum and maximum, at θ = 0° and θ = 60°, respectively). The distribution of C-H⋯H-C contacts is clearly different for individual conformers, as in Figure 10d. The 2D FP changes due to methyl rotation are for all contacts taken together and only C-H⋯H-C contacts of comparable magnitude. The differences between them do not exceed 1%, and the global extremes occur at the same abscissa values. Thus, among the intermolecular interactions, the C-H⋯H-C contacts are mainly affected during the rotation of the methyl group at N(7). Moreover, the 2D FP(θ) dependence suggests that the change in the number of interactions is smaller than the change in the strength of interactions. The magnitude of the percentages, as in Figure 12, is in good agreement with the modulation of the NQR parameters due to rotation, as in Figure 5 and Figure 7, as well as the changes of the total energy upon the rotation of the methyl group, as in Figure 4.
3.3. Characterization of the Strength of the Interactions
The packing similarity between the LT and RT DEF crystal structures is high (99.75%), while that between the LT and RT ABC structures is lower (99.68%). Analysis of the total lattice energy and its terms (electrostatic, polarization, dispersion, and repulsion) derived from DFT calculations for a cluster of 10 Å in diameter, as in Table 8, has revealed that irrespective of the structure (ordered or disordered) and temperature (LT or RT), the attractive interactions contribute about 72% of the total energy and cannot be cancelled by the much smaller repulsion of about 38%.

Table 8.
Separation of electrostatic, Ee, polarization. Ep, dispersion, Ed, and repulsion, and Er, terms for the total lattice energy, Et, calculated with the Spackman scaled approach (optimized proton positions).
At 150 K, the total lattice energy (−105 kJ/mol) is dominated by the dispersion (−177.8 kJ/mol) and electrostatic forces (−105.82 kJ/mol), which are stronger than the polarization (−27 kJ/mol) or repulsion (56.79 kJ/mol). With increasing temperature, all the contributions decrease in absolute value, resulting in a slightly lower total energy, as in Figure 13.
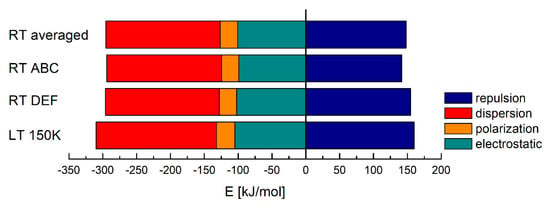
Figure 13.
Contributions to the total lattice energy in paraxanthine, broken down into a few different basic interaction types.
The particular energy terms in all these structures are strongly correlated (the Pearson coefficient exceeds 0.999), Figure S7, but the scattering is moderate for LT versus RT DEF (6.64%), high for LT versus RT ABC (20.63%), and marginal for the LT versus RT averaged (2.79%).
This suggests that LT and RT DEF are “energetically” more similar than LT and RT ABC. The two types of leading interactions, electrostatic (mainly hydrogen bonds; shown in red) and dispersion (mainly π⋯π; shown in green), form networks of non-covalent interactions in two orthogonal directions, as in Figure 14. An increase in temperature only slightly weakens the total energy of the lattice (by 4.06 kJ/mol), and the proportions between individual terms are within 1%, so the temperature slightly affects the shape of this energy skeleton.
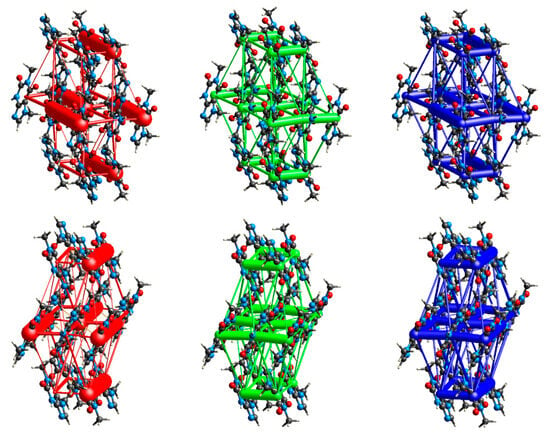
Figure 14.
Energy framework of diagrams for electrostatic (red, left), dispersion (green, center), and total energy (blue, right) visualized by red, green, and blue “sticks” in the paraxanthine structure of RT ABC (upper row) and RT DEF (lower row).
Closer analysis of the data reveals that the major contributions to the total lattice energy, as in Table 9 and Figure S8, come from a pair of strongly concerted N–H⋯O hydrogen bonds (about 31.2 kJ/mol) and a pair of (N7)C–H⋯O(4) bonds (about 13 kJ/mol for LT, RT DEF structures, and 8 kJ/mol for RT ABC structure).

Table 9.
The strength of the particular interactions in paraxanthine (optimized proton positions), estimated using the pairs of molecules (electrostatic, Ee, polarization. Ep, dispersion, Ed, and repulsion, Er, terms for the total lattice energy, Et).
Weak hydrogen bonds C(8)–H⋯O(6) of 14.2 kJ/mol, (N9)C–H⋯C(8), and (N3)C–H⋯(N9) of about 10 kJ/mol and N(1)CH⋯O(6) of about 9 kJ/mol bind the PX molecules together. In addition, non-polar N(1)C–H⋯H–CN(1) dispersive contacts of about 9 kJ/mol bind protons of methyl groups from neighboring molecules. The entire structure is stabilized by the interlayered π⋯π stackings of about 40–50 kJ/mol. The ordering of the most important interactions according to their decreasing energy is as follows: a pair of N–H⋯O > π⋯π stacking > C–H⋯O > C–H⋯N > C–H⋯H–C. Neither temperature nor disorder change it. The N(3)–H⋯O(2) hydrogen bonds and π⋯π stacking are the main driving forces forming the “energetical” skeleton in PX, as shown in Figure 14. However, a significant difference occurs in the (N7)C–H⋯O(6) hydrogen bond and N(7)C–H⋯H–CN(7) dispersive contacts, which are much weaker in RT DEF than in LT or RT ABC. These dihydrogen contacts are subtle but definitely not weak. Apparently, the change in the conformation of the methyl group at N(7) affects the strength of the (N7)C–H⋯O(6) hydrogen bond and dispersive contact N(7)C–H⋯H–CN(7). The change from syn to anti causes their weakening by up to 5.5 kJ/mol, Table 8, but only the cumulative effect of (N7)C–H⋯O(6) and N(7)C–H⋯H–CN(7)) can be assessed. Conformational disorder is clearly visible in Figure S8. The points scattering from ERT(ELT) correspond to repulsion and, to a lesser extent, to electrostatic terms for (N7)C–H⋯O(6) and N(7)C–H⋯H–CN(7), and, in a minor degree, to N(9)⋯H–CN(7). Thus, conformational disorder significantly modulates these two contributions to the total energy.
Although the above analysis provides a preliminary and rough insight into the distribution of the interactions, it is still incomplete. Therefore, the quantum theory of atoms in molecules (QTAIM) was used to verify the presence and estimate the strength of the inter- and intra-molecular interactions. The topological descriptors of electron density (ρ(r), Δρ(r), the HBCP(r), and its components GBCP(r) and VBCP(r)) as well as the strength of all intra- and intermolecular bonds and contacts, are collected in Table S3. The molecular graphs based on the crystalline structure are shown in Figure 15. Overall, the QTAIM analysis confirmed the presence of the intermolecular hydrogen bonds and H⋯H contacts which contribute to the stabilization of the crystalline structure, as detected by the total 2D FP, as in Table 10. For each of the interactions listed in Table S3, the values of ρ(r) in the BCP do not exceed 0.1 a.u., while the values of the Laplacian, ΔρBCP(r), are positive. Thus, according to the Koch and Poplier [] criterion, all these interactions can be defined as non-covalent. Moreover, in each case the –G(rBCP)/V(rBCP) ratio exceeds 1; thus, all of them are truly non-covalent (i.e., none are partially covalent). The energies of the N(3)H⋯O(2) and C(8)H⋯O(6) hydrogen bonds, estimated using QTAIM and Equations (7)–(11), as in Table 10 and Table S3, are in good agreement with those calculated using the classical energy framework approach, but the energies of the remaining non-covalent bonds are much lower. Some contributions are combined, and their energies were misestimated, while others were missed. However, the energies of the C-H⋯H-C dispersive interactions may be underestimated because in QTAIM these bonds are treated individually and the coupling effect between them is ignored. Regardless, these results confirm the conclusion that LT and RT DEF are more similar than LT and RT ABC.
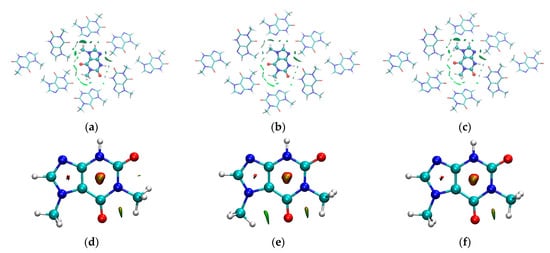
Figure 15.
The molecular graphs cut of the crystalline structure with reduced density gradient isosurfaces (RDG) and sign(λ2)ρBCP mapped over the surface (isovalue 0.35 a.u.). The surfaces indicating intermolecular (a) LT, (b) RT ABC, (c) RT DEF, and intramolecular (d) LT, (e) RT ABC, (f) RT ABC interactions are visualized using a blue–green–red scheme.

Table 10.
The energies of the intermolecular interactions calculated according to the Espinosa (EE), Matta (EM), Emamian (EEM), and Afonin (EA) equations at the M062X/6-311 + G** level.
In contrast to the 2D FP in which intramolecular hydrogen bonds are indistinguishable from intermolecular ones, or simply undetectable, QTAIM detected intramolecular N(1)C–H⋯O(6) hydrogen bond in all LT and RT structures, but N(7)C–H⋯O(6) only in the RT ABC structure. However, in some cases, the standard QTAIM approach is also insufficient to detect all intramolecular interactions, so the isosurface of the reduced density gradient, RDG(r), was investigated. The reduced density gradient isosurfaces with sign(λ2)ρBCP mapped over the surface are shown in Figure 15.
The light cyan slabs between N(3)H and O(2) indicate the presence of stabilizing intermolecular N(3)H⋯O(2) hydrogen bonds. Smaller and green slabs between C(8)H and O(6) suggests the existence of much weaker intermolecular C(8)H⋯O(6) hydrogen bonds. The disc-shaped green surfaces of the reduced density gradient located between the protons from two –N(7)CH3 groups belonging to the neighboring molecules confirm the presence of the dispersive C–H⋯H–C interactions, as in Figure 15a–c. The small green slab that is disc-shaped, located between the proton from –N(1)CH3 and O(6), indicates the presence of the weak attractive intramolecular C–H⋯O hydrogen bond, as in Figure 15d,e. Another, slightly larger green slab, that is also disc-shaped, is located between the proton from –N(7)CH3 and O(6), and confirms our assumptions about the presence of the weak attractive intramolecular C–H⋯O hydrogen bond in RT ABC structure, as in Figure 15e, even though no critical point was detected. The tiny green area between the proton of –N(1)CH3 and O(2) suggests the existence of a very weak attractive intramolecular C–H⋯O hydrogen bond, but only in the LT structure Figure 15d. Both interactions affect the barrier height to the rotation of the methyl group at the N(7) position, which leads to hindered rotation and structural disorder. As illustrated in Figure 15c–e, one or two dark red elliptical slabs are present at the center of the six-membered ring and five-membered ring, respectively. Both indicate a significant classical steric effect (repulsion) that results from the spatial arrangement of N and C atoms in the rings. This steric crowding is stronger in the six-membered ring than in the five-membered ring.
In the RDG(r) versus sign(λ2)ρ(r) plot, as in Figure 16, the non-covalent interactions, i.e., hydrogen bonds (strong and attractive), van der Waals contacts (weak), and steric interactions (ring closures, repulsive) are visible as spikes (on the left, λ2 > 0, strong/weak repulsive, while on the right, λ2 < 0, weak/strong attractive). The spikes on the left correspond to negative sign(λ2)ρ and the most negative value −0.04 a.u. The spikes on the right correspond to positive sign(λ2)ρ, where the least positive value is 0.055 a.u. Such a wide range of sign(λ2)ρ suggests a combination of strong hydrogen bonding, van der Waals, π⋯π stacking, and steric interactions contributing to the stability of the crystal. Moreover, the plot indicates that the RT ABC structure is much less stable than RT DEF or LT. Low RDS spikes at large negative sign(λ2)ρ(r) indicate stabilizing intermolecular N(3)H⋯O(2) and C(8)H⋯O(6) hydrogen bonds. Numerous narrow spikes located in the central part of the plot (i.e., near-zero sign(λ2)ρ(r)) depict dispersive C–H⋯H–C and π⋯π stacking interactions. Their positions for the RT ABC structure differ significantly from those for LT and RT DEF. The RDS spikes at about −0.4 a.u, −0.2 a.u., and −0.15 a.u., as in Figure 16 (top), describe intramolecular N(1)CH⋯O(6), N(1)CH⋯O(2), and N(7)CH⋯O(2) hydrogen bonds. Two spikes at large positive sign(λ2)ρ(r) values for sterically crowded rings indicate the lack of bonding in their central area.
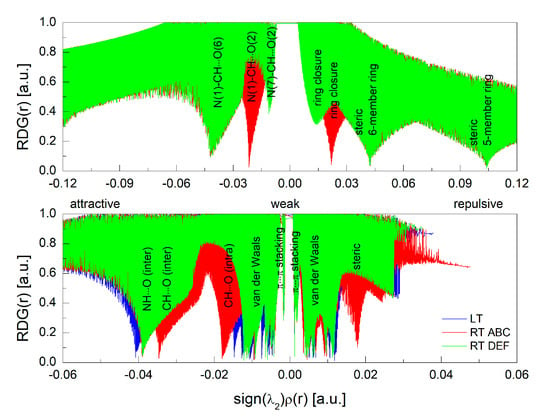
Figure 16.
The RDG(r) versus sign(λ2)ρ(r) plot for LT, RT ABC, and RT DEF: intramolecular (top) and intermolecular (bottom) non-covalent interactions.
The spike positions, assigned to nitrogen interactions, as in Figure 17, vary from one structure to another, but that for RT ABC differs significantly from those for LT and RT DEF.
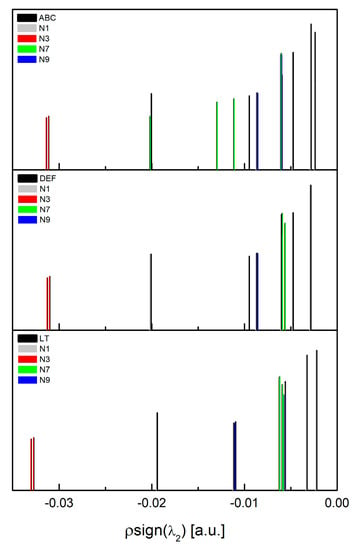
Figure 17.
The peak’s position in the RDG(r) versus sign(λ2)ρ(r) plot broken down into four nitrogen sites in three structures, i.e., RT ABC (top), RT DEF (middle), and LT 150K (bottom).
The most stable peak positions are those describing the N(3)H⋯O hydrogen bond, while the most shifted ones are those describing non-covalent interactions in which N(7) and N(9) are involved. This confirms the greater sensitivity of the five-membered ring to the methyl rotation. Moreover, the positions of the peaks describing non-covalent interactions in which N(1) is involved are relatively stable, which confirms the conclusion about the completely different nature of the two methyl groups in PX. The positions of the spikes in the plot of RDG(r) versus sign(λ2)ρ(r) for N(3) and N(9), both of which have a direct involvement in hydrogen bonds, are quite well correlated with e2qQ/h.
3.4. Binding Mode of Paraxanthine with A2A Receptor
PX has a similar structure to adenosine and, like caffeine, acts as a competitive antagonist to adenosine receptors (A1 and A2A). Unfortunately, the structure of the PX complex with A2A has not yet been experimentally investigated. Therefore, to determine which conformation of the methyl group at N(7) is preferred in a protein–ligand complex, we used molecular docking. The crystal structure of stabilized A2A adenosine receptor A2AR-StaR2-bRIL in complex with caffeine, 5MZP [], was retrieved from the PDB database. The receptor was prepared by removing caffeine and water molecules. However, two water molecules binding the actual caffeine ligand have been retained and treated as part of the receptor environment. The potential binding site (cavity) of 124.416 Å3 in volume was detected. This cavity is formed by the following receptor residues: Phe163, Leu249, Ile274, Asn253, Met177, Ile66, Val84, and Glu169 (all except polar Asn253 are hydrophobic). Its shape provides the largest contact area between the ligand and receptor surfaces. The search space of the simulation exploited in the docking studies was defined as a subset region of 9.0–15.0 Å around the active site cleft. To evaluate the docking process, we performed a redocking evaluation task. The ligand was removed from the crystal structure and redocked in the initial ligand-binding pocket of the receptor. The redocking protocol was successful, as the root-mean-square deviation (RMSD) was only 0.11 Å. PX was then docked to a rigid protein structure in exactly the same way. The best pose of conformer that leads to the stabilization of the complex with the highest binding/docking score was selected after docking (the approach for docking the ligands in the protein pocket was the same as reported previously []).
The stability of the binding of a complex resulting from molecular docking is often verified by means of molecular dynamics simulations. In this case, random jumps of functional groups are observed, making the study of the binding modes of individual conformers problematic. Therefore, we prepared and docked twelve conformers of the methyl group at N(7) differing in the θ angle 0° ≤ θ ≤ 120° (rotation about its threefold symmetry axis). The strength of the binding between the protein and ligand, measured by the total binding energy and docking score, are strongly influenced by θ. However, both show global minima at 60°, as in Figure 18.
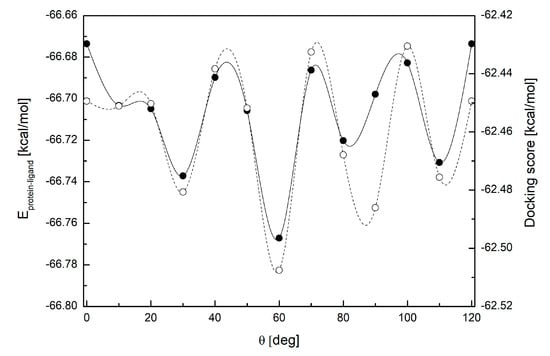
Figure 18.
The changes in the docking score (open circles and dashed line) and total binding energy (solid circles and line) upon the rotation of the methyl group at N(7); a global minimum near θ = 60°.
Regardless of the conformer, oxygen O(6) formed two O–H⋯O hydrogen bonds with nearby water molecules, and oxygen O(2) of PX formed one N–H⋯O hydrogen bond with the Asn253 residue. However, the length and strength of N–H⋯O bond, which seems to be a key factor in the A2A receptor–PX interaction, depends on the θ, as in Figure 19.
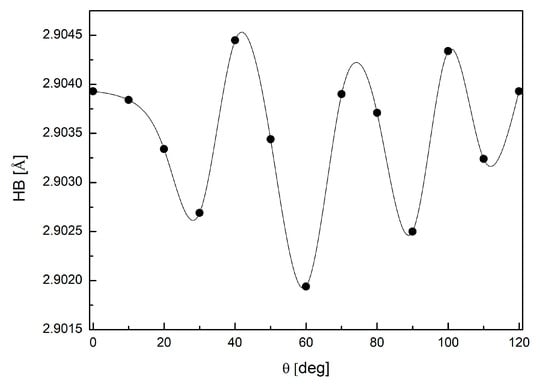
Figure 19.
The changes in the strength of hydrogen bond N–H⋯O linking the PX (ligand) with Asn253 (protein residue) upon the rotation of the methyl group at N(7); a global minimum near θ = 60°.
The best score conformers (global minimum at θ = 60°), as depicted in Figure 20, participate in the strongest hydrogen bond (of 2.902 Å), which is only marginally weaker than that in the actual caffeine ligand (of 2.894 Å). The best score conformer of the methyl group at N(7) in PX is very close to that of the actual ligand (caffeine) in the 5MZP (angle deviation does not exceed 1°). Moreover, the PX moiety in the protein–ligand complex has adopted the same methyl group conformation at N(7) as in the solid state (i.e., the RT DEF conformer).
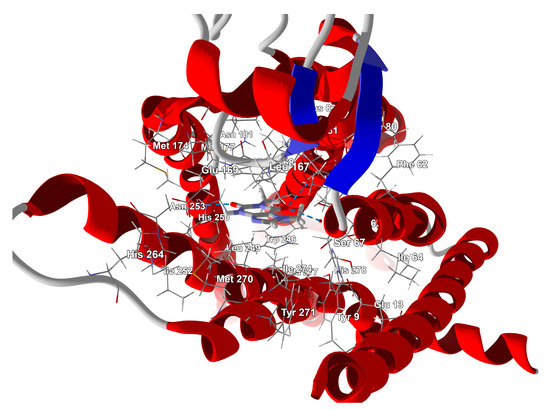
Figure 20.
The docked pose of PX (conformer θ = 60°) in a binding site of A2A. The protein backbone is represented as a cartoon, the binding cavity residues are shown as thin sticks, docked ligands are shown as sticks, while the hydrogen bonds with Asn253 and two water molecules are depicted with dashed blue lines.
Detailed insight into the binding mode with LigPlot+ [,] confirms the above observations and reveals a set of hydrophobic interactions binding PX with Phe163, Ile66, Ile274, Leu249, Met177, and Val84, as in Figure 21, which further stabilizes the protein–ligand complex.
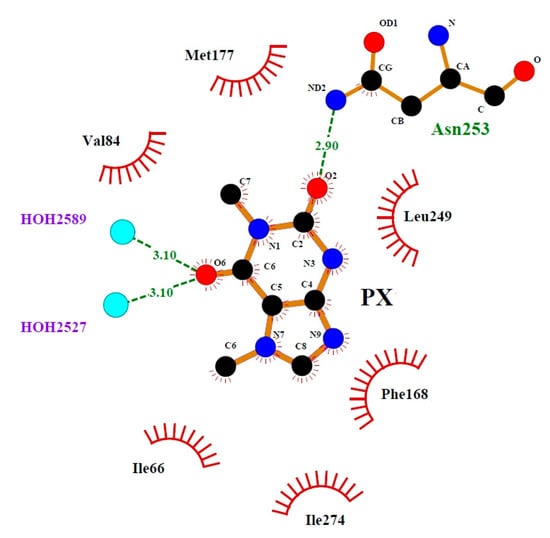
Figure 21.
A LigPlot+ schematic 2D representation of the PX–protein interactions. The hydrogen bonds formed by the protein and two water molecules with the PX atoms are shown as green dashed lines, while the residues involved in hydrophobic contacts are shown as red arcs and labeled.
It should be noted that LigPlot+ suggests a similar set of hydrophobic interactions for the caffeine binding with the same protein. The hydrophobic interaction energies obtained from molecular docking are listed in Table 11. All of them, apart from the binding between the ligand and Val84, are stronger when the ligand is caffeine.

Table 11.
The energies of the hydrophobic protein–ligand interactions.
The sign[λ2(r)]ρ(r) surface mapped to the RDG(r) isosurface in the red–green–blue scheme for the protein–ligand complex is shown in Figure 22. This surface visualizes the binding mode and reveals the nature of the non-covalent interactions between the A2A protein and PX ligand. In general, the protein environment makes the electronic density slightly less localized and smooth. Weak van der Waals-type interactions clearly dominate, which is indicated by the green colour of the surface. Most of them are C-H⋯H-C interactions involving the methyl group at the ligand’s N(7) nitrogen and the methyl groups of Ile66, Ile274, and Ala63, and the methyl group at the ligands’s N(1) nitrogen and the methyl groups of Leu249 and Met177 residues. The large and nearly flat green area above the six-membered ring of the PX ring proves π⋯π-stacking between the ligand and Phe163 (average π-stack contact distance: 3.4 Å; center-to-center axis deviation: 2°). The N–H⋯O hydrogen bond is clearly visible, and is depicted by a small light cyan disc-shaped area near O(2).
Figure 22.
The sign[λ2(r)]ρ(r) surface mapped to the RDG(r) isosurface (isocontour value 0.4 a.u.) PX–A2A complex with best PX pose conformer θ = 60°. The protein backbone is represented as a cartoon (color by ResID).
Conformation changes have a significant effect on the protein–ligand binding, as in Figure 23. The mutual shift in the red and green areas and the red and green spikes, respectively, shows the differences in the binding mode caused by the conformational change from θ = 0° to θ = 60°. In general, the distance from the ligand and the shape of the surface of the binding regions differ among conformers. However, the differences in non-covalent intermolecular interactions are relatively small compared to intramolecular interactions.
Figure 23.
The overlap of the RDG isosurfaces for two conformers θ = 0° (red surface) and θ = 60° (green surface) (left) and the RDG(r) versus sign(λ2)ρ(r) plot for two conformers: θ = 60° (top) and θ = 0° (bottom) (right).
Although the methyl group is not directly involved in any strong non-covalent protein–ligand bond, it does contribute to the overall strength of the ligand-to-protein binding. This indirect effect is related to the hydrophobic interactions and the modulation of the electron density throughout the ligand due to the rotation of the methyl group. However, methyl group jumps, if they occur, will cause a subtle effect that will modify but not destroy the key protein–ligand bond. Involvement of the methyl group at N(7) in a strong intramolecular C–H⋯O hydrogen bond supported by dispersive C–H⋯H–C interactions, appears to be a source of disorder as well as an important factor in the formation of protein–ligand complexes.
4. Conclusions
Three factors determine the structural disorder in PX: larger crystal voids near methyl at N(7) than N(1), opening the path for disorder, hyperconjugation that strongly affects the density distribution in the five-membered ring, and the involvement of the methyl group at N(7) in many non-covalent bonds that intercept subsequent jumping protons. By the modulation of the strong hyperconjugation effect, the rotation of the methyl group at the N(7) position affects the electron density in the entire molecule. Therefore, the disorder, that is considered to be local and restricted to the N(7) site, actually affects the entire molecule. As a consequence, methyl rotation significantly modulates the components of the EFG tensor and slightly alters the orientation of its axes for each nitrogen.
Changes in the global 2P FP caused by the rotation of the methyl group at N(7), quantified using the Pompeiu–Hausdorff and Bhattacharayya metrics and the Wasserstein distance, confirm the changes in the distribution and strength of non-covalent interactions occurring throughout the molecule. The influence of methyl group rotation on the pattern of interactions is clearly visible regardless of the type of metric. The magnitude of these percentages is consistent with the changes in the total energy and modulation of the NQR spectra due to the methyl group rotation.
Non-covalent interactions of four types, namely intermolecular hydrogen bonds N−H⋯O, C−H⋯N and C−H⋯O, weak C−H⋯O intramolecular hydrogen bonds (closing 6-member rings and stiffening the structure), numerous H⋯H dispersive interactions, and π⋯π stacking, form the bonding network in PX. The rotation of methyl groups slightly affects the shape of the PX crystal’s energy skeleton, but in-depth analysis reveals differences in the strength of individual interactions and their total distribution. In the LT and RT DEF structures, N(1) participates in two intermolecular hydrogen bonds of different strengths, i.e., C–H⋯O and C–H⋯N, with one dispersive H⋯H contact and one intramolecular hydrogen bond C–H⋯O, while –N(7) participates in one C–H⋯N intermolecular hydrogen bond, two dispersive H⋯H contacts, and a van der Waals N⋯O contact. Nitrogen N(3) acts as a strong proton donor and is involved only in the N–H⋯O bond, while –N(9)= is involved only in the weak C–H⋯N intermolecular hydrogen bond. Thus, only N(3) and N(9) are involved in hydrogen bonds directly, while N(1) and N(7) contribute as the donors of methyl groups, indirectly. Two additional interactions play an important role in the structure of RT ABC: strong dispersive contacts H⋯H and relatively weak intramolecular bonding of the nitrogen methyl group at N(7), C–H⋯O. In the RT ABC structure both methyl groups at N(1) and N(7) seem to be involved in the intramolecular hydrogen bonds C–H⋯O, while in LT and RT DEF only the methyl substituted at N(7) is involved in such a bond. Thus, in RT ABC, the two oxygen atoms strongly bind N(1) with intramolecular hydrogen bonds, resulting in a high increase in the rotation barrier of the methyl group at N(1). Moreover, in the structure of RT ABC, the nitrogen N(7) binds oxygen almost as strongly as N(1) and a few times stronger than in LT or RT DEF. During the rotation of the methyl group, the strength of two intramolecular hydrogen bonds changes significantly. In addition, during rotation, the protons of the methyl group are captured and bound by the CH⋯O bond, which temporarily stabilizes the structure.
The PX moiety in the A2A adenosine receptor–ligand complex has adopted the same methyl group conformation at N(7) as in the solid state (i.e., RT DEF conformer). Thus, the interplay between the intramolecular C−H⋯O hydrogen bonds and C−H⋯H−C dispersive interactions is a key factor in hindering methyl rotation and introducing structural disorder, and an important factor in the formation of protein–ligand complexes. In addition, dispersion interactions play an important role in molecular associations, regardless of the state (solid or protein–ligand complex).
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/pr11092740/s1, Table S1. The 14N NQR parameters for PX calculated theoretically at the GGA/RPBE level with TS DFT-D correction. Table S2. The 14N NQR parameters for PX calculated theoretically at the m-GGA/RSCAN level. Table S3. Topological parameters describing the interactions in PX (electron density at bond critical point, BCP, (ρBCP(r)), its Laplacian (ΔρBCP(r)), the potential electron energy density (VBCP(r)), the kinetic electron energy density (GBCP(r)) and the total electron energy density (HBCP(r)) calculated at the M062X/6-311+G** level. Figure S1. The 14N NQR spectrum in PX: experimental (a) and simulated at the GGA/RBPE of theory (b) LT, (c) averaged model at RT (RT ABCDEF) and d) direct disorder model. Figure S2. The correlation between the NQR frequencies experimental and calculated at M062X level. Figure S3 The resonance line positions in NQR spectrum simulated at the M062X level: (a) cluster, LT, (b) cluster, averaged model RT ABCDEF. Figure S4. The correlation between the EFG tensor components. Figure S5. The changes in the FWHM of the resonance line upon the rotation of the methyl group at N(7). Figure S6. Local 2D molecular fingerprinting of the interactions pattern in PX (protons optimized). Figure S7. The correlation between the total energy and its components (data from Table 6) for LT, RT ABC and RT DEF structures (solid line ERT=ELT). Figure S8. Interactions pattern in the PX structure (along the a-axis): (a) LT, (b) RT ABC and (c) RT DEF.
Author Contributions
Conceptualization, methodology J.N.L.; experimental investigations, J.S. and V.Ž.; description of the experimental part, J.S.; quantum chemical calculations, molecular docking and modelling, J.N.L.; visualizations, M.L.; writing—original draft preparation and revision, J.N.L.; writing—review and editing, J.N.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Allotment of computer time from the Wrocław Supercomputing and Networking Center (WCSS) is gratefully acknowledged.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zrenner, R.; Stitt, M.; Sonnewald, U.; Boldt, R. Pyrimidine and Purine Biosynthesis and Degradation in Plants. Annu. Rev. Plant Biol. 2006, 57, 805–836. [Google Scholar] [CrossRef]
- Monteiro, J.; Alves, M.G.; Oliveira, P.F.; Silva, B.M. Pharmacological potential of methylxanthines: Retrospective analysis and future expectations. Crit. Rev. Food Sci. Nutr. 2018, 59, 2597–2625. [Google Scholar] [CrossRef]
- Arnaud, M.J. The pharmacology of caffeine. Prog. Drug Res. 1987, 31, 273–313. [Google Scholar] [CrossRef] [PubMed]
- Orrú, M.; Guitart, X.; Karcz-Kubicha, M.; Solinas, M.; Justinova, Z.; Barodia, S.K.; Zanoveli, J.; Cortes, A.; Lluis, C.; Casado, V.; et al. Psychostimulant pharmacological profile of paraxanthine, the main metabolite of caffeine in humans. Neuropharmacology 2013, 67, 476–484. [Google Scholar] [CrossRef]
- Caffeine. In IARC Monographs on the Evaluation of Carcinogenic Risks to Humans; World Health Organization, International Agency for Research on Cancer: Lyon, France, 1991; Volume 51, pp. 291–390.
- Tassaneeyakul, W.; Birkett, D.J.; McManus, M.E.; Tassaneeyakul, W.; Veronese, M.E.; Andersson, T.; Tukey, R.H.; Miners, J.O. Caffeine metabolism by human hepatic cytochromes P450: Contributions of 1A2, 2E1 and 3A isoforms. Biochem. Pharmacol. 1994, 47, 1767–1776. [Google Scholar] [CrossRef]
- Cornelis, M.C.; El-Sohemy, A.; Campos, H. Genetic polymorphism of the adenosine A2A receptor is associated with habitual caffeine consumption. Am. J. Clin. Nutr. 2007, 86, 240–244. [Google Scholar] [CrossRef]
- Lajin, B.; Schweighofer, N.; Goessler, W.; Obermayer-Pietsch, B. The determination of the Paraxanthine/Caffeine ratio as a metabolic biomarker for CYP1A2 activity in various human matrices by UHPLC-ESIMS/MS. Talanta 2021, 234, 122658. [Google Scholar] [CrossRef] [PubMed]
- Mazzafera, P. Catabolism of caffeine in plants and microorganisms. Front. Biosci. 2004, 9, 1348. [Google Scholar] [CrossRef]
- Berthou, F.; Guillois, B.; Riche, C.; Dreano, Y.; Jacqz-Aigrain, E.; Beaune, P.H. Interspecies variations in caffeine metabolism related to cytochrome P4501A enzymes. Xenobiotica Fate Foreign Compd. Biol. Syst. 1992, 22, 671–680. [Google Scholar] [CrossRef]
- Ashihara, H.; Sano, H.; Crozier, A. Caffeine and related purine alkaloids: Biosynthesis, catabolism, function and genetic engineering. Phytochemistry 2008, 69, 841–856. [Google Scholar] [CrossRef]
- Gao, Z.-G.; Jacobson, K.A. Emerging adenosine receptor agonists. Expert Opin. Emerg. Drugs 2007, 12, 479–492. [Google Scholar] [CrossRef] [PubMed]
- Dulloo, A.G.; Seydoux, J.; Girardier, L. Paraxanthine (metabolite of caffeine) mimics caffeine’s interaction with sympathetic control of thermogenesis. Am. J. Physiol. 1994, 267 Pt 1, E801–E804. [Google Scholar] [CrossRef] [PubMed]
- Benowitz, N.L.; Jacob, P.; Mayan, H.; Denaro, C. Sympathomimetic effects of paraxanthine and caffeine in humans. Clin. Pharmacol. Ther. 1995, 58, 684–691. [Google Scholar] [CrossRef]
- Han, Y.; Xun, L.; Wang, X.; Yang, S.; Sun, Z.; Shi, H.; Xu, X.; Hu, S. Detection of caffeine and its main metabolites for early diagnosis of Parkinson’s disease using micellar electrokinetic capillary chromatography. Electrophoresis 2020, 41, 1392–1399. [Google Scholar] [CrossRef] [PubMed]
- Barr, R.G. Methylxanthines for exacerbations of chronic obstructive pulmonary disease: Meta-analysis of randomised trials. BMJ 2003, 327, 643. [Google Scholar] [CrossRef]
- Xing, D.; Yoo, C.; Gonzalez, D.; Jenkins, V.; Nottingham, K.; Dickerson, B.; Leonard, M.; Ko, J.; Faries, M.; Kephart, W.; et al. Dose-Response of Paraxanthine on Cognitive Function: A Double Blind, Placebo Controlled, Crossover Trial. Nutrients 2021, 13, 4478. [Google Scholar] [CrossRef]
- Ferré, S. An update on the mechanisms of the psychostimulant effects of caffeine. J. Neurochem. 2008, 105, 1067–1079. [Google Scholar] [CrossRef]
- Yoo, C.; Xing, D.; Gonzalez, D.; Jenkins, V.; Nottingham, K.; Dickerson, B.; Leonard, M.; Ko, J.; Faries, M.; Kephart, W.; et al. Acute Paraxanthine Ingestion Improves Cognition and Short-Term Memory and Helps Sustain Attention in a Double-Blind, Placebo-Controlled, Crossover Trial. Nutrients 2021, 13, 3980. [Google Scholar] [CrossRef]
- Ferre, S.; Orru, M.; Guitart, X. Paraxanthine: Connecting Caffeine to Nitric Oxide Neurotransmission. J. Caffeine Res. 2013, 3, 72–78. [Google Scholar] [CrossRef]
- Guerreiro, S.; Toulorge, D.; Hirsch, E.; Marien, M.; Sokoloff, P.; Michel, P.P. Paraxanthine, the primary metabolite of caffeine, provides protection against dopaminergic cell death via stimulation of ryanodine receptor channels. Mol. Pharmacol. 2008, 74, 980–989. [Google Scholar] [CrossRef]
- Costentin, J. Main neurotropic and psychotropic effects of methylxanthines (caffeine, theophylline, theobromine, paraxanthine). PSN 2010, 8, 182–186. [Google Scholar] [CrossRef]
- Mitchell, L.; MacFarlane, P.M. Mechanistic actions of oxygen and methylxanthines on respiratory neural control and for the treatment of neonatal apnea. Respir. Physiol. Neurobiol. 2020, 273, 103318. [Google Scholar] [CrossRef] [PubMed]
- Gressner, O.A.; Lahme, B.; Siluschek, M.; Gressner, A.M. Identification of paraxanthine as the most potent caffeine-derived inhibitor of connective tissue growth factor expression in liver parenchymal cells. Liver Int. 2009, 29, 886–897. [Google Scholar] [CrossRef] [PubMed]
- Sasamoto, H.; Fujii, Y.; Ashihara, H. Effect of Purine Alkaloids on the Proliferation of Lettuce Cells Derived from Protoplasts. Nat. Prod. Commun. 2015, 10, 1934578X1501000. [Google Scholar] [CrossRef]
- Razavi, S.M.; Asadi, N. Physiological and biochemical responses of lettuce plant to the allochemical compound of paraxanthine. J. Plant Process Funct. 2022, 10, 51–60. [Google Scholar]
- Hosseini, A.; Mirmahdi, E.; Moghaddam, M.A. A new strategy for treatment of Anosmia and Ageusia in COVID-19 patients. Integr. Respir. Med. 2020, 1, 2. [Google Scholar] [CrossRef]
- Khani, E.; Khiali, S.; Beheshtirouy, S.; Entezari-Maleki, T. Potential pharmacologic treatments for COVID-19 smell and taste loss: A comprehensive review. Eur. J. Pharmacol. 2021, 912, 174582. [Google Scholar] [CrossRef]
- Kohli, P.; Soler, Z.M.; Nguyen, S.A.; Muus, J.S.; Schlosser, R.J. The Association Between Olfaction and Depression: A Systematic Review. Chem. Senses 2016, 41, 479–486. [Google Scholar] [CrossRef]
- Alharbi, O.; Xu, Y.; Goodacre, R. Simultaneous multiplexed quantification of caffeine and its major metabolites theobromine and paraxanthine using surface-enhanced Raman scattering. Anal. Bioanal. Chem. 2015, 407, 8253–8261. [Google Scholar] [CrossRef]
- Seliger, J.; Zagar, V.; Apih, T.; Gregorovic, A.; Latosińska, M.; Olejniczak, G.A.; Latosińska, J.N. Polymorphism and disorder in natural active ingredients. Low and high-temperature phases of anhydrous caffeine: Spectroscopic (1H-14N NMR-NQR/14N NQR) and solid-state computational modelling (DFT/QTAIM/RDS) study. Eur. J. Pharm. Sci. 2016, 85, 18–30. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Olejniczak, G.A.; Seliger, J.; Zagar, V. Topology of the interactions pattern in pharmaceutically relevant polymorphs of methylxanthines (caffeine, theobromine, and theophiline): Combined experimental (1H-14N nuclear quadrupole double resonance) and computational (DFT and Hirshfeld-based) study. J. Chem. Inf. Model. 2014, 54, 2570–2584. [Google Scholar] [CrossRef] [PubMed]
- Yalkowsky, S.H.; He, Y.; Jain, P. Handbook of Aqueous Solubility Data; CRC Press: Boca Raton, FL, USA, 2016; p. 1620. [Google Scholar]
- Carlucci, L.; Gavezzotti, A. Molecular Recognition and Crystal Energy Landscapes: An X-ray and Computational Study of Caffeine and Other Methylxanthines. Chem.—A Eur. J. 2005, 11, 271–279. [Google Scholar] [CrossRef]
- Echeverría, J.; Aullón, G.; Alvarez, S. Dihydrogen intermolecular contacts in group 13 compounds: H⋯H or E⋯H (E = B, Al, Ga) interactions? Dalton Trans. 2017, 46, 2844–2854. [Google Scholar] [CrossRef] [PubMed]
- Rösel, S.; Quanz, H.; Logemann, C.; Becker, J.; Mossou, E.; Cañadillas-Delgado, L.; Caldeweyher, E.; Grimme, S.; Schreiner, P.R. London Dispersion Enables the Shortest Intermolecular Hydrocarbon H⋯H Contact. J. Am. Chem. Soc. 2017, 139, 7428–7431. [Google Scholar] [CrossRef] [PubMed]
- Hajji, M.; Al-Otaibi, J.S.; Belkhiria, M.; Dhifaoui, S.; Habib, M.A.; Elmgirhi, S.M.H.; Mtiraoui, H.; Bel-Hadj-Tahar, R.; Msaddek, M.; Guerfel, T. Structural and computational analyses of a 2-propanolammonium-chlorocadmate(II) assembly: Pivotal role of hydrogen bonding and H–H interactions. J. Mol. Struct. 2021, 1223, 128998. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Orzeszko, A.; Maurin, J.K. Synthesis and Crystal Structure of Adamantylated 4,5,6,7-Tetrahalogeno-1H-benzimidazoles Novel Multi-Target Ligands (Potential CK2, M2 and SARS-CoV-2 Inhibitors); X-ray/DFT/QTAIM/Hirshfeld Surfaces/Molecular Docking Study. Molecules 2022, 28, 147. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Latosińska, M.; Seliger, J.; Žagar, V.; Apih, T.; Grieb, P. Elucidating the Role of Noncovalent Interactions in Favipiravir, a Drug Active against Various Human RNA Viruses; a 1H-14N NQDR/Periodic DFT/QTAIM/RDS/3D Hirshfeld Surfaces Combined Study. Molecules 2023, 28, 3308. [Google Scholar] [CrossRef]
- Latosińska, J.N. NQR parameters: Electric field gradient tensor and asymmetry parameter studied in terms of density functional theory. Int. J. Quantum Chem. 2003, 91, 284–296. [Google Scholar] [CrossRef]
- Bader, R. Atoms in Molecules: A Quantum Theory (International Series of Monographs on Chemistry); Oxford University Press: New York, NY, USA, 1994. [Google Scholar]
- Johnson, E.R.; Keinan, S.; Mori-Sánchez, P.; Contreras-García, J.; Cohen, A.J.; Yang, W. Revealing Noncovalent Interactions. J. Am. Chem. Soc. 2010, 132, 6498–6506. [Google Scholar] [CrossRef]
- Spackman, M.A.; Jayatilaka, D. Hirshfeld surface analysis. CrystEngComm 2009, 11, 19. [Google Scholar] [CrossRef]
- Spackman, M.A.; McKinnon, J.J. Fingerprinting intermolecular interactions in molecular crystalsBased on the presentation given at CrystEngComm Discussion, 29th June 1st July 2002, Bristol, UK. CrystEngComm 2002, 4, 378. [Google Scholar] [CrossRef]
- Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. 1965, 140, A1133–A1138. [Google Scholar] [CrossRef]
- Levy, M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2007, 120, 215–241. [Google Scholar] [CrossRef]
- Latosińska, J.N.; Koput, J. Analysis of the NQR parameters in 2-nitro-5-methylimidazole derivatives by quantum chemical calculations. Phys. Chem. Chem. Phys. 2000, 2, 145–150. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Rev. C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Zhang, Y.; Yang, W. Comment on “Generalized Gradient Approximation Made Simple”. Phys. Rev. Lett. 1998, 80, 890. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Wu, Z.; Cohen, R.E. More accurate generalized gradient approximation for solids. Phys. Rev. B 2006, 73, 235116. [Google Scholar] [CrossRef]
- Perdew, J.P.; Ruzsinszky, A.; Csonka, G.I.; Vydrov, O.A.; Scuseria, G.E.; Constantin, L.A.; Zhou, X.; Burke, K. Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces. Phys. Rev. Lett. 2008, 100, 136406. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, molecules, solids, and surfaces: Applications of the generalized gradient approximation for exchange and correlation. Phys. Rev. B 1992, 46, 6671–6687, Erratum in Phys. Rev. B 1993, 48, 4978. [Google Scholar] [CrossRef]
- Tkatchenko, A.; Scheffler, M. Accurate Molecular Van Der Waals Interactions from Ground-State Electron Density and Free-Atom Reference Data. Phys. Rev. Lett. 2009, 102, 073005. [Google Scholar] [CrossRef] [PubMed]
- Peng, H.; Yang, Z.H.; Perdew, J.P.; Sun, J. Versatile van der Waals Density Functional Based on a Meta-Generalized Gradient Approximation. Phys. Rev. X 2016, 6, 041005. [Google Scholar] [CrossRef]
- Sun, J.; Ruzsinszky, A.; Perdew, J.P. Strongly Constrained and Appropriately Normed Semilocal Density Functional. Phys. Rev. Lett. 2015, 115, 036402. [Google Scholar] [CrossRef]
- Bartók, A.P.; Yates, J.R. Regularized SCAN functional. J. Chem. Phys. 2019, 150, 161101. [Google Scholar] [CrossRef]
- Pyykkö, P. Year-2008 nuclear quadrupole moments. Mol. Phys. 2008, 106, 1965–1974. [Google Scholar] [CrossRef]
- Abramov, Y.A. On the Possibility of Kinetic Energy Density Evaluation from the Experimental Electron-Density Distribution. Acta Crystallogr. Sect. A Found. Crystallogr. 1997, 53, 264–272. [Google Scholar] [CrossRef]
- Espinosa, E.; Molins, E.; Lecomte, C. Hydrogen bond strengths revealed by topological analyses of experimentally observed electron densities. Chem. Phys. Lett. 1998, 285, 170–173. [Google Scholar] [CrossRef]
- Mata, I.; Alkorta, I.; Espinosa, E.; Molins, E. Relationships between interaction energy, intermolecular distance and electron density properties in hydrogen bonded complexes under external electric fields. Chem. Phys. Lett. 2011, 507, 185–189. [Google Scholar] [CrossRef]
- Emamian, S.; Lu, T.; Kruse, H.; Emamian, H. Exploring Nature and Predicting Strength of Hydrogen Bonds: A Correlation Analysis Between Atoms-in-Molecules Descriptors, Binding Energies, and Energy Components of Symmetry-Adapted Perturbation Theory. J. Comput. Chem. 2019, 40, 2868–2881. [Google Scholar] [CrossRef]
- Afonin, A.V.; Vashchenko, A.V.; Sigalov, M.V. Estimating the energy of intramolecular hydrogen bonds from 1H NMR and QTAIM calculations. Org. Biomol. Chem. 2016, 14, 11199–11211. [Google Scholar] [CrossRef]
- Nikolaienko, T.Y.; Bulavin, L.A.; Hovorun, D.M. Bridging QTAIM with vibrational spectroscopy: The energy of intramolecular hydrogen bonds in DNA-related biomolecules. Phys. Chem. Chem. Phys. 2012, 14, 7441. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD: Visual molecular dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Jelsch, C.; Ejsmont, K.; Huder, L. The enrichment ratio of atomic contacts in crystals, an indicator derived from the Hirshfeld surface analysis. IUCrJ 2014, 1, 119–128. [Google Scholar] [CrossRef] [PubMed]
- Hausdorff, F. Grundzüge der Mengenlehre; Leipzig Viet; Gerstein-University of Toronto: Toronto, ON, Canada, 1914. [Google Scholar]
- Bhattacharyya, A. On a Measure of Divergence between Two Multinomial Populations. Sankhyā Indian J. Stat. (1933–1960) 1946, 7, 401–406. [Google Scholar]
- Vaserstein, L.N. Markov processes on countable space products describing large systems of automata. Probl. Inform. Transm. 1969, 5, 47–52. [Google Scholar]
- Latosińska, J.N.; Latosińska, M.; Szafrański, M.; Seliger, J.; Žagar, V.; Burchardt, D.V. Impact of structural differences in carcinopreventive agents indole-3-carbinol and 3,3′-diindolylmethane on biological activity. An X-ray, 1H–14N NQDR, 13C CP/MAS NMR, and periodic hybrid DFT study. Eur. J. Pharm. Sci. 2015, 77, 141–153. [Google Scholar] [CrossRef]
- Trott, O.; Olson, A.J. AutoDock Vina: Improving the speed and accuracy of docking with a new scoring function, efficient optimization, and multithreading. J. Comput. Chem. 2009, 31, 455–461. [Google Scholar] [CrossRef]
- Eberhardt, J.; Santos-Martins, D.; Tillack, A.F.; Forli, S. AutoDock Vina 1.2.0: New Docking Methods, Expanded Force Field, and Python Bindings. J. Chem. Inf. Model. 2021, 61, 3891–3898. [Google Scholar] [CrossRef]
- Wallace, A.C.; Laskowski, R.A.; Thornton, J.M. LIGPLOT: A program to generate schematic diagrams of protein-ligand interactions. Protein Eng. Des. Sel. 1995, 8, 127–134. [Google Scholar] [CrossRef]
- Laskowski, R.A.; Swindells, M.B. LigPlot+: Multiple Ligand–Protein Interaction Diagrams for Drug Discovery. J. Chem. Inf. Model. 2011, 51, 2778–2786. [Google Scholar] [CrossRef]
- Seliger, J.; Žagar, V.; Blinc, R. 1H-14N Nuclear Quadrupole Double Resonance with Multiple Frequency Sweeps. Z. Naturforschung A 1994, 49, 31–34. [Google Scholar] [CrossRef]
- Seliger, J.; Zagar, V.; Blinc, R. A New Highly Sensitive 1H-14N Nuclear-Quadrupole Double-Resonance Technique. J. Magn. Reson. 1994, 106, 214–222. [Google Scholar] [CrossRef]
- Etter, M.C. Encoding and decoding hydrogen-bond patterns of organic compounds. Acc. Chem. Res. 2002, 23, 120–126. [Google Scholar] [CrossRef]
- Gilli, G.; Gilli, P. The Nature of the Hydrogen Bond: Outline of a Comprehensive Hydrogen Bond Theory, 1st ed.; Oxford Academic: Oxford, UK, 2009. [Google Scholar]
- Koch, U.; Popelier, P.L.A. Characterization of C-H-O Hydrogen Bonds on the Basis of the Charge Density. J. Phys. Chem. 2002, 99, 9747–9754. [Google Scholar] [CrossRef]
- Cheng, R.K.Y.; Segala, E.; Robertson, N.; Deflorian, F.; Doré, A.S.; Errey, J.C.; Fiez-Vandal, C.; Marshall, F.H.; Cooke, R.M. Structures of Human A 1 and A 2A Adenosine Receptors with Xanthines Reveal Determinants of Selectivity. Structure 2017, 25, 1275–1285.e4. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).