Semantic Hybrid Signal Temporal Logic Learning-Based Data-Driven Anomaly Detection in the Textile Process
Abstract
:1. Introduction
- (1)
- Based on signal temporal logic (STL), we constructed a more expressive hybrid signal temporal logic (HSTL) system to learn human-readable data semantic features;
- (2)
- A data-driven semantic anomaly detector (SeAD) was established using the logic formula, which can realize online anomaly detection;
- (3)
- The effectiveness of our model was demonstrated via the polymerization data of the textile process.
2. Semantic Hybrid Signal Temporal Logic
2.1. Signal Temporal Logic
2.2. The Proposition of Semantic Hybrid Signal Temporal Logical
3. Problem Statement
3.1. Hybrid Signal Temporal Logic Learning
3.2. Anomaly-Detection-Model-Based Hybrid Signal Temporal Logic
| Algorithm 1: HSTL Fault Diagnosis Model. |
| Input: A segmented data set: Dimension: 2 1: Generate basic HSTL formulas 2: Formula parameterization do 9: else |
3.3. Complexity
4. Case Study
4.1. Preliminary Analysis of Selected Components
4.2. Anomaly Detection Semantic Learning
4.3. Comparison of Experimental Results
4.4. Ablation Analyses
4.5. Semantic Anomaly Detector Transfer Detection
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- He, C.; Zhang, C.; Bai, T.; Jiao, K.; Su, W.; Wu, K.; Su, A. A Review on Artificial Intelligence Enabled Design, Synthesis, and Process Optimization of Chemical Products for Industry 4.0. Processes 2023, 11, 330. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhao, J. A deep belief network based fault diagnosis model for complex chemical processes. Comput. Chem. Eng. 2017, 107, 395–407. [Google Scholar] [CrossRef]
- Kumar, A.; Jaiswal, A. A Deep Swarm-Optimized Model for Leveraging Industrial Data Analytics in Cognitive Manufacturing. IEEE Trans. Ind. Inform. 2021, 17, 2938–2946. [Google Scholar] [CrossRef]
- Su, A.; Zhang, C.; She, Y.-B.; Yang, Y.-F. Exploring Deep Learning for Metalloporphyrins: Databases, Molecular Representations, and Model Architectures. Catalysts 2022, 12, 1485. [Google Scholar] [CrossRef]
- Yasenjiang, J.; Xu, C.; Zhang, S.; Zhang, X. Fault Diagnosis and Prediction of Continuous IndustrialProcesses Based on Hidden Markov Model-BayesianNetwork Hybrid Model. Int. J. Chem. Eng. 2022, 2022, 3511073. [Google Scholar] [CrossRef]
- Yan, L.; Peng, X.; Tone, C.; Luo, L. A Multigroup Fault Detection and Diagnosis Scheme for Multivariate Systems. Ind. Eng. Chem. Res. 2020, 59, 20767–20778. [Google Scholar] [CrossRef]
- Hatamleh, M.; Chong, J.W.; Tan, R.R.; Aviso, K.B.; Janairo, J.I.B.; Chemmangattuvalappil, N.G. Design of mosquito repellent molecules via the integration of hyperbox machine learning and computer aided molecular design. Digit. Chem. Eng. 2022, 3, 100018. [Google Scholar] [CrossRef]
- Jian, C.; Yang, K.; Ao, Y. Industrial fault diagnosis based on active learning and semi-supervised learning using small training set. Eng. Appl. Artif. Intel. 2021, 104, 104365. [Google Scholar] [CrossRef]
- Kourtis, G.; Kavakli, E.; Sakellariou, R. A Rule-Based Approach Founded on Description Logics for Industry 4.0 Smart Factories. IEEE Trans. Ind. Inform. 2019, 15, 4888–4899. [Google Scholar] [CrossRef]
- Chen, G.; Liu, M.; Kong, Z. Temporal-Logic-Based Semantic Fault Diagnosis with Time-Series Data From Industrial Internet of Things. IEEE Trans. Ind. Electron. 2021, 68, 4393–44035. [Google Scholar] [CrossRef]
- Huo, X.; Hao, K.; Chen, L.; Tang, X.; Wang, T.; Cai, X. A dynamic soft sensor of industrial fuzzy time series with propositional linear temporal logic. Expert Sys. Appl. 2022, 201, 117176. [Google Scholar] [CrossRef]
- Pnueli, A. The temporal semantics of concurrent programs. Theoretical Comput. Sci. 1981, 13, 45–60. [Google Scholar] [CrossRef]
- Bringsjord, S. The logicist manifesto: At long last let logic-based artificial intelligence become a field unto itself. J. Appl. Logic. 2008, 6, 502–525. [Google Scholar] [CrossRef]
- Bartocci, E.; Gol, E.A.; Haghighi, I.; Belta, C. A formal methods approach to pattern recognition and synthesis in reaction diffusion networks. IEEE Trans. Control Netw. Syst. 2018, 5, 308–320. [Google Scholar] [CrossRef]
- Kong, Z.; Jones, A.; Belta, C. Temporal logics for learning and detection of anomalous behavior. IEEE Trans. Autom. Control. 2017, 62, 1210–1222. [Google Scholar] [CrossRef]
- Bombara, G.; Vasile, C.I.; Penedo, F.; Yasuoka, H.; Belta, C. A decision tree approach to data classification using signal temporal logic. In Proceedings of the ACM International Conference on Hybrid Systems: Computation and Control (HSCC), Vienna, Austria, 12–14 April 2016; pp. 1–10. [Google Scholar]
- Liu, K.; Lin, H.; Fei, Z.; Liang, J. Spatially–temporally online fault detection using timed multivariate statistical logic. Eng. Appl. Artif. Intell. 2017, 65, 51–59. [Google Scholar] [CrossRef]
- Kong, Z.; Jones, A.; Ayala, A.M.; Gol, E.A.; Belta, C. Temporal logic inference for classification and prediction from data. In Proceedings of the ACM International Conference on Hybrid Systems: Computation and Control (HSCC), Philadelphia, PA, USA, 15–17 April 2014; pp. 273–282. [Google Scholar]
- Gabbay, D.M.; Guenthner, F. Handbook of Philosophical Logic, 2nd ed.; Springer Publishing: New York, NY, USA, 2014; p. 62. [Google Scholar]
- Blackburn, P.; Tzakova, M. Hybrid Languages and Temporal Logic. Logic J. IGPL 1999, 7, 27–54. [Google Scholar] [CrossRef]
- Prior, A.N.; Hasle, P.F.V. Papers on Time and Tense; Oxford University Press: Oxford, UK, 2003; pp. 93–171. [Google Scholar]
- Brauner, T. Hybrid Logic and Its Proof-Theory; Springer Publishing: New York, NY, USA, 2001; pp. 21–56. [Google Scholar]
- Trinh, C.; Meimaroglou, D.; Hoppe, S. Machine Learning in Chemical Product Engineering: The State of the Art and a Guide for Newcomers. Processes 2021, 9, 1456. [Google Scholar] [CrossRef]
- Marin, C.; Popescu, D.; Petre, E. Modeling and Control of the Orthogonalization Plants in Textile Industry. IEEE Trans. Ind. Appl. 2019, 55, 4247–4257. [Google Scholar] [CrossRef]
- Jian, N.L.; Zabiri, H.; Ramasamy, M. Data-Based Modeling of a Nonexplicit Two-Time Scale Process via Multiple Time-Scale Recurrent Neural Networks. Ind. Eng. Chem. Res. 2022, 61, 9356–9365. [Google Scholar] [CrossRef]
- Jieyang, P.; Kimmig, A.; Dongkun, W.; Niu, Z.; Zhi, F.; Jiahai, W.; Liu, X.; Ovtcharova, J. A systematic review of data-driven approaches to fault diagnosis and early warning. J. Intell. Manuf. 2022, 1–28. [Google Scholar] [CrossRef]
- Deng, X.; Tian, X. A new fault isolation method based on unified contribution plots. In Proceedings of the 30th Chinese Control Conference, Yantai, China, 22–24 July 2011; pp. 4280–4285. [Google Scholar]
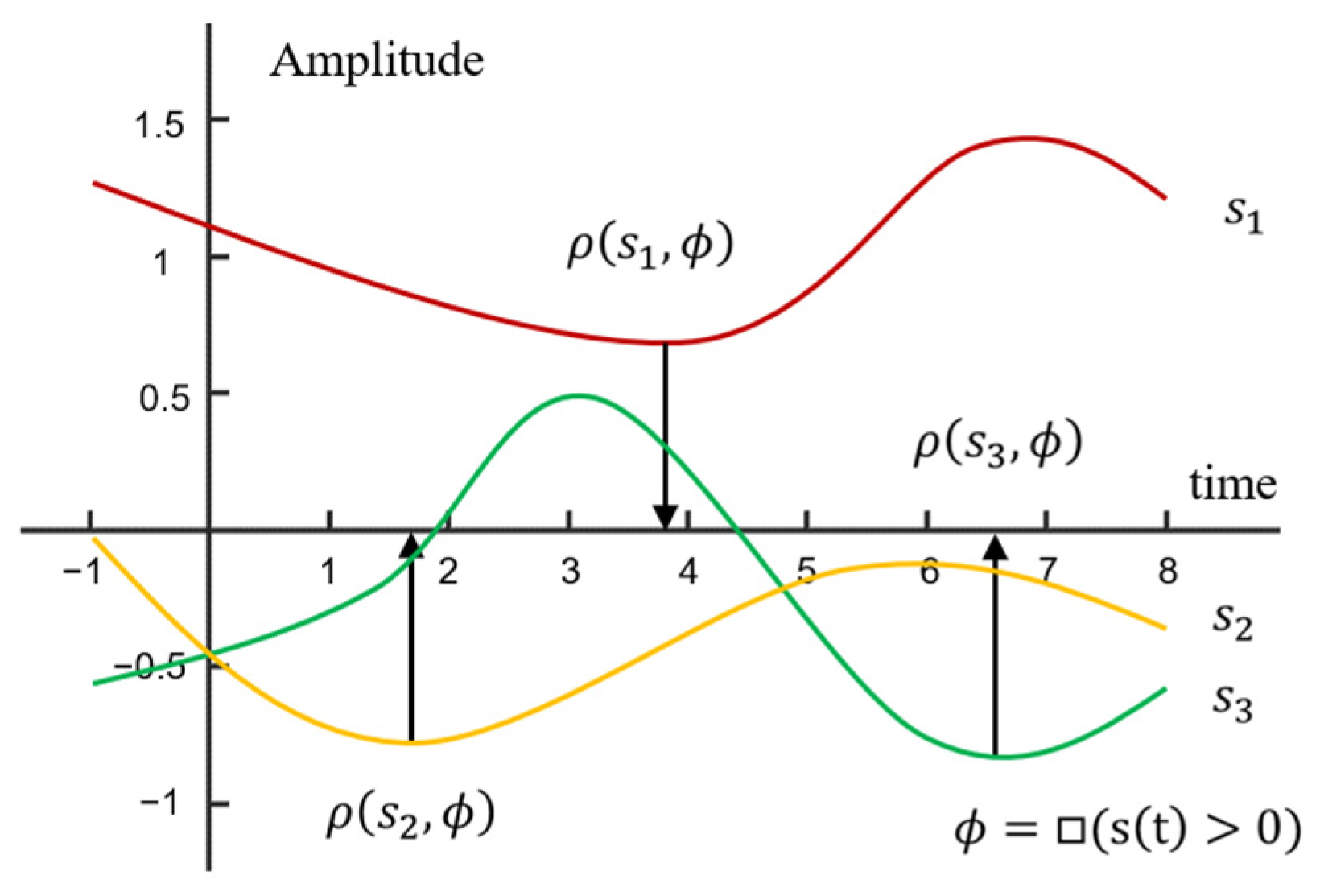
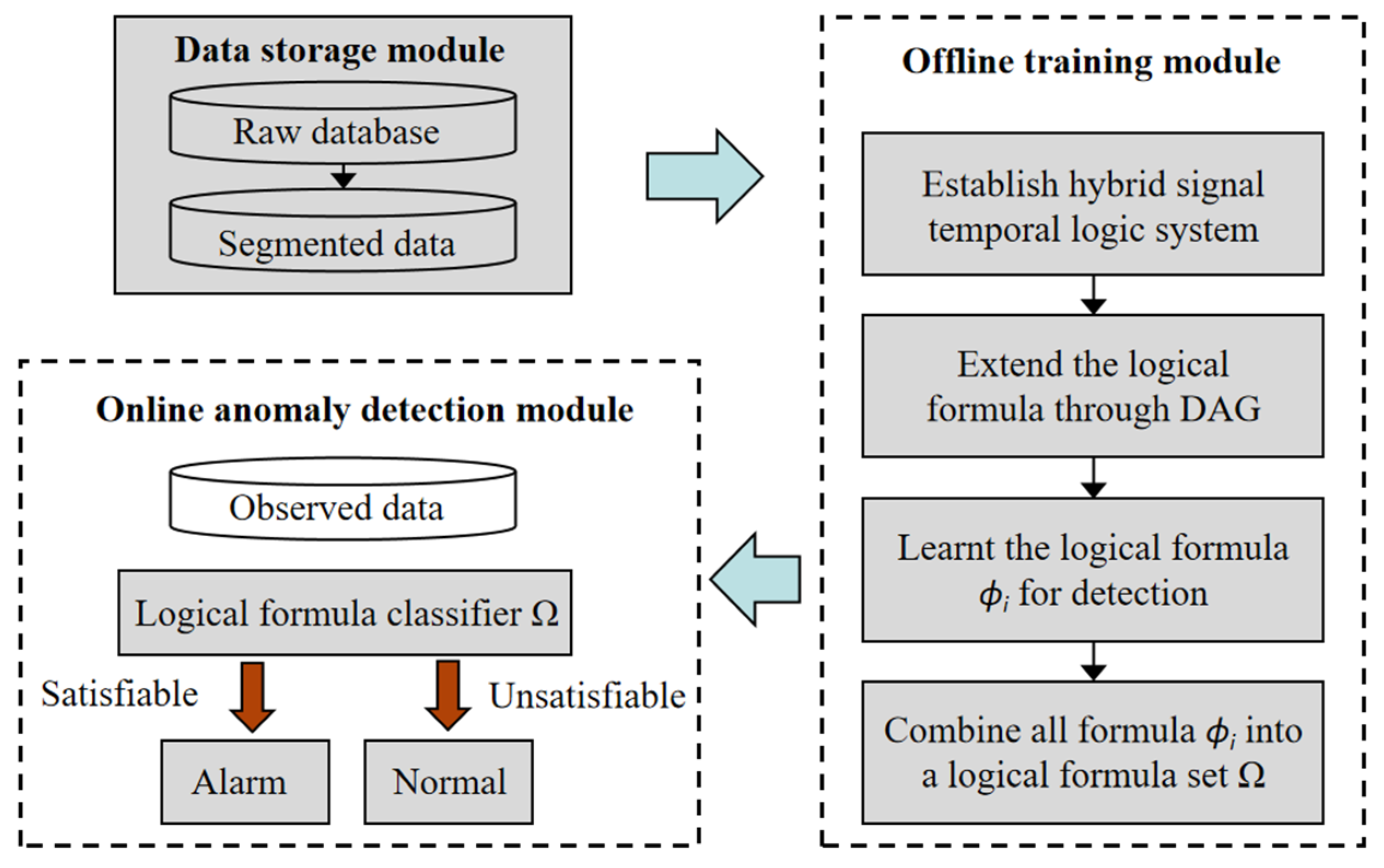
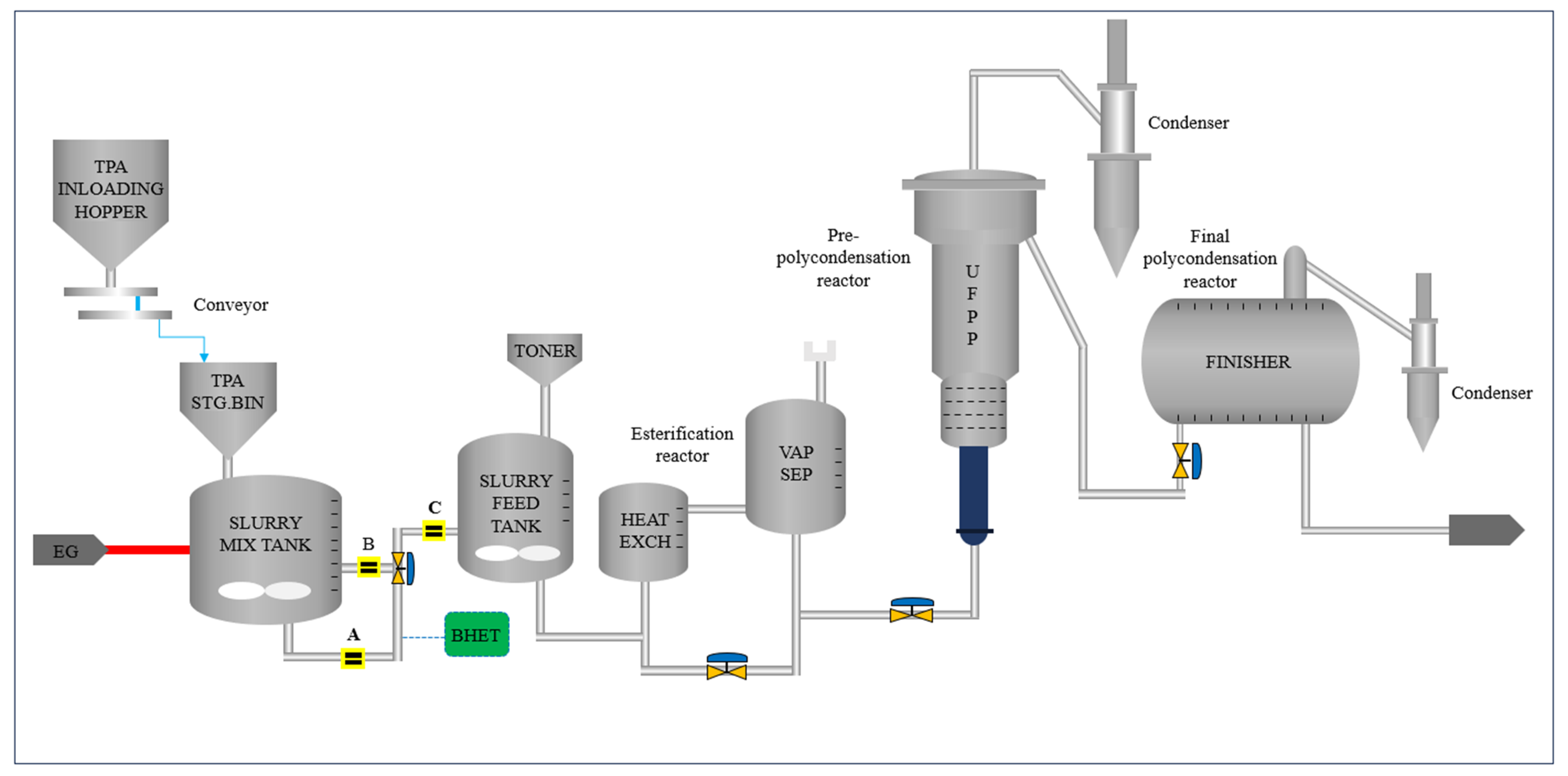
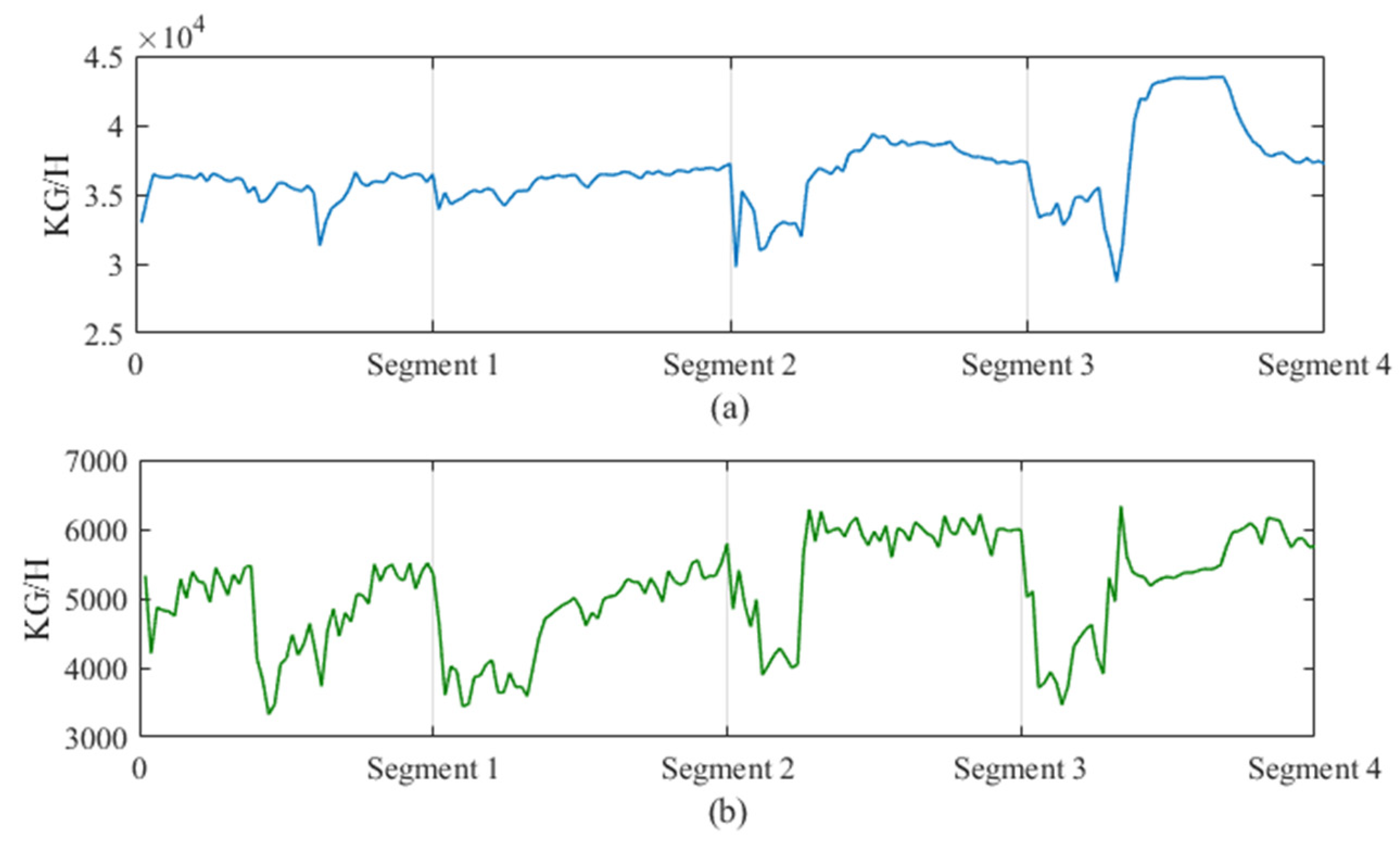
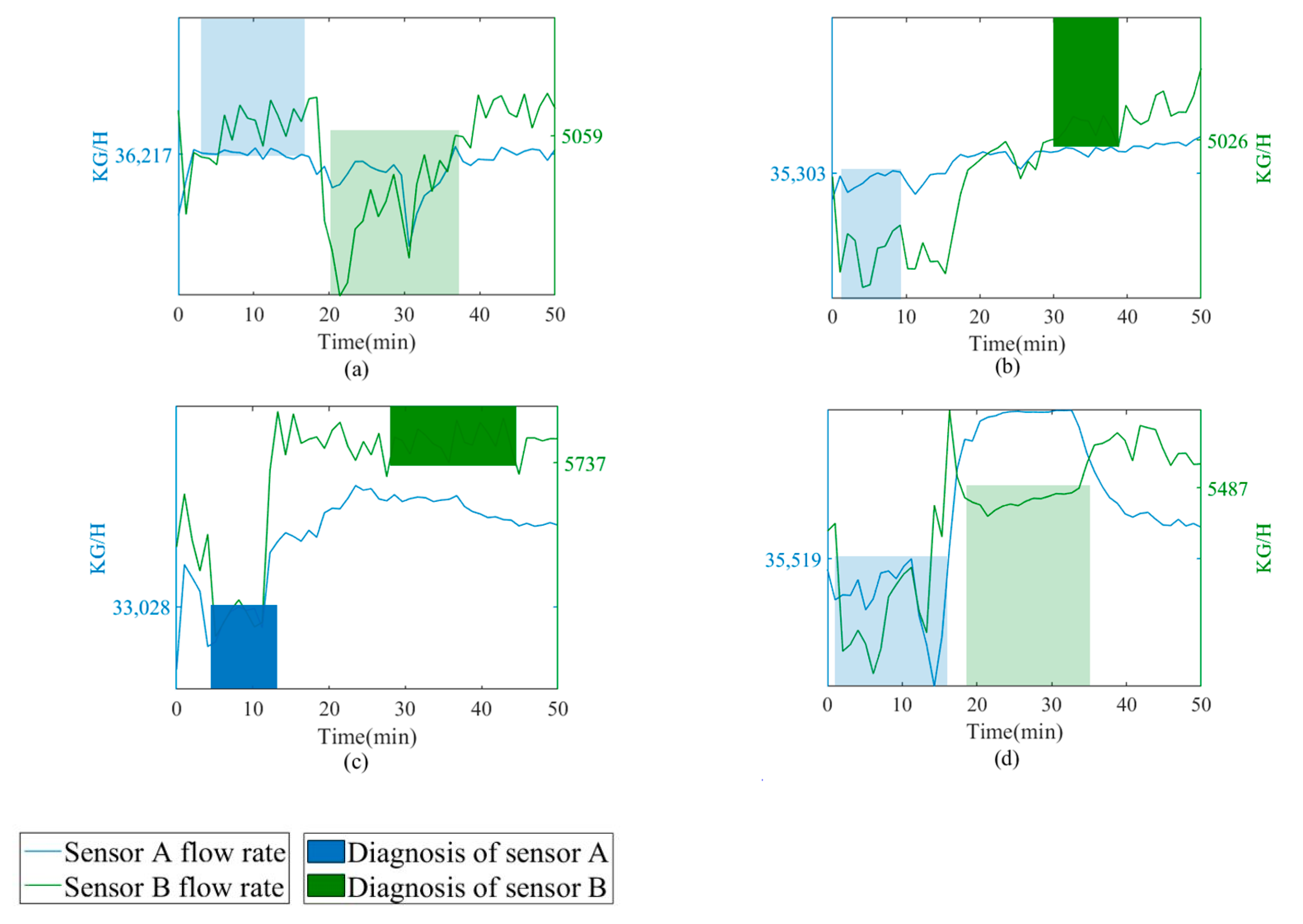



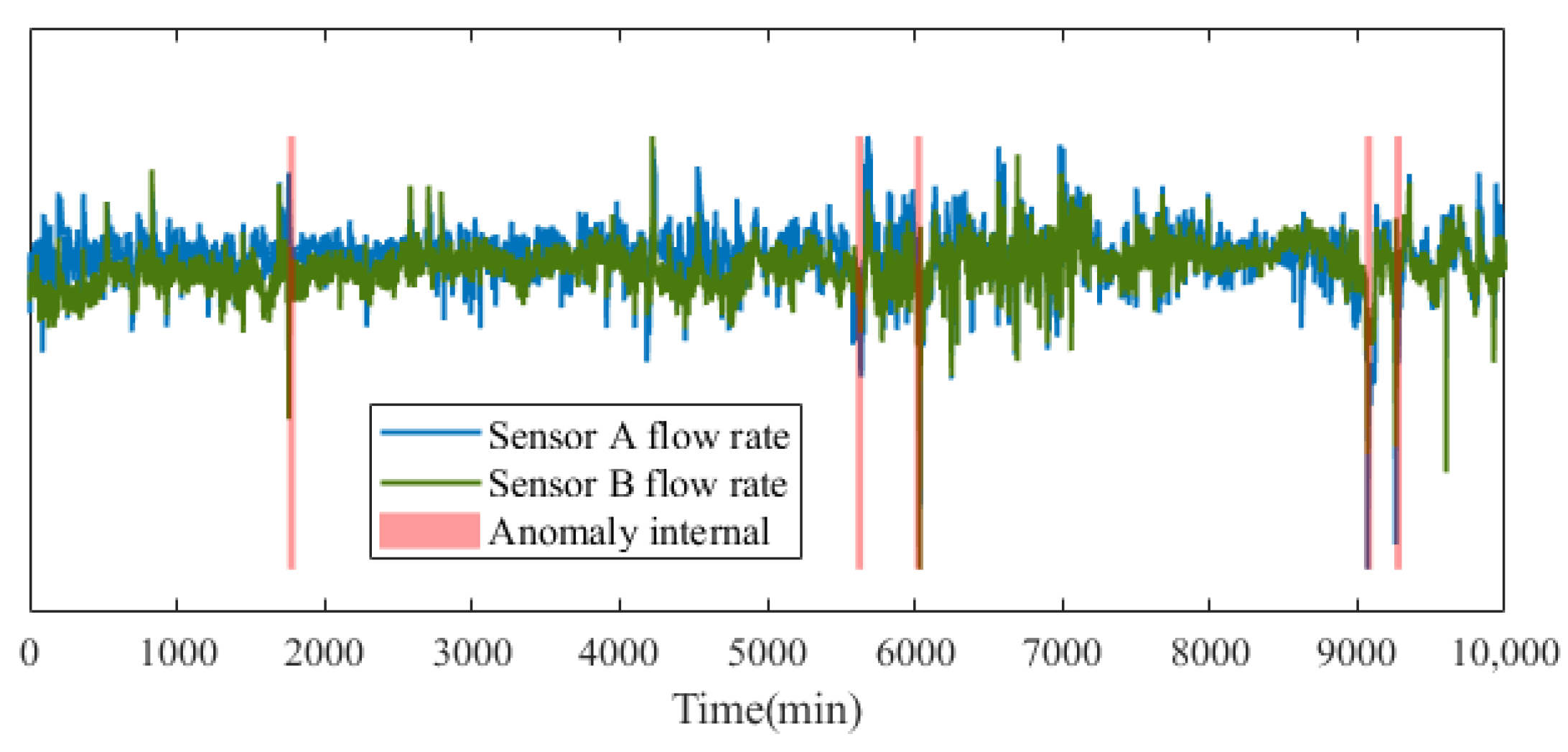

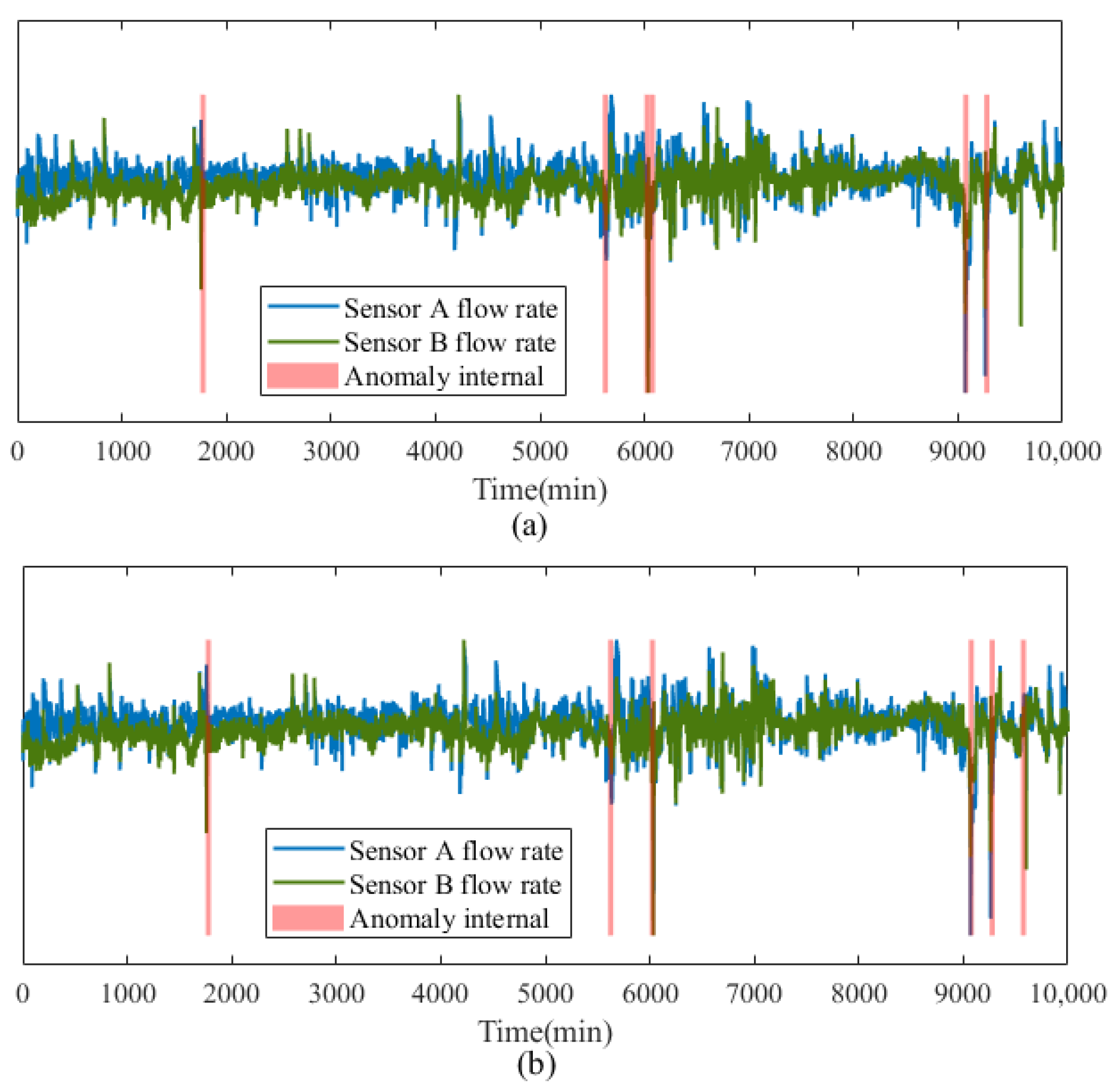


| Literature | Approach | Result Achieved | Application Background |
|---|---|---|---|
| Kong et al. (2014) [18] | Parameter signal temporal logic (PSTL) | Discover temporal logic properties of a system from data. | Herding Synthetic biology |
| Kong et al. (2017) [15] | Inference parametric signal temporal logic (iPSTL) | Use data to construct a signal temporal logic (STL) formula that describes normal system behavior. | Naval surveillance Train braking system |
| Liu et al. (2017) [17] | Timed multivariate statistical logic (TMSL) | Specify not only spatial features but also temporal dynamics of systems in a formal manner. | Robot arm system |
| Bartocci et al. (2018) [14] | Tree-spatial superposition logic (TSSL) | A formal framework for specifying, detecting, and generating spatial patterns in reaction–diffusion networks. | Turing’s reaction–diffusion system |
| Chen et al. (2021) [10] | Agenda-based, learning-enabled algorithm | Construct the formal specifications of faults directly from data collected from IIoT-enabled systems. | Iron-making factory |
| Formulas | Semantic Anomaly Detection |
|---|---|
| From 0 to 50, the flow rate from Sensor A is higher than 36,217 at least once from time 3 to 18; as a result, the flow rate from Sensor B is lower than 5059 at least once from time 20 to 39. | |
| From 0 to 50, the flow rate from Sensor A is lower than 35,303 at least once from time 2 to 8; as a result, the flow rate from Sensor B is higher than 5026 the entire time from 30 to 38. | |
| From 0 to 50, the flow rate from Sensor A is lower than 33,028 the entire time from 5 to 12; as a result, the flow rate from Sensor B is higher than 5737 the entire time from 29 to 44. | |
| From 3 to 50, the flow rate from Sensor A is lower than 35,519 at least once from time 1 to 16; as a result, the flow rate from Sensor B is lower than 5487 at least once from time 19 to 34. |
| Precision | Recall | F1 | Rank | |
|---|---|---|---|---|
| PCA (SPE) | 1 | 0.7138 | 0.8330 | 7 |
| PCA (T2) | 1 | 0.7908 | 0.8832 | 6 |
| Deng [27] | 0.9875 | 0.8546 | 0.9161 | 5 |
| Huo [11] | 1 | 0.9245 | 0.9608 | 4 |
| LSTM | 0.9760 | 1 | 0.9879 | 3 |
| GRU | 0.9823 | 1 | 0.9911 | 2 |
| HSTL | 0.9999 | 0.9829 | 0.9913 | 1 |
| Precision | Recall | F1 | Time (s) | |
|---|---|---|---|---|
| HSTL with SA | 0.9999 | 0.9829 | 0.9913 | 5.17 |
| HSTL with PSO | 0.9967 | 0.9904 | 0.9935 | 6.32 |
| HSTL with GA | 1 | 0.9879 | 0.9939 | 22.57 |
| Variance | Decrease | ||
|---|---|---|---|
| Before Detection | After Detection | ||
| Sensor A | 6204.2 | 4724.5 | 23.85% |
| Sensor C | 2906.3 | 1982.8 | 31.78% |
| Formulas | Semantic Anomaly Detection |
|---|---|
| From 0 to 50, the flow rate from sensor A is higher than 36,217 at least once from time 3 to 18; as a result, the flow rate from Sensor C is lower than 31,014 at least once from time 20 to 39. | |
| From 0 to 50, the flow rate from Sensor A is lower than 35,303 at least once within Time 2 to 8; as a result, the flow rate from Sensor C is higher than 30,950 the entire time from 30 to 38. | |
| From 0 to 50, the flow rate from Sensor A is lower than 33,028 the entire time from 5 to 12; as a result, the flow rate from Sensor C is higher than 32,330 the entire time from 29 to 44. | |
| From 3 to 50, the flow rate from Sensor A is lower than 35,519 at least once from time 1 to 16; as a result, the flow rate from Sensor C is lower than 31,845 at least once from time 19 to 34. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, X.; Hao, K. Semantic Hybrid Signal Temporal Logic Learning-Based Data-Driven Anomaly Detection in the Textile Process. Processes 2023, 11, 2804. https://doi.org/10.3390/pr11092804
Huo X, Hao K. Semantic Hybrid Signal Temporal Logic Learning-Based Data-Driven Anomaly Detection in the Textile Process. Processes. 2023; 11(9):2804. https://doi.org/10.3390/pr11092804
Chicago/Turabian StyleHuo, Xu, and Kuangrong Hao. 2023. "Semantic Hybrid Signal Temporal Logic Learning-Based Data-Driven Anomaly Detection in the Textile Process" Processes 11, no. 9: 2804. https://doi.org/10.3390/pr11092804
APA StyleHuo, X., & Hao, K. (2023). Semantic Hybrid Signal Temporal Logic Learning-Based Data-Driven Anomaly Detection in the Textile Process. Processes, 11(9), 2804. https://doi.org/10.3390/pr11092804






