Dynamic Pressure Analysis of Shale Gas Wells Considering Three-Dimensional Distribution and Properties of the Hydraulic Fracture Network
Abstract
:1. Introduction
2. Methodology
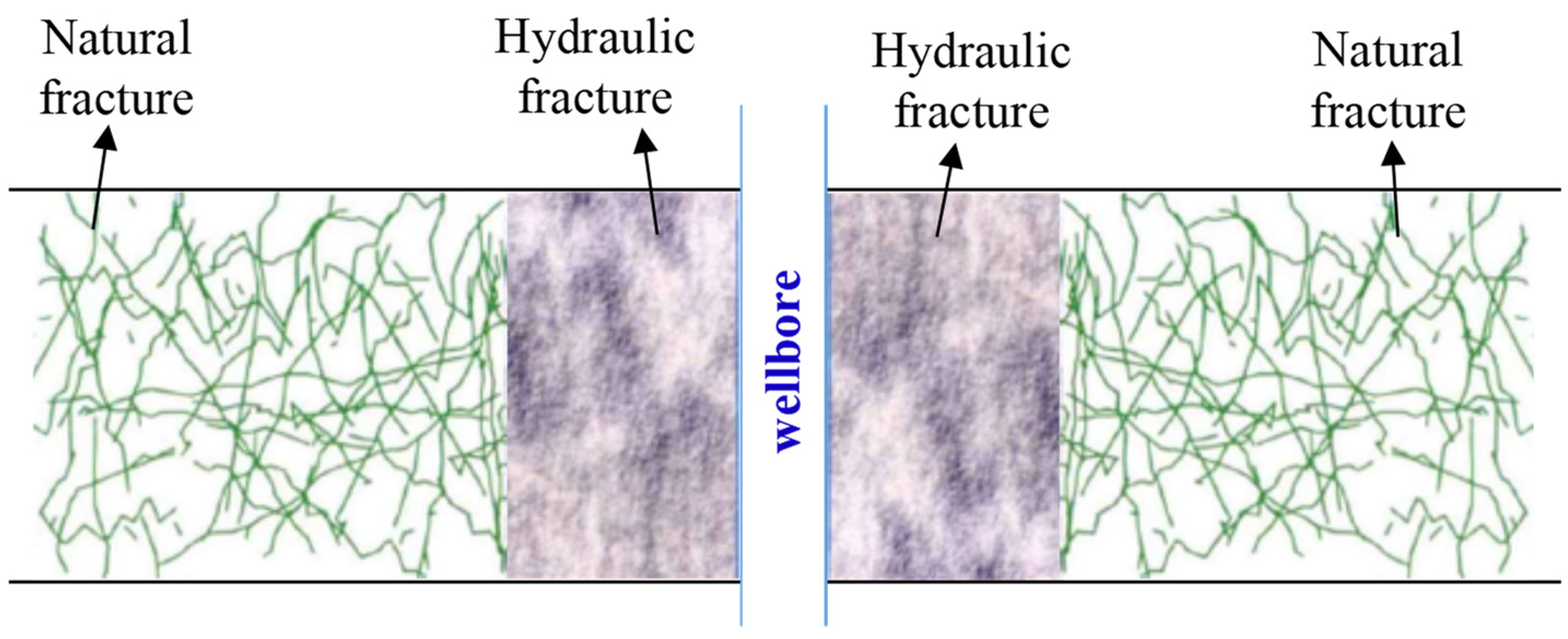
2.1. Model Assumption
2.2. Mathematical Model
2.2.1. Fluid Flow in the Hydraulic Fracture
2.2.2. Fluid Flow in the Shale Gas Reservoir
2.3. Solution to Mathematical Model
2.3.1. Dimensionless Mathematical Model
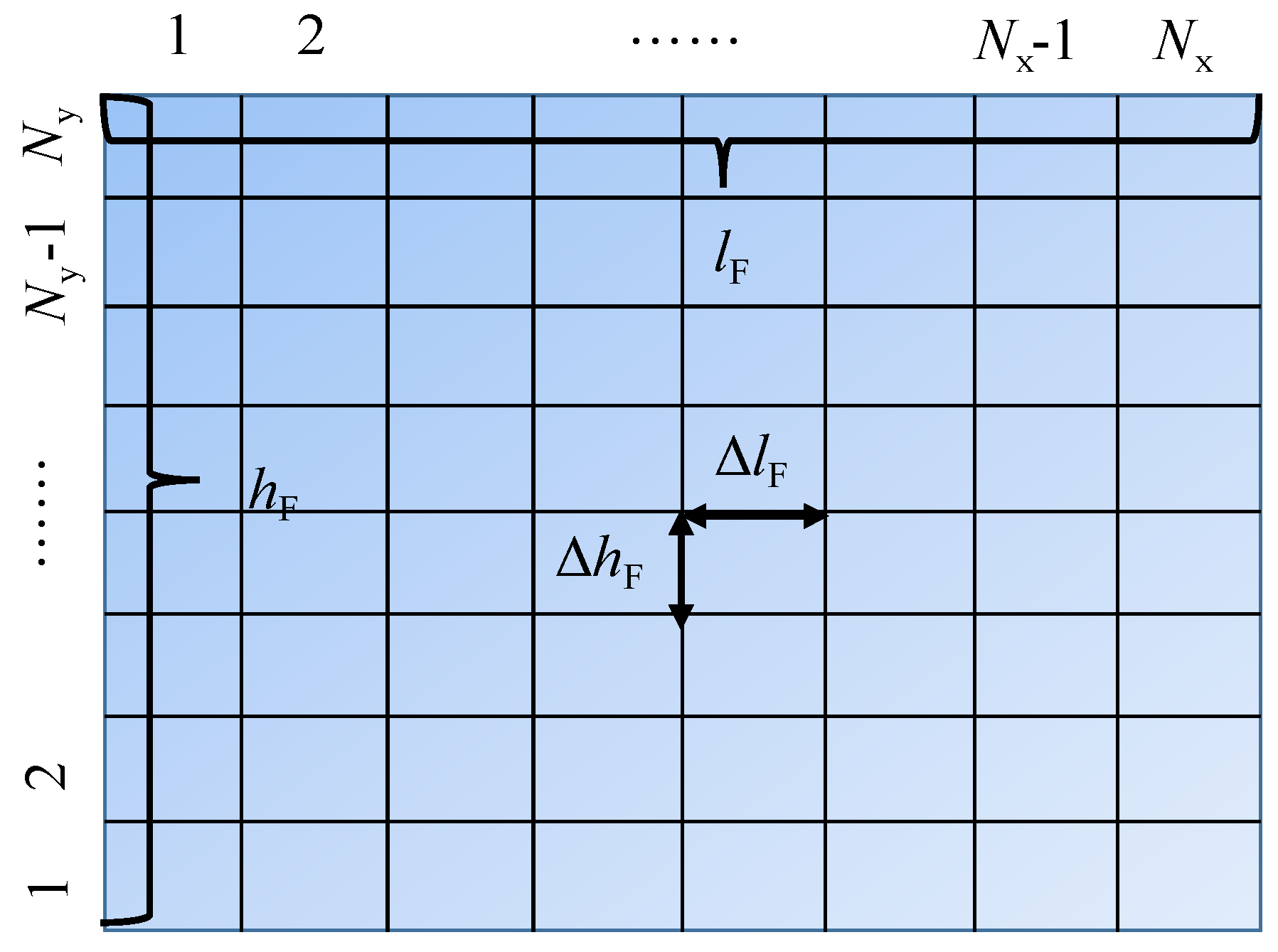
2.3.2. Solution of the Numerical Fracture Flow Model
2.3.3. Solution of the Reservoir Flow Model
2.3.4. Coupling Conditions for Flow in the Two Systems
3. Results and Discussion
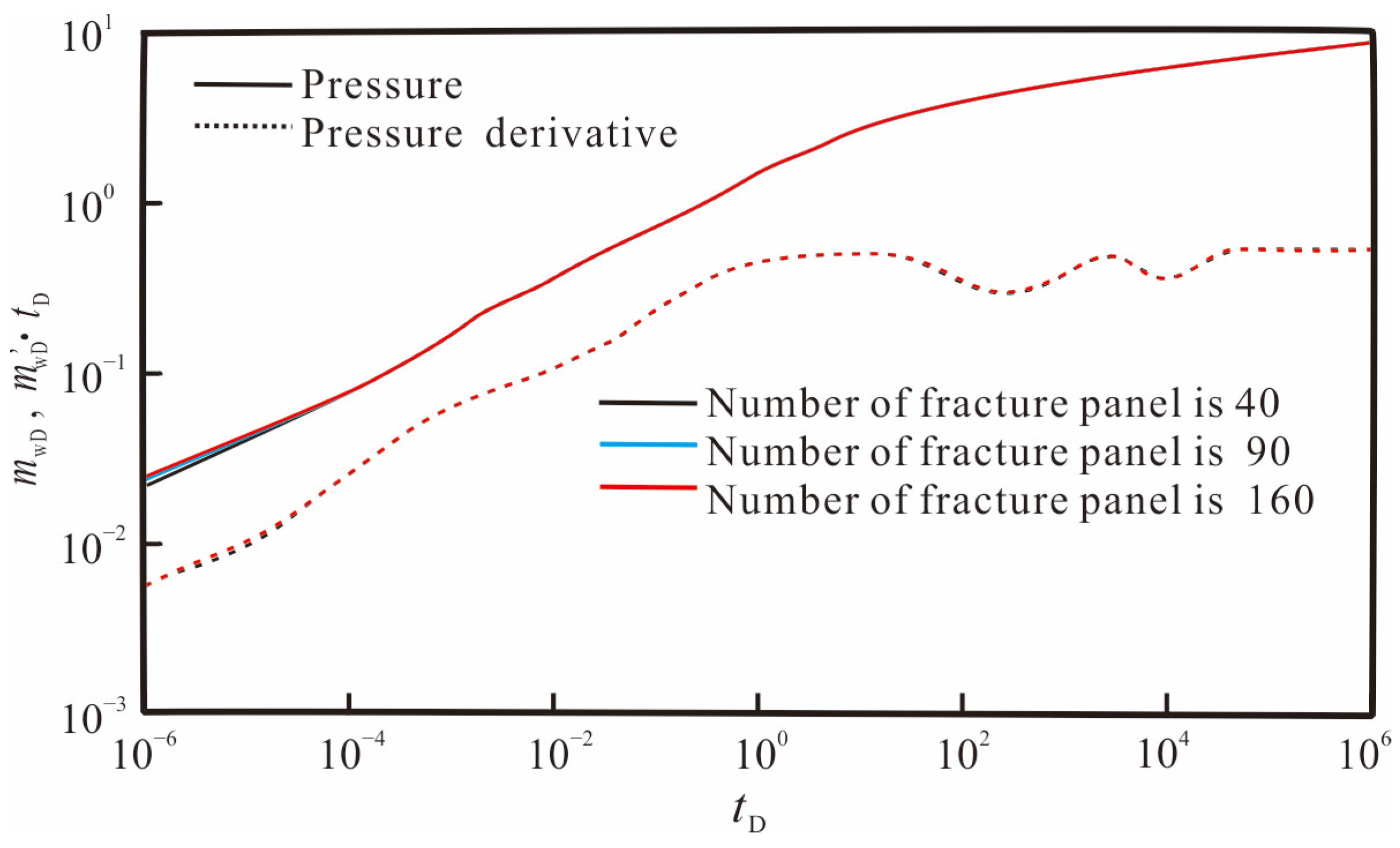
3.1. Model Verification
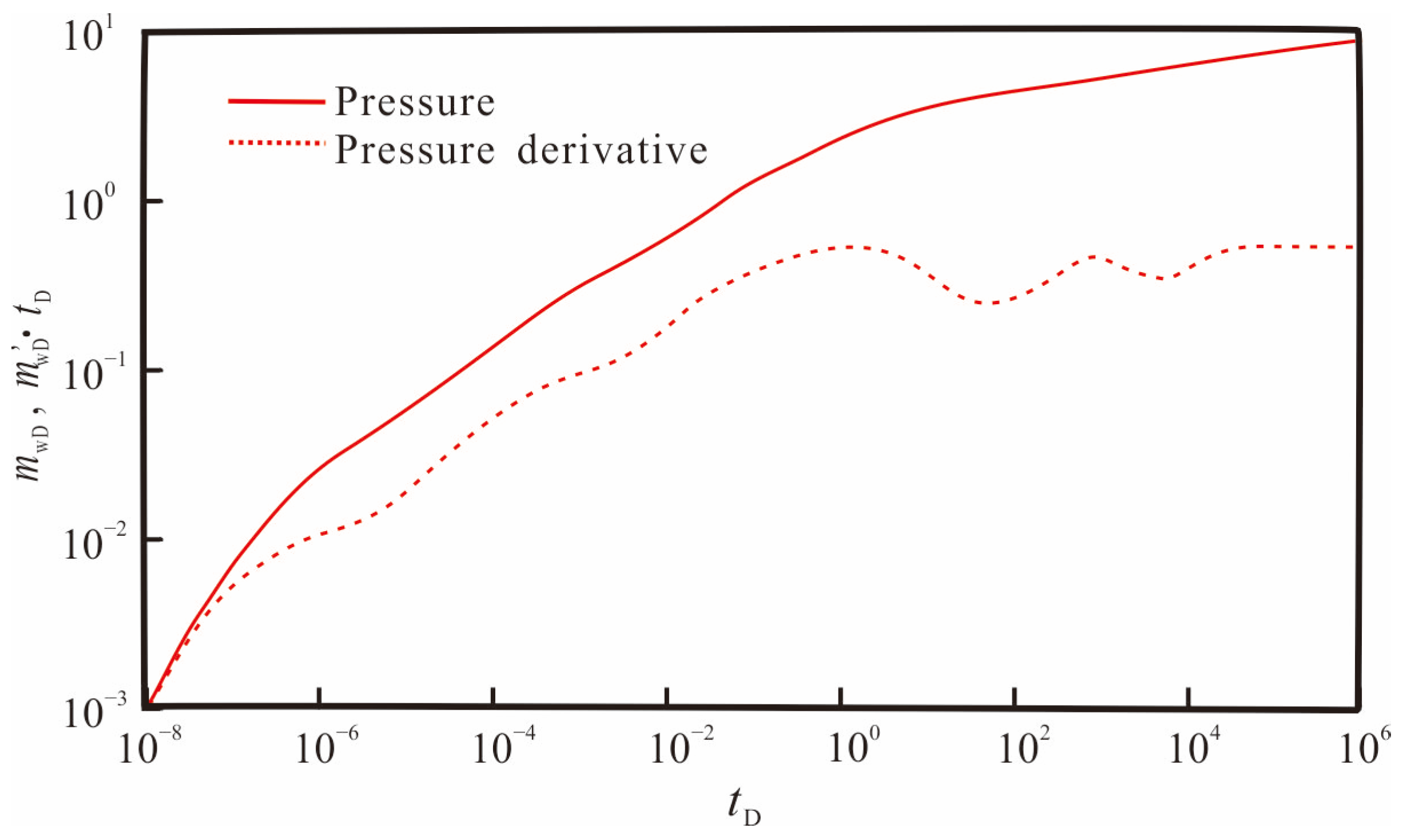
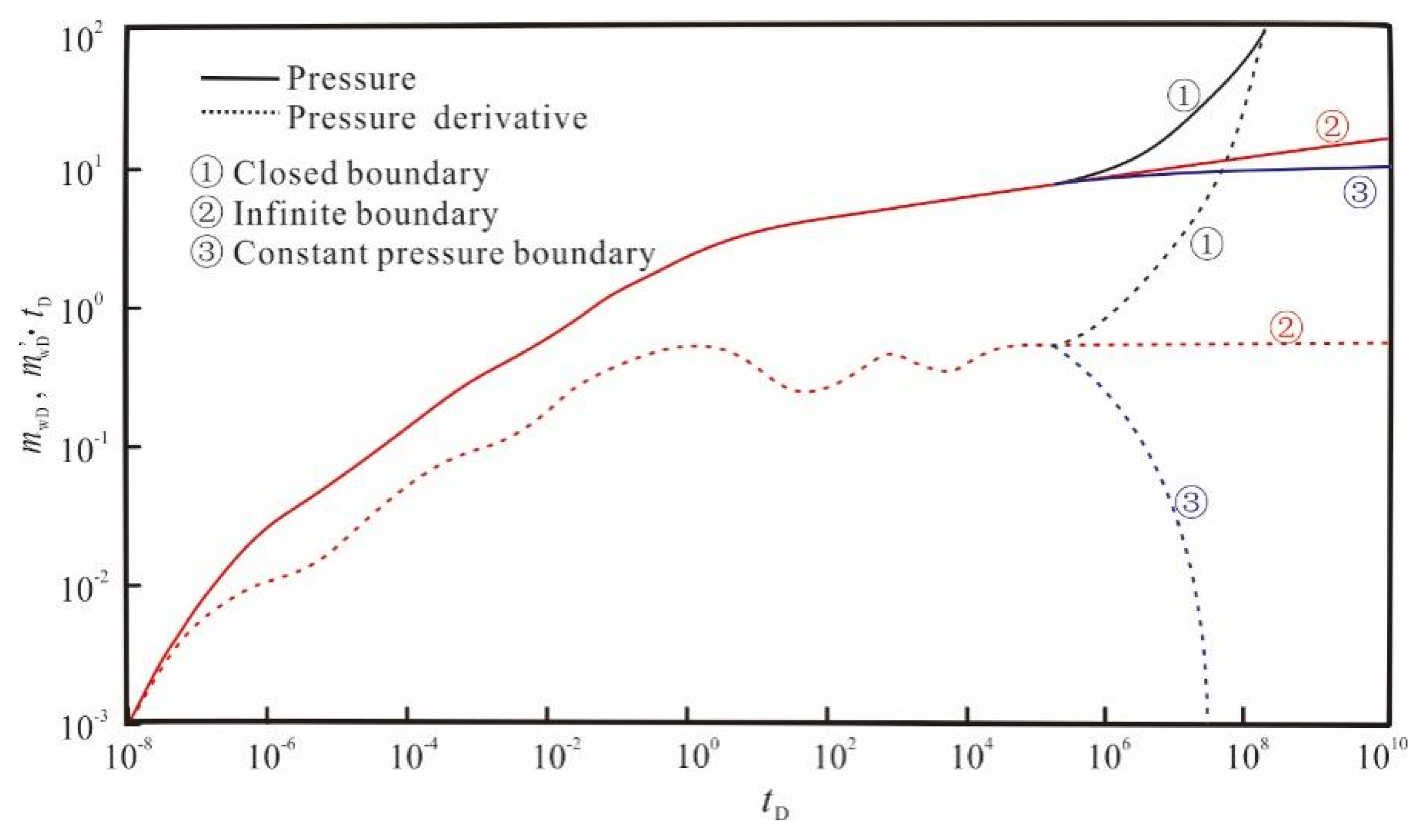
3.2. Flow Regime Identification
- (1)
- First radial flow regime of the hydraulic fracture
- (2)
- Bi-linear flow regime
- (3)
- Linear flow regime in the formation
- (4)
- The second radial flow regime
- (5)
- Horizontal elliptical flow regime
- (6)
- Adsorbed gas desorption and diffusion regime
- (7)
- Inter-porosity flow from the matrix to the micro-fractures
- (8)
- Boundary dominated flow regime
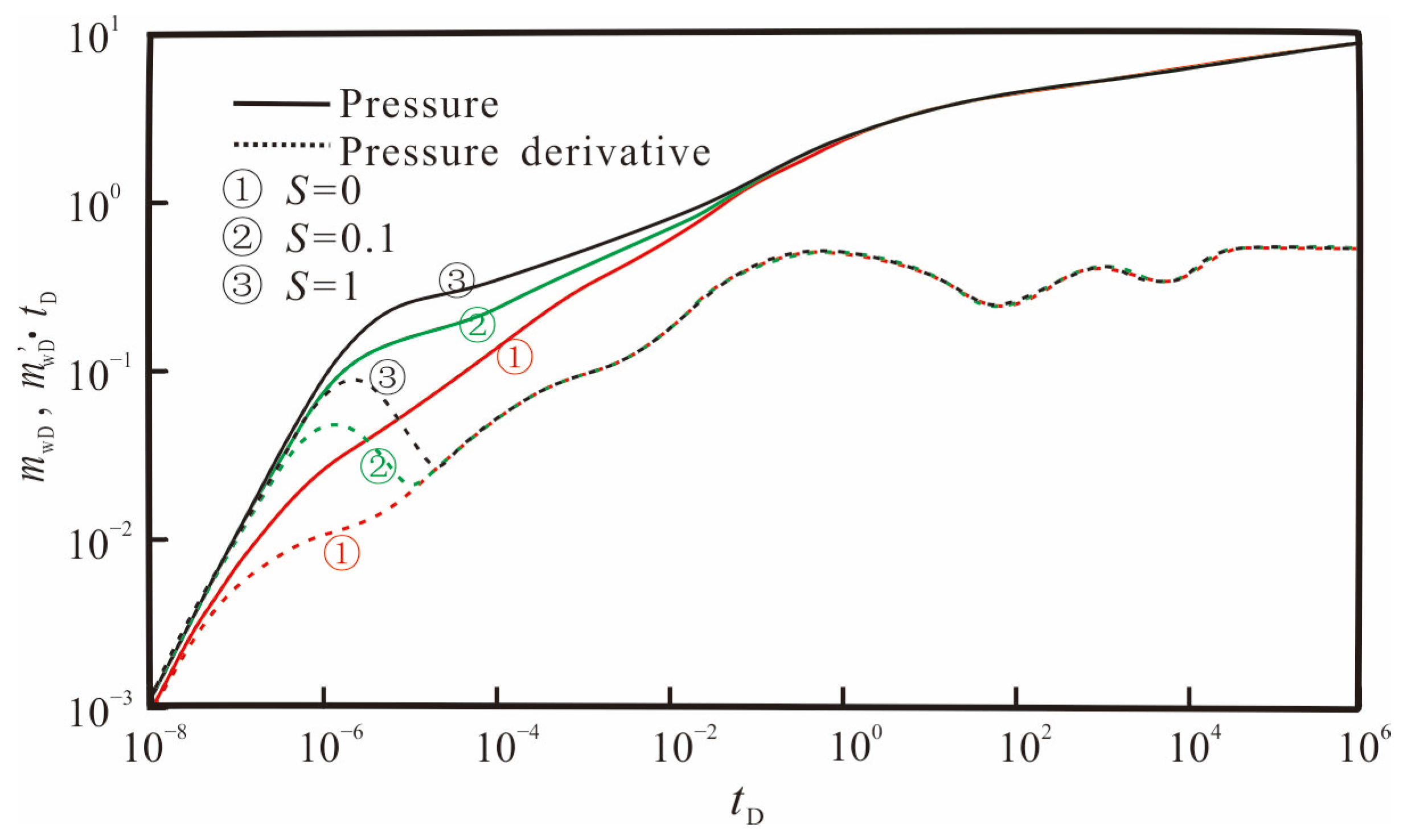
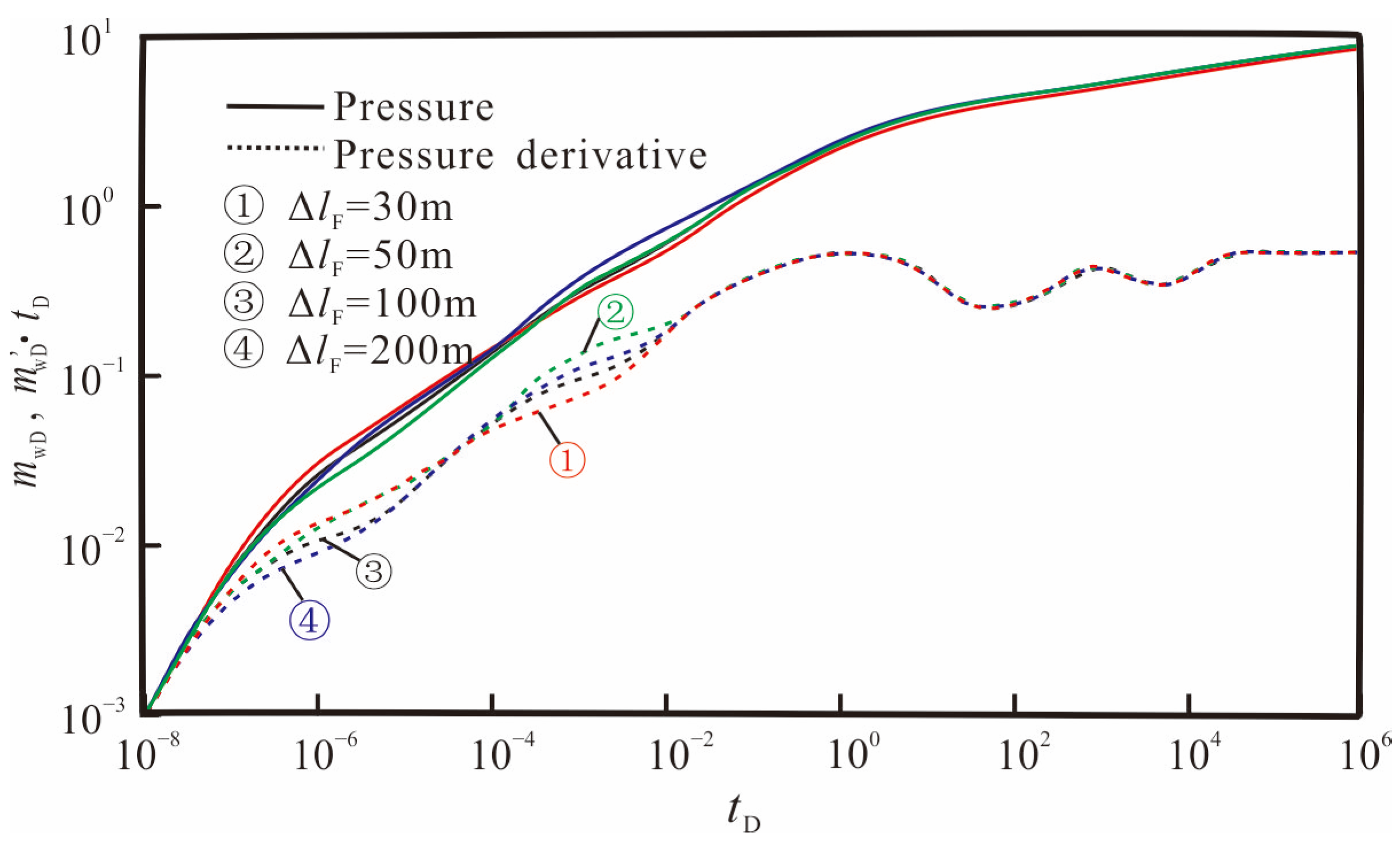
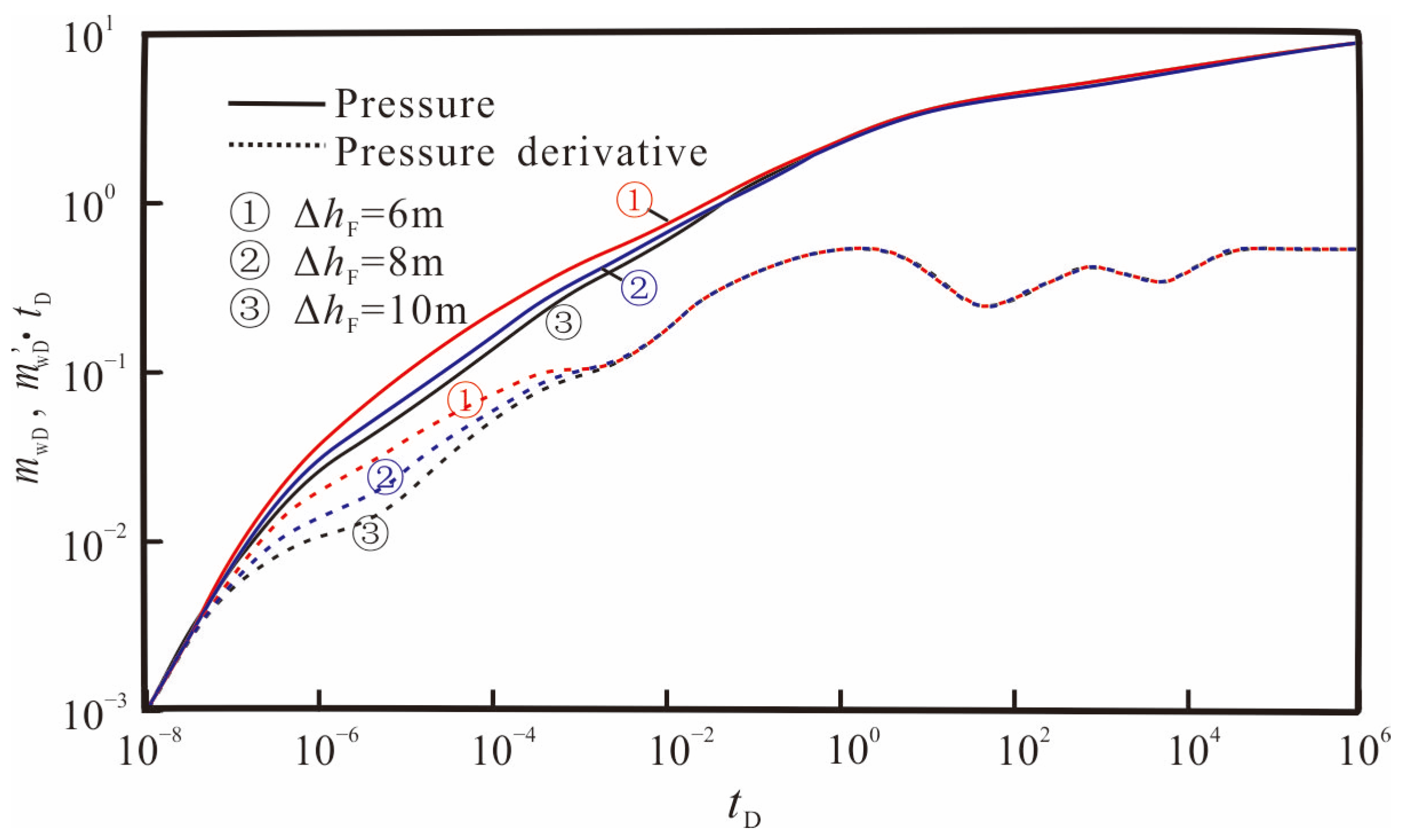
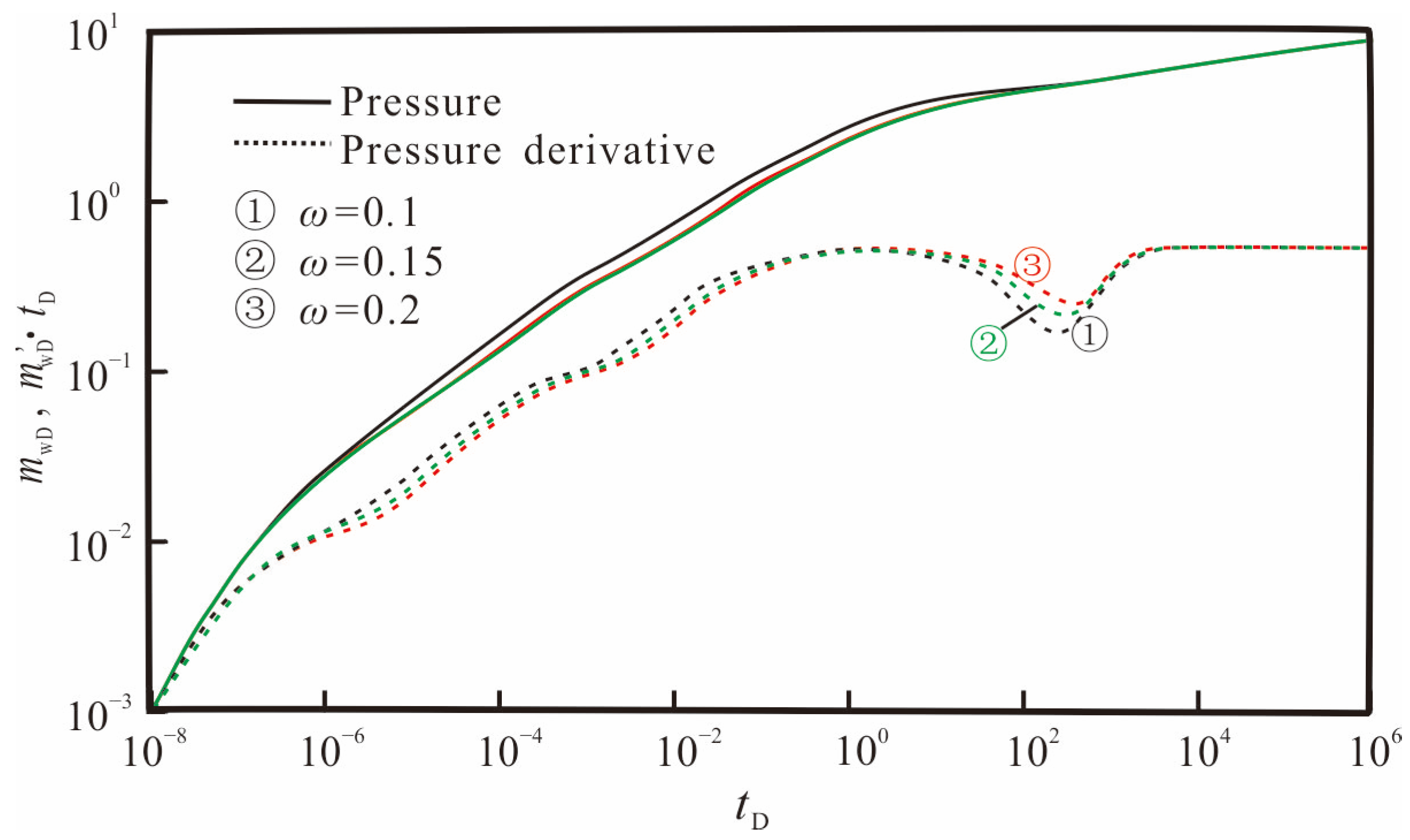
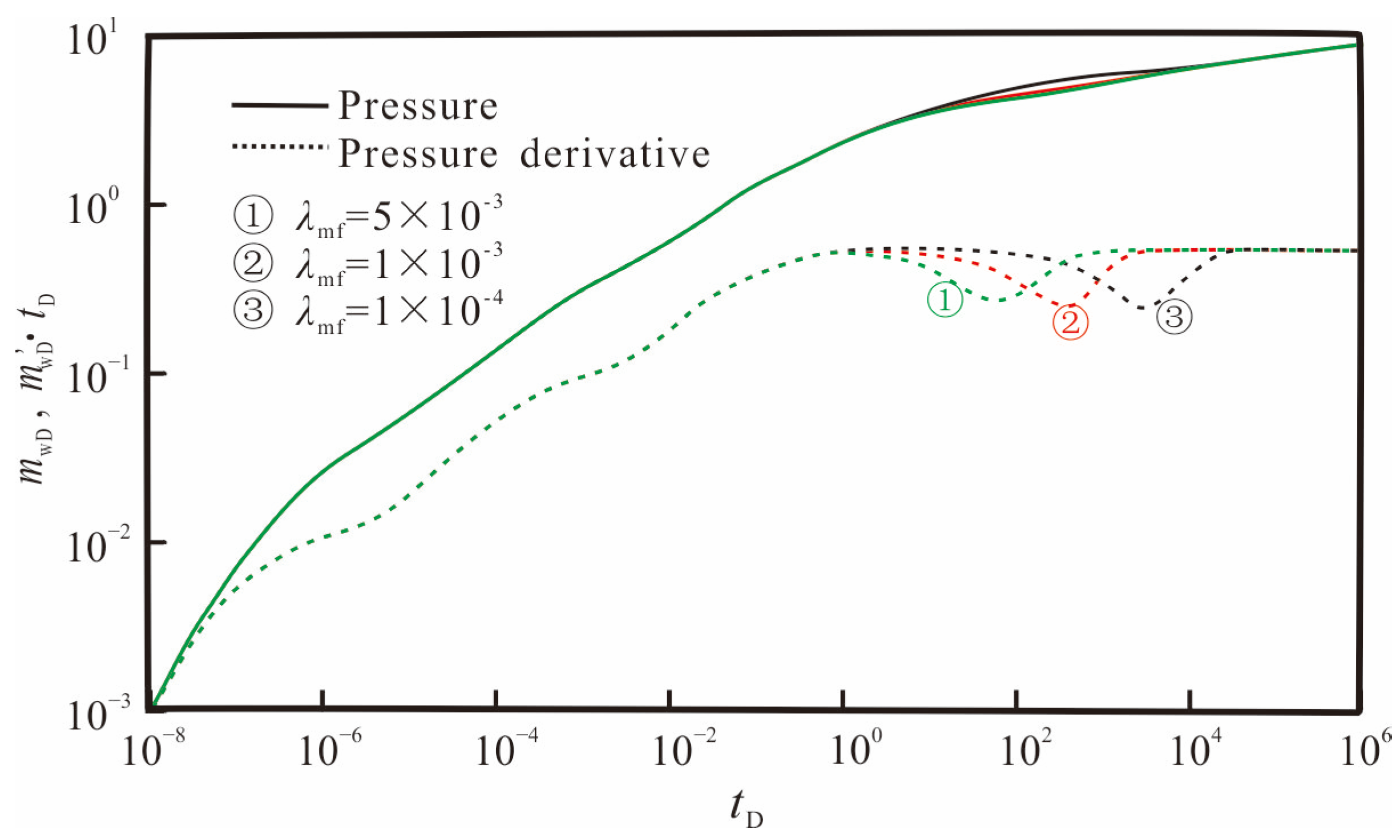
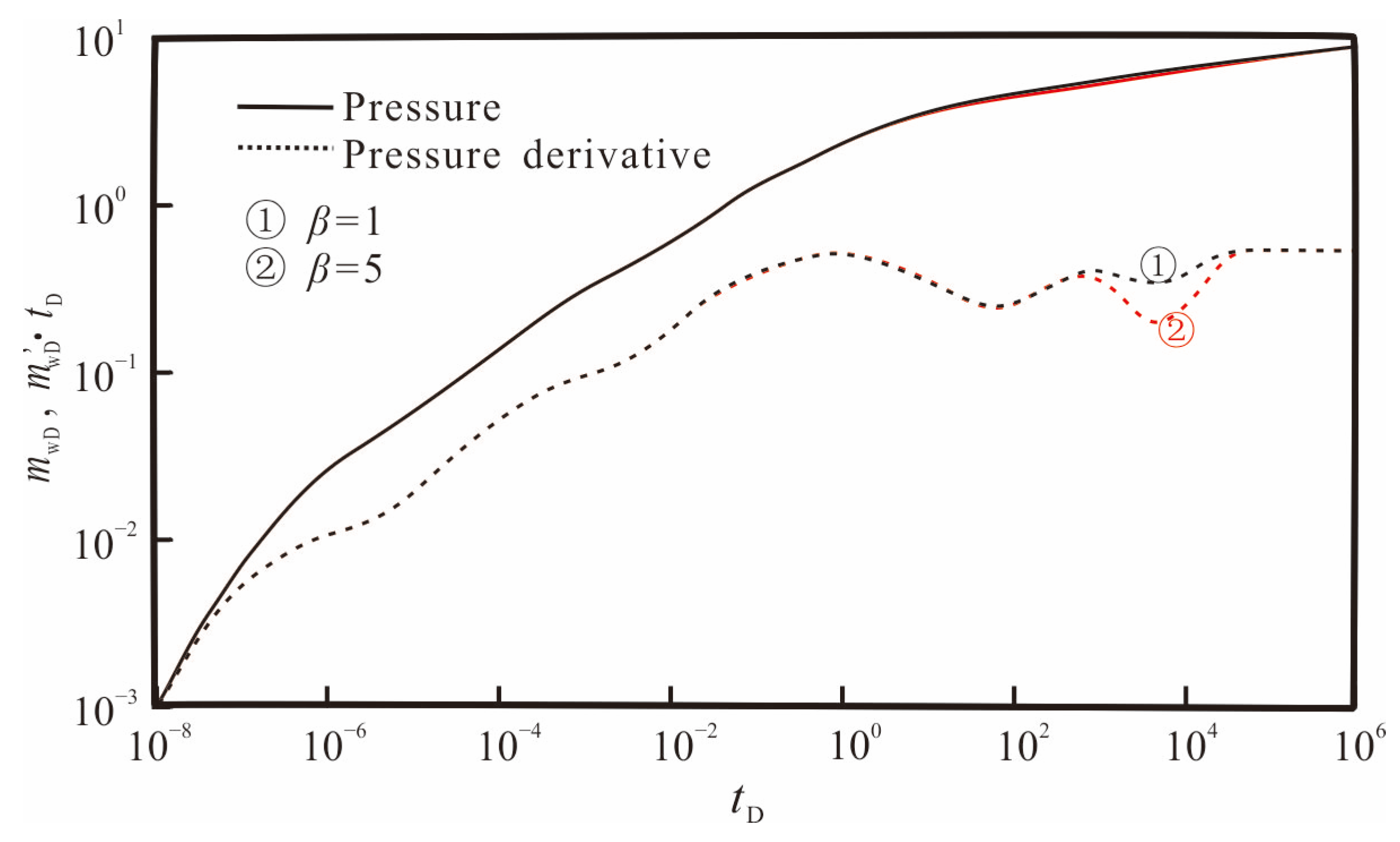
3.3. Sensitivity Analysis
4. Conclusions
- The semi-analytical model employs only a small number of grid divisions for the fracture network, thereby reducing the number of grids required while allowing for a flexible description of the three-dimensional fracture distribution, leading to significant improvements in calculation efficiency. Additionally, the coupling solution method of the three-dimensional discrete fracture flow numerical solution and the reservoir flow analytical solution enhances the accuracy of the early flow simulation;
- The shale gas well testing interpretation curve obtained in this research comprises nine main flow stages: early wellbore storage and skin effect stage, first radial flow stage of fracture, bilinear flow stage, formation linear flow stage, second radial flow stage of fracture, horizontal elliptical flow stage, adsorption gas diffusion and seepage stage, inter-porosity flow stage, and outer boundary reaction stage;
- Unlike conventional gas reservoirs, shale gas reservoirs incorporate adsorbed gas. Consequently, when the pressure wave propagates to the formation, the pressure drop of shale gas reservoirs is lower than that of conventional gas reservoirs due to the replenishment of desorbed gas. The conventional gas reservoir exhibits a curve position higher than that of the shale gas reservoir on the pseudo-pressure and pseudo-pressure derivative curves;
- Under certain reservoir conditions, the artificial fracture flow capacity, fracture length, and height are the main engineering factors affecting the pressure responses of shale gas wells. The larger the fracture flow capacity, fracture length, and height, the smaller the flow resistance of shale gas, and the smaller the production pressure difference under the same production rate. Therefore, maximizing the degree and scope of reconstruction can enhance the gas well production capacity during fracturing construction.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cao, P.; Liu, J.; Leong, Y.-K. A fully coupled multiscale shale deformation-gas transport model for the evaluation of shale gas extraction. Fuel 2016, 178, 103–117. [Google Scholar] [CrossRef]
- Wang, H.; Chen, L.; Qu, Z.; Yin, Y.; Kang, Q.; Yu, B.; Tao, W.-Q. Modeling of multi-scale transport phenomena in shale gas production—A critical review. Appl. Energy 2020, 262, 114575. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, L.; Xiong, Y.; Zhou, Y.; Liu, Q.; Chen, D. Pressure response and production performance for multi-fractured horizontal wells with complex seepage mechanism in box-shaped shale gas reservoir. J. Nat. Gas Sci. Eng. 2016, 32, 66–80. [Google Scholar] [CrossRef]
- Zhao, X.; Rui, Z.; Liao, X.; Zhang, R. A simulation method for modified isochronal well testing to determine shale gas well productivity. J. Nat. Gas Sci. Eng. 2015, 27, 479–485. [Google Scholar] [CrossRef]
- Huang, T.; Guo, X.; Chen, F. Modeling transient flow behavior of a multiscale triple porosity model for shale gas reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 33–46. [Google Scholar] [CrossRef]
- Wei, S.; Xia, Y.; Jin, Y.; Chen, M.; Chen, K. Quantitative study in shale gas behaviors using a coupled triple-continuum and discrete fracture model. J. Pet. Sci. Eng. 2019, 174, 49–69. [Google Scholar] [CrossRef]
- Lin, L.; Li, G.; Zhao, J.; Ren, L.; Wu, J. Productivity model of shale gas fractured horizontal well considering complex fracture morphology. J. Pet. Sci. Eng. 2022, 208, 109511. [Google Scholar]
- Zhao, Y.-L.; Zhang, L.-H.; Zhao, J.-Z.; Luo, J.-X.; Zhang, B.-N. “Triple porosity” modeling of transient well test and rate decline analysis for multi-fractured horizontal well in shale gas reservoirs. J. Pet. Sci. Eng. 2013, 110, 253–262. [Google Scholar] [CrossRef]
- Yu, W.; Xu, Y.; Liu, M.; Wu, K.; Sepehrnoori, K. Simulation of shale gas transport and production with complex fractures using embedded discrete fracture model. AIChE J. 2018, 64, 2251–2264. [Google Scholar] [CrossRef]
- Zhao, Y.; Lu, G.; Zhang, L.; Wei, Y.; Guo, J.; Chang, C. Numerical simulation of shale gas reservoirs considering discrete fracture network using a coupled multiple transport mechanisms and geomechanics model. J. Pet. Sci. Eng. 2020, 195, 107588. [Google Scholar] [CrossRef]
- Tian, L.; Xiao, C.; Liu, M.; Gu, D.; Song, G.; Cao, H.; Li, X. Well testing model for multi-fractured horizontal well for shale gas reservoirs with consideration of dual diffusion in matrix. J. Nat. Gas Sci. Eng. 2014, 21, 283–295. [Google Scholar] [CrossRef]
- Ren, J.; Guo, P. A novel semi-analytical model for finite-conductivity multiple fractured horizontal wells in shale gas reservoirs. J. Nat. Gas Sci. Eng. 2015, 24, 35–51. [Google Scholar] [CrossRef]
- Xu, Y.; Liu, X.; Hu, Z.; Duan, X.; Chang, J. Bottom-hole pressure drawdown management of fractured horizontal wells in shale gas reservoirs using a semi-analytical model. Sci. Rep. 2022, 12, 22490. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Cheng, L.; Huang, S.; Jia, P.; Zhang, J.; Lan, X.; Huang, H. A practical method for production data analysis from multistage fractured horizontal wells in shale gas reservoirs. Fuel 2016, 186, 821–829. [Google Scholar] [CrossRef]
- Fan, D.; Ettehadtavakkol, A. Semi-analytical modeling of shale gas flow through fractal induced fracture networks with microseismic data. Fuel 2017, 193, 444–459. [Google Scholar] [CrossRef]
- Yang, R.; Huang, Z.; Li, G.; Yu, W.; Sepehrnoori, K.; Lashgari, H.R.; Tian, S.; Song, X.; Sheng, M. A semianalytical approach to model two-phase flowback of shale-gas wells with complex-fracture-network geometries. SPE J. 2017, 22, 1808–1833. [Google Scholar] [CrossRef]
- Huang, S.; Ding, G.; Wu, Y.; Huang, H.; Lan, X.; Zhang, J. A semi-analytical model to evaluate productivity of shale gas wells with complex fracture networks. J. Nat. Gas Sci. Eng. 2018, 50, 374–383. [Google Scholar] [CrossRef]
- Xu, B.; Wu, Y.; Cheng, L.; Huang, S.; Bai, Y.; Chen, L.; Liu, Y.; Yang, Y.; Yang, L. Uncertainty quantification in production forecast for shale gas well using a semi-analytical model. J. Pet. Explor. Prod. Technol. 2019, 9, 1963–1970. [Google Scholar] [CrossRef]
- Fang, B.; Hu, J.; Xu, J.; Zhang, Y. A semi-analytical model for horizontal-well productivity in shale gas reservoirs: Coupling of multi-scale seepage and matrix shrinkage. J. Pet. Sci. Eng. 2020, 195, 107869. [Google Scholar] [CrossRef]
- Chen, Z.; Liao, X.; Zhao, X.; Dou, X.; Zhu, L. Performance of horizontal wells with fracture networks in shale gas formation. J. Pet. Sci. Eng. 2015, 133, 646–664. [Google Scholar] [CrossRef]
- Ren, L.; Lin, R.; Zhao, J.; Rasouli, V.; Zhao, J.; Yang, H. Stimulated reservoir volume estimation for shale gas fracturing: Mechanism and modeling approach. J. Pet. Sci. Eng. 2018, 166, 290–304. [Google Scholar] [CrossRef]
- Wang, H. Discrete fracture networks modeling of shale gas production and revisit rate transient analysis in heterogeneous fractured reservoirs. J. Pet. Sci. Eng. 2018, 169, 796–812. [Google Scholar] [CrossRef]
- Wang, T.; Tian, S.; Zhang, W.; Ren, W.; Li, G. Production model of a fractured horizontal well in shale gas reservoirs. Energy Fuels 2020, 35, 493–500. [Google Scholar] [CrossRef]
- Dai, C.; Liu, H.; Wang, Y.; Li, X.; Wang, W. A simulation approach for shale gas development in China with embedded discrete fracture modeling. Mar. Pet. Geol. 2019, 100, 519–529. [Google Scholar] [CrossRef]
- Zhang, D.; Dai, Y.; Ma, X.; Zhang, L.; Zhong, B.; Wu, J.; Tao, Z. An analysis for the influences of fracture network system on multi-stage fractured horizontal well productivity in shale gas reservoirs. Energies 2018, 11, 414. [Google Scholar] [CrossRef]
- Mi, L.; Jiang, H.; Mou, S.; Li, J.; Pei, Y.; Liu, C. Numerical simulation study of shale gas reservoir with stress-dependent fracture conductivity using multiscale discrete fracture network model. Part. Sci. Technol. 2018, 36, 202–211. [Google Scholar]
- Wu, Y.; Cheng, L.; Huang, S.; Bai, Y.; Jia, P.; Wang, S.; Xu, B.; Chen, L. An approximate semianalytical method for two-phase flow analysis of liquid-rich shale gas and tight light-oil wells. J. Pet. Sci. Eng. 2019, 176, 562–572. [Google Scholar] [CrossRef]
- Wang, S.; Bai, Y.; Xu, B.; Li, Y.; Chen, L.; Dong, Z.; Li, W.; Zheng, X.; Wang, X. A hybrid model for simulating fracturing fluid flowback in tight sandstone gas wells considering a three-dimensional discrete fracture. Lithosphere 2021, 2021, 7673447. [Google Scholar] [CrossRef]
- Jia, Y.-L.; Wang, B.-C.; Nie, R.-S.; Wang, D.-L. New transient-flow modelling of a multiple-fractured horizontal well. J. Geophys. Eng. 2014, 11, 15013. [Google Scholar] [CrossRef]
- Xu, J.; Wu, K.; Yang, S.; Cao, J.; Chen, Z.; Pan, Y.; Yan, B. Real gas transport in tapered noncircular nanopores of shale rocks. AIChE J. 2017, 63, 3224–3242. [Google Scholar] [CrossRef]
- Xu, J.; Wu, K.; Li, R.; Li, Z.; Li, J.; Xu, Q.; Li, L.; Chen, Z. Nanoscale pore size distribution effects on gas production from fractal shale rocks. Fractals 2019, 27, 1950142. [Google Scholar] [CrossRef]
- Wang, S.; Li, D.; Li, W. A Semi-Analytical Model for Production Prediction of Deep CBM Wells Considering Gas-Water Two-Phase Flow. Processes 2023, 11, 3022. [Google Scholar] [CrossRef]
- Bai, Y.; Wang, S.; Xu, B.; Li, D.; Fan, W.; Wu, J.; Huang, S. Prediction Model for Tight Gas Wells with Time-Dependent Mechanism and Stress Sensitivity Effect. ACS Omega 2023, 8, 43037–43050. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Cheng, L.; Huang, S.; Liu, H. Transient behavior of complex fracture networks. J. Pet. Sci. Eng. 2015, 132, 1–17. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]





| Parameters | Symbol | Definition |
|---|---|---|
| Dimensionless pseudo pressure of the hydraulic fracture | ||
| Dimensionless pseudo pressure of the micro-fracture | ||
| Dimensionless pseudo time | ||
| Dimensionless hydraulic fracture conductivity | ||
| Dimensionless hydraulic fracture pressure transmitting coefficient | ||
| Dimensionless gas flux entering the fracture from the matrix at a point on the fracture surface per unit volume | ||
| Dimensionless gas production rate per unit volume | ||
| Dimensionless fracture aperture | ||
| Dimensionless reservoir thickness | ||
| Dimensionless distance in the x direction | ||
| Dimensionless distance in the y direction | ||
| Dimensionless distance in the z direction | ||
| Dimensionless outer boundary in the x direction | ||
| Dimensionless outer boundary in the y direction | ||
| Dimensionless length of the fracture panel | ||
| Dimensionless height of the fracture panel | ||
| Dimensionless adsorption concentration of the matrix | ||
| Dimensionless equilibrium adsorption concentration | ||
| Adsorption coefficient | ||
| Capacitance coefficient of the micro-fracture | ||
| Diffusion flow coefficient | ||
| Capacitance coefficient of matrix | ||
| Inter-porosity flow factor of matrix system into micro-fracture system |
| Parameters | Symbol | Value |
|---|---|---|
| Dimensionless fracture conductivity | CFD | 50 |
| Dimensionless half-length of hydraulic fracture | xFD | 1 |
| Dimensionless half-height of hydraulic fracture | hFD | 0.1 |
| Dimensionless width of hydraulic fracture | wFD | 1.7 × 10−4 |
| Dimensionless outer boundary in the x direction | xeD | 16.67 |
| Dimensionless outer boundary in the y direction | yeD | 16.67 |
| Dimensionless outer boundary in the z direction | zeD | 0.43 |
| Parameters | Symbol | Units | Value |
|---|---|---|---|
| Initial formation pressure | pi | MPa | 22 |
| Initial formation temperature | Ti | K | 320.3 |
| Formation thickness | h | m | 26 |
| Number of hydraulic fracture panels | N | Dimensionless | 90 |
| Permeability of the hydraulic fracture | kF | mD | 300 |
| Half-length of hydraulic fracture | lF | m | 60 |
| Half-height of hydraulic fracture | hF | m | 5 |
| Width of hydraulic fracture [34] | wF | m | 0.001 |
| Porosity of hydraulic fracture [34] | ΦF | Fraction | 0.4 |
| Porosity of the matrix | Φm | Fraction | 0.05 |
| Permeability of the matrix | kM | mD | 0.0005 |
| Langmuir pressure | pL | MPa | 2.5 |
| Langmuir volume | VL | m3/m3 | 3 |
| Parameters | Symbol | Units | Value |
|---|---|---|---|
| Skin factors | S | Dimensionless | 0, 0.1, 1 |
| Dimensionless hydraulic fracture conductivity | CFD | Dimensionless | 30, 50, 100 |
| Half-length of hydraulic fracture | ΔlF | Dimensionless | 30, 50, 100, 200 |
| Half-height of hydraulic fracture | ΔhF | Dimensionless | 6, 8, 10 |
| Storage ratio | ωf | Dimensionless | 0.1, 0.15, 0.2 |
| Inter-porosity flow factor | λMf | Dimensionless | 1 × 10−4, 1 × 10−3, 5 × 10−3 |
| Adsorption coefficient | β | Dimensionless | 1, 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, L.; Wang, G.; Zhang, X.; Guo, W.; Liang, B.; Jiang, P.; Liu, Y.; Gao, J.; Liu, D.; Yu, R.; et al. Dynamic Pressure Analysis of Shale Gas Wells Considering Three-Dimensional Distribution and Properties of the Hydraulic Fracture Network. Processes 2024, 12, 286. https://doi.org/10.3390/pr12020286
Kang L, Wang G, Zhang X, Guo W, Liang B, Jiang P, Liu Y, Gao J, Liu D, Yu R, et al. Dynamic Pressure Analysis of Shale Gas Wells Considering Three-Dimensional Distribution and Properties of the Hydraulic Fracture Network. Processes. 2024; 12(2):286. https://doi.org/10.3390/pr12020286
Chicago/Turabian StyleKang, Lixia, Gaocheng Wang, Xiaowei Zhang, Wei Guo, Bin Liang, Pei Jiang, Yuyang Liu, Jinliang Gao, Dan Liu, Rongze Yu, and et al. 2024. "Dynamic Pressure Analysis of Shale Gas Wells Considering Three-Dimensional Distribution and Properties of the Hydraulic Fracture Network" Processes 12, no. 2: 286. https://doi.org/10.3390/pr12020286
APA StyleKang, L., Wang, G., Zhang, X., Guo, W., Liang, B., Jiang, P., Liu, Y., Gao, J., Liu, D., Yu, R., & Sun, Y. (2024). Dynamic Pressure Analysis of Shale Gas Wells Considering Three-Dimensional Distribution and Properties of the Hydraulic Fracture Network. Processes, 12(2), 286. https://doi.org/10.3390/pr12020286








