Study of Acid Fracturing Strategy with Integrated Modeling in Naturally Fractured Carbonate Reservoirs
Abstract
1. Introduction
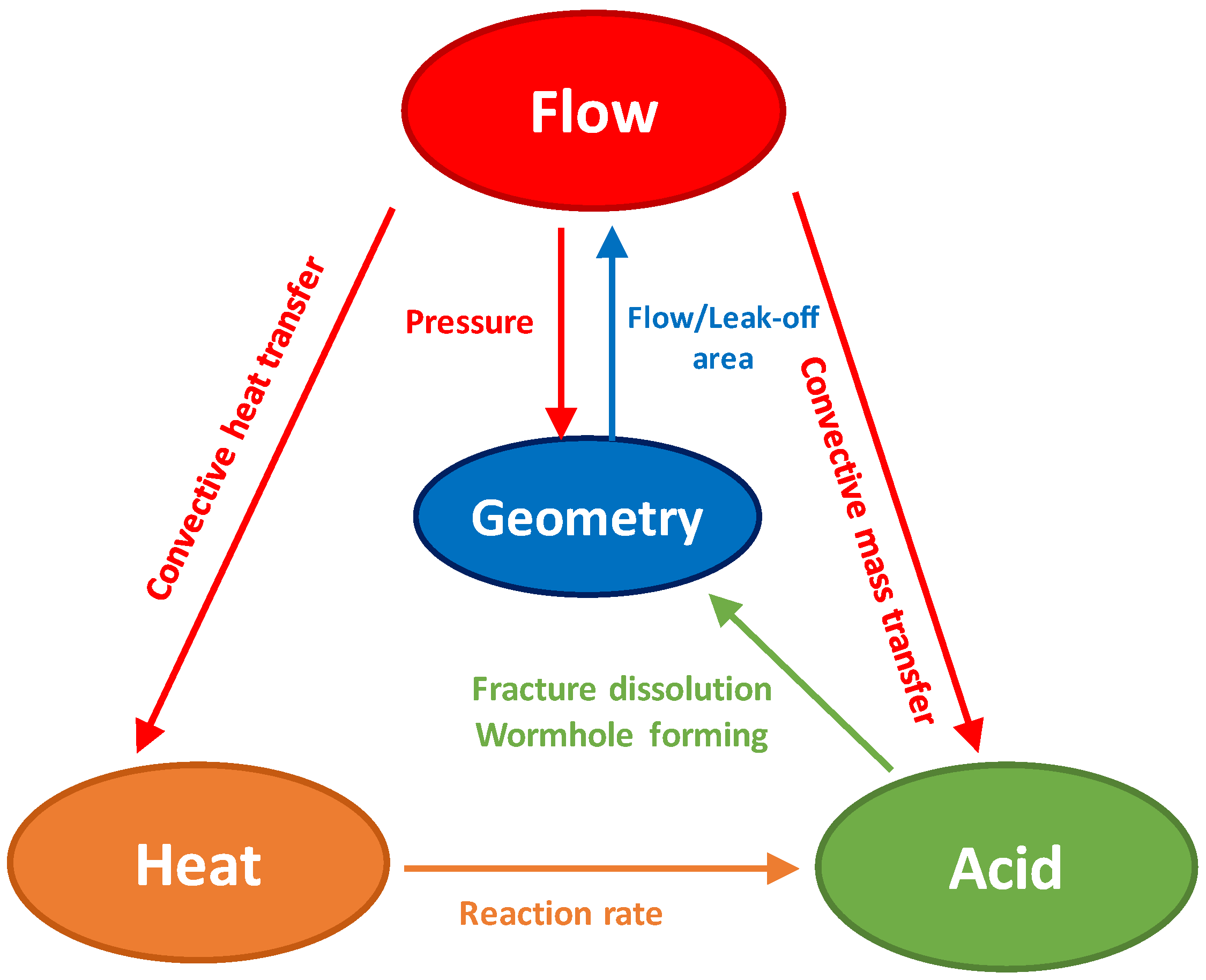
2. Mathematical Model
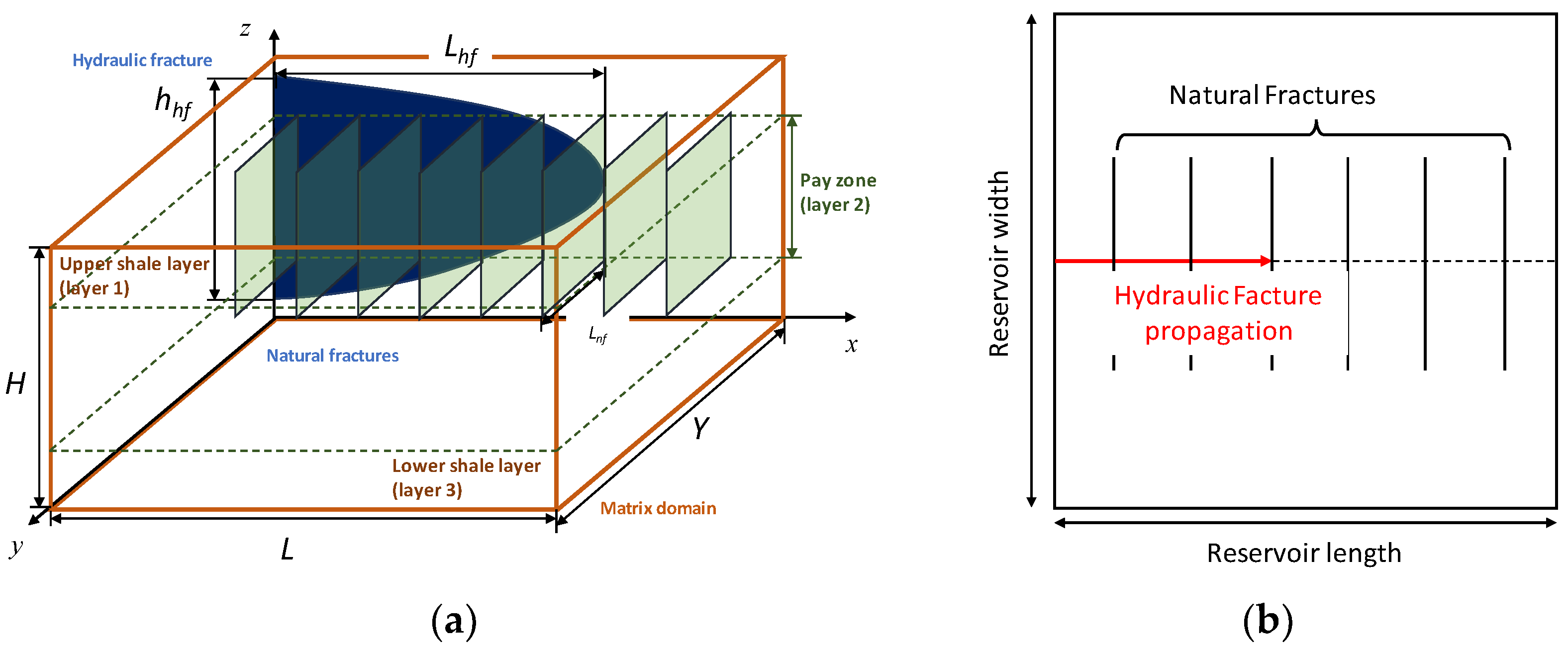
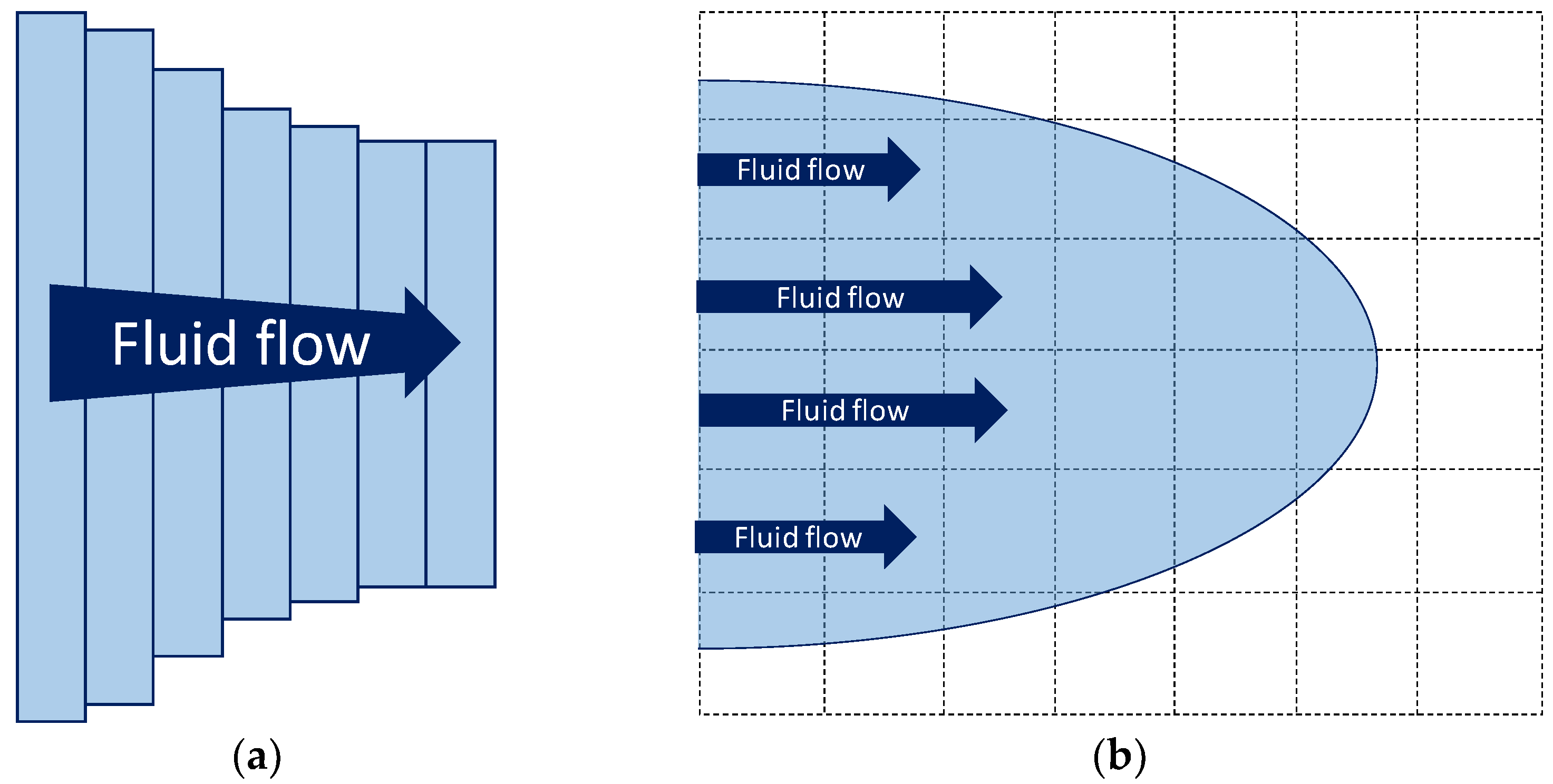
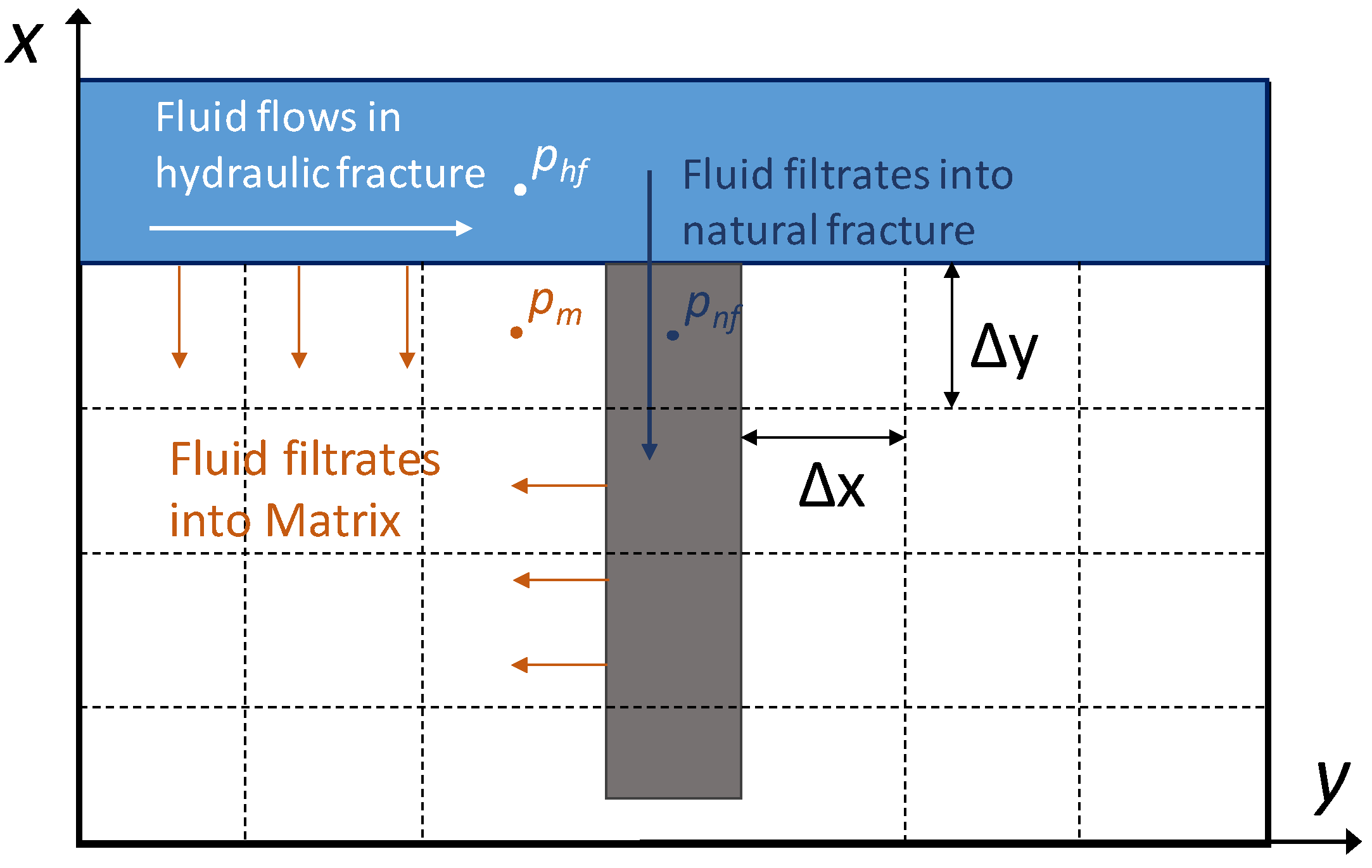
2.1. Geometry Model
2.2. Fluid Flow and Leak-Off Model
2.3. Heat Transfer Model
2.4. Acid Model
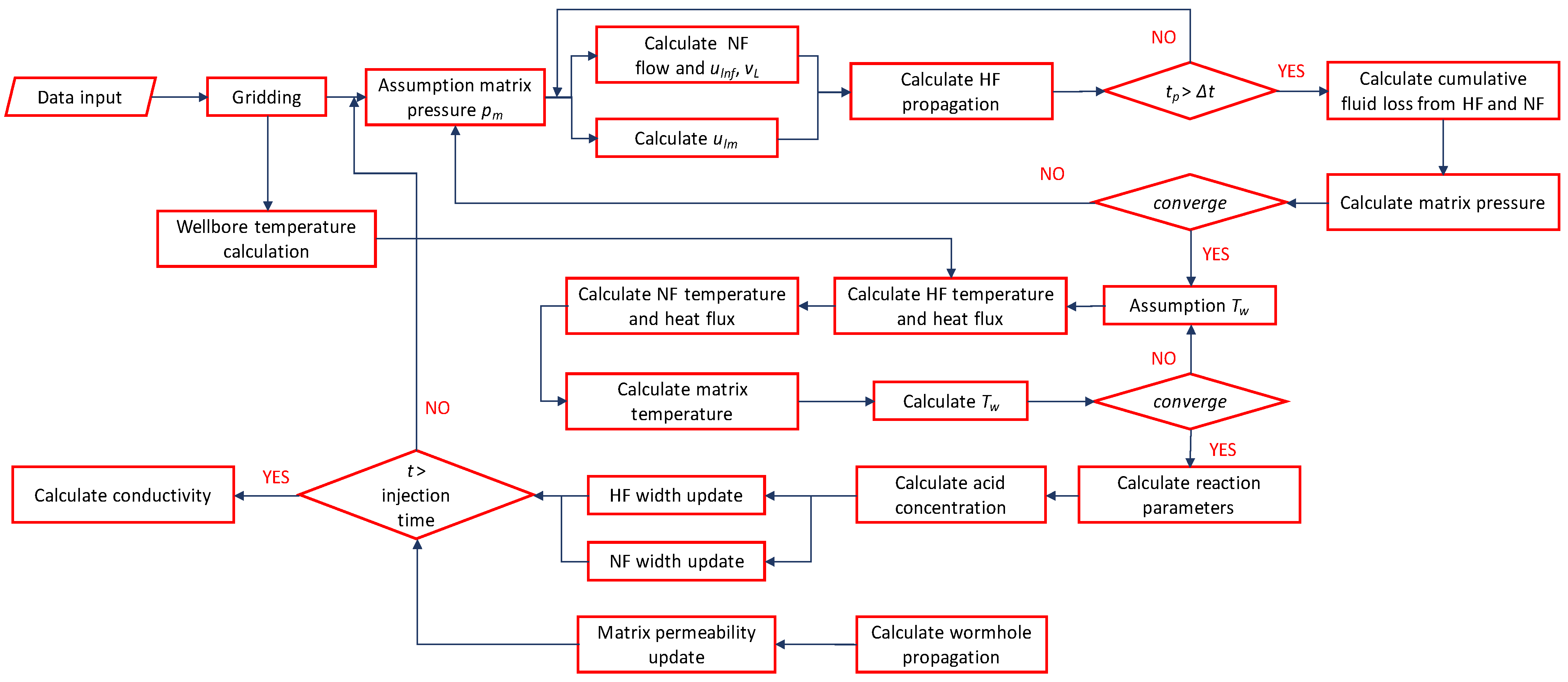
3. Calculation Approach
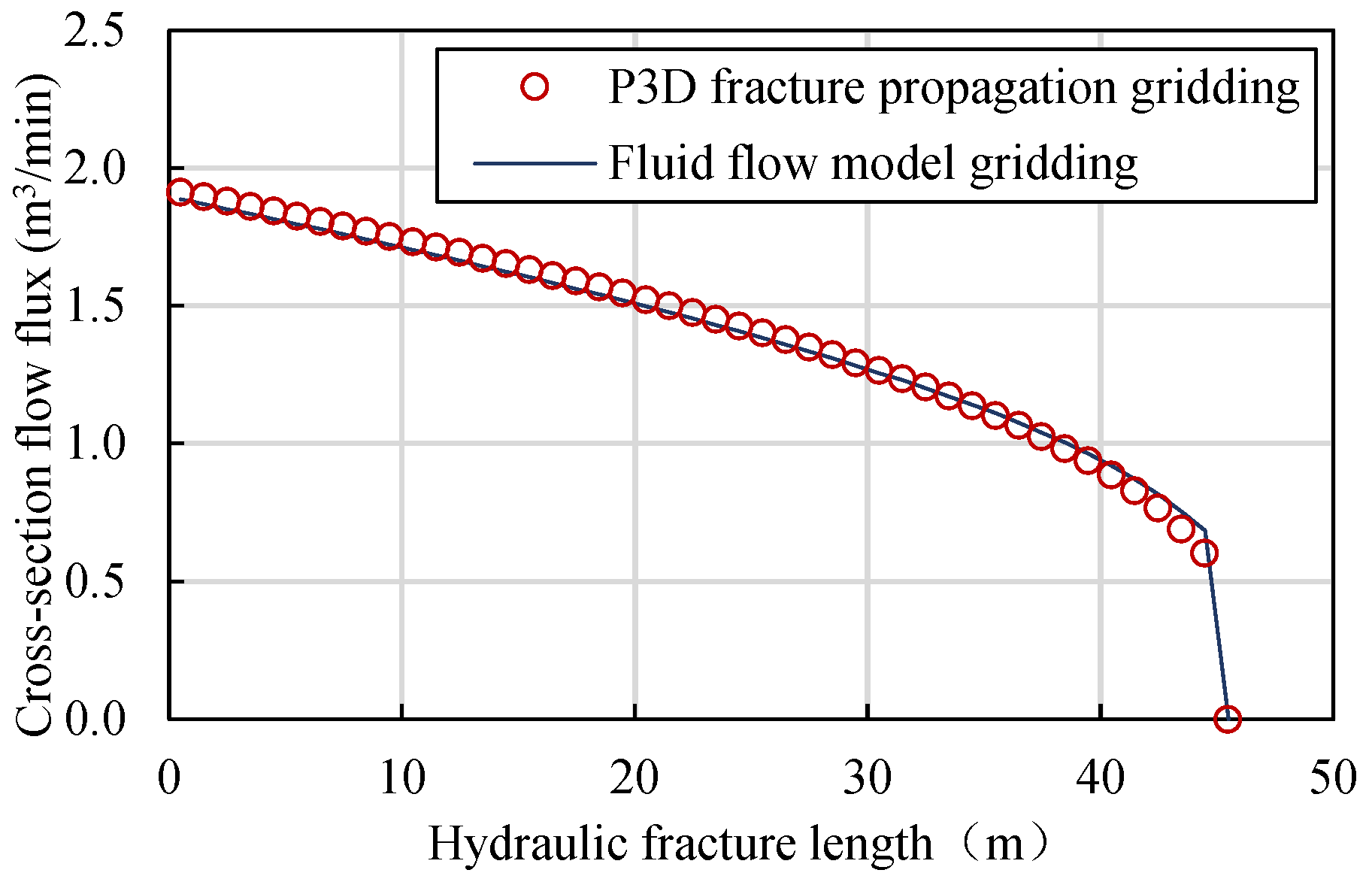
4. Model Validation
5. Results
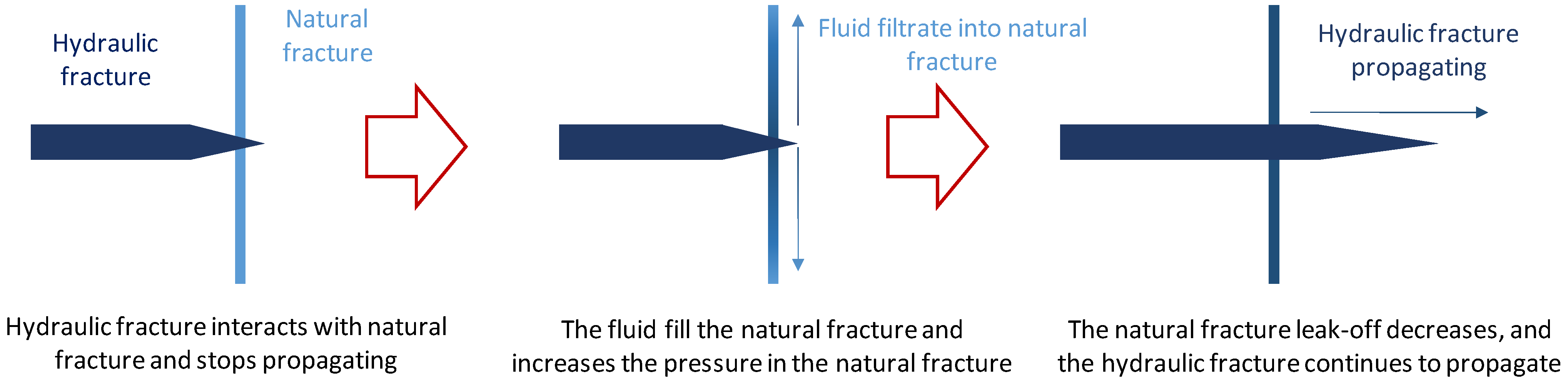
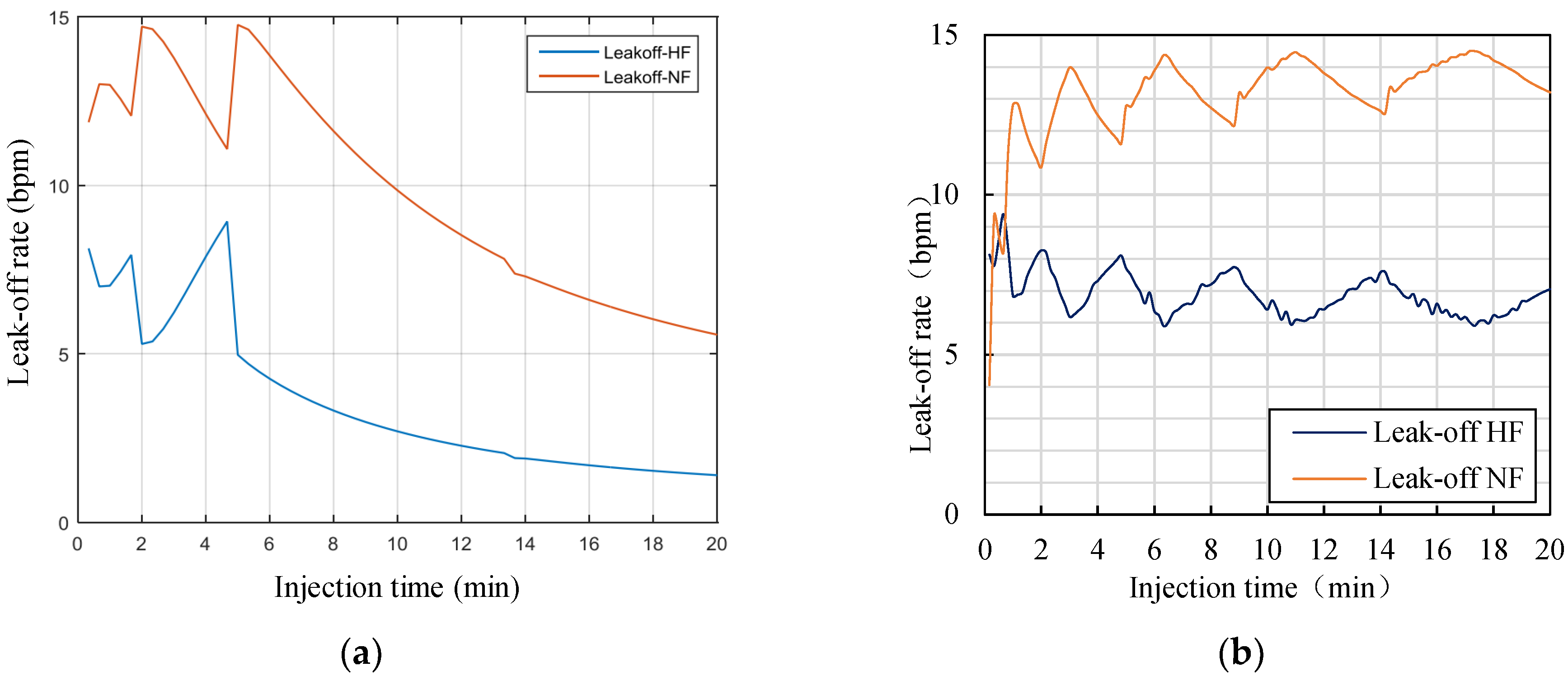
5.1. Natural Fracture Leak-Off Behavior
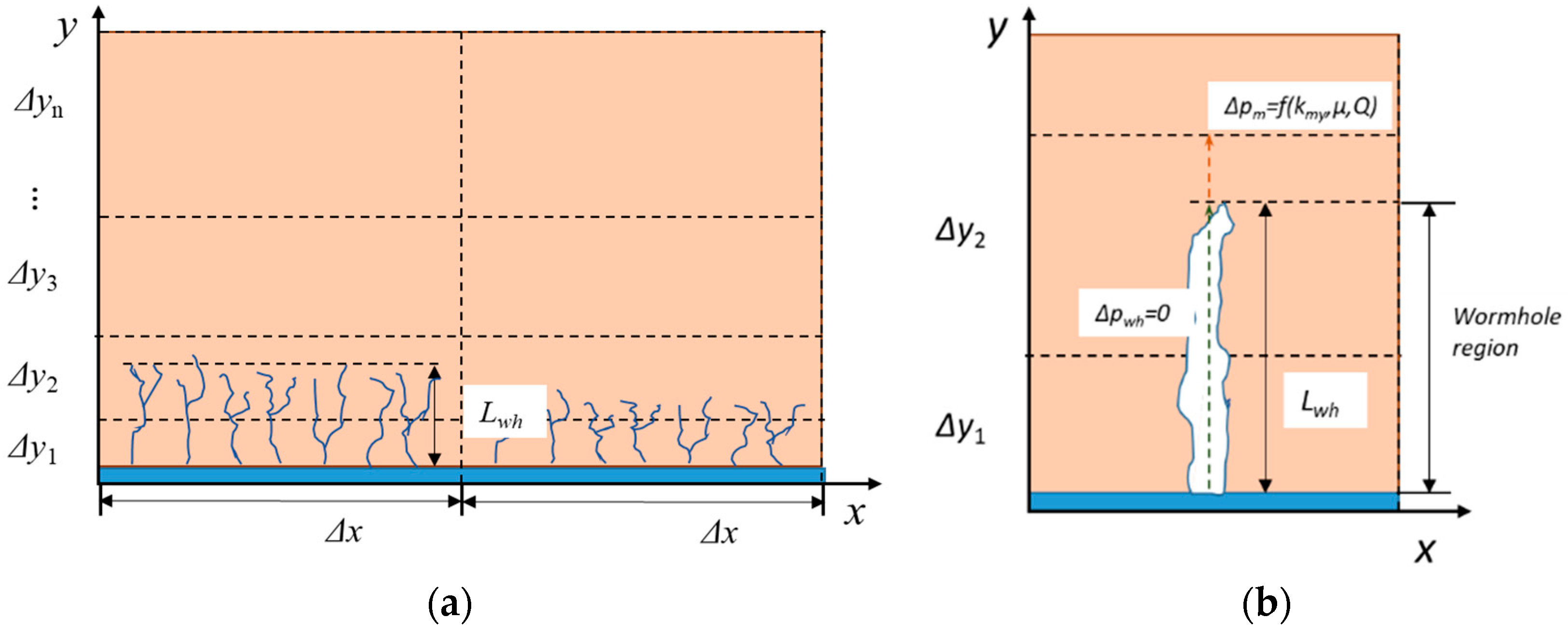
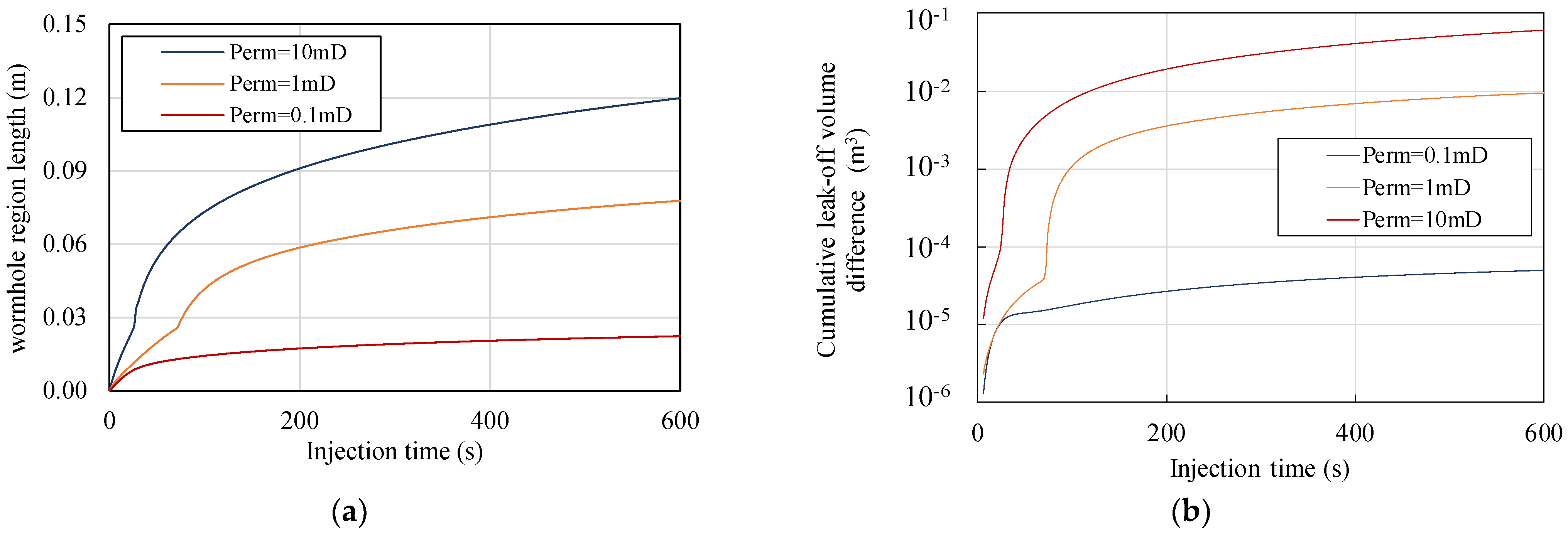
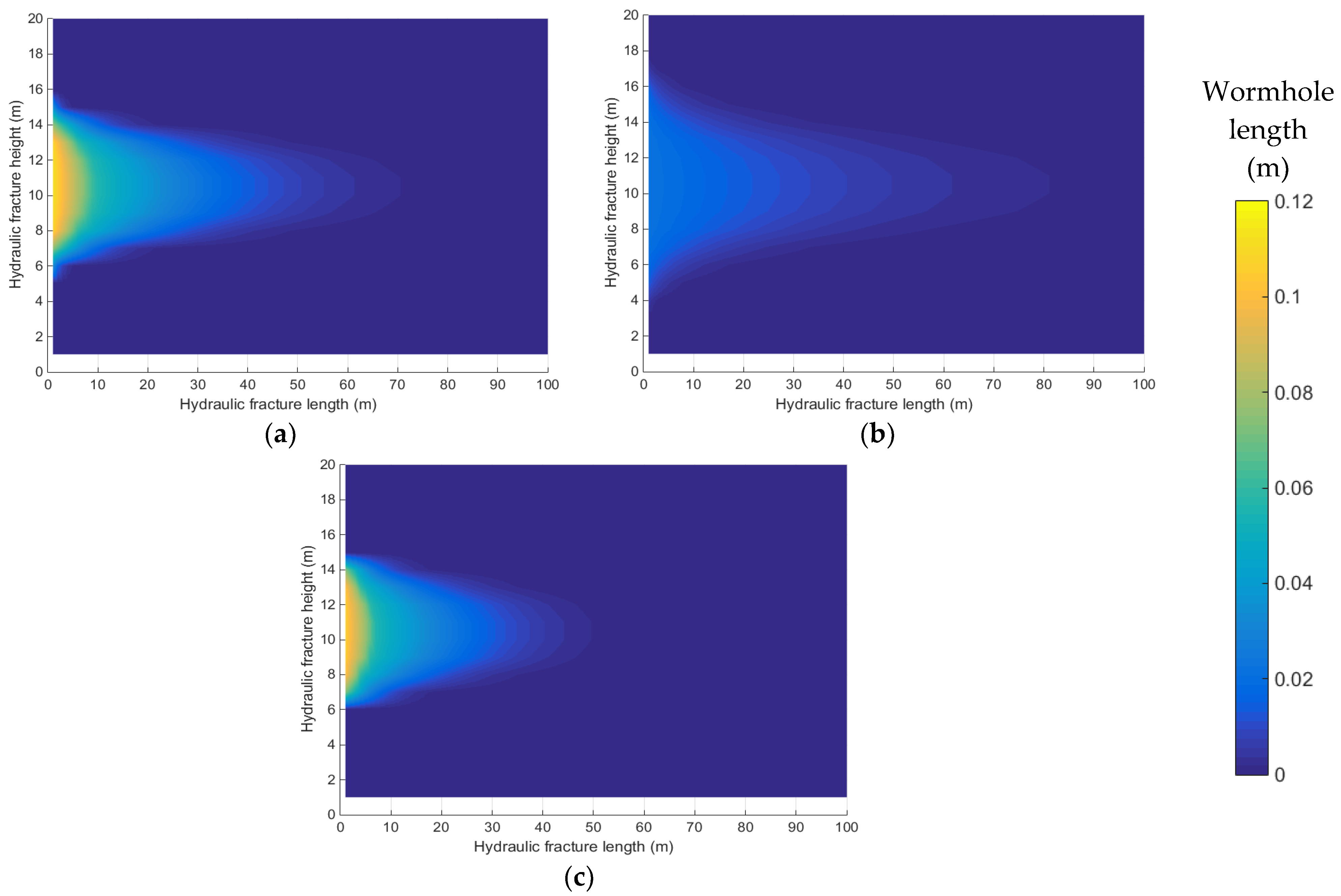
5.2. Wormhole Leak-Off Behavior
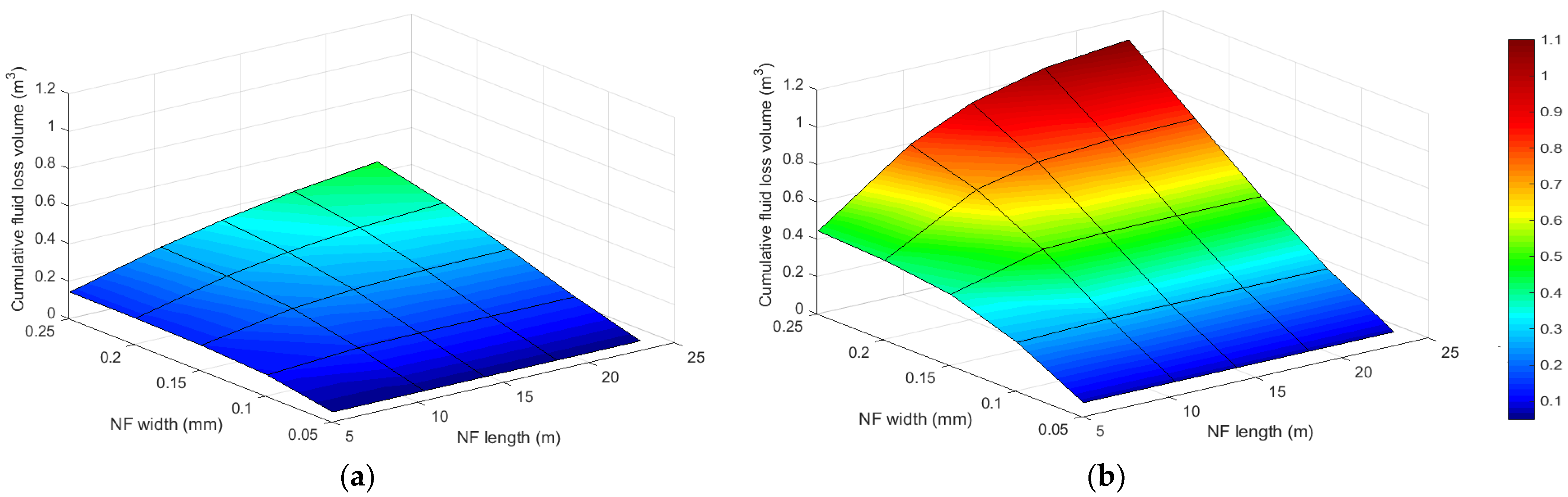
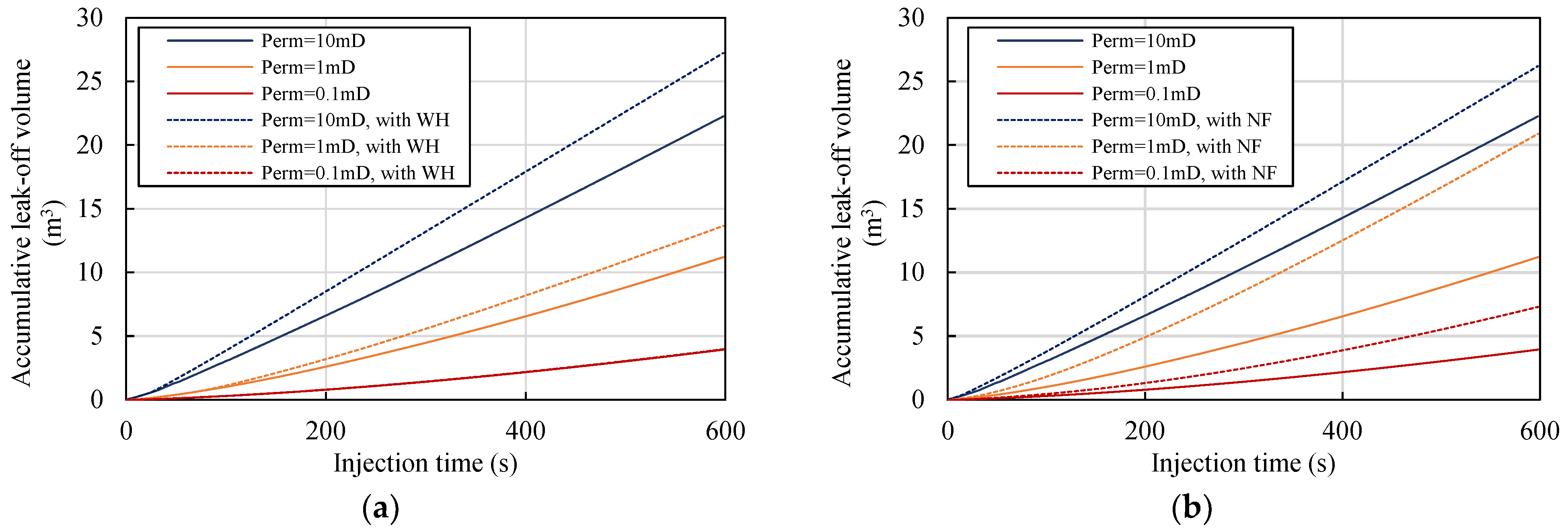
5.3. Cumulative Leak-Off Volume and Hydraulic Fracture Propagation
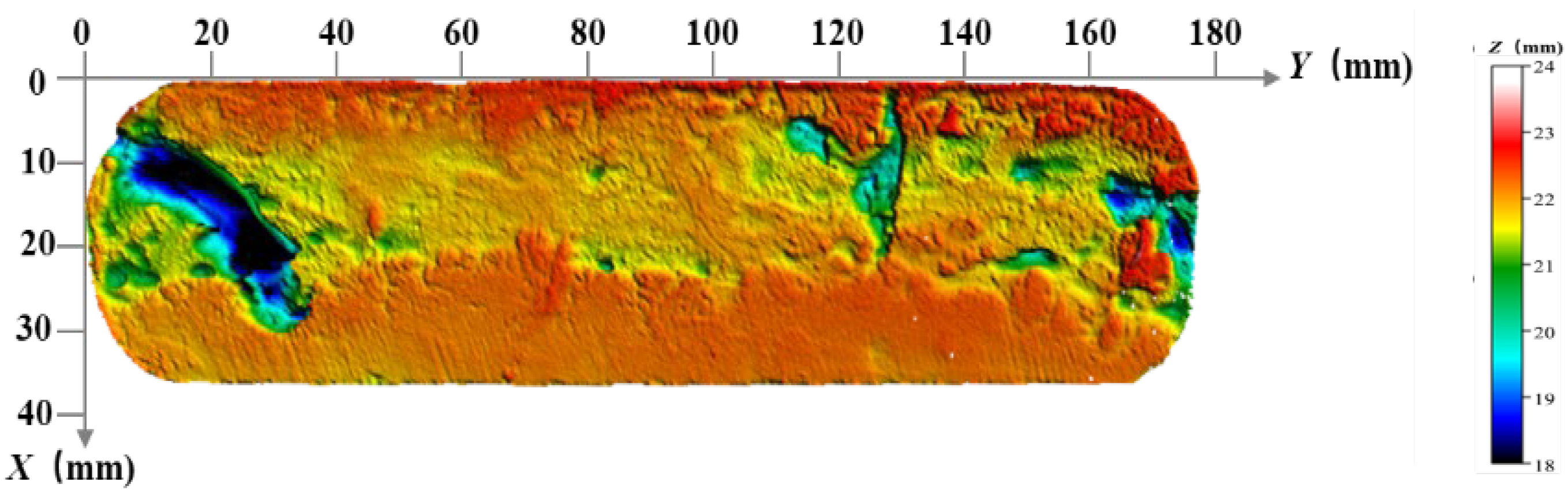
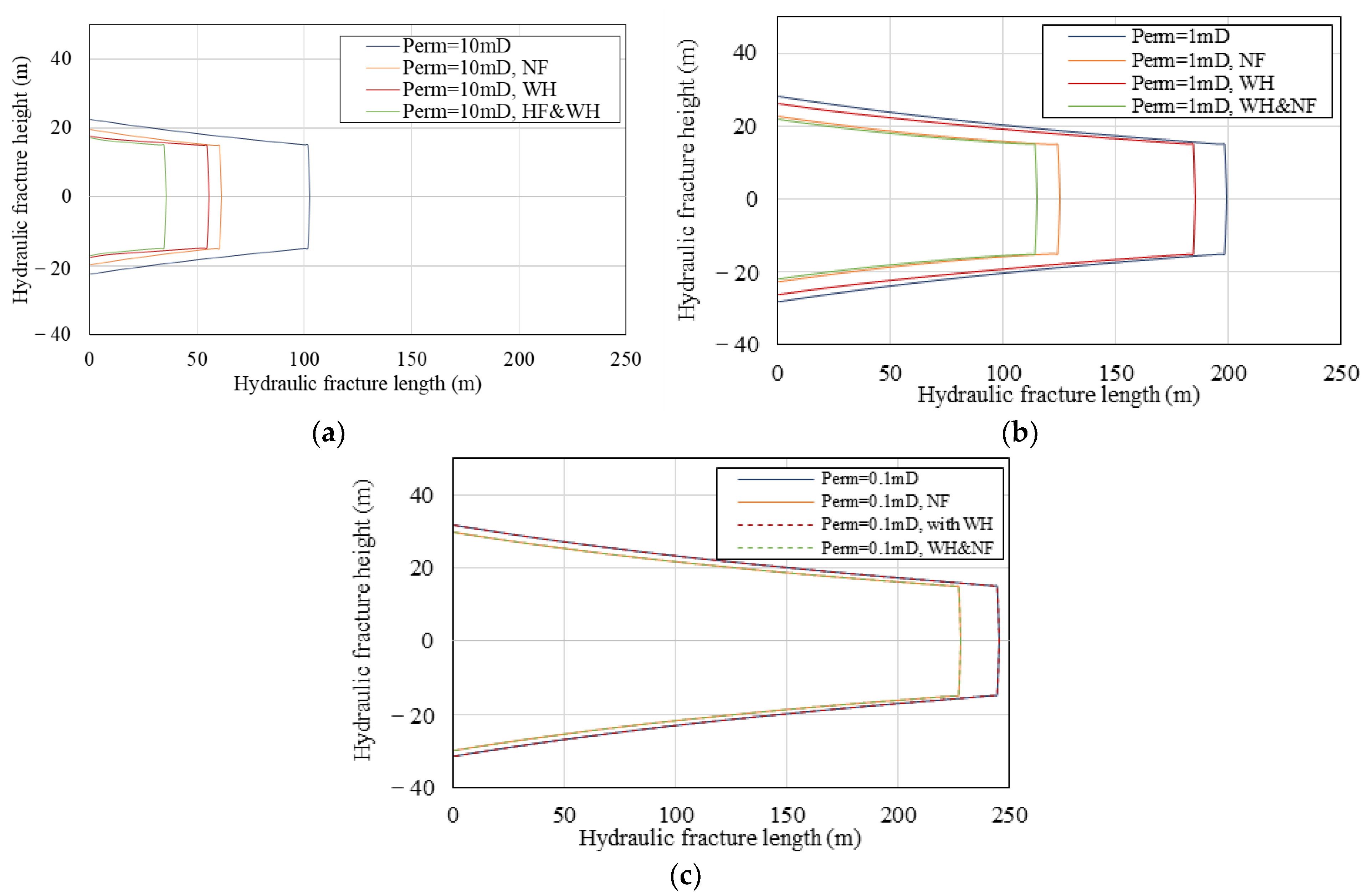
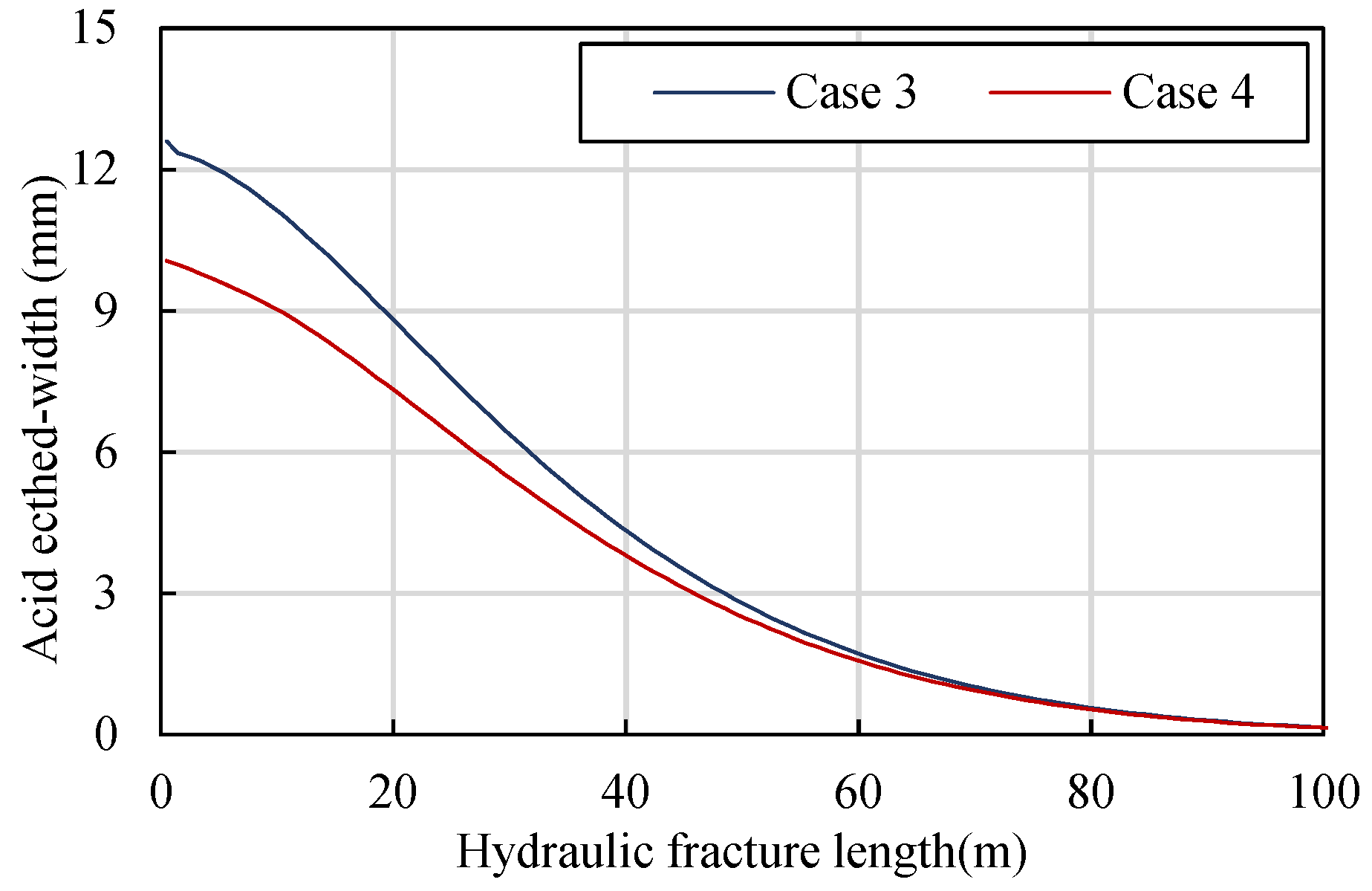
5.4. Acid Etching in Hydraulic Fracture
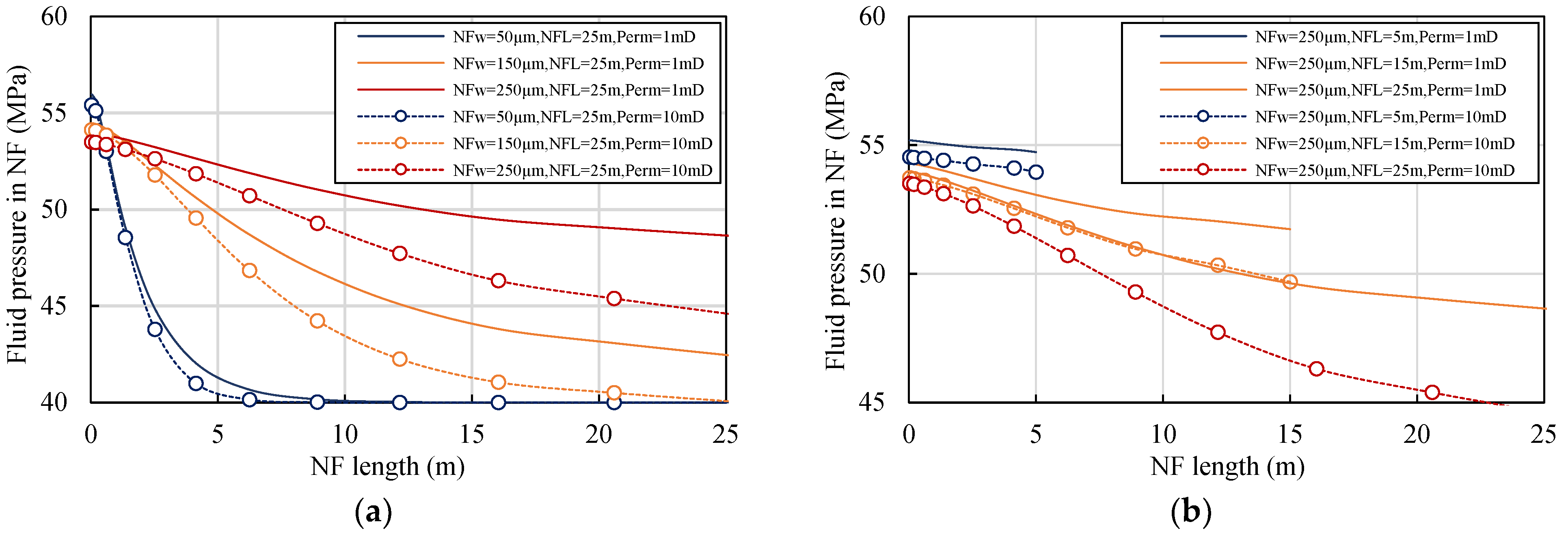
5.5. Acid Etching in Natural Fractures
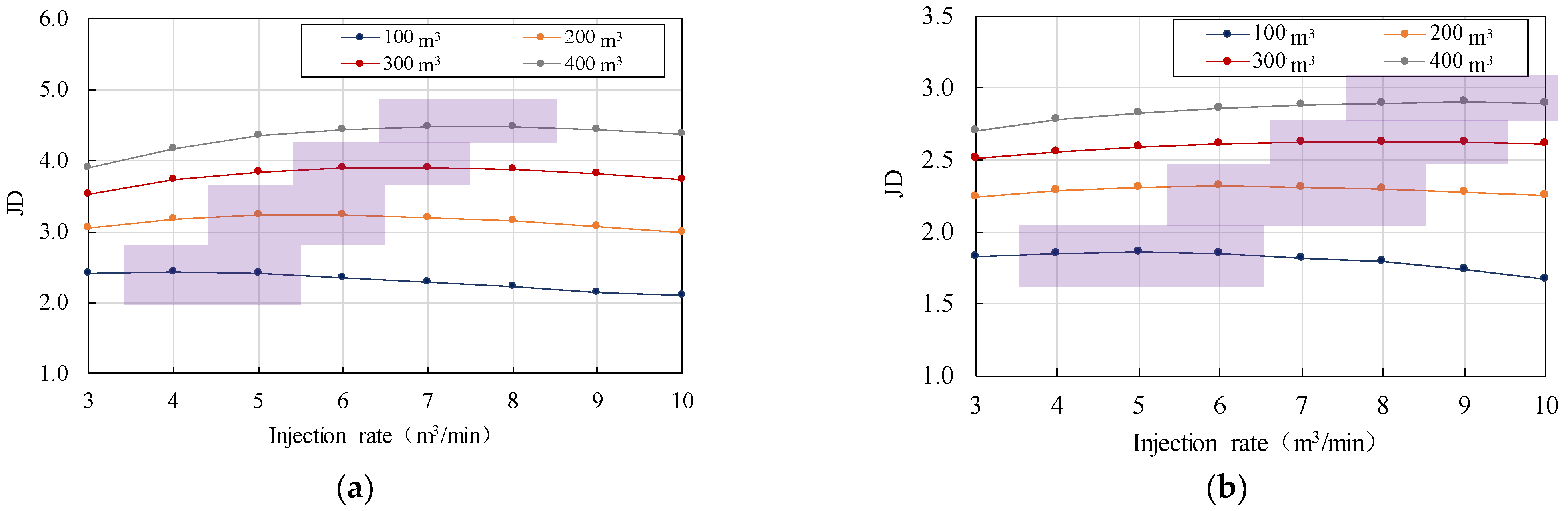
5.6. Acid Fracturing Strategy Study
5.7. 10 mD Permeability: Case 1 and Case 2
5.8. 1 mD Permeability: Case 3 and Case 4
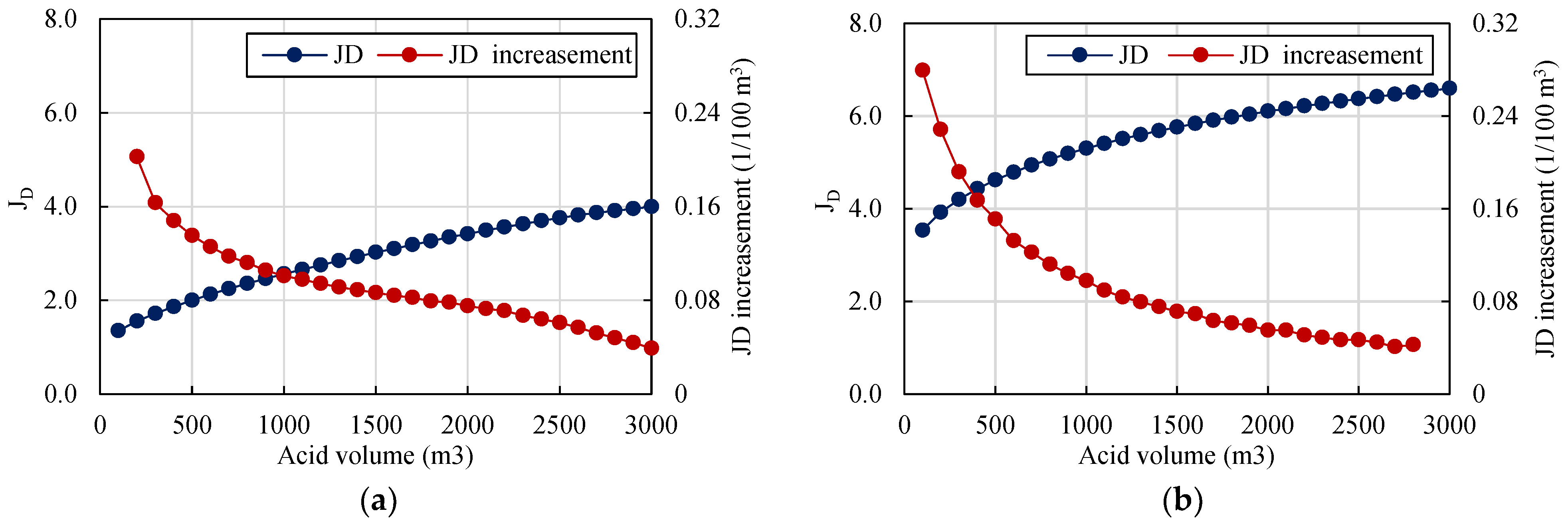
5.9. Effects of Treatment Volume on Dimensionless Production Index
6. Discussions
7. Conclusions
- 1.
- Both geometric parameters and matrix permeability govern the acid leak-off of natural fractures, and it only increases significantly while all three parameters grow together. Therefore, natural fractures significantly affect the hydraulic geometry and acid-etching profile. It is necessary to take natural fractures into the simulation in naturally fractured reservoirs.
- 2.
- Wormholes significantly influence leak-off behavior and hydraulic fracture propagation. They also substantially change the etched-width profile near the hydraulic entrance where the wormholes are well developed. Therefore, wormholes must be considered in the acid fracturing simulation, especially in a high-permeability reservoir (≥1 mD).
- 3.
- For all the simulated cases, there is an optimal acid injection rate that can obtain the highest productivity under various treatment volumes. The optimal parameters strongly depend on natural fracture geometry and reservoir permeability.
- 4.
- In high-permeability fractured reservoirs, creating a more conductive fracture is preferable. The optimal injection rate does not always increase with treatment volume but depends on natural fracture. The conductive natural fracture case shows the highest stimulation potential by acid fracturing, and a lower injection rate should be adopted to obtain better productivity.
- 5.
- In low-permeability fractured reservoirs, a higher injection rate is recommended to create a longer acid-etched fracture, and the optimal injection rate increases with treatment volume. The natural fracture network case shows the highest stimulation potential by acid fracturing, and the highest injection rate should be adopted to obtain better productivity.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ahf | cross-sectional area of hydraulic fracture, m2; |
| Ct | total compress coefficient, Pa−1; |
| Chf, Cnf | average acid concentration across the fracture width, mol/m3; |
| cl | specific heat of fluid, J/(kg·K); |
| cm | specific heat of porous medium, J/(kg·K); |
| E | Young’s modulus, Pa; |
| G | shear modulus, Pa; |
| hhf | hydraulic fracture height, m; |
| hpay | pay zone height, m; |
| hi | hydraulic fracture height in the ith layer, m; |
| KIu and KIl | stress intensity factors of the top and bottom tips of the hydraulic fracture, Pa·m1/2; |
| KIc | stress intensity factor, Pa·m1/2; |
| kc | acid reaction constant, m/s; kg is the mass transfer coefficient, m/s; |
| kmx, kmy, and kmz | matrix permeability in x, y, and z directions, m2; |
| kwh | permeability of the matrix grid with wormholes at the y direction, m2; |
| Lnf | natural fracture length, m; |
| Lwh | wormhole length, m; |
| Lwh, tip | wormhole length at the element where the wormhole tip is located, m. |
| M | mole weight of the rock, kg/mol; |
| NAC | acid capacity number; |
| phf | fluid pressure in hydraulic fracture, Pa; |
| pnf | fluid pressure in natural fracture, Pa; |
| pcp | fluid pressure at the centerline of the hydraulic fracture, Pa; |
| pm | fluid pressure in matrix, Pa; |
| PVbt,opt | optimal breakthrough volume, dimensionless; |
| qf | fluid leak-off source term, kg·m−3·s−1; |
| qL,nf | natural fracture leak-off volume, m3; |
| qh,m | energy source term, J/(m3·s). |
| Thf, Tnf | average temperature across the fracture width, K; |
| Tm | temperature of the porous medium, K; |
| average flow velocity through hydraulic fracture cross-section, m/s; | |
| ux, uy, uz | flow velocity in the x, y, z direction, m/s; |
| v | Poisson’s ratio, dimensionless; |
| vL,hf | fluid leak-off velocity in the hydraulic fracture, m/s; |
| vwh | wormhole growth velocity, m/s; |
| vi, tip | average interstitial velocity in the wormhole front, m/s; |
| vi,opt | optimal injection velocity, m/s; |
| whf | hydraulic fracture width, m; |
| wtip | width at the tip element of the hydraulic fracture, m; |
| μ | fluid viscosity, mPa·s; |
| β | dissolving power of acid on rock, kg rock/kg acid; |
| σpay | closure stress of pay zone, Pa; |
| Δσ | stress difference between pay zone and shale layer, Pa; |
| σi | closure stresses in the ith layer; |
| ϕ | rock porosity, dimensionless; |
| ρl | fluid density, kg/m3; |
| ρm | density of porous medium, kg/m3; |
| ρr | density of rock, kg/m3; |
| λl | thermal conductance of fluid, W/(m·K); |
| λm | thermal conductance of porous medium, W/(m·K); |
| η | fraction of the leaking acid that reacts at the fracture surfaces; |
| Δytip | length of the grid where the wormhole tip is located, m. |
References
- Li, Y.; Kang, Z.; Xue, Z.; Zheng, S. Theories and practices of carbonate reservoirs development in China. Pet. Explor. Dev. 2018, 45, 669–678. [Google Scholar] [CrossRef]
- Brenda, A.; Aguilera, R. Buildup Evaluation of a Tight Overpressured Naturally Fractured Carbonate Reservoir with the Use of a Semi-Empirical Model. SPE Res. Eval. Eng. 2023, 26, 1498–1513. [Google Scholar]
- Chen, L.; Liu, F.; Yang, J. Horizontal well staged acid fracturing technology for deep and ultra-deep carbonate gas reservoirs in the Sichuan Basin. Nat. Gas. Ind. 2022, 42, 56–64. [Google Scholar]
- Farouk, S.; Sen, S.; Abuseda, H.; El-Shamly, Y.; Salam, A.; Elhossainy, M.M. Petrophysical Characterization of the Turonian and Cenomanian Intervals in the Abu Gharadig Field, Western Desert, Egypt: Inferences on Reservoir Quality and Resource Development. Nat. Resour. Res. 2022, 31, 1793–1824. [Google Scholar] [CrossRef]
- Yi, M.; Shen, X.; Jin, L.; Wang, J.; Huang, Z.; Shen, G. Forward Modeling of Natural Fractures within Carbonate Rock Formations with Continuum Damage Mechanics and Its Application in Fuman Oilfield. Energies 2022, 15, 6318. [Google Scholar] [CrossRef]
- Aljawad, M.; Aljulaih, H.; Mahmoud, M.; Desouky, M. Integration of field, laboratory, and modeling aspects of acid fracturing: A comprehensive review. J. Pet. Sci. Eng. 2019, 181, 106158. [Google Scholar] [CrossRef]
- Mou, J.; Zhang, S.; Zhang, Y. Acid leak-off mechanism in acid fracturing of naturally fractured carbonate oil reservoirs. Transp. Porous Media 2012, 91, 573–584. [Google Scholar] [CrossRef]
- Ugursal, A.; Zhu, D.; Hill, A.D. Development of Acid Fracturing Model for Naturally Fractured Reservoirs. SPE Prod. Oper. 2019, 34, 735–748. [Google Scholar] [CrossRef]
- Hawkins, M.F., Jr. A Note on the Skin Effect. J. Pet. Technol. 1956, 8, 65–66. [Google Scholar] [CrossRef]
- Akanni, O.O.; Nasr-El-Din, H.A. Modeling of Wormhole Propagation During Matrix Acidizing of Carbonate Reservoirs by Organic Acids and Chelating Agents. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, United Arab Emirates, 26–28 September 2016. [Google Scholar]
- De Oliveira, T.J.L.; De Melo, A.R.; Oliveira, J.A.A.; Pereira, A.Z. Numerical Simulation of the Acidizing Process and PVBT Extraction Methodology Including Porosity/Permeability and Mineralogy Heterogeneity. In Proceedings of the SPE International Symposium and Exhibition on Formation Damage Control, Lafayette, LA, USA, 15–17 February 2012. [Google Scholar]
- Kalia, N.; Balakotaiah, V. Effect of medium heterogeneities on reactive dissolution of carbonates. Chem. Eng. Sci. 2009, 64, 376–390. [Google Scholar] [CrossRef]
- Palharini, S.M.; Zhu, D.; Hill, A.D. Anisotropic-Wormhole-Network Generation in Carbonate Acidizing and Wormhole-Model Analysis through Averaged-Continuum Simulations. SPE Prod. Oper. 2019, 34, 90–108. [Google Scholar]
- Palharini, S.M.; Hill, A.D.; Zhu, D. A New Up-Scaled Wormhole Model Grounded on Experimental Results and in 2-Scale Continuum Simulations. In Proceedings of the SPE International Conference on Oilfield Chemistry, Galveston, TX, USA, 8–9 April 2019. [Google Scholar]
- Panga, M.K.R.; Ziauddin, M.; Balakotaiah, V. Two-Scale Continuum Model for Simulation of Wormholes in Carbonate Acidization. AIChE J. 2005, 51, 3231–3248. [Google Scholar] [CrossRef]
- Dang, L.; Zhou, C.; Huang, M.; Jiang, D. Simulation of effective fracture length of prepad acid fracturing considering multiple leak-off effect. Nat. Gas. Ind. B 2019, 6, 64–70. [Google Scholar] [CrossRef]
- Economides, M.J.; Zhu, D.; Hill, A.D.; Ehlig-Economides, C. Petroleum Production Systems, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2013. [Google Scholar]
- Buijse, M.A.; Glasbergen, G. A semi-empirical model to calculate wormhole growth in carbonate acidizing. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 9–12 October 2005. [Google Scholar]
- Furui, K.; Burton, R.C.; Burkhead, D.W.; Abdelmalek, N.A.; Hill, A.D.; Zhu, D.; Nozaki, M. A Comprehensive Model of High-Rate Matrix-Acid Stimulation for Long Horizontal Wells in Carbonate Reservoirs: Part II—Wellbore/Reservoir Coupled-Flow Modeling and Field Application. SPE J. 2012, 17, 280–291. [Google Scholar] [CrossRef]
- Hill, A.D.; Zhu, D.; Wang, Y. The Effect of Wormholing on the Fluid Loss Coefficient in Acid Fracturing. SPE Prod. Oper. 1995, 10, 257–264. [Google Scholar] [CrossRef]
- Economides, M.J.; Nolte, K.G. Reservoir Stimulation, 3rd ed.; Prentice Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Olson, J.E. Fracture Aperture, Length and Pattern Geometry Development under Biaxial Loading: A Numerical Study with Applications to Natural, Cross-Jointed Systems; Special Publications; Geological Society of London: London, UK, 2007; Volume 289, pp. 123–142. [Google Scholar]
- Dong, C.; Zhu, D.; Hill, A.D. Modeling of the Acidizing Process in Naturally Fractured Carbonates. SPE J. 2002, 7, 400–408. [Google Scholar] [CrossRef]
- Nolte, K.G.; Economides, M.J. (Eds.) Reservoir Stimulation; John Wiley and Sons: Chichester, NY, USA, 2000. [Google Scholar]
- Eickmeier, J.R.; Ersoy, D.; Ramey, H.J. Wellbore temperatures and heat losses during production or injection operations. J. Can. Pet. Technol. 1970, 9, 115–121. [Google Scholar] [CrossRef]
- Kaviany, M. Principles of Heat Transfer in Porous Media; Springer Science and Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Roberts, L.D.; Guin, J.A. A New Method for Predicting Acid Penetration Distance. SPE J. 1975, 15, 277–286. [Google Scholar] [CrossRef]
- Deng, J.; Mou, J.; Hill, A.D.; Zhu, D. A New Correlation of Acid-Fracture Conductivity Subject to Closure Stress. SPE Prod. Oper. 2012, 27, 158–169. [Google Scholar] [CrossRef]
- Nordgren, R.P. Propagation of a vertical hydraulic fracture. SPE J. 1972, 12, 306–314. [Google Scholar] [CrossRef]
- Schechter, R.S. Oil Well Stimulation; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1992. [Google Scholar]
- Terrill, R.M. Heat Transfer in Laminar Flow Between Parallel Porous Plates. Int. J. Heat. Mass. Transfer. 1965, 8, 1491–1497. [Google Scholar] [CrossRef]
- Ugursal, A.; Schwalbert, M.P.; Zhu, D.; Hill, A.D. Acid Fracturing Productivity Model for Naturally Fractured Carbonate Reservoirs. In Proceedings of the SPE International Hydraulic Fracturing Technology Conference and Exhibition, Muscat, Oman, 16–18 October 2018. [Google Scholar]
- Etten, J.; Zhu, D.; Hill, A.D. The Combined Effect of Permeability and Pore Structure on Carbonate Matrix Acidizing. In Proceedings of the EUROPEC 2015, Madrid, Spain, 1–4 June 2015. [Google Scholar]




| Input Data | SI Unit | Input Data | SI Unit |
|---|---|---|---|
| Wellbore properties | |||
| Inner tube diameter, r0 | 0.062 m | Outer casing diameter, r3 | 0.127 m |
| Outer tube diameter, r1 | 0.073 m | Ground surface temperature, TG | 25 °C |
| Inner casing diameter, r2 | 0.103 m | Steel thermal conductance, λs | 45 W/(m·K) |
| Steel specific heat capacity, cs | 460 J/(kg·K) | ||
| Reservoir properties | |||
| Reservoir pressure, Pe | 4 × 107 Pa | Minimum horizontal stress in pay zone, σh | 5 × 107 Pa |
| Total compressibility, Ct | 2.2 × 10−9 Pa−1 | Minimum horizontal stress in shale layer, σhs | 5.8 × 107 Pa |
| Reservoir fluid viscosity, µo | 0.01 Pa·s | Reservoir fluid density, ρo | 850 kg/m3 |
| Reservoir width, Ly | 500 m | Reservoir length, Lx | 500 m |
| Pay zone height, hpay | 30 m | Reservoir height, Lz | 200 m |
| Limestone-specific heat capacity, cr | 850 J/(kg·K) | Reservoir temperature, Te | 439 K |
| Limestone thermal conductance, λr | 1.57 W/(m·K) | Limestone density, ρr | 2600 kg/m3 |
| Young’s modulus, E | 6 × 1010 Pa | Poisson’s ratio, v | 0.15 |
| Acid properties | |||
| Acid density, ρl | 1100 kg/m3 | Acid initial concentration, C0 | 6020 mol/m3 |
| Acid viscosity, µl | 0.03 Pa·s | Acid-specific heat capacity, cl | 4200 J/(kg·K) |
| Acid thermal conductance, λl | 0.7 W/(m·K); | Frequency factor, k | 0.003 m/s |
| Activation energy, Ea | 16,000 J/mol | Reference diffusion coefficient, De0 | 5.6 × 10−9 m2/s |
| Reference temperature, T0 | 323 K | ||
| Mou-Deng conductivity correlation parameters | |||
| Horizontal correlation length, λDx | 1 | Vertical correlation length, λDx | 0.05 |
| Normalized permeability standard deviation, σD | 0.4 | Closure pressure, σc | 3 × 107 Pa |
| Permeability, mD | NF Width, μm | NF Length, m | Spacing, m | |
|---|---|---|---|---|
| Case 1 | 10 | 250 | 25 | 1 |
| Case 2 | 10 | 50 | 25 | 0.2 |
| Case 3 | 1 | 150 | 15 | 1 |
| Case 4 | 1 | 50 | 25 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Ren, J.; Xin, S.; Guan, C.; Zhao, B.; Xu, P. Study of Acid Fracturing Strategy with Integrated Modeling in Naturally Fractured Carbonate Reservoirs. Processes 2024, 12, 808. https://doi.org/10.3390/pr12040808
Cao X, Ren J, Xin S, Guan C, Zhao B, Xu P. Study of Acid Fracturing Strategy with Integrated Modeling in Naturally Fractured Carbonate Reservoirs. Processes. 2024; 12(4):808. https://doi.org/10.3390/pr12040808
Chicago/Turabian StyleCao, Xusheng, Jichuan Ren, Shunyuan Xin, Chencheng Guan, Bing Zhao, and Peixuan Xu. 2024. "Study of Acid Fracturing Strategy with Integrated Modeling in Naturally Fractured Carbonate Reservoirs" Processes 12, no. 4: 808. https://doi.org/10.3390/pr12040808
APA StyleCao, X., Ren, J., Xin, S., Guan, C., Zhao, B., & Xu, P. (2024). Study of Acid Fracturing Strategy with Integrated Modeling in Naturally Fractured Carbonate Reservoirs. Processes, 12(4), 808. https://doi.org/10.3390/pr12040808





