Rapid Classification and Diagnosis of Gas Wells Driven by Production Data
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Preparation and Feature Engineering
2.1.1. Raw Data Acquisition
2.1.2. Feature Engineering
- (1)
- Liquid Discharge Capacity Features
- (2)
- Liquid Production Intensity Features.
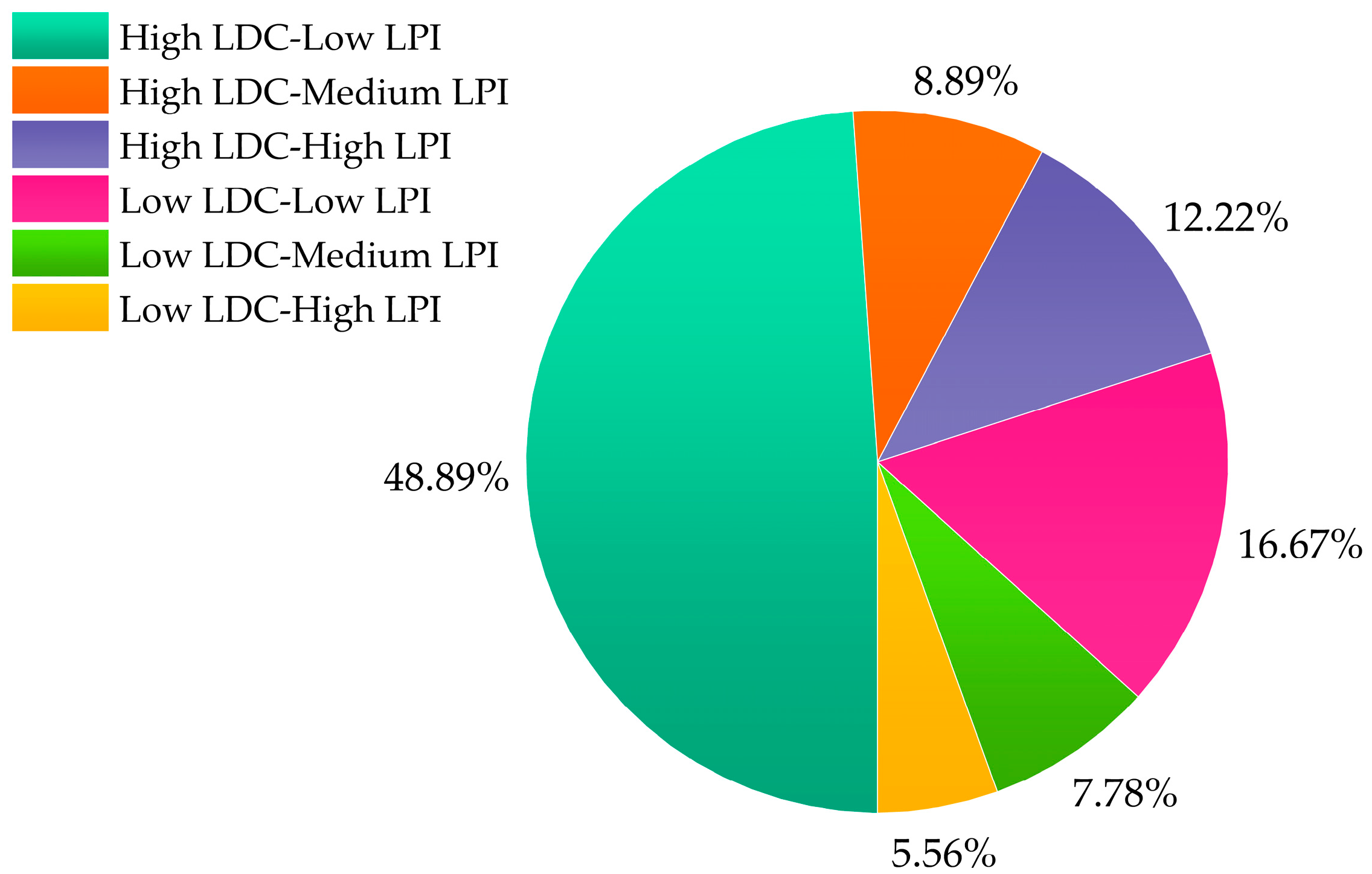
2.1.3. Sample Generation and Labeling
2.2. Procedures and Methods
2.2.1. Dimensionality Reduction Techniques
- (1)
- Principal Component Analysis (PCA)
- (2)
- Linear Discriminant Analysis (LDA)
- (3)
- Locality Preserving Projection (LPP)
- (4)
- Independent Component Analysis (ICA)
2.2.2. Classification Algorithms
- (1)
- Naive Bayes (NB)
- (2)
- Discriminant Analysis (DA)
- (3)
- K-Nearest Neighbor (KNN)
- (4)
- Support Vector Machine (SVM)
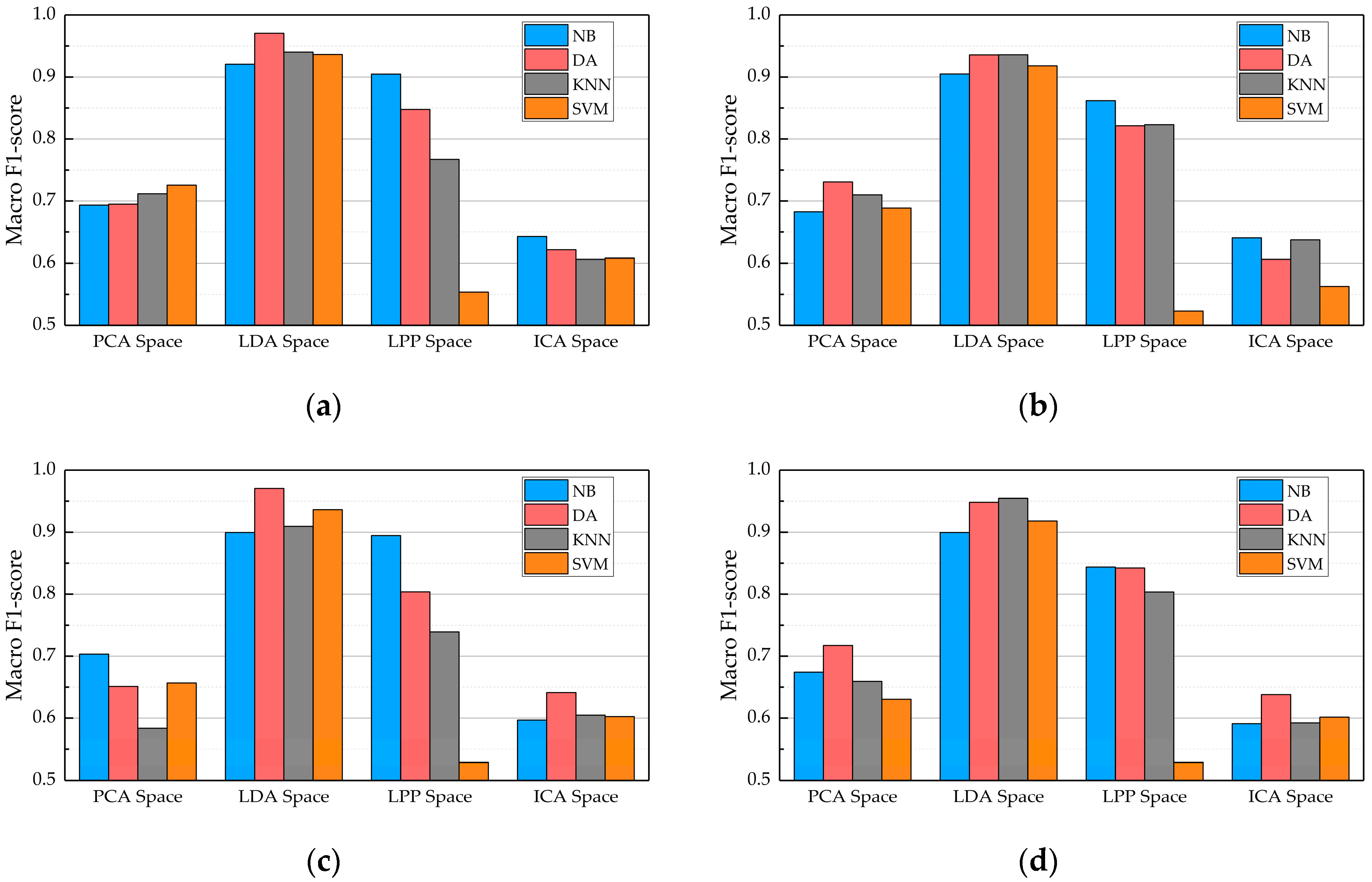
2.2.3. Model Training and Evaluation
3. Results and Discussion
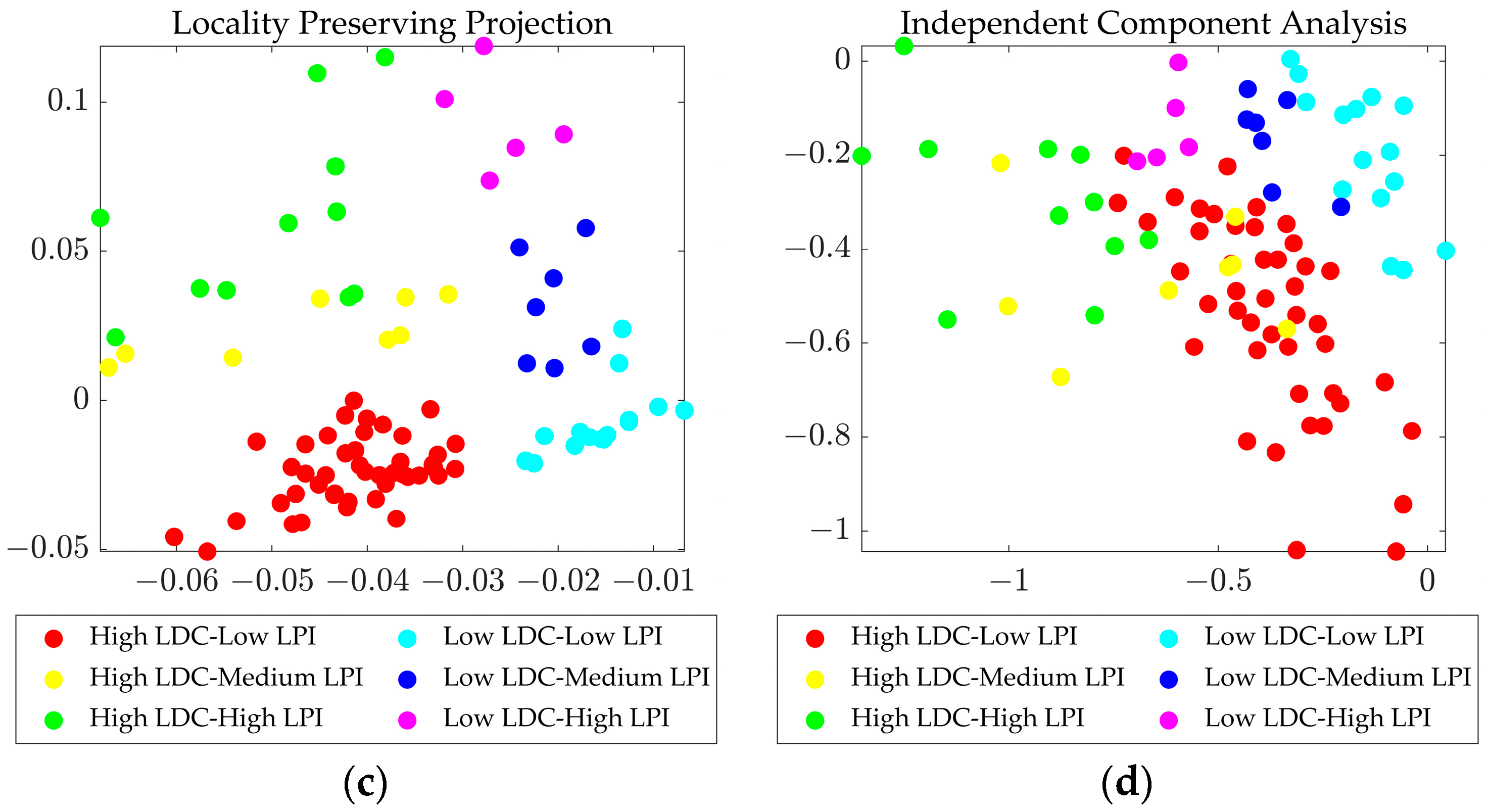
3.1. New Feature Spaces and 2D Samples
3.2. Classification Map Establishment
3.2.1. Construction of Decision Space
3.2.2. Determination of Classification Boundary
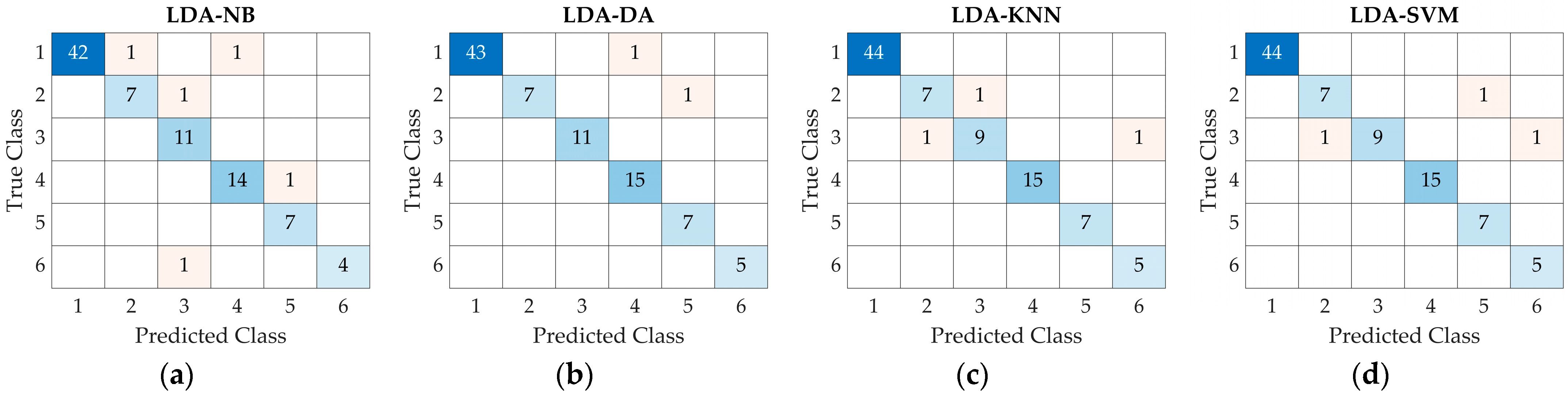
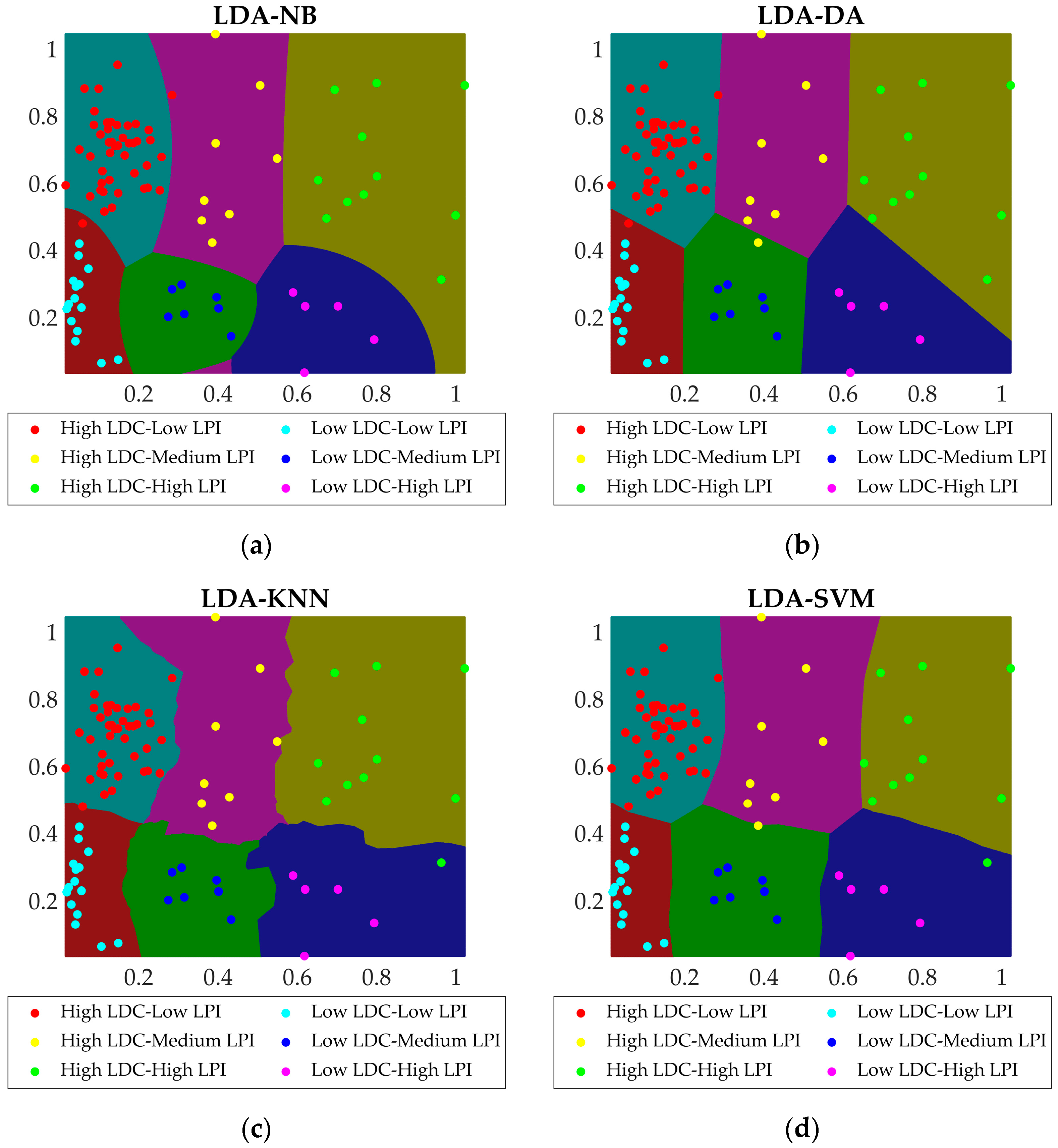
3.2.3. Combination Model and Classification Maps
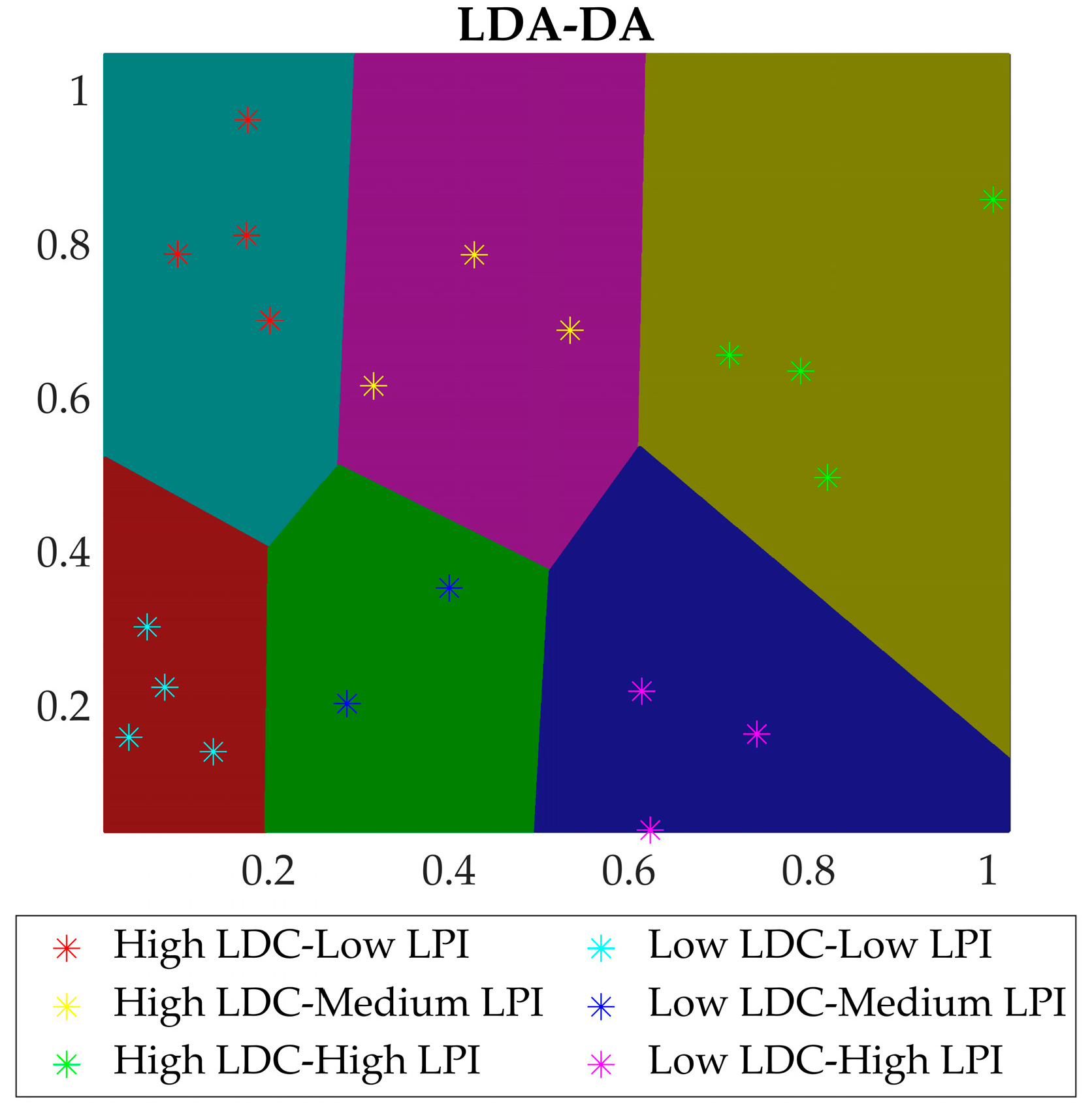
3.3. Test and Verification
4. Conclusions
- (1)
- A production data-driven method for gas well classification is proposed, which classifies gas wells from the perspective of instant evaluation and short-term management strategy decision making, and establishes classification rules through the analysis and mining of production data. This offers new ideas on gas well classification, expanding its content and scope, and thus holds certain guiding significance for research in this field.
- (2)
- Feature engineering is the foundation of gas well classification. This paper applies domain knowledge to feature engineering, successfully interpreting and processing the gas well production data according to the current usage scenario, ensuring the pertinence and purposiveness of feature extraction. In similar classification tasks, if unavoidable considerations from other aspects arise, it is necessary to re-implement feature engineering.
- (3)
- The classification map can be continuously updated in field applications. It means that new samples are constantly added, inapplicable samples are removed, and the upgraded sample set is used to regenerate the map. This allows the classification map to continuously acquire new knowledge to adapt to the gas reservoir development process. Additionally, if an automatic data collection system is deployed in the field and the data processing flow described in this paper is integrated into program modules, the current work has the potential to evolve into an online, self-updating gas well classification and diagnostic system, providing real-time decision-making support for the routine management of gas wells.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| No. | SP | C-GFR | SRGP | C-LFR | LGR-SD | Type Label |
|---|---|---|---|---|---|---|
| MPa | 104 m3/d | 104 m | m3/d | Fraction | ||
| Sample 1 | 4.58 | 6.0673 | 513.6821 | 3.04 | 0.1414 | High LDC-Low LPI |
| Sample 2 | 14.93 | 5.0011 | 46.8987 | 4.06 | 0.6075 | High LDC-Low LPI |
| Sample 3 | 10.82 | 4.9097 | 238.5747 | 4.42 | 0.4535 | High LDC-Low LPI |
| Sample 4 | 10.24 | 6.2026 | 216.4255 | 3.72 | 0.3669 | High LDC-Low LPI |
| Sample 5 | 4.04 | 5.5031 | 152.4439 | 4.76 | 0.2802 | High LDC-Low LPI |
| Sample 6 | 11.20 | 4.2300 | 253.7963 | 1.84 | 0.4617 | High LDC-Low LPI |
| Sample 7 | 11.70 | 5.3509 | 98.6469 | 3.21 | 0.3536 | High LDC-Low LPI |
| Sample 8 | 8.10 | 5.8325 | 73.8774 | 3.42 | 0.3306 | High LDC-Low LPI |
| Sample 9 | 12.30 | 4.0500 | 103.1890 | 0.65 | 0.2157 | High LDC-Low LPI |
| Sample 10 | 17.99 | 5.8083 | 64.1500 | 0.89 | 0.0461 | High LDC-Low LPI |
| Sample 11 | 8.08 | 6.4205 | 903.6039 | 3.21 | 0.1649 | High LDC-Low LPI |
| Sample 12 | 12.58 | 4.8423 | 519.2204 | 1.45 | 0.0000 | High LDC-Low LPI |
| Sample 13 | 2.92 | 6.1777 | 389.0311 | 4.03 | 0.2285 | High LDC-Low LPI |
| Sample 14 | 5.90 | 6.3000 | 320.8326 | 1.26 | 0.0733 | High LDC-Low LPI |
| Sample 15 | 3.20 | 4.3200 | 726.2535 | 0.43 | 0.0020 | High LDC-Low LPI |
| Sample 16 | 2.60 | 5.2000 | 238.9909 | 1.04 | 0.0167 | High LDC-Low LPI |
| Sample 17 | 6.50 | 4.8200 | 213.0983 | 0.89 | 0.0093 | High LDC-Low LPI |
| Sample 18 | 3.70 | 5.4000 | 221.3011 | 1.67 | 0.0089 | High LDC-Low LPI |
| Sample 19 | 7.60 | 5.0600 | 111.2244 | 1.57 | 0.0100 | High LDC-Low LPI |
| Sample 20 | 3.12 | 3.9800 | 996.1924 | 3.98 | 0.6116 | High LDC-Low LPI |
| Sample 21 | 2.50 | 5.0600 | 991.1733 | 1.52 | 0.8166 | High LDC-Low LPI |
| Sample 22 | 2.70 | 5.8000 | 609.4280 | 2.32 | 0.7455 | High LDC-Low LPI |
| Sample 23 | 5.60 | 5.7400 | 384.8057 | 4.59 | 0.5743 | High LDC-Low LPI |
| Sample 24 | 3.40 | 6.8200 | 620.1848 | 4.77 | 0.6063 | High LDC-Low LPI |
| Sample 25 | 8.60 | 6.1000 | 237.8302 | 1.40 | 0.0157 | High LDC-Low LPI |
| Sample 26 | 12.90 | 5.8700 | 663.3872 | 1.29 | 0.0100 | High LDC-Low LPI |
| Sample 27 | 6.20 | 5.4200 | 206.1093 | 1.25 | 0.0196 | High LDC-Low LPI |
| Sample 28 | 4.70 | 6.2300 | 130.7468 | 1.43 | 0.0147 | High LDC-Low LPI |
| Sample 29 | 3.40 | 5.8100 | 534.2683 | 1.34 | 0.0198 | High LDC-Low LPI |
| Sample 30 | 9.10 | 5.8800 | 58.7946 | 1.35 | 0.0141 | High LDC-Low LPI |
| Sample 31 | 2.80 | 6.2400 | 187.1762 | 1.06 | 0.0374 | High LDC-Low LPI |
| Sample 32 | 6.30 | 6.0000 | 581.8307 | 1.02 | 0.0400 | High LDC-Low LPI |
| Sample 33 | 2.30 | 6.2800 | 458.7685 | 1.07 | 0.0417 | High LDC-Low LPI |
| Sample 34 | 6.86 | 6.3600 | 282.1879 | 3.23 | 0.0735 | High LDC-Low LPI |
| Sample 35 | 11.20 | 5.9300 | 312.4548 | 2.67 | 0.0490 | High LDC-Low LPI |
| Sample 36 | 5.30 | 6.0600 | 266.6547 | 2.85 | 0.0402 | High LDC-Low LPI |
| Sample 37 | 0.90 | 4.9600 | 550.8149 | 1.63 | 0.1554 | High LDC-Low LPI |
| Sample 38 | 5.40 | 4.8200 | 174.4959 | 2.04 | 0.1534 | High LDC-Low LPI |
| Sample 39 | 1.80 | 5.9400 | 320.8622 | 2.08 | 0.1510 | High LDC-Low LPI |
| Sample 40 | 7.10 | 6.1000 | 183.1287 | 3.05 | 0.0564 | High LDC-Low LPI |
| Sample 41 | 14.40 | 5.7900 | 127.4232 | 2.90 | 0.1184 | High LDC-Low LPI |
| Sample 42 | 2.00 | 6.1000 | 347.8464 | 1.22 | 0.0598 | High LDC-Low LPI |
| Sample 43 | 6.50 | 5.4300 | 342.3038 | 0.71 | 0.0000 | High LDC-Low LPI |
| Sample 44 | 13.10 | 6.4100 | 365.2630 | 0.83 | 0.1177 | High LDC-Low LPI |
| Sample 45 | 8.05 | 5.7952 | 274.0215 | 3.39 | 0.3287 | High LDC-Low LPI |
| Sample 46 | 16.27 | 6.0183 | 63.8500 | 0.91 | 0.0453 | High LDC-Low LPI |
| Sample 47 | 9.57 | 7.0454 | 514.0142 | 2.95 | 0.0814 | High LDC-Low LPI |
| Sample 48 | 9.89 | 6.2014 | 390.2455 | 2.94 | 0.2305 | High LDC-Low LPI |
| Sample 49 | 5.01 | 5.1780 | 326.4224 | 7.25 | 0.9633 | High LDC-Medium LPI |
| Sample 50 | 2.92 | 4.5452 | 541.0575 | 7.74 | 1.0562 | High LDC-Medium LPI |
| Sample 51 | 17.65 | 6.8952 | 372.8574 | 11.17 | 1.1152 | High LDC-Medium LPI |
| Sample 52 | 3.05 | 5.1397 | 331.8989 | 8.33 | 1.2472 | High LDC-Medium LPI |
| Sample 53 | 3.95 | 4.5540 | 250.6186 | 7.38 | 1.2337 | High LDC-Medium LPI |
| Sample 54 | 3.88 | 6.4151 | 327.8478 | 11.55 | 1.1086 | High LDC-Medium LPI |
| Sample 55 | 13.54 | 8.1299 | 348.2563 | 4.31 | 1.6300 | High LDC-Medium LPI |
| Sample 56 | 19.80 | 5.8700 | 64.5558 | 8.39 | 0.9318 | High LDC-Medium LPI |
| Sample 57 | 11.04 | 6.5031 | 352.4357 | 7.75 | 1.2896 | High LDC-Medium LPI |
| Sample 58 | 8.62 | 6.2695 | 244.0125 | 12.69 | 0.6965 | High LDC-Medium LPI |
| Sample 59 | 15.05 | 4.9272 | 345.2147 | 5.04 | 1.5985 | High LDC-Medium LPI |
| Sample 60 | 10.34 | 8.0005 | 477.3014 | 26.60 | 1.0942 | High LDC-High LPI |
| Sample 61 | 16.87 | 6.6822 | 97.6272 | 20.71 | 0.5261 | High LDC-High LPI |
| Sample 62 | 10.65 | 5.2715 | 143.9851 | 15.70 | 1.4965 | High LDC-High LPI |
| Sample 63 | 2.52 | 6.2500 | 285.8750 | 16.00 | 1.9721 | High LDC-High LPI |
| Sample 64 | 2.32 | 7.1369 | 84.7497 | 11.90 | 3.2389 | High LDC-High LPI |
| Sample 65 | 2.75 | 4.6095 | 411.8543 | 23.05 | 2.3925 | High LDC-High LPI |
| Sample 66 | 3.88 | 8.1454 | 276.9023 | 14.66 | 1.0607 | High LDC-High LPI |
| Sample 67 | 3.57 | 6.1817 | 276.7646 | 16.71 | 0.5284 | High LDC-High LPI |
| Sample 68 | 7.49 | 5.7473 | 159.6393 | 20.88 | 0.0990 | High LDC-High LPI |
| Sample 69 | 15.10 | 5.5800 | 44.6502 | 30.69 | 0.0000 | High LDC-High LPI |
| Sample 70 | 20.40 | 7.6200 | 68.5990 | 22.86 | 0.0000 | High LDC-High LPI |
| Sample 71 | 3.32 | 7.1369 | 85.0572 | 11.82 | 3.1957 | High LDC-High LPI |
| Sample 72 | 10.24 | 7.8594 | 397.2941 | 25.92 | 1.1026 | High LDC-High LPI |
| Sample 73 | 10.62 | 6.2054 | 277.0124 | 16.64 | 1.4294 | High LDC-High LPI |
| Sample 74 | 3.48 | 5.7215 | 260.1546 | 21.24 | 0.9811 | High LDC-High LPI |
| Sample 75 | 2.47 | 3.2674 | 214.4573 | 0.49 | 0.0361 | Low LDC-Low LPI |
| Sample 76 | 2.17 | 2.6074 | 12.4141 | 0.62 | 0.1170 | Low LDC-Low LPI |
| Sample 77 | 2.30 | 2.5400 | 159.6520 | 0.51 | 0.1487 | Low LDC-Low LPI |
| Sample 78 | 6.86 | 1.8181 | 79.5665 | 3.29 | 0.8144 | Low LDC-Low LPI |
| Sample 79 | 2.26 | 3.5623 | 371.9818 | 1.07 | 0.0283 | Low LDC-Low LPI |
| Sample 80 | 7.36 | 2.9129 | 20.4926 | 0.87 | 0.0424 | Low LDC-Low LPI |
| Sample 81 | 4.12 | 3.5207 | 188.0475 | 1.35 | 0.1131 | Low LDC-Low LPI |
| Sample 82 | 2.58 | 3.0815 | 5.3586 | 0.88 | 0.0000 | Low LDC-Low LPI |
| Sample 83 | 4.87 | 2.8991 | 37.5312 | 0.32 | 0.0000 | Low LDC-Low LPI |
| Sample 84 | 0.20 | 2.4900 | 415.1497 | 0.69 | 0.1414 | Low LDC-Low LPI |
| Sample 85 | 0.60 | 3.3800 | 152.4396 | 0.34 | 0.0012 | Low LDC-Low LPI |
| Sample 86 | 0.20 | 4.0200 | 324.8085 | 0.45 | 0.0015 | Low LDC-Low LPI |
| Sample 87 | 2.60 | 3.3800 | 108.1089 | 0.68 | 0.0087 | Low LDC-Low LPI |
| Sample 88 | 9.20 | 1.5000 | 77.8309 | 3.50 | 0.4578 | Low LDC-Low LPI |
| Sample 89 | 0.20 | 2.4600 | 41.8323 | 0.79 | 0.0142 | Low LDC-Low LPI |
| Sample 90 | 2.86 | 2.3218 | 178.4257 | 3.26 | 0.5158 | Low LDC-Low LPI |
| Sample 91 | 3.76 | 3.2245 | 186.2547 | 1.34 | 0.1085 | Low LDC-Low LPI |
| Sample 92 | 2.60 | 3.1015 | 5.5473 | 0.87 | 0.3154 | Low LDC-Low LPI |
| Sample 93 | 2.20 | 2.5864 | 12.3851 | 0.64 | 0.1120 | Low LDC-Low LPI |
| Sample 94 | 2.31 | 3.1089 | 69.3973 | 9.45 | 1.2972 | Low LDC-Medium LPI |
| Sample 95 | 2.81 | 3.2089 | 319.3973 | 8.45 | 1.4972 | Low LDC-Medium LPI |
| Sample 96 | 2.85 | 2.5598 | 412.9353 | 9.15 | 0.1697 | Low LDC-Medium LPI |
| Sample 97 | 5.04 | 3.5535 | 157.4053 | 8.88 | 0.1556 | Low LDC-Medium LPI |
| Sample 98 | 5.06 | 3.6700 | 51.4432 | 5.14 | 1.0126 | Low LDC-Medium LPI |
| Sample 99 | 1.85 | 3.8400 | 76.2545 | 8.65 | 0.9242 | Low LDC-Medium LPI |
| Sample 100 | 2.58 | 3.2548 | 71.2578 | 9.05 | 0.1055 | Low LDC-Medium LPI |
| Sample 101 | 5.36 | 3.1536 | 8.5190 | 5.41 | 1.0790 | Low LDC-Medium LPI |
| Sample 102 | 1.20 | 4.5100 | 74.7258 | 8.45 | 0.7977 | Low LDC-Medium LPI |
| Sample 103 | 5.04 | 2.3750 | 151.4633 | 15.05 | 1.8396 | Low LDC-High LPI |
| Sample 104 | 2.14 | 4.0774 | 77.0765 | 12.62 | 1.9720 | Low LDC-High LPI |
| Sample 105 | 2.35 | 3.2859 | 342.5112 | 17.30 | 2.8055 | Low LDC-High LPI |
| Sample 106 | 2.74 | 4.0912 | 176.9306 | 12.58 | 1.7582 | Low LDC-High LPI |
| Sample 107 | 5.18 | 3.7125 | 291.0768 | 14.75 | 2.5740 | Low LDC-High LPI |
| Sample 108 | 2.15 | 3.9524 | 76.9765 | 12.59 | 1.9625 | Low LDC-High LPI |
| Sample 109 | 2.38 | 2.2037 | 341.9542 | 17.28 | 1.2984 | Low LDC-High LPI |
| Sample 110 | 5.21 | 3.7225 | 18.9524 | 15.21 | 2.6050 | Low LDC-High LPI |
Appendix B



References
- Liu, J.; Zhu, Z.; Hong, J.; Feng, X.; Yang, Y.; Guo, J.; Wang, D. Gas well classification method based on production data characteristic analysis. Oil Drill. Prod. Technol. 2021, 43, 510–517. [Google Scholar] [CrossRef]
- Liu, C. Analysis of Production Characteristics and Technical Countermeasures of Gas Wells in Shenmu Gas Field. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2018. [Google Scholar]
- Joseph, A.; Sand, C.M.; Ajienka, J.A. Classification and Management of Liquid Loading in Gas Wells. In Proceedings of the SPE Nigeria Annual International Conference and Exhibition, Lagos, Nigeria, 5–7 August 2013. [Google Scholar]
- Wei, Y.; Jia, A.; He, D.; Liu, Y.; Ji, G.; Cui, B.; Ren, L. Classification and evaluation of horizontal well performance in Sulige tight gas reservoirs, Ordos Basin. Nat. Gas Ind. 2013, 33, 47–51. [Google Scholar]
- Zhang, N. Classification evaluation of production dynamic for horizontal well in Su 53 block. Unconv. Oil Gas 2021, 8, 88–94. [Google Scholar] [CrossRef]
- Qiu, L. Dynamic Analysis of Tight Water-Producing Gas Reservoirs and Evaluation of Water Production Impact in Western Sulige Area. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2020. [Google Scholar]
- Shang, Y.; Zhai, S.; Lin, X.; Li, X.; Li, H.; Feng, Q. Dynamic and static integrated classification model for low permeability tight gas wells based on XGBoost algorithm. Spec. Oil Gas Reserv. 2023, 30, 135–143. [Google Scholar]
- Zhang, Z. Well Management and Dynamic Analysis of Eastern Sulige Gasfield. Master’s Thesis, Xi’an Shiyou University, Xi’an, China, 2016. [Google Scholar]
- Sharma, A.; Srinivasan, S.; Lake, L.W. Classification of Oil and Gas Reservoirs Based on Recovery Factor: A Data-Mining Approach. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Lee, B.B.; Lake, L.W. Using Data Analytics to Analyze Reservoir Databases. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 28–30 September 2015. [Google Scholar]
- Barone, A.; Sen, M.K. An Improved Classification Method That Combines Feature Selection with Nonlinear Bayesian Classification and Regression: A Case Study on Pore-Fluid Prediction. In Proceedings of the 2017 SEG International Exposition and Annual Meeting, Houston, TX, USA, 24–29 September 2017. [Google Scholar]
- Viggen, E.M.; Løvstakken, L.; Ma, S.-E.; Merciu, I.A. Better automatic interpretation of cement evaluation logs through feature engineering. SPE J. 2021, 26, 2894–2913. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, J.; Zhang, Q. Application of locality preserving projection-based unsupervised learning in predicting the oil production for low-permeability reservoirs. SPE J. 2021, 26, 1302–1313. [Google Scholar] [CrossRef]
- Liao, L.; Zeng, Y.; Liang, Y.; Zhang, H. Data Mining: A Novel Strategy for Production Forecast in Tight Hydrocarbon Resource in Canada by Random Forest Analysis. In Proceedings of the International Petroleum Technology Conference, Dhahran, Saudi Arabia, 13–15 January 2020. [Google Scholar]
- Ahmadi, R.; Aminshahidy, B.; Shahrabi, J. Data-driven analysis of stimulation treatments using association rule mining. SPE Prod. Oper. 2023, 38, 552–564. [Google Scholar] [CrossRef]
- Ejim, C.; Xiao, J. Screening Artificial Lift and Other Techniques for Liquid Unloading in Unconventional Gas Wells. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 9–12 November 2020. [Google Scholar]
- Veeken, C.; Al Kharusi, D. Selecting Artificial Lift or Deliquification Measures for Deep Gas Wells in The Sultanate of Oman. In Proceedings of the SPE Kuwait Oil and Gas Show and Conference, Mishref, Kuwait, 13–16 October 2019. [Google Scholar]
- Tharwat, A. Principal component analysis—A tutorial. Int. J. Appl. Pattern Recognit. 2016, 3, 197–240. [Google Scholar] [CrossRef]
- Ye, J.; Janardan, R.; Li, Q. Two-Dimensional Linear Discriminant Analysis. In Proceedings of the Advances in Neural Information Processing Systems, Vancouver, BC, Canada, 13–18 December 2004. [Google Scholar]
- Phinyomark, A.; Hu, H.; Phukpattaranont, P.; Limsakul, C. Application of linear discriminant analysis in dimensionality reduction for hand motion classification. Meas. Sci. Rev. 2012, 12, 82–89. [Google Scholar] [CrossRef]
- Yu, W.; Teng, X.; Liu, C. Face recognition using discriminant locality preserving projections. Image Vision Comput. 2006, 24, 239–248. [Google Scholar] [CrossRef]
- Zhang, L.; Qiao, L.; Chen, S. Graph-optimized locality preserving projections. Pattern Recogn. 2010, 43, 1993–2002. [Google Scholar] [CrossRef]
- Stone, J.V. Independent Component Analysis: A Tutorial Introduction; The MIT Press: London, UK, 2004; pp. 5–11. [Google Scholar]
- Zhang, H. The Optimality of Naive Bayes. In Proceedings of the Seventeenth International Florida Artificial Intelligence Research Society Conference, Miami Beach, FL, USA, 16–18 January 2004. [Google Scholar]
- Webb, G.I. Naïve Bayes. In Encyclopedia of Machine Learning and Data Mining; Sammut, C., Webb, G.I., Eds.; Springer: Boston, MA, USA, 2016; pp. 1–2. [Google Scholar]
- Brown, M.T.; Wicker, L.R. 8—Discriminant analysis. In Handbook of Applied Multivariate Statistics and Mathematical Modeling; Tinsley, H.E.A., Brown, S.D., Eds.; Academic Press: San Diego, CA, USA, 2000; pp. 209–235. [Google Scholar]
- Mclachlan, G.J. General introduction. In Discriminant Analysis and Statistical Pattern Recognition; Mclachlan, G.J., Ed.; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 1992; pp. 1–26. [Google Scholar]
- Alouhali, R.; Aljubran, M.; Gharbi, S.; Al-yami, A. Drilling Through Data: Automated Kick Detection Using Data Mining. In Proceedings of the SPE International Heavy Oil Conference and Exhibition, Kuwait City, Kuwait, 10–12 December 2018. [Google Scholar]
- Bize-Forest, N.; Lima, L.; Baines, V.; Boyd, A.; Abbots, F.; Barnett, A. Using Machine-Learning for Depositional Facies Prediction in a Complex Carbonate Reservoir. In Proceedings of the SPWLA 59th Annual Logging Symposium, London, UK, 2–6 June 2018. [Google Scholar]
- Biswas, D. Adapting Shallow and Deep Learning Algorithms to Examine Production Performance—Data Analytics and Forecasting. In Proceedings of the SPE/IATMI Asia Pacific Oil & Gas Conference and Exhibition, Bali, Indonesia, 29–31 October 2019. [Google Scholar]
- Saini, I.; Singh, D.; Khosla, A. QRS detection using K-Nearest Neighbor algorithm (KNN) and evaluation on standard ECG databases. J. Adv. Res. 2013, 4, 331–344. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y. An evaluation of statistical approaches to text categorization. Inf. Retr. 1999, 1, 69–90. [Google Scholar] [CrossRef]
- Durand, T.; Mehrasa, N.; Mori, G. Learning a Deep ConvNet for Multi-Label Classification With Partial Labels. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019. [Google Scholar]
- Magno, G.; Rodrigues, T.; Almeida, V.A.F. Detecting Spammers on Twitter. In Proceedings of the Seventh annual Collaboration, Electronic messaging, AntiAbuse and Spam Conference, Redmond, WA, USA, 13–14 July 2010. [Google Scholar]




| No. | SP | C-GFR | SRGP | C-LFR | LGR-SD | Type Label |
|---|---|---|---|---|---|---|
| MPa | 104 m3/d | 104 m | m3/d | Fraction | ||
| Sample 1 | 4.58 | 6.0673 | 513.6821 | 3.04 | 0.1414 | High LDC-Low LPI |
| Sample 2 | 14.93 | 5.0011 | 46.8987 | 4.06 | 0.6075 | High LDC-Low LPI |
| Sample 3 | 10.82 | 4.9097 | 238.5747 | 4.42 | 0.4535 | High LDC-Low LPI |
| Sample 4 | 5.01 | 5.1780 | 326.4224 | 7.25 | 0.9633 | High LDC-Medium LPI |
| Sample 5 | 2.92 | 4.5452 | 541.0575 | 7.74 | 1.0562 | High LDC-Medium LPI |
| Sample 6 | 17.65 | 6.8952 | 372.8574 | 11.17 | 1.1152 | High LDC-Medium LPI |
| Sample 7 | 10.34 | 8.0005 | 477.3014 | 26.60 | 1.0942 | High LDC-High LPI |
| Sample 8 | 16.87 | 6.6822 | 97.6272 | 20.71 | 0.5261 | High LDC-High LPI |
| Sample 9 | 10.65 | 5.2715 | 143.9851 | 15.70 | 1.4965 | High LDC-High LPI |
| Sample 10 | 2.47 | 3.2674 | 214.4573 | 0.49 | 0.0361 | Low LDC-Low LPI |
| Sample 11 | 2.17 | 2.6074 | 12.4141 | 0.62 | 0.1170 | Low LDC-Low LPI |
| Sample 12 | 2.30 | 2.5400 | 159.6520 | 0.51 | 0.1487 | Low LDC-Low LPI |
| Sample 13 | 2.31 | 3.1089 | 69.3973 | 9.45 | 1.2972 | Low LDC-Medium LPI |
| Sample 14 | 2.81 | 3.2089 | 319.3973 | 8.45 | 1.4972 | Low LDC-Medium LPI |
| Sample 15 | 2.85 | 2.5598 | 412.9353 | 9.15 | 0.1697 | Low LDC-Medium LPI |
| Sample 16 | 5.04 | 2.3750 | 151.4633 | 15.05 | 1.8396 | Low LDC-High LPI |
| Sample 17 | 2.14 | 4.0774 | 77.0765 | 12.62 | 1.9720 | Low LDC-High LPI |
| Sample 18 | 2.35 | 3.2859 | 342.5112 | 17.30 | 2.8055 | Low LDC-High LPI |
| DR Technique | Projection Vector | Vector Value | ||||
|---|---|---|---|---|---|---|
| PCA | Vector 1 | (−0.0726 | 0.4697 | 0.5183 | 0.6021 | 0.3781)T |
| Vector 2 | (−0.0579 | −0.4028 | −0.5381 | 0.3690 | 0.6392)T | |
| LDA | Vector 1 | (−0.0827 | 0.1917 | −0.0616 | 0.9299 | 0.2965)T |
| Vector 2 | (0.2540 | 0.9157 | 0.2033 | −0.2089 | −0.1092)T | |
| LPP | Vector 1 | (−0.0222 | −0.0405 | −0.0242 | −0.0047 | −0.0048)T |
| Vector 2 | (−0.0352 | −0.0269 | −0.0206 | 0.0926 | 0.1022)T | |
| ICA | Vector 1 | (0.2955 | −0.3957 | −0.5513 | −0.6128 | −0.2769)T |
| Vector 2 | (−0.8122 | −0.4856 | 0.0624 | 0.3164 | 0.0213)T | |
| Combination Case | Accuracy (%) | Macro | Micro | ||||
|---|---|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1-score (%) | Precision (%) | Recall (%) | F1-score (%) | ||
| PCA-NB | 92.963 | 67.649 | 72.341 | 69.321 | 78.889 | 78.889 | 78.889 |
| PCA-DA | 92.963 | 69.275 | 73.862 | 69.473 | 78.889 | 78.889 | 78.889 |
| PCA-KNN | 93.704 | 69.861 | 77.594 | 71.153 | 81.111 | 81.111 | 81.111 |
| PCA-SVM | 94.074 | 73.591 | 78.270 | 72.547 | 82.222 | 82.222 | 82.222 |
| Combination Case | Accuracy (%) | Macro | Micro | ||||
|---|---|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1-score (%) | Precision (%) | Recall (%) | F1-score (%) | ||
| LDA-NB | 98.148 | 92.158 | 92.715 | 92.066 | 94.444 | 94.444 | 94.444 |
| LDA-DA | 99.259 | 96.875 | 97.538 | 97.049 | 97.778 | 97.778 | 97.778 |
| LDA-KNN | 98.889 | 93.472 | 94.886 | 94.021 | 96.667 | 96.667 | 96.667 |
| LDA-SVM | 98.889 | 93.056 | 94.886 | 93.624 | 96.667 | 96.667 | 96.667 |
| Combination Case | Accuracy (%) | Macro | Micro | ||||
|---|---|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1-score (%) | Precision (%) | Recall (%) | F1-score (%) | ||
| LPP-NB | 98.148 | 90.593 | 92.828 | 90.464 | 94.444 | 94.444 | 94.444 |
| LPP-DA | 97.037 | 84.306 | 86.281 | 84.752 | 91.111 | 91.111 | 91.111 |
| LPP-KNN | 95.556 | 76.369 | 79.758 | 76.705 | 86.667 | 86.667 | 86.667 |
| LPP-SVM | 90.370 | 56.878 | 61.885 | 55.359 | 71.111 | 71.111 | 71.111 |
| Combination Case | Accuracy (%) | Macro | Micro | ||||
|---|---|---|---|---|---|---|---|
| Precision (%) | Recall (%) | F1-score (%) | Precision (%) | Recall (%) | F1-score (%) | ||
| ICA-NB | 90.370 | 64.395 | 66.407 | 64.264 | 0.71111 | 71.111 | 71.111 |
| ICA-DA | 89.630 | 61.236 | 67.361 | 62.146 | 0.68889 | 68.889 | 68.889 |
| ICA-KNN | 87.037 | 60.265 | 65.933 | 60.624 | 0.61111 | 61.111 | 61.111 |
| ICA-SVM | 90.741 | 61.215 | 67.985 | 60.806 | 0.72222 | 72.222 | 72.222 |
| No. | SP | C-GFR | SRGP | C-LFR | LGR-SD | Type Label |
|---|---|---|---|---|---|---|
| MPa | 104 m3/d | 104 m | m3/d | Fraction | ||
| Sample 1 | 16.27 | 6.0183 | 63.8500 | 0.91 | 0.0453 | High LDC-Low LPI |
| Sample 2 | 8.05 | 5.7952 | 274.0215 | 3.39 | 0.3287 | High LDC-Low LPI |
| Sample 3 | 9.57 | 7.0454 | 514.0142 | 2.95 | 0.0814 | High LDC-Low LPI |
| Sample 4 | 9.89 | 6.2014 | 390.2455 | 2.94 | 0.2305 | High LDC-Low LPI |
| Sample 5 | 11.04 | 6.5031 | 352.4357 | 7.75 | 1.2896 | High LDC-Medium LPI |
| Sample 6 | 8.62 | 6.2695 | 244.0125 | 12.69 | 0.6965 | High LDC-Medium LPI |
| Sample 7 | 15.05 | 4.9272 | 345.2147 | 5.04 | 1.5985 | High LDC-Medium LPI |
| Sample 8 | 3.32 | 7.1369 | 85.0572 | 11.82 | 3.1957 | High LDC-High LPI |
| Sample 9 | 10.24 | 7.8594 | 397.2941 | 25.92 | 1.1026 | High LDC-High LPI |
| Sample 10 | 10.62 | 6.2054 | 277.0124 | 16.64 | 1.4294 | High LDC-High LPI |
| Sample 11 | 3.48 | 5.7215 | 260.1546 | 21.24 | 0.9811 | High LDC-High LPI |
| Sample 12 | 2.86 | 2.3218 | 178.4257 | 3.26 | 0.5158 | Low LDC-Low LPI |
| Sample 13 | 3.76 | 3.2245 | 186.2547 | 1.34 | 0.1085 | Low LDC-Low LPI |
| Sample 14 | 2.60 | 3.1015 | 5.5473 | 0.87 | 0.3154 | Low LDC-Low LPI |
| Sample 15 | 2.20 | 2.5864 | 12.3851 | 0.64 | 0.1120 | Low LDC-Low LPI |
| Sample 16 | 5.36 | 3.1536 | 8.5190 | 5.41 | 1.0790 | Low LDC-Medium LPI |
| Sample 17 | 1.20 | 4.5100 | 74.7258 | 8.45 | 0.7977 | Low LDC-Medium LPI |
| Sample 18 | 2.15 | 3.9524 | 76.9765 | 12.59 | 1.9625 | Low LDC-High LPI |
| Sample 19 | 2.38 | 2.2037 | 341.9542 | 17.28 | 1.2984 | Low LDC-High LPI |
| Sample 20 | 5.21 | 3.7225 | 18.9524 | 15.21 | 2.6050 | Low LDC-High LPI |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Z.; Han, G.; Liang, X.; Chang, S.; Yang, B.; Yang, D. Rapid Classification and Diagnosis of Gas Wells Driven by Production Data. Processes 2024, 12, 1254. https://doi.org/10.3390/pr12061254
Zhu Z, Han G, Liang X, Chang S, Yang B, Yang D. Rapid Classification and Diagnosis of Gas Wells Driven by Production Data. Processes. 2024; 12(6):1254. https://doi.org/10.3390/pr12061254
Chicago/Turabian StyleZhu, Zhiyong, Guoqing Han, Xingyuan Liang, Shuping Chang, Boke Yang, and Dingding Yang. 2024. "Rapid Classification and Diagnosis of Gas Wells Driven by Production Data" Processes 12, no. 6: 1254. https://doi.org/10.3390/pr12061254
APA StyleZhu, Z., Han, G., Liang, X., Chang, S., Yang, B., & Yang, D. (2024). Rapid Classification and Diagnosis of Gas Wells Driven by Production Data. Processes, 12(6), 1254. https://doi.org/10.3390/pr12061254








