Predicting Multi-Dense Jet Concentration Fields Using a Field Reconstruction Machine Learning Framework
Abstract
1. Introduction
2. Materials and Methods
2.1. Overall Research Approach
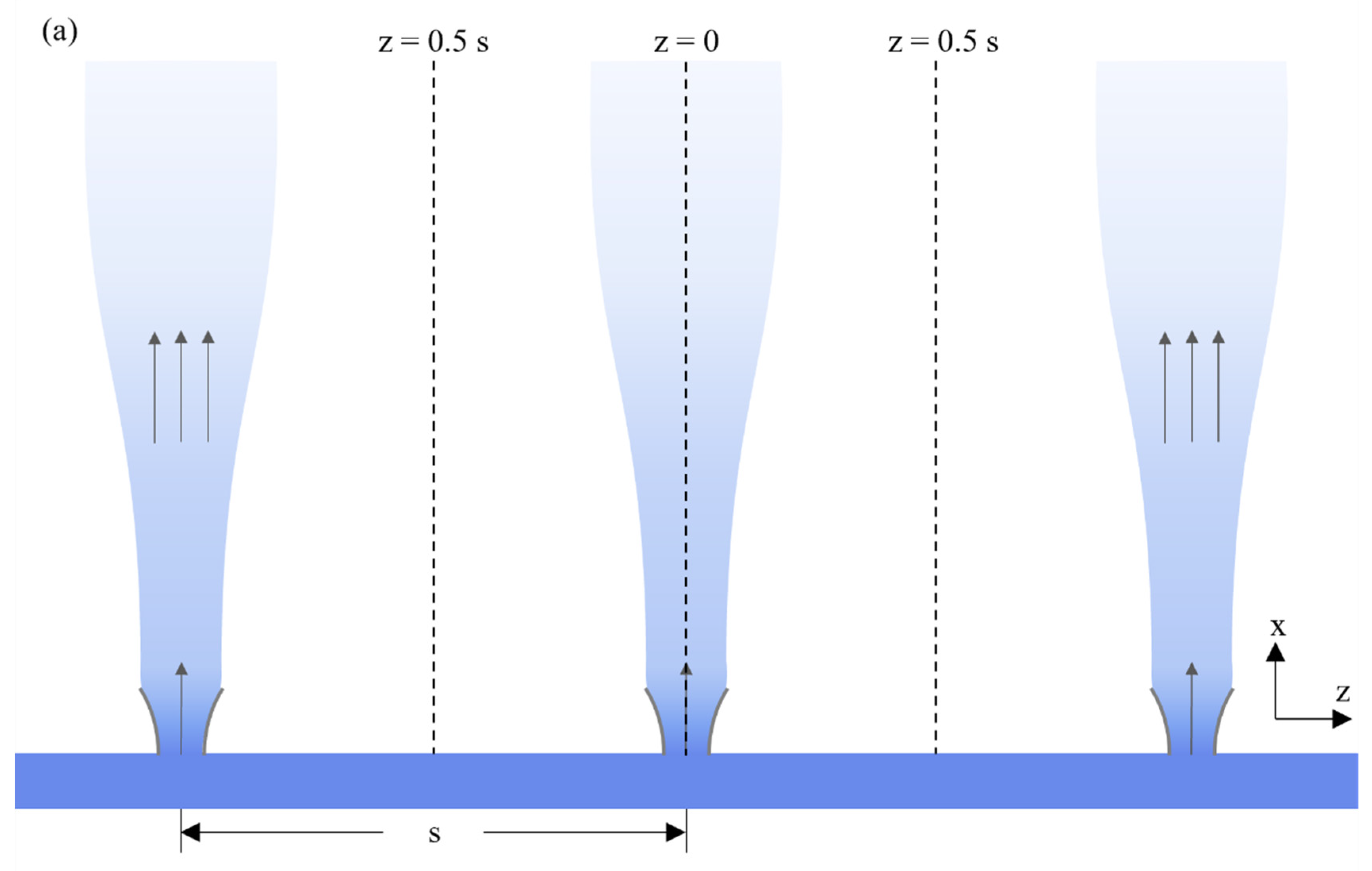
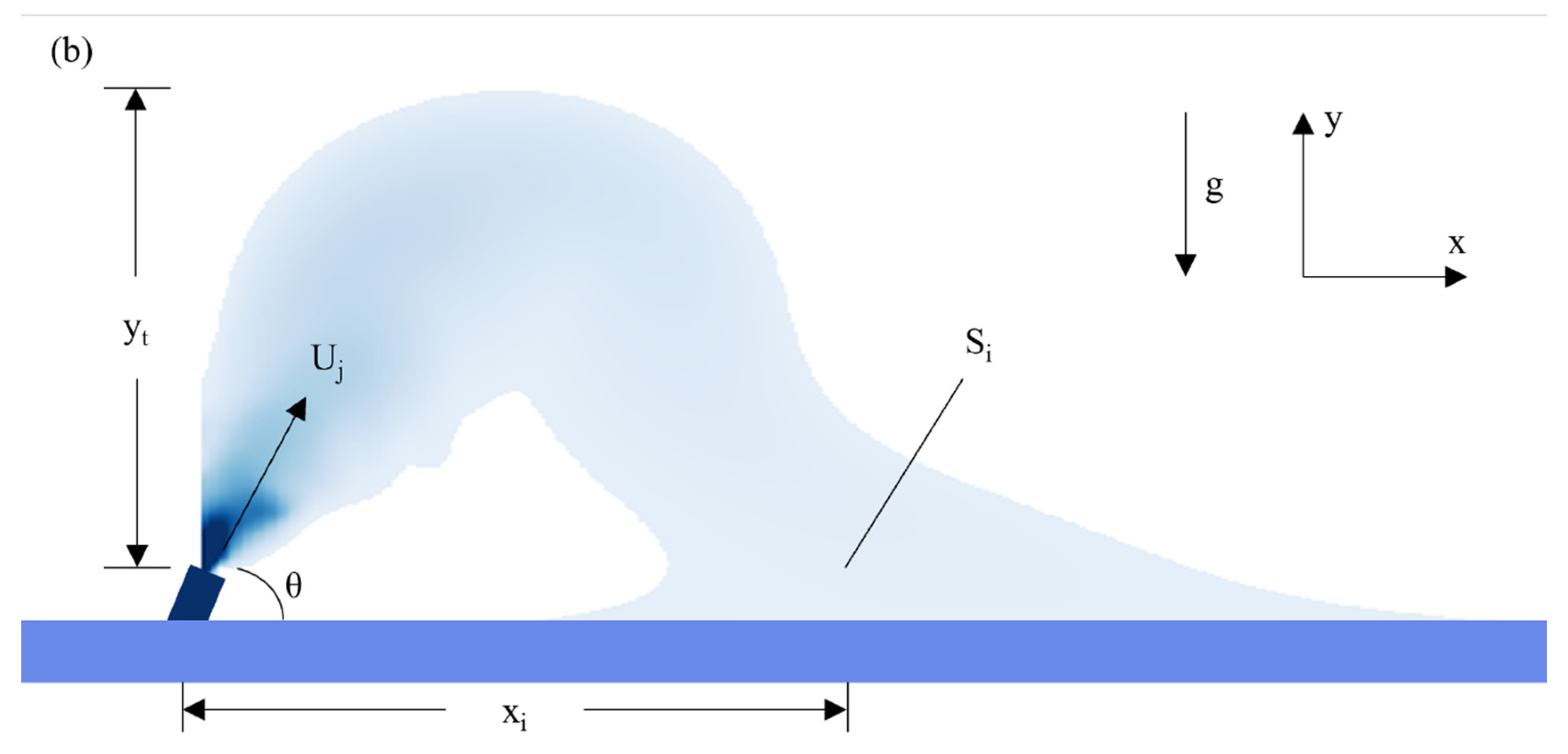
2.2. Physical Phenomenon
2.3. Physical Representation
2.4. Numerical Experiments
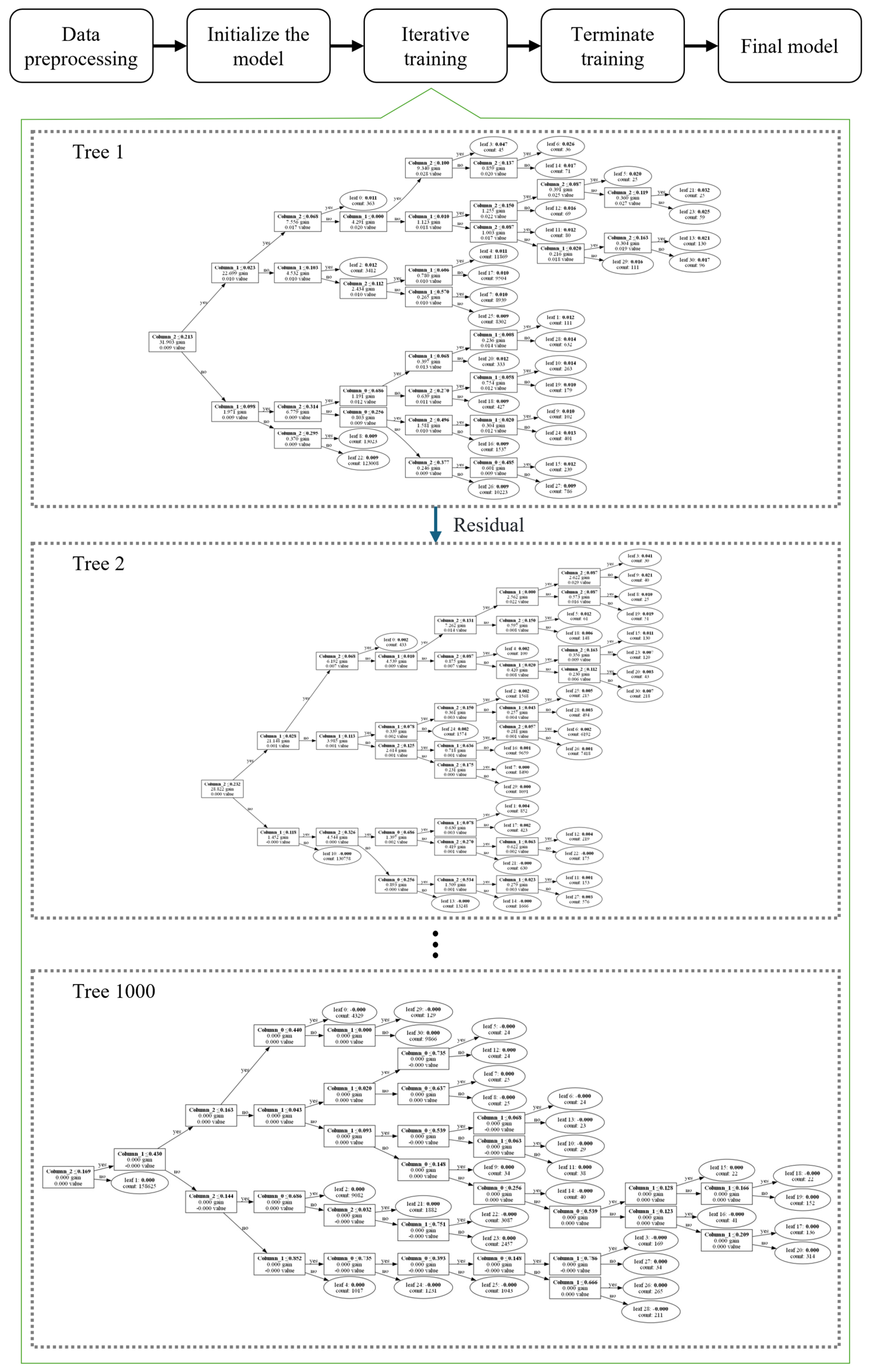
2.5. Field Reconstruction LightGBM Algorithm
2.6. Reference Methods
2.6.1. GradientBoostingRegressor
2.6.2. XGBoost
2.6.3. K-Nearest Neighbors
3. Results
3.1. Numerical Results
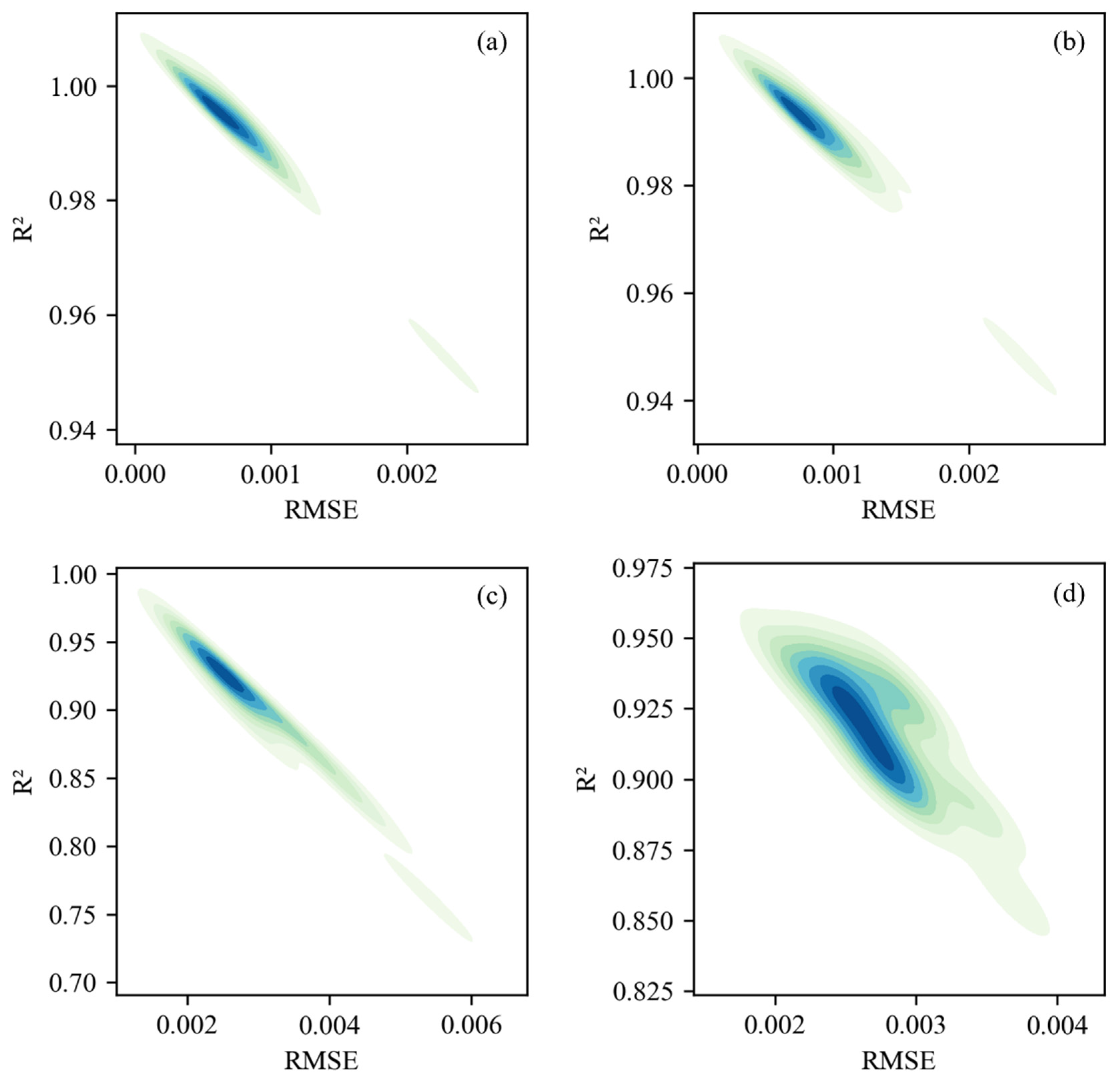
3.2. Performance of the LightGBM Method
3.3. Performance of the Reference Methods
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Campos, C.J.A.; Morrisey, D.J.; Barter, P. Principles and technical application of mixing zones for wastewater discharges to freshwater and marine environments. Water 2022, 14, 1201. [Google Scholar] [CrossRef]
- Alavian, V.; Jirka, G.H.; Denton, R.A.; Johnson, M.C.; Stefan, H.G. Density currents entering lakes and reservoirs. J. Hydraul. Eng. 1992, 118, 1464–1489. [Google Scholar] [CrossRef]
- Yannopoulos, P.C.; Noutsopoulos, G.C. Interaction of vertical round turbulent buoyant jets—Part I: Entrainment restriction approach. J. Hydraul. Res. 2006, 44, 218–232. [Google Scholar] [CrossRef]
- Brunton, S.L.; Noack, B.R.; Koumoutsakos, P. Machine learning for fluid mechanics. Annu. Rev. Fluid Mech. 2020, 52, 477–508. [Google Scholar] [CrossRef]
- Lindberg, W.R. Experiments on Negatively Buoyant Jets, with and Without Cross-Flow. In Recent Research Advances in the Fluid Mechanics of Turbulent Jets and Plumes; Springer: Dordrecht, The Netherlands, 1994; pp. 131–145. [Google Scholar]
- Cipollina, A.; Brucato, A.; Grisafi, F.; Nicosia, S. Bench-scale investigation of inclined dense jets. J. Hydraul. Eng. 2005, 131, 1017–1022. [Google Scholar] [CrossRef]
- Ferrari, S.; Querzoli, G. Mixing and re-entrainment in a negatively buoyant jet. J. Hydraul. Res. 2010, 48, 632–640. [Google Scholar] [CrossRef]
- Shao, D.; Law, A.W.-K. Mixing and boundary interactions of 30 and 45 inclined dense jets. Environ. Fluid Mech. 2010, 10, 521–553. [Google Scholar] [CrossRef]
- Jiang, M.; Chen, W.; Law, A.W.-K. Mixing characteristics of 45° inclined duckbill dense jets in co-flowing currents. J. Hydro-Environ. Res. 2021, 36, 77–86. [Google Scholar] [CrossRef]
- Gungor, E.; Roberts, P.J.W. Experimental studies on vertical dense jets in a flowing current. J. Hydraul. Eng. 2009, 135, 935–948. [Google Scholar] [CrossRef]
- Abessi, O.; Roberts, P.J.W. Effect of nozzle orientation on dense jets in stagnant environments. J. Hydraul. Eng. 2015, 141, 06015009. [Google Scholar] [CrossRef]
- Pagliara, S.; Palermo, M. Scour process caused by multiple subvertical non-crossing jets. Water Sci. Eng. 2017, 10, 17–24. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C. Spreading of round dense jets impinging on a horizontal bottom. J. Hydro-Environ. Res. 2010, 4, 289–300. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 1: Geometrical characteristics. J. Hydraul. Res. 2011, 49, 3–12. [Google Scholar] [CrossRef]
- Papakonstantis, I.G.; Christodoulou, G.C.; Papanicolaou, P.N. Inclined negatively buoyant jets 2: Concentration measurements. J. Hydraul. Res. 2011, 49, 13–22. [Google Scholar] [CrossRef]
- Lai, C.C.; Lee, J.H. Mixing of inclined dense jets in stationary ambient. J. Hydro-Environ. Res. 2012, 6, 9–28. [Google Scholar] [CrossRef]
- Kikkert, G.A.; Davidson, M.J.; Nokes, R.I. Inclined negatively buoyant discharges. J. Hydraul. Eng. 2007, 133, 545–554. [Google Scholar] [CrossRef]
- Choi, K.W.; Lai, C.C.K.; Lee, J.H.W. Mixing in the intermediate field of dense jets in cross currents. J. Hydraul. Eng. 2016, 142, 04015041. [Google Scholar] [CrossRef]
- Bombardelli, F.A.; Palermo, M.; Pagliara, S. Temporal evolution of jet induced scour depth in cohesionless granular beds and the phenomenological theory of turbulence. Phys. Fluids 2018, 30, 085109. [Google Scholar] [CrossRef]
- Ma, Y.; Li, P.; Zhu, D.Z.; Khan, A. Air flow inside a vertical pipe induced by a free-falling water jet. J. Hydro-Environ. Res. 2022, 44, 23–34. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.; Zhao, B. Large eddy simulations of turbulent circular wall jets. Int. J. Heat Mass Transf. 2015, 80, 72–84. [Google Scholar] [CrossRef]
- Zhang, S.; Law, A.W.-K.; Jiang, M. Large eddy simulations of 45 and 60 inclined dense jets with bottom impact. J. Hydro-Environ. Res. 2017, 15, 54–66. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, H.; Abali, B.E.; Müller, W.H. Investigating the Morphology of a Free-Falling Jet with an Accurate Finite Element and Level Set Modeling. Fluids 2024, 9, 264. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Numerical modeling of multiple inclined dense jets discharged from moderately spaced ports. Water 2019, 11, 2077. [Google Scholar] [CrossRef]
- Nikiforakis, I.K.; Stamou, A.I.; Christodoulou, G.C. A modified integral model for negatively buoyant jets in a stationary ambient. Environ. Fluid Mech. 2015, 15, 939–957. [Google Scholar] [CrossRef]
- Lou, Y.; He, Z.; Jiang, H.; Han, X. Numerical simulation of two coalescing turbulent forced plumes in linearly stratified fluids. Phys. Fluids 2019, 31, 037111. [Google Scholar] [CrossRef]
- Li, G.; Wang, B. Simulation of the flow field and scour evolution by turbulent wall jets under a sluice gate. J. Hydro-Environ. Res. 2022, 43, 22–32. [Google Scholar] [CrossRef]
- Yan, X.; Mohammadian, A. Evolutionary modeling of inclined dense jets discharged from multiport diffusers. J. Coast. Res. 2020, 36, 362–371. [Google Scholar] [CrossRef]
- Beheshtian, S.; Roodbari, S.K.; Ghorbani, H.; Azodinia, M.; Mudabbir, M. Machine Learning Prediction of Gas Hydrates Phase Equilibrium in Porous Medium. In Proceedings of the 2024 IEEE 18th International Symposium on Applied Computational Intelligence and Informatics (SACI), Timisoara, Romania, 23–25 May 2024; IEEE: Piscataway, NJ, USA, 2024. [Google Scholar]
- Zou, F.; Wang, W.; Cai, Q.; Guo, F.; Shi, R. Dynamic Generation Method of Highway ETC Gantry Topology Based on LightGBM. Mathematics 2023, 11, 3413. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, L.; Chen, G.; Gu, Z.; Tian, Z.; Du, X.; Guizani, M. STG2P: A two-stage pipeline model for intrusion detection based on improved LightGBM and K-means. Simul. Model. Pract. Theory 2022, 120, 102614. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, T.; Zhang, D. Fault Detection of Flow Control Valves Using Online LightGBM and STL Decomposition. Actuators 2024, 13, 222. [Google Scholar] [CrossRef]
- Holzmann, T. Mathematics, Numerics, Derivations and OpenFOAM®; Holzmann CFD: Loeben, Germany, 2016. [Google Scholar]
- The OpenCFD Foundation. OpenFOAM User Guide; Version 4.0; The OpenCFD Foundation: London, UK, 2016. [Google Scholar]
- Zhang, S.; Jiang, B.; Law, A.W.K.; Zhao, B. Large eddy simulations of 45 inclined dense jets. Environ. Fluid Mech. 2016, 16, 101–121. [Google Scholar] [CrossRef]
- Lai, A.C.; Zhao, B.; Law, A.W.K.; Adams, E.E. A numerical and analytical study of the effect of aspect ratio on the behavior of a round thermal. Environ. Fluid Mech. 2015, 15, 85–108. [Google Scholar] [CrossRef]

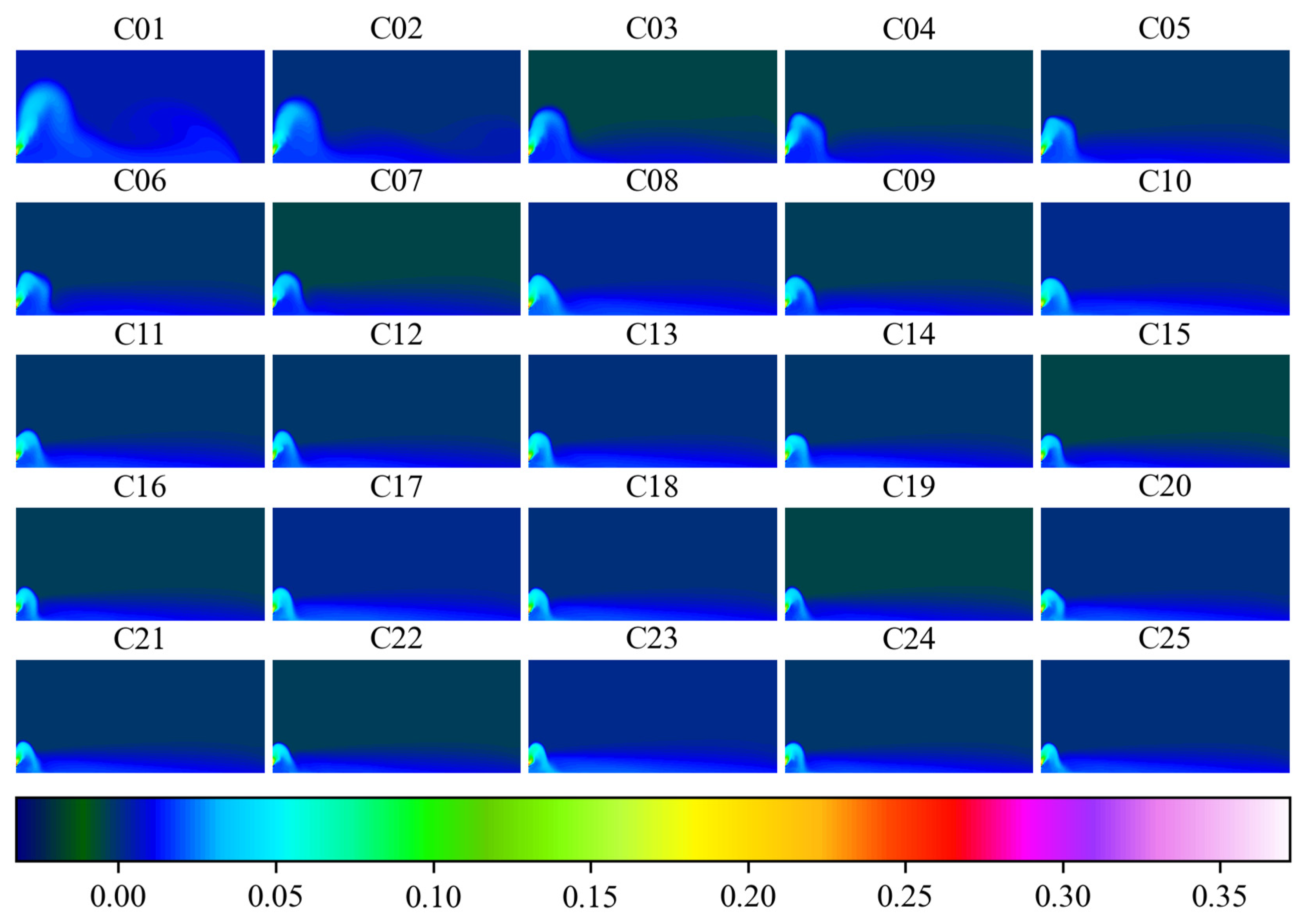
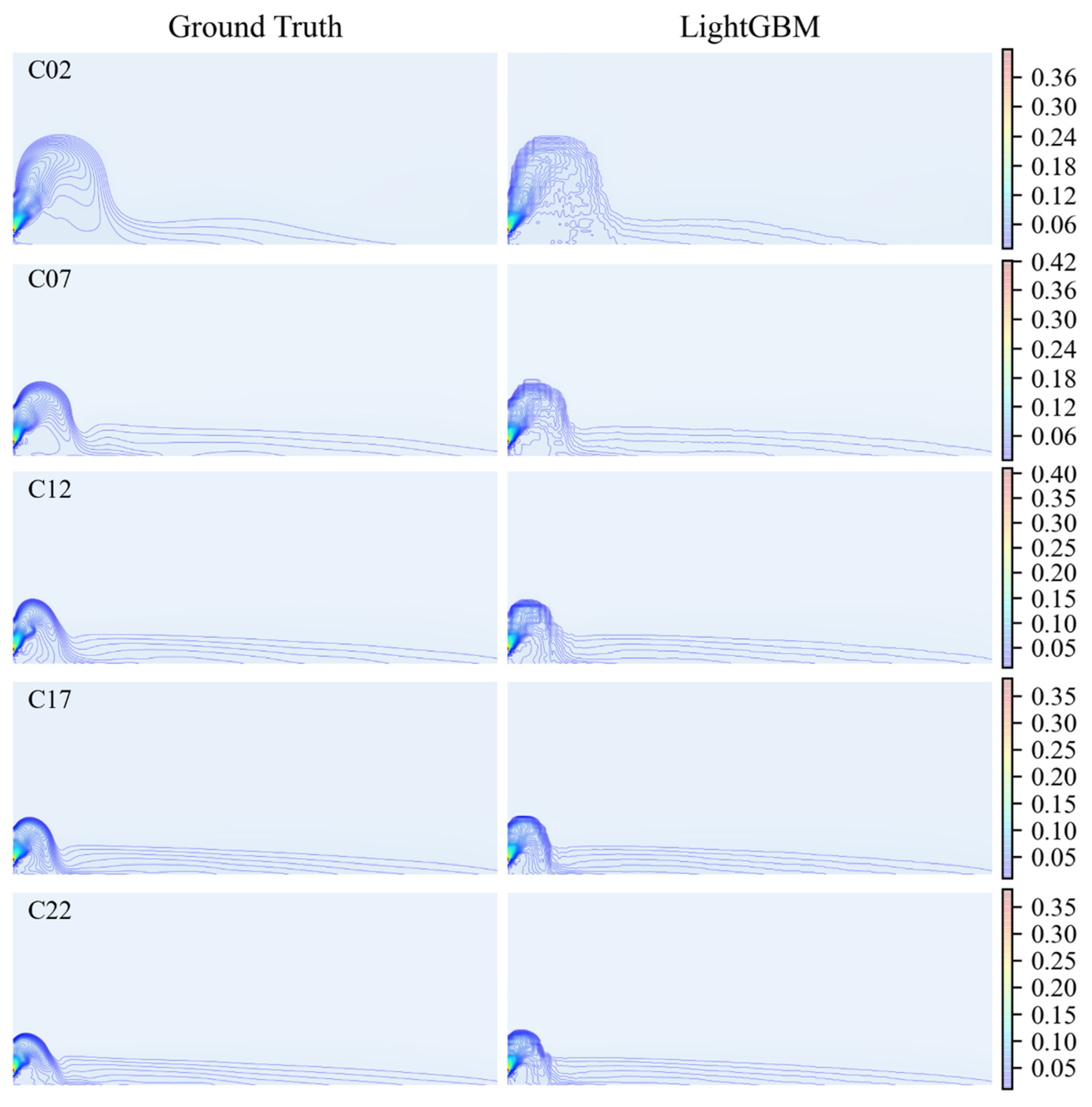
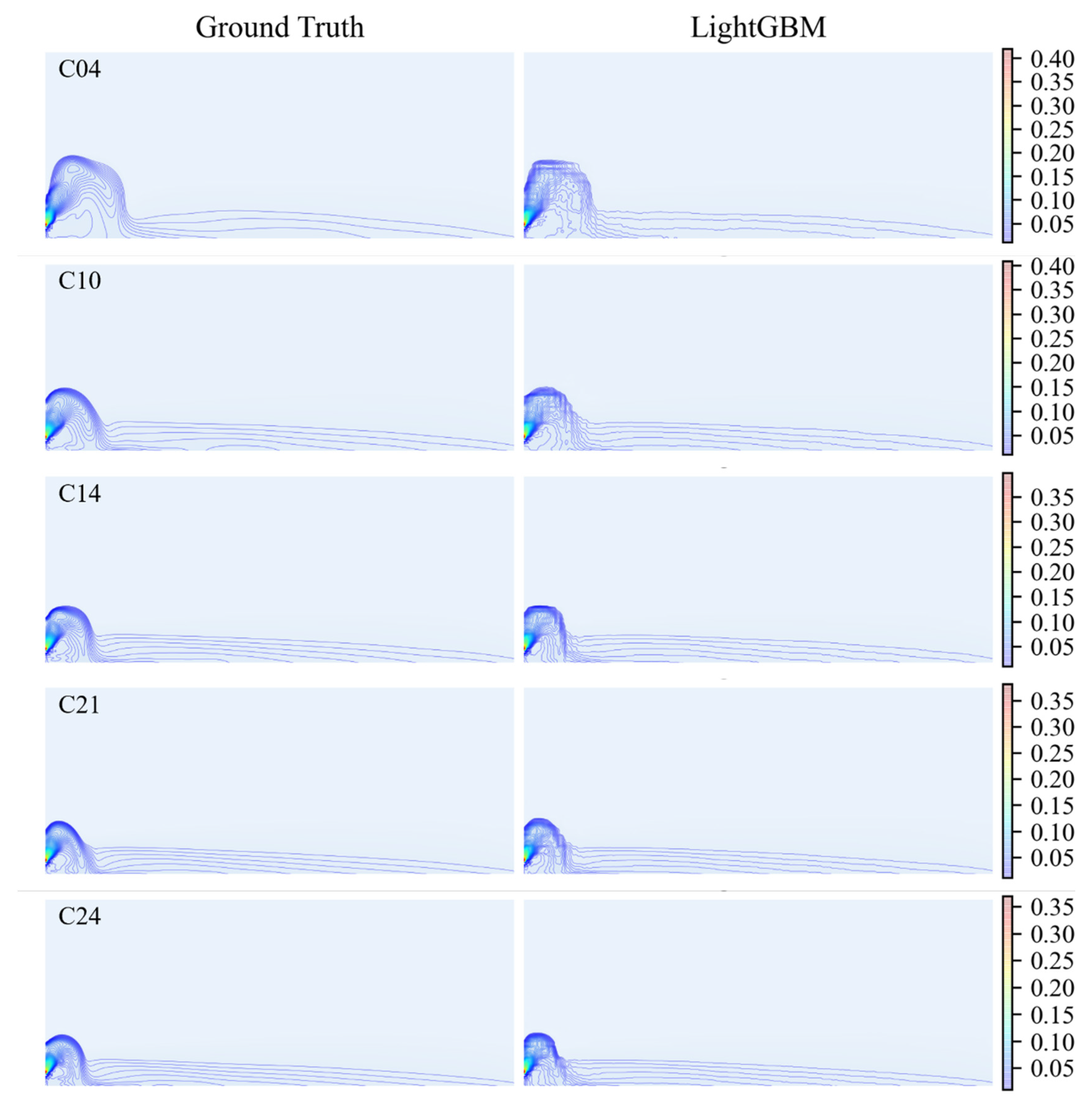

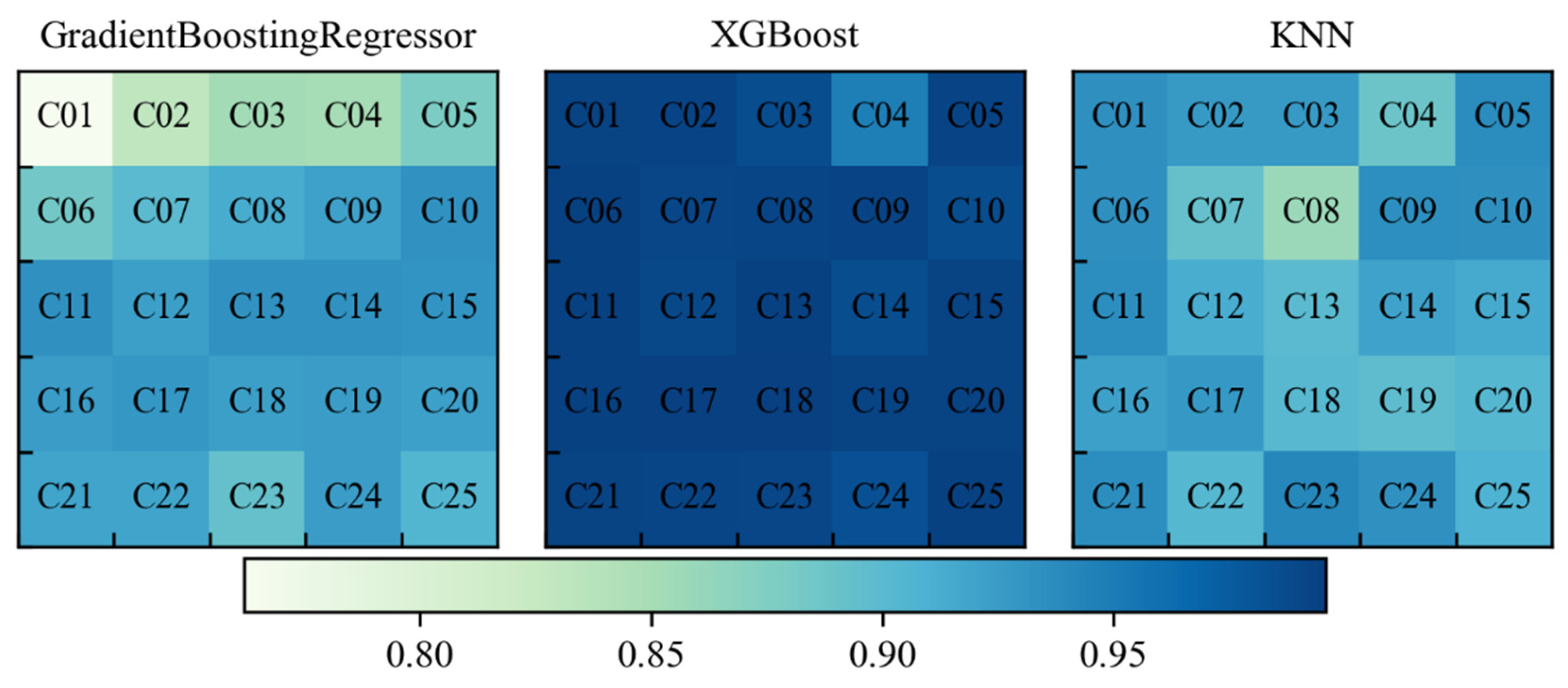
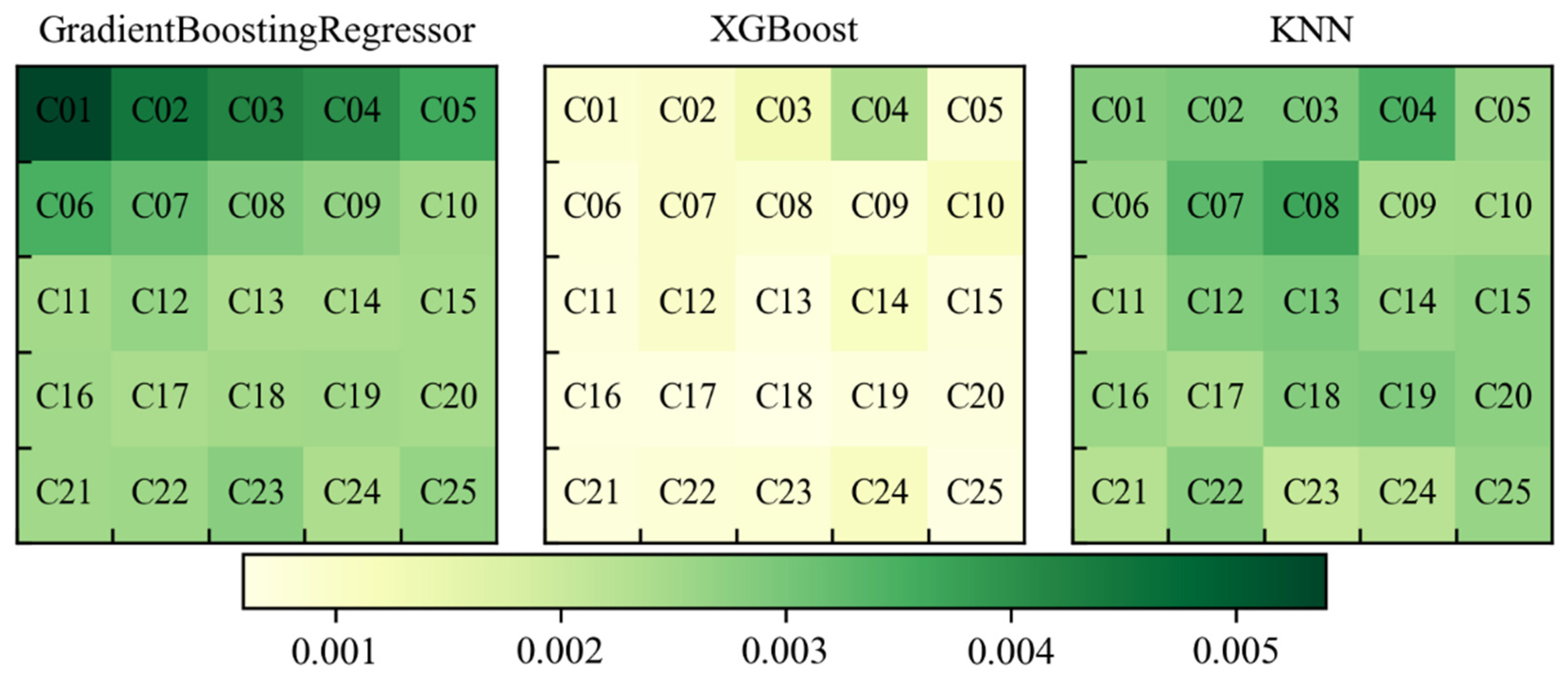
| Cases | ρjet | Fr | s/(d·Fr) | Cases | ρjet | Fr | s/(d·Fr) |
|---|---|---|---|---|---|---|---|
| C00 | 1029 | 81.1 | 0.73 | C13 | 1336 | 24.9 | 2.37 |
| C01 | 1021 | 93.8 | 0.63 | C14 | 1362 | 24.0 | 2.46 |
| C02 | 1047 | 64.9 | 0.91 | C15 | 1388 | 23.2 | 2.54 |
| C03 | 1076 | 51.7 | 1.14 | C16 | 1414 | 22.5 | 2.63 |
| C04 | 1103 | 44.6 | 1.32 | C17 | 1440 | 21.8 | 2.71 |
| C05 | 1129 | 40.0 | 1.48 | C18 | 1466 | 21.2 | 2.79 |
| C06 | 1154 | 36.6 | 1.61 | C19 | 1492 | 20.6 | 2.86 |
| C07 | 1180 | 33.9 | 1.74 | C20 | 1518 | 20.1 | 2.94 |
| C08 | 1207 | 31.7 | 1.86 | C21 | 1544 | 19.6 | 3.01 |
| C09 | 1233 | 29.9 | 1.98 | C22 | 1570 | 19.2 | 3.08 |
| C10 | 1259 | 28.4 | 2.08 | C23 | 1596 | 18.8 | 3.15 |
| C11 | 1276 | 27.5 | 2.15 | C24 | 1622 | 18.4 | 3.22 |
| C12 | 1310 | 25.9 | 2.28 | C25 | 1649 | 18.0 | 3.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Luo, C.; Wang, Z.; Liu, S.; Zhu, Z. Predicting Multi-Dense Jet Concentration Fields Using a Field Reconstruction Machine Learning Framework. Processes 2025, 13, 863. https://doi.org/10.3390/pr13030863
Yan X, Luo C, Wang Z, Liu S, Zhu Z. Predicting Multi-Dense Jet Concentration Fields Using a Field Reconstruction Machine Learning Framework. Processes. 2025; 13(3):863. https://doi.org/10.3390/pr13030863
Chicago/Turabian StyleYan, Xiaohui, Chuyao Luo, Zhuo Wang, Sidi Liu, and Zuhao Zhu. 2025. "Predicting Multi-Dense Jet Concentration Fields Using a Field Reconstruction Machine Learning Framework" Processes 13, no. 3: 863. https://doi.org/10.3390/pr13030863
APA StyleYan, X., Luo, C., Wang, Z., Liu, S., & Zhu, Z. (2025). Predicting Multi-Dense Jet Concentration Fields Using a Field Reconstruction Machine Learning Framework. Processes, 13(3), 863. https://doi.org/10.3390/pr13030863








