A Data-Driven Algorithm for Dynamic Parameter Estimation of an Alkaline Electrolysis System Combining Online Reinforcement Learning and k-Means Clustering Analysis
Abstract
1. Introduction
2. The Models of the AEL System and Estimated Parameters
2.1. Electrochemical Model and Parameters
2.2. Heat Transfer Model and Parameters
2.3. Mass Transfer Model and Parameters
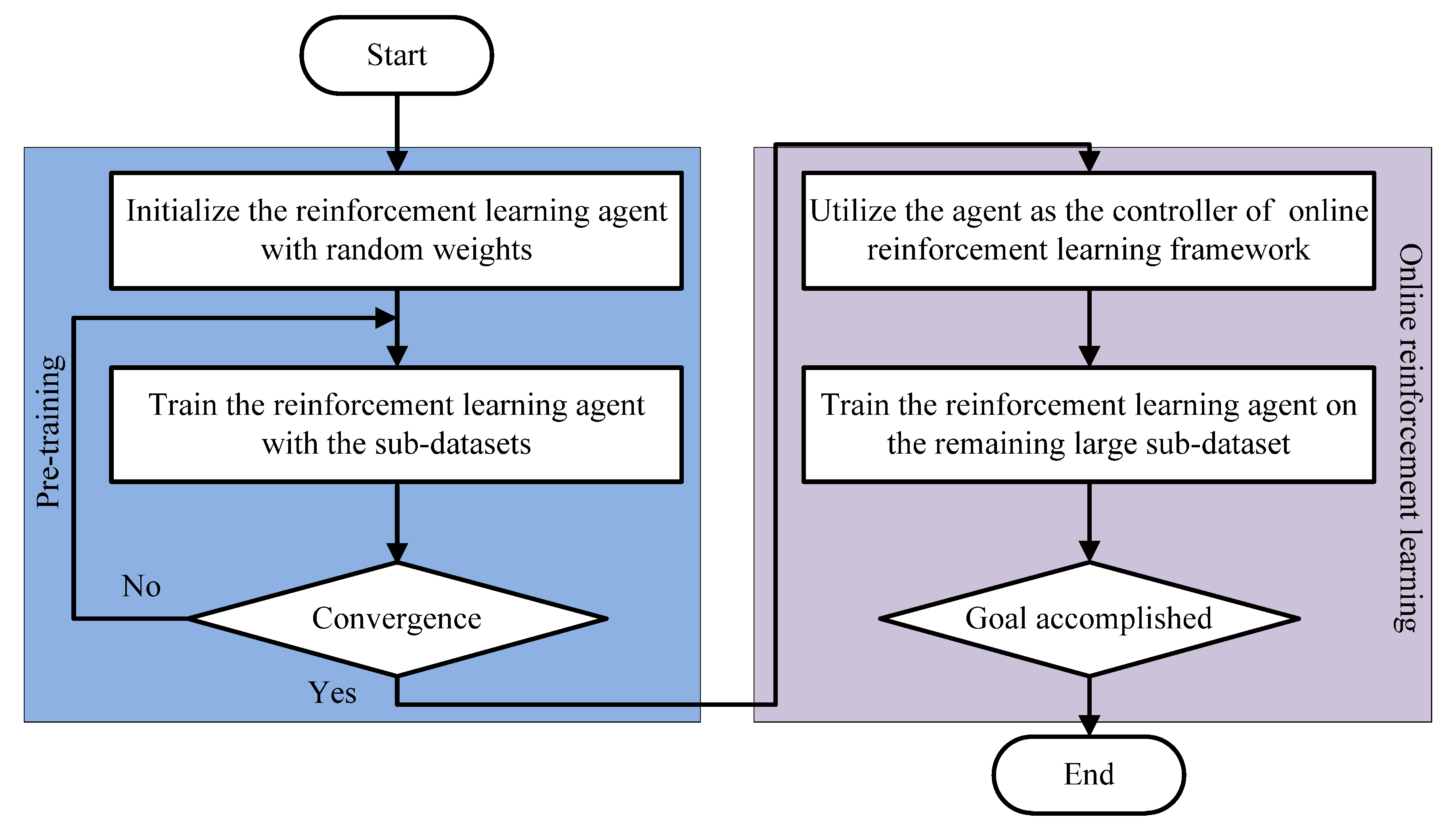
3. The Proposed Model
3.1. The Architecture of the Proposed Model
3.2. K-Means Clustering Analysis
3.3. Notation of Reinforcement Learning
3.4. Online Reinforcement Learning
4. Results
4.1. Experiment Data
4.2. Performance Metrics
4.3. Case Study
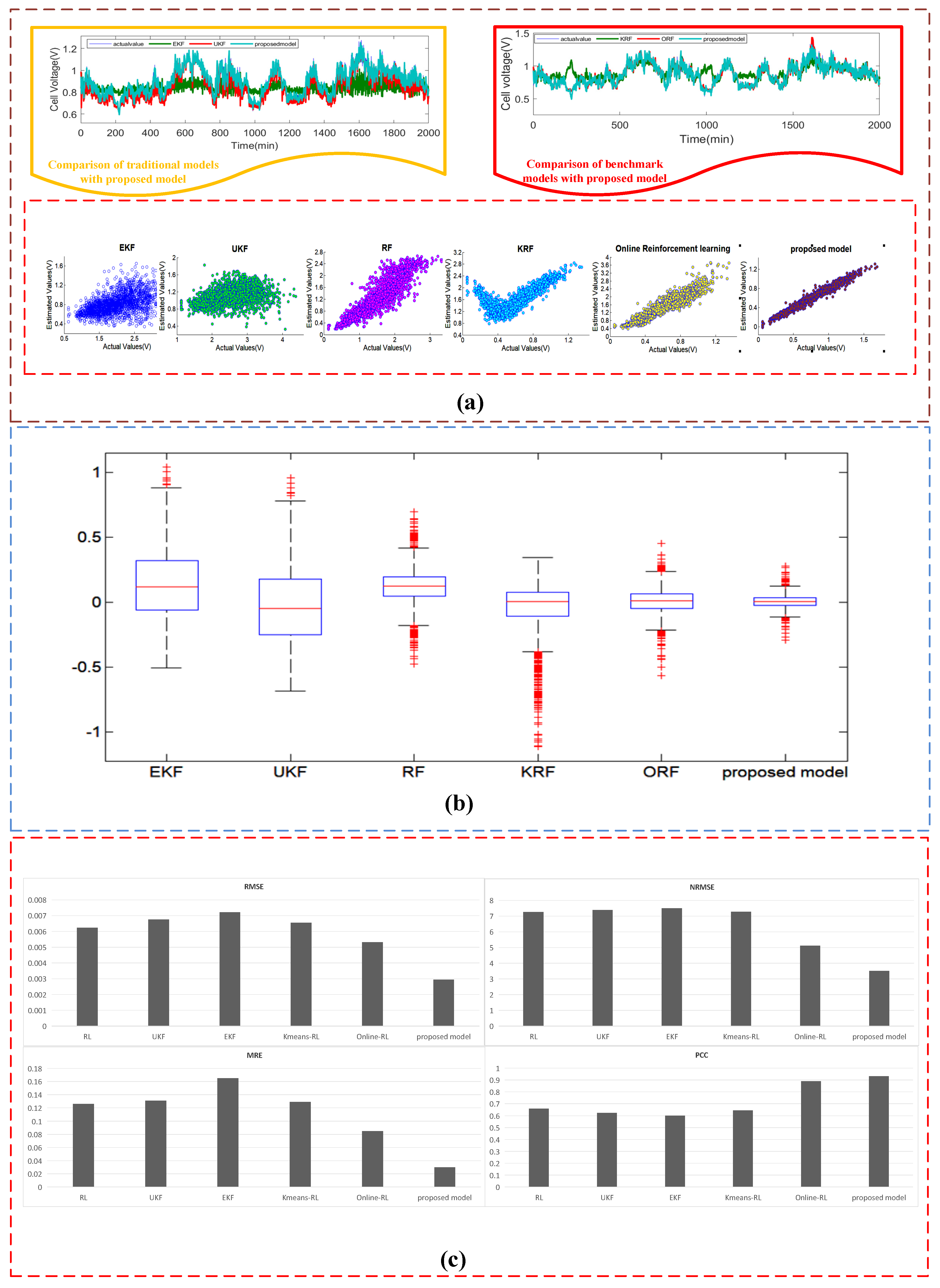
4.3.1. Case I: The Estimated Results of the Dataset #1
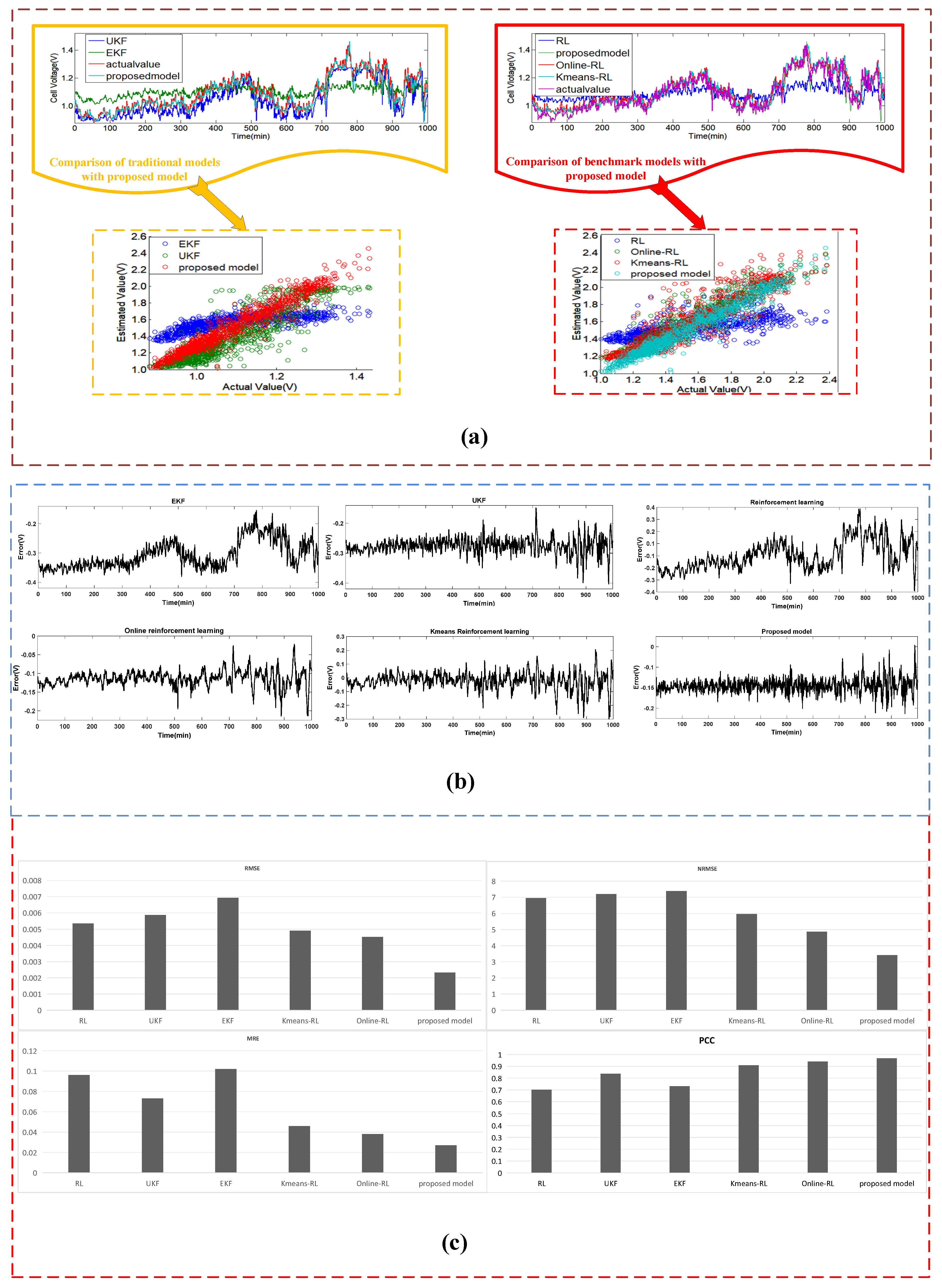
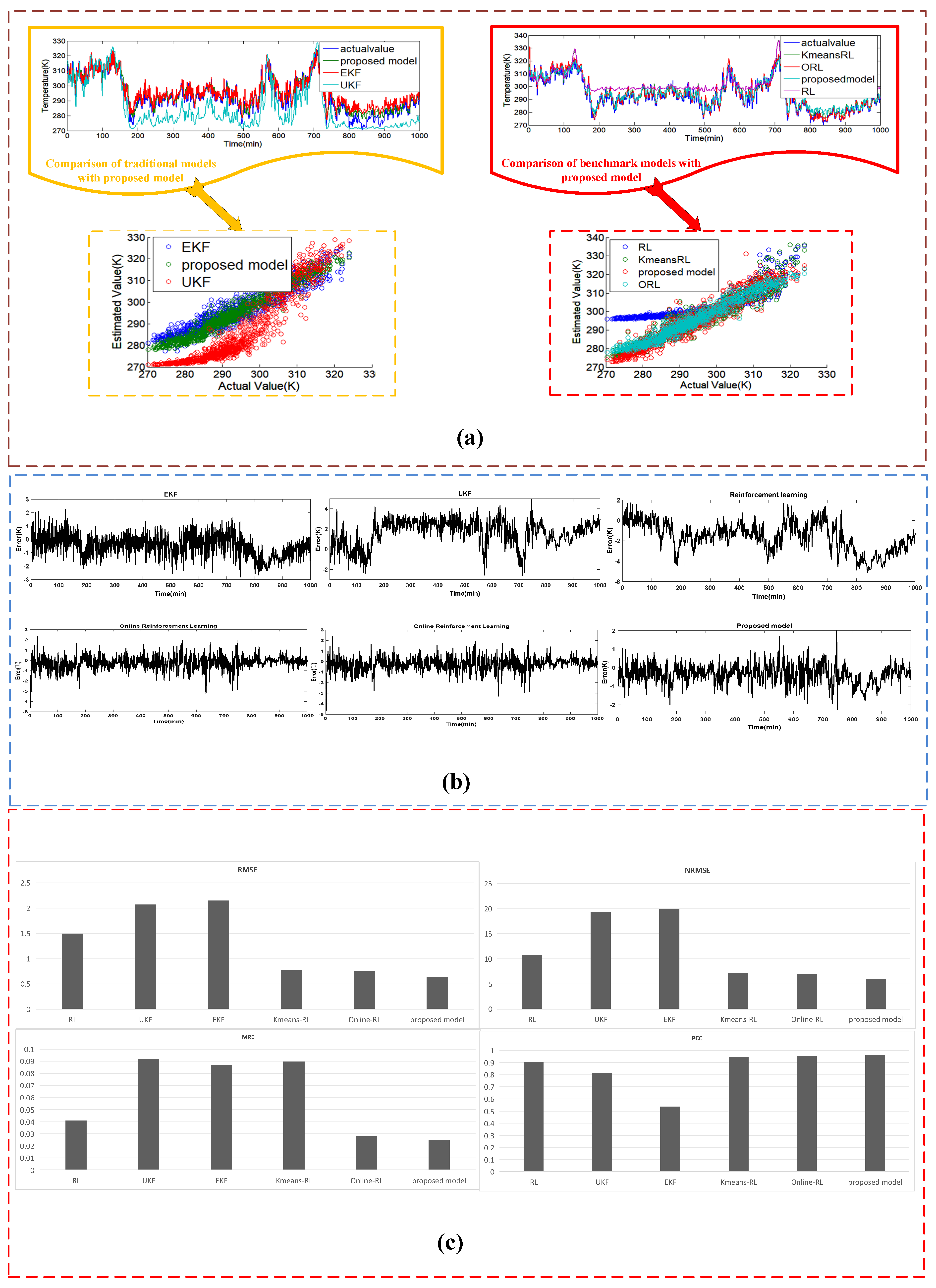
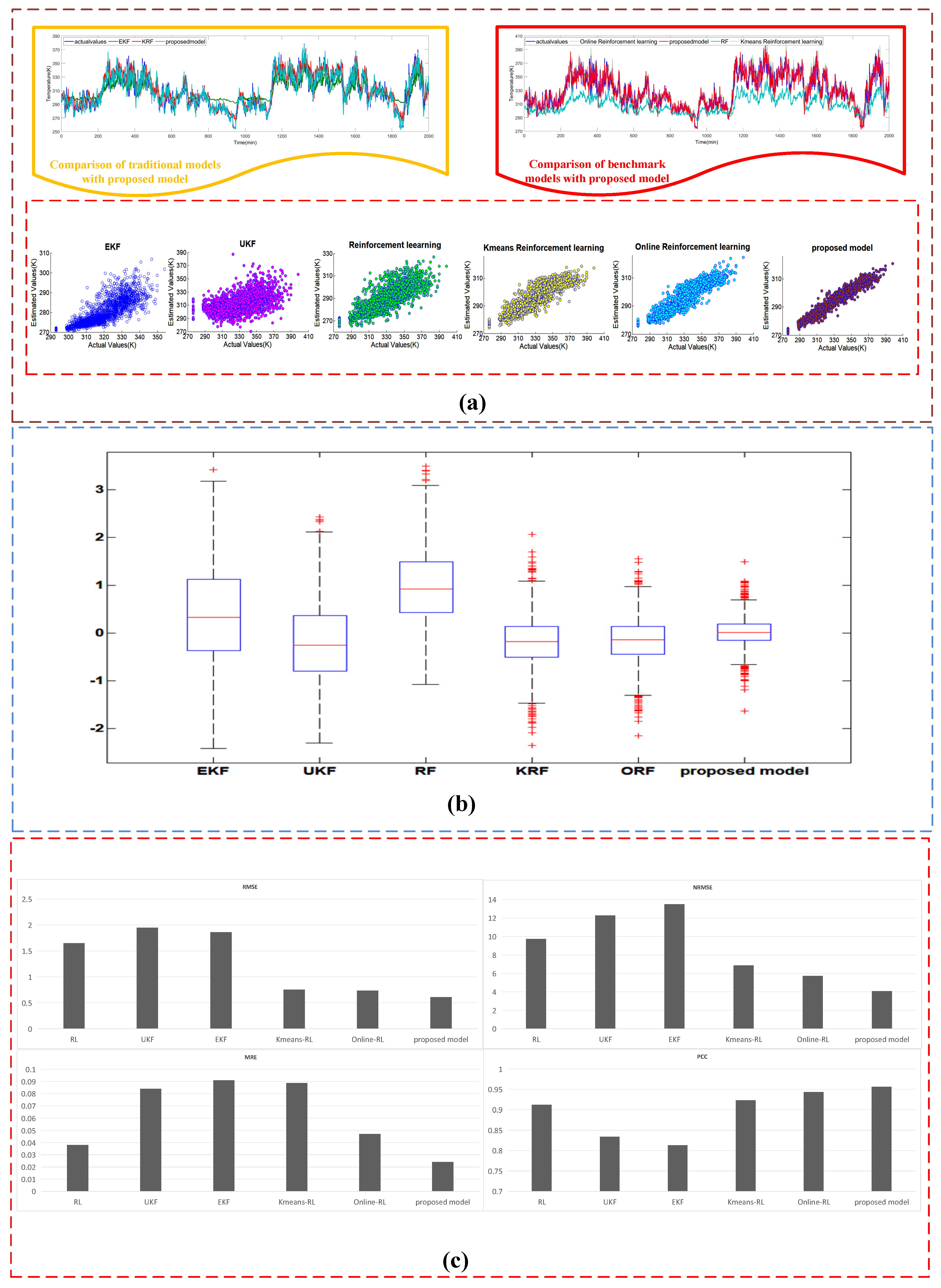
4.3.2. Case II: The Estimated Results of the Dataset #2
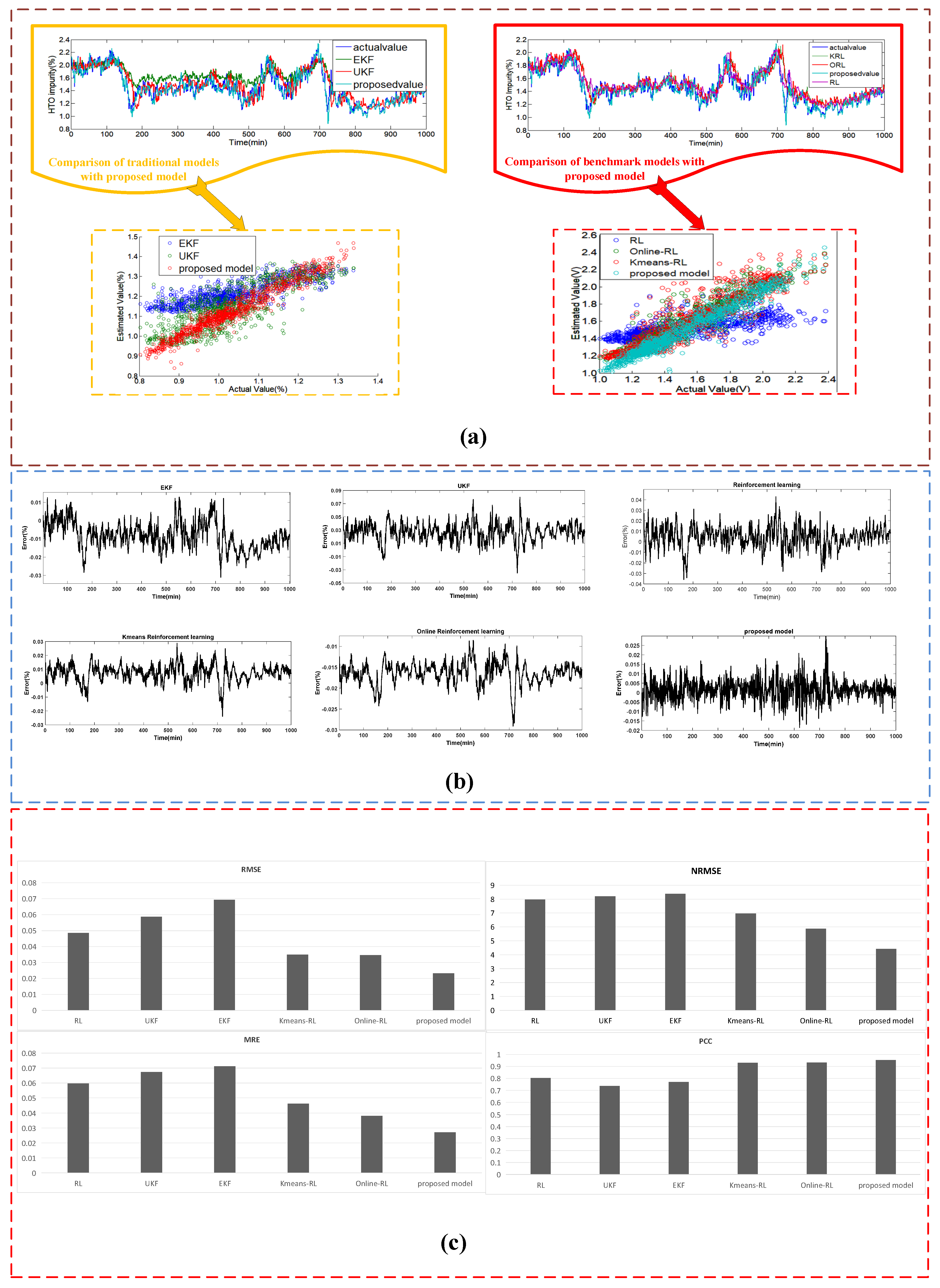
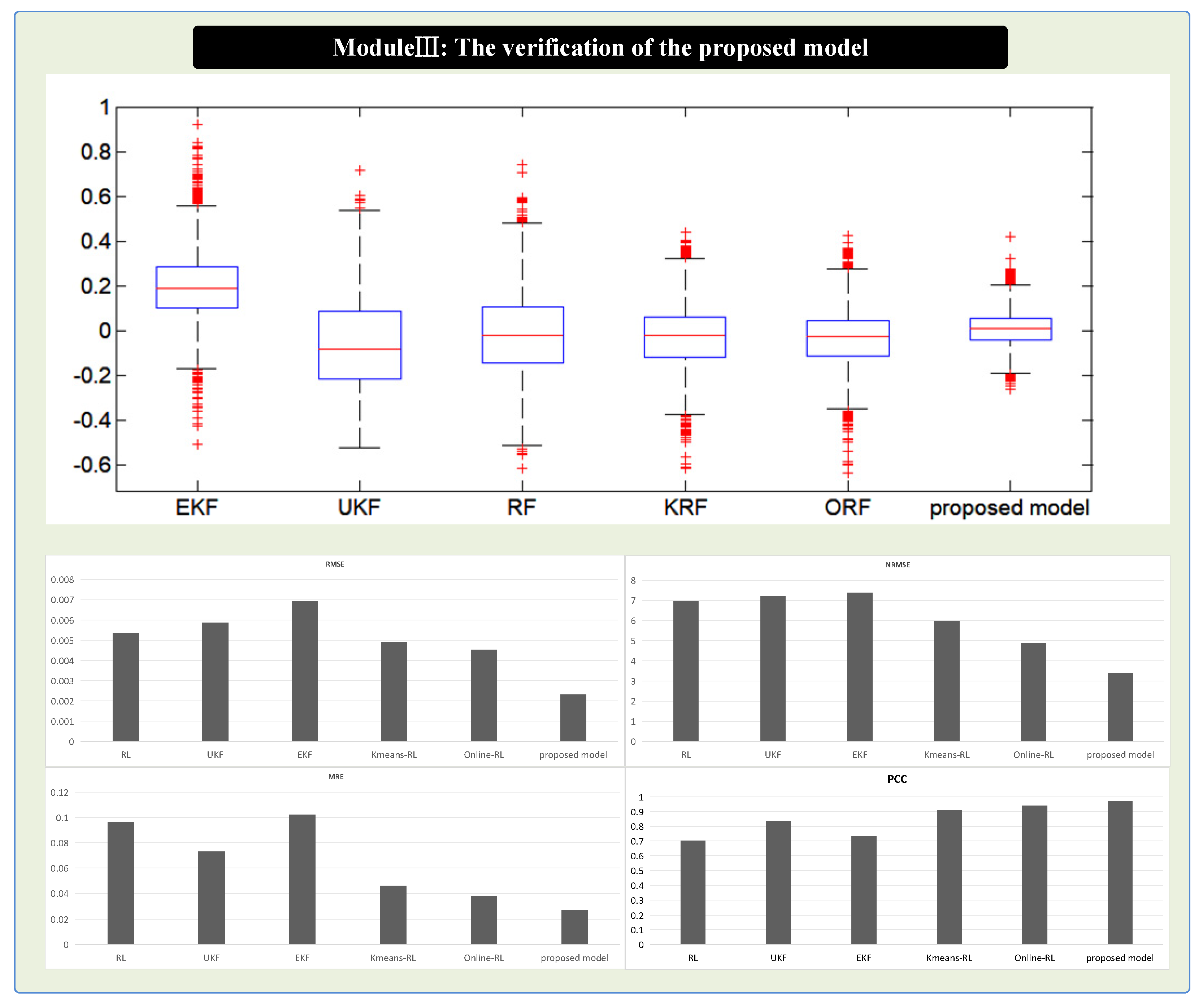
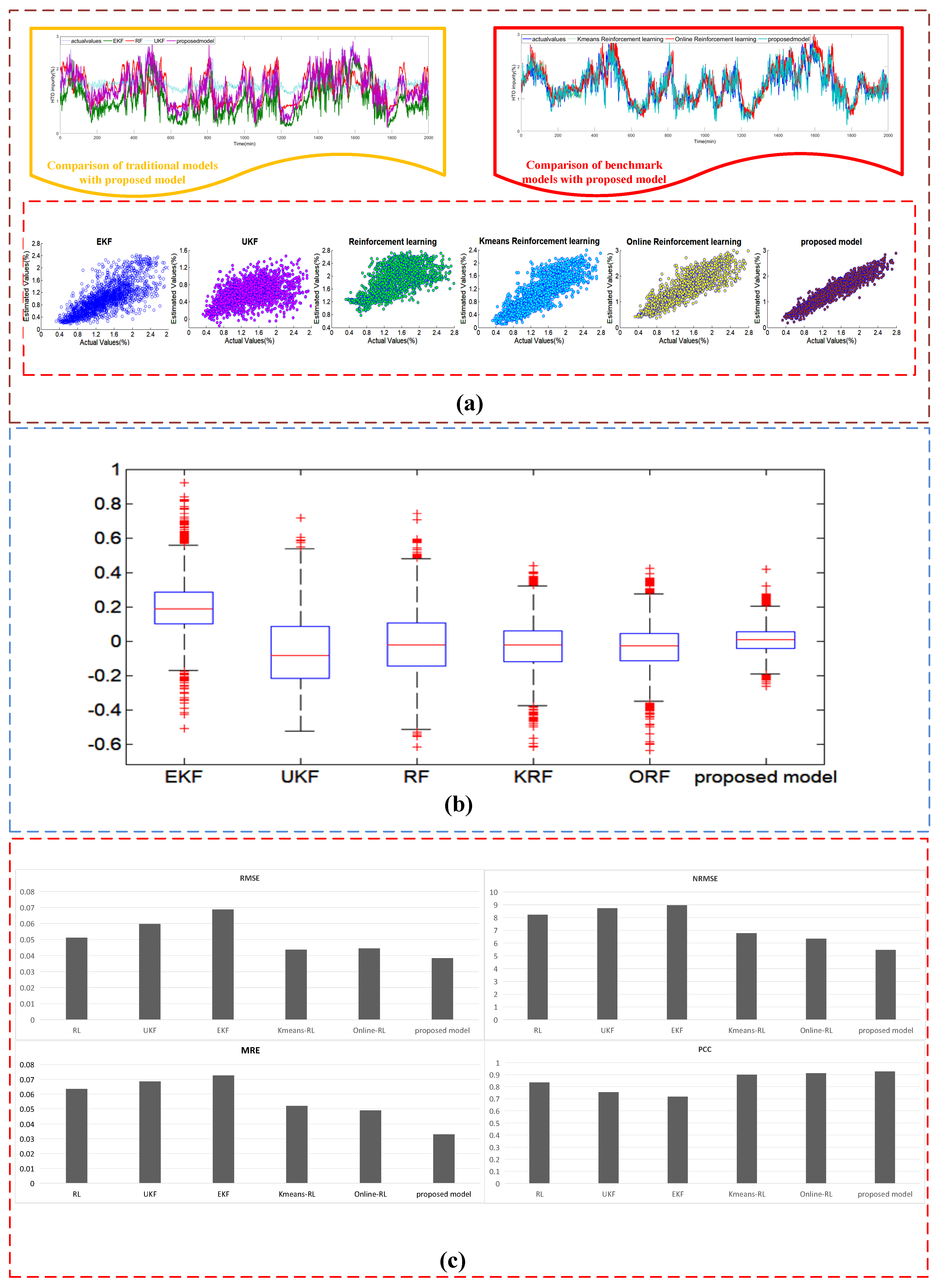
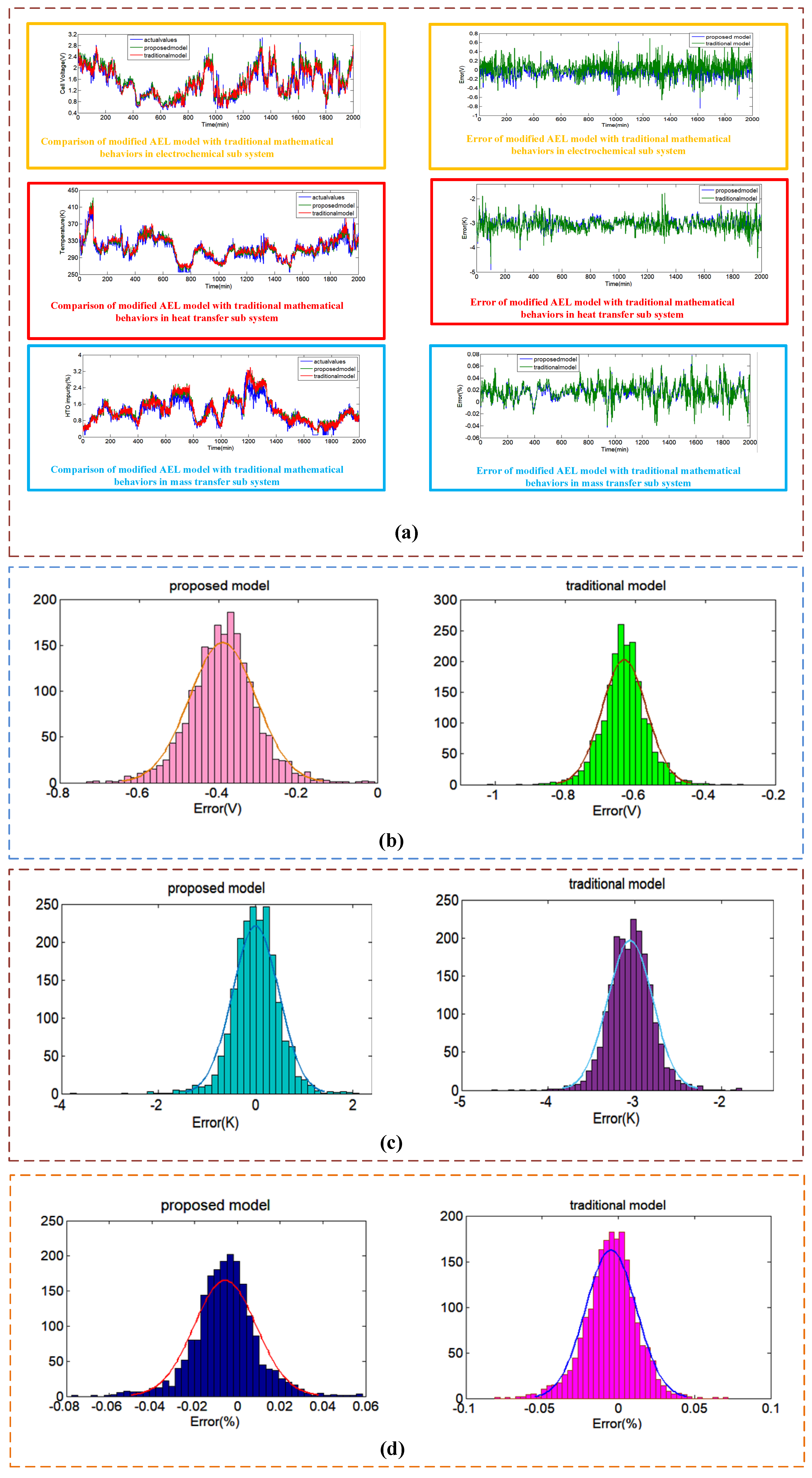
4.3.3. Case III Comparison with the Modified AEL Systems for Dataset #3
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, Y.; Lv, H.; Lu, H.; Quan, Q.; Li, W.; Cui, X.; Liu, G.; Jiang, L. Mg/seawater batteries driven self-powered direct seawater electrolysis systems for hydrogen production. Nano Energy 2022, 98, 107295. [Google Scholar] [CrossRef]
- Qiu, X.; Zhang, H.; Qiu, Y.; Zhou, Y.; Zang, T.; Zhou, B.; Qi, R.; Lin, J.; Wang, J. Dynamic parameter estimation of the alkaline electrolysis system combining Bayesian inference and adaptive polynomial surrogate models. Appl. Energy 2023, 348, 121533. [Google Scholar] [CrossRef]
- Panah, P.G.; Cui, X.; Bornapour, M.; Hooshmand, R.-A.; Guerrero, J.M. Marketability analysis of green hydrogen production in Denmark: Scale-up effects on grid-connected electrolysis. Int. J. Hydrogen Energy 2022, 47, 12443–12455. [Google Scholar] [CrossRef]
- Sebbahi, S.; Assila, A.; Belghiti, A.A.; Laasri, S.; Kaya, S.; Hlil, E.K.; Rachidi, S.; Hajjaji, A. A comprehensive review of recent advances in alkaline water electrolysis for hydrogen production. Int. J. Hydrogen Energy 2024, 82, 583–599. [Google Scholar] [CrossRef]
- de Groot, M.T.; Kraakman, J.; Barros, R.L.G. Optimal operating parameters for advanced alkaline water electrolysis. Int. J. Hydrogen Energy 2022, 47, 34773–34783. [Google Scholar] [CrossRef]
- Sanchez, M.; Amores, E.; Rodriguez, L.; Clemente-Jul, C. Semi-empirical model and experimental validation for the performance evaluation of a 15 kW alkaline water electrolyzer. Int. J. Hydrogen Energy 2018, 43, 20332–20345. [Google Scholar] [CrossRef]
- Huang, D.; Xiong, B.; Fang, J.; Hu, K.; Zhong, Z.; Ying, Y.; Ai, X.; Chen, Z. A multiphysics model of the compactly-assembled industrial alkaline water electrolysis cell. Appl. Energy 2022, 314, 118987. [Google Scholar] [CrossRef]
- Kim, H.; Park, M.; Lee, K.S. One-dimensional dynamic modeling of a high-pressure water electrolysis system for hydrogen production. Int. J. Hydrogen Energy 2013, 38, 2596–2609. [Google Scholar] [CrossRef]
- Sakas, G.; Ibanez-Rioja, A.; Ruuskanen, V.; Kosonen, A.; Ahola, J.; Bergmann, O. Dynamic energy and mass balance model for an industrial alkaline water electrolyzer plant process. Int. J. Hydrogen Energy 2022, 47, 4328–4345. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, X. Digital twin of wind farms via physics-informed deep learning. Energy Convers. Manag. 2023, 293, 117507. [Google Scholar] [CrossRef]
- Abomazid, A.M.; El-Taweel, N.A.; Farag, H.E. Novel analytical approach for parameters identification of PEM electrolyzer. IEEE Trans. Ind. Inf. 2022, 18, 5870–5881. [Google Scholar]
- El-Fergany, A.A. Extracting optimal parameters of PEM fuel cells using Salp Swarm Optimizer. Renew. Energy 2018, 119, 641–648. [Google Scholar]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar]
- Ben Messaoud, R.; Midouni, A.; Hajji, S. PEM fuel cell model parameters extraction based on moth-flame optimization. Chem. Eng. Sci. 2021, 229, 116100. [Google Scholar]
- Chen, K.; Peng, H.; Zhang, J.; Chen, P.; Ruan, J.; Li, B.; Wang, Y. Optimized Demand-Side Day-Ahead Generation Scheduling Model for a Wind-Photovoltaic-Energy Storage Hydrogen Production System. ACS Omega 2022, 7, 43036–43044. [Google Scholar]
- Abaza, A.; El-Sehiemy, R.A.; Mahmoud, K.; Lehtonen, M.; Darwish, M.M. Optimal estimation of proton exchange membrane fuel cells parameter based on coyote optimization algorithm. Appl. Sci. 2021, 11, 2052. [Google Scholar] [CrossRef]
- Gunay, M.E.; Tapan, N.A.; Akkoc, G. Analysis and modeling of high-performance polymer electrolyte membrane electrolyzers by machine learning. Int. J. Hydrogen Energy 2022, 47, 2134–2151. [Google Scholar]
- Wang, M.; Zhu, H. Machine learning for transition-metal-based hydrogen generation electrocatalysts. ACS Catal. 2021, 11, 3930–3937. [Google Scholar]
- Jang, D.; Choi, W.; Cho, H.-S.; Cho, W.C.; Kim, C.H.; Kang, S. Numerical modeling and analysis of the temperature effect on the performance of an alkaline water electrolysis system. J. Power Sources 2021, 506, 230106. [Google Scholar]
- Li, Y.; Zhang, T.; Ma, J.; Deng, X.; Gu, J.; Yang, F.; Ouyang, M. Study the effect of lye flow rate, temperature, system pressure and different current density on energy consumption in catalyst test and 500W commercial alkaline water electrolysis. Mater. Today Phys. 2022, 22, 100606. [Google Scholar]
- Qiu, Y.; Zhou, B.; Zang, T.; Zhou, Y.; Chen, S.; Qi, R.; Li, J.; Lin, J. Extended load flexibility of utility-scale P2H plants: Optimal production scheduling considering dynamic thermal and HTO impurity effects. Renew. Energy 2023, 217, 119198. [Google Scholar]
- Kojima, H.; Nagasawa, K.; Todoroki, N.; Ito, Y.; Matsui, T.; Nakajima, R. Influence of renewable energy power fluctuations on water electrolysis for green hydrogen production. Int. J. Hydrogen Energy 2023, 48, 4572–4593. [Google Scholar]
- Jang, D.; Cho, H.-S.; Kang, S. Numerical modeling and analysis of the effect of pressure on the performance of an alkaline water electrolysis system. Appl. Energy 2021, 287, 116554. [Google Scholar]
- Rodriguez, J.; Amores, E. CFD modeling and experimental validation of an alkaline water electrolysis cell for hydrogen production. Processes 2020, 8, 1634. [Google Scholar] [CrossRef]
- Haverkort, J.W.; Rajaei, H. Voltage losses in zero-gap alkaline water electrolysis. J. Power Sources 2021, 497, 229864. [Google Scholar]
- Hammoudi, M.; Henao, C.; Agbossou, K.; Dubé, Y.; Doumbia, M.L. New multi-physics approach for modelling and design of alkaline electrolyzers. Int. J. Hydrogen Energy 2012, 37, 13895–13913. [Google Scholar]
- Qi, R.; Gao, X.; Lin, J.; Song, Y.; Wang, J.; Qiu, Y.; Liu, M. Pressure control strategy to extend the loading range of an alkaline electrolysis system. Int. J. Hydrogen Energy 2021, 46, 35997–36011. [Google Scholar]
- Qi, R.; Li, J.; Lin, J.; Song, Y.; Wang, J.; Cui, Q.; Qiu, Y.; Tang, M.; Wang, J. Thermal modeling and controller design of an alkaline electrolysis system under dynamic operating conditions. Appl. Energy 2023, 332, 120551. [Google Scholar]
- Xia, Y.H.; Cheng, H.R.; He, H.H.; Hu, Z.Y.; Wei, W. Efficiency Enhancement for Alkaline Water Electrolyzers Directly Driven by Fluctuating PV Power. IEEE Trans. Ind. Electron. 2024, 71, 5755–5765. [Google Scholar]
- Cantisani, N.; Dovits, J.; Jørgensen, J. Dynamic modeling of an alkaline electrolyzer plant for process simulation and optimization. arXiv 2023, arXiv:2311.09882. [Google Scholar]




| Sub-System | Parameters | Unit | Description |
|---|---|---|---|
| Electrochemical model | V | Voltage of the electrolysis cell | |
| A | Current of the electrolysis cell | ||
| K | Temperature of the electrolysis cell | ||
| MPa | Operating stress | ||
| Heat transfer model | K | Heat capacity of the lye in the separators | |
| K | Resistance of the lye in the electrolysis stack | ||
| K | Heat capacity of the lye in the electrolysis stack | ||
| K | Resistance in the electrolysis stack | ||
| K | Heat capacities of the heat exchangers | ||
| K | Outlet temperature of the water in the cooling coil | ||
| K | Inlet temperature of the water in the cooling coil | ||
| Mass transfer model | % | Hydrogen-to-oxygen impurity |
| Sub-System | Parameters | Unit | Description |
|---|---|---|---|
| Electrochemical model | Ω m2 | Parameter related to ohmic resistance | |
| Ω m2 | Parameter related to ohmic resistance (pressure) | ||
| Ω m2 | Parameter related to ohmic resistance (temperature) | ||
| V | Coefficient for overvoltage on Electrodes | ||
| m2/A | Coefficient for overvoltage on Electrodes (temperature) | ||
| m2/A | |||
| m2/A | |||
| Heat transfer model | J/K | Heat capacity of the lye in the separators | |
| J/K | Heat capacities of the gas–liquid separators | ||
| K/W | Resistance of the lye in the electrolysis stack | ||
| J/K | Heat capacity of the lye in the electrolysis stack | ||
| K/W | Resistance in the electrolysis stack | ||
| J/K | Heat capacities of the heat exchangers | ||
| Mass transfer model | µm | Thickness of the diaphragm | |
| mol/m3 | Ability of solubility of hydrogen |
| AEL Model | Measured Parameters |
|---|---|
| Electrochemical model | , , , |
| Heat transfer model | , , , , , , |
| Mass transfer model | , , T, |
| Sub-System | Parameters | Value | Unit |
|---|---|---|---|
| Electrochemical model | Ω m2 | ||
| Ω m2 | |||
| Ω m2 | |||
| V | |||
| −0.29 | m2/A | ||
| −0.35 | m2/A | ||
| 0.12 | m2/A | ||
| Heat transfer model | J/K | ||
| J/K | |||
| K/W | |||
| J/K | |||
| K/W | |||
| J/K | |||
| Mass transfer model | 610~700 | µm | |
| 0.53~1.24 | mol/m3 |
| Estimating Approaches | Sub System | MRE | RMSE | NRMSE | PCC |
|---|---|---|---|---|---|
| EKF | heat transfer | 0.087 | 2.148 | 19.9 | 0.536 |
| electrochemical | 0.102 | 0.00693 | 7.385 | 0.731 | |
| mass transfer | 0.07102 | 0.0693 | 8.385 | 0.769 | |
| UKF | heat transfer | 0.092 | 2.07 | 19.3 | 0.813 |
| electrochemical | 0.073 | 0.00587 | 7.201 | 0.837 | |
| mass transfer | 0.0673 | 0.0587 | 8.201 | 0.737 | |
| RL | heat transfer | 0.041 | 1.492 | 10.81 | 0.905 |
| electrochemical | 0.096 | 0.005353 | 6.958 | 0.702 | |
| mass transfer | 0.0596 | 0.0485 | 7.958 | 0.802 | |
| ORL | heat transfer | 0.028 | 0.748 | 6.9 | 0.953 |
| electrochemical | 0.038 | 0.004521 | 4.865 | 0.94 | |
| mass transfer | 0.038 | 0.0345 | 5.865 | 0.931 | |
| KRL | heat transfer | 0.039 | 0.768 | 7.15 | 0.945 |
| electrochemical | 0.046 | 0.00491 | 5.958 | 0.909 | |
| mass transfer | 0.046 | 0.03491 | 6.958 | 0.929 | |
| Proposed model | heat transfer | 0.025 | 0.635 | 5.9 | 0.963 |
| electrochemical | 0.027 | 0.00232 | 3.41 | 0.968 | |
| mass transfer | 0.027 | 0.0232 | 4.41 | 0.952 |
| Sub-System | Parameters | Value | Unit |
|---|---|---|---|
| Electrochemical model | Ω m2 | ||
| Ω m2 | |||
| Ω m2 | |||
| V | |||
| −0.51 | m2/A | ||
| −0.65 | m2/A | ||
| 0.02 | m2/A | ||
| Heat transfer model | J/K | ||
| J/K | |||
| K/W | |||
| J/K | |||
| K/W | |||
| J/K | |||
| Mass transfer model | 600~690 | µm | |
| 0.42~1.15 | mol/m3 |
| Estimating Approaches | Sub system | MRE | RMSE | NRMSE | PCC |
|---|---|---|---|---|---|
| EKF | heat transfer | 0.091 | 1.86 | 13.5 | 0.813 |
| electrochemical | 0.165 | 0.00721 | 7.498 | 0.601 | |
| mass transfer | 0.07255 | 0.0688 | 8.972 | 0.716 | |
| UKF | heat transfer | 0.084 | 1.95 | 12.3 | 0.834 |
| electrochemical | 0.131 | 0.006765 | 7.391 | 0.624 | |
| mass transfer | 0.0685 | 0.0597 | 8.731 | 0.754 | |
| RL | heat transfer | 0.038 | 1.651 | 9.73 | 0.912 |
| electrochemical | 0.126 | 0.006238 | 7.265 | 0.659 | |
| mass transfer | 0.06346 | 0.0512 | 8.234 | 0.834 | |
| ORL | heat transfer | 0.047 | 0.735 | 5.73 | 0.943 |
| electrochemical | 0.085 | 0.00532 | 5.112 | 0.89 | |
| mass transfer | 0.049 | 0.0445 | 6.345 | 0.912 | |
| KRL | heat transfer | 0.08865 | 0.7548 | 6.86 | 0.923 |
| electrochemical | 0.129 | 0.00655 | 7.288 | 0.643 | |
| mass transfer | 0.052 | 0.0437 | 6.774 | 0.898 | |
| Proposed model | heat transfer | 0.024 | 0.612 | 4.09 | 0.956 |
| electrochemical | 0.03 | 0.00295 | 3.51 | 0.932 | |
| mass transfer | 0.033 | 0.0384 | 5.47 | 0.926 |
| Sub-System | Parameters | Value | Unit |
|---|---|---|---|
| Electrochemical model | Ω m2 | ||
| Ω m2 | |||
| Ω m2 | |||
| V | |||
| −0.62 | m2/A | ||
| −0.60 | m2/A | ||
| 0.11 | m2/A | ||
| Heat transfer model | J/K | ||
| J/K | |||
| K/W | |||
| J/K | |||
| K/W | |||
| J/K | |||
| Mass transfer model | 620~700 | µm | |
| 0.38~1.03 | mol/m3 |
| Estimating Approaches | Sub System | MRE | RMSE | NRMSE | PCC |
|---|---|---|---|---|---|
| Traditional AEL system | heat transfer | 0.042 | 0.724 | 5.36 | 0.922 |
| electrochemical | 0.081 | 0.00632 | 5.768 | 0.854 | |
| mass transfer | 0.041 | 0.0398 | 6.553 | 0.865 | |
| Proposed AEL system | heat transfer | 0.039 | 0.685 | 4.75 | 0.933 |
| electrochemical | 0.075 | 0.00611 | 5.431 | 0.875 | |
| mass transfer | 0.032 | 0.0348 | 6.12 | 0.911 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, Z.; Zhang, T.; Zhang, J.; Zhao, M.; Wan, Z.; Chen, H. A Data-Driven Algorithm for Dynamic Parameter Estimation of an Alkaline Electrolysis System Combining Online Reinforcement Learning and k-Means Clustering Analysis. Processes 2025, 13, 1009. https://doi.org/10.3390/pr13041009
Sun Z, Zhang T, Zhang J, Zhao M, Wan Z, Chen H. A Data-Driven Algorithm for Dynamic Parameter Estimation of an Alkaline Electrolysis System Combining Online Reinforcement Learning and k-Means Clustering Analysis. Processes. 2025; 13(4):1009. https://doi.org/10.3390/pr13041009
Chicago/Turabian StyleSun, Zexian, Tao Zhang, Jiaming Zhang, Mingyu Zhao, Zhiyu Wan, and Honglei Chen. 2025. "A Data-Driven Algorithm for Dynamic Parameter Estimation of an Alkaline Electrolysis System Combining Online Reinforcement Learning and k-Means Clustering Analysis" Processes 13, no. 4: 1009. https://doi.org/10.3390/pr13041009
APA StyleSun, Z., Zhang, T., Zhang, J., Zhao, M., Wan, Z., & Chen, H. (2025). A Data-Driven Algorithm for Dynamic Parameter Estimation of an Alkaline Electrolysis System Combining Online Reinforcement Learning and k-Means Clustering Analysis. Processes, 13(4), 1009. https://doi.org/10.3390/pr13041009





