Linking Catalyst Development and Chemical Reactor Design with Ethanol to Butadiene Processes

Abstract

This study explores the relation between catalyst research and chemical reaction engineering for developing ethanol to butadiene (ETB) technologies. An ETB process involves two distinct steps: ethanol dehydrogenation to acetaldehyde and butadiene synthesis. The catalyst functions can be tailored separately or imbedded in a single formulation, leading to two-stage and one-stage processes. The performance of selected ETB catalysts is confronted with predictions based on chemical equilibrium, considering the simultaneous formation of products, by-products and impurities. The analysis shows that, essentially, the performance of ETB catalysts is controlled by kinetic factors. A shortlist of relevant catalysts for industrial implementation is proposed. The analysis highlights two key issues for industrial reactor design: catalyst deactivation/regeneration and the use of inert gas as a major process cost. The first issue is addressed by developing a comprehensive fluidized bed reactor model operating in the bubbling regime, capable of handling complex reaction kinetics. Good performance close to plug flow is obtained with bubbles at a size of 4 to 8 cm and with intensive mass transfer. The simulation reveals an autocatalytic effect of acetaldehyde on the butadiene formation favored by a well-mixed dense phase. The second study investigates the optimization of the chemical reaction section in a reactor–separation–recycle system via economic potential. The costs associated with the catalytic reactor and the catalyst charge, including regeneration, along with the costs of recycling reactants and of an inert gas if used, are key factors in determining the optimal operation region. This approach, verified by simulation in Aspen Plus^TM, points out that better robustness and a limited use of an inert gas are necessary for developing industrial catalysts for the one-stage ETB process.

1. Introduction

1,3-Butadiene (BD) is a top chemical intermediate used mainly as a monomer in the production of elastomers and industrial copolymers, with 27% of its total production going towards styrene–butadiene rubber, 26% towards polybutadiene rubber, 13% towards latex butadiene rubber, 12% towards acrylonitrile butadiene styrene, 6% towards adiponitrile, and the other 16% being used to manufacture other important chemicals for a variety of applications [1]. Currently, 95% of BD originates from oil refining as a by-product of naphtha steam cracking. Its global production capacity should grow by 32% from 18 Mtpa in 2021 to 23.7 Mtpa in 2026, mainly attributed to the development of the Asian market. The decarbonation of chemical process industries sets tough challenges for chemical engineering research in developing sustainable processes based on renewable raw materials [2]. Notably, ethanol appears to be suitable since, currently, it is a top feedstock, with 80.1 million tons being produced in 2019 and a cumulated annual growth rate of 4.8% in the next decade (Grand View Research, 2023, https://www.grandviewresearch.com, accessed on 23 December 2023). Major industrial companies are currently involved in the development of ethanol to butadiene (ETB) processes. One example is the BioButterfly project, connecting the leading tire producer Michelin in an alliance with IFP Energies Nouvelles and Axens (https://www.axens.net/resources-events/news/pr-michelin-ifp-energies-nouvelles-and-axens-give-new-dimension-biobutterfly, accessed on 1 February 2025).

Two ETB processes were invented in the early twentieth century by Russian scientists: the first of these was the two-stage process, developed by Ostromislensky (1916) in the USA, and the second was the one-stage process, developed by Lebedev in the former Soviet Union (1935). These were both abandoned after 1960 because of the urgent need for cheaper feedstock from oil refineries and more efficient manufacturing processes.

In recent years, the interest in ETB processes has been revived, making the research of new catalysts more active and selective. The manufacturing of BD from bioethanol should bring a notable advantage in terms of reducing the greenhouse gas footprint. This seems to be significant when using feedstock from Brazilian sugarcane and US corn stover [3]. Furthermore, this change in production method should also be stimulated by the fall in butadiene production from oil refineries due to the development of renewable energies.

The use of renewable resources other than bioethanol is explored for manufacturing butadiene, using resources such as biomass (Farzad, et al. [4]), C6 sugars (Moncada, et al. [5]) and paper mill and lignocellulosic feedstock (Rodgers, et al. [6]). However, these studies are devoted to technological and ecological aspects and not the issues regarding the design process.

An impressive number of papers have been published in the last decade in this field with the goal of discovering new formulations for boosting catalyst performance in terms of ethanol conversion and butadiene selectivity, particularly for the one-stage process that seems to offer technical and economic advantages. The experiments have been conducted in microreactor devices with small catalyst amounts but employed sophisticated methods for chemical analysis and physical characterization. The research focused primarily on understanding the rationale of catalyst formulation in relation to the activity and reaction mechanism. However, from the viewpoint of reaction engineering and process design, the research was limited. In fact, the designer needs much more data for developing an industrial process, namely the detailed description of species distribution at different operation parameters, such as temperature, pressure and WHSV, as well as data regarding the catalyst deactivation and regeneration. We should underline the importance of data over impurities formation, which, even in small amounts, may require costly separation techniques. At the highest level, detailed kinetic modeling is necessary for the reliable design of the chemical reaction system. On this basis, one can proceed by developing a realistic process flowsheet, applying systematic methods and advanced simulation tools [7]. At the end of this process, the assessment of capital and operation costs validates the industrial feasibility of the proposed catalyst.

The first process design study for a two-stage ETB process using detailed kinetics was published by Dimian et al. [8]. This made use of a CuO/Cr₂O₃ catalyst for acetaldehyde production and a Ta₂O₅/SiO₂ catalyst for butadiene synthesis, for which a reliable 21-reaction model was available (Dussol et al. [9]). Complete reaction and separation schemes were developed, and the processing equipment was designed and sized. Minimum energy consumption was achieved via process integration and intensification methods. Rigorous simulation in Aspen Plus^TM resulted in performance indices among the best obtained so far: butadiene carbon (C-) yield 83.7%, mass yield 0.495 kg/kg-ethanol (theoretical 0.587), waste of 0.257 kg/kg, thermal utility of 16 MJ/kg and catalyst productivity of 0.253 kg/(kg-cat·h).

Important contributions in terms of experimental investigation and process design studies have been published by researchers at the University of Seville, Spain. An interesting paper by Cabrera Camacho et al. [10] discusses the techno-economic comparison of one-stage and two-stage processes, the first employing an Hf/Zn catalyst and the second using tantalum on mesoporous silica. The results seem to indicate a slight advantage of the one-stage process, despite a much better butadiene yield for the two-stage process, which cannot compensate for the larger energy cost. However, this result seems questionable since it strongly depends on several design decisions. A major one is scaling up the catalyst performance from lab to industrial stages, disregarding the effect of inert gas on the design of the chemical reaction system and, in general, the substantial processing costs.

A comparison of the two ETB processes has also been investigated by Dimian and Bildea [11]. This time, the process design considers the effect of an inert gas. It is noteworthy that the use of inert gas in various proportions appears as a common feature to almost all one-stage catalysts developed so far. To handle this situation, the paper proposes applying radial-flow adiabatic reactor technology. The study demonstrates that even if a high butadiene-C selectivity of 84% would be achievable in both competing ETB processes, the total product cost would remain notably higher in the case of the one-stage process when an inert gas is used. The difference may drop below 10% by applying an inert-to-ethanol molar ratio below one. The study highlights that one-stage process catalyst research should continue to target a higher butadiene C-yield, from 75% achievable today to over 80%, while also being able to operate without or with a reduced amount of inert gas.

The current study deals with the relationship between catalyst research and chemical reaction engineering for developing ethanol-to-butadiene (ETB) technologies. The first part presents the progress achieved to date in the development of ETB catalysts. The chemistry section presents the currently agreed upon complex reaction mechanism. In addition to the path leading from ethanol to 1,3 butadiene, the chemical reaction network involves the formation of numerous by-products and impurities. These are related to the catalyst formulation and have a strong impact on the feasibility of an industrial process.

The next section presents a selection of high-performing ETB catalysts developed in recent years. Key criteria include ethanol conversion, butadiene yield, as well as operating conditions, primarily the ethanol partial pressure (EPP) related to the use of inert gas.

The performance of the selected catalysts is subjected to a thermodynamic analysis. This allows for evaluating the role of chemical equilibrium on species distribution and selecting the operation parameters for process design. Extending a previous study [12], the analysis examines the simultaneous occurrence of competing reactions in both acetaldehyde and butadiene synthesis pathways, including products, by-products, and impurities. The comparison of predictions with experimental data allows for assessing the role of thermodynamics versus kinetic factors. The analysis demonstrates that ethanol conversion and species selectivity are intimately related to the mechanism of catalytic processes and ultimately to the catalyst synthesis procedure. Based on this, a shortlist of catalysts relevant to industrial application is proposed. From a process engineering perspective, enhancing ETB catalyst robustness and studying the effect of inert gas on butadiene selectivity are recommended.

The final section presents two studies regarding chemical reactor design issues in relation to ETB catalyst development. These studies are novel and complement the reactor designs developed in previous papers by Dimian and Bildea [11] as well as Bozga et al. [13]. The first study addresses the design of a fluid bed reactor as an effective alternative for catalyst regeneration, using the kinetic model developed by Brosteanu et al. [14] based on data provided by Da Ros et al. [15]. The second study examines the optimal design of the chemical reactor through analysis in the reactor–separation recycle (RSR) system using the economic potential to estimate the processing costs at successive design levels. The analysis demonstrates that the optimal operation zone is significantly influenced by the costs of the reactor, catalyst load and the regeneration procedure, as well as by substantial processing costs associated with the use of the inert gas, if required. Consequently, this aspect should receive more attention in catalyst research.

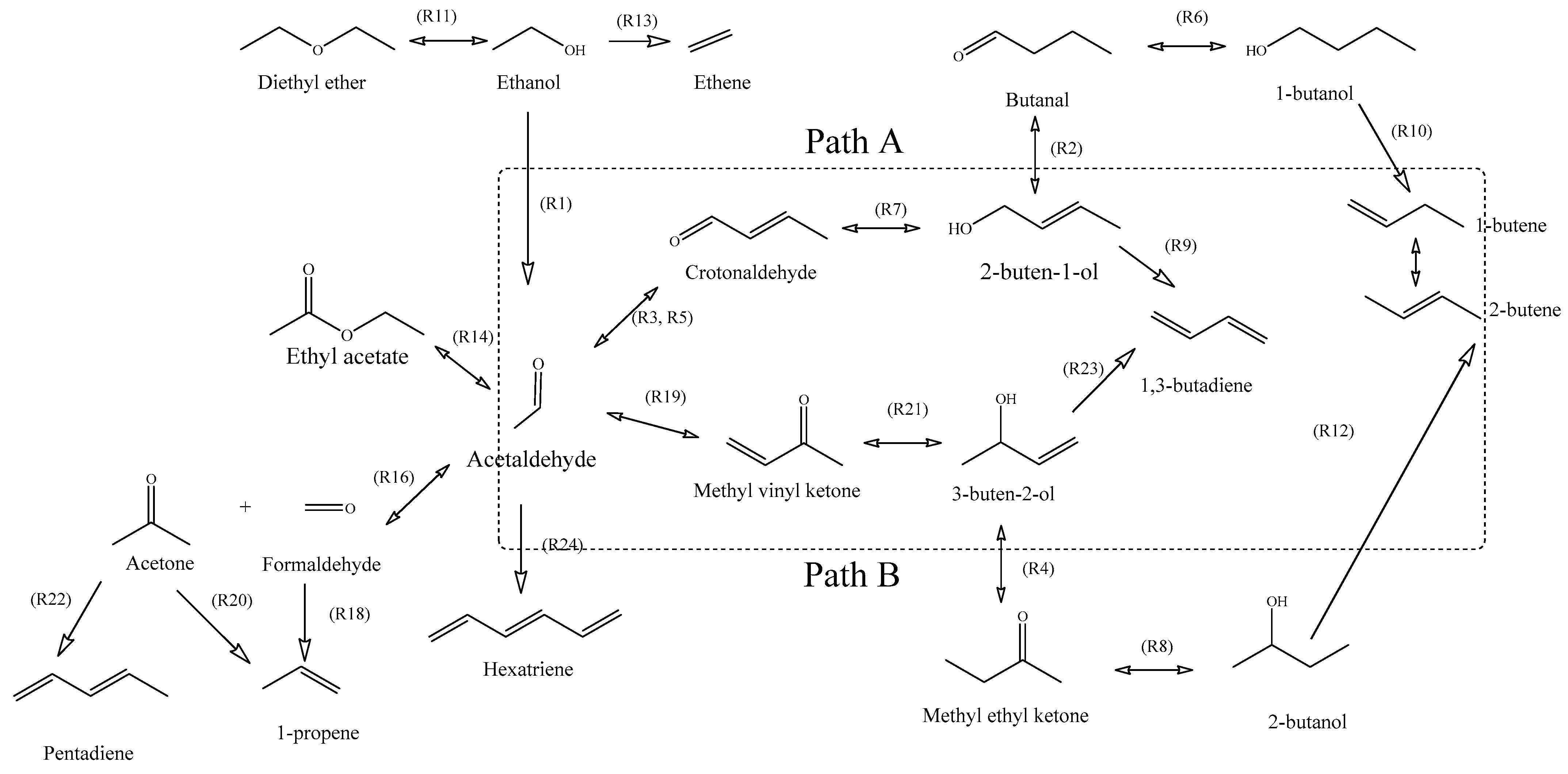
2. Chemistry

The industrial ETB processes can be described by the following overall stoichiometric equations:

One stage (1StP)

$$\begin{array}{l}2 {\mathrm{C}}_2{\mathrm{H}}_5-\mathrm{OH}\Rightarrow {\mathrm{H}}_2{\mathrm{C}=\mathrm{CH}-\mathrm{CH}=\mathrm{CH}}_2+2 {\mathrm{H}}_2{\mathrm{O}+\mathrm{H}}_2, {\mathsf{\Delta }\mathrm{H}}_{\mathrm{R}}^{298\mathrm{K}}=47.7 \mathrm{kJ}/\mathrm{molEtOH}\\ \left(\mathrm{EtOH}\right) \left(\mathrm{BD}\right)\end{array}$$

(1)

Two stages (2StP)

$$\begin{array}{l}{\mathrm{C}}_2{\mathrm{H}}_5-\mathrm{OH}\Rightarrow {\mathrm{CH}}_3{-\mathrm{CHO}+\mathrm{H}}_2, {\mathsf{\Delta }\mathrm{H}}_{\mathrm{R}}^{298\mathrm{K}}=68.6 \mathrm{kJ}/\mathrm{mol}\\ \left(\mathrm{EtOH}\right) \left(\mathrm{ACH}\right)\end{array}$$

(2)

$${\mathrm{C}}_2{\mathrm{H}}_5{-\mathrm{OH}+\mathrm{CH}}_3-\mathrm{CHO}\Rightarrow {\mathrm{H}}_2{\mathrm{C}=\mathrm{CH}-\mathrm{CH}=\mathrm{CH}}_2+2 {\mathrm{H}}_2\mathrm{O}, {\mathsf{\Delta }\mathrm{H}}_{\mathrm{R}}^{298\mathrm{K}}=31.5 \mathrm{kJ}/\mathrm{mol}$$

(3)

In fact, the chemistry of the ETB processes involves a complex network of reactions, including the formation of numerous chemical species, such as intermediates, by-products and impurities. The occurrence of these species strongly depends on the catalyst used, as well as the operation parameters. Figure 1 illustrates the reactions involved in the complex network, while Table S1 provides the corresponding stoichiometry [9,12].

The BD synthesis in both processes starts with the formation of acetaldehyde by ethanol dehydrogenation. In addition to the main reaction, this step involves the formation of by-products, such as ethylene (C2=), diethyl ether (DEE) and ethyl acetate (EtAc), whose amounts depend primarily on the catalyst employed. Then, EtOH and ACH react in a complex chain of reactions leading to BD, as depicted in Figure 1 in the framed drawing. The synthesis chain begins with the condensation of ACH to acetaldol, a very unstable species that can quickly evolve via two paths. Path A, attributed to Kagan et al. [16] and Toussaint et al. [17], is the most accepted. This consists of acetaldol dehydration to crotonaldehyde, then to crotyl alcohol (2-butene-1-ol) through reduction with ethanol via the Meerwein–Ponndorff–Verley (MPV) reaction and finally to BD through water elimination. For Path B, attributed to Inoue et al. [18], acetaldol converts to the isomer 4-hydroxi-butane-2-one and further to methyl-vinyl-ketone (MVK). This gives 3-buten-2-ol via the MPV reaction and, finally, BD through water elimination. The existence of these two reaction paths can explain the formation of numerous impurities that appear in the ETB processes, such as butanal, 1-butanol, butene-1 from 2-buten-ol, and methyl-ethyl-ketone (MEK), 2-butan-ol, and butene-2 from 3-buten-2-ol. Note that butadiene itself is not the origin of these impurities but rather concurrent reactions. Another observation regards the key role of the acetaldehyde, which initiates the synthesis by aldol formation but also sustains it through the MPV reaction. This behavior suggests the characteristics of an autocatalytic reaction.

Other impurities are generated by acetaldehyde degradation reactions, such as formaldehyde, acetone, ethyl acetate, unsaturated hydrocarbons, like propylene, pentadiene and hexadiene, as well as various heavies. The above components exhibit large differences in volatility and chemical affinity, necessitating a complicated separation system with a significant impact on the process flowsheet and process economics [8].

It can be concluded that the occurrence of numerous by-products and impurities has a strong impact on catalyst development for ETB processes. Therefore, catalyst performance is the determining factor for the process design of a sustainable process.

3. Catalysts

A large number of published studies have been devoted in the last decade to the development of performant catalysts for ETB processes. Comprehensive reviews have been published by Pomalaza et al. [19,20] and Kyriienko et al. [21]. Most of the research deals with the one-stage process, which is supposed to offer a technological advantage over the two-stage process by using a single catalyst, but this opinion is debatable. Typically, experiments are performed in microreactor devices at atmospheric pressure under inert gas flow (N₂, Ar, He), which means lower ethanol partial pressure (EPP), mostly around 0.1 to 0.3 bar. The use of an inert gas may be justified in laboratory research, but this becomes problematic in industrial conditions, such as continuous operation and high throughput. As demonstrated by Dimian and Bildea [11], recycling large amounts of inert gas involves costly separation, recycling, and gas compression equipment, which ultimately affects process profitability. Recently, Makhin et al. [22] brought the same observation and performed experiments in more realistic conditions, in the absence of inert gas and with acetaldehyde recycling.

Note that under industrial conditions, achieving higher product selectivity is preferable to obtaining high conversion, as the former typically offers more advantages in terms of economic profitability. As a rule of thumb, productivity of 0.15 kg/kg/h can be considered the lower limit for industrial feasibility.

Table 1. Selection of candidate catalysts for ETB processes.

	Catalyst	EPP [bar]	Conv [%]	BD sel. [%]	Temp. [°C]	WHSV [kg/kg/h]	Prod. [kg/kg/h]	Reference
1	MgO/SiO2	0.06	95	77	450	4.1	1.35	Huang et al. [30]
2	MgO/SiO2	0.15	50	60	300	0.5	-	Szabó et al. [31]
3	Au/MgO/SiO2	0.20	60	78.3	300	1.1	0.506	Shylesh et al. [3]
4	K/Zr/Zn/MgO/SiO2	0.4–0.8	41.8	50.1	400	0.21	0.21	Da Ros et al. [32]
5	1Ag/10ZrO2/SiO2	0.5	45.6	73	320	0.32	0.06	Sushkevich et al. [23]
6	Ag/ZrO2/SiO2	0.5	89	73.6	325	0.47	0.17	Dagle et al. [33]
7	Ag/ZrO2/SiO2	0.29	87	71.8	325	0.47		Li et al. [34]
8	Cu/TaSiBEA	0.3	88	72.6	325	0.40	0.19	Kyriienko et al. [35]
9	La/ZnSiO2	0.18	36	70	325	1	0.15	Larina et al. [36]
10	Hf/Zn/SiO2	0.025	98.8	70.0	360	0.64	0.26	De Baerdemaeker et al. [37]
11	Hf/Zn/SiO2	0.21	81.9	58.8	380	1.12	1.15	Cabello González et al. [38]
12	CuO/La2O3/ZrO2/SiO2	1.013	48	60	340	1.3	0.32	Makhin et al. [22]
13 *	Ta2O2/SiO2 mol EtOH/ACH = 2.5	Atm	Xtot = 43	>75	340	1.18	-	Dussol et al. [9]
14 *	Ta-SBA-15 mol EtOH/ACH = 1.7	Atm	68	75	325	1.03	-	Cabello González et al. [39]
15 *	Ta/SMS	Atm.	56.7	70.5	350	-	-	Kim et al. [40]

* ETB second stage.

presents a selection of high-performance catalysts developed over the past decade. Although commercial implementation has not yet been achieved, significant progress has been made in understanding the complex roles of the components and optimizing their formulations. Among the numerous studies, the publications of Sushkevich et al. [23] and Kyriienko et al. [21] are noteworthy. They suggest that a multifunctional ETB catalyst formulation can be represented as M/MOx/SiO₂. The investigation of the reaction mechanism proved that the key steps of butadiene synthesis are ethanol dehydrogenation, aldol-crotonic condensation, MPV reduction and unsaturated-C4 alcohol dehydration. In the dehydrogenation step, the most important step (Kyriienko et al. [21]), the presence of metal promotors M, such as Cu, Ag, Au, and La, is necessary to enhance the reaction rate, which is otherwise less efficient with base sites originating from MOx, the mixed oxide employed. Among mixed oxides, the most successful so far are MgO, ZrO₂ and HfO₂. The condensation step may be driven by both base and acid sites formed through the interaction of MOx with the SiO₂ support, though acid sites are preferred due to their resistance to deactivation. The MPV step is also catalyzed by MOx components, with ZrO₂ showing superior performance (Sushkevich and Ivanova [24]). The presence of Lewis acid sites (LASs) is needed for the final dehydration step. Overall, a balanced ratio of base and acid sites is desirable for achieving high butadiene selectivity (Kyriienko et al. [21]). A study by Santos et al. [25] demonstrated that a high ratio of acid to base sites favored ethanol dehydration products, whereas a lower acid-to-base ratio facilitated the aldol condensation of ACH, results which are also supported by Wang et al. [26]. Other studies concluded that the cooperative interaction between acidic and basic sites promotes the formation of acetaldehyde, a key intermediate in the Lebedev process [27,28]. In a Lebedev catalyst, magnesium silicate hydrates provide a balance of surface acidity and basicity, significantly improving butadiene formation [29]. Additionally, the physical properties of the SiO₂ support and its interaction with other catalyst components are crucial for forming intermediate species involved in the reaction mechanism.

Lebedev’s MgO/SiO₂ formulation still provides a realistic basis for developing effective ETB catalysts (lines 1 to 4). Thus, Huang et al. [30] achieved 77% BD selectivity at 95% ethanol conversion (EC), with a remarkable productivity of 1.35 kg 1,3-BD/kg-cat/h, albeit at very low EPP. Szabó et al. [31] showed that a catalyst based on natural talc can yield good results. The use of promoters may have a significant impact on the catalyst’s performance. For example, the catalyst proposed by Shylesh et al. [3] delivers 78.3% BD selectivity at 60% EC and 0.20 bar EPP. Da Ros et al. [32] obtained comparable results at higher EPP levels, between 0.4 and 0.8 bar.

The use of zirconium in formulation may enhance performance and robustness. The Ag-doped ZrO₂/SiO₂ catalyst proposed by Sushkevich et al. [23] achieved a BD selectivity of 73% at 45.6% EC and an EPP of 0.5. By improving the silicate support, Dagle et al. [33] obtained 73.6% BD selectivity at 89% EC but under a milder temperature at 325 °C.

Doping TaSiBEA zeolites with transitional metals such as Ag, Cu and Zn leads to high-performance catalysts, achieving 72.6% BD selectivity at 88% EC and 0.3 bar EPP [35]. A similar outcome was found by incorporating Lanthanum in a silica gel-type catalyst [36]. Using transition metals from groups 4 and 5 has also been explored, as illustrated in Table 1 with the Hf(IV)/Zn(II) catalysts.

The by-products and impurities include olefines (ethylene, propylene, butenes), oxygenated components (alcohols, aldehydes, ketones, ethers), as well as other hydrocarbons and heavy compounds. Some of the reactions shown in Figure 1 occur with the formation of intermediary products that are rarely or not observed experimentally [9,19]. For example, the transformation of acetaldehyde to crotonaldehyde proceeds via acetaldol (reactions R3 and R5, Table S1), which is not detected experimentally. Similarly, the formation of methyl-vinyl-ketone from acetaldehyde (reaction R19) is hypothesized to involve 4-hydroxy-2 butanone as an intermediary product, which is also not observed experimentally. In addition, during the transformation of crotonaldehyde to 1,3-butadiene (reactions R7 and R9), crotyl alcohol (2-buten-1-ol) acts as an intermediary. This compound is generally not observed in the reaction mixture due to its rapid dehydration. However, its presence has been experimentally confirmed.

This essential information in process design is absent in most publications. The origin of the aforementioned species is also significant. In general, thermodynamic chemical equilibrium offers useful predictions over the feasibility of chemical reactions, but the presence of catalysts can profoundly affect this capability. In fact, catalysis is primarily a non-equilibrium phenomenon [41]. This aspect is examined in the next section, where the predictions offered by thermodynamics are confronted with “kinetic” data delivered by a catalyst in specific operation conditions.

4. Thermodynamic Analysis

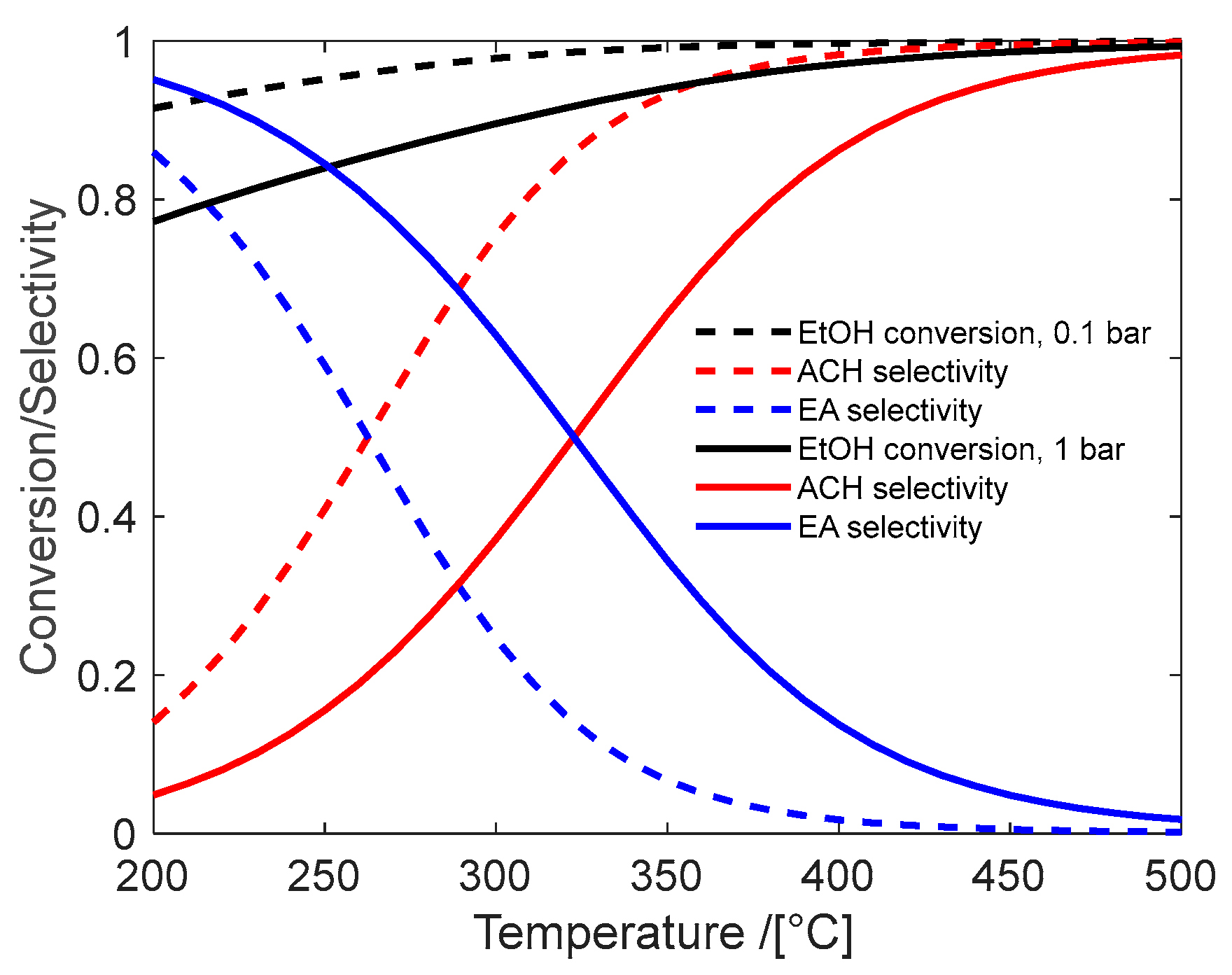
4.1. Acetaldehyde Synthesis

The synthesis of acetaldehyde through ethanol dehydrogenation plays a crucial role as the initial step that triggers the complex chemistry involved in both ETB processes (reaction (4)). The secondary species that may affect the yield include ethylene, diethyl ether, and ethyl acetate (reactions (5) to (7)):

$$C_2{H}_5-OH\iff C{H}_3-CHO+H_2$$

(4)

$$C_2{H}_5-OH\iff H_{2}C=C{H}_2+H_{2}O$$

(5)

$$\begin{array}{l}2C_2{H}_5-OH\iff {\left(C_2{H}_5\right)}_{2}O+H_{2}O\\ \left(DEE\right)\end{array}$$

(6)

$$\begin{array}{l}2C_2{H}_5-OH\iff C{H}_3-CO-O-C_2{H}_5+2H_2\\ \left(EA\right)\end{array}$$

(7)

The relative extent of these reactions depends on the catalyst employed. Figure 2B shows the dependence of the ethanol conversion at equilibrium (reaction (1)) on pressure and temperature within a workable range. One may observe that ethanol partial pressure is a key process variable. For instance, reaching 90% ethanol conversion at 250 °C occurs at 0.1 bar but needs 360 °C at 1 bar. As one may see from Table 2 that practically all the experiments regarding the one-stage process employed inert gas (nitrogen, argon, helium) to ensure low-ethanol partial pressure, mostly around 0.2 bar, with a single exception (Makhin et al. [22]) that worked at atmospheric pressure. However, the use of inert gas in the one-stage process implies costly equipment for vacuum and separation/recycling operations (Dimian and Bildea [11]). In contrast, the two-stage process allows dehydrogenation to occurs at pressures above atmospheric levels, thereby reducing processing costs (Dimian et al. [8]). Consequently, exploring the role of ethanol partial pressure should be an important research direction for developing industrial one-stage catalysts.

Next, the situation where reactions (4) to (7) occur simultaneously is examined. Figure 2A presents the equilibrium constants profiles versus temperature at atmospheric pressure within a range of 200 to 500 °C. For the formation of acetaldehyde, ethylene and ethyl acetate, the equilibrium constants increase substantially with temperature, whereas they decrease for diethyl ether is due to the exothermic reaction. Figure 2B shows that, across the practical range of 0.1 to 3 bar, the equilibrium conversion can reach values above 97.5%.

Figure 3 presents the selectivity profile for the simultaneous formation of acetaldehyde, ethylene, diethyl ether and ethyl acetate as a function of temperature at pressures between 0.1 and 3 bar. Figure 3A shows that the acetaldehyde selectivity is very low at temperatures below 300 °C and only increases to about 10% at 500 °C. Figure 3B reveals that the ethylene formation largely dominates the equilibrium process, while diethyl ether and ethyl acetate (Figure 3C,D) should appear only in small amounts. The results show that, in a catalytic process governed by equilibrium, secondary reactions would significantly reduce the acetaldehyde yield, rendering the ETB process infeasible. A deeper insight pinpoints fundamental differences in the mechanism of competing reactions. Specifically, the acetaldehyde and ethyl acetate formation implies ethanol dehydrogenation (reactions (4) and (7)), while ethylene and diethyl ether result from ethanol dehydration. The catalysts required for these reactions are fundamentally distinct.

Figure 4 illustrates the dehydrogenation scenario where acetaldehyde competes with ethyl acetate as a by-product. Under atmospheric pressure and in the absence of inert gas, the acetaldehyde formation is favored by higher temperature: 97% EtOH conversion and 86% ACH selectivity at 400 °C, but only 89.5% and 37.1% at 300 °C. Dropping the pressure to 0.1 bar shows a significant boost in ACH selectivity, as in EtOH conversion. Conversely, increasing the pressure above atmospheric levels reverses this effect, with ethyl acetate selectivity becoming dominant at lower temperatures (200 to 300 °C). This behavior is applied in an efficient hydrogen storage and usage method [42]. Concerning dehydration reactions, the chemical equilibrium calculations indicate that ethylene formation is much more favored than the diethyl ether.

The above predictions in terms of conversion, selectivity and stability (time on stream) are compared with the experimental data in Table 2. From the abundant literature, only relevant papers are presented. For ethanol dehydrogenation to acetaldehyde (ETA), typical heterogeneous catalysts are as follows: (1) noble metals, such as Pd, Au, Ru, and Ag; (2) non-noble metals, such as Cu and Co; and (3) others, such as carbide and nitride, and metal oxide catalysts [43]. Among these, Cu-based catalysts have been the most extensively investigated and are considered highly effective from an industrial perspective. Using CuO on an asbestos support, Franckaerts and Froment [44] found that over 95% ACH selectivity can be obtained within a temperature range of 225 to 285 °C and pressure range of 1 to 10 atm, and, on this basis, they developed a kinetic model. Similarly, Peloso et al. [45] employed a commercial cooper chromite catalyst with a particle size of 3 mm and found that in the same conditions, the ACH selectivity reached almost 100%. This kinetic model that includes the catalyst effectiveness factor was applied by Dimian et al. [8] to the design of a two-stage process. In another study, Santacesaria et al. [42] employed a commercial chromite catalyst to achieve high selectivity in ethanol dehydrogenation to ethyl acetate working at pressures exceeding 20 bar, while at atmospheric pressure, acetaldehyde was obtained. It may be observed that the above results deviate significantly from the thermodynamic predictions mentioned above, reinforcing the observation that the species’ selectivity of a catalytic process may be controlled not by thermodynamics but by “kinetic reasons” arising from the catalyst employed that can selectively favor certain reaction pathways.

From an industrial viewpoint, the drawback of using metal-based catalysts for ethanol dehydrogenation is the rapid loss of activity that requires frequent regeneration. It was found that the improvement in catalyst robustness involves optimizing both the metal deposition and the support structure. Hence, Li et al. [46] obtained high EtOH conversion and excellent ACH selectivity through better Cu dispersion by modifying the SiO₂ with SiC. Similarly, Garbarino et al. [47] obtained comparable results using a Zn aluminate-based support. Zhang et al. [48] reported an efficient and robust Cu/SiO₂ catalyst (500 h TOS) prepared via the ammonia evaporation method. However, it is worth noting that these catalysts operate at low-ethanol partial pressure using inert gas. However, Raynes and Taylor [49] achieved notable progress developing a ZnO/Mordenite catalyst, which, at ethanol atmospheric pressure and 400 °C, achieved a 40% conversion rate with over 80% ACH selectivity, minimal ethylene formation, and low coking, while maintaining excellent stability over 120 h TOS. Additionally, this catalyst gives results close to the thermodynamic predictions (Figure 4).

Employing acidic catalysts also favors ethanol dehydration to diethyl ether (DEE). Since this component complicates the design of the separation section, limiting its occurrence is highly desirable (Dimian et al. [8]). Phung and Busca [50] identified the reaction mechanism that can explain the large variation in selectivity when working with aluminosilicates. While ethylene is formed by the elimination of an ethoxy group, DEE needs the activation of a second adsorbed but non-dissociated ethanol molecule. Therefore, DEE tends to form at lower SiO₂/Al₂O₃ ratios, where Lewis sites are more frequently surrounded by alumina-like surface. In addition, DEE occurrence is favored at lower temperatures, while ethylene is predominant at higher ones. For instance, with a catalyst sample containing 87% wt. SiO_2, the DEE selectivity was 69.5% at 250 °C but dropped to only 0.4% at 350 °C.

From the above analysis, it can be concluded that efficient aldehyde production in a two-stage process can be ensured with high selectivity by employing dedicated catalysts. In contrast, achieving this in a one-stage process with a single multifunctional catalyst is much more challenging, as simultaneous ethanol dehydration reactions may produce significant amounts of ethylene, DEE, and other impurities. As demonstrated using isotopic methods by Sushkevich et al. [51] for the Ag/SiO₂ catalyst and by DeWilde et al. [52] for the γ-Al₂O₃ catalyst, the formation of both acetaldehyde and ethylene proceeds, however, through a common surface intermediate. The C-H bond cleavage is the kinetic limiting factor for both products, although the presence of strong acidic sites favors ethylene selectivity. Recently, Abdulrazzaq et al. [53] observed a similar mechanism with the undoped MgO-SiO₂ (Lebedev) catalyst. This catalyst may offer both weak and strong acid Lewis sites, with the former contributing to acetaldehyde occurrence and the latter facilitating BD synthesis (Table 2, lines 1–2). Moreover, the use of promotors, such as metal oxides (K₂O, CuO, ZnO) and noble metals (Au, Ag, La), can further enhance the catalyst’s performance in terms of ethanol conversion and butadiene selectivity (Table 2, lines 3 to 11).

Table 2. Selectivity performance of some catalysts used for ethanol to acetaldehyde production.

	Catalyst	Temp. °C	PEtOH bar	Conv. EtOH	Sel ACH	Sel C2H4	Sel DEE	Sel EA	TOS h	Reference
1	CuO-asbest	225–285	1–10	<0.50	96	0	0	3	-	Franckaerts and Froment [44]
2	CuO-Cr2O3	225–285	1–10	<0.25	99	-	-	1	150	Peloso et al. [45]
3	Cu-1234	200–290	20–30	<0.6	> 98	-	-	1.5	-	Santacesaria et al. [42]
4	Cu/C/SiC	280	0.05	0.814	99	-	-	-	8	Li et al. [46]
5	Cu/ZnAl2O4	200–400	0.07	<0.95	> 95	0	0	0	-	Garbarino et al. [47]
6	Cu/SiO2	280	0.04	0.90	>98	-	-		500	Zhang et al. [48]
7	ZnO/MOR	400	Atm.	0.4	89	4	4	3	120	Raynes and Taylor [49]
8	γ-Al2O3	350–400	<0.16	0.1	30	60	10	-	-	DeWilde et al. [52]
9	SiO2/Al2O3	150–450	Atm	0–100	0	0–100	60–0	0	-	Phung and Busca [50]
10	MgO-SiO2	325	0.037	-	20	80	-	-	12	Abdulrazzaq et al. [53]

Table 2. Selectivity performance of some catalysts used for ethanol to acetaldehyde production.

	Catalyst	Temp. °C	PEtOH bar	Conv. EtOH	Sel ACH	Sel C2H4	Sel DEE	Sel EA	TOS h	Reference
1	CuO-asbest	225–285	1–10	<0.50	96	0	0	3	-	Franckaerts and Froment [44]
2	CuO-Cr2O3	225–285	1–10	<0.25	99	-	-	1	150	Peloso et al. [45]
3	Cu-1234	200–290	20–30	<0.6	> 98	-	-	1.5	-	Santacesaria et al. [42]
4	Cu/C/SiC	280	0.05	0.814	99	-	-	-	8	Li et al. [46]
5	Cu/ZnAl2O4	200–400	0.07	<0.95	> 95	0	0	0	-	Garbarino et al. [47]
6	Cu/SiO2	280	0.04	0.90	>98	-	-		500	Zhang et al. [48]
7	ZnO/MOR	400	Atm.	0.4	89	4	4	3	120	Raynes and Taylor [49]
8	γ-Al2O3	350–400	<0.16	0.1	30	60	10	-	-	DeWilde et al. [52]
9	SiO2/Al2O3	150–450	Atm	0–100	0	0–100	60–0	0	-	Phung and Busca [50]
10	MgO-SiO2	325	0.037	-	20	80	-	-	12	Abdulrazzaq et al. [53]

4.2. Butadiene Synthesis

The BD synthesis consists of a complex reaction network, as illustrated in Figure 1, where the dotted-line frame highlights the key reactions. Two paths to BD can be identified. Path A regards the widely acknowledged route proposed by the works of Kagan et al. [16] and Toussaint et al. [17]. The first step is the condensation of two acetaldehyde molecules to form acetaldol, an unstable intermediate that rapidly dehydrates to crotonaldehyde. This is further reduced with ethanol via the Meerwein–Pondorf–Verley (MVP) reaction to 2-buten1-ol (crotyl alcohol), which ultimately produces 1,3 butadiene through dehydration. In Path B, attributed to Inoue et al. [18], acetaldol may isomerize to 4-hydroxy-butan-2-one, which dehydrates to methyl-vinyl-ketone (MVK), then by MPV reaction giving 3-buten-2-ol and, finally, 1,3 butadiene. The existence of two synthesis paths has been experimentally proved (Dussol et al. [9]). This scheme can also explain the formation of numerous oxygenated and hydrocarbon impurities, such as aldehydes/ketones, butanols and butenes.

Table 3. Chemical equilibrium for ethanol-to butadiene chemistry at 350 °C and 1 atm.

	BD1	BD1 + BD2	BD1 + C2H4	BD1 + BUTAL *	BD1 + C2H4 + BUTAL	BD1 + BD2 + BUTOLS *	BD1 + BD2 + BUTENES
Total kmoles	1.9981	1.998	1.9995	1.943	1.9864	1.7210	1.5120
ETOH	0.0019	0.002	0.0005	0.002	0.0005	0.0013	4.35 × 10−5
ACH	0.0395	0.038	0.0357	0.035	0.0336	0.0310	0.0165
H2	0.5190	0.536	0.1415	0.517	0.1461	0.3994	0.0216
CROT-ALD *	2.06 × 10−4	1.90 × 10−4	1.68 × 10−4	1.74 × 10−4	0.0002	1.51 × 10−4	3.52 × 10−5
CROT-OL *	1.71 × 10−6	1.62 × 10−6	3.78 × 10−7	1.48 × 10−6	3.12 × 10−7	1.12 × 10−6	1.60 × 10−8
MVK *	NONE	0.018	NONE	NONE	NONE	0.0023	0.0005
3BTE2OL *	NONE	1.32 × 10−19	NONE	NONE	NONE	9.57 × 10−6	1.37 × 10−7
H2O	0.9584	0.9426	0.9637	0.9075	0.9526	0.8055	0.9821
BD	0.4798	0.4623	0.1054	0.4261	0.0990	0.3216	0.0033
C2H4	-	NONE	0.7526	NONE	0.7412	NONE	NONE
DEE	-	NONE	NONE	NONE	NONE	NONE	NONE
BUTAL *	-	NONE	NONE	0.055	0.0552	0.0417	5.99 × 10−4
1-BUTOL *	-	NONE	-	NONE	NONE	0.1118	9.88 × 10−5
2-BUTOL *	-	NONE	-	-	-	0.0061	5.42 × 10−6
1-BUTENE	-	-	-	-	-	-	0.1926
2-BUTENE	-	-	-	-	-	-	0.2945

* butanal (BUTAL), butanols (BUTOLS), croton aldehyde (CROT-ALD), crotyl alcohol (CROT-OL), 3-butene-2-ol (3BTE2OL), 1(2)—butanol (1(2)-BUTOL), methyl-vinyl ketone (MVK).

presents chemical equilibrium computations regarding the Path A and Path B ways starting from 1 kmol/h at 350 °C and 1 atm. The computation was carried out using Aspen Plus^TM v.14 simulation software and the REQUIL reactor unit, with enthalpy of formation and Gibbs free energy of formation available from the Aspen database. To check the accuracy, an estimation procedure based on the second-order methods of Gani and Benson was applied. In most cases, the errors are negligible, bound by about +/− 1 kcal/mol. By neglecting secondary reactions, Path A leads to a theoretically high BD yield of 0.4798 kmol/kmol EtOH. The intermediate species crotonaldehyde and 2-buten-1-ol appear only in very low amounts. When considering both Path A and B, the butadiene yield is slightly lower due to the formation of MVK and 3-buten-2-ol. Thus, in the absence of other reactions, the formation of 1.3 butadiene by assuming the above pathways is thermodynamically feasible.

The thermodynamic behavior of the network of reactions can be investigated more realistically when the simultaneous formation of some by-products and impurities is considered. Firstly, the occurrence of ethylene and diethyl ether from ethanol dehydration is examined. The result is that the BD yield drops significantly to 0.1054, with a large amount of ethylene but little DEE. As previously shown, the dehydration reactions are related to strong acidic catalyst sites necessary for assisting other elementary steps in the BD synthesis process, namely the dehydration of unsaturated intermediates 2-buten-1-ol and 3-buten-2-ol to 1,3-butadiene.

Oxygenated species are an important category of by-products and impurities. As shown in Figure 1, following Path A, the butanal may appear due to the parallel reaction with butadiene formation through the dehydration of 2-buten-1-ol; in this case, the BD yield at equilibrium drops slightly to 0.4261. If ethylene formation is added, the BD yield falls sharply below 0.099. We may proceed further by considering the formation of butanols and butenes by Path A and Path B, the result being a moderate decrease in the BD yield to 0.3216 with significant amounts of butanols. The dehydration of alcohols to 1-butene and 2-butene leads to a negligible BD yield. In practice, the formation of butene cis- and trans-isomers is important for the assessment of the butadiene purification section, as this may involve substantial capital and utility costs (Dimian et al. [8]).

To conclude this section, we note that recent molecular simulation methods make use of density functional theory (DFT) algorithms, which are based on structural catalyst models for calculating the formation of Gibbs energy of different intermediates and transition states. This approach brings valuable insights into elucidating the reaction mechanism related to the catalytic process and can theoretically explain the differences encountered with classical thermodynamics. We specifically mention the papers by Chieregato et al. [54], Zhang et al. [55], and Taifan and Baltrusaitis [56].

4.3. Catalyst Selection for Process Design

The analysis presented so far shows that the catalysts for ETB processes must consider the interplay of two functions in their formulation: dehydrogenation and dehydration. These depend rather on the kinetic factors occurring from the intermediate steps of the catalytic process and less on the thermodynamic chemical equilibrium. The analysis identifies that a large amount of inert gas (lower ethanol partial pressure) was applied systematically in laboratory research to achieve higher butadiene selectivity. From an industrial viewpoint, the use of inert gas can involve high processing costs. As a result, only a few catalyst formulations from Table 1 remain of interest for industrial applications, as presented in

Table 4. Suitable catalysts for ETB process design.

	Catalyst	EPP [bar]	Conv. [%]	Temp. [°C]	BD %	ACH %	Olefin %	DEE %	Oxy %	References
1	Ag/ZrO2/SiO2	0.5	30	320	73.8	-	8.6	3.7	4.6	Sushkevich et al. [51]
2	K/Zr/Zn/MgO/SiO2	0.6	41.8	400	50.1	22.0	20.1	2.4	-	Da Ros et al. [15]
3	Cu/TaSiBEA	0.3	88	325	72.6	15.0	2.7	1.0	8.5	Kyriienko et al. [35]
4	Ag/ZrO2/SiO2	0.5	89	325	73.6	6.7	12.2	3.0	2.7	Dagle et al. [57]
5	Ag/ZrO2/SiO2	0.29	86.9	325	71.8	5.1	7.8	4.9	4.1	Li et al. [34]
6	Cu/La/ZrO2/SiO2	1.0	47.7	340	60.3	-	15.1	-	12.3	Makhin et al. [22]

. Replacing MgO in the Lebedev catalyst formulation with ZrO₂ appears to be a major improvement. The catalyst proposed by Dagle et al. [57], for which a patent application exists (2018; 2020), appears to be the best performer, offering high conversion of 90% at 0.5 bar ethanol partial pressure and 325 °C with the benefit of lower energy consumption. The cumulative selectivity of BD and ACH, which is 72.6 + 6.7 = 80.3%, forecasts a BD yield over 80% in a process with recycles. Similar behavior is shown by the catalysts developed by Sushkevich et al. [58] and by Li et al. [34]. Unfortunately, no kinetic models are proposed. In this study, we apply the catalyst developed by Da Ros et al. [15] with the kinetic model developed by Brosteanu et al. [14]. Here, we may mention the recent paper of Makhin et al. [22] as the only one working at atmospheric pressure without inert gas. A BD selectivity of about 60% is lower than the 70–74% achieved with inert gas by EPP of 0.3 to 0.6 bar but still high enough to encourage further improvements. The paper also demonstrates that ACH recycling is beneficial for raising the BD yield.

5. Chemical Reaction Engineering Issues

This section develops the design of a fluidized bed reactor for the one-stage ETB using the detailed kinetic model by Brosteanu et al. [14] based on the MgO/SiO₂ catalyst proposed by Da Ros et al. [15]. The presented approach is original for developing ETB technologies and more general in the case of processes involving complex chemistry.

The design of fluidized bed reactors is a difficult topic not covered by commercial software, except for a model in Aspen Plus^TM v14 (Aspen Technology, Inc., Bedford, MA, USA) dealing with circulating fluid bed (CFB) reactors. For this reason, the presented model is developed in Matlab^TM 2024b (The MathWorks, Inc.; Natick, MA, USA), starting with the formulation of equations. The two-phase model (TPM) is capable of capturing a realistic physical description of coupled hydrodynamic and mass transfer phenomena while limiting the number of parameters involved in the algorithm. On this basis, a somewhat more rigorous approach may be developed, such as the Kunii–Levenspiel model [59], but the estimation and accuracy of additional parameters may raise questions.

The kinetic modelling used in this paper is based on the experimental data published by Da Ros et al. [15], which used a K/Zr/Zn/MgO/SiO₂ catalyst. The packed-bed reactor was filled with 25 mg catalyst and operated at reaction temperatures ranging from 300 to 400 °C, with WHSV between 0.31 and 2.49 h⁻¹, fed with ethanol/nitrogen mixtures at atmospheric pressure with the molar fractions of 0.41–0.85. The working conditions for the designed fluidized bed reactor fall within these intervals.

5.1. Fluidized Bed Reactor for ETB Process

5.1.1. Two-Phase Fluidized Bed Modelling

The fluidized bed is structured in two phases (zones): the dense (emulsion) phase and the bubble phase. Practically all the catalyst is confined in the dense phase, with the bubble phase containing negligible amounts. The gas flowing through the dense phase corresponds to the minimum fluidization velocity, while the excess gas passes through the catalyst bed as a sequence of bubbles.

The TPM model developed in this section can be characterized as involving a single parameter, the bubble size. As underlined by Levenspiel [60], the power of this approach should be apparent since the model parameter can be easily adjusted as a function of experimental evidence and, thus, offers useful insights for the fluidized bed reactor design.

Generally, the gas bubble phase is assumed to be in plug flow, while for the dense phase, both plug flow and completely mixed assumptions are used. However, in the bubbling regime, the most appropriate dense phase flow pattern appears to be complete mixing. It is expected that the values of conversion, selectivity and yield achievable in the TPM are within the range defined by the two patterns. Two versions of the TPM were published by Orcutt and Grace [61]. Orcutt’s model assumes plug flow (PF) in the bubble phase and perfect mixing (CSTR) in the dense phase. Additionally, the Grace model considers that a small catalyst amount is shared in the bubble phase, which is important in the case of rapid reactions. It is accepted that TPM provides a good preliminary evaluation of bubbling fluidized bed reactor performance, particularly for slow reactions (Sundaresan and Amundson [62]; Werther [63]; Chaouki et al. [64]; Jafari et al. [65]).

Table 5. Constructive and operating parameters of the simulated fluidized bed reactor.

Parameter	Value	Parameter	Value
Weight space velocity (WHSV)	1.3 h−1	Amount of catalyst	2537 kg
Reactor feed rate, Fm	3800 kg/h	Feed ethanol molar fraction	0.80
Feed pressure of reactants, P0	1.5 bar	Reaction temperature, T	673 K
Catalyst particle diameter, dp	100 μm	Min fluidization velocity, umf	5.7 mm/s
Superficial feed gas velocity, u0	(10 ÷ 40) umf	Terminal velocity, ut	0.26 m/s
Catalyst particle density, ρp	1250 kg/m3	Bubble diameter, Db	0.08 m

presents the data applied for the simulation model developed in Matlab^TM.

The size and properties of the catalyst particles correspond to their inclusion in the category of fine particles and in group A of the Geldart classification (Rowe and Yates [66]; Grace et al. [67]). The gas volume fractions in the expanded bed fall between the values ε_f ~ 0.58 (for u₀ = 10 u_mf) and ε_f ~ 0.66 (for u₀ = 40 u_mf), corresponding to solid volume fractions between 0.42 and 0.34.

5.1.2. Reactor Model Equations

The modelling assumptions are as follows: (i) negligible internal diffusion and heat transport on the global process kinetics due to small catalyst particles; (ii) the influence of gas–solid mass and heat transfer on process kinetics is neglected; (iii) heat for the reaction is supplied via horizontal pipes traversing the bed using Dowtherm A vapors, but the presence of internal heat transfer pipes and the use of internal dispersing devices may limit the maximum gas bubble size; (iv) the reaction in the freeboard neglected; (v) the presence of catalyst particles in bubbles is neglected; (vi) isothermal operation.

(a)

Plug flow of gas in both phases (PFb-PFd)

-

balance equation of species j in the bubble phase:

$${\displaystyle \frac{{\mathrm{dF}}_{\mathrm{Mj}}^{(\mathrm{b})}}{\mathrm{dz}}}= \mathrm{S} {\mathrm{K}}_{\mathrm{bd}}{\epsilon }_{\mathrm{b}}\left[{\mathrm{C}}_{\mathrm{j}}^{\left(\mathrm{d}\right)}-{\mathrm{C}}_{\mathrm{j}}^{\left(\mathrm{b}\right)}\right] ; \mathrm{z}={0, \mathrm{F}}_{\mathrm{Mj}}^{(\mathrm{b})}={\mathrm{F}}_{\mathrm{Mj},0}^{(\mathrm{b})}, j=1,2\dots N_c-1$$

(8)

-

balance equation of species j in the dense phase:

$${\displaystyle \frac{{\mathrm{dF}}_{\mathrm{Mj}}^{(\mathrm{d})}}{\mathrm{dz}}}=\mathrm{S} {\mathrm{K}}_{\mathrm{bd}}{\epsilon }_{\mathrm{b}}\left[{\mathrm{C}}_{\mathrm{j}}^{\left(\mathrm{b}\right)}-{\mathrm{C}}_{\mathrm{j}}^{\left(\mathrm{d}\right)}\right]+ \mathrm{S} {(1-\epsilon }_{\mathrm{b}}{) (1-\epsilon }_{\mathrm{mf}} ) {\mathrm{r}}_{\mathrm{v}}^{(\mathrm{j})}; \mathrm{z}={0, \mathrm{F}}_{\mathrm{Mj}}^{(\mathrm{d})}={\mathrm{F}}_{\mathrm{Mj},0}^{(\mathrm{d})}$$

(9)

-

pressure variation along the bed:

$${\displaystyle \frac{\mathrm{dP}}{\mathrm{dz}}} = - {(1-\epsilon }_{\mathrm{b}}{)(1-\epsilon }_{\mathrm{mf}}{)\mathsf{\rho }}_{\mathrm{p}} \mathrm{g}; \mathrm{z}=0, {\mathrm{P}=\mathrm{P}}_0$$

(10)

(b)

Plug flow of gas into the bubble phase and full mixing into dense phase (PFb-CSTRd)

-

the balance of species j in the bubble phase is expressed by Equation (8)

-

the balance equation of species j in the dense phase:

$${\mathrm{F}}_{\mathrm{Mj},0}^{(\mathrm{d})}+ \mathrm{S} {\displaystyle \underset{0}{\overset{\mathrm{H}}{\int }}{\mathrm{K}}_{\mathrm{bd}} {\epsilon }_{\mathrm{b}}\left[{\mathrm{C}}_{\mathrm{j}}^{\left(\mathrm{b}\right)}{-\mathrm{C}}_{\mathrm{j}}^{\left(\mathrm{d}\right)}\right]} \mathrm{dz}+ \mathrm{S} \mathrm{H} {(1- \epsilon }_{\mathrm{b}}{) (1-\epsilon }_{\mathrm{mf}} ) {\mathrm{r}}_{\mathrm{v}}^{(\mathrm{j})} - {\mathrm{F}}_{\mathrm{Mj}}^{(\mathrm{d})}=0, {\mathrm{j}=1,\mathrm{N}}_{\mathrm{c}}-1$$

(11)

-

the pressure variation along the bed is defined by Equation (10).

In the equations presented above, the notations are as follows:

N_c—number of components in the reaction mixture including inert gas; ${\mathrm{F}}_{\mathrm{Mj}}^{(\mathrm{b})}, {\mathrm{F}}_{\mathrm{Mj}}^{(\mathrm{d})}$—molar flowrate of species j in the bubble and dense phase, respectively; ${\mathrm{C}}_{\mathrm{j}}^{(\mathrm{b})}, {\mathrm{C}}_{\mathrm{j}}^{(\mathrm{d})}$—gas concentrations of species j in the two phases; S—the cross-section area of the fluidized bed; K_bd—the interphase mass transfer coefficient reported to bubble volume; ${\epsilon }_{\mathrm{b}}$—fraction of the bed occupied by bubbles; ${\epsilon }_{\mathrm{mf}}$—void fraction of the dense phase (identical to that at the point of minimum fluidization); ${\mathrm{r}}_{\mathrm{v}}^{(\mathrm{j})}$—rate of formation for species j, calculated at the composition of the gas in the dense phase (reported to volume of catalyst particle); g—acceleration of gravity; ρ_p—catalyst particle density; z—axial coordinate. The overbar designates the average value along the bed.

The parameters K_bd, ε_b, ε_mf were evaluated using correlations published by Rowe and Yates [66], Kunii and Levenspiel [59] and Grace et al. [67], respectively.

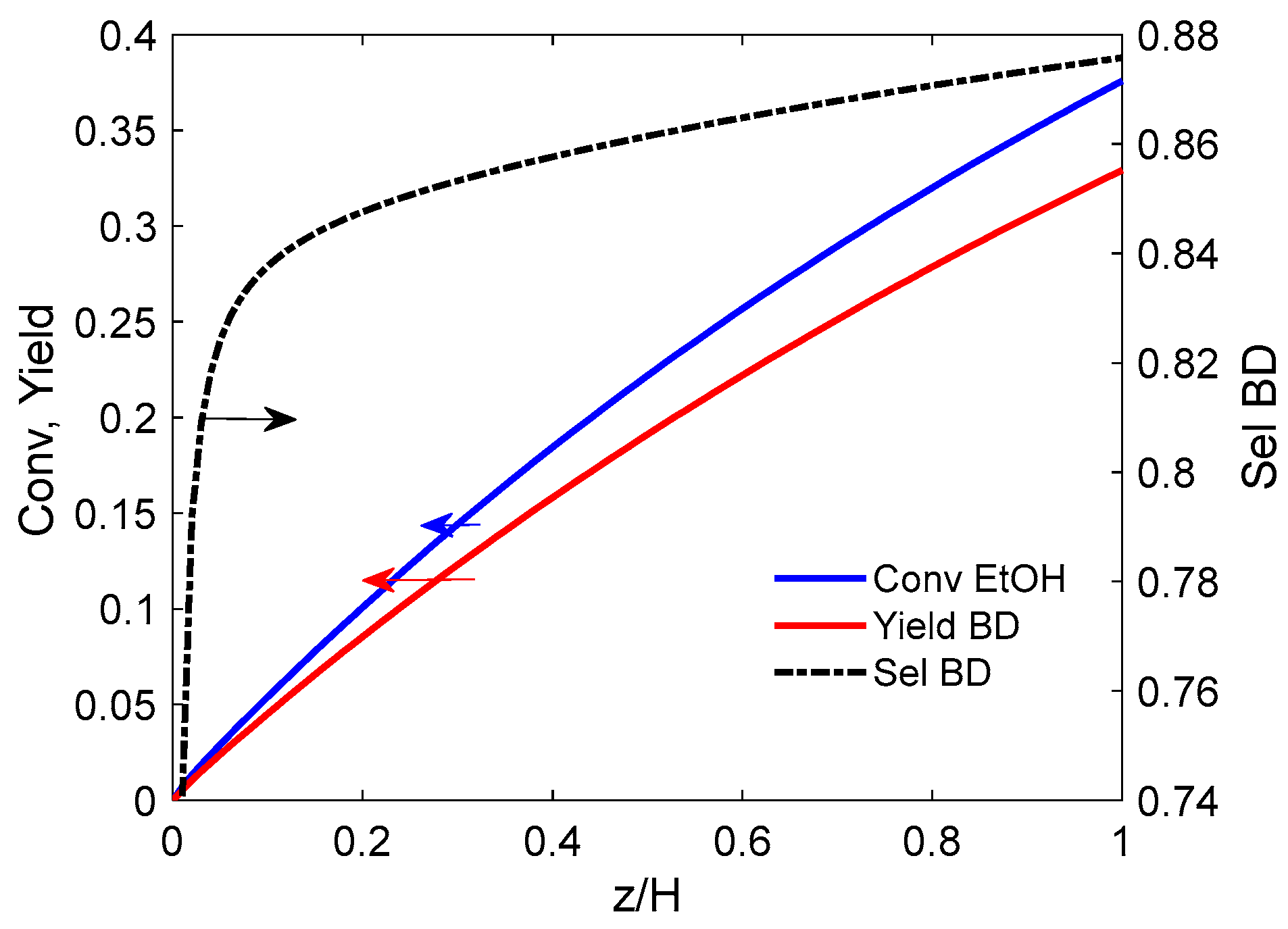
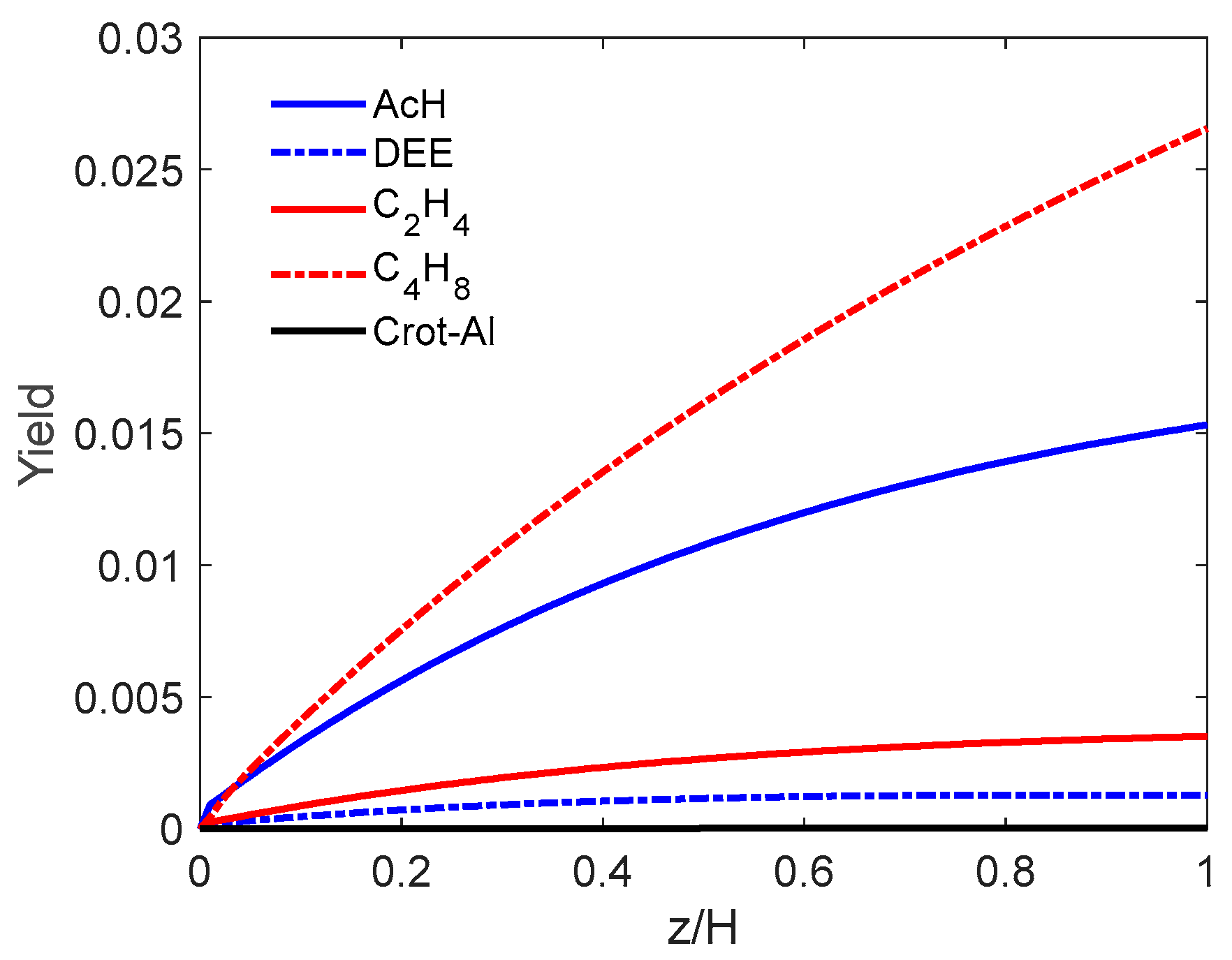
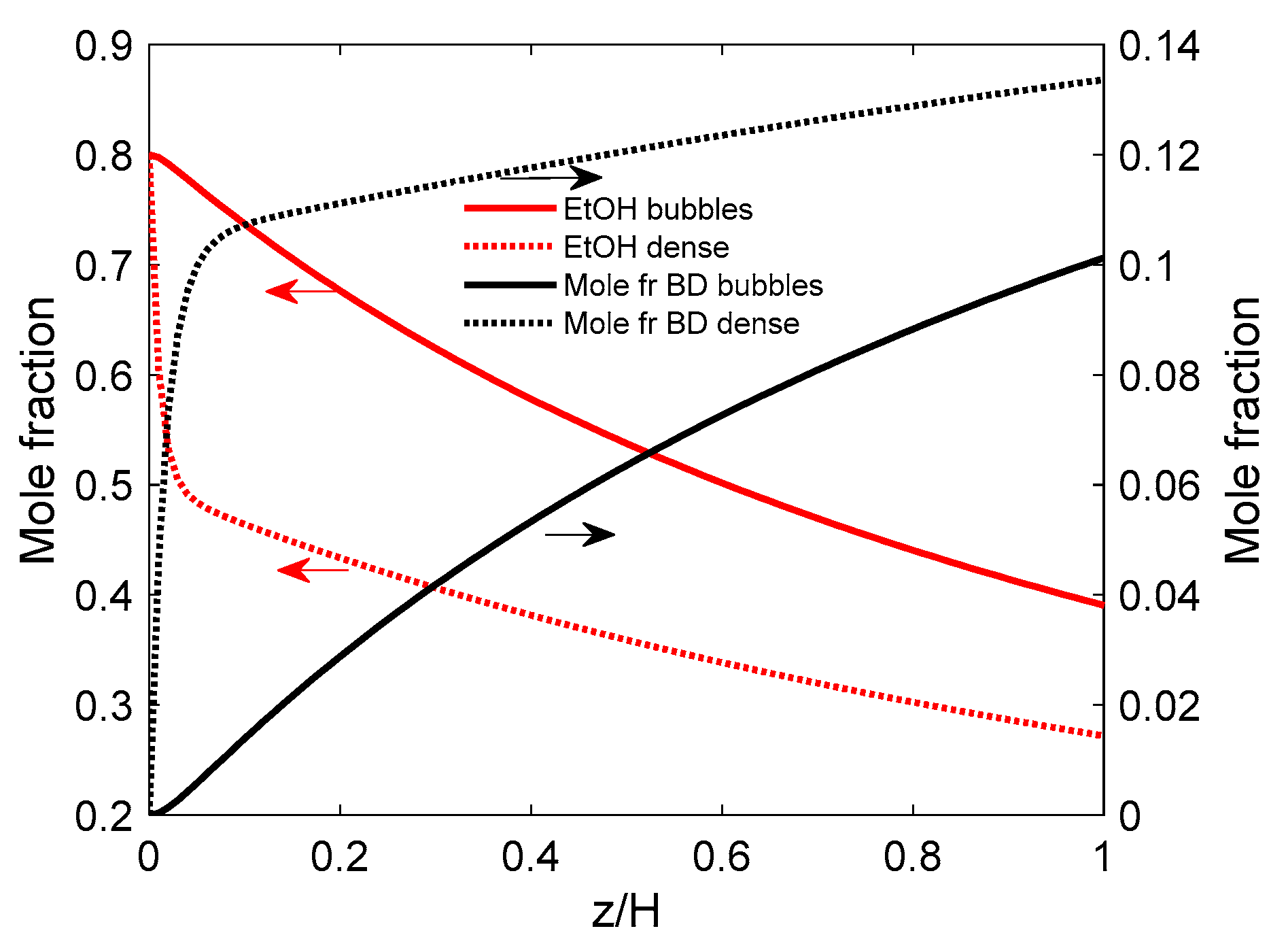
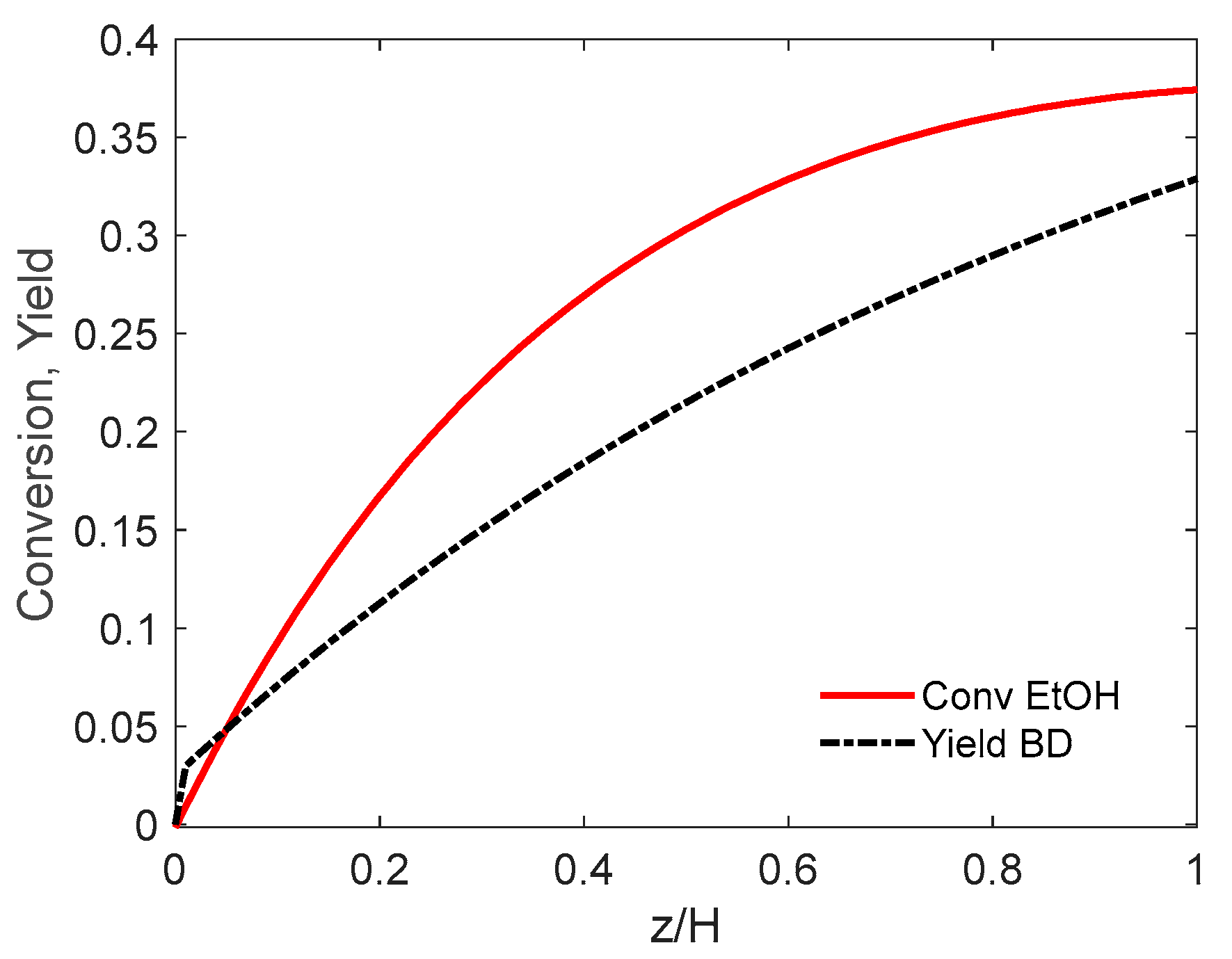
5.1.3. Simulation Results

The system of ordinary differential Equations (8)–(10), for the PFb-PFd gas flow pattern and the system of differential-algebraic Equations (8), (10) and (11) for the PFb-CSTRd gas flow, were integrated numerically using the MATLAB^® programming package.

The bubble diameter is considered constant along the fluidized bed, whereas the bubble velocity and bubble volume fraction are calculated using published correlations. The accuracy of integration was checked by the atomic balance between the reactor’s entry and exit. This balance is fulfilled with negligible errors for the PFb-PFd gas flow (errors in the atomic balance of C ~10⁻⁷%) but relatively larger for the PFb- CSTRd (~0.03%), due to difficulty in determining the accurate solution for dense-phase balance equations. We also note some convergence problems in the solution of balance Equation (11), at low bubble diameters (smaller than 4 cm).

(a)

PFb-PFd hypothesis

Figure 5, Figure 6, Figure 7 and Figure 8 present simulation results for the data given in Table 5 and a ratio u_0/u_mf = 30, which corresponds to a bed diameter of 2.6 m and an extended bed height H = 1.1 m. The total gas flow rate, calculated by the integration of the mass balance equations, increases along the bed, inducing an increasing bubble volume fraction (from 0.21 to 0.27) and bubble velocity, respectively (from ~0.8 to ~0.86 m/s).

The evolution of the ethanol interphase mass transfer coefficient, K_bd, presents a minimum along the bed, due to the opposite influences of the ethanol diffusion coefficient (decreasing along the bed) and of the bubble velocity (increasing along the bed) (Figure 5). Figure 6 depicts the evolutions of ethanol conversion, BD yield and BD selectivity. As seen, the BD selectivity shows a steep increase in the distributor vicinity, followed by a flattening tendency after 0.1 m up the bed. In addition to butadiene, significant amounts of by-products are also generated (Figure 7). Among these, the most notable appear to be butene (yield ~2.7%), acetaldehyde (~1.5%) and ethylene (~0.35%).

Figure 8 shows the evolution of ethanol and BD concentrations in the two phases. A steep decrease in ethanol concentration and steep increase in BD concentration in the dense phase are observed in the entry section, a consequence of low gas velocity (high reaction time) and higher reaction rate in this region due to ethanol concentration. These evolutions explain the shape of the BD selectivity curve, already shown in Figure 6.

• (b) PFb-CSTRd flow

The calculated ethanol conversion and BD yield in the PFb-CSTRd flow hypothesis are slightly smaller but rather close to those obtained considering gas plug flow in both phases. This is explained by the complete mixing of gas in the dense phase and the important gas exchange between the two phases (see below). A few results are presented in Figure 9 and Figure 10. Figure 9 shows a short zone near the feed section where the BD yield is higher than the ethanol conversion, explained by the effect of the completely mixed dense phase.

5.1.4. Influence of the Gas Feed Velocity

Table 6. Influence of gas velocity on fluidized bed reactor performances (T = 400 °C; D_b = 8 cm).

Fluidized Bed		Flow Model		Kbd tb
		PFb-PFd	PFb-CSTRd
u0 = 10 umf	Conv EtOH	0.280	0.289	0.57
	Yield BD	0.252	0.260
	Sel BD	0.898	0.90
u0 = 20 umf	Conv EtOH	0.340	0.348	1.18
	Yield BD	0.301	0.310
	Sel BD	0.885	0.887
u0 = 30 umf	Conv EtOH	0.376	0.374	1.890
	Yield BD	0.329	0.329
	Sel BD	0.876	0.879
u0 = 40 umf	Conv EtOH	0.396	0.382	2.48
	Yield BD	0.345	0.334
	Sel BD	0.871	0.875
Mixed fluidized bed T = 400 °C	Conv EtOH	0.385
	Yield BD	0.334
	Sel BD	0.868
Fixed bed dp = 3 mm; T = 400 °C	Conv EtOH	0.413
	Yield BD	0.355
	Sel BD	0.860
	Vbed/Dv0	4.43 s

presents the values of ethanol conversion, BD selectivity, and BD yield, calculated at different values of the gas superficial velocity (operating conditions given in Table 5). As can be seen from the table, the ethanol conversion and BD yield values are not essentially different for the two flow patterns (PFb-PFd and PFb-CSTRd) (see also Figure 6 and Figure 9). These results agree with other published studies, which report that the flow models in the dense phase, whether assumed to be plug flow or completely mixed, do not significantly affect the predictions (Ho [68]).

The examination of the results regarding the PFb-CSTRd model reveals that in the BFB regime, the performance of a mixed flow is somewhat superior to the plug flow in the range u_o/u_min ratio of 10 to 30, but the situation changes towards an advantage of plug flow models at a ratio of 40. This behavior is rather surprising! However, looking deeper into the kinetics of complex reaction systems, it can be seen that acetaldehyde action has an autocatalytic character: initiating the butadiene synthesis chain by aldol condensation of two ACH molecules, while at a later stage, one ACH molecule is restored by the MPV reduction of ethanol. This mechanism supports an acceleration action by recycling the acetaldehyde identified experimentally (Da Ros et al. [69]; Makhin et al. [22]).

The beneficial influence of the u₀/u_mf ratio on the transformation is explained by the intensification of the gas transfer between the bubble and dense phases, with an increase in this ratio. Quantitatively, this intensification can be expressed by the ratio (r_t) between the volume of gas transferred between the two phases and the volume of gas captured in the bubble phase:

$${\mathrm{r}}_{\mathrm{t}}={\displaystyle \frac{\mathrm{H} \mathrm{S} {\epsilon }_{\mathrm{b}}{\mathrm{K}}_{\mathrm{bd}}{\mathrm{t}}_{\mathrm{b}}}{\mathrm{H} \mathrm{S} {\epsilon }_{\mathrm{b}}}} = {\mathrm{K}}_{\mathrm{b}\mathrm{d}}{\mathrm{t}}_{\mathrm{b}}$$

(12)

In this relationship, t_b represents the time taken for a bubble to cross the bed:

$${\mathrm{t}}_{\mathrm{b}}={\displaystyle \frac{\mathrm{H} }{{\mathrm{u}}_{\mathrm{b}}}}$$

(13)

Table 6 illustrates the approach. For example, at u₀/u_mf = 10 (relatively small gas velocity), r_t = 0.57, i.e., 57% of the inlet gas is transferred to the dense phase for sustaining the catalytic reaction. At u₀/u_mf = 40, close to the turbulent fluidization flow, r_t = 2.48 means that the exchanged gas volume is 2.48-times larger than the bubble gas volume. Note that for u₀/u_mf = 10, 90% of the gas input goes through the bed as bubbles, while for u₀/u_mf = 40, this fraction rises to 97.5%.

Increasing the superficial gas velocity u₀ leads to more intensive mass transfer between the two phases. As shown by Table 6, the fluidized bed performance for both fluid patterns rises significantly with the ratio u₀/u_min, namely in the range of ratios 10 to 30, for which the operation takes place in the BFB regime, as represented in a general flow diagram (Figure 20.5 from Levenspiel [60]). In the case of the PFb-PFd model, the ethanol conversion rises from 0.28 to 0.376, while the BD yield rises from 0.252 to 0.329. Further raising of u₀/u_min to 40 shifts the operation close to the turbulent fluidized bed (TFB), where the bubbles agglomerate in slugs and the behavior is approaching a PF reactor with axial dispersion.

5.1.5. Influence of Bubble Size

Figure 11 presents the influence of the bubble diameter on the fluidized bed reactor performance, such as ethanol conversion and BD yield (left axis) and selectivity (right axis). The PFb/PFd and PFb/CSTRd patterns are compared. The results are of interest since the bubble diameter is a parameter that the designer can manipulate:

-

Increasing the bubble diameter from 4 to 20 cm drops both the ethanol conversion and BD yield by about 2.4-times. This effect, common to both flow patterns, is due to lower interphase mass transfer (K_bd) and lower bubble residence time (t_b).

-

At small bubble diameters, the performance of the PFd model is better, but at bubble diameters larger than 8 cm, the CSTRd pattern seems slightly superior. This may be explained again by the autocatalytic effect of the recycled acetaldehyde on the butadiene synthesis rate.

-

An interesting aspect is that in the range of smaller diameters (4 to 8 cm), the performance of the CSTRd seems to be insensitive to the bubble diameters. Therefore, this bubble size range is recommended for designing the gas distribution and redistribution devices. In this way, the reactor performance should be high but not greatly affected by the mixing model.

In a nutshell, the analysis demonstrates that the development of a fluidized bed reactor for the one-stage ETB process is realistic, with the performance approaching the fixed bed reactor but offering the clear advantage of efficient continuous catalyst regeneration. The application of a simple two-phase model allows us to obtain a robust comparison of the two limiting models for the reactive catalytic dense phase, plug flow and mixed flow. The modelling provides insights for reactor design: place the operation in the BFB region at the highest gas ratio u₀/u_mf to provide intense interphase mass transfer; ensure a bubble size distribution in a range of 4 to 8 cm.

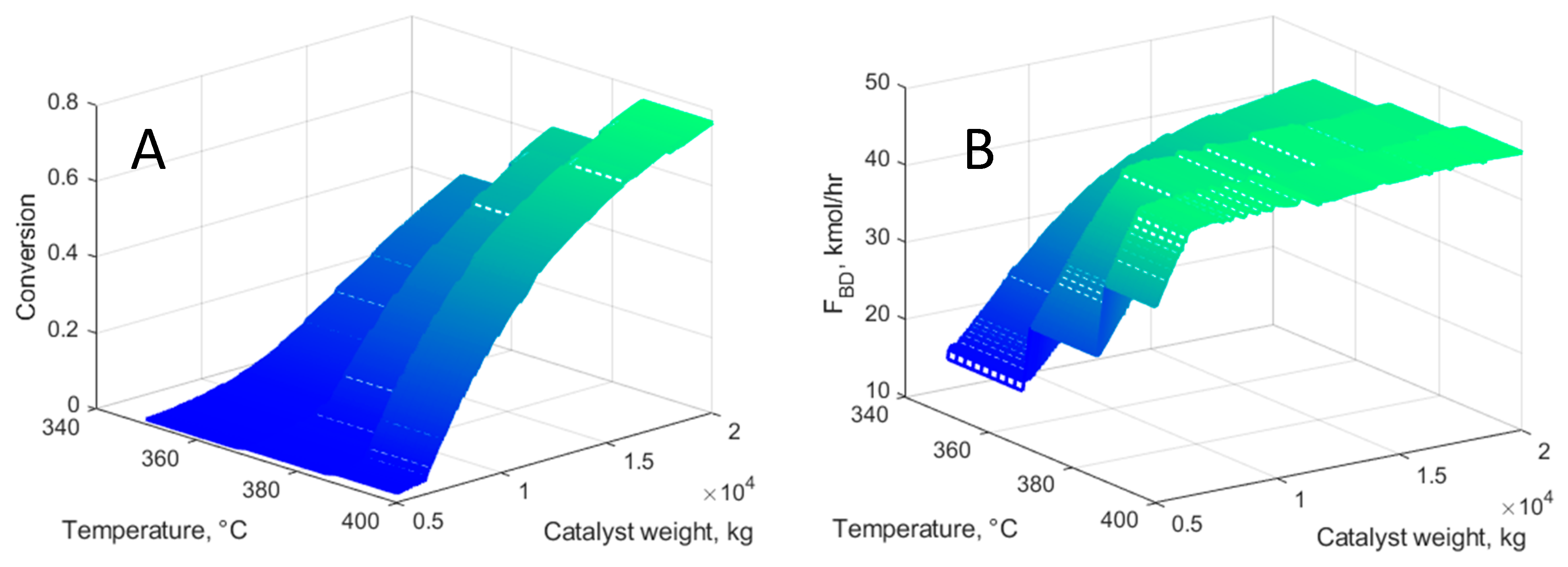
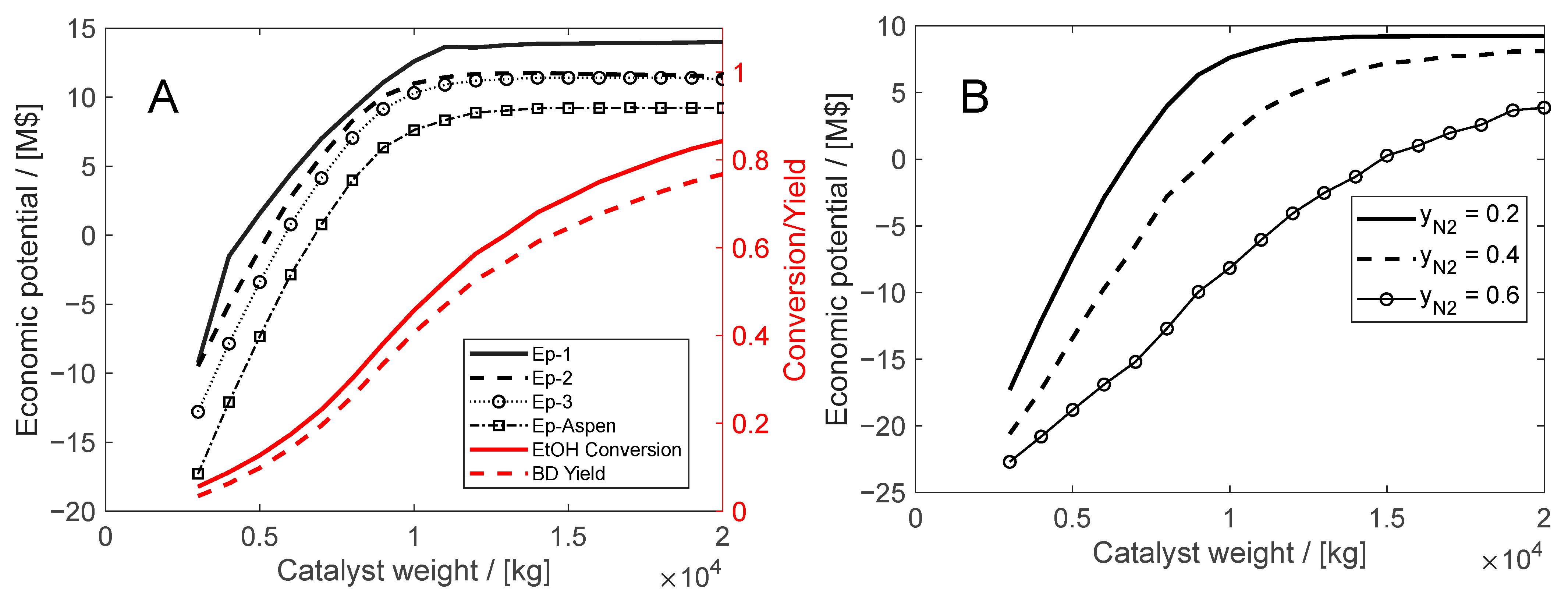
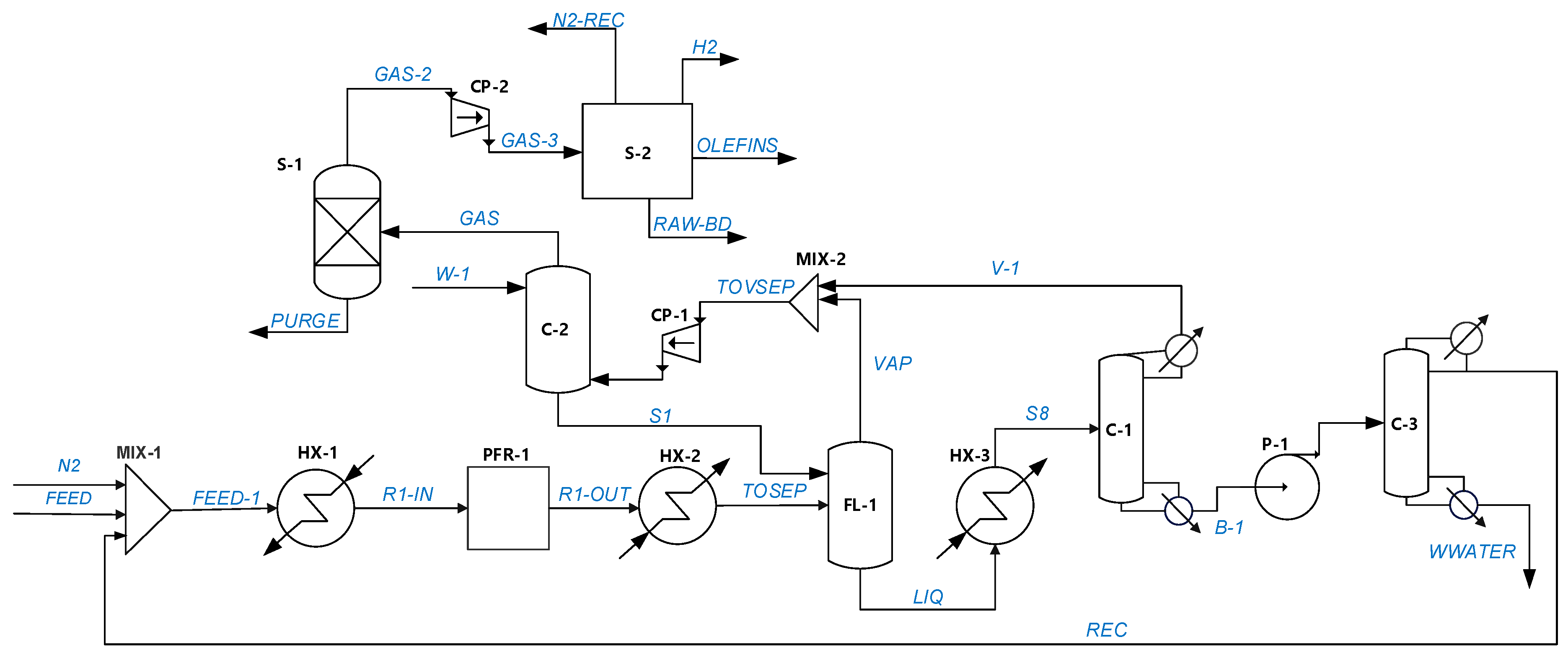
5.2. ETB Reactor Design in a Recycle Structure

This section presents the design of a catalytic chemical reactor for the one-stage ETB process within a reactor–separation–recycle (RSR) structure. Unlike the standalone analysis, this approach considers the relation between the reactor performance and the process design, particularly focusing on the separation system. Key advantages include the optimal design of the chemical reactor before the full process synthesis and insights over the plantwide control of the material and heat balances (Dimian et al. [7], Bîldea et al. [70], Brosteanu et al. [71]).

The analysis of the chemical reactor in a simplified RSR structure is described in Figure 12. In this particular case, the reactor is a shell-and-tube heat exchanger with a catalyst in the tubes and Dowtherm vapor in the shell. Previous analysis examined the effectiveness factor, dealing with complex reaction kinetics, and proposed an effective numerical method coded in Matlab^TM to solve this difficult problem [13]. More specifically, it was found that for a MgO/SiO₂ catalyst (Da Ros et al. [15]), the butadiene yield was controlled by the accumulation of ethanol reactant and the key intermediates as acetaldehyde and crotonaldehyde in the particles, governed by the internal chemical reaction with diffusion and external mass and heat transport rates. Catalyst particles in the range 2 to 3 mm with tubes of diameter 25 to 40 mm are the most efficient for achieving 80% butadiene carbon selectivity. This modelling approach is generic for designing catalytic chemical reactors involving complex reactions.

As depicted in Figure 12, the fresh feed and recycle stream containing ethanol and acetaldehyde are mixed in MIX-1 with the inert gas (nitrogen) set by a design specification to obtain the desired inert volumetric fraction. The heating and cooling of the mixture are simulated by the heat exchange units HX-1 and HX-2, respectively. After the reaction, the outlet mixture enters a black-box separation unit that mimics the separation system, delivering the stream of products (butadiene, hydrogen, water, by-products and nitrogen) and the recycle stream containing non-converted ethanol and acetaldehyde. As demonstrated by several works, including Da Ros et al. [69], adding acetaldehyde to the ethanol feed significantly increases the butadiene yield.

In this way, one can simulate a complete description of the reactor performance as a function of the operating parameters, namely catalyst load, temperature, pressure and inert fraction. Figure 13 displays, in a 3D representation, the ethanol conversion and butadiene production at atmospheric pressure with an inert fraction of 0.2, temperature of 350 to 400 °C, and 2000 to 20,000 kg catalyst. In the temperature range of 360 to 370 °C, a large amount of catalyst (20,000 kg) is necessary to obtain a modest BD yield of 40% at an ethanol conversion of around 50%. To achieve a higher yield, the operating temperature must be raised to the maximum, 400 °C in this case. This operation drops the catalyst load to below 15,000 kg, increasing the BD yield to about 43.5%. It is worth noting that the BD yield is most sensitive to ethanol recycle and inert gas flow rates. These fall from large to moderate values as the conversion increases from small to moderate. This trend has a significant effect on the reactor sizing, catalyst load and operation costs.

Following the hierarchical approach of process synthesis, the assessment of different design alternatives can be performed in terms of the economic potential (EP). This represents the difference between the revenues obtained by selling the products and the expenses involved in manufacturing, as raw materials, utilities and annualized capital costs (Dimian et al. [7]). EP can be applied for the chemical reactor design and optimization in an RSR system by applying the following cost function:

$$\mathrm{EP}=\mathrm{EP}(\mathrm{I}/\mathrm{O})-\left\{\mathrm{Cos}{\mathrm{t}}_{\mathrm{Reactor}}+\mathrm{Cos}{\mathrm{t}}_{\mathrm{Catalyst}}+\mathrm{Cos}{\mathrm{t}}_{\mathrm{Utilities}}\right\}-\mathrm{Cos}{\mathrm{t}}_{\mathrm{Recycles}}$$

(14)

The catalyst load is the independent variable. EP(I/O) is the economic potential at the first input/output level, noted here as EP-1, calculated only from the products’ selling and the raw materials’ cost. Further, the expenses occurred at the reactor level (EP-2) and the recycle level (EP-3) are subtracted. The assumptions in this case are as follows:

(a)

Butadiene cost of 1.5 USD/kg, medium in the 2010–2020 period (www.intratec.us, accessed on 1 February 2025), and bioethanol cost of 0.45 USD/kg as internal biorefinery production price.

(b)

The multitube reactor cost is based on heat transfer area A estimated as A = 4W/ρ_cD_t. (W: weight of catalyst; D_t: tube diameter; ρ_c: catalyst bed density). The equipment purchasing cost is C = a + bAⁿ (USD) with a = 32,000, b = 70 and n = 1.2 [7]. In addition, material factors of 2 and installation of 3 are considered. The reactor cost is annualized by assuming an ROI of 0.2.

(c)

Catalyst cost estimation assumes regeneration/replacement each month over 12 months. To simplify, we assume the same cost for new and regenerated catalysts. This is 5 USD/kg, considering the cost of MgO and SiO₂ raw materials 1.5 USD/kg plus 3.5 USD/kg additional costs for on-site production and regeneration.

(d)

The reactor duty is calculated by multiplying the butadiene production rate with the enthalpy of reaction (2 × 44.7 MJ/kmol) for an efficiency factor of 0.85.

(e)

The energy cost of ethanol recycling is approximated from the molar flow, enthalpy of vaporization of 37.6 MJ/kmol and a reflux ratio of 1.75.

(f)

The inert (nitrogen) flow is varied by a ‘design specification’ to keep constant a molar fraction of 0.2 at the rector inlet. The inert (nitrogen) recycling cost is calculated from the compression energy from 1.1 to 25 bar (to butadiene separation). The specific consumption determined by simulation is 0.12 kWh/kg.

(g)

The energy prices have a strong impact on the procedure in today’s unstable market. There are large differences in industrial prices between the USA (www.eia.gov, accessed on 1 February 2025) and Europe (https://ec.europa.eu/eurostat, accessed on 1 February 2025), as 80 vs. 200 USD /MWh for electricity and 15 vs. 22 USD/GJ for thermal energy. US prices are used here as a benchmark.

Figure 14A represents the variation in the EP with the catalyst load, starting from the first level EP-1 (details in Supplementary Material). Initially, the EP-1 rises linearly to a plateau trend at USD 13 starting with 10,000 kg/h. The next level EP-2 considers the impact of the chemical reactor, including reactor annualized costs over 5 years and the cost of catalyst and reactor heating. The trend shows a similar trajectory, but the plateau drops to USD 11.8. At 14000 kg, the above contributions are USD 0.67, 0.84 and 0.2. It can be seen that the shift from EP-1 to EP-2 is significant. This effect can be explained by the large amount of catalyst needed to achieve the target production related to a modest catalyst productivity of 0.15 kg/kg catalyst/h. Next, the EP-3 level considers the recycling cost of ethanol and acetaldehyde, as well as of the inert gas. The ethanol recycling flow rate is high at small conversion, but it drops rapidly to a limit when the ethanol conversion does not increase. The trend of inert recycling is similar. The relative costs of ethanol and inert gas recycling at 14,000 kg/h are USD 0.3 and 0.1. Finally, the EP-3 shows a fair maximum at USD 11.4.

To evaluate the worth of the RSR analysis, we proceed with the process synthesis of the ETB process. Figure 15 presents the flowsheet used for simulation in Aspen Plus v14. Fresh feed and recycle stream containing ethanol enter the mixer MIX-1 together with controlled inert flow set to 0.2 molar fraction. After cooling to 33 °C, the outlet reaction mixture is submitted to vapor/liquid separation in FL-1. The vapor phase captures most of the BD, but a high recovery of 99.5% is boosted with the re-boiled stripping column C-1. After vapor-phase compression in CP-1 from 1.1 to 5 bar, the small amounts of oxygenated species are removed by water washing in the column C-2. Then, the cleaned gas containing butadiene, hydrogen, ethylene, butene and nitrogen is sent to separation of BD, olefin, nitrogen and hydrogen, simulated by the black-box separator S-2. The separation methods refer to standard cryogenic and membrane techniques.

The RSR analysis demonstrates that the design of the chemical reactor, including the catalyst and the structure of recycles, is the determinant factor in designing an ETB process. It should be noted that product selectivity in stand-alone reactor design becomes the overall product yield at the level of the process with recycles. Therefore, in such a process, the operation point should select the best selectivity that can be achieved, not necessarily at high conversion. If the catalyst deactivates frequently, its regeneration may be cost limiting.

The simulation carried out in the Aspen Plus process simulator provides a more accurate estimation at the third level. This includes the design and cost estimation of separation columns and more accurate estimation of recycling costs. It can be observed that the EP-ASPEN curve shifts below the EP-3 curve in the RSR system, but the optimum zone is preserved. Finally, the optimal reactor design involves a catalyst load of 14,000 kg that delivers butadiene production of 44.42 kmol/h or 2057 kg/h that results in a productivity of 0.15 kg/(kg-cat·h).

Figure 14B displays the role of the inert amount about the economic potential and, thus, on process feasibility. For a nitrogen molar fraction of 0.2, the optimal EP-3 is USD 8.99, in which the share of catalyst fees is 9.3% and of recycle fees is 3.6%. If the inert molar fraction rises to 0.4, then the above values become 6.48, 13 and 10.2%. A further rise in the nitrogen fraction to 0.6 shifts the EP-3 in the negative domain, making the process infeasible.

The above analysis demonstrates the importance of carefully scaling up the effect of using inert gas when investigating catalyst performance. A quantitative assessment can be performed in an RSR analysis via a kinetic model that incorporates this effect.

6. Conclusions

• This study investigates the relationship between the development of ethanol to butadiene (ETB) catalysts and the design of the chemical reaction system. The ETB catalyst must achieve two tasks, converting ethanol into a substantial amount of acetaldehyde and performing butadiene synthesis through a multi-step reaction chain. While specialized catalysts can fulfill these requirements efficiently, combining them into a multifunctional performant single catalyst is much more challenging. Additionally, the formation of numerous by-products and impurities seriously affects the butadiene yield.
• A thermodynamic analysis is performed in Aspen Plus^TM for both acetaldehyde and butadiene synthesis steps, with the original feature of considering the simultaneous formation of the main products, by-products and impurities. Comparing the predictions with selected experimental data demonstrates that the performance of the ETB catalysts is controlled essentially by kinetic factors and not by thermodynamics. This study highlights the constraint of using inert gas at industrial scale to achieve a higher butadiene yield due to large additional processing costs. This requirement restricts the catalyst selection to a shortlist based essentially on mixed oxides, namely ZrO₂, and on SiO₂-type support boosted by metal promoters for ethanol dehydrogenation, such as Cu, Ag, Au, and La. The catalyst proposed by Da Ros et al. [15], with kinetic modelling developed by the authors, appears suitable for testing conceptual reactor designs.
• From an industrial perspective, the ETB catalyst assessment should consider the catalyst deactivation and regeneration. As a novelty, this study addresses this topic by analyzing the application of a fluidized bed reactor. A thorough two-phase simulation model was implemented in Matlab^TM, which was successful in solving the algorithmic challenges arising from the complex chemical kinetics.
• The simulation demonstrates the feasibility of operating the reactor in the bubble fluidization bed (BFB) regime. High superficial velocity ratios u₀/u_min, and bubble sizes in the range 4 to 8 cm favor the reactor performance (ethanol conversion and butadiene yield). The simulation reveals an autocatalytic effect due to acetaldehyde chemistry. Surprisingly, the performance of a well-mixed dense phase becomes better compared to the plug flow model, though the differences are minimal due to limited ethanol conversion (around 50%).
• A second case study deals with the optimization of the ETB reaction section. This approach is generic and takes place in the reactor–separation–recycle (RSR) structure by evaluating the economic potential in relation to the costs of the reactor, catalyst, and recycling operations. The RSR analysis demonstrates the importance in the economic assessment of inert gas recycling, which the designer should consider if involved in catalyst development. In the present case, the recycling of nitrogen might shift the operation into the infeasible region, findings confirmed by rigorous simulation in Aspen Plus^TM.
• The insights from this study can be applied for developing suitable industrial catalysts for the one-stage ETB process. The recommendations are as follows: (1) targeting higher butadiene C-selectivity (over 80 to 85%), including acetaldehyde at reasonable ethanol conversion; (2) suppressing or limiting the use of inert gas; (3) improving catalyst robustness; (4) performing more kinetic investigations for catalyst assessment by process design; (5) targeting productivity better than 0.15 kg butadiene/kg cat/h.