Machine Learning-Based Sizing Model for Tapered Electrical Submersible Pumps Under Multiple Operating Conditions
Abstract
:1. Introduction
2. Overview of ESP Hybrid Sizing Model
2.1. Conventional Design Methods
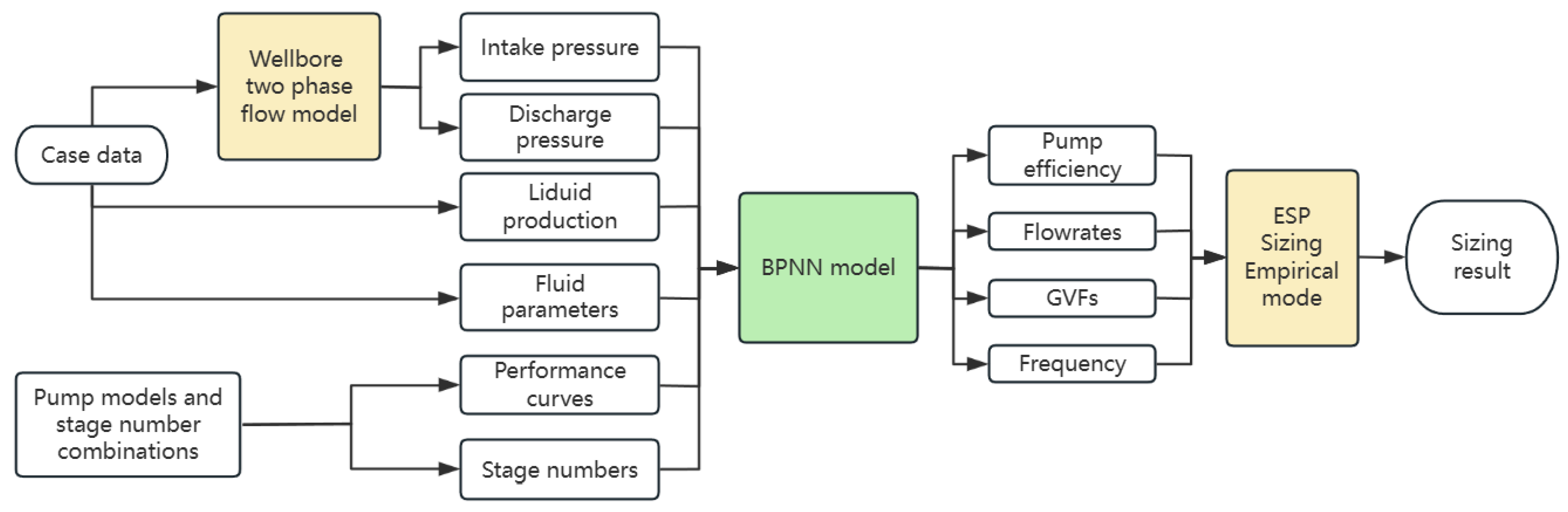
2.2. Hybrid Model Framework
- Wellbore two-phase flow calculation: Using the gas reservoir numerical simulation results, the bottom hole flowing pressure for each given working condition is determined. This pressure serves as the starting point to calculate the pump intake parameters (before the separator) under each working condition using the wellbore two-phase flow calculating model, including total fluid flow, pressure, and GVF. A reasonable separator is then selected, and the separating efficiency is determined. Then, the pump intake (after the separator) parameters are calculated. Then, using the wellbore two-phase flow model, the pump discharge data under each working condition are calculated, starting from the wellhead tubing pressure.
- Pump efficiency calculation: After obtaining the pump intake and discharge working data, the stage-by-stage pump calculation model is used to calculate pump efficiency, operating frequency, and other data for the inlet and outlet of each pump under different pump models and stage number combinations.
- Pump selection and optimization: The primary objective of this process is to eliminate designs that may cause operational failures and to maximize the overall pump efficiency of tapered ESP systems under multiple operating conditions. To avoid operational failures, the key constraints include GVF inside two pumps that must be below the pump limit to prevent gas locking; and the operating frequency must remain within a certain range to ensure proper lubrication and avoid increased equipment costs. To maximize the pump efficiency, each operating condition is assigned a weight, and the pump efficiency is calculated as a weighted average; the weighted average efficiencies for various pump models and stage numbers are then compared to determine the optimal combination of the pump model and stage number.
2.3. ESP Sizing Empirical Model
- GVF constraint: The constraint of filtering out designs with a gas volume fraction (GVF) exceeding 30% [24,25,26] at the intake of the upper pump is based on well-established engineering principles and field experience. Conventional pumps with mixed-flow designs are not capable of handling high GVF conditions efficiently, as excessive gas content can lead to gas locking, reduced pump efficiency, and even operational failure. By excluding such designs, we ensure that the selected pump configurations operate within their recommended performance range, thereby maintaining high efficiency and reliability.
- Frequency range: The minimum operating frequency of all working conditions should not be less than 35 Hz. Based on field experience, ESP systems should run under a frequency of at least 35 Hz to ensure proper lubrication of the seal bearing and prevent failure. The maximum operating frequency of all working conditions should be close to the design frequency. When the design frequency is set at 60 Hz, in some cases, the pump model and stage number combination with the highest weighted pump efficiency may result in a maximum operating frequency significantly lower than 60 Hz. While this design may provide higher pump efficiency, it can also lead to a higher number of ESP stages and increased equipment costs, which is not optimal. Therefore, the model restricts the maximum operating frequency range to 59–60 Hz across all working conditions. The model is flexible in adjusting this frequency range to accommodate specific field conditions. Users can modify the lower frequency limit and design frequency within the model’s input parameters, allowing for customization based on well-specific requirements or operational constraints. For example, in wells with lower liquid production rates, the lower frequency limit can be reduced to 30 Hz, while in high-flow-rate wells, the design frequency can be increased to 70 Hz [27].
- Weighted averaging of pump efficiencies: After screening, the ESP operating conditions are assigned weights based on factors such as condition duration. The objective function for the optimization is defined as the maximization of the weighted pump efficiency across all operating conditions. Mathematically, the objective function can be expressed as the following:where n is the total number of operating conditions, ηweighted is the weighted pump efficiency, fraction; ηi is the total pump efficiency for working condition i, fraction; and wi is the weight assigned to the operating condition i, reflecting its relative importance. This objective function ensures that the optimization process prioritizes designs that perform well under the most critical operating conditions while maintaining high efficiency across all scenarios.
3. Tapered ESP Operating Parameters FCNN Model
3.1. Mechanism Model for Calculating the Operating Parameters of Tapered ESP
- (1)
- Set initial frequencies f1 and f2 to 0 Hz and 100 Hz, respectively.
- (2)
- Calculate the median value of f1 and f2, denoted as f3, and use the ESP affinity law [11] to calculate the head and efficiency performance curves for the two pumps under f3.
- (3)
- Perform stage-by-stage calculations in the pump. Starting from the pump intake, obtain the head of the first-stage pump based on the pump intake flow rate from the performance curve. This is then converted into a pressure boost, and the fluid pressure and flow rate at the outlet of this stage are calculated. These values are used as the intake parameters for the second-stage pump to calculate the discharge pressure and flow rate of the second-stage pump. This step is repeated until the last pump is calculated.
- (4)
- If the discharge pressure of the last pump exceeds the design discharge pressure, assign the value of f3 to f2; otherwise, assign f3 to f1.
- (5)
- If the difference between f2 and f1 is less than 0.2 Hz, the final operating frequency is the median value of f1 and f2. If the difference is greater than 0.2 Hz, return to step 2 to recalculate.
- (6)
- For the final operating frequency, perform stage-by-stage calculation and save the flow rate and GVF at the pump intake, the connection point between the two pumps, and the pump discharge. During the stage-by-stage calculation process, the power consumption of each stage is calculated. The power consumption at each stage is then used to calculate the total efficiency of the ESP. The formula for calculating the total pump efficiency is as follows:where η is the total pump efficiency, dimensionless; n1 and n2 are the stage numbers of two pumps; ρi is the average density of the fluid in the i-th stage pump, which is the average density of the fluid at the inlet and outlet of this stage pump, kg/m3; g is the acceleration of gravity, which is 9.81 m/s2; Hi is the head of the i-th stage pump, which is read through the performance curve, m; Qi is the fluid flow rate of the i-th stage pump, which is the average flow rate of the fluid at the inlet and outlet of this stage pump, m3/s; Pi is the power of the i-th stage pump, W; and ηi is the efficiency of the i-th stage pump, which is read through the performance curve, fraction.
3.2. Data Genreration and Preprocessing
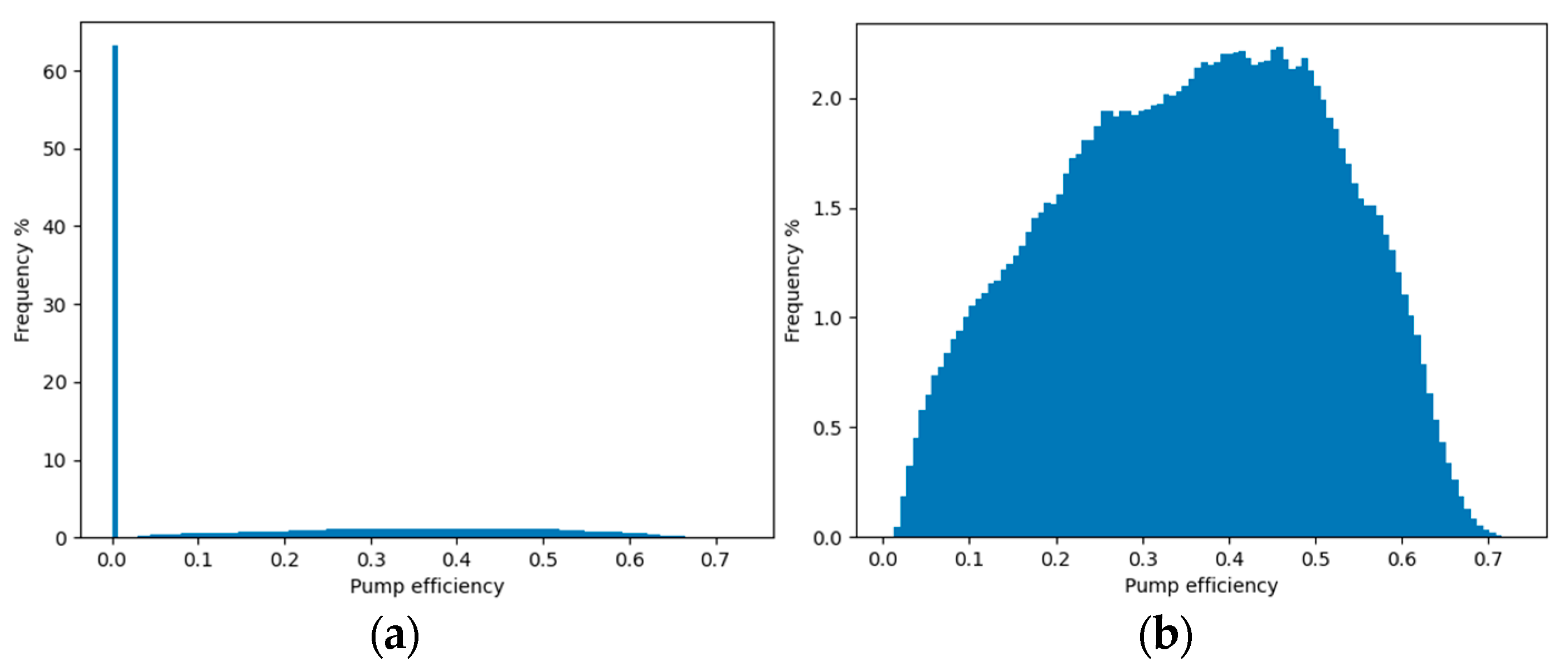
- Screening out data with a pump efficiency of 0:
- Screening out data with an operating frequency greater than 99 Hz:
- Parameter normalization:
- Data set division:
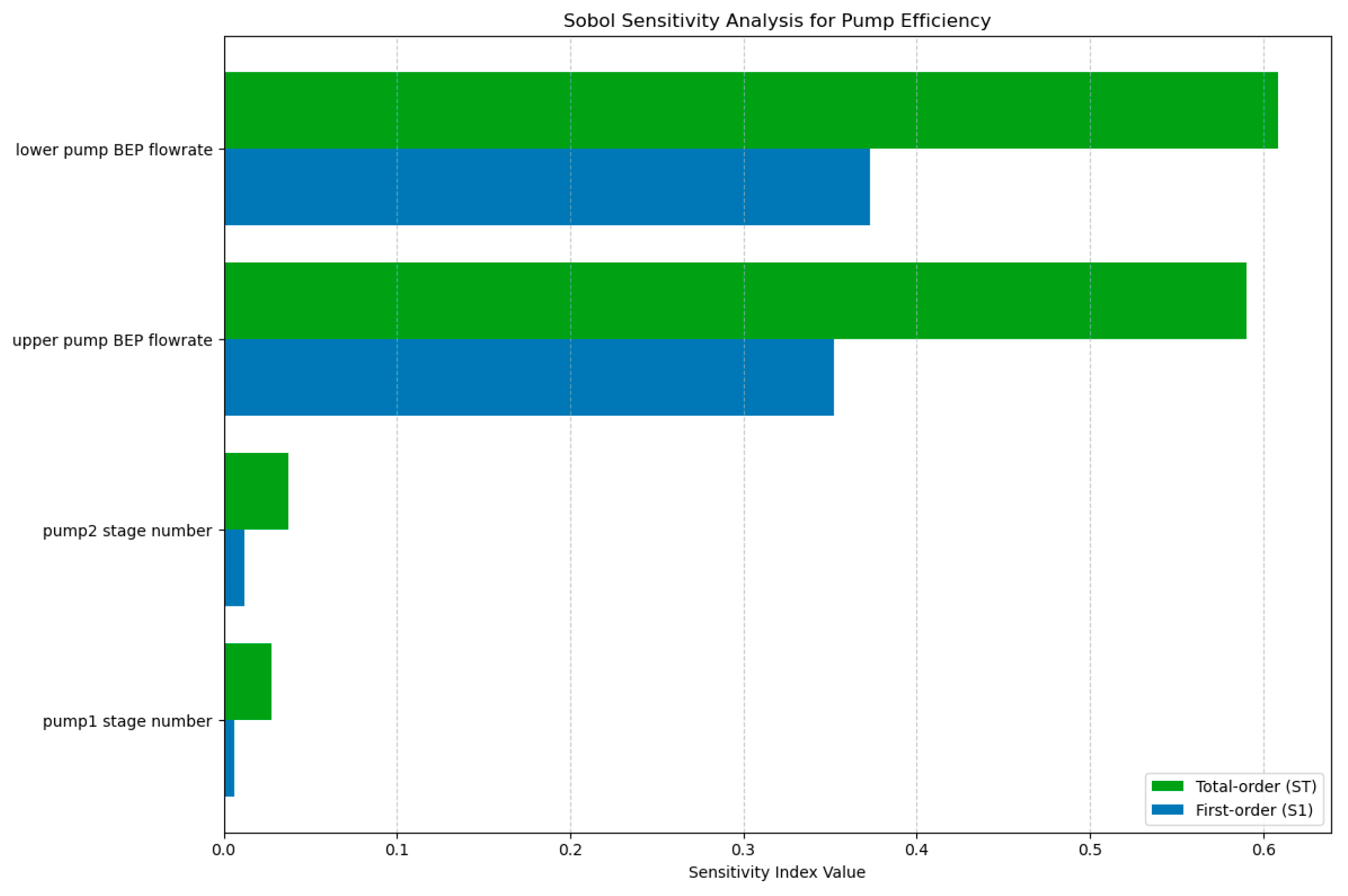
- Sensitivity analysis of input parameters:
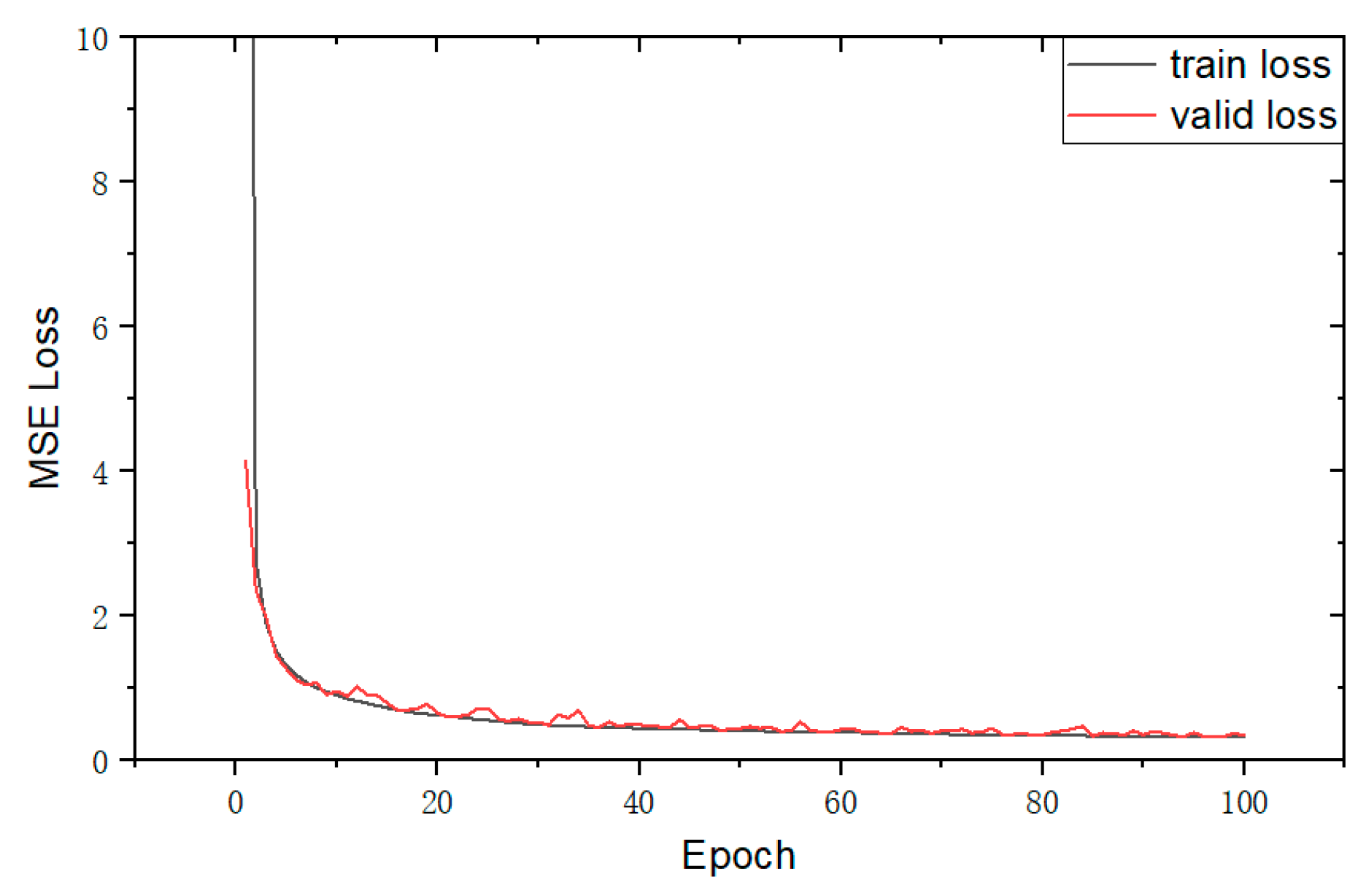
3.3. Model Building and Training
4. Case Study and Validation
4.1. Case Description
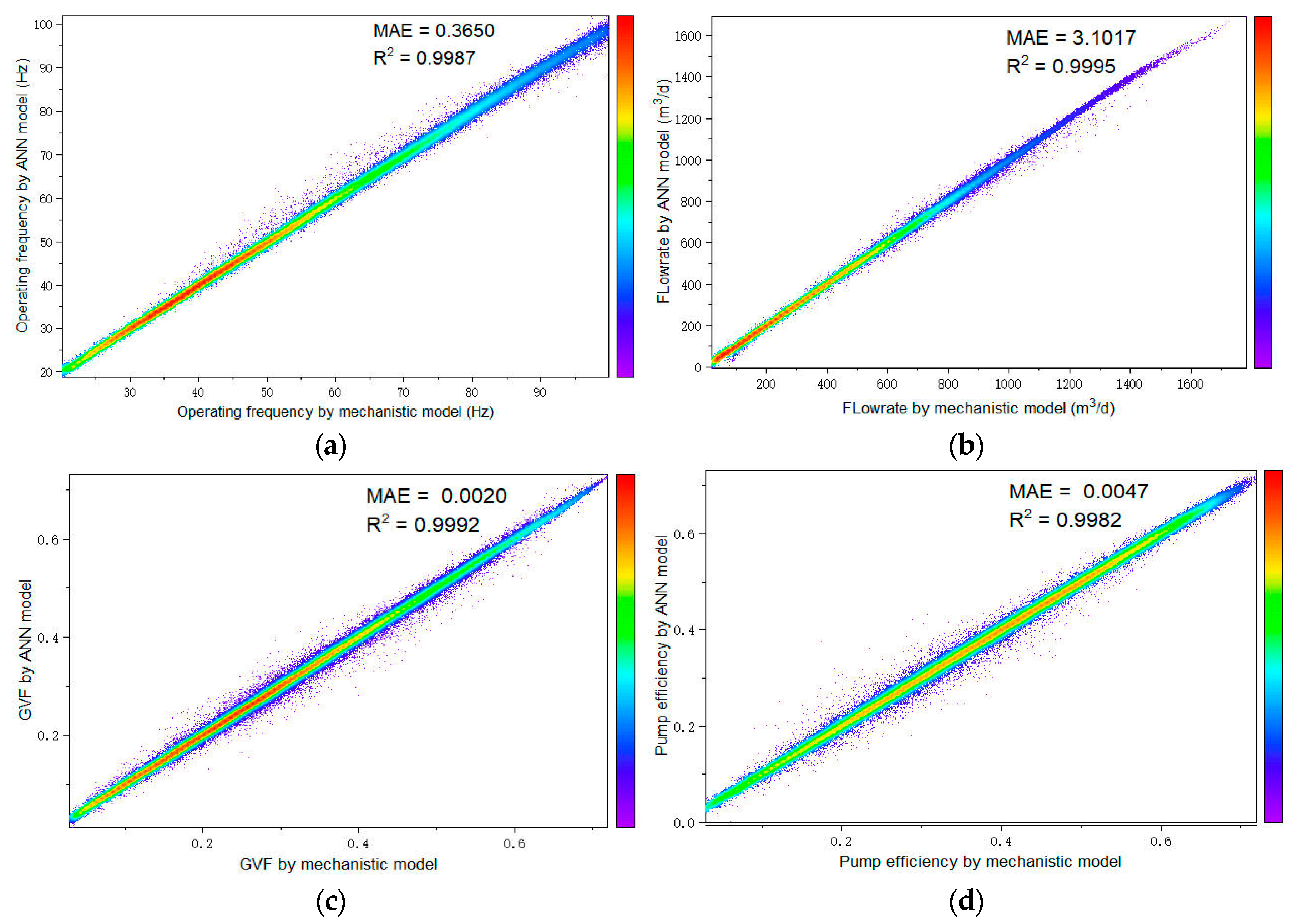
4.2. FCNN Model Calculation Results
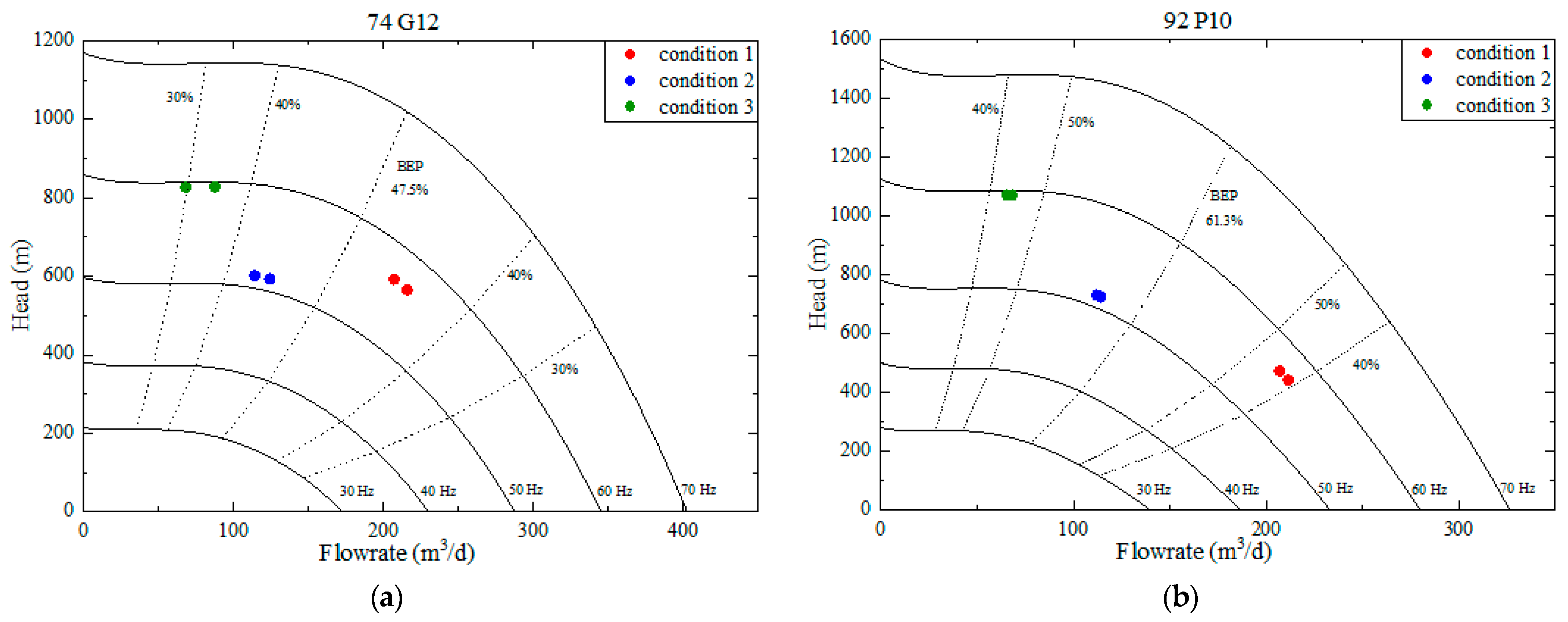
4.3. Sizing Results Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ESP | Electrical Submersible Pump |
| GVF | Gas Volume Fraction |
| GLR | Gas Liquid Ratio |
| FCNN | Fully Connected Neural Network |
| BP | Backpropagation |
| MSE | Mean Squared Error |
| MAE | Mean Absolute Error |
References
- Janadeleh, M.; Ghamarpoor, R.; Abbood, N.K.; Seyednooroldin, H.; Hasan, N.; Ali, Z.H. Evaluation and selection of the best artificial lift method for optimal production using pipesim software. Heliyon 2024, 10, e36934. [Google Scholar] [CrossRef] [PubMed]
- Drozdov, A.N.; Bulatov, G.G.; Lapoukhov, A.N.; Mamedov, E.A.; Malyavko, E.A.; Alekseev, Y.L. Artificial-lift operation technologies of low-pressure flooded gas and gas-condensate wells. In Proceedings of the SPE Trinidad and Tobago Section Energy Resources Conference, Port-of-Spain, Trinidad, 11 June 2012. [Google Scholar] [CrossRef]
- Pant, H. Best Pumping Practices to Optimize Dewatering in CBM wells: Lessons Learned Developing Raniganj East Field, India. In Proceedings of the SPE Unconventional Resources Conference and Exhibition-Asia Pacific, Brisbane, Australia, 11 November 2013. [Google Scholar] [CrossRef]
- Bassett, L. Successful Strategies for Dewatering Wells Using ESP’s. In Proceedings of the SPE Eastern Regional Meeting, Charleston, SC, USA, 23 September 2009. [Google Scholar] [CrossRef]
- Liang, X.; Xing, Z.; Yue, Z.; Ma, H.; Shu, J.; Han, G. Optimization of Energy Consumption in Oil Fields Using Data Analysis. Processes 2024, 12, 1090. [Google Scholar] [CrossRef]
- Buluttekin, M.B.; Ulusoy, B.; Dorscher, D. Simulations and challenges of ESP applications in high GOR wells at south east of Turkey. In Proceedings of the 22nd World Petroleum Congress, Istanbul, Turkey, 9 July 2017. [Google Scholar]
- Zhou, D.; Sachdeva, R. Design Tapered Electric Submersible Pumps For Gassy Wells. In Proceedings of the Indian Oil and Gas Technical Conference and Exhibition, Mumbai, India, 4 March 2008. [Google Scholar] [CrossRef]
- Peng, Y.; Ye, C.; Sun, F.; Wang, X.; Zhu, P.; Zhu, Q.; Zhang, Y.; Wang, W. Drainage gas recovery technology for high-sulfur gas wells by a canned ESP system. Nat. Gas Ind. B 2018, 5, 452–458. [Google Scholar] [CrossRef]
- Kadio-Morokro, B.; Curay, F.; Fernandez, J.; Salazar, V. Extending ESP run life in gassy wells application. In Proceedings of the SPE Electric Submersible Pump Symposium, The Woodlands, TX, USA, 24 April 2017. [Google Scholar] [CrossRef]
- Takacs, G. Electrical Submersible Pump Components and Their Operational Features. In Electrical Submersible Pumps Manual, 2nd ed.; Gulf Professional Publishing: Waltham, MA, USA, 2018; pp. 55–152. [Google Scholar] [CrossRef]
- Yao, J.; Han, G.; Zhang, Z. Method of Automatic Sizing and Selection of Tapered Electrical Submersible Pump System Based on Multiple Operating Cases. In Proceedings of the International Conference on Computational & Experimental Engineering and Sciences, Singapore, 21 August 2024. [Google Scholar] [CrossRef]
- Agwu, O.E.; Alkouh, A.; Alatefi, S.; Azim, R.A.; Ferhadi, R. Utilization of machine learning for the estimation of production rates in wells operated by electrical submersible pumps. J. Pet. Explor. Prod. Technol. 2024, 14, 1205–1233. [Google Scholar] [CrossRef]
- Yang, P.; Chen, J.; Wu, L.; Li, S. Fault Identification of Electric Submersible Pumps Based on Unsupervised and Multi-Source Transfer Learning Integration. Sustainability 2022, 14, 9870. [Google Scholar] [CrossRef]
- Peng, L.; Han, G.; Pagou, A.L.; Shu, J. Electric submersible pump broken shaft fault diagnosis based on principal component analysis. J. Pet. Sci. Eng. 2020, 191, 107154. [Google Scholar] [CrossRef]
- Wan, M.; Gou, M. Research on fault diagnosis of electric submersible pump based on improved convolutional neural network with Bayesian optimization. Rev. Sci. Instrum. 2023, 94, 115109. [Google Scholar] [CrossRef] [PubMed]
- Han, G.; Lu, X.; Zhang, H.; Sui, X.; Wang, B.; Liang, K. ESP Wells Dynamic Survival Analysis and Lifespan Prediction Using Machine Learning Algorithms. In Proceedings of the SPE Annual Technical Conference and Exhibition, New Orleans, LA, USA, 20 September 2024. [Google Scholar] [CrossRef]
- Abdalla, R.; Samara, H.; Perozo, N.; Carvajal, C.P. Machine learning approach for predictive maintenance of the electrical submersible pumps (ESPS). ACS Omega 2022, 7, 17641–17651. [Google Scholar] [CrossRef] [PubMed]
- Costa, E.A.; Rebello, C.M.; Santana, V.V.; Reges, G.; Silva, T.O.; Abreu, O.S.L.; Ribeiro, M.P.; Foresti, B.P.; Fontana, M.; Nogueira, I.B.R.; et al. An uncertainty approach for Electric Submersible Pump modeling through Deep Neural Network. Heliyon 2024, 10, e24047. [Google Scholar] [CrossRef]
- Iranzi, J.; Son, H.; Lee, Y.; Wang, J. A Nodal Analysis Based Monitoring of an Electric Submersible Pump Operation in Multiphase Flow. Appl. Sci. 2022, 12, 2825. [Google Scholar] [CrossRef]
- Beggs, D.H.; Brill, J.P. A study of two-phase flow in inclined pipes. J. Pet. Technol. 1973, 25, 607–617. [Google Scholar] [CrossRef]
- Heidaryan, E.; Salarabad, A.; Moghadasi, J. A novel correlation approach for prediction of natural gas compressibility factor. J. Nat. Gas Chem. 2010, 19, 189–192. [Google Scholar] [CrossRef]
- Bahadori, A.; Mokhatab, S.; Towler, B.F. Rapidly estimating natural gas compressibility factor. J. Nat. Gas Chem. 2007, 16, 349–353. [Google Scholar] [CrossRef]
- Hall, K.R.; Yaborough, L. A new equation of state for Z-factor calculations. Oil Gas J. 1973, 71, 82–92. [Google Scholar]
- Zhu, J.; Zhu, H.; Wang, Z.; Zhang, J.; Cuamatzi-Melendez, R.; Farfan, J.A.M.; Zhang, H.Q. Surfactant effect on air/water flow in a multistage electrical submersible pump (ESP). Exp. Therm. Fluid. Sci. 2018, 98, 95–111. [Google Scholar] [CrossRef]
- Ali, A.; Yuan, J.; Deng, F.; Wang, B.; Liu, L.; Si, Q.; Buttar, N.A. Research Progress and Prospects of Multi-Stage Centrifugal Pump Capability for Handling Gas–Liquid Multiphase Flow: Comparison and Empirical Model Validation. Energies 2021, 14, 896. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, H.-Q. A Review of Experiments and Modeling of Gas-Liquid Flow in Electrical Submersible Pumps. Energies 2018, 11, 180. [Google Scholar] [CrossRef]
- Andagoya, K.; Villalobos, J.; León, F.; Hidalgo, M.; Vela, N.; Sotomayor, A.; Orozco, A.; Ekambaram, R.; Koduru, P.; Reyes, C.; et al. Ultrahigh Speed ESP Technology Solution for a 11,400-ft Well: First Successful Deployment with Induction Motor in Ecuador. In Proceedings of the SPE Middle East Artificial Lift Conference and Exhibition, Manama, Bahrain, 29 October 2024. [Google Scholar] [CrossRef]
- Powers, M.L. Special considerations for electric submersible pump applications in underpressured reservoirs. SPE Prod. Eng. 1992, 7, 301–306. [Google Scholar] [CrossRef]
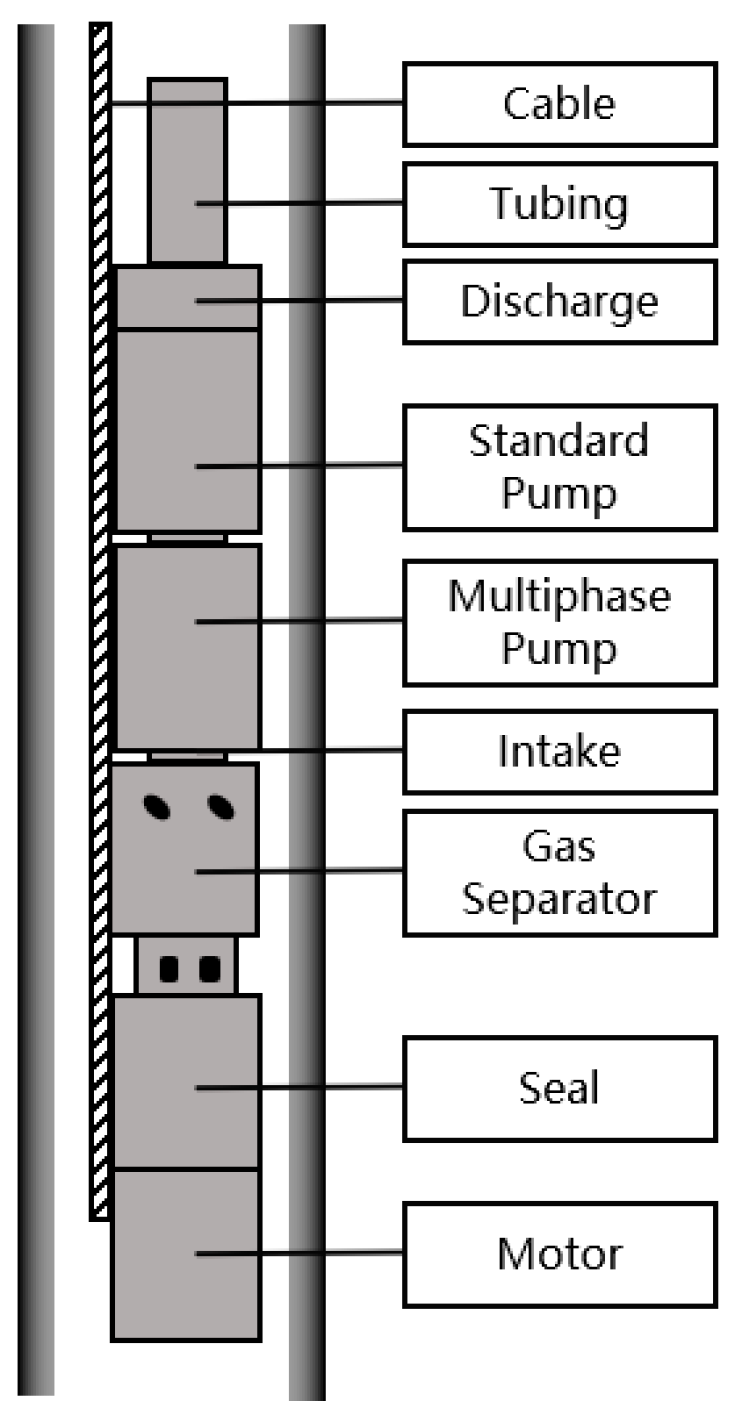
| Parameters | Minimum Value | Maximum Value |
|---|---|---|
| Intake pressure (MPa) | 5 | 16 |
| Discharge pressure (MPa) | Intake pressure + 4 MPa | Intake pressure + 25 MPa |
| Water production rate (m3/d) | 20 | 500 |
| Tubing GLR (m3/m3) | 10 | 110 |
| Water relative density | 1 | 1.1 |
| Gas relative density | 60 | 80 |
| Fluid temperature (K) | 333 | 373 |
| Stage number | 50 | 300 |
| Network Architecture * | Training Time (s) | Test MAE | Test MSE | Test R2 |
|---|---|---|---|---|
| 33-16-8 | 1714.06 | 2.6474 | 16.7345 | 0.9569 |
| 33-64-8 | 1952.41 | 1.1303 | 3.2766 | 0.9910 |
| 33-64-32-8 | 2672.63 | 0.6147 | 0.9529 | 0.9974 |
| 33-64-32-16-8 | 2716.26 | 0.6151 | 0.9172 | 0.9974 |
| 33-128-64-32-8 | 2811.20 | 0.3431 | 0.3231 | 0.9991 |
| 33-128-64-32-16-8 | 3327.19 | 0.3168 | 0.2610 | 0.9993 |
| Network Layer | Parameters | Number of Neurons |
|---|---|---|
| Input layer | Intake pressure | 1 |
| Discharge pressure | 1 | |
| Liquid production rate | 1 | |
| Tubing GLR | 1 | |
| Fluid temperature | 1 | |
| Water relative density | 1 | |
| Water relative density | 1 | |
| Head curve of lower pump | 6 | |
| Efficiency curve of lower pump | 6 | |
| Stage number of lower pump | 1 | |
| Head curve of upper pump | 6 | |
| Efficiency curve of upper pump | 6 | |
| Stage number of upper pump | 1 | |
| Output layer | Operating frequency | 1 |
| Total pump efficiency | 1 | |
| Flow rate at intake/discharge/connection point | 3 | |
| GVF at intake/discharge/connection point | 3 |
| Data | Value | Data | Value |
|---|---|---|---|
| Well structure | Vertical | Tubing ID (mm) | 63 |
| Water relative density | 1.02 | Casing ID (mm) | 121 |
| Gas specific gravity | 0.66 | Pump fluid temperature (K) | 353 |
| Perforation depth (m) | 3200 | Pump hanging depth (m) | 3000 |
| Gas separator efficiency | 0.9 |
| Working Condition Name | Gas Rate (m3/d) | Water Rate (m3/d) | Intake Pressure (MPa) | Discharge Pressure (MPa) | Tubing GLR (m3/m3) | Weight Coefficients |
|---|---|---|---|---|---|---|
| 1 | 20,000 | 200 | 17.90 | 28.04 | 10 | 0.25 |
| 2 | 30,000 | 100 | 13.21 | 24.72 | 30 | 0.25 |
| 3 | 30,000 | 50 | 8.3 | 22.15 | 60 | 0.5 |
| Working Condition | Operating Frequency (Hz) | Intake Flow Rate (m3/d) | Connection Point Flow Rate (m3/d) | Discharge Flow Rate (m3/d) | Intake GVF | Connection Point GVF | Discharge GVF | Pump Efficiency (%) |
|---|---|---|---|---|---|---|---|---|
| 1 | 56.8 | 215.62 | 206.97 | 211.49 | 0.0494 | 0.0481 | 0.0422 | 45.37 |
| 2 | 51.3 | 124.02 | 114.06 | 112.11 | 0.1830 | 0.1396 | 0.1138 | 59.53 |
| 3 | 59.5 | 87.39 | 68.08 | 65.50 | 0.4292 | 0.2991 | 0.2138 | 38.31 |
| Lower Pump | Upper Pump | Condition 1 | Condition 2 | Condition 3 | Weighted Pump Efficiency | |||
|---|---|---|---|---|---|---|---|---|
| Operating Frequency (Hz) | Pump Efficiency | Operating Frequency (Hz) | Pump Efficiency | Operating Frequency (Hz) | Pump Efficiency | |||
| 74-G12 | 92-P10 | 56.8 | 45.37% | 51.3 | 51.45% | 59.5 | 38.31% | 43.36% |
| 100-G22 | 128-P18 | 49.1 | 62.90% | 50.9 | 47.10% | 59.2 | 30.37% | 42.69% |
| 74-G12 | 96-P8 | 60.5 | 38.95% | 51.4 | 51.55% | 59.2 | 39.45% | 42.35% |
| 76-G12 | 96-P12 | 52.5 | 50.84% | 50.4 | 49.79% | 59.5 | 34.01% | 42.16% |
| 98-G22 | 98-P12 | 50.7 | 54.30% | 49.5 | 48.58% | 59.2 | 32.33% | 41.88% |
| 98-G22 | 92-P10 | 55.7 | 45.86% | 50.4 | 49.79% | 59.4 | 35.44% | 41.63% |
| 98-G22 | 94-P8 | 59.4 | 40.22% | 51.8 | 49.02% | 59.5 | 36.27% | 40.44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, J.; Han, G.; Liang, X.; Wang, M. Machine Learning-Based Sizing Model for Tapered Electrical Submersible Pumps Under Multiple Operating Conditions. Processes 2025, 13, 1056. https://doi.org/10.3390/pr13041056
Yao J, Han G, Liang X, Wang M. Machine Learning-Based Sizing Model for Tapered Electrical Submersible Pumps Under Multiple Operating Conditions. Processes. 2025; 13(4):1056. https://doi.org/10.3390/pr13041056
Chicago/Turabian StyleYao, Jinsong, Guoqing Han, Xingyuan Liang, and Mengyu Wang. 2025. "Machine Learning-Based Sizing Model for Tapered Electrical Submersible Pumps Under Multiple Operating Conditions" Processes 13, no. 4: 1056. https://doi.org/10.3390/pr13041056
APA StyleYao, J., Han, G., Liang, X., & Wang, M. (2025). Machine Learning-Based Sizing Model for Tapered Electrical Submersible Pumps Under Multiple Operating Conditions. Processes, 13(4), 1056. https://doi.org/10.3390/pr13041056








