Computational Modeling of the Effect of Nitrogen on the Plasma Spray Process with Ar–H2–N2 Mixtures
Abstract
1. Introduction
2. Methodology
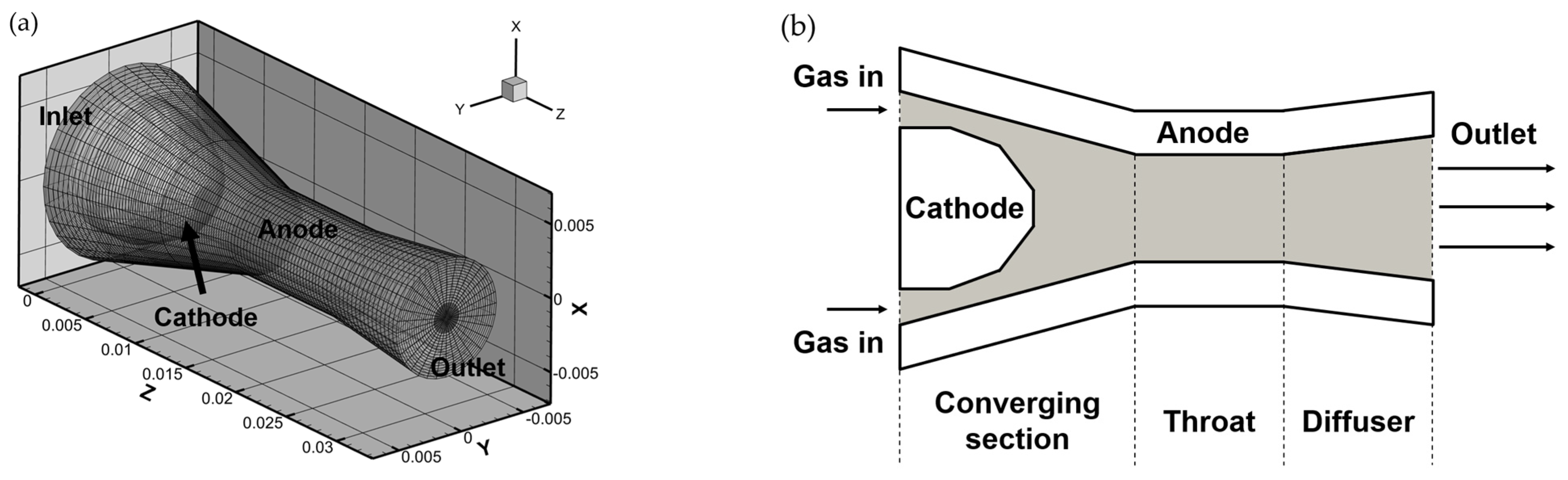
2.1. Geometry and Operating Conditions
2.2. Governing Equations
- Continuity equation
- Momentum conservation equation
- Energy conservation equation
- Electric potential
- Magnetic field
2.3. Boundary Conditions
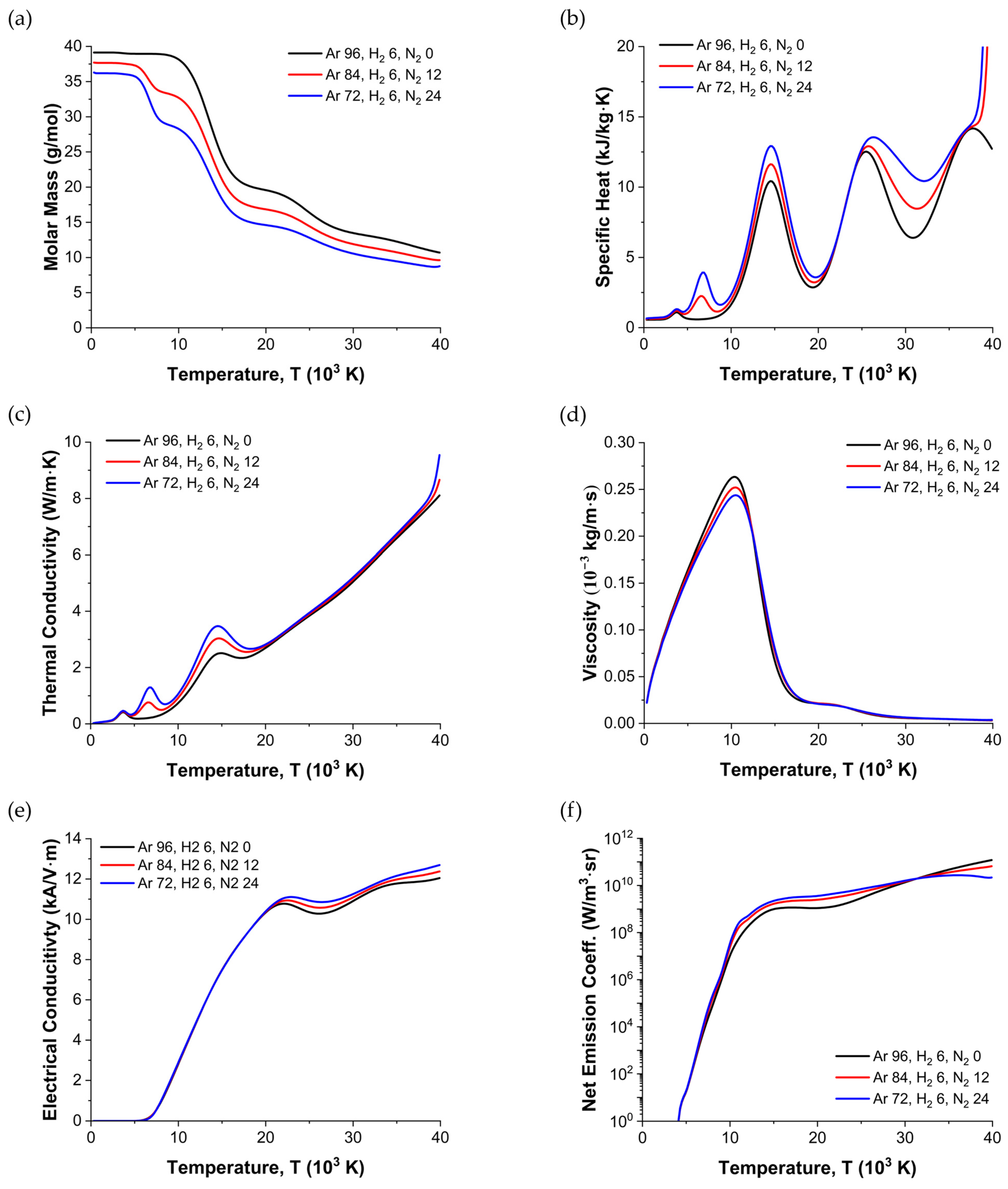
2.4. Thermodynamic and Transport Properties
- Electrical Conductivity: The electrical conductivity increased significantly with the temperature (especially above ∼20,000 K), with a steeper increase as the nitrogen fraction increased, which enhanced the ionization and free-electron density. This property played a key role in determining the arc voltage and current density profiles.
- Net Emission Coefficient: The NEC governed radiative heat losses. While the NEC typically increased with nitrogen at moderate temperatures, it decreased in extremely hot regions (>32,000 K) where N2 was extensively ionized, decreasing the radiative transitions. This variation in the NEC partially explained the temperature changes observed in the torch.
- Thermal Conductivity: Thermal conductivity affects how quickly heat diffuses through the plasma. Elevated nitrogen levels tended to raise the overall thermal conductivity, aiding in the efficient cooling of the plasma core and influencing the temperature field near the outlet.
2.5. Validation
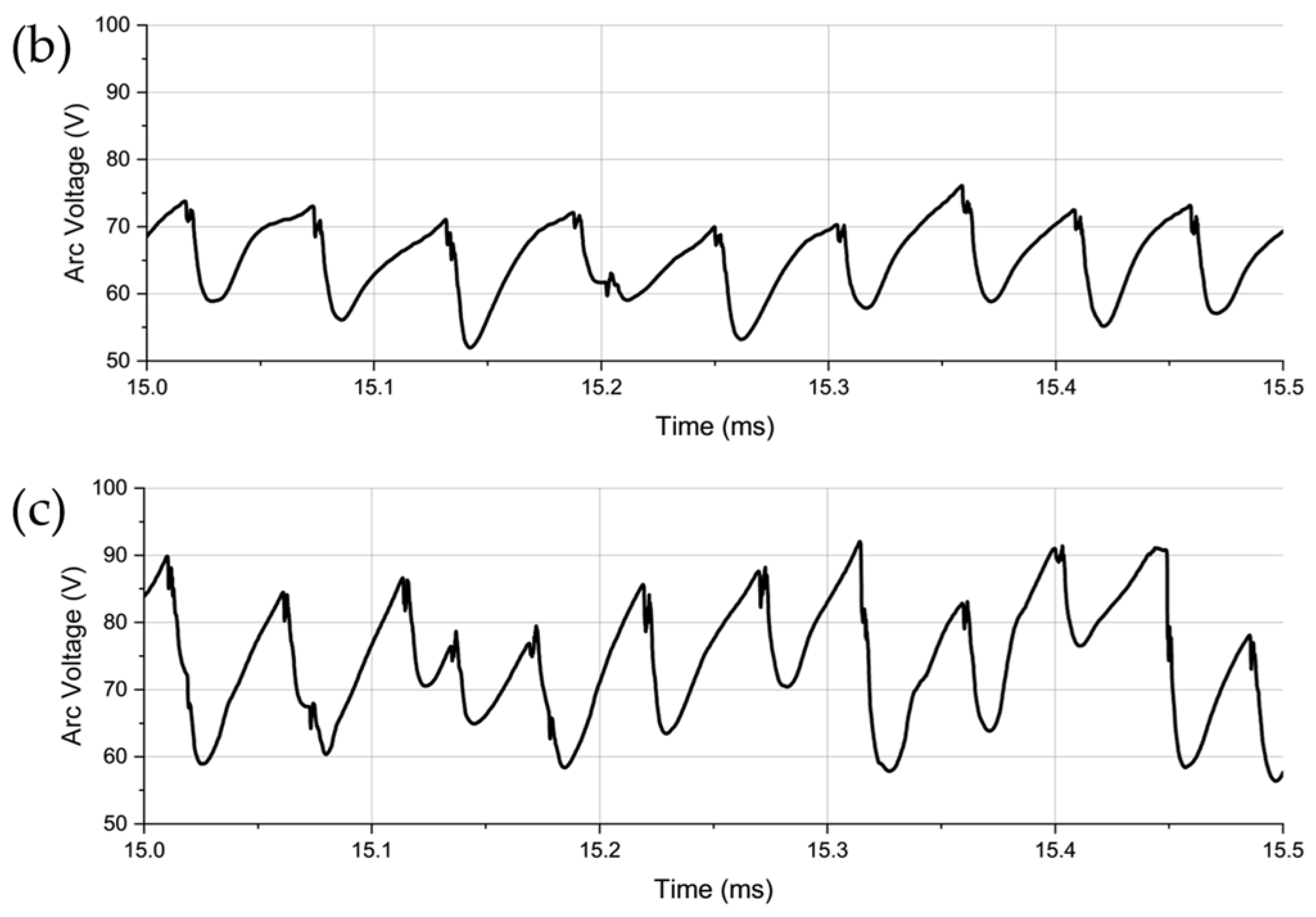
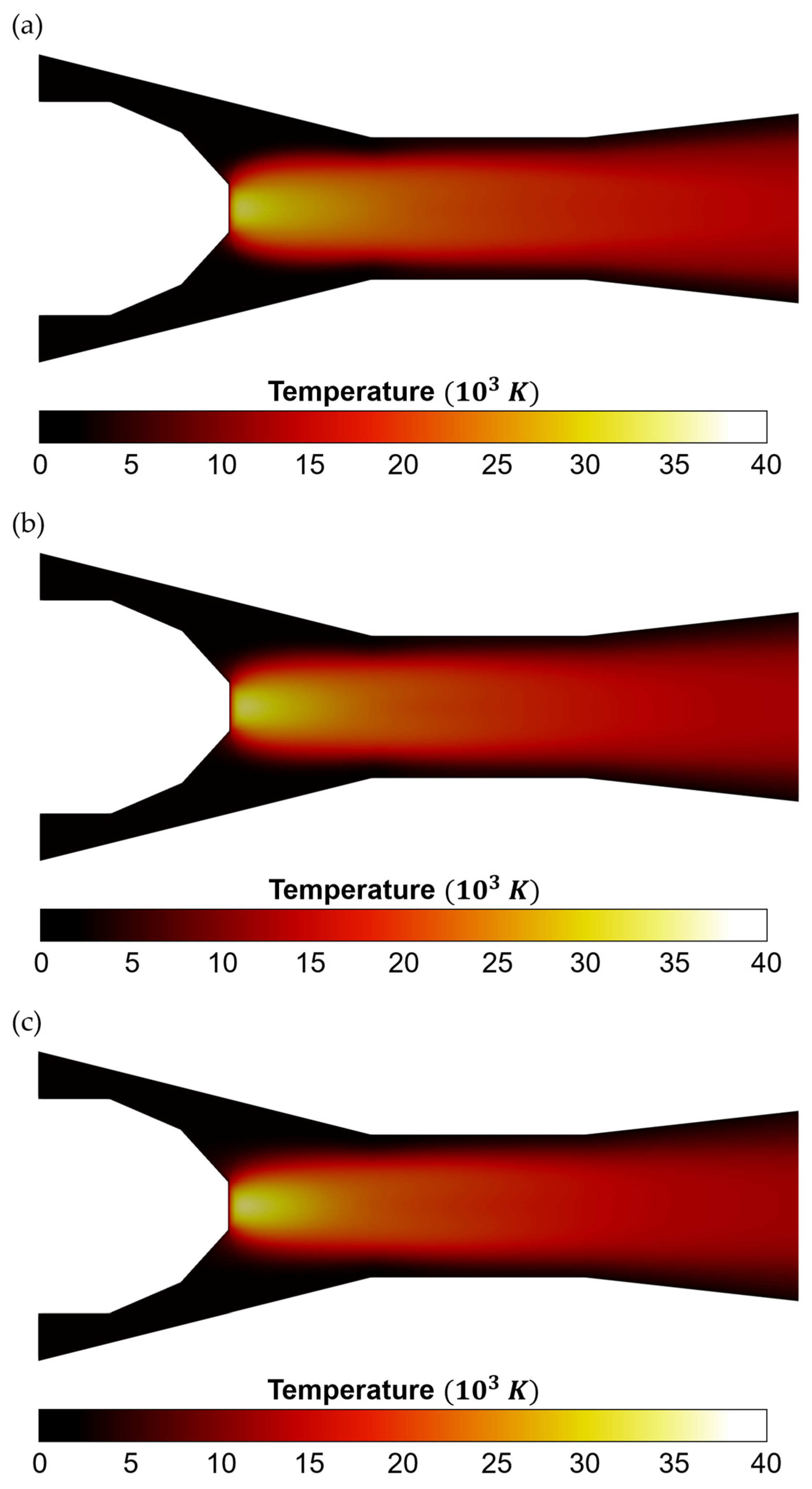
3. Results and Discussion
4. Limitations
5. Conclusions
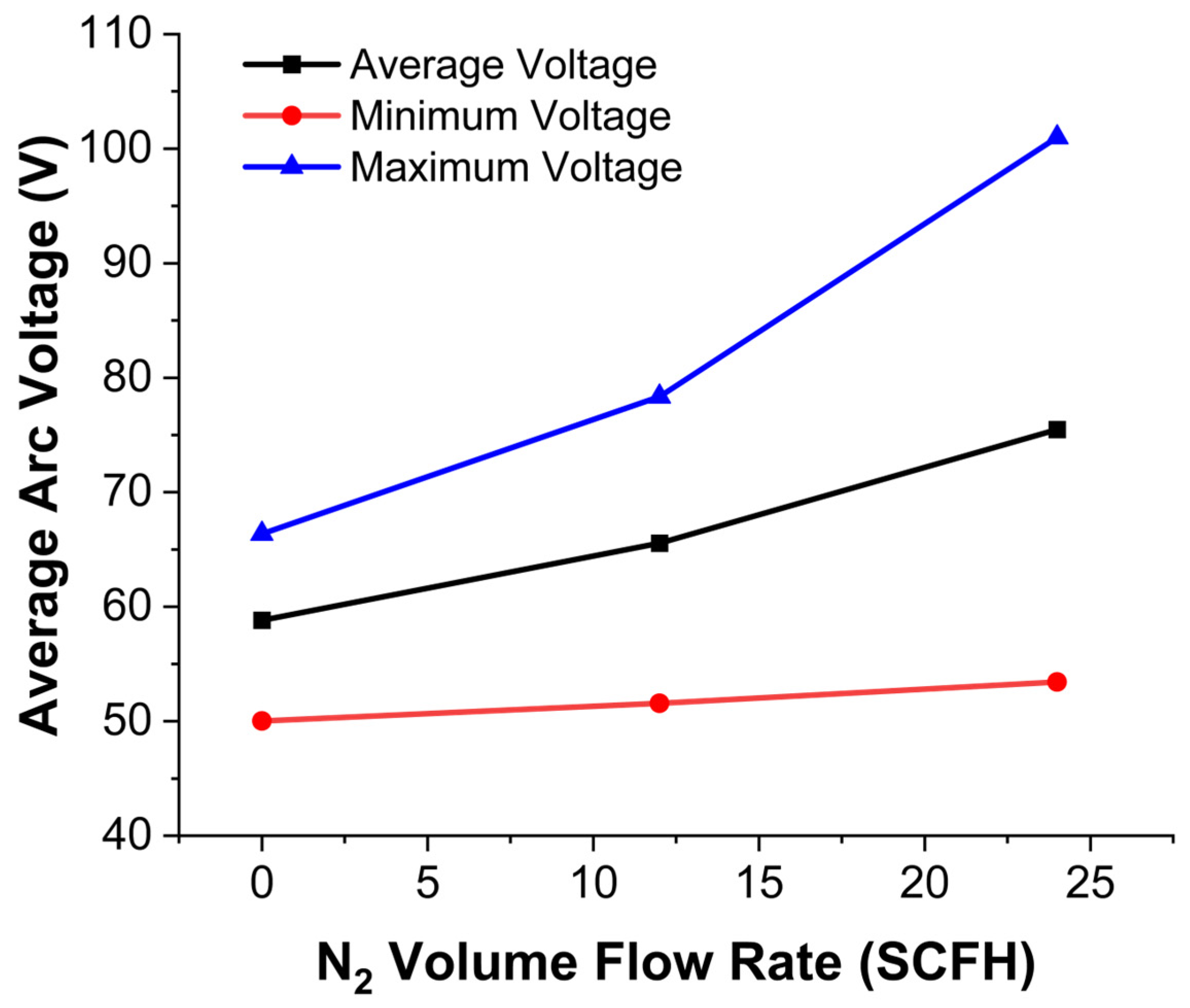
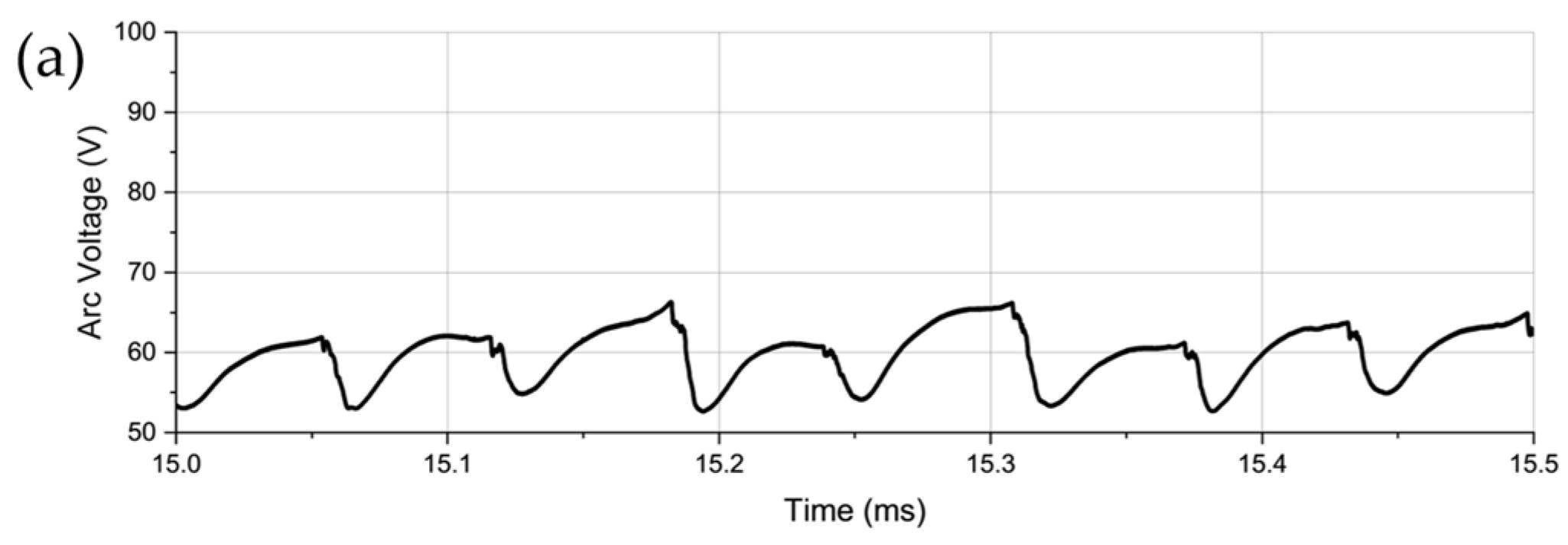
- Arc Voltage and Instability:
- 2.
- Temperature Distribution and Plasma Properties:
- 3.
- Velocity and Mach Number:
- 4.
- Efficiency Trade-Offs:
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fauchais, P.L.; Heberlein, J.V.R.; Boulos, M.I. Thermal Spray Fundamentals; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Boulos, M.I.; Fauchais, P.L.; Pfender, E. Handbook of Thermal Plasmas. 2023. Available online: https://link.springer.com/referencework/10.1007/978-3-030-84936-8?page=2#toc (accessed on 26 February 2025).
- Murphy, A.B. Computational modelling of thermal plasmas for industry. Rev. Mod. Plasma Phys. 2024, 8, 26. [Google Scholar] [CrossRef]
- Murphy, A.B.; Uhrlandt, D. Foundations of High-Pressure Thermal Plasmas. Plasma Sources Sci. Technol. 2018, 27, 063001. [Google Scholar] [CrossRef]
- Wen, K.; Liu, X.; Liu, M.; Zhou, K.; Long, H.; Deng, C.; Mao, J.; Yan, X.; Liao, H. Numerical simulation and experimental study of Ar-H2 DC atmospheric plasma spraying. Surf. Coat. Technol. 2019, 371, 312–321. [Google Scholar] [CrossRef]
- Dalir, E.; Dolatabadi, A.; Mostaghimi, J. Modeling of Suspension Plasma Spraying Process Including Arc Movement Inside the Torch. J. Therm. Spray Technol. 2019, 28, 1105–1125. [Google Scholar] [CrossRef]
- Guo, Z.; Yin, S.; Liao, H.; Gu, S. Three-dimensional simulation of an argon–hydrogen DC non-transferred arc plasma torch. Int. J. Heat Mass Transf. 2015, 80, 644–652. [Google Scholar] [CrossRef]
- Kwon, H.; Kang, Y.-j.; Yoo, Y.W.; Kim, D.H.; Park, Y.; Lee, S.; Park, H. Effect of Process-Gas Composition on In-Flight and Deposition Characteristics of Atmospheric Plasma-Sprayed Ni Particles. Met. Mater. Int. 2022, 29, 1825–1840. [Google Scholar] [CrossRef]
- Perambadur, J.K.; Rat, V.; Niane, T.N.; Chazelas, C. Simulation of the Axial III Plus Plasma Torch and Its Arc Fluctuations. J. Therm. Spray Technol. 2024, 33, 2526–2547. [Google Scholar] [CrossRef]
- Wen, K.; Liu, X.; Zhou, K.; Liu, M.; Zhu, H.; Huang, J.; Zhang, Z.; Huang, R.; Mao, J.; Yan, X.; et al. 3D time-dependent numerical simulation for atmospheric plasma spraying. Surf. Coat. Technol. 2019, 371, 344–354. [Google Scholar] [CrossRef]
- Liu, S.H.; Trelles, J.P.; Murphy, A.B.; Li, L.; Zhang, S.L.; Yang, G.J.; Li, C.X.; Li, C.J. Numerical simulation of the flow characteristics inside a novel plasma spray torch. J. Phys. D Appl. Phys. 2019, 52, 335203. [Google Scholar] [CrossRef]
- Bobzin, K.; Heinemann, H.; Erck, M.; Warkentin, S.; Mokrov, O.; Sharma, R.; Reisgen, U.; Jasutyn, K. Modeling of arcs with binary gas mixtures in a multi-arc plasma generator. Mater. Werkst. 2024, 56, 77–87. [Google Scholar] [CrossRef]
- Zhang, T.; Mariaux, G.; Vardelle, A.; Li, C.J. Numerical simulation of plasma jet characteristics under very low-pressure plasma spray conditions. Coatings 2021, 11, 726. [Google Scholar] [CrossRef]
- Ivchenko, D.; Zhang, T.; Mariaux, G.; Vardelle, A.; Goutier, S.; Itina, T.E. On the Validity of Continuum Computational Fluid Dynamics Approach Under Very Low-Pressure Plasma Spray Conditions. J. Therm. Spray Technol. 2018, 27, 3–13. [Google Scholar] [CrossRef]
- Liu, S.-H.; Trelles, J.P.; Li, C.-J.; Li, C.-X.; Guo, H.-B. A review and progress of multiphase flows in atmospheric and low pressure plasma spray advanced coating. Mater. Today Phys. 2022, 27, 100832. [Google Scholar] [CrossRef]
- Liu, S.H.; Trelles, J.P.; Murphy, A.B.; He, W.T.; Shi, J.; Li, S.; Li, C.J.; Li, C.X.; Guo, H.B. Low-pressure plasma-induced physical vapor deposition of advanced thermal barrier coatings: Microstructures, modelling and mechanisms. Mater. Today Phys. 2021, 21, 100481. [Google Scholar] [CrossRef]
- Murphy, A.B. Calculation and application of combined diffusion coefficients in thermal plasmas. Sci. Rep. 2014, 4, 4304. [Google Scholar] [CrossRef]
- Zhang, X.N.; Murphy, A.B.; Li, H.P.; Xia, W.D. Combined diffusion coefficients for a mixture of three ionized gases. Plasma Sources Sci. Technol. 2014, 23, 065044. [Google Scholar] [CrossRef]
- Park, H.; Trautmann, M.; Tanaka, K.; Tanaka, M.; Murphy, A.B. Mixing of multiple metal vapours into an arc plasma in gas tungsten arc welding of stainless steel. J. Phys. D-Appl. Phys. 2017, 50, 43LT03. [Google Scholar] [CrossRef]
- Park, H.; Trautmann, M.; Tanaka, K.; Tanaka, M.; Murphy, A.B. A computational model of gas tungsten arc welding of stainless steel: The importance of considering the different metal vapours simultaneously. J. Phys. D Appl. Phys. 2018, 51, 395202. [Google Scholar] [CrossRef]
- Dolmaire, A.; Hartikainen, E.; Goutier, S.; Béchade, E.; Vardelle, M.; Geffroy, P.-M.; Joulia, A. Benefits of Hydrogen in a Segmented-Anode Plasma Torch in Suspension Plasma Spraying. J. Therm. Spray Technol. 2021, 30, 236–250. [Google Scholar] [CrossRef]
- Joeris, J.; Tiwari, A.; Brinckmann, S.; Kurze, F.; Guillon, O.; Vaßen, R. Evaluation of major factors influencing the TBC topcoat formation in axial suspension plasma spraying (SPS). Int. J. Appl. Ceram. Technol. 2023, 20, 884–895. [Google Scholar] [CrossRef]
- Xiang, J.; Chen, F.F.; Park, H.; Tanaka, K.; Shigeta, M.; Tanaka, M.; Murphy, A.B. Numerical study of the metal vapour transport in tungsten inert-gas welding in argon for stainless steel. Appl. Math. Model. 2020, 79, 713–728. [Google Scholar] [CrossRef]
- Baeva, M.; Benilov, M.S.; Zhu, T.; Testrich, H.; Kewitz, T.; Foest, R. Modelling and experimental evidence of the cathode erosion in a plasma spray torch. J. Phys. D Appl. Phys. 2022, 55, 365202. [Google Scholar] [CrossRef]
- Saifutdinov, A.I.; Timerkaev, B.A.; Ibragimov, A.R. Numerical Simulation of Temperature Fields in a Direct-Current Plasma Torch. Tech. Phys. Lett. 2018, 44, 164–166. [Google Scholar] [CrossRef]
- Zhukovskii, R.; Chazelas, C.; Vardelle, A.; Rat, V.; Distler, B. Effect of Electromagnetic Boundary Conditions on Reliability of Plasma Torch Models. J. Therm. Spray Technol. 2020, 29, 894–907. [Google Scholar] [CrossRef]
- Zhukovskii, R.; Chazelas, C.; Rat, V.; Vardelle, A.; Molz, R. Predicted Anode Arc Attachment by LTE (Local Thermodynamic Equilibrium) and 2-T (Two-Temperature) Arc Models in a Cascaded-Anode DC Plasma Spray Torch. J. Therm. Spray Technol. 2022, 31, 28–45. [Google Scholar] [CrossRef]
- Zhang, H.; Mauer, G.; Liu, S.; Liu, M.; Jia, Y.; Li, C.; Li, C.; Vaßen, R. Modeling of the Effect of Carrier Gas Injection on the Laminarity of the Plasma Jet Generated by a Cascaded Spray Gun. Coatings 2022, 12, 1416. [Google Scholar] [CrossRef]
- Anders, A. Glows, arcs, ohmic discharges: An electrode-centered review on discharge modes and the transitions between them. Appl. Phys. Rev. 2024, 11, 031310. [Google Scholar] [CrossRef]
- Tsonev, I.; Boothroyd, J.; Kolev, S.; Bogaerts, A. Simulation of glow and arc discharges in nitrogen: Effects of the cathode emission mechanisms. Plasma Sources Sci. Technol. 2023, 32, 054002. [Google Scholar] [CrossRef]
- Benilov, M.S. Multiple solutions in the theory of dc glow discharges and cathodic part of arc discharges. Application of these solutions to the modeling of cathode spots and patterns: A review. Plasma Sources Sci. Technol. 2014, 23, 054019. [Google Scholar] [CrossRef]
- Xiong, H.-B.; Zheng, L.-L.; Sampath, S.; Williamson, R.L.; Fincke, J.R. Three-dimensional simulation of plasma spray: Effects of carrier gas flow and particle injection on plasma jet and entrained particle behavior. Int. J. Heat Mass Transf. 2004, 47, 5189–5200. [Google Scholar] [CrossRef]
- Martínez-Villegas, I.; Mora-García, A.G.; Ruiz-Luna, H.; McKelliget, J.; Poblano-Salas, C.A.; Muñoz-Saldaña, J.; Trápaga-Martínez, G. Swirling Effects in Atmospheric Plasma Spraying Process: Experiments and Simulation. Coatings 2020, 10, 388. [Google Scholar] [CrossRef]
- Weller, H.G.; Tabor, G.; Jasak, H.; Fureby, C. A tensorial approach to computational continuum mechanics using object-oriented techniques. Comput. Phys. 1998, 12, 620–631. [Google Scholar] [CrossRef]
- Trelles, J.P.; Modirkhazeni, S.M. Variational multiscale method for nonequilibrium plasma flows. Comput. Methods Appl. Mech. Eng. 2014, 282, 87–131. [Google Scholar] [CrossRef]
- Bobzin, K.; Heinemann, H.; Dokhanchi, A. Numerical and Experimental Analysis of a Solid Shroud in Multi-arc Plasma Spraying. J. Therm. Spray Technol. 2024, 33, 1191–1204. [Google Scholar] [CrossRef]
- Huang, R.; Fukanuma, H.; Uesugi, Y.; Tanaka, Y. Simulation of Arc Root Fluctuation in a DC Non-Transferred Plasma Torch with Three Dimensional Modeling. J. Therm. Spray Technol. 2012, 21, 636–643. [Google Scholar] [CrossRef]
- Lowke, J.J.; Tanaka, M. ‘LTE-diffusion approximation’ for arc calculations. J. Phys. D Appl. Phys. 2006, 39, 3634. [Google Scholar] [CrossRef]
- Murphy, A.B. Transport coefficients of plasmas in mixtures of nitrogen and hydrogen. Chem. Phys. 2012, 398, 64–72. [Google Scholar] [CrossRef]
- Murphy, A.B.; Arundelli, C.J. Transport coefficients of argon, nitrogen, oxygen, argon-nitrogen, and argon-oxygen plasmas. Plasma Chem. Plasma Process. 1994, 14, 451–490. [Google Scholar] [CrossRef]
- Cram, L.E. Statistical evaluation of radiative power losses from thermal plasmas due to spectral lines. J. Phys. D Appl. Phys. 1985, 18, 401–411. [Google Scholar] [CrossRef]
- Cressault, Y.; Rouffet, M.E.; Gleizes, A.; Meillot, E. Net emission of Ar–H 2 –He thermal plasmas at atmospheric pressure. J. Phys. D Appl. Phys. 2010, 43, 335204. [Google Scholar] [CrossRef]
- Ernst, K.A.; Kopainsky, J.G.; Maecker, H.H. The Energy Transport, Including Emission and Absorption, in N2-Arcs of Different Radii. IEEE Trans. Plasma Sci. 1973, 1, 3–16. [Google Scholar] [CrossRef]
- Murphy, A.B.; Tanaka, M.; Tashiro, S.; Sato, T.; Lowke, J.J. A computational investigation of the effectiveness of different shielding gas mixtures for arc welding. J. Phys. D Appl. Phys. 2009, 42, 115205. [Google Scholar] [CrossRef]
- Coudert, J.F.; Planche, M.P.; Fauchais, P. Characterization of d.c. plasma torch voltage fluctuations. Plasma Chem. Plasma Process. 1995, 16, S211–S227. [Google Scholar] [CrossRef]
- Trelles, J.P.; Heberlein, J.V.R.; Pfender, E. Non-equilibrium modelling of arc plasma torches. J. Phys. D Appl. Phys. 2007, 40, 5937. [Google Scholar] [CrossRef]






| Case | Ar | H2 | N2 |
|---|---|---|---|
| Volume Flow Rate (SCFH) | Volume Flow Rate (SCFH) | Volume Flow Rate (SCFH) | |
| 1 | 96 | 6 | 0 |
| 2 | 84 | 6 | 12 |
| 3 | 72 | 6 | 24 |
| Boundary | Pressure | Velocity | Temperature | Electric Potential | Magnetic Potential |
|---|---|---|---|---|---|
| Inlet | Flow rate | 0 | |||
| Cathode | 0 | ||||
| Anode | 0 | 0 | |||
| Outlet | Ambient P |
| Case | Input (kW) | Output (kW) | Efficiency (%) | Temperature (K) | Velocity (m/s) |
|---|---|---|---|---|---|
| 1 | 37.797 | 23.626 | 62.51 | 7850 | 754 |
| 2 | 43.875 | 23.776 | 54.19 | 7530 | 763 |
| 3 | 52.276 | 26.548 | 50.78 | 7390 | 818 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, B.; Kwon, H.; Yoo, Y.W.; Kim, D.H.; Park, Y.; Kang, Y.-j.; Murphy, A.B.; Park, H. Computational Modeling of the Effect of Nitrogen on the Plasma Spray Process with Ar–H2–N2 Mixtures. Processes 2025, 13, 1155. https://doi.org/10.3390/pr13041155
Jeon B, Kwon H, Yoo YW, Kim DH, Park Y, Kang Y-j, Murphy AB, Park H. Computational Modeling of the Effect of Nitrogen on the Plasma Spray Process with Ar–H2–N2 Mixtures. Processes. 2025; 13(4):1155. https://doi.org/10.3390/pr13041155
Chicago/Turabian StyleJeon, Byeongryun, Hansol Kwon, Yeon Woo Yoo, Do Hyun Kim, Youngjin Park, Yong-jin Kang, Anthony B. Murphy, and Hunkwan Park. 2025. "Computational Modeling of the Effect of Nitrogen on the Plasma Spray Process with Ar–H2–N2 Mixtures" Processes 13, no. 4: 1155. https://doi.org/10.3390/pr13041155
APA StyleJeon, B., Kwon, H., Yoo, Y. W., Kim, D. H., Park, Y., Kang, Y.-j., Murphy, A. B., & Park, H. (2025). Computational Modeling of the Effect of Nitrogen on the Plasma Spray Process with Ar–H2–N2 Mixtures. Processes, 13(4), 1155. https://doi.org/10.3390/pr13041155






